Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

6 Week 5 Introduction to Hypothesis Testing Reading
An introduction to hypothesis testing.
What are you interested in learning about? Perhaps you’d like to know if there is a difference in average final grade between two different versions of a college class? Does the Fort Lewis women’s soccer team score more goals than the national Division II women’s average? Which outdoor sport do Fort Lewis students prefer the most? Do the pine trees on campus differ in mean height from the aspen trees? For all of these questions, we can collect a sample, analyze the data, then make a statistical inference based on the analysis. This means determining whether we have enough evidence to reject our null hypothesis (what was originally assumed to be true, until we prove otherwise). The process is called hypothesis testing .
A really good Khan Academy video to introduce the hypothesis test process: Khan Academy Hypothesis Testing . As you watch, please don’t get caught up in the calculations, as we will use SPSS to do these calculations. We will also use SPSS p-values, instead of the referenced Z-table, to make statistical decisions.
The Six-Step Process
Hypothesis testing requires very specific, detailed steps. Think of it as a mathematical lab report where you have to write out your work in a particular way. There are six steps that we will follow for ALL of the hypothesis tests that we learn this semester.
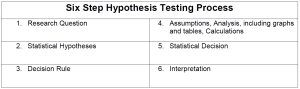
1. Research Question
All hypothesis tests start with a research question. This is literally a question that includes what you are trying to prove, like the examples earlier: Which outdoor sport do Fort Lewis students prefer the most? Is there sufficient evidence to show that the Fort Lewis women’s soccer team scores more goals than the national Division 2 women’s average?
In this step, besides literally being a question, you’ll want to include:
- mention of your variable(s)
- wording specific to the type of test that you’ll be conducting (mean, mean difference, relationship, pattern)
- specific wording that indicates directionality (are you looking for a ‘difference’, are you looking for something to be ‘more than’ or ‘less than’ something else, or are you comparing one pattern to another?)
Consider this research question: Do the pine trees on campus differ in mean height from the aspen trees?
- The wording of this research question clearly mentions the variables being studied. The independent variable is the type of tree (pine or aspen), and these trees are having their heights compared, so the dependent variable is height.
- ‘Mean’ is mentioned, so this indicates a test with a quantitative dependent variable.
- The question also asks if the tree heights ‘differ’. This specific word indicates that the test being performed is a two-tailed (i.e. non-directional) test. More about the meaning of one/two-tailed will come later.
2. Statistical Hypotheses
A statistical hypothesis test has a null hypothesis, the status quo, what we assume to be true. Notation is H 0, read as “H naught”. The alternative hypothesis is what you are trying to prove (mentioned in your research question), H 1 or H A . All hypothesis tests must include a null and an alternative hypothesis. We also note which hypothesis test is being done in this step.
The notation for your statistical hypotheses will vary depending on the type of test that you’re doing. Writing statistical hypotheses is NOT the same as most scientific hypotheses. You are not writing sentences explaining what you think will happen in the study. Here is an example of what statistical hypotheses look like using the research question: Do the pine trees on campus differ in mean height from the aspen trees?
3. Decision Rule
In this step, you state which alpha value you will use, and when appropriate, the directionality, or tail, of the test. You also write a statement: “I will reject the null hypothesis if p < alpha” (insert actual alpha value here). In this introductory class, alpha is the level of significance, how willing we are to make the wrong statistical decision, and it will be set to 0.05 or 0.01.
Example of a Decision Rule:
Let alpha=0.01, two-tailed. I will reject the null hypothesis if p<0.01.
4. Assumptions, Analysis and Calculations
Quite a bit goes on in this step. Assumptions for the particular hypothesis test must be done. SPSS will be used to create appropriate graphs, and test output tables. Where appropriate, calculations of the test’s effect size will also be done in this step.
All hypothesis tests have assumptions that we hope to meet. For example, tests with a quantitative dependent variable consider a histogram(s) to check if the distribution is normal, and whether there are any obvious outliers. Each hypothesis test has different assumptions, so it is important to pay attention to the specific test’s requirements.
Required SPSS output will also depend on the test.
5. Statistical Decision
It is in Step 5 that we determine if we have enough statistical evidence to reject our null hypothesis. We will consult the SPSS p-value and compare to our chosen alpha (from Step 3: Decision Rule).
Put very simply, the p -value is the probability that, if the null hypothesis is true, the results from another randomly selected sample will be as extreme or more extreme as the results obtained from the given sample. The p -value can also be thought of as the probability that the results (from the sample) that we are seeing are solely due to chance. This concept will be discussed in much further detail in the class notes.
Based on this numerical comparison between the p-value and alpha, we’ll either reject or retain our null hypothesis. Note: You may NEVER ‘accept’ the null hypothesis. This is because it is impossible to prove a null hypothesis to be true.
Retaining the null means that you just don’t have enough evidence to prove your alternative hypothesis to be true, so you fall back to your null. (You retain the null when p is greater than or equal to alpha.)
Rejecting the null means that you did find enough evidence to prove your alternative hypothesis as true. (You reject the null when p is less than alpha.)
Example of a Statistical Decision:
Retain the null hypothesis, because p=0.12 > alpha=0.01.
The p-value will come from SPSS output, and the alpha will have already been determined back in Step 3. You must be very careful when you compare the decimal values of the p-value and alpha. If, for example, you mistakenly think that p=0.12 < alpha=0.01, then you will make the incorrect statistical decision, which will likely lead to an incorrect interpretation of the study’s findings.
6. Interpretation
The interpretation is where you write up your findings. The specifics will vary depending on the type of hypothesis test you performed, but you will always include a plain English, contextual conclusion of what your study found (i.e. what it means to reject or retain the null hypothesis in that particular study). You’ll have statistics that you quote to support your decision. Some of the statistics will need to be written in APA style citation (the American Psychological Association style of citation). For some hypothesis tests, you’ll also include an interpretation of the effect size.
Some hypothesis tests will also require an additional (non-Parametric) test after the completion of your original test, if the test’s assumptions have not been met. These tests are also call “Post-Hoc tests”.
As previously stated, hypothesis testing is a very detailed process. Do not be concerned if you have read through all of the steps above, and have many questions (and are possibly very confused). It will take time, and a lot of practice to learn and apply these steps!
This Reading is just meant as an overview of hypothesis testing. Much more information is forthcoming in the various sets of Notes about the specifics needed in each of these steps. The Hypothesis Test Checklist will be a critical resource for you to refer to during homeworks and tests.
Student Course Learning Objectives
4. Choose, administer and interpret the correct tests based on the situation, including identification of appropriate sampling and potential errors
c. Choose the appropriate hypothesis test given a situation
d. Describe the meaning and uses of alpha and p-values
e. Write the appropriate null and alternative hypotheses, including whether the alternative should be one-sided or two-sided
f. Determine and calculate the appropriate test statistic (e.g. z-test, multiple t-tests, Chi-Square, ANOVA)
g. Determine and interpret effect sizes.
h. Interpret results of a hypothesis test
- Use technology in the statistical analysis of data
- Communicate in writing the results of statistical analyses of data
Attributions
Adapted from “Week 5 Introduction to Hypothesis Testing Reading” by Sherri Spriggs and Sandi Dang is licensed under CC BY-NC-SA 4.0 .
Math 132 Introduction to Statistics Readings Copyright © by Sherri Spriggs is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License , except where otherwise noted.
Share This Book
- Data Science
- Data Analysis
- Data Visualization
- Machine Learning
- Deep Learning
- Computer Vision
- Artificial Intelligence
- AI ML DS Interview Series
- AI ML DS Projects series
- Data Engineering
- Web Scrapping
Understanding Hypothesis Testing
Hypothesis testing involves formulating assumptions about population parameters based on sample statistics and rigorously evaluating these assumptions against empirical evidence. This article sheds light on the significance of hypothesis testing and the critical steps involved in the process.
What is Hypothesis Testing?
A hypothesis is an assumption or idea, specifically a statistical claim about an unknown population parameter. For example, a judge assumes a person is innocent and verifies this by reviewing evidence and hearing testimony before reaching a verdict.
Hypothesis testing is a statistical method that is used to make a statistical decision using experimental data. Hypothesis testing is basically an assumption that we make about a population parameter. It evaluates two mutually exclusive statements about a population to determine which statement is best supported by the sample data.
To test the validity of the claim or assumption about the population parameter:
- A sample is drawn from the population and analyzed.
- The results of the analysis are used to decide whether the claim is true or not.
Example: You say an average height in the class is 30 or a boy is taller than a girl. All of these is an assumption that we are assuming, and we need some statistical way to prove these. We need some mathematical conclusion whatever we are assuming is true.
Defining Hypotheses
- Null hypothesis (H 0 ): In statistics, the null hypothesis is a general statement or default position that there is no relationship between two measured cases or no relationship among groups. In other words, it is a basic assumption or made based on the problem knowledge. Example : A company’s mean production is 50 units/per da H 0 : [Tex]\mu [/Tex] = 50.
- Alternative hypothesis (H 1 ): The alternative hypothesis is the hypothesis used in hypothesis testing that is contrary to the null hypothesis. Example: A company’s production is not equal to 50 units/per day i.e. H 1 : [Tex]\mu [/Tex] [Tex]\ne [/Tex] 50.
Key Terms of Hypothesis Testing
- Level of significance : It refers to the degree of significance in which we accept or reject the null hypothesis. 100% accuracy is not possible for accepting a hypothesis, so we, therefore, select a level of significance that is usually 5%. This is normally denoted with [Tex]\alpha[/Tex] and generally, it is 0.05 or 5%, which means your output should be 95% confident to give a similar kind of result in each sample.
- P-value: The P value , or calculated probability, is the probability of finding the observed/extreme results when the null hypothesis(H0) of a study-given problem is true. If your P-value is less than the chosen significance level then you reject the null hypothesis i.e. accept that your sample claims to support the alternative hypothesis.
- Test Statistic: The test statistic is a numerical value calculated from sample data during a hypothesis test, used to determine whether to reject the null hypothesis. It is compared to a critical value or p-value to make decisions about the statistical significance of the observed results.
- Critical value : The critical value in statistics is a threshold or cutoff point used to determine whether to reject the null hypothesis in a hypothesis test.
- Degrees of freedom: Degrees of freedom are associated with the variability or freedom one has in estimating a parameter. The degrees of freedom are related to the sample size and determine the shape.
Why do we use Hypothesis Testing?
Hypothesis testing is an important procedure in statistics. Hypothesis testing evaluates two mutually exclusive population statements to determine which statement is most supported by sample data. When we say that the findings are statistically significant, thanks to hypothesis testing.
One-Tailed and Two-Tailed Test
One tailed test focuses on one direction, either greater than or less than a specified value. We use a one-tailed test when there is a clear directional expectation based on prior knowledge or theory. The critical region is located on only one side of the distribution curve. If the sample falls into this critical region, the null hypothesis is rejected in favor of the alternative hypothesis.
One-Tailed Test
There are two types of one-tailed test:
- Left-Tailed (Left-Sided) Test: The alternative hypothesis asserts that the true parameter value is less than the null hypothesis. Example: H 0 : [Tex]\mu \geq 50 [/Tex] and H 1 : [Tex]\mu < 50 [/Tex]
- Right-Tailed (Right-Sided) Test : The alternative hypothesis asserts that the true parameter value is greater than the null hypothesis. Example: H 0 : [Tex]\mu \leq50 [/Tex] and H 1 : [Tex]\mu > 50 [/Tex]
Two-Tailed Test
A two-tailed test considers both directions, greater than and less than a specified value.We use a two-tailed test when there is no specific directional expectation, and want to detect any significant difference.
Example: H 0 : [Tex]\mu = [/Tex] 50 and H 1 : [Tex]\mu \neq 50 [/Tex]
To delve deeper into differences into both types of test: Refer to link
What are Type 1 and Type 2 errors in Hypothesis Testing?
In hypothesis testing, Type I and Type II errors are two possible errors that researchers can make when drawing conclusions about a population based on a sample of data. These errors are associated with the decisions made regarding the null hypothesis and the alternative hypothesis.
- Type I error: When we reject the null hypothesis, although that hypothesis was true. Type I error is denoted by alpha( [Tex]\alpha [/Tex] ).
- Type II errors : When we accept the null hypothesis, but it is false. Type II errors are denoted by beta( [Tex]\beta [/Tex] ).
Null Hypothesis is True | Null Hypothesis is False | |
|---|---|---|
Null Hypothesis is True (Accept) | Correct Decision | Type II Error (False Negative) |
Alternative Hypothesis is True (Reject) | Type I Error (False Positive) | Correct Decision |
How does Hypothesis Testing work?
Step 1: define null and alternative hypothesis.
State the null hypothesis ( [Tex]H_0 [/Tex] ), representing no effect, and the alternative hypothesis ( [Tex]H_1 [/Tex] ), suggesting an effect or difference.
We first identify the problem about which we want to make an assumption keeping in mind that our assumption should be contradictory to one another, assuming Normally distributed data.
Step 2 – Choose significance level
Select a significance level ( [Tex]\alpha [/Tex] ), typically 0.05, to determine the threshold for rejecting the null hypothesis. It provides validity to our hypothesis test, ensuring that we have sufficient data to back up our claims. Usually, we determine our significance level beforehand of the test. The p-value is the criterion used to calculate our significance value.
Step 3 – Collect and Analyze data.
Gather relevant data through observation or experimentation. Analyze the data using appropriate statistical methods to obtain a test statistic.
Step 4-Calculate Test Statistic
The data for the tests are evaluated in this step we look for various scores based on the characteristics of data. The choice of the test statistic depends on the type of hypothesis test being conducted.
There are various hypothesis tests, each appropriate for various goal to calculate our test. This could be a Z-test , Chi-square , T-test , and so on.
- Z-test : If population means and standard deviations are known. Z-statistic is commonly used.
- t-test : If population standard deviations are unknown. and sample size is small than t-test statistic is more appropriate.
- Chi-square test : Chi-square test is used for categorical data or for testing independence in contingency tables
- F-test : F-test is often used in analysis of variance (ANOVA) to compare variances or test the equality of means across multiple groups.
We have a smaller dataset, So, T-test is more appropriate to test our hypothesis.
T-statistic is a measure of the difference between the means of two groups relative to the variability within each group. It is calculated as the difference between the sample means divided by the standard error of the difference. It is also known as the t-value or t-score.
Step 5 – Comparing Test Statistic:
In this stage, we decide where we should accept the null hypothesis or reject the null hypothesis. There are two ways to decide where we should accept or reject the null hypothesis.
Method A: Using Crtical values
Comparing the test statistic and tabulated critical value we have,
- If Test Statistic>Critical Value: Reject the null hypothesis.
- If Test Statistic≤Critical Value: Fail to reject the null hypothesis.
Note: Critical values are predetermined threshold values that are used to make a decision in hypothesis testing. To determine critical values for hypothesis testing, we typically refer to a statistical distribution table , such as the normal distribution or t-distribution tables based on.
Method B: Using P-values
We can also come to an conclusion using the p-value,
- If the p-value is less than or equal to the significance level i.e. ( [Tex]p\leq\alpha [/Tex] ), you reject the null hypothesis. This indicates that the observed results are unlikely to have occurred by chance alone, providing evidence in favor of the alternative hypothesis.
- If the p-value is greater than the significance level i.e. ( [Tex]p\geq \alpha[/Tex] ), you fail to reject the null hypothesis. This suggests that the observed results are consistent with what would be expected under the null hypothesis.
Note : The p-value is the probability of obtaining a test statistic as extreme as, or more extreme than, the one observed in the sample, assuming the null hypothesis is true. To determine p-value for hypothesis testing, we typically refer to a statistical distribution table , such as the normal distribution or t-distribution tables based on.
Step 7- Interpret the Results
At last, we can conclude our experiment using method A or B.
Calculating test statistic
To validate our hypothesis about a population parameter we use statistical functions . We use the z-score, p-value, and level of significance(alpha) to make evidence for our hypothesis for normally distributed data .
1. Z-statistics:
When population means and standard deviations are known.
[Tex]z = \frac{\bar{x} – \mu}{\frac{\sigma}{\sqrt{n}}}[/Tex]
- [Tex]\bar{x} [/Tex] is the sample mean,
- μ represents the population mean,
- σ is the standard deviation
- and n is the size of the sample.
2. T-Statistics
T test is used when n<30,
t-statistic calculation is given by:
[Tex]t=\frac{x̄-μ}{s/\sqrt{n}} [/Tex]
- t = t-score,
- x̄ = sample mean
- μ = population mean,
- s = standard deviation of the sample,
- n = sample size
3. Chi-Square Test
Chi-Square Test for Independence categorical Data (Non-normally distributed) using:
[Tex]\chi^2 = \sum \frac{(O_{ij} – E_{ij})^2}{E_{ij}}[/Tex]
- [Tex]O_{ij}[/Tex] is the observed frequency in cell [Tex]{ij} [/Tex]
- i,j are the rows and columns index respectively.
- [Tex]E_{ij}[/Tex] is the expected frequency in cell [Tex]{ij}[/Tex] , calculated as : [Tex]\frac{{\text{{Row total}} \times \text{{Column total}}}}{{\text{{Total observations}}}}[/Tex]
Real life Examples of Hypothesis Testing
Let’s examine hypothesis testing using two real life situations,
Case A: D oes a New Drug Affect Blood Pressure?
Imagine a pharmaceutical company has developed a new drug that they believe can effectively lower blood pressure in patients with hypertension. Before bringing the drug to market, they need to conduct a study to assess its impact on blood pressure.
- Before Treatment: 120, 122, 118, 130, 125, 128, 115, 121, 123, 119
- After Treatment: 115, 120, 112, 128, 122, 125, 110, 117, 119, 114
Step 1 : Define the Hypothesis
- Null Hypothesis : (H 0 )The new drug has no effect on blood pressure.
- Alternate Hypothesis : (H 1 )The new drug has an effect on blood pressure.
Step 2: Define the Significance level
Let’s consider the Significance level at 0.05, indicating rejection of the null hypothesis.
If the evidence suggests less than a 5% chance of observing the results due to random variation.
Step 3 : Compute the test statistic
Using paired T-test analyze the data to obtain a test statistic and a p-value.
The test statistic (e.g., T-statistic) is calculated based on the differences between blood pressure measurements before and after treatment.
t = m/(s/√n)
- m = mean of the difference i.e X after, X before
- s = standard deviation of the difference (d) i.e d i = X after, i − X before,
- n = sample size,
then, m= -3.9, s= 1.8 and n= 10
we, calculate the , T-statistic = -9 based on the formula for paired t test
Step 4: Find the p-value
The calculated t-statistic is -9 and degrees of freedom df = 9, you can find the p-value using statistical software or a t-distribution table.
thus, p-value = 8.538051223166285e-06
Step 5: Result
- If the p-value is less than or equal to 0.05, the researchers reject the null hypothesis.
- If the p-value is greater than 0.05, they fail to reject the null hypothesis.
Conclusion: Since the p-value (8.538051223166285e-06) is less than the significance level (0.05), the researchers reject the null hypothesis. There is statistically significant evidence that the average blood pressure before and after treatment with the new drug is different.
Python Implementation of Case A
Let’s create hypothesis testing with python, where we are testing whether a new drug affects blood pressure. For this example, we will use a paired T-test. We’ll use the scipy.stats library for the T-test.
Scipy is a mathematical library in Python that is mostly used for mathematical equations and computations.
We will implement our first real life problem via python,
import numpy as np from scipy import stats # Data before_treatment = np . array ([ 120 , 122 , 118 , 130 , 125 , 128 , 115 , 121 , 123 , 119 ]) after_treatment = np . array ([ 115 , 120 , 112 , 128 , 122 , 125 , 110 , 117 , 119 , 114 ]) # Step 1: Null and Alternate Hypotheses # Null Hypothesis: The new drug has no effect on blood pressure. # Alternate Hypothesis: The new drug has an effect on blood pressure. null_hypothesis = "The new drug has no effect on blood pressure." alternate_hypothesis = "The new drug has an effect on blood pressure." # Step 2: Significance Level alpha = 0.05 # Step 3: Paired T-test t_statistic , p_value = stats . ttest_rel ( after_treatment , before_treatment ) # Step 4: Calculate T-statistic manually m = np . mean ( after_treatment - before_treatment ) s = np . std ( after_treatment - before_treatment , ddof = 1 ) # using ddof=1 for sample standard deviation n = len ( before_treatment ) t_statistic_manual = m / ( s / np . sqrt ( n )) # Step 5: Decision if p_value <= alpha : decision = "Reject" else : decision = "Fail to reject" # Conclusion if decision == "Reject" : conclusion = "There is statistically significant evidence that the average blood pressure before and after treatment with the new drug is different." else : conclusion = "There is insufficient evidence to claim a significant difference in average blood pressure before and after treatment with the new drug." # Display results print ( "T-statistic (from scipy):" , t_statistic ) print ( "P-value (from scipy):" , p_value ) print ( "T-statistic (calculated manually):" , t_statistic_manual ) print ( f "Decision: { decision } the null hypothesis at alpha= { alpha } ." ) print ( "Conclusion:" , conclusion )
T-statistic (from scipy): -9.0 P-value (from scipy): 8.538051223166285e-06 T-statistic (calculated manually): -9.0 Decision: Reject the null hypothesis at alpha=0.05. Conclusion: There is statistically significant evidence that the average blood pressure before and after treatment with the new drug is different.
In the above example, given the T-statistic of approximately -9 and an extremely small p-value, the results indicate a strong case to reject the null hypothesis at a significance level of 0.05.
- The results suggest that the new drug, treatment, or intervention has a significant effect on lowering blood pressure.
- The negative T-statistic indicates that the mean blood pressure after treatment is significantly lower than the assumed population mean before treatment.
Case B : Cholesterol level in a population
Data: A sample of 25 individuals is taken, and their cholesterol levels are measured.
Cholesterol Levels (mg/dL): 205, 198, 210, 190, 215, 205, 200, 192, 198, 205, 198, 202, 208, 200, 205, 198, 205, 210, 192, 205, 198, 205, 210, 192, 205.
Populations Mean = 200
Population Standard Deviation (σ): 5 mg/dL(given for this problem)
Step 1: Define the Hypothesis
- Null Hypothesis (H 0 ): The average cholesterol level in a population is 200 mg/dL.
- Alternate Hypothesis (H 1 ): The average cholesterol level in a population is different from 200 mg/dL.
As the direction of deviation is not given , we assume a two-tailed test, and based on a normal distribution table, the critical values for a significance level of 0.05 (two-tailed) can be calculated through the z-table and are approximately -1.96 and 1.96.
The test statistic is calculated by using the z formula Z = [Tex](203.8 – 200) / (5 \div \sqrt{25}) [/Tex] and we get accordingly , Z =2.039999999999992.
Step 4: Result
Since the absolute value of the test statistic (2.04) is greater than the critical value (1.96), we reject the null hypothesis. And conclude that, there is statistically significant evidence that the average cholesterol level in the population is different from 200 mg/dL
Python Implementation of Case B
import scipy.stats as stats import math import numpy as np # Given data sample_data = np . array ( [ 205 , 198 , 210 , 190 , 215 , 205 , 200 , 192 , 198 , 205 , 198 , 202 , 208 , 200 , 205 , 198 , 205 , 210 , 192 , 205 , 198 , 205 , 210 , 192 , 205 ]) population_std_dev = 5 population_mean = 200 sample_size = len ( sample_data ) # Step 1: Define the Hypotheses # Null Hypothesis (H0): The average cholesterol level in a population is 200 mg/dL. # Alternate Hypothesis (H1): The average cholesterol level in a population is different from 200 mg/dL. # Step 2: Define the Significance Level alpha = 0.05 # Two-tailed test # Critical values for a significance level of 0.05 (two-tailed) critical_value_left = stats . norm . ppf ( alpha / 2 ) critical_value_right = - critical_value_left # Step 3: Compute the test statistic sample_mean = sample_data . mean () z_score = ( sample_mean - population_mean ) / \ ( population_std_dev / math . sqrt ( sample_size )) # Step 4: Result # Check if the absolute value of the test statistic is greater than the critical values if abs ( z_score ) > max ( abs ( critical_value_left ), abs ( critical_value_right )): print ( "Reject the null hypothesis." ) print ( "There is statistically significant evidence that the average cholesterol level in the population is different from 200 mg/dL." ) else : print ( "Fail to reject the null hypothesis." ) print ( "There is not enough evidence to conclude that the average cholesterol level in the population is different from 200 mg/dL." )
Reject the null hypothesis. There is statistically significant evidence that the average cholesterol level in the population is different from 200 mg/dL.
Limitations of Hypothesis Testing
- Although a useful technique, hypothesis testing does not offer a comprehensive grasp of the topic being studied. Without fully reflecting the intricacy or whole context of the phenomena, it concentrates on certain hypotheses and statistical significance.
- The accuracy of hypothesis testing results is contingent on the quality of available data and the appropriateness of statistical methods used. Inaccurate data or poorly formulated hypotheses can lead to incorrect conclusions.
- Relying solely on hypothesis testing may cause analysts to overlook significant patterns or relationships in the data that are not captured by the specific hypotheses being tested. This limitation underscores the importance of complimenting hypothesis testing with other analytical approaches.
Hypothesis testing stands as a cornerstone in statistical analysis, enabling data scientists to navigate uncertainties and draw credible inferences from sample data. By systematically defining null and alternative hypotheses, choosing significance levels, and leveraging statistical tests, researchers can assess the validity of their assumptions. The article also elucidates the critical distinction between Type I and Type II errors, providing a comprehensive understanding of the nuanced decision-making process inherent in hypothesis testing. The real-life example of testing a new drug’s effect on blood pressure using a paired T-test showcases the practical application of these principles, underscoring the importance of statistical rigor in data-driven decision-making.
Frequently Asked Questions (FAQs)
1. what are the 3 types of hypothesis test.
There are three types of hypothesis tests: right-tailed, left-tailed, and two-tailed. Right-tailed tests assess if a parameter is greater, left-tailed if lesser. Two-tailed tests check for non-directional differences, greater or lesser.
2.What are the 4 components of hypothesis testing?
Null Hypothesis ( [Tex]H_o [/Tex] ): No effect or difference exists. Alternative Hypothesis ( [Tex]H_1 [/Tex] ): An effect or difference exists. Significance Level ( [Tex]\alpha [/Tex] ): Risk of rejecting null hypothesis when it’s true (Type I error). Test Statistic: Numerical value representing observed evidence against null hypothesis.
3.What is hypothesis testing in ML?
Statistical method to evaluate the performance and validity of machine learning models. Tests specific hypotheses about model behavior, like whether features influence predictions or if a model generalizes well to unseen data.
4.What is the difference between Pytest and hypothesis in Python?
Pytest purposes general testing framework for Python code while Hypothesis is a Property-based testing framework for Python, focusing on generating test cases based on specified properties of the code.
Please Login to comment...
Similar reads.
- data-science
- Best 10 IPTV Service Providers in Germany
- Python 3.13 Releases | Enhanced REPL for Developers
- IPTV Anbieter in Deutschland - Top IPTV Anbieter Abonnements
- Best SSL Certificate Providers in 2024 (Free & Paid)
- Content Improvement League 2024: From Good To A Great Article
Improve your Coding Skills with Practice
What kind of Experience do you want to share?

Data Science Central
- Author Portal
- 3D Printing
- AI Data Stores
- AI Hardware
- AI Linguistics
- AI User Interfaces and Experience
- AI Visualization
- Cloud and Edge
- Cognitive Computing
- Containers and Virtualization
- Data Science
- Data Security
- Digital Factoring
- Drones and Robot AI
- Internet of Things
- Knowledge Engineering
- Machine Learning
- Quantum Computing
- Robotic Process Automation
- The Mathematics of AI
- Tools and Techniques
- Virtual Reality and Gaming
- Blockchain & Identity
- Business Agility
- Business Analytics
- Data Lifecycle Management
- Data Privacy
- Data Strategist
- Data Trends
- Digital Communications
- Digital Disruption
- Digital Professional
- Digital Twins
- Digital Workplace
- Marketing Tech
- Sustainability
- Agriculture and Food AI
- AI and Science
- AI in Government
- Autonomous Vehicles
- Education AI
- Energy Tech
- Financial Services AI
- Healthcare AI
- Logistics and Supply Chain AI
- Manufacturing AI
- Mobile and Telecom AI
- News and Entertainment AI
- Smart Cities
- Social Media and AI
- Functional Languages
- Other Languages
- Query Languages
- Web Languages
- Education Spotlight
- Newsletters
- O’Reilly Media
An introduction to Statistical Inference and Hypothesis testing
- March 22, 2020 at 10:22 am
In a previous blog ( The difference between statistics and data science ), I discussed the significance of statistical inference. In this section, we expand on these ideas
The goal of statistical inference is to make a statement about something that is not observed within a certain level of uncertainty. Inference is difficult because it is based on a sample i.e. the objective is to understand the population based on the sample . The population is a collection of objects that we want to study/test. For example, if you are studying quality of products from an assembly line for a given day, then the whole production for that day is the population. In the real world, it may be hard to test every product – hence we draw a sample from the population and infer the results based on the sample for the whole population.
In this sense, the statistical model provides an abstract representation of the population and how the elements of the population relate to each other. Parameters are numbers that represent features or associations of the population. We estimate the value of the parameters from the data. A parameter represents a s ummary description of a fixed characteristic or measure of the target population. It represents the true value that would be obtained as if we had taken a census (instead of a sample). Examples of parameters include Mean (μ), Variance (σ²), Standard Deviation (σ), Proportion (π). These values are individually called a statistic. A Sampling Distribution is a probability distribution of a statistic obtained through a large number of samples drawn from the population. In sampling, the confidence interval provides a more continuous measure of un-certainty. The confidence interval proposes a range of plausible values for an unknown parameter (for example, the mean). In other words, the confidence interval represents a range of values we are fairly sure our true value lies in. For example, for a given sample group, the mean height is 175 cms and if the confidence interval is 95%, then it means, 95% of similar experiments will include the true mean, but 5% will not contain the sample.
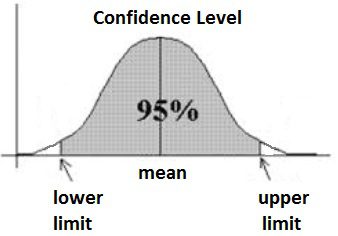
Image source and reference: An introduction to confidence intervals
Hypothesis testing
Having understood sampling and inference, let us now explore hypothesis testing. Hypothesis testing enables us to make claims about the distribution of data or whether one set of results are different from another set of results. Hypothesis testing allows us to interpret or draw conclusions about the population using sample data. In a hypothesis test, we evaluate two mutually exclusive statements about a population to determine which statement is best supported by the sample data. The Null Hypothesis(H0) is a statement of no change and is assumed to be true unless evidence indicates otherwise. The Null hypothesis is the one we want to disprove. The Alternative Hypothesis: (H1 or Ha) is the opposite of the null hypothesis, represents the claim that is being testing. We are trying to collect evidence in favour of the alternative hypothesis. The Probability value (P-Value) represents the probability that the null hypothesis is true based on the current sample or one that is more extreme than the current sample. The Significance Level (α) defines a cut-off p-value for how strongly a sample contradicts the null hypothesis of the experiment. If P-Value < α, then there is sufficient evidence to reject the null hypothesis and accept the alternative hypothesis. If P-Value > α, we fail to reject the null hypothesis.
Central limit theorem
The central limit theorem is at the heart of hypothesis testing. Given a sample where the statistics of the population is unknowable, we need a way to infer statistics across the population. For example, if we want to know the average weight of all the dogs in the world, it is not possible to weigh up each dog and compute the mean. So, we use the central limit theorem and the confidence interval which enables to infer the mean of the population within a certain margin.
So, if we take multiple samples – say the first sample of 40 dogs and compute of the mean for that sample. Again, we take a next sample of say 50 dogs and do the same. We repeat the process by getting a large number of random samples which are independent of each other – then the ‘mean of the means’ of these samples will give the approximate mean of the whole population as per the central limit theorem. Also, the histogram of the means will represent the bell curve as per the central limit theorem. The central limit theorem is significant because this idea applies to an unknown distribution (ex: Binomial or even a completely random distribution) – which means techniques like hypothesis testing can apply to any distribution (not just the normal distribution)
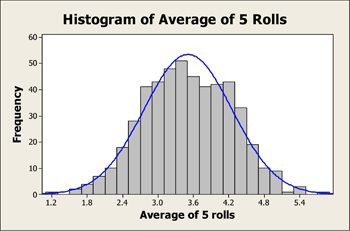
Image source: minitab .
Leave a Reply Cancel reply
Your email address will not be published. Required fields are marked *
Save my name, email, and website in this browser for the next time I comment.
Related Content

- Study Abroad Get upto 50% discount on Visa Fees
- Top Universities & Colleges
- Abroad Exams
- Top Courses
- Read College Reviews
- Admission Alerts 2024
- Education Loan
- Institute (Counselling, Coaching and More)
- Ask a Question
- College Predictor
- Test Series
- Practice Questions
- Course Finder
- Scholarship
- All Courses
- B.Sc (Nursing)
Statistical Inference: Types, Procedure & Examples

Arpita Srivastava
Content Writer
Statistical inference is defined as the process of analysing data and drawing conclusions based on random variation. Hypothesis testing and confidence intervals are two applications of statistical inference.
- Statistical inference is a technique that uses random sampling to make decisions about the parameters of a population.
- The method is based on the concept of probability distribution.
- It allows us to evaluate the relationship between the dependent and independent variables.
- Statistical inference aims to estimate the uncertainty or variation from sample to sample.
- It enables us to provide a range of value for something's true worth in the population.
- The process involves the collection of quantitative data.
- Descriptive Statistics and Inferential Statistics are two types of Statistical inference.
- Polling performed during the election is a real-life example of the inference.
The components used in the statistical inference are as follows:
- Size of the sample
- Sample Size
- Variability in the sample
|
|
Key Terms: Statistical Inference, Probability Distribution, Independent Variables, Dependent Variable, Descriptive Statistics, Inferential Statistics, Bivariate Regression, Multivariate Regression, Anova or T-test, Chi-Square Statistic, Contingency Table
Types of Statistical Inference
[Click Here for Sample Questions]
Different types of statistical inference which are used to draw conclusions are as follows:
Pearson Correlation Coefficient
Pearson Correlation Coefficient is a type of coefficient that specifies the ratio between the covariance of two variables and the product of their standard deviations.
- The value ranges between -1 to 1.
- It can be mathematically represented as:
p x,y = cov (x, y) / σ x σ y
Bivariate Regression
Bivariate Regression Analysis is a form of analysis that specifies the relationship between two variables. It is used for testing the hypothesis of variables. The analysis determines the strength of the relationship between variables.
- One variable acts as the dependent variable, and the other variable acts as the independent variable.
- Bivariate Regression for linear variables are as follows:
y = β 0 + β 1 x + ε
Multivariate Regression
Multivariate Regression is a type of regression that specifies the degree to which more that one dependent variables are related to independent variable. It is the simplest Machine Learning Algorithm.
- Multivariate Regression can mathematically be represented as:
Y = β 0 + β 1 X 1 + β k X k + residual
Anova also known as analysis of variance is a statistical model that is used to determine the relationship between independent variables and the dependent variable.
T-test is an important method is used in the field of statistical inference that determine the difference between the means of two groups. It determine the relationship between two grouped data.
- It can be represented as:
t = m – μ / (s/ √n)
However, the most common and widely used types of statistical inference are
- Interval of Confidence
- Validation of hypotheses
Read More:
|
|
|
|
Statistical Inference Procedure
The Statistical Inference Procedure includes the steps listed below which are as follows:
- Firstly, start with a theory.
- In the next step, create a research hypothesis.
- Put the variables into action.
- Then , recognize the population to which the findings should be applied.
- Create a null hypothesis for this population.
- Begin the study by gathering a sample of children from the general population .
To reject the null hypothesis, use the statistical test to see if the collected sample properties differ from what is expected under the null hypothesis.
Statistical Inference
Statistical Interference Solution
Statistical inference solutions make effective use of statistical data in relation to a group of individuals or trials. It deals with every character, including data collection, investigation, and analysis, as well as data collection organization.
- People can gain knowledge after starting work in a variety of fields by using statistical inference solutions.
The following are some statistical inference solution facts:
- It is a common method for predicting whether the observed samples are independent of a specific population type.
- The method includes poisson or normal distribution methods.
The statistical inference solution aids in evaluating the expected model's parameter(s), such as normal mean or binomial proportion.
Importance of Statistical Inference
The importance of statistical inference is that it helps examine the data properly. To develop an effective solution, accurate data analysis is required to interpret the research findings.
- Inferential statistics is used to forecast the future based on a variety of observations from various fields.
- It allows us to draw conclusions about the data.
- The method also assists us in providing a likely range of values for the true value of something in the population.
Statistical inference is used in a variety of fields, including:
- Business Analysis
- Artificial Intelligence
- Financial Analysis
- Fraud Detection
- Machine Learning
- Pharmaceutical Sector
- Share market.
| Class 12 Mathematics Related Concept | ||
|---|---|---|
Things to Remember
- Statistical inference is used to test hypotheses and calculate confidence intervals.
- It is also referred to as inferential statistics.
- The method consists of analyzing and drawing conclusions from data that is subject to random variation.
- It employs a variety of statistical analysis techniques to reach a conclusion about the population.
- In statistics, descriptive statistics are used to describe data.
- On the other hand, inferential statistics are used to make predictions based on the data.
- Inferential statistics uses data from a sample to generalize to the entire population.
- The students can take help from Class 12 Mathematics Notes .
Sample Questions
Ques: A card is drawn from the shuffled pack of 52 cards. The trial is repeated a total of 400 times, and the different suits of cards are listed below:
|
|
|
|
|
|
|
|
|
|
|
|
What is the likelihood of receiving the following suits if the card is drawn at random? (5 marks)
(A) Diamond Card
(B) Black Card
(C) Except for spade
Ans: Through statistical inference solution.
Total number of events = 400
i.e., 100 + 90+120+90 = 400
(A) The probability of winning a diamond card is:
Total number of trials in which diamond card is drawn= 90
Hence, P(diamond card )= 90/4000
(B) The probability of winning black card is:
Number of trials in which black card appeared = 100 + 90 = 190
Hence, P(black card) = 190./400 = 0.48
(C) Except spade
Number of trials other than spade appeared = 90 + 100 + 120 = 310
Hence, P(except spade) = 310/400 = 0.78
Ques: A bad with two yellow balls, three red balls, and five black balls. From the bag, only one ball is drawn at random. What is the likelihood of drawing the black ball? (3 marks)
Ans: Through statistical inference solution.
- Total number of balls in a bag = 10
- i.e 2 + 3+ 5 = 10
- Number of black balls= 5
- Probability of getting a black ball = Number of black balls/ Total number of balls
Hence, the probability of getting black balls is 1/2.
Ques: A card is drawn at random from a deck of 52. What is the likelihood that the card drawn is a face card (only the Jack, King, and Queen)? (3 marks)
Ans: Total number of cards= 52
- Number of a face card in a pack of 52 cards= 12
- Probability of receiving a face card = 12/52 = 3/13
- Hence, the probability of receiving face card is 3/13
Ques: What exactly is statistics? Describe its various types. (5 marks)
Ans: Statistics is the in-depth study of data collection, organisation, interpretation, and presentation. It is, in other words, a type of mathematical analysis that collects and summarises data. It is used in a variety of fields including business, manufacturing, psychology, government, manufacturing, humanities, and so on.
- Statistics data is gathered through the use of a sample procedure or other methods.
- Descriptive statistics and inferential statistics are the two types of statistical procedures used to analyse data.
- Inferential statistics are used to assess data from a sample using the mean or standard deviation.
- Descriptive statistics are used to assess data from a sample using the mean or standard deviation.
The statistic is divided into two categories. There are two kinds of statics:
- Descriptive Statistics
- Inferential Statistics
Ques: What Is the Purpose of Statistical Inference Training? (3 marks)
Ans: Inferential statistics use data from a sample to draw conclusions about the larger population from which the sample was drawn. The goal of statistical inference is to draw conclusions from a sample and apply them to a large population.
- It employs probability theory to investigate the probabilities of sample characteristics.
- The most commonly used methods are hypothesis tests, analysis of variance, and so on.
Ques: Find the probability of getting an odd number when a die is tossed? (2 marks)
Ans: When a die is tossed there are 6 possible outcomes, S = { 1, 2, 3, 4, 5, 6 }
According to the question, favorable events of getting an even number is { 1,3,5 }
Therefore, no. of favorable event = 3
And the total no. of outcomes = 6
Therefore, the probability of getting an odd number when a die is tossed is 3 / 6 = 1 / 2
Ques: A bad with three yellow balls, three red balls, and six black balls. From the bag, only one ball is drawn at random. What is the likelihood of drawing the yellow ball? (3 marks)
- Total number of balls in a bag = 12
- i.e 3 + 3+ 6 = 12
- Number of yellow balls= 3
- Probability of getting a black ball = Number of yellow balls/ Total number of balls
Hence, the probability of getting yellow balls is 1/4.
Ques: What is the probability of getting a sum of 8 when two dice are thrown? (3 marks)
Ans: There are 36 possibilities when we throw two dice.
The desired outcome is 8. To get 8, we can have three favorable outcomes.
{(4,4),(6,2),(5,3),(3,5), (2,6)}
Probability of an event = number of favorable outcomes/ sample space
Probability of getting number 8 = 5/36
Ques: The correlation coefficient of a set of data is found to be 0.9. The standard deviation of data set x (σ x ) = 1 , and standard deviation of data set y (σ y ) = 1.4. Find out the covariance of the data? (3 marks)
Ans: The relationship between correlation and covariance is given by –
Correlation = p x,y = cov (x, y) / σ x σ y
Values given in the question are,
- Correlation = 0.9
- σ x = 1
- σ y = 1.4
- Therefore, cov(x,y) = 0.9 x 1 x 1.4
Ques: What does a correlation of 0.66 means? ( 2 marks)
Ans: As we know that a correlation of 1 means a perfect positive correlation, thus, a correlation of 0.66 means 66% of the variance in one variable is accounted for by the second variable.
Ques: Find the standard deviation of 4, 9, 11, 15, 17, 5, 8, 12, 10? (4 Marks)
Ans: First find out the mean: 10.11
Now, subtract the mean individually from each of the data set points provided and then square the obtained result, which is equivalent to the (x - μ)² step.
x would refer to the values given in the question.
| X | 4 | 9 | 11 | 15 | 17 | 5 | 8 | 12 | 10 |
| (x - μ)² | 37.33 | 1.23 | 0.79 | 23.91 | 47.47 | 26.11 | 4.45 | 3.57 | 0.0121 |
Now, add up the obtained results (which is the 'sigma' in the formula): 144.87
Now, divide by n. as discussed earlier n is the number of values in the data, so in this example, N is 9. which gives us: 16.09
And lastly, square root it: 4.01
CBSE CLASS XII Related Questions
1. if a'= \(\begin{bmatrix} 3 & 4 \\ -1 & 2 \\ 0 &1 \end{bmatrix}\) \(\begin{bmatrix} -1 & 2 & 1 \\ 1 &2 & 3\end{bmatrix}\) , then verify that (i) \((a+b)'=a'+b' \) (ii) \((a-b)'=a'-b'\), 2. find the vector and the cartesian equations of the lines that pass through the origin and(5,-2,3)., 3. evaluate \(\begin{vmatrix} cos\alpha cos\beta &cos\alpha sin\beta &-sin\alpha \\ -sin\beta&cos\beta &0 \\ sin\alpha cos\beta&sin\alpha\sin\beta &cos\alpha \end{vmatrix}\), 4. let a= \(\begin{bmatrix} 0 & 1 \\ 0 & 0 \end{bmatrix}\) ,show that(ai+ba) n =a n i+na n-1 ba,where i is the identity matrix of order 2 and n∈n, 5. find the inverse of each of the matrices,if it exists \(\begin{bmatrix} 2 & 1 \\ 7 & 4 \end{bmatrix}\), 6. let \(a=\begin{bmatrix}1&-2&1\\ -2&3&1\\ 1&1&5\end{bmatrix}\) verify that - \((i)[adja]^{-1}=adj(a^{-1})\) \((ii)(a^{-1})^{-1}=a\).
Exam Pattern
Paper Analysis
Physics Syllabus
Chemistry Syllabus
Mathematics Syllabus
Biology Syllabus
English Syllabus
Physical Education Syllabus
Computer Science Syllabus
Economics Syllabus
Business Studies Syllabus
Political Science Syllabus
Physics Practical
Chemistry Practical
History Syllabus
Accountancy Syllabus
Chapter Wise Weightage
Geography Syllabus
Biology Practical
Mathematics
SUBSCRIBE TO OUR NEWS LETTER


- Data Science
Hypothesis Testing in Data Science [Types, Process, Example]
Home Blog Data Science Hypothesis Testing in Data Science [Types, Process, Example]
In day-to-day life, we come across a lot of data lot of variety of content. Sometimes the information is too much that we get confused about whether the information provided is correct or not. At that moment, we get introduced to a word called “Hypothesis testing” which helps in determining the proofs and pieces of evidence for some belief or information.
What is Hypothesis Testing?
Hypothesis testing is an integral part of statistical inference. It is used to decide whether the given sample data from the population parameter satisfies the given hypothetical condition. So, it will predict and decide using several factors whether the predictions satisfy the conditions or not. In simpler terms, trying to prove whether the facts or statements are true or not.
For example, if you predict that students who sit on the last bench are poorer and weaker than students sitting on 1st bench, then this is a hypothetical statement that needs to be clarified using different experiments. Another example we can see is implementing new business strategies to evaluate whether they will work for the business or not. All these things are very necessary when you work with data as a data scientist. If you are interested in learning about data science, visit this amazing Data Science full course to learn data science.
How is Hypothesis Testing Used in Data Science?
It is important to know how and where we can use hypothesis testing techniques in the field of data science. Data scientists predict a lot of things in their day-to-day work, and to check the probability of whether that finding is certain or not, we use hypothesis testing. The main goal of hypothesis testing is to gauge how well the predictions perform based on the sample data provided by the population. If you are interested to know more about the applications of the data, then refer to this D ata Scien ce course in India which will give you more insights into application-based things. When data scientists work on model building using various machine learning algorithms, they need to have faith in their models and the forecasting of models. They then provide the sample data to the model for training purposes so that it can provide us with the significance of statistical data that will represent the entire population.
Where and When to Use Hypothesis Test?
Hypothesis testing is widely used when we need to compare our results based on predictions. So, it will compare before and after results. For example, someone claimed that students writing exams from blue pen always get above 90%; now this statement proves it correct, and experiments need to be done. So, the data will be collected based on the student's input, and then the test will be done on the final result later after various experiments and observations on students' marks vs pen used, final conclusions will be made which will determine the results. Now hypothesis testing will be done to compare the 1st and the 2nd result, to see the difference and closeness of both outputs. This is how hypothesis testing is done.
How Does Hypothesis Testing Work in Data Science?
In the whole data science life cycle, hypothesis testing is done in various stages, starting from the initial part, the 1st stage where the EDA, data pre-processing, and manipulation are done. In this stage, we will do our initial hypothesis testing to visualize the outcome in later stages. The next test will be done after we have built our model, once the model is ready and hypothesis testing is done, we will compare the results of the initial testing and the 2nd one to compare the results and significance of the results and to confirm the insights generated from the 1st cycle match with the 2nd one or not. This will help us know how the model responds to the sample training data. As we saw above, hypothesis testing is always needed when we are planning to contrast more than 2 groups. While checking on the results, it is important to check on the flexibility of the results for the sample and the population. Later, we can judge on the disagreement of the results are appropriate or vague. This is all we can do using hypothesis testing.
Different Types of Hypothesis Testing
Hypothesis testing can be seen in several types. In total, we have 5 types of hypothesis testing. They are described below:

1. Alternative Hypothesis
The alternative hypothesis explains and defines the relationship between two variables. It simply indicates a positive relationship between two variables which means they do have a statistical bond. It indicates that the sample observed is going to influence or affect the outcome. An alternative hypothesis is described using H a or H 1 . Ha indicates an alternative hypothesis and H 1 explains the possibility of influenced outcome which is 1. For example, children who study from the beginning of the class have fewer chances to fail. An alternate hypothesis will be accepted once the statistical predictions become significant. The alternative hypothesis can be further divided into 3 parts.
- Left-tailed: Left tailed hypothesis can be expected when the sample value is less than the true value.
- Right-tailed: Right-tailed hypothesis can be expected when the true value is greater than the outcome/predicted value.
- Two-tailed: Two-tailed hypothesis is defined when the true value is not equal to the sample value or the output.
2. Null Hypothesis
The null hypothesis simply states that there is no relation between statistical variables. If the facts presented at the start do not match with the outcomes, then we can say, the testing is null hypothesis testing. The null hypothesis is represented as H 0 . For example, children who study from the beginning of the class have no fewer chances to fail. There are types of Null Hypothesis described below:
Simple Hypothesis: It helps in denoting and indicating the distribution of the population.
Composite Hypothesis: It does not denote the population distribution
Exact Hypothesis: In the exact hypothesis, the value of the hypothesis is the same as the sample distribution. Example- μ= 10
Inexact Hypothesis: Here, the hypothesis values are not equal to the sample. It will denote a particular range of values.
3. Non-directional Hypothesis
The non-directional hypothesis is a tow-tailed hypothesis that indicates the true value does not equal the predicted value. In simpler terms, there is no direction between the 2 variables. For an example of a non-directional hypothesis, girls and boys have different methodologies to solve a problem. Here the example explains that the thinking methodologies of a girl and a boy is different, they don’t think alike.
4. Directional Hypothesis
In the Directional hypothesis, there is a direct relationship between two variables. Here any of the variables influence the other.
5. Statistical Hypothesis
Statistical hypothesis helps in understanding the nature and character of the population. It is a great method to decide whether the values and the data we have with us satisfy the given hypothesis or not. It helps us in making different probabilistic and certain statements to predict the outcome of the population... We have several types of tests which are the T-test, Z-test, and Anova tests.
Methods of Hypothesis Testing
1. frequentist hypothesis testing.
Frequentist hypotheses mostly work with the approach of making predictions and assumptions based on the current data which is real-time data. All the facts are based on current data. The most famous kind of frequentist approach is null hypothesis testing.
2. Bayesian Hypothesis Testing
Bayesian testing is a modern and latest way of hypothesis testing. It is known to be the test that works with past data to predict the future possibilities of the hypothesis. In Bayesian, it refers to the prior distribution or prior probability samples for the observed data. In the medical Industry, we observe that Doctors deal with patients’ diseases using past historical records. So, with this kind of record, it is helpful for them to understand and predict the current and upcoming health conditions of the patient.
Importance of Hypothesis Testing in Data Science
Most of the time, people assume that data science is all about applying machine learning algorithms and getting results, that is true but in addition to the fact that to work in the data science field, one needs to be well versed with statistics as most of the background work in Data science is done through statistics. When we deal with data for pre-processing, manipulating, and analyzing, statistics play. Specifically speaking Hypothesis testing helps in making confident decisions, predicting the correct outcomes, and finding insightful conclusions regarding the population. Hypothesis testing helps us resolve tough things easily. To get more familiar with Hypothesis testing and other prediction models attend the superb useful KnowledgeHut Data Science full course which will give you more domain knowledge and will assist you in working with industry-related projects.
Basic Steps in Hypothesis Testing [Workflow]
1. null and alternative hypothesis.
After we have done our initial research about the predictions that we want to find out if true, it is important to mention whether the hypothesis done is a null hypothesis(H0) or an alternative hypothesis (Ha). Once we understand the type of hypothesis, it will be easy for us to do mathematical research on it. A null hypothesis will usually indicate the no-relationship between the variables whereas an alternative hypothesis describes the relationship between 2 variables.
- H0 – Girls, on average, are not strong as boys
- Ha - Girls, on average are stronger than boys
2. Data Collection
To prove our statistical test validity, it is essential and critical to check the data and proceed with sampling them to get the correct hypothesis results. If the target data is not prepared and ready, it will become difficult to make the predictions or the statistical inference on the population that we are planning to make. It is important to prepare efficient data, so that hypothesis findings can be easy to predict.
3. Selection of an appropriate test statistic
To perform various analyses on the data, we need to choose a statistical test. There are various types of statistical tests available. Based on the wide spread of the data that is variance within the group or how different the data category is from one another that is variance without a group, we can proceed with our further research study.
4. Selection of the appropriate significant level
Once we get the result and outcome of the statistical test, we have to then proceed further to decide whether the reject or accept the null hypothesis. The significance level is indicated by alpha (α). It describes the probability of rejecting or accepting the null hypothesis. Example- Suppose the value of the significance level which is alpha is 0.05. Now, this value indicates the difference from the null hypothesis.
5. Calculation of the test statistics and the p-value
P value is simply the probability value and expected determined outcome which is at least as extreme and close as observed results of a hypothetical test. It helps in evaluating and verifying hypotheses against the sample data. This happens while assuming the null hypothesis is true. The lower the value of P, the higher and better will be the results of the significant value which is alpha (α). For example, if the P-value is 0.05 or even less than this, then it will be considered statistically significant. The main thing is these values are predicted based on the calculations done by deviating the values between the observed one and referenced one. The greater the difference between values, the lower the p-value will be.
6. Findings of the test
After knowing the P-value and statistical significance, we can determine our results and take the appropriate decision of whether to accept or reject the null hypothesis based on the facts and statistics presented to us.
How to Calculate Hypothesis Testing?
Hypothesis testing can be done using various statistical tests. One is Z-test. The formula for Z-test is given below:
Z = ( x̅ – μ 0 ) / (σ /√n)
In the above equation, x̅ is the sample mean
- μ0 is the population mean
- σ is the standard deviation
- n is the sample size
Now depending on the Z-test result, the examination will be processed further. The result is either going to be a null hypothesis or it is going to be an alternative hypothesis. That can be measured through below formula-
- H0: μ=μ0
- Ha: μ≠μ0
- Here,
- H0 = null hypothesis
- Ha = alternate hypothesis
In this way, we calculate the hypothesis testing and can apply it to real-world scenarios.
Real-World Examples of Hypothesis Testing
Hypothesis testing has a wide variety of use cases that proves to be beneficial for various industries.
1. Healthcare
In the healthcare industry, all the research and experiments which are done to predict the success of any medicine or drug are done successfully with the help of Hypothesis testing.
2. Education sector
Hypothesis testing assists in experimenting with different teaching techniques to deal with the understanding capability of different students.
3. Mental Health
Hypothesis testing helps in indicating the factors that may cause some serious mental health issues.
4. Manufacturing
Testing whether the new change in the process of manufacturing helped in the improvement of the process as well as in the quantity or not. In the same way, there are many other use cases that we get to see in different sectors for hypothesis testing.
Error Terms in Hypothesis Testing
1. type-i error.
Type I error occurs during the process of hypothesis testing when the null hypothesis is rejected even though it is accurate. This kind of error is also known as False positive because even though the statement is positive or correct but results are given as false. For example, an innocent person still goes to jail because he is considered to be guilty.
2. Type-II error
Type II error occurs during the process of hypothesis testing when the null hypothesis is not rejected even though it is inaccurate. This Kind of error is also called a False-negative which means even though the statements are false and inaccurate, it still says it is correct and doesn’t reject it. For example, a person is guilty, but in court, he has been proven innocent where he is guilty, so this is a Type II error.
3. Level of Significance
The level of significance is majorly used to measure the confidence with which a null hypothesis can be rejected. It is the value with which one can reject the null hypothesis which is H0. The level of significance gauges whether the hypothesis testing is significant or not.
P-value stands for probability value, which tells us the probability or likelihood to find the set of observations when the null hypothesis is true using statistical tests. The main purpose is to check the significance of the statistical statement.
5. High P-Values
A higher P-value indicates that the testing is not statistically significant. For example, a P value greater than 0.05 is considered to be having higher P value. A higher P-value also means that our evidence and proofs are not strong enough to influence the population.
In hypothesis testing, each step is responsible for getting the outcomes and the results, whether it is the selection of statistical tests or working on data, each step contributes towards the better consequences of the hypothesis testing. It is always a recommendable step when planning for predicting the outcomes and trying to experiment with the sample; hypothesis testing is a useful concept to apply.
Frequently Asked Questions (FAQs)
We can test a hypothesis by selecting a correct hypothetical test and, based on those getting results.
Many statistical tests are used for hypothetical testing which includes Z-test, T-test, etc.
Hypothesis helps us in doing various experiments and working on a specific research topic to predict the results.
The null and alternative hypothesis, data collection, selecting a statistical test, selecting significance value, calculating p-value, check your findings.
In simple words, parametric tests are purely based on assumptions whereas non-parametric tests are based on data that is collected and acquired from a sample.

Gauri Guglani
Gauri Guglani works as a Data Analyst at Deloitte Consulting. She has done her major in Information Technology and holds great interest in the field of data science. She owns her technical skills as well as managerial skills and also is great at communicating. Since her undergraduate, Gauri has developed a profound interest in writing content and sharing her knowledge through the manual means of blog/article writing. She loves writing on topics affiliated with Statistics, Python Libraries, Machine Learning, Natural Language processes, and many more.
Avail your free 1:1 mentorship session.
Something went wrong
Upcoming Data Science Batches & Dates
| Name | Date | Fee | Know more |
|---|
- Math Article
Statistical Inference

Statistics is a branch of Mathematics, that deals with the collection, analysis, interpretation, and the presentation of the numerical data. In other words, it is defined as the collection of quantitative data. The main purpose of Statistics is to make an accurate conclusion using a limited sample about a greater population.
Types of Statistics
Statistics can be classified into two different categories. The two different types of Statistics are:
- Descriptive Statistics
- Inferential Statistics
In Statistics, descriptive statistics describe the data, whereas inferential statistics help you make predictions from the data. In inferential statistics, the data are taken from the sample and allows you to generalize the population. In general, inference means “guess”, which means making inference about something. So, statistical inference means, making inference about the population. To take a conclusion about the population, it uses various statistical analysis techniques. In this article, one of the types of statistics called inferential statistics is explained in detail. Now, you are going to learn the proper definition of statistical inference, types, solutions, and examples.
Statistical Inference Definition
Statistical inference is the process of analysing the result and making conclusions from data subject to random variation. It is also called inferential statistics. Hypothesis testing and confidence intervals are the applications of the statistical inference. Statistical inference is a method of making decisions about the parameters of a population, based on random sampling. It helps to assess the relationship between the dependent and independent variables. The purpose of statistical inference to estimate the uncertainty or sample to sample variation. It allows us to provide a probable range of values for the true values of something in the population. The components used for making statistical inference are:
- Sample Size
- Variability in the sample
- Size of the observed differences
Types of Statistical Inference
There are different types of statistical inferences that are extensively used for making conclusions. They are:
- One sample hypothesis testing
- Confidence Interval
- Pearson Correlation
- Bi-variate regression
- Multi-variate regression
- Chi-square statistics and contingency table
- ANOVA or T-test
Statistical Inference Procedure
The procedure involved in inferential statistics are:
- Begin with a theory
- Create a research hypothesis
- Operationalize the variables
- Recognize the population to which the study results should apply
- Formulate a null hypothesis for this population
- Accumulate a sample from the population and continue the study
- Conduct statistical tests to see if the collected sample properties are adequately different from what would be expected under the null hypothesis to be able to reject the null hypothesis
Statistical Inference Solution
Statistical inference solutions produce efficient use of statistical data relating to groups of individuals or trials. It deals with all characters, including the collection, investigation and analysis of data and organizing the collected data. By statistical inference solution, people can acquire knowledge after starting their work in diverse fields. Some statistical inference solution facts are:
- It is a common way to assume that the observed sample is of independent observations from a population type like Poisson or normal
- Statistical inference solution is used to evaluate the parameter(s) of the expected model like normal mean or binomial proportion
Importance of Statistical Inference
Inferential Statistics is important to examine the data properly. To make an accurate conclusion, proper data analysis is important to interpret the research results. It is majorly used in the future prediction for various observations in different fields. It helps us to make inference about the data. The statistical inference has a wide range of application in different fields, such as:
- Business Analysis
- Artificial Intelligence
- Financial Analysis
- Fraud Detection
- Machine Learning
- Share Market
- Pharmaceutical Sector
Statistical Inference Examples
An example of statistical inference is given below.
Question: From the shuffled pack of cards, a card is drawn. This trial is repeated for 400 times, and the suits are given below:
| Suit | Spade | Clubs | Hearts | Diamonds |
| No.of times drawn | 90 | 100 | 120 | 90 |
While a card is tried at random, then what is the probability of getting a
- Diamond cards
- Black cards
- Except for spade
By statistical inference solution,
Total number of events = 400
i.e.,90+100+120+90=400
(1) The probability of getting diamond cards:
Number of trials in which diamond card is drawn = 90
Therefore, P(diamond card) = 90/400 = 0.225
(2) The probability of getting black cards:
Number of trials in which black card showed up = 90+100 =190
Therefore, P(black card) = 190/400 = 0.475
(3) Except for spade
Number of trials other than spade showed up = 90+100+120 =310
Therefore, P(except spade) = 310/400 = 0.775
Stay tuned with BYJU’S – The Learning App for more Maths-related concepts and download the app for more personalized videos.
| MATHS Related Links | |
Register with BYJU'S & Download Free PDFs
Register with byju's & watch live videos.
An official website of the United States government
The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.
The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.
- Publications
- Account settings
Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .
- Advanced Search
- Journal List
- Indian J Crit Care Med
- v.23(Suppl 3); 2019 Sep
An Introduction to Statistics: Understanding Hypothesis Testing and Statistical Errors
Priya ranganathan.
1 Department of Anesthesiology, Critical Care and Pain, Tata Memorial Hospital, Mumbai, Maharashtra, India
2 Department of Surgical Oncology, Tata Memorial Centre, Mumbai, Maharashtra, India
The second article in this series on biostatistics covers the concepts of sample, population, research hypotheses and statistical errors.
How to cite this article
Ranganathan P, Pramesh CS. An Introduction to Statistics: Understanding Hypothesis Testing and Statistical Errors. Indian J Crit Care Med 2019;23(Suppl 3):S230–S231.
Two papers quoted in this issue of the Indian Journal of Critical Care Medicine report. The results of studies aim to prove that a new intervention is better than (superior to) an existing treatment. In the ABLE study, the investigators wanted to show that transfusion of fresh red blood cells would be superior to standard-issue red cells in reducing 90-day mortality in ICU patients. 1 The PROPPR study was designed to prove that transfusion of a lower ratio of plasma and platelets to red cells would be superior to a higher ratio in decreasing 24-hour and 30-day mortality in critically ill patients. 2 These studies are known as superiority studies (as opposed to noninferiority or equivalence studies which will be discussed in a subsequent article).
SAMPLE VERSUS POPULATION
A sample represents a group of participants selected from the entire population. Since studies cannot be carried out on entire populations, researchers choose samples, which are representative of the population. This is similar to walking into a grocery store and examining a few grains of rice or wheat before purchasing an entire bag; we assume that the few grains that we select (the sample) are representative of the entire sack of grains (the population).
The results of the study are then extrapolated to generate inferences about the population. We do this using a process known as hypothesis testing. This means that the results of the study may not always be identical to the results we would expect to find in the population; i.e., there is the possibility that the study results may be erroneous.
HYPOTHESIS TESTING
A clinical trial begins with an assumption or belief, and then proceeds to either prove or disprove this assumption. In statistical terms, this belief or assumption is known as a hypothesis. Counterintuitively, what the researcher believes in (or is trying to prove) is called the “alternate” hypothesis, and the opposite is called the “null” hypothesis; every study has a null hypothesis and an alternate hypothesis. For superiority studies, the alternate hypothesis states that one treatment (usually the new or experimental treatment) is superior to the other; the null hypothesis states that there is no difference between the treatments (the treatments are equal). For example, in the ABLE study, we start by stating the null hypothesis—there is no difference in mortality between groups receiving fresh RBCs and standard-issue RBCs. We then state the alternate hypothesis—There is a difference between groups receiving fresh RBCs and standard-issue RBCs. It is important to note that we have stated that the groups are different, without specifying which group will be better than the other. This is known as a two-tailed hypothesis and it allows us to test for superiority on either side (using a two-sided test). This is because, when we start a study, we are not 100% certain that the new treatment can only be better than the standard treatment—it could be worse, and if it is so, the study should pick it up as well. One tailed hypothesis and one-sided statistical testing is done for non-inferiority studies, which will be discussed in a subsequent paper in this series.
STATISTICAL ERRORS
There are two possibilities to consider when interpreting the results of a superiority study. The first possibility is that there is truly no difference between the treatments but the study finds that they are different. This is called a Type-1 error or false-positive error or alpha error. This means falsely rejecting the null hypothesis.
The second possibility is that there is a difference between the treatments and the study does not pick up this difference. This is called a Type 2 error or false-negative error or beta error. This means falsely accepting the null hypothesis.
The power of the study is the ability to detect a difference between groups and is the converse of the beta error; i.e., power = 1-beta error. Alpha and beta errors are finalized when the protocol is written and form the basis for sample size calculation for the study. In an ideal world, we would not like any error in the results of our study; however, we would need to do the study in the entire population (infinite sample size) to be able to get a 0% alpha and beta error. These two errors enable us to do studies with realistic sample sizes, with the compromise that there is a small possibility that the results may not always reflect the truth. The basis for this will be discussed in a subsequent paper in this series dealing with sample size calculation.
Conventionally, type 1 or alpha error is set at 5%. This means, that at the end of the study, if there is a difference between groups, we want to be 95% certain that this is a true difference and allow only a 5% probability that this difference has occurred by chance (false positive). Type 2 or beta error is usually set between 10% and 20%; therefore, the power of the study is 90% or 80%. This means that if there is a difference between groups, we want to be 80% (or 90%) certain that the study will detect that difference. For example, in the ABLE study, sample size was calculated with a type 1 error of 5% (two-sided) and power of 90% (type 2 error of 10%) (1).
Table 1 gives a summary of the two types of statistical errors with an example
Statistical errors
| (a) Types of statistical errors | |||
| : Null hypothesis is | |||
| True | False | ||
| Null hypothesis is actually | True | Correct results! | Falsely rejecting null hypothesis - Type I error |
| False | Falsely accepting null hypothesis - Type II error | Correct results! | |
| (b) Possible statistical errors in the ABLE trial | |||
| There is difference in mortality between groups receiving fresh RBCs and standard-issue RBCs | There difference in mortality between groups receiving fresh RBCs and standard-issue RBCs | ||
| Truth | There is difference in mortality between groups receiving fresh RBCs and standard-issue RBCs | Correct results! | Falsely rejecting null hypothesis - Type I error |
| There difference in mortality between groups receiving fresh RBCs and standard-issue RBCs | Falsely accepting null hypothesis - Type II error | Correct results! | |
In the next article in this series, we will look at the meaning and interpretation of ‘ p ’ value and confidence intervals for hypothesis testing.
Source of support: Nil
Conflict of interest: None
Have a language expert improve your writing
Run a free plagiarism check in 10 minutes, generate accurate citations for free.
- Knowledge Base
- Inferential Statistics | An Easy Introduction & Examples
Inferential Statistics | An Easy Introduction & Examples
Published on September 4, 2020 by Pritha Bhandari . Revised on June 22, 2023.
While descriptive statistics summarize the characteristics of a data set, inferential statistics help you come to conclusions and make predictions based on your data.
When you have collected data from a sample , you can use inferential statistics to understand the larger population from which the sample is taken.
Inferential statistics have two main uses:
- making estimates about populations (for example, the mean SAT score of all 11th graders in the US).
- testing hypotheses to draw conclusions about populations (for example, the relationship between SAT scores and family income).
Table of contents
Descriptive versus inferential statistics, estimating population parameters from sample statistics, hypothesis testing, other interesting articles, frequently asked questions about inferential statistics.
Descriptive statistics allow you to describe a data set, while inferential statistics allow you to make inferences based on a data set.
- Descriptive statistics
Using descriptive statistics, you can report characteristics of your data:
- The distribution concerns the frequency of each value.
- The central tendency concerns the averages of the values.
- The variability concerns how spread out the values are.
In descriptive statistics, there is no uncertainty – the statistics precisely describe the data that you collected. If you collect data from an entire population, you can directly compare these descriptive statistics to those from other populations.
Inferential statistics
Most of the time, you can only acquire data from samples, because it is too difficult or expensive to collect data from the whole population that you’re interested in.
While descriptive statistics can only summarize a sample’s characteristics, inferential statistics use your sample to make reasonable guesses about the larger population.
With inferential statistics, it’s important to use random and unbiased sampling methods . If your sample isn’t representative of your population, then you can’t make valid statistical inferences or generalize .
Sampling error in inferential statistics
Since the size of a sample is always smaller than the size of the population, some of the population isn’t captured by sample data. This creates sampling error , which is the difference between the true population values (called parameters) and the measured sample values (called statistics).
Sampling error arises any time you use a sample, even if your sample is random and unbiased. For this reason, there is always some uncertainty in inferential statistics. However, using probability sampling methods reduces this uncertainty.
Receive feedback on language, structure, and formatting
Professional editors proofread and edit your paper by focusing on:
- Academic style
- Vague sentences
- Style consistency
See an example

The characteristics of samples and populations are described by numbers called statistics and parameters :
- A statistic is a measure that describes the sample (e.g., sample mean ).
- A parameter is a measure that describes the whole population (e.g., population mean).
Sampling error is the difference between a parameter and a corresponding statistic. Since in most cases you don’t know the real population parameter, you can use inferential statistics to estimate these parameters in a way that takes sampling error into account.
There are two important types of estimates you can make about the population: point estimates and interval estimates .
- A point estimate is a single value estimate of a parameter. For instance, a sample mean is a point estimate of a population mean.
- An interval estimate gives you a range of values where the parameter is expected to lie. A confidence interval is the most common type of interval estimate.
Both types of estimates are important for gathering a clear idea of where a parameter is likely to lie.
Confidence intervals
A confidence interval uses the variability around a statistic to come up with an interval estimate for a parameter. Confidence intervals are useful for estimating parameters because they take sampling error into account.
While a point estimate gives you a precise value for the parameter you are interested in, a confidence interval tells you the uncertainty of the point estimate. They are best used in combination with each other.
Each confidence interval is associated with a confidence level. A confidence level tells you the probability (in percentage) of the interval containing the parameter estimate if you repeat the study again.
A 95% confidence interval means that if you repeat your study with a new sample in exactly the same way 100 times, you can expect your estimate to lie within the specified range of values 95 times.
Although you can say that your estimate will lie within the interval a certain percentage of the time, you cannot say for sure that the actual population parameter will. That’s because you can’t know the true value of the population parameter without collecting data from the full population.
However, with random sampling and a suitable sample size, you can reasonably expect your confidence interval to contain the parameter a certain percentage of the time.
Your point estimate of the population mean paid vacation days is the sample mean of 19 paid vacation days.
Hypothesis testing is a formal process of statistical analysis using inferential statistics. The goal of hypothesis testing is to compare populations or assess relationships between variables using samples.
Hypotheses , or predictions, are tested using statistical tests . Statistical tests also estimate sampling errors so that valid inferences can be made.
Statistical tests can be parametric or non-parametric. Parametric tests are considered more statistically powerful because they are more likely to detect an effect if one exists.
Parametric tests make assumptions that include the following:
- the population that the sample comes from follows a normal distribution of scores
- the sample size is large enough to represent the population
- the variances , a measure of variability , of each group being compared are similar
When your data violates any of these assumptions, non-parametric tests are more suitable. Non-parametric tests are called “distribution-free tests” because they don’t assume anything about the distribution of the population data.
Statistical tests come in three forms: tests of comparison, correlation or regression.
Comparison tests
Comparison tests assess whether there are differences in means, medians or rankings of scores of two or more groups.
To decide which test suits your aim, consider whether your data meets the conditions necessary for parametric tests, the number of samples, and the levels of measurement of your variables.
Means can only be found for interval or ratio data , while medians and rankings are more appropriate measures for ordinal data .
| test | Yes | Means | 2 samples |
|---|---|---|---|
| Yes | Means | 3+ samples | |
| Mood’s median | No | Medians | 2+ samples |
| Wilcoxon signed-rank | No | Distributions | 2 samples |
| Wilcoxon rank-sum (Mann-Whitney ) | No | Sums of rankings | 2 samples |
| Kruskal-Wallis | No | Mean rankings | 3+ samples |
Correlation tests
Correlation tests determine the extent to which two variables are associated.
Although Pearson’s r is the most statistically powerful test, Spearman’s r is appropriate for interval and ratio variables when the data doesn’t follow a normal distribution.
The chi square test of independence is the only test that can be used with nominal variables.
| Pearson’s | Yes | Interval/ratio variables |
|---|---|---|
| Spearman’s | No | Ordinal/interval/ratio variables |
| Chi square test of independence | No | Nominal/ordinal variables |
Regression tests
Regression tests demonstrate whether changes in predictor variables cause changes in an outcome variable. You can decide which regression test to use based on the number and types of variables you have as predictors and outcomes.
Most of the commonly used regression tests are parametric. If your data is not normally distributed, you can perform data transformations.
Data transformations help you make your data normally distributed using mathematical operations, like taking the square root of each value.
| 1 interval/ratio variable | 1 interval/ratio variable | |
| 2+ interval/ratio variable(s) | 1 interval/ratio variable | |
| Logistic regression | 1+ any variable(s) | 1 binary variable |
| Nominal regression | 1+ any variable(s) | 1 nominal variable |
| Ordinal regression | 1+ any variable(s) | 1 ordinal variable |
If you want to know more about statistics , methodology , or research bias , make sure to check out some of our other articles with explanations and examples.
- Confidence interval
- Measures of central tendency
- Correlation coefficient
Methodology
- Cluster sampling
- Stratified sampling
- Types of interviews
- Cohort study
- Thematic analysis
Research bias
- Implicit bias
- Cognitive bias
- Survivorship bias
- Availability heuristic
- Nonresponse bias
- Regression to the mean
Descriptive statistics summarize the characteristics of a data set. Inferential statistics allow you to test a hypothesis or assess whether your data is generalizable to the broader population.
A statistic refers to measures about the sample , while a parameter refers to measures about the population .
A sampling error is the difference between a population parameter and a sample statistic .
Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics. It is used by scientists to test specific predictions, called hypotheses , by calculating how likely it is that a pattern or relationship between variables could have arisen by chance.

Cite this Scribbr article
If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.
Bhandari, P. (2023, June 22). Inferential Statistics | An Easy Introduction & Examples. Scribbr. Retrieved August 29, 2024, from https://www.scribbr.com/statistics/inferential-statistics/
Is this article helpful?

Pritha Bhandari
Other students also liked, parameter vs statistic | definitions, differences & examples, descriptive statistics | definitions, types, examples, hypothesis testing | a step-by-step guide with easy examples, what is your plagiarism score.
Tutorial Playlist
Statistics tutorial, everything you need to know about the probability density function in statistics, the best guide to understand central limit theorem, an in-depth guide to measures of central tendency : mean, median and mode, the ultimate guide to understand conditional probability.
A Comprehensive Look at Percentile in Statistics
The Best Guide to Understand Bayes Theorem
Everything you need to know about the normal distribution, an in-depth explanation of cumulative distribution function, a complete guide to chi-square test, what is hypothesis testing in statistics types and examples, understanding the fundamentals of arithmetic and geometric progression, the definitive guide to understand spearman’s rank correlation, mean squared error: overview, examples, concepts and more, all you need to know about the empirical rule in statistics, the complete guide to skewness and kurtosis, a holistic look at bernoulli distribution.
All You Need to Know About Bias in Statistics
A Complete Guide to Get a Grasp of Time Series Analysis
The Key Differences Between Z-Test Vs. T-Test
The Complete Guide to Understand Pearson's Correlation
A complete guide on the types of statistical studies, everything you need to know about poisson distribution, your best guide to understand correlation vs. regression, the most comprehensive guide for beginners on what is correlation, hypothesis testing in statistics - types | examples.
Lesson 10 of 24 By Avijeet Biswal

Table of Contents
In today’s data-driven world, decisions are based on data all the time. Hypothesis plays a crucial role in that process, whether it may be making business decisions, in the health sector, academia, or in quality improvement. Without hypothesis & hypothesis tests, you risk drawing the wrong conclusions and making bad decisions. In this tutorial, you will look at Hypothesis Testing in Statistics.
The Ultimate Ticket to Top Data Science Job Roles
What Is Hypothesis Testing in Statistics?
Hypothesis Testing is a type of statistical analysis in which you put your assumptions about a population parameter to the test. It is used to estimate the relationship between 2 statistical variables.
Let's discuss few examples of statistical hypothesis from real-life -
- A teacher assumes that 60% of his college's students come from lower-middle-class families.
- A doctor believes that 3D (Diet, Dose, and Discipline) is 90% effective for diabetic patients.
Now that you know about hypothesis testing, look at the two types of hypothesis testing in statistics.
Hypothesis Testing Formula
Z = ( x̅ – μ0 ) / (σ /√n)
- Here, x̅ is the sample mean,
- μ0 is the population mean,
- σ is the standard deviation,
- n is the sample size.
How Hypothesis Testing Works?
An analyst performs hypothesis testing on a statistical sample to present evidence of the plausibility of the null hypothesis. Measurements and analyses are conducted on a random sample of the population to test a theory. Analysts use a random population sample to test two hypotheses: the null and alternative hypotheses.
The null hypothesis is typically an equality hypothesis between population parameters; for example, a null hypothesis may claim that the population means return equals zero. The alternate hypothesis is essentially the inverse of the null hypothesis (e.g., the population means the return is not equal to zero). As a result, they are mutually exclusive, and only one can be correct. One of the two possibilities, however, will always be correct.
Your Dream Career is Just Around The Corner!
Null Hypothesis and Alternative Hypothesis
The Null Hypothesis is the assumption that the event will not occur. A null hypothesis has no bearing on the study's outcome unless it is rejected.
H0 is the symbol for it, and it is pronounced H-naught.
The Alternate Hypothesis is the logical opposite of the null hypothesis. The acceptance of the alternative hypothesis follows the rejection of the null hypothesis. H1 is the symbol for it.
Let's understand this with an example.
A sanitizer manufacturer claims that its product kills 95 percent of germs on average.
To put this company's claim to the test, create a null and alternate hypothesis.
H0 (Null Hypothesis): Average = 95%.
Alternative Hypothesis (H1): The average is less than 95%.
Another straightforward example to understand this concept is determining whether or not a coin is fair and balanced. The null hypothesis states that the probability of a show of heads is equal to the likelihood of a show of tails. In contrast, the alternate theory states that the probability of a show of heads and tails would be very different.
Become a Data Scientist with Hands-on Training!
Hypothesis Testing Calculation With Examples
Let's consider a hypothesis test for the average height of women in the United States. Suppose our null hypothesis is that the average height is 5'4". We gather a sample of 100 women and determine that their average height is 5'5". The standard deviation of population is 2.
To calculate the z-score, we would use the following formula:
z = ( x̅ – μ0 ) / (σ /√n)
z = (5'5" - 5'4") / (2" / √100)
z = 0.5 / (0.045)
We will reject the null hypothesis as the z-score of 11.11 is very large and conclude that there is evidence to suggest that the average height of women in the US is greater than 5'4".
Steps in Hypothesis Testing
Hypothesis testing is a statistical method to determine if there is enough evidence in a sample of data to infer that a certain condition is true for the entire population. Here’s a breakdown of the typical steps involved in hypothesis testing:
Formulate Hypotheses
- Null Hypothesis (H0): This hypothesis states that there is no effect or difference, and it is the hypothesis you attempt to reject with your test.
- Alternative Hypothesis (H1 or Ha): This hypothesis is what you might believe to be true or hope to prove true. It is usually considered the opposite of the null hypothesis.
Choose the Significance Level (α)
The significance level, often denoted by alpha (α), is the probability of rejecting the null hypothesis when it is true. Common choices for α are 0.05 (5%), 0.01 (1%), and 0.10 (10%).
Select the Appropriate Test
Choose a statistical test based on the type of data and the hypothesis. Common tests include t-tests, chi-square tests, ANOVA, and regression analysis. The selection depends on data type, distribution, sample size, and whether the hypothesis is one-tailed or two-tailed.
Collect Data
Gather the data that will be analyzed in the test. This data should be representative of the population to infer conclusions accurately.
Calculate the Test Statistic
Based on the collected data and the chosen test, calculate a test statistic that reflects how much the observed data deviates from the null hypothesis.
Determine the p-value
The p-value is the probability of observing test results at least as extreme as the results observed, assuming the null hypothesis is correct. It helps determine the strength of the evidence against the null hypothesis.
Make a Decision
Compare the p-value to the chosen significance level:
- If the p-value ≤ α: Reject the null hypothesis, suggesting sufficient evidence in the data supports the alternative hypothesis.
- If the p-value > α: Do not reject the null hypothesis, suggesting insufficient evidence to support the alternative hypothesis.
Report the Results
Present the findings from the hypothesis test, including the test statistic, p-value, and the conclusion about the hypotheses.
Perform Post-hoc Analysis (if necessary)
Depending on the results and the study design, further analysis may be needed to explore the data more deeply or to address multiple comparisons if several hypotheses were tested simultaneously.
Types of Hypothesis Testing
To determine whether a discovery or relationship is statistically significant, hypothesis testing uses a z-test. It usually checks to see if two means are the same (the null hypothesis). Only when the population standard deviation is known and the sample size is 30 data points or more, can a z-test be applied.
A statistical test called a t-test is employed to compare the means of two groups. To determine whether two groups differ or if a procedure or treatment affects the population of interest, it is frequently used in hypothesis testing.
Chi-Square
You utilize a Chi-square test for hypothesis testing concerning whether your data is as predicted. To determine if the expected and observed results are well-fitted, the Chi-square test analyzes the differences between categorical variables from a random sample. The test's fundamental premise is that the observed values in your data should be compared to the predicted values that would be present if the null hypothesis were true.
Hypothesis Testing and Confidence Intervals
Both confidence intervals and hypothesis tests are inferential techniques that depend on approximating the sample distribution. Data from a sample is used to estimate a population parameter using confidence intervals. Data from a sample is used in hypothesis testing to examine a given hypothesis. We must have a postulated parameter to conduct hypothesis testing.
Bootstrap distributions and randomization distributions are created using comparable simulation techniques. The observed sample statistic is the focal point of a bootstrap distribution, whereas the null hypothesis value is the focal point of a randomization distribution.
A variety of feasible population parameter estimates are included in confidence ranges. In this lesson, we created just two-tailed confidence intervals. There is a direct connection between these two-tail confidence intervals and these two-tail hypothesis tests. The results of a two-tailed hypothesis test and two-tailed confidence intervals typically provide the same results. In other words, a hypothesis test at the 0.05 level will virtually always fail to reject the null hypothesis if the 95% confidence interval contains the predicted value. A hypothesis test at the 0.05 level will nearly certainly reject the null hypothesis if the 95% confidence interval does not include the hypothesized parameter.
Become a Data Scientist through hands-on learning with hackathons, masterclasses, webinars, and Ask-Me-Anything! Start learning now!
Simple and Composite Hypothesis Testing
Depending on the population distribution, you can classify the statistical hypothesis into two types.
Simple Hypothesis: A simple hypothesis specifies an exact value for the parameter.
Composite Hypothesis: A composite hypothesis specifies a range of values.
A company is claiming that their average sales for this quarter are 1000 units. This is an example of a simple hypothesis.
Suppose the company claims that the sales are in the range of 900 to 1000 units. Then this is a case of a composite hypothesis.
One-Tailed and Two-Tailed Hypothesis Testing
The One-Tailed test, also called a directional test, considers a critical region of data that would result in the null hypothesis being rejected if the test sample falls into it, inevitably meaning the acceptance of the alternate hypothesis.
In a one-tailed test, the critical distribution area is one-sided, meaning the test sample is either greater or lesser than a specific value.
In two tails, the test sample is checked to be greater or less than a range of values in a Two-Tailed test, implying that the critical distribution area is two-sided.
If the sample falls within this range, the alternate hypothesis will be accepted, and the null hypothesis will be rejected.
Become a Data Scientist With Real-World Experience
Right Tailed Hypothesis Testing
If the larger than (>) sign appears in your hypothesis statement, you are using a right-tailed test, also known as an upper test. Or, to put it another way, the disparity is to the right. For instance, you can contrast the battery life before and after a change in production. Your hypothesis statements can be the following if you want to know if the battery life is longer than the original (let's say 90 hours):
- The null hypothesis is (H0 <= 90) or less change.
- A possibility is that battery life has risen (H1) > 90.
The crucial point in this situation is that the alternate hypothesis (H1), not the null hypothesis, decides whether you get a right-tailed test.
Left Tailed Hypothesis Testing
Alternative hypotheses that assert the true value of a parameter is lower than the null hypothesis are tested with a left-tailed test; they are indicated by the asterisk "<".
Suppose H0: mean = 50 and H1: mean not equal to 50
According to the H1, the mean can be greater than or less than 50. This is an example of a Two-tailed test.
In a similar manner, if H0: mean >=50, then H1: mean <50
Here the mean is less than 50. It is called a One-tailed test.
Type 1 and Type 2 Error
A hypothesis test can result in two types of errors.
Type 1 Error: A Type-I error occurs when sample results reject the null hypothesis despite being true.
Type 2 Error: A Type-II error occurs when the null hypothesis is not rejected when it is false, unlike a Type-I error.
Suppose a teacher evaluates the examination paper to decide whether a student passes or fails.
H0: Student has passed
H1: Student has failed
Type I error will be the teacher failing the student [rejects H0] although the student scored the passing marks [H0 was true].
Type II error will be the case where the teacher passes the student [do not reject H0] although the student did not score the passing marks [H1 is true].
Our Data Scientist Master's Program covers core topics such as R, Python, Machine Learning, Tableau, Hadoop, and Spark. Get started on your journey today!
Limitations of Hypothesis Testing
Hypothesis testing has some limitations that researchers should be aware of:
- It cannot prove or establish the truth: Hypothesis testing provides evidence to support or reject a hypothesis, but it cannot confirm the absolute truth of the research question.
- Results are sample-specific: Hypothesis testing is based on analyzing a sample from a population, and the conclusions drawn are specific to that particular sample.
- Possible errors: During hypothesis testing, there is a chance of committing type I error (rejecting a true null hypothesis) or type II error (failing to reject a false null hypothesis).
- Assumptions and requirements: Different tests have specific assumptions and requirements that must be met to accurately interpret results.
Learn All The Tricks Of The BI Trade
After reading this tutorial, you would have a much better understanding of hypothesis testing, one of the most important concepts in the field of Data Science . The majority of hypotheses are based on speculation about observed behavior, natural phenomena, or established theories.
If you are interested in statistics of data science and skills needed for such a career, you ought to explore the Post Graduate Program in Data Science.
If you have any questions regarding this ‘Hypothesis Testing In Statistics’ tutorial, do share them in the comment section. Our subject matter expert will respond to your queries. Happy learning!
1. What is hypothesis testing in statistics with example?
Hypothesis testing is a statistical method used to determine if there is enough evidence in a sample data to draw conclusions about a population. It involves formulating two competing hypotheses, the null hypothesis (H0) and the alternative hypothesis (Ha), and then collecting data to assess the evidence. An example: testing if a new drug improves patient recovery (Ha) compared to the standard treatment (H0) based on collected patient data.
2. What is H0 and H1 in statistics?
In statistics, H0 and H1 represent the null and alternative hypotheses. The null hypothesis, H0, is the default assumption that no effect or difference exists between groups or conditions. The alternative hypothesis, H1, is the competing claim suggesting an effect or a difference. Statistical tests determine whether to reject the null hypothesis in favor of the alternative hypothesis based on the data.
3. What is a simple hypothesis with an example?
A simple hypothesis is a specific statement predicting a single relationship between two variables. It posits a direct and uncomplicated outcome. For example, a simple hypothesis might state, "Increased sunlight exposure increases the growth rate of sunflowers." Here, the hypothesis suggests a direct relationship between the amount of sunlight (independent variable) and the growth rate of sunflowers (dependent variable), with no additional variables considered.
4. What are the 3 major types of hypothesis?
The three major types of hypotheses are:
- Null Hypothesis (H0): Represents the default assumption, stating that there is no significant effect or relationship in the data.
- Alternative Hypothesis (Ha): Contradicts the null hypothesis and proposes a specific effect or relationship that researchers want to investigate.
- Nondirectional Hypothesis: An alternative hypothesis that doesn't specify the direction of the effect, leaving it open for both positive and negative possibilities.
Find our PL-300 Microsoft Power BI Certification Training Online Classroom training classes in top cities:
| Name | Date | Place | |
|---|---|---|---|
| 7 Sep -22 Sep 2024, Weekend batch | Your City | ||
| 21 Sep -6 Oct 2024, Weekend batch | Your City | ||
| 12 Oct -27 Oct 2024, Weekend batch | Your City |
About the Author
Avijeet is a Senior Research Analyst at Simplilearn. Passionate about Data Analytics, Machine Learning, and Deep Learning, Avijeet is also interested in politics, cricket, and football.
Recommended Resources
Free eBook: Top Programming Languages For A Data Scientist
Normality Test in Minitab: Minitab with Statistics
Machine Learning Career Guide: A Playbook to Becoming a Machine Learning Engineer
- PMP, PMI, PMBOK, CAPM, PgMP, PfMP, ACP, PBA, RMP, SP, and OPM3 are registered marks of the Project Management Institute, Inc.
- Skip to secondary menu
- Skip to main content
- Skip to primary sidebar
Statistics By Jim
Making statistics intuitive
Types I & Type II Errors in Hypothesis Testing
By Jim Frost 8 Comments
In hypothesis testing, a Type I error is a false positive while a Type II error is a false negative. In this blog post, you will learn about these two types of errors, their causes, and how to manage them.
Hypothesis tests use sample data to make inferences about the properties of a population . You gain tremendous benefits by working with random samples because it is usually impossible to measure the entire population.
However, there are tradeoffs when you use samples. The samples we use are typically a minuscule percentage of the entire population. Consequently, they occasionally misrepresent the population severely enough to cause hypothesis tests to make Type I and Type II errors.
Potential Outcomes in Hypothesis Testing
Hypothesis testing is a procedure in inferential statistics that assesses two mutually exclusive theories about the properties of a population. For a generic hypothesis test, the two hypotheses are as follows:
- Null hypothesis : There is no effect
- Alternative hypothesis : There is an effect.
The sample data must provide sufficient evidence to reject the null hypothesis and conclude that the effect exists in the population. Ideally, a hypothesis test fails to reject the null hypothesis when the effect is not present in the population, and it rejects the null hypothesis when the effect exists.
Statisticians define two types of errors in hypothesis testing. Creatively, they call these errors Type I and Type II errors. Both types of error relate to incorrect conclusions about the null hypothesis.
The table summarizes the four possible outcomes for a hypothesis test.
|
|
| |
|
|
|
Related post : How Hypothesis Tests Work: P-values and the Significance Level
Fire alarm analogy for the types of errors

Using hypothesis tests correctly improves your chances of drawing trustworthy conclusions. However, errors are bound to occur.
Unlike the fire alarm analogy, there is no sure way to determine whether an error occurred after you perform a hypothesis test. Typically, a clearer picture develops over time as other researchers conduct similar studies and an overall pattern of results appears. Seeing how your results fit in with similar studies is a crucial step in assessing your study’s findings.
Now, let’s take a look at each type of error in more depth.
Type I Error: False Positives
When you see a p-value that is less than your significance level , you get excited because your results are statistically significant. However, it could be a type I error . The supposed effect might not exist in the population. Again, there is usually no warning when this occurs.
Why do these errors occur? It comes down to sample error. Your random sample has overestimated the effect by chance. It was the luck of the draw. This type of error doesn’t indicate that the researchers did anything wrong. The experimental design, data collection, data validity , and statistical analysis can all be correct, and yet this type of error still occurs.
Even though we don’t know for sure which studies have false positive results, we do know their rate of occurrence. The rate of occurrence for Type I errors equals the significance level of the hypothesis test, which is also known as alpha (α).
The significance level is an evidentiary standard that you set to determine whether your sample data are strong enough to reject the null hypothesis. Hypothesis tests define that standard using the probability of rejecting a null hypothesis that is actually true. You set this value based on your willingness to risk a false positive.
Related post : How to Interpret P-values Correctly
Using the significance level to set the Type I error rate
When the significance level is 0.05 and the null hypothesis is true, there is a 5% chance that the test will reject the null hypothesis incorrectly. If you set alpha to 0.01, there is a 1% of a false positive. If 5% is good, then 1% seems even better, right? As you’ll see, there is a tradeoff between Type I and Type II errors. If you hold everything else constant, as you reduce the chance for a false positive, you increase the opportunity for a false negative.
Type I errors are relatively straightforward. The math is beyond the scope of this article, but statisticians designed hypothesis tests to incorporate everything that affects this error rate so that you can specify it for your studies. As long as your experimental design is sound, you collect valid data, and the data satisfy the assumptions of the hypothesis test, the Type I error rate equals the significance level that you specify. However, if there is a problem in one of those areas, it can affect the false positive rate.
Warning about a potential misinterpretation of Type I errors and the Significance Level
When the null hypothesis is correct for the population, the probability that a test produces a false positive equals the significance level. However, when you look at a statistically significant test result, you cannot state that there is a 5% chance that it represents a false positive.
Why is that the case? Imagine that we perform 100 studies on a population where the null hypothesis is true. If we use a significance level of 0.05, we’d expect that five of the studies will produce statistically significant results—false positives. Afterward, when we go to look at those significant studies, what is the probability that each one is a false positive? Not 5 percent but 100%!
That scenario also illustrates a point that I made earlier. The true picture becomes more evident after repeated experimentation. Given the pattern of results that are predominantly not significant, it is unlikely that an effect exists in the population.
Type II Error: False Negatives
When you perform a hypothesis test and your p-value is greater than your significance level, your results are not statistically significant. That’s disappointing because your sample provides insufficient evidence for concluding that the effect you’re studying exists in the population. However, there is a chance that the effect is present in the population even though the test results don’t support it. If that’s the case, you’ve just experienced a Type II error . The probability of making a Type II error is known as beta (β).
What causes Type II errors? Whereas Type I errors are caused by one thing, sample error, there are a host of possible reasons for Type II errors—small effect sizes, small sample sizes, and high data variability. Furthermore, unlike Type I errors, you can’t set the Type II error rate for your analysis. Instead, the best that you can do is estimate it before you begin your study by approximating properties of the alternative hypothesis that you’re studying. When you do this type of estimation, it’s called power analysis.
To estimate the Type II error rate, you create a hypothetical probability distribution that represents the properties of a true alternative hypothesis. However, when you’re performing a hypothesis test, you typically don’t know which hypothesis is true, much less the specific properties of the distribution for the alternative hypothesis. Consequently, the true Type II error rate is usually unknown!
Type II errors and the power of the analysis
The Type II error rate (beta) is the probability of a false negative. Therefore, the inverse of Type II errors is the probability of correctly detecting an effect. Statisticians refer to this concept as the power of a hypothesis test. Consequently, 1 – β = the statistical power. Analysts typically estimate power rather than beta directly.
If you read my post about power and sample size analysis , you know that the three factors that affect power are sample size, variability in the population, and the effect size. As you design your experiment, you can enter estimates of these three factors into statistical software and it calculates the estimated power for your test.
Suppose you perform a power analysis for an upcoming study and calculate an estimated power of 90%. For this study, the estimated Type II error rate is 10% (1 – 0.9). Keep in mind that variability and effect size are based on estimates and guesses. Consequently, power and the Type II error rate are just estimates rather than something you set directly. These estimates are only as good as the inputs into your power analysis.
Low variability and larger effect sizes decrease the Type II error rate, which increases the statistical power. However, researchers usually have less control over those aspects of a hypothesis test. Typically, researchers have the most control over sample size, making it the critical way to manage your Type II error rate. Holding everything else constant, increasing the sample size reduces the Type II error rate and increases power.
Learn more about Power in Statistics .
Graphing Type I and Type II Errors
The graph below illustrates the two types of errors using two sampling distributions. The critical region line represents the point at which you reject or fail to reject the null hypothesis. Of course, when you perform the hypothesis test, you don’t know which hypothesis is correct. And, the properties of the distribution for the alternative hypothesis are usually unknown. However, use this graph to understand the general nature of these errors and how they are related.

The distribution on the left represents the null hypothesis. If the null hypothesis is true, you only need to worry about Type I errors, which is the shaded portion of the null hypothesis distribution. The rest of the null distribution represents the correct decision of failing to reject the null.
On the other hand, if the alternative hypothesis is true, you need to worry about Type II errors. The shaded region on the alternative hypothesis distribution represents the Type II error rate. The rest of the alternative distribution represents the probability of correctly detecting an effect—power.
Moving the critical value line is equivalent to changing the significance level. If you move the line to the left, you’re increasing the significance level (e.g., α 0.05 to 0.10). Holding everything else constant, this adjustment increases the Type I error rate while reducing the Type II error rate. Moving the line to the right reduces the significance level (e.g., α 0.05 to 0.01), which decreases the Type I error rate but increases the type II error rate.
Is One Error Worse Than the Other?
As you’ve seen, the nature of the two types of error, their causes, and the certainty of their rates of occurrence are all very different.
A common question is whether one type of error is worse than the other? Statisticians designed hypothesis tests to control Type I errors while Type II errors are much less defined. Consequently, many statisticians state that it is better to fail to detect an effect when it exists than it is to conclude an effect exists when it doesn’t. That is to say, there is a tendency to assume that Type I errors are worse.
However, reality is more complex than that. You should carefully consider the consequences of each type of error for your specific test.
Suppose you are assessing the strength of a new jet engine part that is under consideration. Peoples lives are riding on the part’s strength. A false negative in this scenario merely means that the part is strong enough but the test fails to detect it. This situation does not put anyone’s life at risk. On the other hand, Type I errors are worse in this situation because they indicate the part is strong enough when it is not.
Now suppose that the jet engine part is already in use but there are concerns about it failing. In this case, you want the test to be more sensitive to detecting problems even at the risk of false positives. Type II errors are worse in this scenario because the test fails to recognize the problem and leaves these problematic parts in use for longer.
Using hypothesis tests effectively requires that you understand their error rates. By setting the significance level and estimating your test’s power, you can manage both error rates so they meet your requirements.
The error rates in this post are all for individual tests. If you need to perform multiple comparisons, such as comparing group means in ANOVA, you’ll need to use post hoc tests to control the experiment-wise error rate or use the Bonferroni correction .
Share this:

Reader Interactions
June 4, 2024 at 2:04 pm
Very informative.
June 9, 2023 at 9:54 am
Hi Jim- I just signed up for your newsletter and this is my first question to you. I am not a statistician but work with them in my professional life as a QC consultant in biopharmaceutical development. I have a question about Type I and Type II errors in the realm of equivalence testing using two one sided difference testing (TOST). In a recent 2020 publication that I co-authored with a statistician, we stated that the probability of concluding non-equivalence when that is the truth, (which is the opposite of power, the probability of concluding equivalence when it is correct) is 1-2*alpha. This made sense to me because one uses a 90% confidence interval on a mean to evaluate whether the result is within established equivalence bounds with an alpha set to 0.05. However, it appears that specificity (1-alpha) is always the case as is power always being 1-beta. For equivalence testing the latter is 1-2*beta/2 but for specificity it stays as 1-alpha because only one of the null hypotheses in a two-sided test can fail at one time. I still see 1-2*alpha as making more sense as we show in Figure 3 of our paper which shows the white space under the distribution of the alternative hypothesis as 1-2 alpha. The paper can be downloaded as open access here if that would make my question more clear. https://bioprocessingjournal.com/index.php/article-downloads/890-vol-19-open-access-2020-defining-therapeutic-window-for-viral-vectors-a-statistical-framework-to-improve-consistency-in-assigning-product-dose-values I have consulted with other statistical colleagues and cannot get consensus so I would love your opinion and explanation! Thanks in advance!
June 10, 2023 at 1:00 am
Let me preface my response by saying that I’m not an expert in equivalence testing. But here’s my best guess about your question.
The alpha is for each of the hypothesis tests. Each one has a type I error rate of 0.05. Or, as you say, a specificity of 1-alpha. However, there are two tests so we need to consider the family-wise error rate. The formula is the following:
FWER = 1 – (1 – α)^N
Where N is the number of hypothesis tests.
For two tests, there’s a family-wise error rate of 0.0975. Or a family-wise specificity of 0.9025.
However, I believe they use 90% CI for a different reason (although it’s a very close match to the family-wise error rate). The 90% CI provides consistent results with the two one-side 95% tests. In other words, if the 90% CI is within the equivalency bounds, then the two tests will be significant. If the CI extends above the upper bound, the corresponding test won’t be significant. Etc.
However, using either rational, I’d say the overall type I error rate is about 0.1.
I hope that answers your question. And, again, I’m not an expert in this particular test.
July 18, 2022 at 5:15 am
Thank you for your valuable content. I have a question regarding correcting for multiple tests. My question is: for exactly how many tests should I correct in the scenario below?
Background: I’m testing for differences between groups A (patient group) and B (control group) in variable X. Variable X is a biological variable present in the body’s left and right side. Variable Y is a questionnaire for group A.
Step 1. Is there a significant difference within groups in the weight of left and right variable X? (I will conduct two paired sample t-tests)
If I find a significant difference in step 1, then I will conduct steps 2A and 2B. However, if I don’t find a significant difference in step 1, then I will only conduct step 2C.
Step 2A. Is there a significant difference between groups in left variable X? (I will conduct one independent sample t-test) Step 2B. Is there a significant difference between groups in right variable X? (I will conduct one independent sample t-test)
Step 2C. Is there a significant difference between groups in total variable X (left + right variable X)? (I will conduct one independent sample t-test)
If I find a significant difference in step 1, then I will conduct with steps 3A and 3B. However, if I don’t find a significant difference in step 1, then I will only conduct step 3C.
Step 3A. Is there a significant correlation between left variable X in group A and variable Y? (I will conduct Pearson correlation) Step 3B. Is there a significant correlation between right variable X in group A and variable Y? (I will conduct Pearson correlation)
Step 3C. Is there a significant correlation between total variable X in group A and variable Y? (I will conduct a Pearson correlation)
Regards, De
January 2, 2021 at 1:57 pm
I should say that being a budding statistician, this site seems to be pretty reliable. I have few doubts in here. It would be great if you can clarify it:
“A significance level of 0.05 indicates a 5% risk of concluding that a difference exists when there is no actual difference. ”
My understanding : When we say that the significance level is 0.05 then it means we are taking 5% risk to support alternate hypothesis even though there is no difference ?( I think i am not allowed to say Null is true, because null is assumed to be true/ Right)
January 2, 2021 at 6:48 pm
The sentence as I write it is correct. Here’s a simple way to understand it. Imagine you’re conducting a computer simulation where you control the population parameters and have the computer draw random samples from the populations that you define. Now, imagine you draw samples from two populations where the means and standard deviations are equal. You know this for a fact because you set the parameters yourself. Then you conduct a series of 2-sample t-tests.
In this example, you know the null hypothesis is correct. However, thanks to random sampling error, some proportion of the t-tests will have statistically significant results (i.e., false positives or Type I errors). The proportion of false positives will equal your significance level over the long run.
Of course, in real-world experiments, you never know for sure whether the null is true or not. However, given the properties of the hypothesis, you do know what proportion of tests will give you a false positive IF the null is true–and that’s the significance level.
I’m thinking through the wording of how you wrote it and I believe it is equivalent to what I wrote. If there is no difference (the null is true), then you have a 5% chance of incorrectly supporting the alternative. And, again, you’re correct that in the real world you don’t know for sure whether the null is true. But, you can still know the false positive (Type I) error rate. For more information about that property, read my post about how hypothesis tests work .
July 9, 2018 at 11:43 am
I like to use the analogy of a trial. The null hypothesis is that the defendant is innocent. A type I error would be convicting an innocent person and a type II error would be acquitting a guilty one. I like to think that our system makes a type I error very unlikely with the trade off being that a type II error is greater.
July 9, 2018 at 12:03 pm
Hi Doug, I think that is an excellent analogy on multiple levels. As you mention, a trial would set a high bar for the significance level by choosing a very low value for alpha. This helps prevent innocent people from being convicted (Type I error) but does increase the probability of allowing the guilty to go free (Type II error). I often refer to the significant level as a evidentiary standard with this legalistic analogy in mind.
Additionally, in the justice system in the U.S., there is a presumption of innocence and the prosecutor must present sufficient evidence to prove that the defendant is guilty. That’s just like in a hypothesis test where the assumption is that the null hypothesis is true and your sample must contain sufficient evidence to be able to reject the null hypothesis and suggest that the effect exists in the population.
This analogy even works for the similarities behind the phrases “Not guilty” and “Fail to reject the null hypothesis.” In both cases, you aren’t proving innocence or that the null hypothesis is true. When a defendant is “not guilty” it might be that the evidence was insufficient to convince the jury. In a hypothesis test, when you fail to reject the null hypothesis, it’s possible that an effect exists in the population but you have insufficient evidence to detect it. Perhaps the effect exists but the sample size or effect size is too small, or the variability might be too high.
Comments and Questions Cancel reply
Inferential Statistics for Hypothesis Testing
- First Online: 15 May 2020
Cite this chapter

- Ray W. Cooksey 2
1718 Accesses
3 Citations
This chapter discusses and illustrates inferential statistics for hypothesis testing. The procedures and fundamental concepts reviewed in this chapter can help to accomplish the following goals: (1) evaluate the statistical and practical significance of the difference between a specific statistic (e.g. a proportion, a mean, a regression weight, or a correlation coefficient) and its hypothesised value in the population; and/or (2) evaluate the statistical and practical significance of the difference between some combination of statistics (e.g. group means) and some combination of their corresponding population parameters. Such comparisons/tests may be relatively simple or multivariate in nature. In this chapter, you will explore various procedures (e.g. t- tests, analysis of variance, multiple regression, multivariate analysis of variance and covariance, discriminant analysis, logistic regression) that can be employed in different hypothesis testing situations and research designs to inform the judgments of significance. You will also learn that statistical significance is not the only way to address hypotheses—practical significance (e.g., effect size) is almost always relevant as well; in some cases, even more relevant. Finally, you will explore several fundamental concepts dealing with the logic of statistical inference, the general linear model, research design, sampling and, for complex designs, the concept of interaction.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Subscribe and save.
- Get 10 units per month
- Download Article/Chapter or eBook
- 1 Unit = 1 Article or 1 Chapter
- Cancel anytime
- Available as PDF
- Read on any device
- Instant download
- Own it forever
- Available as EPUB and PDF
- Compact, lightweight edition
- Dispatched in 3 to 5 business days
- Free shipping worldwide - see info
- Durable hardcover edition
Tax calculation will be finalised at checkout
Purchases are for personal use only
Institutional subscriptions
References for Fundamental Concept V
Cohen, J. (1988). Statistical power analysis for the behavioral sciences (2nd ed.). Hillsdale: Lawrence Erlbaum Associates.
MATH Google Scholar
Cohen, J., Cohen, P., West, S. G., & Aiken, L. S. (2003). Applied multiple regression/correlation analysis for the behavioral sciences (3rd ed.). Mahwah: Lawrence Erlbaum Associates. Ch. 1, 2.
Google Scholar
Field, A. (2018). Discovering statistics using SPSS for Windows (5th ed.). Los Angeles: Sage. Section 2.9.
Judd, C. M., McClelland, G. H., & Ryan, C. S. (2017). Data analysis: A model-comparison approach (3rd ed.). New York: Routledge. Ch. 4 onward.
Book Google Scholar
Paul, F., Erdfelder, E., Lang, A.-G., & Buchner, A. (2007). G∗Power 3: A flexible statistical power analysis program for the social, behavioral, and biomedical sciences. Behavior Research Methods, 39 (2), 175–191.
Article Google Scholar
Tabachnick, B. G., & Fidell, L. S. (2019). Using multivariate statistics (7th ed.). New York: Pearson Education. Ch. 4.
Useful Additional Reading for Fundamental Concept V
Argyrous, G. (2011). Statistics for research: with a guide to SPSS (3rd ed.). London: Sage. Ch. 14, 15, 27.
De Vaus, D. (2002). Analyzing social science data: 50 key problems in data analysis . Sage, London: . Ch. 23, 24, 25 and 39.
Glass, G. V., & Hopkins, K. D. (1996). Statistical methods in education and psychology (3rd ed.). Upper Saddle River: Pearson. Ch. 10–12.
Gravetter, F. J., & Wallnau, L. B. (2017). Statistics for the behavioural sciences (10th ed.). Belmont: Wadsworth Cengage. Ch. 7, 8.
Henkel, R. E. (1976). Tests of significance . Beverly Hills: Sage. Ch. 3.
Howell, D. C. (2013). Statistical methods for psychology (8th ed.). Belmont: Cengage Wadsworth. Ch. 4, 18.
Lewis-Beck, M. S. (1995). Data analysis: An introduction . Thousand Oaks: Sage.
Meyers, L. S., Gamst, G. C., & Guarino, A. (2017). Applied multivariate research: Design and interpretation (3rd ed.). Thousand Oaks: Sage. Ch. 2.
Mohr, L. B. (1990). Understanding significance testing . Newbury Park: Sage.
Steinberg, W. J. (2011). Statistics alive (2nd ed.). Los Angeles: Sage. Ch. 12–15, 19.
References for Fundamental Concept VI
Cohen, J., Cohen, P., West, S. G., & Aiken, L. S. (2003). Applied multiple regression/correlation analysis for the behavioral sciences (3rd ed.). Mahwah: Lawrence Erlbaum Associates. Ch. 8.
Judd, C. M., McClelland, G. H., & Ryan, C. S. (2017). Data analysis: A model-comparison approach (3rd ed.). New York: Routledge. Ch. 1.
Useful Additional Reading for for Fundamental Concept VI
Haase, R. F. (2011). Multivariate general linear models . Los Angeles: Sage.
Hardy, M. A. (1993). Regression with dummy variables . Los Angeles: Sage.
Hardy, M. A., & Reynolds, J. (2004). Incorporating categorical information into regression models: The utility of dummy variables. In M. Hardy & A. Bryman (Eds.), Handbook of data analysis (pp. 209–236). London: Sage.
Chapter Google Scholar
Miles, J., & Shevlin, M. (2001). Applying regression & correlation: A guide for students and researchers . Los Angeles: Sage. Ch. 1–3.
Pedhazur, E. J. (1997). Multiple regression in behavioral research: Explanation and prediction (3rd ed.). South Melbourne: Wadsworth Thomson Learning. Ch. 11.
Tabachnick, B. G., & Fidell, L. S. (2019). Using multivariate statistics (7th ed.). New York: Pearson Education. Ch. 18.
Vik, P. (2013). Regression, ANOVA and the general linear model: A statistics primer . Los Angeles: Sage.
References for Fundamental Concept VII
Campbell, D. T., & Stanley, J. C. (1966). Experimental and quasi-experimental designs for research . Boston: Houghton Mifflin.
Cook, T. D., & Campbell, D. T. (1979). Quasi-experimentation: Design and analysis issues for field settings . Chicago: Rand McNally.
Cooksey, R. W., & McDonald, G. (2019). Surviving and thriving in postgraduate research (2nd ed., pp. 653–654–676–677). Singapore,. Ch. 14, section 14.3.2: Springer.
Keppel, G., & Wickens, T. D. (2004). Design and analysis: A researcher’s handbook (4th ed.). Upper Saddle River: Prentice Hall. Ch. 1.
Kirk, R. E. (2013). Experimental design: Procedures for behavioral sciences (4th ed.). Thousand Oaks: Sage. Ch. 10 and 12.
Shadish, W. R., Cook, T. D., & Campbell, D. T. (2001). Experimental and quasi-experimental designs for generalized causal inference (2nd ed.). Boston: Cengage.
Useful Additional Reading for Fundamental Concept VII
Edmonds, W. E., & Kennedy, T. D. (2013). An applied reference guide to research designs: Quantitative, qualitative and mixed methods . Los Angeles: Sage. Ch. 1–8.
Jackson, S. L. (2012). Research methods and statistics: A critical thinking approach (4th ed.). Belmont: Wadsworth Cengage Learning. Ch. 9, 11–13.
Levin, I. P. (1999). Relating statistics and experimental design: An introduction . Thousand Oaks: Sage Publications.
Rosenthal, R., & Rosnow, R. L. (1991). Essentials of behavioral research: Methods and data analysis (2nd ed.). New York: McGraw-Hill. Ch. 4, 5, 6, 16 and 18.
Spector, P. (1981). Research designs . Beverly Hills: Sage.
References for Fundamental Concept VIII
Cooksey, R. W., & McDonald, G. (2019). Surviving and thriving in postgraduate research (2nd ed.). Singapore: Springer. Ch. 19.
Fink, A. (2002). How to sample in surveys (2nd ed.). Thousand Oaks: Sage.
Useful Additional Reading for Fundamental Concept VIII
Argyrous, G. (2011). Statistics for research: With a guide to SPSS (3rd ed.). London: Sage. Ch. 14.
De Vaus, D. (2002). Analyzing social science data: 50 key problems in data analysis . London: Sage. Ch. 20, 21, 22 and 26.
Fricker, R. D. (2008). Sampling methods for web and e-mail surveys. In N. Fielding, R. M. Lee, & G. Blank (Eds.), The Sage handbook of online research methods (pp. 195–217). London: Sage Publications.
Glass, G. V., & Hopkins, K. D. (1996). Statistical methods in education and psychology (3rd ed.). Upper Saddle River: Pearson. Ch. 10.
Kalton, G. (1983). Introduction to survey sampling . Beverly Hills: Sage.
Book MATH Google Scholar
Rosenthal, R., & Rosnow, R. L. (1991). Essentials of behavioral research: Methods and data analysis (2nd ed.). New York: McGraw-Hill. Ch. 10.
Scheaffer, R. L., Mendenhall, W., III, Ott, L., & Kerow, K. G. (2012). Elementary survey sampling (7th ed.). Boston: Brooks/Cole Cengage Learning.
Reference for Procedure 7.1
Everitt, B. S. (1992). The analysis of contingency tables (2nd ed.). London: Chapman & Hall. Ch. 3.
Useful Additional Reading for Procedure 7.1
Agresti, A. (2018). Statistical methods for the social sciences (5th ed.). Boston: Pearson. Ch. 8.
Allen, P., Bennett, K., & Heritage, B. (2019). SPSS statistics: A practical guide (4th ed.). South Melbourne: Cengage Learning Australia Pty. Ch. 17.
Argyrous, G. (2011). Statistics for research: With a guide to SPSS (3rd ed.). London: Sage. Ch. 23.
Field, A. (2018). Discovering statistics using SPSS for Windows (5th ed.). Los Angeles: Sage. Ch. 19, (Sections 19.1 to 19.3).
George, D., & Mallery, P. (2019). IBM SPSS statistics 25 step by step: A simple guide and reference (15th ed.). New York: Routledge. Ch. 8.
Hildebrand, D. K., Laing, J. D., & Rosenthal, H. (1977). The analysis of ordinal data . Beverly Hills: Sage.
Liebetrau, A. M. (1983). Measures of association . Beverly Hills: Sage.
Reynolds, H. T. (1984). Analysis of nominal data (2nd ed.). Beverly Hills: Sage.
Smithson, M. J. (2000). Statistics with confidence . London: Sage. Ch. 9.
Steinberg, W. J. (2011). Statistics alive (2nd ed.). Los Angeles: Sage. Ch. 31.
Reference for for Procedure 7.2
Field, A. (2018). Discovering statistics using SPSS for Windows (5th ed.). Los Angeles: Sage. Ch. 10 (sections 10.1 to 10.8 and 10.10).
Useful Additional Reading for Procedure 7.2
Allen, P., Bennett, K., & Heritage, B. (2019). SPSS statistics: A practical guide (4th ed.). South Melbourne: Cengage Learning Australia Pty. Ch. 5.
Argyrous, G. (2011). Statistics for research: With a guide to SPSS (3rd ed.). London: Sage. Ch. 18.
George, D., & Mallery, P. (2019). IBM SPSS statistics 25 step by step: A simple guide and reference (15th ed.). New York: Routledge. Ch. 11.
Glass, G. V., & Hopkins, K. D. (1996). Statistical methods in education and psychology (3rd ed.). Upper Saddle River: Pearson. Ch. 12.
Gravetter, F. J., & Wallnau, L. B. (2017). Statistics for the behavioural sciences (10th ed.). Belmont: Wadsworth Cengage. Ch. 10.
Howell, D. C. (2013). Statistical methods for psychology (8th ed.). Belmont: Cengage Wadsworth. Ch. 7.
Rosenthal, R., & Rosnow, R. L. (1991). Essentials of behavioral research: Methods and data analysis (2nd ed.). New York: McGraw-Hill. Ch. 15.
Steinberg, W. J. (2011). Statistics alive (2nd ed.). Los Angeles: Sage. Ch. 20–21, 23.
Reference for for Procedure 7.3
Siegel, S., & Castellan, N. J., Jr. (1988). Nonparametric statistics (2nd ed., pp. 128–137). New York: McGraw-Hill. Ch. 6.
Useful Additional Reading for Procedure 7.3
Argyrous, G. (2011). Statistics for research: With a guide to SPSS (3rd ed.). London: Sage. Ch. 25.
Corder, G. W., & Foreman, D. I. (2009). Nonparametric statistics for non-statisticians: A step-by-step approach . Hoboken: Wiley. Ch. 4.
Field, A. (2018). Discovering statistics using SPSS for Windows (5th ed.). Los Angeles: Sage. Ch. 7, Sections 7.1 to 7.4.
Gibbons, J. D. (1993). Nonparametric statistics: An introduction . Beverly Hills: Sage. Ch. 4.
Howell, D. C. (2013). Statistical methods for psychology (8th ed.). Belmont: Cengage Wadsworth. Ch. 18.
Neave, H. R., & Worthington, P. L. (1988). Distribution-free statistics . London: Unwin Hyman. Ch. 5, 6, and 7.
Reference for Procedure 7.4
Field, A. (2018). Discovering statistics using SPSS for Windows (5th ed.). Los Angeles: Sage. Ch. 10, Sections 10.9 to 10.11.
Useful Additional Reading for Procedure 7.4
Allen, P., Bennett, K., & Heritage, B. (2019). SPSS statistics: A practical guide (4th ed.). South Melbourne: Cengage Learning Australia Pty. Ch. 6.
Argyrous, G. (2011). Statistics for research: With a guide to SPSS (3rd ed.). London: Sage. Ch. 20.
Gravetter, F. J., & Wallnau, L. B. (2017). Statistics for the behavioural sciences (10th ed.). Belmont: Wadsworth Cengage. Ch. 11.
Steinberg, W. J. (2011). Statistics alive (2nd ed.). Los Angeles: Sage. Ch. 22.
Reference for Procedure 7.5
Siegel, S., & Castellan, N. J., Jr. (1988). Nonparametric statistics (2nd ed., pp. 87–95). New York,. Ch. 5: McGraw-Hill.
Useful Additional Reading for Procedure 7.5
Field, A. (2018). Discovering statistics using SPSS for Windows (5th ed.). Los Angeles: Sage. Ch. 6, Section 7.5.
Gibbons, J. D. (1993). Nonparametric statistics: An introduction . Beverly Hills: Sage. Ch. 3.
Neave, H. R., & Worthington, P. L. (1988). Distribution-free statistics . London: Unwin Hyman. Ch. 8.
References for Procedure 7.6
Field, A. (2018). Discovering statistics using SPSS for Windows (5th ed.). Los Angeles: Sage. Ch. 12.
Field, A., Miles, J., & Field, Z. (2012). Discovering statistics using R . London: Sage. Ch. 10.
Iversen, G. R., & Norpoth, H. (1987). Analysis of variance (2nd ed.). Newbury Park: Sage. Ch. 2 and 4.
Useful Additional Reading for Procedure 7.6
Allen, P., Bennett, K., & Heritage, B. (2019). SPSS statistics: A practical guide (4th ed.). South Melbourne: Cengage Learning Australia Pty. Ch. 7.
Argyrous, G. (2011). Statistics for research: With a guide to SPSS (3rd ed.). London: Sage. Ch. 19.
Everitt, B. S. (1995). Making sense of statistics in psychology: A second level course . Oxford: Oxford University Press. Ch. 3.
Glass, G. V., & Hopkins, K. D. (1996). Statistical methods in education and psychology (3rd ed.). Upper Saddle River: Pearson. Ch. 15.
Gravetter, F. J., & Wallnau, L. B. (2017). Statistics for the behavioural sciences (10th ed.). Belmont: Wadsworth Cengage. Ch. 12.
Howell, D. C. (2013). Statistical methods for psychology (8th ed.). Belmont: Cengage Wadsworth. Ch. 11.
Steinberg, W. J. (2011). Statistics alive (2nd ed.). Los Angeles: Sage. Ch. 24 and 25.
References for Procedure 7.7
Field, A. (2018). Discovering statistics using SPSS for Windows (5th ed.). Los Angeles: Sage. Ch. 12, Sections 12.10; see also ch. 7, sections 7.4.5, 7.5.5 and 7.6.7.
Hays, W. L. (1988). Statistics (3rd ed.). New York: Holt, Rinehart, & Winston. Ch. 8, pp. 306–313; Ch. 10, p. 369 and pp. 374–376.
Tabachnick, B. G., & Fidell, L. S. (2019). Using multivariate statistics (7th ed.). New York: Pearson Education. Ch. 3, Section 3.4.
Useful Additional Reading for Procedure 7.7
Cortina, J., & Nouri, H. (2000). Effect size for ANOVA designs . Thousand Oaks: Sage.
Keppel, G., & Wickens, T. D. (2004). Design and analysis: A researcher's handbook (4th ed.). Upper Saddle River: Prentice Hall. Ch. 8.
Rosenthal, R., & Rosnow, R. L. (1991). Essentials of behavioral research: Methods and data analysis (2nd ed.). New York: McGraw-Hill. Ch. 15, pp. 317–318; Ch. 16, pp. 351–352.
References for Procedure 7.8
Cohen, J., Cohen, P., West, S. G., & Aiken, L. S. (2003). Applied multiple regression/correlation analysis for the behavioral sciences (3rd ed.). Mahwah: Lawrence Erlbaum Associates. Ch. 6 and 8.
Keppel, G., & Wickens, T. D. (2004). Design and analysis: A researcher’s handbook (4th ed.). Upper Saddle River: Prentice Hall. Ch. 4, 5 and 6.
Klockars, A. (1986). Multiple comparisons . Beverly Hills: Sage.
Kirk, R. E. (2013). Experimental design: Procedures for behavioral sciences (4th ed.). Thousand Oaks: Sage. Ch. 4.
Toothaker, L. E. (1993). Multiple comparison procedures . Newbury Park: Sage.
Useful Additional Reading for Procedure 7.8
Field, A. (2018). Discovering statistics using SPSS for Windows (5th ed.). Los Angeles: Sage. Section 12.5 and 12.6.
Howell, D. C. (2013). Statistical methods for psychology (8th ed.). Belmont: Cengage Wadsworth. Ch. 12.
Rosenthal, R., & Rosnow, R. L. (1991). Essentials of behavioral research: Methods and data analysis (2nd ed.). New York: McGraw-Hill. Ch. 21.
Tabachnick, B. G., & Fidell, L. S. (2019). Using multivariate statistics (7th ed.). New York: Pearson Education. Ch. 3.
References for Procedure 7.9
Field, A. (2018). Discovering statistics using SPSS for Windows (5th ed.). Los Angeles: Sage. Section 7.6.
Field, A., Miles, J., & Field, Z. (2012). Discovering statistics using R (pp. 674–686). London,. Ch. 15: Sage.
Siegel, S., & Castellan, N. J., Jr. (1988). Nonparametric statistics (2nd ed.). New York: McGraw-Hill. Ch. 8, which also discusses multiple comparison methods.
Useful Additional Reading for Procedure 7.9
Gibbons, J. D. (1993). Nonparametric statistics: An introduction . Beverly Hills: Sage.
Neave, H. R., & Worthington, P. L. (1988). Distribution-free statistics . London: Unwin Hyman. Ch. 13, which also discusses multiple comparison methods.
References for Procedure 7.10
Cohen, J., Cohen, P., West, S. G., & Aiken, L. S. (2003). Applied multiple regression/correlation analysis for the behavioral sciences (3rd ed.). Mahwah: Lawrence Erlbaum Associates. Ch. 5, 6, 8 and 9.
Cooksey, R. W., & McDonald, G. (2019). Surviving and thriving in postgraduate research (2nd ed.). Singapore: Springer. Ch. 14, section 14.3.2 and pp. 676–677.
Field, A. (2018). Discovering statistics using SPSS for Windows (5th ed.). Los Angeles: Sage. Ch. 14.
Field, A., Miles, J., & Field, Z. (2012). Discovering statistics using R . London: Sage. Ch. 12.
Judd, C. M., McClelland, G. H., & Ryan, C. S. (2017). Data analysis: A model-comparison approach (3rd ed.). New York: Routledge. Ch. 9.
Keppel, G., & Wickens, T. D. (2004). Design and analysis: A researcher’s handbook (4th ed.). Upper Saddle River: Prentice Hall. Ch. 10, 11, 12, 13, 14, 21, 22, 25 and 26.
Kirk, R. E. (2013). Experimental design: Procedures for behavioral sciences (4th ed.). Thousand Oaks: Sage. Ch. 6, 9, 10 and 11.
Useful Additional Reading for Procedure 7.10
Allen, P., Bennett, K., & Heritage, B. (2019). SPSS statistics: A practical guide (4th ed.). South Melbourne: Cengage Learning Australia Pty. Ch. 8.
Brown, S. R., & Melamed, L. E. (1990). Experimental design and analysis . Newbury Park: Sage.
Gravetter, F. J., & Wallnau, L. B. (2017). Statistics for the behavioural sciences (10th ed.). Belmont: Wadsworth Cengage. Ch. 14.
Howell, D. C. (2013). Statistical methods for psychology (8th ed.). Belmont: Cengage Wadsworth. Ch. 13.
Rosenthal, R., & Rosnow, R. L. (1991). Essentials of behavioral research: Methods and data analysis (2nd ed.). New York: McGraw-Hill. Ch. 16 and 17.
References for Fundamental Concept IX
Cohen, J., Cohen, P., West, S. G., & Aiken, L. S. (2003). Applied multiple regression/correlation analysis for the behavioral sciences (3rd ed.). Mahwah: Lawrence Erlbaum Associates. Ch. 9.
Hayes, A. F. (2018). Introduction to mediation, moderation and conditional process analysis: A regression-based approach (3rd ed.). New York: The Guilford Press. Ch. 7.
Keppel, G., & Wickens, T. D. (2004). Design and analysis: A researcher’s handbook (4th ed.). Upper Saddle River: Prentice Hall. Ch. 12 and 13.
Kirk, R. E. (2013). Experimental design: Procedures for behavioral sciences (4th ed.). Thousand Oaks: Sage. Ch. 9.
Miles, J., & Shevlin, M. (2001). Applying regression & correlation: A guide for students and researchers . Los Angeles: Sage. Ch. 7.
Useful Additional Reading for Fundamental Concept IX
Field, A. (2018). Discovering statistics using SPSS for Windows (5th ed.). Los Angeles: Sage. Sections 14.6 and 14.7.
Jaccard, J. (1997). Interaction effects in factorial analysis of variance . Thousand Oaks: Sage.
Jaccard, J., & Turrisi, R. (2003). Interaction effects in multiple regression (2nd ed.). Thousand Oaks: Sage.
Jose, P. E. (2013). Doing statistical mediation and moderation . New York: The Guilford Press.
Judd, C. M., McClelland, G. H., & Ryan, C. S. (2017). Data analysis: A model-comparison approach (3rd ed.). New York: Routledge. Ch. 7, 9.
Majoribanks, K. M. (1997). Interaction, detection, and its effects. In J. P. Keeves (Ed.), Educational research, methodology, and measurement: An international handbook (2nd ed., pp. 561–571). Oxford: Pergamon Press.
Pedhazur, E. J. (1997). Multiple regression in behavioral research: Explanation and prediction (3rd ed.). South Melbourne: Wadsworth Thomson Learning. Ch. 12.
Rosenthal, R., & Rosnow, R. L. (1991). Essentials of behavioral research: Methods and data analysis (2nd ed.). New York: McGraw-Hill. Ch. 17.
Vik, P. (2013). Regression, ANOVA and the General Linear Model: A statistics primer . Los Angeles: Sage. Ch. 10 and 12.
References for Procedure 7.11
Field, A. (2018). Discovering statistics using SPSS for Windows (5th ed.). Los Angeles: Sage. Ch. 15 and 16.
Keppel, G., & Wickens, T. D. (2004). Design and analysis: A researcher’s handbook (4th ed.). Upper Saddle River: Prentice Hall. Ch. 16–20, 23.
Tabachnick, B. G., & Fidell, L. S. (2019). Using multivariate statistics (7th ed.). New York: Pearson Education. Ch. 8.
Polhemus, N. W. (2006). How to: Analyze a repeated measures experiment using STATGRAPHICS Centurion . Document downloaded from http://cdn2.hubspot.net/hubfs/402067/PDFs/How_To_Analyze_a_Repeated_Measures_Experiment.pdf . Accessed 1 Oct 2019.
Useful Additional Reading for Procedure 7.11
Allen, P., Bennett, K., & Heritage, B. (2019). SPSS statistics: A practical guide (4th ed.). South Melbourne: Cengage Learning Australia Pty. Ch. 9.
Cohen, J., Cohen, P., West, S. G., & Aiken, L. S. (2003). Applied multiple regression/correlation analysis for the behavioral sciences (3rd ed.). Mahwah: Lawrence Erlbaum Associates. Ch. 15.
Girden, E. R. (1992). ANOVA repeated measures . Newbury Park: Sage.
Grimm, L. G., & Yarnold, P. R. (Eds.). (2000). Reading and understanding more multivariate statistics . Washington, DC: American Psychological Association (APA). Ch. 10.
Howell, D. C. (2013). Statistical methods for psychology (8th ed.). Belmont: Cengage Wadsworth. Ch. 14.
Judd, C. M., McClelland, G. H., & Ryan, C. S. (2017). Data analysis: A model-comparison approach (3rd ed.). New York: Routledge. Ch. 11.
Rosenthal, R., & Rosnow, R. L. (1991). Essentials of behavioral research: Methods and data analysis (2nd ed.). New York: McGraw-Hill. Ch. 18.
References for Procedure 7.12
Field, A. (2018). Discovering statistics using SPSS for Windows (5th ed.). Los Angeles: Sage. Section 7.7.
Field, A., Miles, J., & Field, Z. (2012). Discovering statistics using R (pp. 686–692). London,. Ch. 15: Sage.
Siegel, S., & Castellan, N. J., Jr. (1988). Nonparametric statistics (2nd ed.). New York: McGraw-Hill. Ch. 7, which also discusses multiple comparison methods.
Useful Additional Reading for Procedure 7.12
Neave, H. R., & Worthington, P. L. (1988). Distribution-free statistics . London: Unwin Hyman. Ch. 14, which also discusses multiple comparison methods.
References for Procedure 7.13
Berry, W. (1993). Understanding regression assumptions . Beverly Hills: Sage.
Cohen, J., Cohen, P., West, S. G., & Aiken, L. S. (2003). Applied multiple regression/correlation analysis for the behavioral sciences (3rd ed.). Mahwah: Lawrence Erlbaum Associates. Ch. 3, 4, 5, 6–9, 10 provide comprehensive coverage of multiple regression concepts at a good conceptual and technical level].
Dunteman, G. (2005). Introduction to generalized linear models . Thousand Oaks: Sage.
Field, A. (2018). Discovering statistics using SPSS for Windows (5th ed.). Los Angeles: Sage. Ch. 6 and 9.
Field, A., Miles, J., & Field, Z. (2012). Discovering statistics using R . London: Sage. Ch. 7.
Fox, J. (1991). Regression diagnostics: An introduction . Beverly Hills: Sage.
Fox, J. (2000). Multiple and generalized nonparametric regression . Thousand Oaks: Sage.
Gill, J. (2000). Generalized linear models: A unified approach . Thousand Oaks: Sage.
Hair, J. F., Black, B., Babin, B., & Anderson, R. E. (2010). Multivariate data analysis: A global perspective (7th ed.). Upper Saddle River: Pearson Education. Ch. 4.
Judd, C. M., McClelland, G. H., & Ryan, C. S. (2017). Data analysis: A model-comparison approach (3rd ed.). New York: Routledge. Ch. 6.
Lewis-Beck, M. S. (1980). Applied regression: An introduction . Newbury Park: Sage.
Miles, J., & Shevlin, M. (2001). Applying regression & correlation: A guide for students and researchers . London: Sage. Ch. 2–7 provide comprehensive coverage of multiple regression concepts at a good conceptual level.
Pedhazur, E. J. (1997). Multiple regression in behavioral research: Explanation and prediction (3rd ed.). South Melbourne: Wadsworth Thomson Learning. Ch. 3, 5–15 provide comprehensive coverage of multiple regression concepts at a more technical level.
Useful Additional Reading for Procedure 7.13
Agresti, A. (2018). Statistical methods for the social sciences (5th ed.). Boston: Pearson. Ch. 12.
Allen, P., Bennett, K., & Heritage, B. (2019). SPSS statistics: A practical guide (4th ed.). South Melbourne: Cengage Learning Australia Pty. Ch. 13.
Darlington, R. B., & Hayes, A. F. (2017). Regression analysis and linear models: Concepts, applications, and implementation . New York: The Guilford Press.
Grimm, L. G., & Yarnold, P. R. (1995). Reading and understanding multivariate statistics . Washington, DC: American Psychological Association. Ch. 2.
Hardy, M. (1993). Regression with dummy variables . Thousand Oaks: Sage.
Howell, D. C. (2013). Statistical methods for psychology (8th ed.). Belmont: Cengage Wadsworth. Ch. 15.
George, D., & Mallery, P. (2019). IBM SPSS statistics 25 step by step: A simple guide and reference (15th ed.). New York: Routledge. Ch. 16 and 28.
Meyers, L. S., Gamst, G. C., & Guarino, A. (2017). Applied multivariate research: Design and interpretation (3rd ed.). Thousand Oaks: Sage. Ch. 5A, 5B, 6A, 6B.
Schroeder, L. D., Sjoquist, D. L., & Stephan, P. E. (1986). Understanding regression analysis: An introductory guide . Beverly Hills: Sage.
Tabachnick, B. G., & Fidell, L. S. (2019). Using multivariate statistics (7th ed.). New York: Pearson Education. Ch. 5.
References for Procedure 7.14
Cohen, J., Cohen, P., West, S. G., & Aiken, L. S. (2003). Applied multiple regression/correlation analysis for the behavioral sciences (3rd ed.). Mahwah: Lawrence Erlbaum Associates. Ch. 13.
Everitt, B. S., & Hothorn, T. (2006). A handbook of statistical analyses using R . Boca Raton: Chapman & Hall/CRC.
Field, A. (2018). Discovering statistics using SPSS for Windows (5th ed.). Los Angeles: Sage. Ch. 20.
Miles, J., & Shevlin, M. (2001). Applying regression & correlation: A guide for students and researchers . London: Sage. Ch. 6.
Pedhazur, E. J. (1997). Multiple regression in behavioral research: Explanation and prediction (3rd ed.). South Melbourne: Wadsworth Thomson Learning. Ch. 17.
Tabachnick, B. G., & Fidell, L. S. (2019). Using multivariate statistics (7th ed.). New York: Pearson Education. Ch. 10.
Useful Additional Reading for Procedure 7.14
Agresti, A. (2018). Statistical methods for the social sciences (5th ed.). Boston: Pearson. Ch. 13.
Allen, P., Bennett, K., & Heritage, B. (2019). SPSS statistics: A practical guide (4th ed.). South Melbourne: Cengage Learning Australia Pty. Ch. 14.
Grimm, L. G., & Yarnold, P. R. (Eds.). (1995). Reading and understanding multivariate statistics . Washington, DC: American Psychological Association (APA). Ch. 7.
George, D., & Mallery, P. (2019). IBM SPSS statistics 25 step by step: A simple guide and reference (15th ed.). New York: Routledge. Ch. 25.
Hair, J. F., Black, B., Babin, B., & Anderson, R. E. (2010). Multivariate data analysis: A global perspective (7th ed.). Upper Saddle River: Pearson Education. Ch. 7.
Menard, S. (2002). Applied logistic regression analysis (2nd ed.). Thousand Oaks: Sage.
Meyers, L. S., Gamst, G. C., & Guarino, A. (2017). Applied multivariate research: Design and interpretation (3rd ed.). Thousand Oaks: Sage. Ch. 9A, 9B.
Pampel, F. (2000). Logistic regression: A primer . Thousand Oaks: Sage.
References for Procedure 7.15
Field, A. (2018). Discovering statistics using SPSS for Windows (5th ed.). Los Angeles: Sage. Ch. 13.
Field, A., Miles, J., & Field, Z. (2012). Discovering statistics using R . London: Sage. Ch. 11.
Tabachnick, B. G., & Fidell, L. S. (2019). Using multivariate statistics (7th ed.). New York: Pearson Education. Ch. 6.
Wildt, A. R., & Ahtola, O. T. (1978). Analysis of covariance . Beverly Hills: Sage.
Useful Additional Reading for Procedure 7.15
Allen, P., Bennett, K., & Heritage, B. (2019). SPSS statistics: A practical guide (4th ed.). South Melbourne: Cengage Learning Australia Pty. Ch. 10.
Judd, C. M., McClelland, G. H., & Ryan, C. S. (2017). Data analysis: A model-comparison approach (3rd ed.). New York: Routledge. Ch. 10.
Keppel, G., & Wickens, T. D. (2004). Design and analysis: A researcher’s handbook (4th ed.). Upper Saddle River: Prentice Hall. Ch. 15.
Kirk, R. E. (2013). Experimental design: Procedures for behavioral sciences (4th ed.). Thousand Oaks: Sage. Ch. 13.
Pedhazur, E. J. (1997). Multiple regression in behavioral research: Explanation and prediction (3rd ed.). South Melbourne: Wadsworth Thomson Learning. Ch. 15.
References for Procedure 7.16
Bray, J. H., & Maxwell, S. E. (1985). Multivariate analysis of variance . Beverly Hills: Sage.
Field, A. (2018). Discovering statistics using SPSS for Windows (5th ed.). Los Angeles: Sage. Ch. 17.
Field, A., Miles, J., & Field, Z. (2012). Discovering statistics using R . London: Sage. Ch. 16.
Hair, J. F., Black, B., Babin, B., & Anderson, R. E. (2010). Multivariate data analysis: A global perspective (7th ed.). Upper Saddle River: Pearson Education. Ch. 8.
Tabachnick, B. G., & Fidell, L. S. (2019). Using multivariate statistics (7th ed.). New York: Pearson Education. Ch. 7.
Useful Additional Reading for Procedure 7.16
Allen, P., Bennett, K., & Heritage, B. (2019). SPSS statistics: A practical guide (4th ed.). South Melbourne: Cengage Learning Australia Pty. Ch. 11.
George, D., & Mallery, P. (2019). IBM SPSS statistics 25 step by step: A simple guide and reference (15th ed.). New York: Routledge. Ch. 23.
Grimm, L. G., & Yarnold, P. R. (1995). Reading and understanding multivariate statistics . Washington, DC: American Psychological Association. Ch. 8.
Meyers, L. S., Gamst, G. C., & Guarino, A. (2017). Applied multivariate research: Design and interpretation (3rd ed.). Thousand Oaks: Sage. Ch. 18A, 18B.
References for Procedure 7.17
Huberty, C. J. (1984). Issues in the use and interpretation of discriminant analysis. Psychological Bulletin, 95 (1), 156–171.
Klecka, W. R. (1980). Discriminant analysis . Beverly Hills: Sage.
Tabachnick, B. G., & Fidell, L. S. (2019). Using multivariate statistics (7th ed.). New York: Pearson Education. Ch. 9.
Useful Additional Reading for Procedure 7.17
Field, A. (2018). Discovering statistics using SPSS for Windows (5th ed.). Los Angeles: Sage. Sections 17.9 to 17.11.
George, D., & Mallery, P. (2019). IBM SPSS statistics 25 step by step: A simple guide and reference (15th ed.). New York: Routledge. Ch. 22.
Grimm, L. G., & Yarnold, P. R. (1995). Reading and understanding multivariate statistics . Washington, DC: American Psychological Association. Ch. 9.
Lohnes, P. R. (1997). Discriminant analysis. In J. P. Keeves (Ed.), Educational research, methodology, and measurement: An international handbook (2nd ed., pp. 503–508). Oxford: Pergamon Press.
Meyers, L. S., Gamst, G. C., & Guarino, A. (2017). Applied multivariate research: Design and interpretation (3rd ed.). Thousand Oaks: Sage. Ch. 19A, 19B.
References for Procedure 7.18
Anderton, D. L., & Cheney, E. (2004). Log-linear analysis. In M. Hardy & A. Bryman (Eds.), Handbook of data analysis (pp. 285–306). London: Sage.
Field, A., Miles, J., & Field, Z. (2012). Discovering statistics using R . London: Sage. Ch. 18.
Knoke, D., & Burke, P. J. (1980). Log-linear models . Beverly Hills: Sage.
Norušis, M. J. (2012). IBM SPSS Statistics 19: Advanced statistical procedures companion . Upper Saddle River: Prentice Hall. Ch. 1 and 2.
Tabachnick, B. G., & Fidell, L. S. (2019). Using multivariate statistics (7th ed.). New York: Pearson Education. Ch. 16.
Useful Additional Reading for Procedure 7.18
Everitt, B. S. (1977). The analysis of contingency tables . New York: Wiley. Ch. 5.
Field, A. (2018). Discovering statistics using SPSS for Windows (5th ed.). Los Angeles: Sage. Section 19.9 to 19.11.
George, D., & Mallery, P. (2019). IBM SPSS statistics 25 step by step: A simple guide and reference (15th ed.). New York: Routledge. Ch. 26 and 27.
Grimm, L. G., & Yarnold, P. R. (1995). Reading and understanding multivariate statistics . Washington, DC: American Psychological Association. Ch. 6.
Kennedy, J. J., & Tam, H. K. (1997). Log-linear models. In J. P. Keeves (Ed.), Educational research, methodology, and measurement: An international handbook (2nd ed., pp. 571–580). Oxford: Pergamon Press.
Download references
Author information
Authors and affiliations.
UNE Business School, University of New England, Armidale, NSW, Australia
Ray W. Cooksey
You can also search for this author in PubMed Google Scholar
Rights and permissions
Reprints and permissions
Copyright information
© 2020 Springer Nature Singapore Pte Ltd.
About this chapter
Cooksey, R.W. (2020). Inferential Statistics for Hypothesis Testing. In: Illustrating Statistical Procedures: Finding Meaning in Quantitative Data . Springer, Singapore. https://doi.org/10.1007/978-981-15-2537-7_7
Download citation
DOI : https://doi.org/10.1007/978-981-15-2537-7_7
Published : 15 May 2020
Publisher Name : Springer, Singapore
Print ISBN : 978-981-15-2536-0
Online ISBN : 978-981-15-2537-7
eBook Packages : Mathematics and Statistics Mathematics and Statistics (R0)
Share this chapter
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative
- Publish with us
Policies and ethics
- Find a journal
- Track your research
User Preferences
Content preview.
Arcu felis bibendum ut tristique et egestas quis:
- Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
- Duis aute irure dolor in reprehenderit in voluptate
- Excepteur sint occaecat cupidatat non proident
Keyboard Shortcuts
Statistical inference and estimation, review of introductory inference.
|
Sampling distribution & Central Limit Theorem Basic concepts of estimation: Review of Introductory Inference -test |
Statistical Inference, Model & Estimation
Recall, a statistical inference aims at learning characteristics of the population from a sample; the population characteristics are parameters and sample characteristics are statistics .
A statistical model is a representation of a complex phenomena that generated the data.
- It has mathematical formulations that describe relationships between random variables and parameters.
- It makes assumptions about the random variables, and sometimes parameters.
- A general form: data = model + residuals
- Model should explain most of the variation in the data
- Residuals are a representation of a lack-of-fit, that is of the portion of the data unexplained by the model.
Estimation represents ways or a process of learning and determining the population parameter based on the model fitted to the data.
Point estimation and interval estimation, and hypothesis testing are three main ways of learning about the population parameter from the sample statistic.
An estimator is particular example of a statistic, which becomes an estimate when the formula is replaced with actual observed sample values.
Point estimation = a single value that estimates the parameter. Point estimates are single values calculated from the sample
Confidence Intervals = gives a range of values for the parameter Interval estimates are intervals within which the parameter is expected to fall, with a certain degree of confidence.
Hypothesis tests = tests for a specific value(s) of the parameter.
In order to perform these inferential tasks, i.e., make inference about the unknown population parameter from the sample statistic, we need to know the likely values of the sample statistic. What would happen if we do sampling many times?
We need the sampling distribution of the statistic
- It depends on the model assumptions about the population distribution, and/or on the sample size.
- Standard error refers to the standard deviation of a sampling distribution.
| We are interested in estimating the true average height of the student population at Penn State. We collect a simple random sample of 54 students. Here is a graphical summary of that sample.
|
Central Limit Theorem
Sampling distribution of the sample mean:
If numerous samples of size n are taken, the frequency curve of the sample means ( \(\bar{X}\)‘s) from those various samples is approximately bell shaped with mean μ and standard deviation, i.e. standard error \(\bar{X}/ \sim N(\mu , \sigma^2 / n)\)
- X is normally distributed
- X is NOT normal, but n is large (e.g. n >30) and μ finite.
- For continuous variables
For categorical data, the CLT holds for the sampling distribution of the sample proportion.
Proportions in Newspapers
As found in CNN in June, 2006:
The parameter of interest in the population is the proportion of U.S. adults who disapprove of how well Bush is handling Iraq, p .
The sample statistic, or point estimator is \(\hat{p}\), and an estimate, based on this sample is \(\hat{p}=0.62\).
Next question ...
If we take another poll, we are likely to get a different sample proportion, e.g. 60%, 59%,67%, etc..
So, what is the 95% confidence interval? Based on the CLT, the 95% CI is \(\hat{p}\pm 2 \ast \sqrt{\frac{\hat{p}(1-\hat{p})}{n}}\).
We often assume p = 1/2 so \(\hat{p}\pm 2 \ast \sqrt{\frac{\frac{1}{2}\ast\frac{1}{2} }{n}}=\hat{p}\pm\frac{1}{\sqrt{n}}=\hat{p}\pm\text{MOE}\).
The margin of error (MOE) is 2 × St.Dev or \(1/\sqrt{n}\).
Module 8: Inference for One Proportion
Hypothesis testing (2 of 5), learning outcomes.
- Recognize the logic behind a hypothesis test and how it relates to the P-value.
In this section, our focus is hypothesis testing, which is part of inference. On the previous page, we practiced stating null and alternative hypotheses from a research question. Forming the hypotheses is the first step in a hypothesis test. Here are the general steps in the process of hypothesis testing. We will see that hypothesis testing is related to the thinking we did in Linking Probability to Statistical Inference .
Step 1: Determine the hypotheses.
The hypotheses come from the research question.
Step 2: Collect the data.
Ideally, we select a random sample from the population. The data comes from this sample. We calculate a statistic (a mean or a proportion) to summarize the data.
Step 3: Assess the evidence.
Assume that the null hypothesis is true. Could the data come from the population described by the null hypothesis? Use simulation or a mathematical model to examine the results from random samples selected from the population described by the null hypothesis. Figure out if results similar to the data are likely or unlikely. Note that the wording “likely or unlikely” implies that this step requires some kind of probability calculation.
Step 4: State a conclusion.
We use what we find in the previous step to make a decision. This step requires us to think in the following way. Remember that we assume that the null hypothesis is true. Then one of two outcomes can occur:
- One possibility is that results similar to the actual sample are extremely unlikely. This means that the data do not fit in with results from random samples selected from the population described by the null hypothesis. In this case, it is unlikely that the data came from this population, so we view this as strong evidence against the null hypothesis. We reject the null hypothesis in favor of the alternative hypothesis.
- The other possibility is that results similar to the actual sample are fairly likely (not unusual). This means that the data fit in with typical results from random samples selected from the population described by the null hypothesis. In this case, we do not have evidence against the null hypothesis, so we cannot reject it in favor of the alternative hypothesis.
Data Use on Smart Phones

According to an article by Andrew Berg (“Report: Teens Texting More, Using More Data,” Wireless Week , October 15, 2010), Nielsen Company analyzed cell phone usage for different age groups using cell phone bills and surveys. Nielsen found significant growth in data usage, particularly among teens, stating that “94 percent of teen subscribers self-identify as advanced data users, turning to their cellphones for messaging, Internet, multimedia, gaming, and other activities like downloads.” The study found that the mean cell phone data usage was 62 MB among teens ages 13 to 17. A researcher is curious whether cell phone data usage has increased for this age group since the original study was conducted. She plans to conduct a hypothesis test.
The null hypothesis is often a statement of “no change,” so the null hypothesis will state that there is no change in the mean cell phone data usage for this age group since the original study. In this case, the alternative hypothesis is that the mean has increased from 62 MB.
- H 0 : The mean data usage for teens with smart phones is still 62 MB.
- H a : The mean data usage for teens with smart phones is greater than 62 MB.
The next step is to obtain a sample and collect data that will allow the researcher to test the hypotheses. The sample must be representative of the population and, ideally, should be a random sample. In this case, the researcher must randomly sample teens who use smart phones.
For the purposes of this example, imagine that the researcher randomly samples 50 teens who use smart phones. She finds that the mean data usage for these teens was 75 MB with a standard deviation of 45 MB. Since it is greater than 62 MB, this sample mean provides some evidence in favor of the alternative hypothesis. But the researcher anticipates that samples will vary when the null hypothesis is true. So how much of a difference will make her doubt the null hypothesis? Does she have evidence strong enough to reject the null hypothesis?
To assess the evidence, the researcher needs to know how much variability to expect in random samples when the null hypothesis is true. She begins with the assumption that H 0 is true – in this case, that the mean data usage for teens is still 62 MB. She then determines how unusual the results of the sample are: If the mean for all teens with smart phones actually is 62 MB, what is the chance that a random sample of 50 teens will have a sample mean of 75 MB or higher? Obviously, this probability depends on how much variability there is in random samples of this size from this population.
The probability of observing a sample mean at least this high if the population mean is 62 MB is approximately 0.023 (later topics explain how to calculate this probability). The probability is quite small. It tells the researcher that if the population mean is actually 62 MB, a sample mean of 75 MB or higher will occur only about 2.3% of the time. This probability is called the P-value .
Note: The P-value is a conditional probability, discussed in the module Relationships in Categorical Data with Intro to Probability . The condition is the assumption that the null hypothesis is true.
Step 4: Conclusion.
The small P-value indicates that it is unlikely for a sample mean to be 75 MB or higher if the population has a mean of 62 MB. It is therefore unlikely that the data from these 50 teens came from a population with a mean of 62 MB. The evidence is strong enough to make the researcher doubt the null hypothesis, so she rejects the null hypothesis in favor of the alternative hypothesis. The researcher concludes that the mean data usage for teens with smart phones has increased since the original study. It is now greater than 62 MB. ( P = 0.023)
Notice that the P-value is included in the preceding conclusion, which is a common practice. It allows the reader to see the strength of the evidence used to draw the conclusion.
How Small Does the P-Value Have to Be to Reject the Null Hypothesis?
A small P-value indicates that it is unlikely that the actual sample data came from the population described by the null hypothesis. More specifically, a small P-value says that there is only a small chance that we will randomly select a sample with results at least as extreme as the data if H 0 is true. The smaller the P-value, the stronger the evidence against H 0 .
But how small does the P-value have to be in order to reject H 0 ?
In practice, we often compare the P-value to 0.05. We reject the null hypothesis in favor of the alternative if the P-value is less than (or equal to) 0.05.
Note: This means that sampling variability will produce results at least as extreme as the data 5% of the time. In other words, in the long run, 1 in 20 random samples will have results that suggest we should reject H 0 even when H 0 is true. This variability is just due to chance, but it is unusual enough that we are willing to say that results this rare suggest that H 0 is not true.
Statistical Significance: Another Way to Describe Unlikely Results
When the P-value is less than (or equal to) 0.05, we also say that the difference between the actual sample statistic and the assumed parameter value is statistically significant . In the previous example, the P-value is less than 0.05, so we say the difference between the sample mean (75 MB) and the assumed mean from the null hypothesis (62 MB) is statistically significant. You will also see this described as a significant difference . A significant difference is an observed difference that is too large to attribute to chance. In other words, it is a difference that is unlikely when we consider sampling variability alone. If the difference is statistically significant, we reject H 0 .
Other Observations about Stating Conclusions in a Hypothesis Test
In the example, the sample mean was greater than 62 MB. This fact alone does not suggest that the data supports the alternative hypothesis. We have to determine that the data is not only larger than 62 MB but larger than we would expect to see in a random sampling if the population mean is 62 MB. We therefore need to determine the P-value. If the sample mean was less than or equal to 62 MB, it would not support the alternative hypothesis. We don’t need to find a P-value in this case. The conclusion is clear without it.
We have to be very careful in how we state the conclusion. There are only two possibilities.
- We have enough evidence to reject the null hypothesis and support the alternative hypothesis.
- We do not have enough evidence to reject the null hypothesis, so there is not enough evidence to support the alternative hypothesis.
If the P-value in the previous example was greater than 0.05, then we would not have enough evidence to reject H 0 and accept H a . In this case our conclusion would be that “there is not enough evidence to show that the mean amount of data used by teens with smart phones has increased.” Notice that this conclusion answers the original research question. It focuses on the alternative hypothesis. It does not say “the null hypothesis is true.” We never accept the null hypothesis or state that it is true. When there is not enough evidence to reject H 0 , the conclusion will say, in essence, that “there is not enough evidence to support H a .” But of course we will state the conclusion in the specific context of the situation we are investigating.
We compared the P-value to 0.05 in the previous example. The number 0.05 is called the significance level for the test, because a P-value less than or equal to 0.05 is statistically significant (unlikely to have occurred solely by chance). The symbol we use for the significance level is α (the lowercase Greek letter alpha). We sometimes refer to the significance level as the α-level. We call this value the significance level because if the P-value is less than the significance level, we say the results of the test showed a significant difference.
If the P-value ≤ α, we reject the null hypothesis in favor of the alternative hypothesis.
If the P-value > α, we fail to reject the null hypothesis.
In practice, it is common to see 0.05 for the significance level. Occasionally, researchers use other significance levels. In particular, if rejecting H 0 will be controversial or expensive, we may require stronger evidence. In this case, a smaller significance level, such as 0.01, is used. As with the hypotheses, we should choose the significance level before collecting data. It is treated as an agreed-upon benchmark prior to conducting the hypothesis test. In this way, we can avoid arguments about the strength of the data. We will look more at how to choose the significance level later. On this page, we continue to use a significance level of 0.05.
First, work through the interactive exercise below to practice the four steps of hypothesis testing and related concepts and terms.
Next, let’s look at some exercises that focus on the P-value and its meaning. Then we’ll try some that cover the conclusion.
For many years, working full-time has meant working 40 hours per week. Nowadays, it seems that corporate employers expect their employees to work more than this amount. A researcher decides to investigate this hypothesis.
- H 0 : The average time full-time corporate employees work per week is 40 hours.
- H a : The average time full-time corporate employees work per week is more than 40 hours.
To substantiate his claim, the researcher randomly selects 250 corporate employees and finds that they work an average of 47 hours per week with a standard deviation of 3.2 hours.
According to the Centers for Disease Control (CDC), roughly 21.5% of all high school seniors in the United States have used marijuana. (The data were collected in 2002. The figure represents those who smoked during the month prior to the survey, so the actual figure might be higher.) A sociologist suspects that the rate among African American high school seniors is lower. In this case, then,
- H 0 : The rate of African American high-school seniors who have used marijuana is 21.5% (same as the overall rate of seniors).
- H a : The rate of African American high-school seniors who have used marijuana is lower than 21.5%.
To check his claim, the sociologist chooses a random sample of 375 African American high school seniors and finds that 16.5% of them have used marijuana.
Contribute!
Improve this page Learn More
- Interactive: Concepts in Statistics - Hypothesis Testing (2 of 5). Authored by : Deborah Devlin and Lumen Learning. Located at : https://lumenlearning.h5p.com/content/1291194018762009888 . License : CC BY: Attribution
- Concepts in Statistics. Provided by : Open Learning Initiative. Located at : http://oli.cmu.edu . License : CC BY: Attribution


IMAGES
VIDEO
COMMENTS
2. Statistical Hypotheses. A statistical hypothesis test has a null hypothesis, the status quo, what we assume to be true. Notation is H 0, read as "H naught". The alternative hypothesis is what you are trying to prove (mentioned in your research question), H 1 or H A. All hypothesis tests must include a null and an alternative hypothesis.
To bridge this gap, we develop a new statistical inference procedure for high-dimensional Hawkes processes. The key ingredient for the inference procedure is a new concentration inequality on the first- and second-order statistics for integrated stochastic processes, which summarize the entire history of the process.
instance of a multinomial distribution. The only simple statistical test, other than modeling, suggested for testing multinomial distributions is Pearson's Chi-Squared in a goodness of fit mode. The usual path recommended in education research textbooks to follow is thus: 1. Decide on a sampling statistic; Pearson's Chi-Squared in this case. 2.
Notes: The table reports the descriptive statistics of target children in the bottom 50% (column 1) and top 50% (column 2) of the predicted Conditional Average Treatment Effect (CATE) on the skills index. Column 3 reports the difference between column 1 and 2. Column 4 shows the p-value of the t-test adjusted for multiple hypothesis testing.
Statistical inference is the process of using a sample to infer the properties of a population. Statistical procedures use sample data to estimate the characteristics of the whole population from which the sample was drawn. Scientists typically want to learn about a population. When studying a phenomenon, such as the effects of a new medication ...
Present the findings in your results and discussion section. Though the specific details might vary, the procedure you will use when testing a hypothesis will always follow some version of these steps. Table of contents. Step 1: State your null and alternate hypothesis. Step 2: Collect data. Step 3: Perform a statistical test.
Hypothesis testing is a statistical method that is used to make a statistical decision using experimental data. Hypothesis testing is basically an assumption that we make about a population parameter. It evaluates two mutually exclusive statements about a population to determine which statement is best supported by the sample data.
Step 7: Based on Steps 5 and 6, draw a conclusion about H 0. If F calculated is larger than F α, then you are in the rejection region and you can reject the null hypothesis with ( 1 − α) level of confidence. Note that modern statistical software condenses Steps 6 and 7 by providing a p -value. The p -value here is the probability of getting ...
Hypothesis testing allows us to interpret or draw conclusions about the population using sample data. In a hypothesis test, we evaluate two mutually exclusive statements about a population to determine which statement is best supported by the sample data. The Null Hypothesis (H0) is a statement of no change and is assumed to be true unless ...
A statistical hypothesis test is a method of statistical inference used to decide whether the data sufficiently supports a particular hypothesis. A statistical hypothesis test typically involves a calculation of a test statistic. Then a decision is made, either by comparing the test statistic to a critical value or equivalently by evaluating a ...
Hypothesis testing is a crucial procedure to perform when you want to make inferences about a population using a random sample. These inferences include estimating population properties such as the mean, differences between means, proportions, and the relationships between variables. This post provides an overview of statistical hypothesis testing.
Statistical inference is defined as the process of analysing data and drawing conclusions based on random variation. Hypothesis testing and confidence intervals are two applications of statistical inference. Statistical inference is a technique that uses random sampling to make decisions about the parameters of a population.
hypothesis test is a binary question about the data distribution. Our goal is to either accept a null hypothesis H0 (which speci es something about this distribution) or to reject it in favor of an alternative hypothesis H1. If H0 (similarly H1) completely speci es the probability distribution for the data, then the hypothesis is simple.
Hypothesis testing is an integral part of statistical inference. It is used to decide whether the given sample data from the population parameter satisfies the given hypothetical condition. So, it will predict and decide using several factors whether the predictions satisfy the conditions or not.
Statistical inference is the process of analysing the result and making conclusions from data subject to random variation. It is also called inferential statistics. Hypothesis testing and confidence intervals are the applications of the statistical inference. Statistical inference is a method of making decisions about the parameters of a ...
The Four Steps in Hypothesis Testing. STEP 1: State the appropriate null and alternative hypotheses, Ho and Ha. STEP 2: Obtain a random sample, collect relevant data, and check whether the data meet the conditions under which the test can be used. If the conditions are met, summarize the data using a test statistic.
Steps in the Application of the Logic of Statistical Testing. Step 1. Determine the hypothesis-specific partition of the parameter space associated with the data generating process. How this is achieved depends on the substance and logic of the research being pursued and is not merely a question of statistics. Step 2.
HYPOTHESIS TESTING. A clinical trial begins with an assumption or belief, and then proceeds to either prove or disprove this assumption. In statistical terms, this belief or assumption is known as a hypothesis. Counterintuitively, what the researcher believes in (or is trying to prove) is called the "alternate" hypothesis, and the opposite ...
Hypothesis testing. Hypothesis testing is a formal process of statistical analysis using inferential statistics. The goal of hypothesis testing is to compare populations or assess relationships between variables using samples. Hypotheses, or predictions, are tested using statistical tests. Statistical tests also estimate sampling errors so that ...
Hypothesis plays a crucial role in that process, whether it may be making business decisions, in the health sector, academia, or in quality improvement. Without hypothesis & hypothesis tests, you risk drawing the wrong conclusions and making bad decisions. ... Hypothesis testing is a statistical method used to determine if there is enough ...
A hypothesis is any statement about an unknown aspect of a distribution. In a hypothesis test, we have two hypotheses: { H 0, the null hypothesis, and { H 1, the alternative hypothesis. Often a hypothesis is stated in terms of the value of one or more unknown parameters, in which case it is called a parametric hypothesis. Speci cally,
Ideally, a hypothesis test fails to reject the null hypothesis when the effect is not present in the population, and it rejects the null hypothesis when the effect exists. Statisticians define two types of errors in hypothesis testing. Creatively, they call these errors Type I and Type II errors.
Step 7: Based on steps 5 and 6, draw a conclusion about H0. If the F\calculated F \calculated from the data is larger than the Fα F α, then you are in the rejection region and you can reject the null hypothesis with (1 − α) ( 1 − α) level of confidence. Note that modern statistical software condenses steps 6 and 7 by providing a p p -value.
This chapter discusses and illustrates inferential statistics for hypothesis testing. The procedures and fundamental concepts reviewed in this chapter can help to accomplish the following goals: (1) evaluate the statistical and practical significance of the difference between a specific statistic (e.g. a proportion, a mean, a regression weight, or a correlation coefficient) and its ...
A statistical model is a representation of a complex phenomena that generated the data. It has mathematical formulations that describe relationships between random variables and parameters. It makes assumptions about the random variables, and sometimes parameters. Residuals are a representation of a lack-of-fit, that is of the portion of the ...
Here are the general steps in the process of hypothesis testing. We will see that hypothesis testing is related to the thinking we did in Linking Probability to Statistical Inference. Step 1: Determine the hypotheses. The hypotheses come from the research question. Step 2: Collect the data.
A statistical hypothesis is an assumption about a population parameter.. For example, we may assume that the mean height of a male in the U.S. is 70 inches. The assumption about the height is the statistical hypothesis and the true mean height of a male in the U.S. is the population parameter.. A hypothesis test is a formal statistical test we use to reject or fail to reject a statistical ...