phd thesis geophysics

Home > FACULTIES > Earth Sciences > GEOPHYSICS-ETD

Geophysics Theses and Dissertations

This collection contains theses and dissertations from the Department of Geophysics, collected from the Scholarship@Western Electronic Thesis and Dissertation Repository

Theses/Dissertations from 2024 2024

Development of a Regional Geodatabase and 3D Models of Metro Vancouver and Their Use and Impact to Regional Seismic Hazard Mapping , Sujan Raj Adhikari

Theses/Dissertations from 2023 2023

Observation and Modelling of Meter-Class Earth impacting Asteroids , David L. Clark

Evaluation of Effectiveness in Seismic Microzonation Hazard Mapping in Canada: Communication, Use, Standardization and Levels , Meredith L. Fyfe

Empirical nonlinear site response applicable to Greater Vancouver, British Columbia , Natalia Gomez Jaramillo

Probabilistic seismic liquefaction hazard mapping of western Metro Vancouver, British Columbia, Canada , Alireza Javanbakht Samani

Petrophysical Properties of the HED Meteorites and the Bushveld Igneous Complex: Implications for Future Asteroid Prospecting Missions , Lukas Louwerse

Probabilistic Tsunami Hazard Analysis of the Makran Region , Payam Momeni

Revealing the Core Dynamics of Vesta: Insights from Experimental Investigations of Electrical Resistivity and Thermal Conductivity , Oluwasanmi A. Orole Mr

Topographic Effects of Shallow Crustal Earthquakes in the Greater Vancouver Region , Alex Vanderhoeff

Theses/Dissertations from 2022 2022

Heat flow in terrestrial-type bodies from high P,T electrical resistivity measurements of Au, Fe-Si and Fe-Ni-Si solid and liquid alloys , Meryem Berrada

Approaches to model non-uniqueness and site complexity for non-invasive shear-wave depth profiling , Christopher Boucher

Testing Aftershock Forecasts Using Bayesian Methods , Elisa Dong

Using Craters to Study Carbon and Nitrogen Compounds on Icy Worlds , Joshua E. Hedgepeth

Geomechanical Modeling of a Fault During Fluid Injection , Charles KW Hulls

Examining κ, the high frequency spectral decay parameter, in Eastern Canada , Samantha M. Palmer

Oxygen Speciation in Potassium Silicate and Potassium Aluminosilicate Glasses: Insights From X-Ray Photoelectron Spectroscopy , Ryan Sawyer

Soil Amplification and Peak Frequencies from Thousands of Passive Seismic Measurements Across Metro Vancouver, British Columbia, Canada , Aamna A. Sirohey

Theses/Dissertations from 2021 2021

Investigation of the Energy Source for an Early Dynamo in Vesta from Experiments on Electrical Resistivity of Liquid Fe-10wt%Ni at High Pressures , Eric M. Lenhart

Heat Flow in the Core of Ganymede: High Pressure-Temperature Electrical Resistivity Measurements of Solid and Liquid Ag and Fe-S Alloys , Joshua A.H. Littleton

Stochastic Source Modelling and Tsunami Analysis of the 2012 Mw 7.8 Haida Gwaii Earthquake , Karina Martinez Alcala

Seismic Imaging in Crystalline Terrains of the Superior Province, Canada , Brian Villamizar

Time-and space-dependent earthquake rupture simulation for Nankai-Tonankai Trough in Japan incorporating multivariate Bernoulli method and stochastic slip models , Yusong Yang

Theses/Dissertations from 2020 2020

A Periglacial Landsystem Analysis in the Canadian High Arctic: A Tool for Planetary Geomorphology , Chimira Nicole Andres

Source Parameters of Induced Seismicity in North America , Joanna M. Holmgren

Earthquake site characterization of rock sites in Eastern Canada and stiff ground sites in Vancouver, British Columbia , Sameer Ladak

Physical Dispersions of Meteor Showers Through High Precision Optical Observations , Denis Vida

Raman Spectroscopy and Synchrotron X-ray Diffraction Study of Lunar and Terrestrial Plagioclase Feldspar at High-Pressure and High-Temperature Conditions , Tianqi Xie

Theses/Dissertations from 2019 2019

Statistical Modeling and Characterization of Induced Seismicity within the Western Canada Sedimentary Basin , Sid Kothari

Considering a Seismically Active Leech River Valley Fault Zone in Southwestern British Columbia , Jacob J. Kukovica

Theses/Dissertations from 2018 2018

Robust Earthquake Site Classification Assessment at Ontario Bridge Sites. , Alex Bilson Darko

Impact Craters on Titan: Finalizing Titan's Crater Population , Joshua E. Hedgepeth

Empirical Characterization of Induced Seismicity in Alberta and Oklahoma , Mark Novakovic

Evaluation of Raman Spectroscopic Geothermometry of Graphitic Carbon as a Mineral Exploration Tool. A Case Study of the San Sebastian Au-Ag Mine, Durango, Mexico , Justin Daniel Rumney

Electrical resistivity of nickel, iron and iron-silicon alloy melts at high pressure with implications for the thermal conductivity of the Earth’s core , Reynold E. Silber

Compositional Variations of Titan's Impact Craters Indicates Active Surface Erosion , Alyssa Werynski

Geomechanical Modelling of Induced Seismicity , Bodi Zhao

Theses/Dissertations from 2017 2017

Developing and Testing a Model of Site Amplification for Southern Ontario , Sebastian Braganza

Full-Waveform Inversion with Scaled-Sobolev Preconditioning Applied to Vibroseis Field Data , Benjamin Paul Consolvo

Experimental Studies of Electrical Resistivity Behavior of Cu, Zn and Co Along Their Melting Boundaries: Implications for Heat Flux at Earth’s Inner Core Boundary , Innocent Chinweikpe Ezenwa

The First Earthquake Site Assessments in Alberta, Canada , Joseph J. Farrugia

Using Bolide Airwaves To Estimate Meteoroid Source Characteristics And Window Damage Potential , Nayeob Gi

Petrophysical Investigations of the Marathon Cu-PGE Deposit, Marathon, ON , Hiruni Gunawardana

Assessment of Earthquake Site Amplification and Application of Passive Seismic Methods for Improved Site Classification in the Greater Vancouver Region, British Columbia , Frederick Andrew Jackson

A Comparison of Ground Motion Characteristics from Induced Seismic Events in Alberta with those in Oklahoma , Krista M. Kaski

Investigating the mechanism of deep-focus earthquakes via in-situ acoustic emission experiments on Fe2SiO4 at high temperature and pressure , Timothy Officer

New GPS Time Series Analysis and a Simplified Model to Compute an Accurate Seasonal Amplitude of Tropospheric Delay , Hadis Samadi Alinia

Time Series Analysis of Surface Deformation Associated With Fluid Injection and Induced Seismicity in Timpson, Texas Using DInSAR Methods , Simon Thorpe

Mitigating non-linearity in full waveform inversion using scaled-Sobolev norms , Mohammad Akbar Hosain Zuberi

Geophysical Study of Complex Meteorite Impact Structures , William Zylberman

Theses/Dissertations from 2016 2016

Anisotropic Waveform Tomography: Application to Crosshole data for Transversely Isotropic Media , Shaun Michael Hadden

Ground-Motion Prediction Equations for Central and Eastern North America, with Emphasis on Site Effects , Behzad Hassani

The Application of Geophysical Inversion Techniques to the Nechalacho Rare Earth Element Deposit, NT , Derek W. Kouhi

Using Physical and Social Sensors in Real-Time Data Streaming for Natural Hazard Monitoring and Response , Yelena Kropivnitskaya

Theses/Dissertations from 2015 2015

Characterizing Seismicity in Alberta for Induced-Seismicity Applications , Luqi Cui

High Pressure and High Temperature Study of Magnesiochromite and Its Geophysical Implications , N M Tauhid Belal Khan

Strength Study of Zircon Under High Pressure , Ievgeniia Morozova

Regionally-Adjustable Generic Ground-Motion Prediction Equation , Emrah Yenier

Theses/Dissertations from 2014 2014

Magnitude Estimation for Earthquake and Tsunami Early Warning Systems , Attieh Eshaghi

Seismicity Processes in the Charlevoix Seismic Zone, Eastern Canada , Azadeh Fereidoni

Statistical Analysis and Computer Modelling of Volcanic Eruptions , Laura Anabelle Sanchez

Theses/Dissertations from 2013 2013

Application of Differential and Polarimetric Synthetic Aperture Radar (SAR) Interferometry for Studying Natural Hazards , Samira Alipour

Variability in Characteristics of Ground Motions Across North America , Alireza Babaie Mahani

Spatial Heterogeneities in a Simple Earthquake Fault Model , Javad Kazemian

High Pressure- Temperature Electrical Resistivity Experiments on Fe-Si Alloys Bearing on Conductive Heat Flow at the Top of the Outer Core , Soushyant Kiarasi

Theses/Dissertations from 2012 2012

Estimating Subsurface Anisotropy: Combining Waveform Tomography and Simulated Annealing , Michael Victor Afanasiev

Technique Design To Increase In-Situ Electrical Connections In A Cubic Anvil Press , Marie April Burford

An investigation into earthquake ground motion characteristics in Japan with emphasis on the 2011 M9.0 Tohoku earthquake , Hadi Ghofrani

Studies of Aftershock Sequences of Large Subduction Zone Earthquakes , Armick Ivanian

Strategies for visco-acoustic waveform inversion in the Laplace-Fourier domain, with application to the Nankai subduction zone , Rie Kamei

Strength, Elasticity and Phase Transition Study on NaCl and MgO-NaCl Mixture to Mantle Pressures , Zhongying MI

Relationships between Earthquake Ground Motions and Modified Mercalli Intensity , Andrea Sweny

Theses/Dissertations from 2011 2011

Strategies for Waveform Tomography of Long-Offset, 2-D Exploration Seismic Data , Andrew J. Brenders

Ergodicity and seismicity clustering with applications in statistical seismology , Nelson Cho

Thermal Plume Transport From Sand and Gravel Pits Potential Thermal Impacts on Cool-Water Streams , Jeffrey M. Markle

• Accessible Formats

Advanced Search

• Notify me via email or RSS
• Expert Gallery
• Online Journals
• eBook Collections
• Reports and Working Papers
• Conferences and Symposiums
• Electronic Theses and Dissertations
• Digitized Special Collections
• All Collections
• Disciplines

Author Corner

• Submit Thesis/Dissertation

Home | About | FAQ | My Account | Accessibility Statement | Privacy | Copyright

©1878 - 2016 Western University

Skip to Content

Other ways to search:

• Events Calendar
• Geophysics Ph.D. Program

Once entered into the Geophysics Ph.D. Program, degree requirements explained below include course requirements, the Comprehensive Examination, and the dissertation defense.

Course Requirements

The geophysics Ph.D. course requirements, residency requirements, and the requirements for the Comprehensive Examination are formulated within the regulations of the  Graduate School . Students are referred to the document,  Graduate School Checklist for Graduation and Other Helpful Information , and the  University Catalog  for general information on requirements for the Ph.D. degree. In case of a conflict between those documents and the requirements stated here, the rules of the Graduate School apply.

A  core of graduate courses , included in the minimum of 30 semester hours required for all Ph.D.'s, is specified for students completing the Ph.D. in geophysics. This core coursework is designed to assure competency in appropriate subject matter at the Ph.D. level. The number of required courses is limited, so that the student is free to design an overall academic program that meets his or her needs in terms of specialized scholarly interests.

The required courses for the Geophysics Ph.D. include the following:

• A three-semester sequence of geophysics courses:  Earth and Planetary Physics I, II, and III  (course numbers 6610, 6620, and 6630, cross-listed in the Geology, Physics, and Astrophysical and Planetary Sciences Departments). These three courses do not have to be taken in any particular order. A student may petition the  Geophysics Program Committee  to substitute another course for one of these three core courses, but not for more than one.
• One semester of graduate-level applied mathematics selected from the list of  Approved Math Courses  on the Academics page. The student may petition the  Geophysics Program Committee  to substitute a comparable mathematics course for one of these courses. It is recommended, though not required, that students fulfill this requirement either before, or at the same time as, they take their first of the  three core Earth and Planetary Physics  courses.
• The student is also expected to take irregularly scheduled seminars on topics in solid earth geophysics, notably  ASTR/GEOL/PHYS 6650.  
• The student must take additional courses of his or her own choosing. The CU Graduate School requires a total of at least 30 semester credit hours. It is expected that the student, in consultation with his or her thesis advisor, will choose courses that are compatible with the student's research interests.  Possible additional courses  could include, but are not restricted to those listed on the  Academics  page. 

Comprehensive Examination

A research project, preferably involving original research, must be written up as a paper (comparable to publishable quality) and provided to the committee members 2 weeks before the oral examination, where the student will briefly present the paper and answer any questions the committee has. Such a research project may be in the student's proposed thesis area but could also be in an unrelated area of geophysics. There should be at least 2 faculty from the geophysics program on the exam committee (which, per Graduate School rules, must have 5 faculty members), the composition of which should be approved by the chair of the geophysics program. Preferably the chair of the committee will  not  be the student's research advisor. The oral exam can include basic questions of geophysics to test the student's understanding of fundamental concepts. It is recommended that geophysics students complete their comps exam before the end of their 5th semester.

The proposed exam tests both geophysics knowledge as well as research skills. 

By the time of the Comprehensive Examination, the student  has applied for and been admitted  to the Geophysics Program. Geophysics should be listed as the department on both the candidacy form and the examination report. 

Dissertation Defense

The public defense of the dissertation is conducted in the  usual way  by a committee of 5 or more faculty, as approved by the  geophysics program chair . The chair of the defense committee is normally the student's research advisor. Because the geophysics faculty is broadly interdisciplinary, the requirement that not all of the committee members for the defense be from one department is usually automatically satisfied.

If the student has a grievance that falls within the framework of the Program, every effort should be made to settle the difficulty by the discussion between the student and the faculty member or members directly involved. If such discussion fails to yield a resolution of the problem, the aggrieved student shall prepare a written statement describing the situation and present it to the Committee. The Committee shall meet with the student and the faculty members involved and shall render its decision on the appropriate resolution of the problem. If the student remains dissatisfied with the Committee's decision, he or she may file a formal complaint with the Dean of the Graduate School, who will involve the Graduate School's normal procedures for reaching a final resolution.

• Undergraduate Programs
• Graduate Courses
• Prospective Post Docs & Visiting Scientists

• Skip to Content
• Catalog Home
• Institution Home
• Programs A-Z
• Courses A-Z
• Academic Calendar

• Undergraduate
• General Information
• The Graduate School
• Admission to the Graduate School
• Student Life at Mines
• Registration and Tuition Classification
• Academic Regulations
• Tuition, Fees, Financial Assistance
• General Requirements
• Applied Mathematics &​ Statistics
• Chemical &​ Biological Engineering
• Civil &​ Environmental Engineering
• Computer Science
• Economics &​ Business
• Engineering, Design, &​ Society
• Electrical Engineering
• Geology &​ Geological Engineering
• Humanities, Arts, &​ Social Sciences
• Mechanical Engineering
• Metallurgical &​ Materials Engineering
• Mining Engineering
• Petroleum Engineering
• Interdisciplinary Graduate Programs
• Combined Undergraduate/​Graduate Degree Programs
• Directory of the School
• Policies &​ Procedures
• Previous Catalogs/​Bulletins
• Catalog Addendum
• Catalog Home /
• Departmental Graduate Programs /

Degrees Offered  

• Graduate Certificate (Energy Geophysics)
• Master of Science (Geophysics) (Non-Thesis)
• Master of Science (Geophysical Engineering) (Non-Thesis)
• Master of Science (Geophysics)
• Master of Science (Geophysical Engineering)
• Doctor of Philosophy (Geophysics)
• Doctor of Philosophy (Geophysical Engineering)

Program Description

Founded in 1926, the Department of Geophysics at Colorado School of Mines is recognized and respected around the world for its programs in applied geophysical research and education. Geophysics is a multidisciplinary field that blends geology, physics, mathematics, computer science, and electrical engineering. Professionals working in geophysics often come with training from programs in these allied disciplines, as well as from formal programs in geophysics.   

Geophysicists study and explore the interior of the Earth (and other planetary bodies) through physical measurements collected at its surface and in the subsurface, as well as remotely via airborne and satellite platforms. Using a combination of mathematical analyses based on data collected using a multitude of sensitive sensors, and insight into physical and chemical processes cast in the relevant geological contexts, geophysicists reveal the detailed structure of the Earth’s interior and explain a multitude of societally relevant natural processes. Noninvasive imaging beneath the surface of geologic bodies by geophysicists is directly analogous to noninvasive imaging of the human body by medical specialists.   

Earth supplies all the materials needed by our society, serves as the repository of used products, and provides a home to all its inhabitants. Geophysicists and geophysical engineers have important roles to play in solving challenging problems facing the inhabitants of the Earth, such as providing fresh water, food, and energy for its growing population, evaluating sites for underground construction and containment of hazardous waste, noninvasive monitoring of aging infrastructure (water and telecommunication conduits, transportation networks), mitigating the threat of geohazards to populated areas (earthquakes, volcanoes, landslides, avalanches), aid homeland security (through detection of underground activity and removal of unexploded ordnance or land mines), evaluating changes in climate and managing humankind’s response to them, as well as satisfying the human thirst for knowledge by exploring Earth and other planetary bodies.

Energy and mineral companies employ geophysicists to explore subsurface resources worldwide. Engineering firms hire geophysical engineers to assess Earth’s near-surface properties for large construction and infrastructure projects. Environmental organizations rely on geophysics to conduct groundwater surveys and to track the flow, distribution, and concentration of contaminants. Geophysicists employed by universities and government agencies (e.g., US Geological Survey or NASA), study dynamic Earth processes at all scales, from its deep interior to the oceans, ice sheets, and atmosphere.   

With 12 full-time faculty members and small class sizes, Geophysics students receive individualized attention in a close-knit environment. Given the multidisciplinary nature of geophysics, the graduate curriculum equips students with a broad skillset including applied mathematics and physics, geology, computing, and sensor engineering, in addition to theoretical and practical aspects of the geophysical field and laboratory methodologies.   

Geophysicists are highly sought-after, and for the past decade, 95% of Mines’ geophysics graduates found employment in their chosen field within six months of graduation.  

Research Emphasis  

The Department conducts research in a wide variety of areas that are mostly related, but not restricted, to applied geophysics. Candidates interested in the current research activities of specific faculty members are encouraged to visit the Department's website and to contact faculty members directly to gain insight into their scholarship . To give prospective candidates an idea of the types of research activities available in geophysics at Mines , a brief summary of research emphases and strengths in the Department is given below.

Discov ering E arth and other p lanet ary bodies . Earth is a dynamic planet evolving over geologic and human time scales . Using geophysical data and methods, the Department explore s Earth from its surface to its core  at all spatial and temporal scales . This broad perspective allows investigation of a wide range of topics including plate tectonics, natural hazards, mineral exploration, and ocean-atmosphere interactions . The Department also uses geophysical and computational approaches to study other planet-lik e bodies to better under stand the origin and evolution of the solar system and to explore space resources.  

S ec u r ing e nerg y and mineral resources . Affordable and abundant energy and minerals have facilitated and accelerated humankind’s growth and development . Responding to energy b alance chang es due to technolog ical advances and greater societal demands for sustainable resource use , the Depar tment 's teaching and research adapts rapidly to maintain its integral role in innovation for effective and responsib le access to Earth resources. T he Department is a leader in conventional and unconventional hydrocarbon resource evaluation, in exploration for essential critical minerals, as well as in underground carbon capture and st orag e . The Department approaches these societal challenges through theoretical advancements, the development of multi-physics techniques , as well as state-of-the-art data analysis and high-performance computing.  

Sustaining communities and the e n v ironment . Environmental assessment through geophysics is integral to humankind ’s interaction with the uppermost Earth crust , where humans live and develop thriving economies . The Department excels at advancing near-surface geophysics through theoretical and technological advancements, develop ment of low-cost instrumentation, working with communities to improve their understanding of environmental issues , and promoting society-informed science and communication. Active research in the Department includes projects related to freshwater resources, subsurface contamination, climate dynamics, and sustainable energy and minerals exploration.  

T hese research endeavors are supported through diverse funding sources includ ing US government agencies, international agencies/ universities , and industry. Research funding supports multiple research groups within the Department .   

Center for Wave Phenomena (CWP) focuses on seismic modeling, imaging, and inversion methods for realistic highly heterogeneous geologic structures through the development and application of high-performance computing and advancement of innovative technologies (e.g., r obotics and distributed acoustic sensing [ DAS ] ).  

Reservoir Characterization Project (RCP ) utilizes a unique research model emphasizing multidisciplinary, collaborative research integrating multicomponent time-lapse 3D seismic reflection data, downhole data, reservoir geology and production data, distributed acoustic sensing (DAS), machine learning, and compressive sensing to solve complex reservoir challenges and optimize reservoir development on active industry projects.  

Center for Gravity, Electrical & Magnetic St udies (CGEM) brings together diverse expertise t o quanti t atively interpret and integrate g ravity, magnetic, electrical and electromagnetic, as well as nuclear magnetic resonance data to advanc e geophysical data interpretation for real-world problems (e.g., mineral exploration , hydrogeophysics , geotechnical problems ) .  

Center for Rock and Fluid Multiphysics (CRFM ) uses advanced laboratory experimental techniques and machine learning to study fluid distributions in rocks and how these distributions affect characteristics such as wave attenuation, velocity dispersion, and seismic signature.  

Global and Computational Seismology Group uses high-performance computing for wave- propagation models and full-waveform inversion with data from Earth and other planetary bodies to investigate the composition and dynamics of planetary interiors, plate tectonics, and hazards related to earthquakes.  

Hydrogeology and Geomechanics Laboratory integrates data from laboratory and field experiments at various scales to inform process-based models of near-surface problems including coastal freshwater, contaminant plumes, geothermal systems, landslides, leakage in earth dams and embankments, and volcanic processes.  

Glaciology Laboratory uses satellite remote sensing techniques in combination with field-based and airborne geophysical methods to understand physical processes of Earth’s glaciers and ice sheets and to overcome the inherent difficulty of observing continent-scale ice masses that drive and react to other components of the Earth’s global climate system.  

Geophysical Oceanography Group combines high-resolution observations of winds, currents, and waves with theory and modeling to bridge the gap between the ocean and the atmosphere and further our understanding of how coupled air-sea interactions affect the environment including through wave dynamics and heat transfer.  

Professors Emeriti

Thomas L. Davis

Alexander A. Kaufman

Kenneth L. Larner

Gary R. Olhoeft

Phillip R. Romig, Jr.

Terence K. Young

Emeritus Associate Professor

Thomas M. Boyd

University Distinguished Professors

Kamini Singha

Ilya D. Tsvankin

John H. Bradford, Vice President for Global Initiatives

Brandon Dugan, Associate Department Head, Baker Hughes Chair of Petrophysics and Borehole Geophysics

Manika Prasad

Paul C. Sava, Department Head, C.H. Green Chair of Exploration Geophysics

Roelof K. Snieder, W.M. Keck Distinguished Professor of Professional Development Education

Associate Professors

Jeffrey C. Shragge

Assistant Professors

Eileen Martin

Matthew Siegfried

Bia Villas Bôas

Joint appointments with loci within Geophysics

Eileen Martin, Assistant Professor in Applied Mathematics and Statistics

Joint appointments with loci outside of Geophysics

Eric Anderson, Associate Professor, Civil and Environmental Engineering

Ebru Bozdag, Associate Professor, Applied Mathematics and Statistics

Elizabeth Reddy, Assistant Professor, Engineering, Design and Society

Danica Roth, Assistant Professor, Geology and Geological Engineering

Kamini Singha, Professor, Geology and Geological Engineering

Research Professor

Jeffrey Lee

Research Associate Professors

Richard Krahenbuhl

James L. Simmons

Adjunct Faculty

Jyoti Behura, Founder & CEO, Seismic Science LLC

Timothy Collett, Senior Scientist, US Geological Survey

Morgan Moschetti, Research Geophysicist, US Geological Survey

Ryan North, Principal Geophysicist, ISC Geoscience

Nathaniel Putzig, Senior Scientist, Planetary Science Institute

Affiliate Faculty

Andrei Swidinsky, Associate Professor, University of Toronto

Whitney Trainor-Guitton, Geoscience Researcher, National Renewable Energy Laboratory

David Wald, Research Geophysicist, US Geological Survey

Joint Appointments

Fred Day-Lewis, Chief Geophysicist, Pacific Northwest National Laboratory

Program Requirements

The Department offers both traditional, research-oriented graduate programs and a non-thesis professional education program designed to meet specific career objectives. The program of study is selected by the student, in consultation with an advisor, and with thesis committee approval, according to the student’s career needs and interests. Specific degrees have specific requirements as detailed below.

Geophysics and Geophysical Engineering Program Objectives

The principal objective for students pursuing the PhD degree in Geophysics or Geophysical Engineering is for Geophysics PhD graduates to be regarded by their employers as effective educators and/or innovative researchers in their early-career peer group. In support of this objective, the PhD programs in the Department of Geophysics are aimed at achieving these student outcomes:

• Graduates will command superior knowledge of Geophysics and fundamental related disciplines.
• Graduates will independently be able to conduct research leading to significant new knowledge and geophysical techniques.
• Graduates will be able to report their findings orally and in writing.

The chief objective for students pursuing the MS degree in Geophysics or Geophysical Engineering is for Geophysics MS graduates to be regarded by their employers as effective practitioners addressing earth, energy, and environmental problems with geophysical techniques. In support of this objective, the MS programs in the Department of Geophysics aim to achieve these student outcomes:

• Graduates will be able to conduct original research that results in new knowledge and geophysical techniques.

Master of Science Degrees (Non-Thesis): Geophysics and Geophysical Engineering

Students may obtain a Master of Science (MS) Degree (Non-Thesis) in either Geophysics or Geophysical Engineering, pursuant to the general and individual program requirements outlined below. 

For either Master of Science (Non-Thesis) degree, the minimum credits required include:

(1) The lists of pre-approved elective courses satisfying the Theory, Application, Computational and Earth & Space Coursework requirements may be found below.

The student and advisor determine individual courses constituting the degree. The courses applied to all MS degrees must satisfy the following specific criteria:

• The 30-credit hour minimum total must include 15 credit hours of GPGN-listed courses.
• A maximum of 6 credit hours of independent study may be counted toward the degree program.
• All course, transfer, residence, and thesis requirements are as described in Registration and Tuition Classification and Graduate Degrees and Requirements sections of the Catalog.
• Up to 6 credits of graduate level work may be double counted in the undergraduate and graduate degree for students enrolled in the Combined Degree.
• Up to 9 credits may be satisfied through 400 (senior) level coursework.  All remaining course credits applied to the degree must be at the 500 level or above.
• Additional courses may also be required by the student's advisor and committee to fulfill background requirements.

The coursework for the degree Master of Science, Geophysical Engineering, must meet the following specific requirements. Note that these requirements are in addition to those associated with the Master of Science in Geophysics.

• Students must complete, either prior to their arrival at Mines or while at Mines, no fewer than 16 credits of engineering coursework. What constitutes coursework considered as engineering is determined by the Geophysics faculty.

Computational Geophysics Track

The Computational Geophysics Track has the same requirements as the Geophysics Master's of Science (Non-Thesis) Degree program described above except that students are expected to choose coursework that satisfies a minimum of 15 credit hours, of which a minimum of 6 credits hours must be GPGN listed, from the list of pre-approved Computational Coursework electives may be found below.

Master of Science Degrees: Geophysics and Geophysical Engineering

Students may obtain a Master of Science (MS) Degree in either Geophysics or Geophysical Engineering, pursuant to the general and individual program requirements outlined below. 

For either Master of Science degree, the minimum credits required include:

(2) With the approval of the student's thesis committee, up to 4 additional GPGN707 research credits beyond the 6 GPGN707 credits required for the degree program can counted toward satisfying the Additional Coursework requirement.

The student and advisor, with approval from the thesis committee, determines individual courses constituting the degree.  The courses applied to all MS degrees must satisfy the following specific criteria:

• All course, research, transfer, residence, and thesis requirements are as described in Registration and Tuition Classification and Graduate Degrees and Requirements sections of the Catalog.
• Up to 6 credits of graduate level work may be double counted in the undergraduate and graduate degree for students enrolled in the Combined Degree.

The coursework and thesis topic for the degree Master of Science, Geophysical Engineering, must meet the following specific requirements. Note that these requirements are in addition to those associated with the Master of Science in Geophysics.

• The student’s dissertation topic must be appropriate for inclusion as part of an Engineering degree, as determined by the Geophysics faculty.

As described in the Master of Science, Thesis and Thesis Defense section of this Catalog, all MS candidates must successfully defend their MS thesis in a public oral Thesis Defense. The guidelines for the Thesis Defense enforced by the Department of Geophysics generally follow those outlined in in the Graduate Departments and Programs section of the Catalog, with one exception. The Department of Geophysics requires students submit the final draft of their written thesis to their thesis committee a minimum of three weeks prior to the thesis defense date.

Mines' Combined Undergraduate/Graduate Degree Program

Students enrolled in Mines’ combined undergraduate/graduate program may double count up to six credits of graduate coursework to fulfill requirements of both their undergraduate and graduate degree programs. These courses must have been passed with “B-” or better, not be substitutes for required coursework, and meet all other University, Department, and Program requirements for graduate credit.

Students are advised to consult with their undergraduate and graduate advisors for appropriate courses to double count upon admission to the combined program.

Doctor of Philosophy Degrees: Geophysics and Geophysical Engineering

We invite applications to our Doctor of Philosophy (PhD) program not only from those individuals with a background in geophysics, but also from those whose background is in allied disciplines such as geology, physics, mathematics, computer science, or electrical engineering.

Students may obtain a PhD Degree in either Geophysics or Geophysical Engineering, pursuant to the general and individual program requirements outlined below.  

For either PhD degree, at least 72 credits beyond the Bachelor's Degree are required.  Of that total, at least 24 research credits are required.  At least 12 course credits must be completed in a minor program of study, approved by the candidate's PhD thesis committee. Up to 36 course credits may be awarded by the candidate's committee for completion of a thesis-based Master's Degree. Graduate-level coursework completed as part of a thesis-based Master’s Degree with a focus on the Theory, Application, Computational or Earth & Space coursework may be used to satisfy the related theme with approval of the candidate’s committee.

While individual courses constituting the degree are determined by the student and approved by the student's advisor and committee, courses applied to all PhD degrees must satisfy the following criteria:

• The 72-credit hour minimum total must include 36 credit hours of GPGN-listed courses.
• All course, research, minor degree programs, transfer, residence, and thesis requirements are as described in Registration and Tuition Classification and Graduate Degrees and Requirements sections of the Catalog.
• Up to 9 credits may be satisfied through 400 (senior) level coursework. All remaining course credits applied to the degree must be at the 500 level or above.
• Students must include the following courses in their PhD program:

(1)  The lists of pre-approved elective courses satisfying the Theory, Application, Computational and Earth & Space Coursework requirements may be found below.

(2) With approval of the student's thesis committee, additional GPGN707 research credits beyond the 24 GPGN707 required for the degree program can counted toward satisfying the Additional Coursework requirement.

(3) The complementary coursework requirement may be satisfied by minor, graduate certificate, or set of courses that provide the spirit of minor or graduate certificate, as approved by the PhD Committee, the Geophysics Graduate Advisory Committee, and the Geophysics Department.

Additional courses may also be required by the student's advisor and committee to fulfill background requirements described below. The coursework and thesis topic for the degree Doctor of Philosophy, Geophysical Engineering, must meet the following additional requirements:

Students in both PhD programs are also required to participate in a practical teaching experience. This requirement must be fulfilled, within a single semester and course, under observation and evaluation by the course instructor of record, and include:

• Planning and delivery of a minimum of 6 lecture hours, or 4 lecture hours and 2 labs;
• Creating and evaluating students' homework and laboratory reports, if appropriate; and
• Holding office hours if necessary.

In both PhD programs, students must demonstrate the potential for successful completion of independent research and enhance the breadth of their expertise by completing a Doctoral Research Qualifying Examination not later than two years from the date of enrollment in the program. An extension of one additional year may be petitioned by students through their thesis committees.  In the Department of Geophysics, the Doctoral Research Qualifying Examination consists of the preparation, presentation, and defense of one research project and a thesis proposal. The research project and thesis proposal used in this process must conform to the standards posted on the Department of Geophysics website. As described in the Doctor of Philosophy Thesis Defense section of this catalog, all PhD candidates must successfully defend their PhD thesis in an open oral Thesis Defense. The guidelines for the Thesis Defense enforced by the Department of Geophysics follow those outlined in the Graduate Departments and Programs section of the Catalog, with one exception. The Department of Geophysics requires students submit the final draft of their written thesis to their thesis committee a minimum of three weeks prior to the thesis defense date.

Acceptable Thesis Formats

In addition to traditional dissertations, the Department of Geophysics also accepts dissertations that are compendia of papers published or submitted to peer-reviewed journals. Dissertations submitted in the latter format must adhere to the following guidelines.

• All papers included in the dissertation must have a common theme, as approved by a student’s thesis committee.
• Papers should be submitted for inclusion in a dissertation in a uniform format and typeset.
• In addition to the individual papers, students must prepare abstract, introduction, discussion, and conclusions sections of the thesis that tie together the individual papers into a unified dissertation.
• A student’s thesis committee might also require the preparation and inclusion of various appendices with the dissertation in support of the papers prepared explicitly for publication.

Graduate Program Background Requirements

All graduate programs in Geophysics require that applicants have a background that includes the equivalent of adequate undergraduate preparation in the following areas:

• Mathematics – Linear Algebra or Linear Systems, Differential Equations, and Computer Programming
• Physics – Classical Mechanics, and Electromagnetism
• Geology – Structural Geology and Stratigraphy
• Geophysics – Courses that include theory and application in three of the following areas: gravity/magnetics, seismology, electrical/electromagnetics, borehole geophysics, remote sensing, geodynamics, oceanography and fluid dynamics.
• Field and computational experience in the hands-on application or implementation of several geophysical methods
• In addition, candidates in the Doctoral program are required to have no less than one year of college-level or two years of high-school-level courses in a single foreign language, or be able to demonstrate fluency in at least one language other than English.

Theory, Application, Computational and Earth & Space Coursework Definitions

• Provides graduate-level foundation in geophysical theory while allowing flexibility based on interest and/or need.
•  Key Learning Outcome: Use  first principles of mathematics and physics to derive models that explain fundamental processes of the Earth and other planetary bodies.
• Application Coursework (pre-approved 500/600 level course electives)
• Provides graduate-level foundation in applied geophysics while allowing flexibility based on interest and/or need.
• Key Learning Outcome: Ability to design and execute experiments to collect, process, and interpret data in order to gain knowledge about the Earth and other planetary bodies.
•  Provides graduate-level foundation in computational geophysics while allowing flexibility based on interest and/or need.
• Key Learning Outcome: Familiarization with numerical implementation of geophysical theory and modern computational techniques, such as data science, machine learning, algorithm development, cluster computing, and parallel processing.
• Provides graduate-level foundation in conceptual modeling of the earth while allowing flexibility based on interest and/or need.
• Key Learning Outcome: Development of conceptual models to explain the observed natural complexity of earth materials and processes.

Graduate Certificate in Energy Geophysics

The Graduate Certificate in Energy Geophysics will be a fully online certificate.  The applicant is required to have an undergraduate degree to be admitted into the program. Students working towards their Graduate Certificate are required to take 12 credits from the following list of approved courses:

Students must achieve a minimum average grade of B (3.0) for the four required courses.  

GPGN503. INTEGRATED EXPLORATION AND DEVELOPMENT. 3.0 Semester Hrs.

(I) Students work alone and in teams to study reservoirs from fluvial-deltaic and valley fill depositional environments. This is a multidisciplinary course that shows students how to characterize and model subsurface reservoir performance by integrating data, methods and concepts from geology, geophysics and petroleum engineering. Activities include field trips, computer modeling, written exercises and oral team presentations. Prerequisite: none. 2 hours lecture, 3 hours lab; 3 semester hours. Offered fall semester, odd years.

GPGN509. INVERSION. 3.0 Semester Hrs.

This course introduces the fundamentals of inverse problem theory as applied to geophysics. Students explore the fundamental concepts of inversion in probabilistic and deterministic frameworks, as well as practical methods for solving discrete inverse problems. Topics studied include optimization criteria, optimization methods, and error and resolution analysis. Weekly homework assignments addressing either theoretical or numerical problems through programming assignments illustrate the concepts discussed in class. 3 hours lecture; 3 semester hours.

GPGN511. ADVANCED GRAVITY AND MAGNETIC METHODS. 3.0 Semester Hrs.

This course presents the theory and methods for processing and interpreting gravity and magnetic data acquired in geoscience applications. The course covers four major topic areas in the gravity and magnetic methods: (1) the data quantities measured in field surveys; (2) the methods for modeling, processing, and analyzing gravity, gravity gradient, and magnetic data; (3) 3D inversion of gravity and magnetic data; and (4) integrated interpretation of gravity and magnetic data through inversion and geology differentiation for extracting geology information. Prerequisites: GPGN314, GPGN328 .

GPGN519. ADVANCED FORMATION EVALUATION. 3.0 Semester Hrs.

A detailed review of well logging and other formation evaluation methods will be presented. Course includes an overview of the logging environment, how different basic and advanced logging tools work, how logging measurements are converted to geophysical properties, how geophysical properties relate to physical and chemical properties of fluids and rocks, and how log data are tied with seismic data.

GPGN520. ELECTRICAL AND ELECTROMAGNETIC EXPLORATION. 3.0 Semester Hrs.

(II) Electromagnetic theory. Instrumentation. Survey planning. Processing of data. Geologic interpretations. Methods and limitations of interpretation. Offered Spring semester in conjunction with GPGN420 . Prerequisite: GPGN314. 3 hours lecture; 3 semester hours.

GPGN530. APPLIED GEOPHYSICS. 3.0 Semester Hrs.

(II) Introduction to geophysical techniques used in a variety of industries (mining, petroleum, environmental and engineering) in exploring for new deposits, site design, etc. The methods studied include gravity, magnetic, electrical, seismic, radiometric and borehole techniques. Emphasis on techniques and their applications are tailored to student interests. The course, intended for non-geophysics students, will emphasize the theoretical basis for each technique, the instrumentation used and data collection, processing and interpretation procedures specific to each technique so that non-specialists can more effectively evaluate the results of geophysical investigations. 3 hours lecture; 3 semester hours.

GPGN533. GEOPHYSICAL DATA INTEGRATION & GEOSTATISTICS. 3.0 Semester Hrs.

(I) Students will learn the fundamentals of and explore opportunities for further development of geostatistical data integration techniques for subsurface earth modeling. The class will build on probability theory, spatial correlations and geostatistics algorithms for combing data of diverse support and resolution into subsurface models. The emphasis of the material will be on stochastic methods for combining quantitative and qualitative data into many equi-probable realizations. Activities include computer modeling, written exercises, oral team presentations, and a semester project with opportunity to enhance student?s respective research projects. Also, we will read, discuss and implement current research articles the in literature to encourage implementation of state-of-the-art practices and/or highlighting current opportunities for research. 3 hours lecture; 3 semester hours.

GPGN536. ADVANCED GEOPHYSICAL COMPUTING I. 3.0 Semester Hrs.

This course extends the principles of geophysical computing in the context of simulating and validating numerical solutions to geophysical data processing challenges and 2D/3D partial differential equations commonly found in geophysical investigations. Students develop 2D and 3D numerical solutions to geophysical problems through prototyping and validating code in both high- (e.g., Python) and low-level (e.g., C/C++/F90) languages. Offered in conjunction with GPGN435. Prerequisite: CSCI250 or instructor consent.

GPGN537. ADVANCED GEOPHYSICAL COMPUTING II. 3.0 Semester Hrs.

A survey of computer programming skills most relevant to geophysical modeling, data processing, visualization, and analysis. Skills enhanced include effective use of multiple programming languages, multicore systems, computer memory hierarchies, GPUs, and parallel computing strategies. Problems addressed include multidimensional geophysical partial differential equations, geophysical image processing, regularization of geophysical data acquired at scattered locations, and other geophysical computing problems encountered in research by students. Prerequisite: GPGN536 or instructor consent.

GPGN543. MINERAL EXPLORATION GEOPHYSICS. 3.0 Semester Hrs.

This course focuses on geophysical methods in mineral exploration by integrating mineral deposit theory and commonly employed geophysical methods. We begin with a background discussion on the geological setting and physical property characteristics of major deposit types to lay the foundational understanding for different geophysical method. We will then discuss the physical principles and operations of different geophysical methods, and the interpretation of geophysical data sets to extract geological information through geophysical inversion. We will then discuss the emerging methods for efficient data acquisition, and integrated exploration methodology of geology differentiation that combines the geologic, physical property, and geophysical information to produce a quasi-geology model to image the geology.

GPGN545. INTRODUCTION TO DISTRIBUTED FIBER-OPTIC SENSING AND ITS APPLICATIONS. 3.0 Semester Hrs.

This course will first introduce the fundamentals of Distributed Fiber-optic Sensing (DFOS) technologies, including the measuring principles, calibration process, advantages, and limitations. Then we will explore the recent development of DFOS applications in geophysics, petroleum engineer, smart city, hydrology, and other fields. Three major technologies of DFOS will be introduced: distributed acoustic sensing (DAS), distributed temperature sensing (DTS), and distributed strain sensing (DSS). Prerequisite: Python programming, signal processing.

GPGN547. PHYSICS, MECHANICS, AND PETROPHYSICS OF ROCKS. 3.0 Semester Hrs.

This course will discuss topics in rock physics, rock mechanics and petrophysics as outlined below. The class is a combination of lectures, practical sessions, and critical reading and discussion of papers. Topics addressed: Segment in Rock physics: stress, strain, stiffness, modulus, attenuation and dispersion, Segment in Petrophysics: seismic & log expression of various formations, wettability, shale analysis, diagenesis, formation evaluation.

GPGN551. WAVE PHENOMENA SEMINAR. 1.0 Semester Hr.

(I, II) Students will probe a range of current methodologies and issues in seismic data processing, and discuss their ongoing and planned research projects. Topic areas include: Statics estimation and compensation, deconvolution, multiple suppression, wavelet estimation, imaging and inversion, anisotropic velocity and amplitude analysis, seismic interferometry, attenuation and dispersion, extraction of stratigraphic and lithologic information, and correlation of surface and borehole seismic data with well log data. Every student registers for GPGN551 in only the first semester in residence and receives a grade of PRG. The grade is changed to a letter grade after the student's presentation of thesis research. Prerequisite: none. 1 hour seminar; 1 semester hour.

GPGN552. INTRODUCTION TO SEISMOLOGY I. 3.0 Semester Hrs.

(I) Introduction to basic principles of elasticity including Hooke's law, equation of motion, representation theorems, and reciprocity. Representation of seismic sources, seismic moment tensor, radiation from point sources in homogeneous isotropic media. Boundary conditions, reflection/transmission coefficients of plane waves, plane-wave propagation in stratified media. Basics of wave propagation in attenuative media, brief description of seismic modeling methods. 3 hours lecture; 3 semester hours.

GPGN553. INTRODUCTION TO SEISMOLOGY II. 3.0 Semester Hrs.

(II) This course is focused on the physics of wave phenomena and the importance of wave-theory results in exploration and earthquake seismology. Includes reflection and transmission problems for spherical waves, methods of steepest descent and stationary phase, point-source radiation in layered isotropic media, surface and non-geometrical waves. Discussion of seismic modeling methods, fundamentals of wave propagation in anisotropic and attenuative media. Prerequisite: GPGN552 . 3 hours lecture; 3 semester hours. Offered spring semester, even years.

GPGN555. EARTHQUAKE SEISMOLOGY. 3.0 Semester Hrs.

Equivalent with GPGN455 , (I) Earthquakes are amongst the most significant natural hazards faced by mankind, with millions of fatalities forecast this century. They are also our most accessible source of information on Earth's structure, rheology and tectonics, which are what ultimately govern the distribution of its natural resources. This course provides an overview of how earthquake seismology, complemented by geodesy and tectonic geomorphology, can be used to determine Earth structure, earthquake locations, depths and mechanisms; understand Earth's tectonics and rheology; establish long-term earthquake histories and forecast future recurrence; and mitigate against seismic hazards. GPGN555 differs from GPGN455 in that the assignments are approximately 20% longer and encompass more challenging questions. GPGN555 is the appropriate course for graduate students and for undergraduates who expect to go on to study earthquake seismology at graduate school. 3 hours lecture; 3 semester hours.

GPGN558. SEISMIC DATA INTERPRETATION AND QUANTITATIVE ANALYSIS. 3.0 Semester Hrs.

This course gives participants an understanding of how to model, understand, interpret and analyze seismic data in a quantitative manner on several worldwide projects. When you look at seismic data, how does it relate to the rock properties, what do the amplitudes mean, what is tuning, what is a wavelet, how does the seismic relate to structure, and what are seismic attributes and inversion products? How do you use this information in exploration, production and basic volumetric and economics calculations? The course will go over these topics. Students will work in teams on several modeling and seismic field data exercises around the world in most widely used software platforms (Ikon-RokDoc, Schlumberger-Petrel, GEOX, CGG-HampsonRussell). The course aims to give participants knowledge and information to assist in professional and career development and to be operationally prepared for the work environment. Prerequisites: GPGN461 or GPGN 561 and GEOL309 or GEOL314 .

GPGN559. RESERVOIR CHARACTERIZATION SEMINAR. 1.0 Semester Hr.

Students will probe a range of current methodologies and issues in integrated reservoir characterization and discuss their ongoing and planned research projects, both in oral presentations and interdisciplinary class discussions. Topic areas include geophysical and geological reservoir characterization, fluid flow and simulation, distributed acoustic and temperature sensing, machine learning and data analytics, compressive sensing for seismic data acquisition, and enhanced oil recovery for unconventionals. Students receive real-time feedback on their research progress and presentations from Geophysics faculty and potentially professionals in the local geophysics community.

GPGN561. SEISMIC DATA PROCESSING I. 4.0 Semester Hrs.

This course covers the basic processing steps required to create images of the earth using 2D and 3D reflection seismic data. Topics include data organization and domains, signal processing to enhance temporal and spatial resolution, identification and suppression of incoherent and coherent noise, velocity analysis, near-surface statics, datuming, normal- and dip-moveout corrections, common-midpoint stacking, principles and methods used for poststack and prestack time and depth imaging, post-imaging enhancement techniques. Field data are extensively used throughout the course. A three-hour lab introduces the student to hands-on data processing using a Seismic Unix software package. The final project consists of processing a 2D seismic line with oral presentation of the results.

GPGN570. APPLICATIONS OF SATELLITE REMOTE SENSING. 3.0 Semester Hrs.

(II) An introduction to geoscience applications of satellite remote sensing of the Earth and planets. The lectures provide background on satellites, sensors, methodology, and diverse applications. Topics include visible, near infrared, and thermal infrared passive sensing, active microwave and radio sensing, and geodetic remote sensing. Lectures and labs involve use of data from a variety of instruments, as several applications to problems in the Earth and planetary sciences are presented. Students will complete independent term projects that are presented both written and orally at the end of the term. Prerequisites: PHGN200 and MATH225 . 2 hours lecture, 2 hours lab; 3 semester hours.

GPGN574. ADVANCED HYDROGEOPHYSICS. 3.0 Semester Hrs.

(II) Application of geophysical methods to groundwater problems from the grain scale to the basin scale. course introduces the groundwater flow and solute transport equations to understand the parameters controlling flow. Geophysical and numerical modeling techniques are introduced as a means to constrain transport parameters. Geophysical topics include electrical methods, seismic methods, downhole logging, and nuclear magnetic resonance. Modeling techniques include forward and inversion approaches for groundwater flow, solute transport, and geophysical data. Readings and discussions will be used to bring state-of-the-art applications of course content. 3 hours lecture; 3 semester hours.

GPGN577. HUMANITARIAN GEOSCIENCE. 3.0 Semester Hrs.

(II) This interdisciplinary course introduces the concepts and practice of geoscientific investigations in humanitarian projects. Students will evaluate humanitarian geoscience case studies, devise the characteristics of successful projects, and identify how these best practices could improve previous case studies. This knowledge will be applied towards a group project. Students will split into groups and pair up with a faculty advisor and a local organization (e.g., NGO or community group) to design, execute and assess the impact of their project. A key emphasis in all aspects of the course will be on community engagement. This course is taught in collaboration with the Mines Engineering Design and Society Division and other participating departments.

GPGN581. GRADUATE SEMINAR. 1.0 Semester Hr.

(I, II) Attendance at scheduled weekly Heiland Distinguished Lectures during each semester of enrollment. Students must complete one individual presentation during the graduate program, at an approved public venue, before degree is granted. Every thesis-based MS student in Geophysics and Geophysical Engineering registers each semester in residence in the program and receive 0.0 credit hours until the last semester in residence. For the last semester, 1.0 credit hours and a grade of PRG are awarded with satisfactory attendance and successful completion of individual presentation requirement.

GPGN583. READING SEMINAR. 1.0 Semester Hr.

This course is designed to broaden the knowledge and perspective of MS students through reading and critiquing scientific publications. Student will read a scientific publication weekly that is related to the Heiland lecture of the week. Every week a student will present and lead the discussion of the paper during the class. Every student need to write a short discussion/summary/thinking/report after the Heiland lecture and post it on Canvas.

GPGN590. INSTRUMENTAL DESIGN IN APPLIED GEOSCIENCES. 3.0 Semester Hrs.

A hands-on course on instrumental design for those interested in developing ?sensors and software? solutions for use in applied geoscience and related engineering disciplines, including environmental, civil, electrical, mining, petroleum, and mechanical engineering. The first half of the course focuses on developing required skill sets in electronics microcomputers and device connectivity that enables students to construct a smart sensing system that is remotely accessible through the internet of things (IoT). The second half of the course consists of project work on multidisciplinary teams who devise, build, and validate usable prototype devices such as a magnetometer, a telemetered sap-monitoring unit, an autonomous ground penetrating radar, or a smart irrigation system. Prerequisite: CSCI250 or instructor consent.

GPGN598. SPECIAL TOPICS IN GEOPHYSICS. 6.0 Semester Hrs.

(I, II, S) Pilot course or special topics course. Topics chosen from special interests of instructor(s) and student(s). Usually the course is offered only once, but no more than twice for the same course content. Prerequisite: none. Variable credit: 0 to 6 credit hours. Repeatable for credit under different titles.

GPGN599. GEOPHYSICAL INVESTIGATIONS MS. 0.5-6 Semester Hr.

(I, II, S) Individual research or special problem projects supervised by a faculty member, also, when a student and instructor agree on a subject matter, content, and credit hours. Prerequisite: ?Independent Study? form must be completed and submitted to the Registrar. Variable credit: 0.5 to 6 credit hours. Repeatable for credit under different topics/experience and maximums vary by department. Contact the Department for credit limits toward the degree.

GPGN605. INVERSION THEORY. 3.0 Semester Hrs.

(II) Introductory course in inverting geophysical observations for inferring earth structure and processes. Techniques discussed include: Monte-Carlo procedures, Marquardt-Levenburg optimization, and generalized linear inversion. In addition, aspects of probability theory, data and model resolution, uniqueness considerations, and the use of a priori constraints are presented. Students are required to apply the inversion methods described to a problem of their choice and present the results as an oral and written report. Prerequisite: MATH225 and knowledge of a scientific programming language. 3 hours lecture; 3 semester hours.

GPGN651. ADVANCED SEISMOLOGY. 3.0 Semester Hrs.

In-depth discussion of wave propagation and seismic processing for anisotropic, heterogeneous media. Topics include influence of anisotropy on plane-wave velocities and polarizations, traveltime analysis for transversely isotropic models, anisotropic velocity-analysis and imaging methods, point-source radiation and Green's function in anisotropic media, inversion and processing of multicomponent seismic data, shear-wave splitting, and basics of seismic fracture characterization. Prerequisite: GPGN552 , GPGN553 .

GPGN658. SEISMIC WAVEFIELD IMAGING. 3.0 Semester Hrs.

(I) Seismic imaging is the process that converts seismograms, each recorded as a function of time, to an image of the earth's subsurface, which is a function of depth below the surface. The course emphasizes imaging applications developed from first principles (elastodynamics relations) to practical methods applicable to seismic wavefield data. Techniques discussed include reverse-time migration and migration by wavefield extrapolation, angle-domain imaging, migration velocity analysis and analysis of angle-dependent reflectivity. Students do independent term projects presented at the end of the term, under the supervision of a faculty member or guest lecturer. Prerequisite: none. 3 hours lecture; 3 semester hours.

GPGN681. GRADUATE SEMINAR - PHD. 1.0 Semester Hr.

(I,II) Presentation describing results of PhD thesis research. All students must present their research at an approved public venue before the degree is granted. Every PhD student registers for GPGN681 only in his/her first semester in residence and receives a grade of PRG. Thereafter, students must attend the weekly Heiland Distinguished Lecture every semester in residence. The grade of PRG is changed to a letter grade after the student's public research presentation and thesis defense are both complete. 1 hour seminar; 1 semester hour.

GPGN698. SPECIAL TOPICS. 6.0 Semester Hrs.

GPGN699. GEOPHYSICAL INVESTIGATION-PHD. 0.5-6 Semester Hr.

GPGN707. GRADUATE THESIS / DISSERTATION RESEARCH CREDIT. 1-15 Semester Hr.

(I, II, S) Research credit hours required for completion of a Masters-level thesis or Doctoral dissertation. Research must be carried out under the direct supervision of the student's faculty advisor. Variable class and semester hours. Repeatable for credit.

SYGN501. RESEARCH SKILLS FOR GRADUATE STUDENTS. 1.0 Semester Hr.

(I, II) This course consists of class sessions and practical exercises. The content of the course is aimed at helping students acquire the skills needed for a career in research. The class sessions cover topics such as the choice of a research topic, making a work plan and executing that plan effectively, what to do when you are stuck, how to write a publication and choose a journal for publication, how to write proposals, the ethics of research, the academic career versus a career in industry, time-management, and a variety of other topics. The course is open to students with very different backgrounds; this ensures a rich and diverse intellectual environment. Prerequisite: None. 1 hour lecture; 1 semester hour.

© 2023-2024 Colorado School of Mines

Print Options

Print this page.

The PDF will include all information unique to this page.

A PDF of the entire Undergraduate catalog.

A PDF of the entire Graduate catalog.

• 2023-2024 Bulletin

• Departments & Programs
• Office of the Dean
• Welcome from the Dean
• By the Numbers
• State of the College 2023
• Information For Faculty & Staff
• Undergraduate Programs
• Undergraduate Certificate Programs
• Dean's List
• Graduate Programs
• Graduate Certificate Programs
• Advising and Support
• Find a Program
• Undergraduate Admissions
• Graduate Admissions
• Financial Aid
• Future Students
• Current Students
• Student Success
• Study Abroad
• Academic Advisors
• Academic Resources
• Career Ready
• Undergraduate Research
• Graduate Research
• Faculty Research
• Research Development
• Centers & Institutes
• Development Office
• Giving Priorities
• Ways to Give

• College of Arts & Sciences News
• Media Relations
• Women in Science
• Teachers & Educators
• K-12 Students

Ph.D. in Geophysics

The Ph.D. in Geophysics will give you a thorough and comprehensive knowledge of geophysics and training in methods of research.

Through this degree program, you will learn how to:

• Explain the scope, significance and limitations of geophysical information to land and environment stewardship and civil infrastructure stakeholders
• Develop new methods to evaluate risk and vulnerability from geological hazards and to make detailed evaluations about quality and quantity of Earth resources
• Determine whether geophysical data indicate a subsurface target of interest so that reliable drilling and excavation decisions can be made
• Design and execute field studies that employ geophysical data to solve a geoscience problem
• Create robust and reliable inferences of fundamental Earth structures and processes from incomplete and possibly inaccurate geological information
• Combine geological and geophysical data to build and assess the implications of integrative models whose value exceeds the sum of its components
• Deliver oral presentations and answer technical questions in plain language, in which you will describe and interpret geophysical information and carefully explain compelling conclusions to the audience
• Prepare and widely circulate well-written and well-structured documents that contain sound reasoning and robust conclusions based on geophysical principles
• Use the full capabilities of commercial software packages to process, display and manipulate geophysical data and work with companies for their further development and refinement
• Use advanced geophysical field and laboratory equipment
• Execute robust and decisive tests of geophysical research hypotheses using advanced principles, data, and techniques
• Apply and further develop advanced principles of scientific uncertainty as they relate to geophysical hypothesis testing
• Be a role model in professional conduct in research and assume leadership roles of professional societies within geological sciences
• Demonstrate exemplary behavior in balancing stakeholder, client and public interest concerns as they pertain to geophysical investigations.

Ph.D. in Geophysics Program Requirements

Earning a Doctoral Degree

The doctoral program gives you a thorough and comprehensive knowledge of your professional field and training in methods of research.

The final basis for granting the degree will be your grasp of the subject matter of a broad field of study and a demonstrated ability to do independent research. You also must have acquired the ability to express thoughts clearly and convincingly in both oral and written form.

The degree is not granted solely for the completion of coursework, residence, and technical requirements, although these must be met.

Steps to Fulfill a Doctoral Program

• What's SLIM
• Alumni (UBC)
• Cloud Computing
• OPTIMUM (UBC)
• YEMOJA (UBC)
• SINBAD (UBC)
• DNOISE (UBC)
• III - Brazil (UBC)
• CHARM (UBC)
• PARTNERS MEETINGS
• OTHER EVENTS
• Technical Reports
• Acquisition
• w/ Curvelets
• Compressive imaging
• Extended Imaging
• Uncertainty-aware imaging
• Imaging with tasks
• Medical imaging
• Time-lapse imaging
• Constrained
• Uncertainty quantification
• Time-lapse FWI
• Time-lapse seismic
• Geological Carbon Storage
• Neural networks
• Seismic data processing
• Structure promoting
• Compressive Sensing
• Collaborations
• SLIM Newcomers
• SLIM Resources
• BibTeX Submission
• Team member registration

Modeling for inversion in exploration geophysics

• Zur Metanavigation
• Zur Hauptnavigation
• Zur Subnavigation
• Zum Seitenfuss

Photo: WIT Consortium

Ph.D. and Habilitation Theses / Dissertationen

• Znak, P. (2019): Wavefront curvatures: dynamic ray focusing and diffraction classification. PhD thesis, University of Hamburg, Germany. (pdf will be availabe soon)
• Glöckner, M. (2019): Advanced Time Imaging. PhD thesis, University of Hamburg, Germany. (pdf )
• Bauer, A. (2019): Utilizing the Unique Properties of Seismic Diffractions. PhD thesis, University of Hamburg, Germany. (pdf)
• Abakumov, I. (2017): Extension of the implicit Common-Reflection-Stacking operator for three-dimensional anisotropic media. PhD thesis, University of Hamburg, Germany. (pdf)
• Vefagh Nematollahy, M. (2017): Multiple attenuation using hyperbolic formulas. PhD thesis, University of Hamburg, Germany. (pdf)
• Xie, Y. (2017): Determination and application of 3-D wavefront attributes. PhD thesis, University of Hamburg, Germany. (pdf)
• Yang, Y. (2017): 2D and 3D seismic imaging by partial time migration and demigration. PhD thesis, University of Hamburg, Germany. (pdf)
• Walda, J. (2016): Determination and application of wavefront attributes. PhD thesis, University of Hamburg, Germany. (pdf)
• Ahmed, K.A. (2015): 3-D seismic processing in crystalline rocks using the common reflection surface stack. PhD thesis, University of Hamburg, Germany. (pdf)
• Behzadi, M. (2015): Microtremor localisation based on cross-correlation stacking. PhD thesis. University of Hamburg, Germany. (pdf)
• Schwarz, B. (2015): Moveout and Geometry. PhD thesis, University of Hamburg, Germany. (pdf)
• Minarto, Eko (2014): Optimization of Common Reflection Surface (CRS) attributes based on conjugate direction approach using Powell search method. PhD thesis, University of Hamburg, Germany. (pdf)
• Zhebel, O. (2013): Imaging of seismic events: the role of imaging conditions, acquisition geometry and source mechanisms. PhD thesis, University of Hamburg, Germany. (pdf)
• Dell, S. (2012): Seismic processing and imaging with diffractions. PhD thesis, University of Hamburg, Germany. (pdf)
• Vanelle, C. (2012): Stacking and migration in an/isotropic media. Habilitation thesis, University of Hamburg, Germany. (pdf)
• Dümmong, S. (2010): Seismic data processing with an expanded Common Reflection Surface workflow. PhD thesis , University of Hamburg, Germany. (pdf)
• Baykulov, M. (2009): Seismic imaging in complex media with the Common Reflection Surface stack. PhD thesis, University of Hamburg, Germany. (pdf)
• Kaschwich, Tina (2006): Traveltime computation and migration in anisotropic media, PhD thesis, University of Hamburg, Germany.  (pdf)
• Golovnina, Svetlana M. (2004): Modeling and inversion in weakly anisotropic media, PhD thesis, University of Hamburg, Germany. (pdf)
• Coman, Radu Aurel (2003): Computation of multivalued traveltimes in three-dimensional heterogeneous media, PhD thesis, University of Hamburg, Germany. (pdf)
• Menyoli, Elive M. (2002): Model Building and Imaging with Reflection Data, PhD thesis, University of Hamburg, Germany. (pdf)
• Vanelle, Claudia (2002): Traveltime-based true-amplitude migration, PhD thesis, University of Hamburg, Germany. (pdf)

College of Natural Sciences and Mathematics    > Department of Earth and Atmospheric Sciences    > Geophysics, PhD

The Department of Earth and Atmospheric Sciences (EAS) offers a wide range of courses leading to the degree of Doctor of Philosophy in Geophysics. A wide variety of electives allows concentration in areas such as exploration, geotechnical, or environmental geophysics, solid earth geophysics, petroleum exploration, marine geophysics, earthquake seismology, and geodynamics. The typical student pursuing this degree is interested in geophysics and has a good background in the geosciences, mathematics, physics, and computing. Graduates will typically pursue careers with resource companies, geophysical service companies, various federal, state, and local government agencies, in the financial sector, or in education/academia.

For more information, please visit: http://www.uh.edu/nsm/earth-atmospheric/graduate/degree-programs/phd-geophysics/ .

Admission Requirements

• Applicant will have earned a Bachelor’s or a Master’s degree
• Scores from the General GRE examination taken in the last 5 years are optional (verbal, quantitative, and analytical writing; advanced GRE is recommended but optional)
• English language proficiency test scores, such as TOEFL or IELTS scores must be provided by applicants who did not earn a prior degree from a US institution or a country where English is the medium of instruction (see list in the  General Admission Policy   ).

Visit  http://www.uh.edu/graduate-school/international-students/ to learn more.

The admissions committee and the department chair will evaluate the credentials of each applicant for the PhD program, considering a broad range of criteria, including:

• Content of the undergraduate program and, if applicable, graduate programs and grades earned, particularly in the areas of Geosciences, Mathematics, Physics, and Chemistry.
• A cumulative GPA of 3.0 or better in the last 60 hours of course work
• Letters of recommendation from three (3) individuals (preferably faculty members), who are able to judge the candidate’s academic abilities and potential for scholarly research.
• GRE scores, if submitted (see above).
• English proficiency test scores, when applicable.
• Scientific, professional, technical publications, and Master’s Thesis (if applicable).

In addition to these requirements, graduate admission may also be contingent upon a faculty advisor agreeing to supervise the applicant.  Therefore, prospective students are strongly encouraged to contact faculty members in the applicant’s field of interest prior to the application deadline.

Deficiencies

Candidates in the Geophysics PhD program must demonstrate general proficiency in mathematics, physics, and geology. Some graduate courses explicitly require prerequisite courses.

The department will determine what deficiencies -if any - are present, and the acceptable means of removing those deficiencies (e.g. course work within and/or outside the department, directed study, research papers). Waivers of requirements will be considered on an individual basis. Applicants with a few deficiencies can satisfy those requirements while also taking graduate courses at the University of Houston. 

Degree Requirements

• All doctoral students must have a minimum of one continuous academic year (two terms (Fall/Spring or Spring/Summer/Fall)) as a full‐time student which consists of 9.0 Credit Hours per term.
• A student working on a dissertation must be continuously enrolled in a minimum of 3.0 Credit Hours of doctoral research each Fall and Spring term, and in a minimum of 3.0 Credit Hours of doctoral dissertation in their final term.
• Up to 6.0 Credit Hours of courses taken outside the department, but relevant to the degree program, can apply to the degree with prior approval from the Geophysics Graduate Faculty Advisor.

Course Requirements

Credit hours required for this degree: 54.0

a) PhD students entering with a MS degree

• Formal EAS courses  Credit  Hours: 18.0
• Letter-graded Doctoral Dissertation course  Credit Hours: 6.0 - 12.0
• The remaining hours may include Coursework, Doctoral Research, Seminars, and Special Problems

b) PhD students entering with a Bachelor’s degree

• Formal EAS elective courses  Credit  Hours: 12.0
• EAS Core Courses  Credit Hours: 12.0 (see list below)
• The remaining hours may include Coursework, Doctoral Research, Seminars and Special Problems

Students are encouraged to consult with the Geophysics Graduate Faculty Advisor to make their selections of graduate courses.

EAS Core Courses

To provide a fundamental background in the essential elements of geophysics, all PhD students entering with a Bachelor’s degree are required to take the following 4 courses:

• GEOL 7324 - Rock Physics Credit Hours: 3.0
• GEOL 7330 - Potntl Fld Mtds-Geophys Credit Hours: 3.0
• GEOL 7333 - Seismic Wave & Ray Theory Credit Hours: 3.0
• GEOL 7341 - Geophysical Data Processing Credit Hours: 3

Course substitutions may be allowed on an individual basis, with prior approval from the Geophysics Graduate Faculty Advisor.

Sequence and Timing

First year in program:

• Appropriate course work
• Removal of all deficiencies
• Establishment of Ph.D. Research Committee

Second year in program:

• Candidacy exam
• Presenting Research and Dissertation Proposals
• Completion of all formal course work
• Initiation of research

Third and successive years:

• Conduct the proposed research
• Submit revised papers
• Completion and defense of dissertation

Academic Policies

• University of Houston Academic Policies     
• Academic Policies: College of Natural Sciences and Mathematics    
• Department/Program Academic Policies:

Scholastic Requirement

• Students not in good standing cannot receive a graduate degree and can be declared ineligible for support with a graduate assistantship (IA, TA, RA/TE or RA).
• Graduate students who receive grades of C+ or lower in 12 or more semester hours of course work attempted for graduate credit are ineligible for any advanced degree at this institution.
• Semester hours of “U” grades in S/U-graded courses apply toward the above 12-hour total.

Research (Dissertation) Advisor/Research Committee

Ph.D. applicants are encouraged to formulate their dissertation committee promptly in order to ensure proper guidance throughout their research.

• a minimum of four members to include three faculty members who have their primary appointment within EAS
• one approved member external to the major department from industry or academia who is acceptable to the department and approved by the college.
• A faculty member with a joint appointment in EAS is considered as an outside member unless he/she chairs the committee. In this case, an additional external member outside the major department is required.
• After these minimum requirements for committee members are satisfied, additional committee members may be approved from industry or academia, but at least 50% of the committee must be tenured/tenure‐track faculty at the University of Houston.
• Research faculty or instructional faculty may serve on dissertation committees, but not chair the committees. However, a research professor may serve as a co‐advisor with a tenured/ tenure‐track faculty.
• Candidates must specify a dissertation committee and have the names on file in the NSM Office of Academic Affairs at least one semester prior to their graduation.

To become a candidate for the doctoral degree a student must meet a set of requirements established by the EAS Department. For all EAS doctoral aspirants, there are two options available to attain candidacy. It is the responsibility of the dissertation advisor to notify the department academic advisor and applicable graduate advisor which path to candidacy the graduate student will undertake by the end of the term preceding the candidacy exam or paper submission (Candidacy Options 1 and 2, respectively. See below).

• It will test the breadth of the candidate’s knowledge within their discipline.
• At the discretion of the examining committee, a student who fails the general examination can be permitted to re‐take it; however, the exam cannot be taken more than twice by the applicant.
• Re‐examination will take place within one (1) month of the initial examination.
• The student must pass the candidacy examination before proceeding to the dissertation proposal.
• All candidacy and proposal requirements must be completed by the end of the 4th term in the program.
• Submission of a manuscript to an Institute for Scientific Information (ISI)‐indexed, peer‐reviewed journal by the 6th week of the fourth semester in the program and approval of an oral and written Ph.D. proposal.
• Research work for the manuscript must have been completed at UH. This timing implies that the student is full‐ time and supported as a Research Assistant (RA) or Teaching Assistant (TA).
• In order to proceed along this pathway for the Ph.D., the dissertation advisor and research committee must agree that the candidate has produced a publishable manuscript capable of passing a rigorous external peer review for a scientific journal and has completed and successfully defended a research proposal.
• Prior to the presentation of the dissertation proposal, the manuscript must be submitted to a peer‐reviewed journal.
• The oral proposal of the dissertation must be presented before the end of the 4th term.

Dissertation Proposal

The oral dissertation proposal will be given during the term in which the candidacy exam has been successfully completed (Candidacy Option 1) or the manuscript has been submitted to an approved peer‐reviewed journal (i.e. before the end of the fourth term) (Candidacy Option 2).

• PhD proposals can take place Monday‐Friday, with starting times between 8:00 a.m. and 4:00 p.m., during the Fall and Spring terms.
• The proposal must be presented by the last day of the semester. Teaching Assistants must present by the first Monday in November in the Fall term, or the first Monday in July in the Summer term..
• Proposals cannot be presented during, vacations, weekends, or over spring break or inter‐semester breaks.
• Summer proposals can be scheduled pending approval of the entire committee.
• A minimum of two hours should be allocated for the dissertation proposal presentation and questions.
• Proposal presentations are preceded by the distribution of a research committee approved 5 to 10 page (10 page maximum for text) written description of the dissertation project.

A one-page abstract must be posted and distributed to all faculty members at least seven calendar days prior to presentation and a digital copy of the full proposal in the final form filed with the department academic advisor and committee members at that time.

• The proposal abstract must contain the title, time, place of the proposal, link for a video conference and the names of the committee members.
• The dissertation advisor and at least one other member of the committee must initial the abstract prior to posting, thus indicating that they approve of the presentation of the proposal.
• The oral presentation, approximately 30 to 45 minutes long, will be followed by a period during which all present can ask questions of the student related to the suitability and feasibility of the project, as well as the student’s ability to perform the research.
• All faculty present can participate in the deliberations.
• Committee members vote on the success or failure of the student’s performance in the dissertation proposal.
• Approval by a majority of those voting is needed to pass the proposal. Upon successful presentation of the dissertation proposal, the student will be granted PhD candidacy status.
• Upon successful presentation of the proposal, a digital copy of the complete proposal with the dissertation advisor’s signature indicating approval of the proposal as originally presented or modified must be placed in the student’s permanent academic file.
• The second presentation must take place within 90 calendar days of the initial presentation.

Dissertation Defense

A public oral defense of the completed dissertation research will be presented to the faculty-at-large and may be attended by any other interested parties.

• The format of the dissertation must follow NSM guidelines.
• Questions pertaining to specific requirements should be addressed to the appropriate advisor.
•  Students that have used candidacy option 1 will submit at least two manuscripts, based on the dissertation research, to a qualified journal. Students that used candidacy option 2 will have a manuscript accepted and another submitted to qualified journals.
• This manuscript must have been judged publication‐ready by the dissertation advisor and at least one other faculty member on the dissertation committee prior to submission.
• For the defense, an abstract, which lists the time and place of the defense, and link for video conference, must be distributed to the EAS faculty and posted publicly at least seven calendar days prior to the scheduled date for the defense.
• The dissertation advisor and at least one other committee member must initial the notice of defense, indicating approval of the defense.

A digital or hard copy of the dissertation/thesis in the final form be submitted at least seven calendar days prior to presentation to the committee members and advising staff that can be provided to EAS faculty upon request.

• PhD defenses can be given Monday‐Friday during the Fall, Spring, and Summer terms with starting times between 8:00 a.m. and 4:00 p.m.
• Defenses cannot be given during vacations, weekends, or final examination periods (nor over spring break or inter‐term breaks).
• Scheduling of defenses is done through the department academic advisor.
• A positive vote by a majority of the dissertation committee is required for successful defense of the dissertation.
• If the student does not complete and successfully defend the PhD dissertation within five years after passing the candidacy examination, retaking of the candidacy examination may be required.
• Once approved by the committee, the dissertation must be submitted to the NSM Office of Academic Affairs no later than the deadline posted on the College website each term.

• Costs, Scholarships & Aid
• Campus Life
• Faculty & Staff
• Family & Visitors
• DFW Community
• Galaxy Login
• Academic Calendar
• Human Resources
• Accessibility

Doctor of Philosophy in Geosciences

Program description.

The PhD Geosciences (Geology/Geophysics) degree program provides a curriculum that is designed to be relevant to many of today’s advanced Sustainable Earth and Environment Science challenges and career prospects, as well as the opportunity to engage in state-of-the-art research with faculty and equipment (computational, laboratory, and fieldwork). Geosciences is one of the original and longest established academic programs at the University of Texas at Dallas. 

The PhD Geosciences degree emphasizes research in several specialized areas of earth, environment, and natural resources science and is designed to prepare graduates for advanced leadership positions in industry, government, or academia. The department requires that a PhD dissertation will consist of a number of independent research contributions, most of which will be published in peer-reviewed geoscience journals. 

Career Opportunities

Graduates of the program seek positions industry, government or academia. 

Marketable Skills

Review the marketable skills for this academic program.

Application Requirements

Degree requirements:  Entering students are expected to have completed the equivalent of the University’s BS and MS degrees in Geosciences, including courses in geology, physics, mathematics and chemistry. Students whose BS or MS training is in a science other than geology or geophysics are admitted to the program when their previous course work complements or supports their intended research interests. Deficiencies in the BS or MS background of admitted students will be addressed through a sequence of required graduate courses. It is understood that the minimum course requirements for the intended degree, as specified below, apply to well-prepared students.  

Test score required:  Highly Encouraged  

Applicants are highly encouraged to take the GRE General Test (Verbal, Quantitative, and Analytical Writing), but the GRE score requirement may be waived upon request. A combined score of greater than 300 on the Verbal and Quantitative portions of the exam is advisable based on our experience with student success in the program.  

Deadlines:  University  deadlines  apply.  

Application procedure : Applicants should secure a PhD supervisor prior to submitting an application . PhD applicants without an agreed faculty supervisor will not be considered for admission. Please contact relevant faculty members directly to inquire about PhD supervision. You may find a complete list of Geoscience faculty, along with their contact information and research interests, on the Geoscience Faculty web page.  

Contact Information

Leah Thompson Email: [email protected] Phone: 972-883-2413 Office: ROC 2.301W

School of Natural Sciences and Mathematics The University of Texas at Dallas 800 W Campbell Rd Richardson, TX 75080-3021

nsm.utdallas.edu

Request More Information

We have received your request for more information. Our admissions team will contact you soon to share details about pursuing your academic goals at UT Dallas.

The University of Texas at Dallas respects your right to privacy . By submitting this form, you consent to receive emails and calls from a representative of the University.

* Required Field

• skip navigation
• Privacy Policy
• Accessibility
• search search
• Campusplan Campus Map

Applied Geophysics

• Prospective students
• Current students

The research section Applied Geophysics focuses on the development of seismic modelling and full waveform inversion methods and their application to a broad range of spatial scales, including non-destructive material testing, shallow targets in environmental geophysics, and imaging of the earth crust. 

Publications

Master's and diploma theses, bachelor's theses.

Attention! Your ePaper is waiting for publication!

By publishing your document, the content will be optimally indexed by Google via AI and sorted into the right category for over 500 million ePaper readers on YUMPU.

This will ensure high visibility and many readers!

Your ePaper is now published and live on YUMPU!

You can find your publication here:

Share your interactive ePaper on all platforms and on your website with our embed function

Ph.D. Thesis - Geophysics - Colorado School of Mines

• gradiometry
• underdetermined
• geophysics.mines.edu

Create successful ePaper yourself

Turn your PDF publications into a flip-book with our unique Google optimized e-Paper software.

CGEM<br />

<strong>Ph</strong>.D. <strong>Thesis</strong><br />

<strong>Colorado</strong> <strong>School</strong> <strong>of</strong> <strong>Mines</strong><br />

Center for Gravity, Electrical<br />

& Magnetic Studies<br />

Nonlinear model appraisal<br />

in gravity gradiometry<br />

imaging; properties and<br />

modeling <strong>of</strong> the resolution<br />

matrix<br />

Barry Kirkendall<br />

Department <strong>of</strong> <strong>Geophysics</strong><br />

Golden, CO 80401<br />

http://www.geophysics.mines.edu/cgem

Defended: May 04, 2007<br />

Co-Advisors:<br />

Committee Chair:<br />

Minor:<br />

Committee Members:<br />

Pr<strong>of</strong>. Yaoguo Li (GP)<br />

Pr<strong>of</strong>. Gary Olhoeft (GP)<br />

Dr. Dag Nummedal (ADMIN)<br />

Pr<strong>of</strong>. Jason Liu (MATH)<br />

Pr<strong>of</strong>. Tom Davis (GP)<br />

Pr<strong>of</strong>. Paul Sava (GP)<br />

Dr. David Simons (LLNL)<br />

NONLINEAR MODEL APPRAISAL IN GRAVITY GRADIOMETRY<br />

IMAGING; PROPERTIES AND MODELING OF THE<br />

RESOLUTION MATRIX<br />

by<br />

Barry Kirkendall

Copyright by Barry Kirkendall 2007<br />

All Rights Reserved

A thesis submitted to the Faculty and Board <strong>of</strong> Trustees <strong>of</strong> the <strong>Colorado</strong> <strong>School</strong> <strong>of</strong><br />

<strong>Mines</strong> in partial fulfillment <strong>of</strong> the requirements for the degree <strong>of</strong> Doctor <strong>of</strong> <strong>Ph</strong>ilosophy<br />

(<strong>Geophysics</strong>).<br />

Golden, <strong>Colorado</strong><br />

Date: May 04, 2007<br />

Author: Barry Kirkendall<br />

<strong>Thesis</strong> Advisor: Dr. Yaoguo Li<br />

<strong>Thesis</strong> Advisor: Dr. Gary Olhoeft<br />

Approved: Dr. Terrence K. Young<br />

Pr<strong>of</strong>essor and Chair<br />

ABSTRACT<br />

In order to study new methods <strong>of</strong> linear and nonlinear error analysis, or model appraisal,<br />

this research uses the framework <strong>of</strong> imaging fissile materials within cargo shipping<br />

containers. I initially propose a gravity gradiometry imaging system to measure the<br />

density distribution within cargo containers and carry out nonlinear geophysical inversion<br />

to recover a model showing the location and value <strong>of</strong> anomalous density signatures.<br />

Gravity gradiometry is clearly shown to have the ability, in the proposed configuration, to<br />

detect high density materials which are possibly fissile in nature. In order to more<br />

accurately recover realistic container geometries, I develop a means to favor the recovery<br />

<strong>of</strong> sharp, rather than blurred, models. While shaper models reduce the uncertainty <strong>of</strong> the<br />

solution, the means to achieve them introduces significant nonlinearity to the problem. I<br />

then develop the centerpiece <strong>of</strong> the thesis which is a set <strong>of</strong> tools used in nonlinear model<br />

appraisal; the resolution matrix for confidence in location and funnel analysis for<br />

confidence in the recovered values. In addition to developing this model appraisal toolset<br />

to the gravity gradient problem, another major part <strong>of</strong> this research is the mathematical<br />

study <strong>of</strong> the symmetry and stability <strong>of</strong> the resolution matrix as a function <strong>of</strong> the ability to<br />

recover sharp models, or L P -norm. After mathematically characterizing the resolution<br />

matrix, I generalize it to two-dimensions, thus eliminating the inherent non-uniqueness<br />

and provide a foundation for extending this work to other physics such as diffusion<br />

electromagnetics. Within this two-dimensional space, the distributions resulting from<br />

two distinct model classes are modeled as a function <strong>of</strong> L P -norm. Aside from numerical<br />

interests, the generalized distributions provide the ability to predict a computationally<br />

intensive high performance model (L 1 -norm) from a less computationally intensive lower<br />

performance model (L 2 -norm). For consistency, the two-dimensional modeling results<br />

are directly applied back into the three-dimensional problem for validation. Also<br />

discussed are practical considerations <strong>of</strong> large-scale three-dimensional calculations that<br />

show a balance between L P -norm and model performance and suggest L 1.1 -norm<br />

solutions be cost substituted for L 1 -norm solutions. Finally, consideration is given to<br />

engineering issues for the construction <strong>of</strong> this imaging system including a flowchart <strong>of</strong><br />

proposed operations and risk analysis. I show that while atmospheric fluctuations will<br />

not affect the sensors, physical impacts to the system, resulting in correlated noise, will<br />

require the container to be rescanned since the data acquisition rate is too low to allow<br />

noise filtering. With the system described in this research, and the use <strong>of</strong> nonlinear<br />

model appraisal tools developed, dense materials that are likely fissile can be detected in<br />

sizes well below 15 cm x 15 cm x 15 cm given the conservative sensor configurations in<br />

this thesis. It is a simple task to decrease this detection size through the addition <strong>of</strong><br />

sensor locations. I finally argue if this technique is used in complement to current<br />

radiological techniques, the false positive detection rates will decrease considerably.<br />

TABLE OF CONTENTS<br />

ABSTRACT………………………………………………………………………………………<br />

LIST OF FIGURES………………………………………………………………………………<br />

LIST OF TABLES………………………………………………………………………………..<br />

ACKNOWLEDGEMENTS………………………………………………………………………<br />

iii<br />

viii<br />

x<br />

xi<br />

Chapter 1 INTRODUCTION……………………………………………………………………. 1<br />

Chapter 2 IMAGING CARGO CONTAINERS USING GRAVITY GRADIOMETRY………. 5<br />

2.1 Introduction…………………………………………………………………………….. 6<br />

2.2 Gravity Gradiometry Technique……………………………………………………….. 8<br />

2.3 Inversion Algorithm to Construct Density Distribution……………………………….. 9<br />

2.3.1 Bound Constrained Inversion with Mean-Square Estimator…………………. 13<br />

2.3.2 Bound Constrained Inversion with Robust Estimator………………………... 15<br />

2.4 A Note on Non-Uniqueness and Global Minima………………………………………. 17<br />

2.5 Conclusion……………………………………………………………………………… 18<br />

2.6 Acknowledgements…………………………………………………………………….. 19<br />

2.7 References……………………………………………………………………………… 19<br />

Chapter 3 APPRAISAL OF RECOVERED MODELS……………………………………….. 31<br />

3.1 Introduction…………………………………………………………………………….. 32<br />

3.2 Funnel Analysis………………………………………………………………………… 32<br />

3.3 Construction <strong>of</strong> Unconstrained (linear) and Bound-Constrained (nonlinear) Resolution 35<br />

Matrices…………………………………………………………………………………<br />

3.4 Analysis <strong>of</strong> Model Appraisal…………………………………………………………… 39<br />

3.5 Experimental Validation………………………………………………………………... 41<br />

3.6 Conclusions…………………………………………………………………………….. 41<br />

3.7 Acknowledgements…………………………………………………………………….. 43<br />

3.8 References……………………………………………………………………………… 43<br />

Chapter 4 SYMMETRY AND STABILITY PROPERTIES OF RESOLUTION MATRICES<br />

51<br />

IN GEOPHYSICAL INVERSION…………………………………………………..<br />

4.1 Introduction…………………………………………………………………………….. 52<br />

4.2 Geophysical Technique and Model…………………………………………………….. 53<br />

4.3 Inversion Technique……………………………………………………………………. 53<br />

4.4 Formation <strong>of</strong> the Resolution Matrix……………………………………………………. 54<br />

4.4.1 Overdetermined and Determined Linear Cases with No Regularization……. 55<br />

4.4.2 Underdetermined Linear Case………………………………………………. 57<br />

4.4.3 Underdetermined Nonlinear Case with Bound Constraints……….………… 57<br />

4.4.4 Underdetermined Nonlinear Case with Bound Constraints and L P -norm…… 58<br />

4.4.5 Assumptions and Limitations in the Formation <strong>of</strong> the Resolution Matrix…… 59<br />

4.5 Symmetry and Scaling Properties <strong>of</strong> the Resolution Matrix…………………………… 60<br />

4.5.1 Numerical Evaluation <strong>of</strong> Asymmetry Versus p-value…….…………………. 60<br />

4.5.2 Resolution Matrix Sensitivity to Discretization………………………………. 62<br />

4.5.3 Quantifying the Resolution from R…………………………………………… 63<br />

4.6 Condition Number and Eigenvalues <strong>of</strong> Resolution Matrices………………………..…. 64<br />

4.7 Conclusions……………………………………………………………..……………… 65<br />

4.8 Acknowledgements…………………………………………………………………….. 67<br />

4.9 References……………………………………………………………………………… 67<br />

Appendix 4.A Determination <strong>of</strong> Symmetry for Underdetermined and Overdetermined<br />

Systems………………………………………………………………………………<br />

Chapter 5 DISTRIBUTIONAL MODELING OF THE RESOLUTION MATRIX……………<br />

5.1 Introduction…………………………………………………………………………..<br />

5.2 Uniqueness <strong>of</strong> the Two-Dimensional Gravity Gradient Inverse…………………….<br />

5.3 Two-Dimensional Gravity Gradient Problem………………………………………..<br />

5.4 Mass Integration Within the Resolution Matrix…………………………………….<br />

5.5 Distributions from Type-1 and Type-2 as Function <strong>of</strong> L P -norm…………………….<br />

5.6 The Generalized Gaussian Distribution (GGD)………………………………………<br />

5.7 Distributional Modeling with GGD…………………………………………………..<br />

76<br />

77<br />

78<br />

80<br />

82<br />

83<br />

84<br />

85<br />

5.8 Application <strong>of</strong> 2-D Results to 3-D Gravity Gradiometry Imaging Problem…………<br />

5.9 Conclusions…………………………………………………………………………..<br />

5.10 Acknowledgements…………………………………………………………………..<br />

5.11 References…………………………………………………………………………….<br />

Chapter 6 PRACTICAL ASPECTS OF LARGE-SCALE 3-D L P -NORM COMPUTATIONS..<br />

6.1 Computation Time as a Function <strong>of</strong> L P -norm………………………………………...<br />

6.2 Model Performance as a Function <strong>of</strong> L P -norm……………………………………..<br />

6.3 Mass Integration Within Resolution Matrix…………………………………………<br />

6.4 Practical Error Considerations………………………………………………………<br />

6.5 Wavelet Compression to Create Sparse Matrices……………………………………<br />

6.6 Acknowledgements…………………………………………………………………..<br />

6.7 References…………………………………………………………………………….<br />

Chapter 7 ENGINEERING ISSUES ASSOCIATED WITH THE DEVELOPMENT OF A<br />

GRAVITY GRADIOMETRY IMAGING SYSTEM………………………………..<br />

7.1 Sensor Quality and Location………………………………………………………….<br />

7.2 Noise………………………………………………………………………………….<br />

7.2.1 Noise from Atmospheric Fluctuations………………………………………..<br />

7.3 Frequency Response <strong>of</strong> Sensor……………………………………………………….<br />

7.4 Time Optimization……………………………………………………………………<br />

7.5 Probabilistic Risk Assessment for Deployed Imaging System………………………<br />

7.6 Technological Requirements for Successful Demonstration <strong>of</strong> Concept……………<br />

7.7 Flowcharts………….…………………………………………………………………<br />

7.8 Conclusions…………………………………………………………………………..<br />

7.9 Acknowledgements…………………………………………………………………..<br />

7.10 References…………………………………………………………………………….<br />

Chapter 8 GENERAL CONCLUSIONS AND NEAR-FUTURE RESEARCH………………...<br />

86<br />

87<br />

88<br />

121<br />

122<br />

123<br />

124<br />

125<br />

131<br />

132<br />

134<br />

135<br />

136<br />

137<br />

138<br />

140<br />

141<br />

143<br />

LIST OF FIGURES<br />

Figure 2.1 Geometry <strong>of</strong> proposed technique and axis coordinates……………........................... 22<br />

Figure 2.2 Discretization and proposed sensor placement for imaging system............................ 23<br />

Figure 2.3 Model <strong>of</strong> Plutonium pit and depleted Uranium rods………………………………... 24<br />

Figure 2.4 T YZ -component <strong>of</strong> the resulting synthetic dataset…………………........................... 25<br />

Figure 2.5 Recovered model with bound constraints and p=2………………….......................... 26<br />

Figure 2.6 Conceptual explanation <strong>of</strong> Huber norm……………………………………………... 27<br />

Figure 2.7 Recovered model with bound constraints and p=1………………………………….. 28<br />

Figure 2.8 Anatomy <strong>of</strong> a piezoelectric accelerometer………………………………………….. 29<br />

Figure 2.9 Manner <strong>of</strong> using two accelerometers to measure gravity gradient………………….. 30<br />

Figure 3.1 Funnel analysis results from Plutonium and Uranium models……............................ 45<br />

Figure 3.2 Orthogonal slices through the resolution matrix as a function <strong>of</strong> L P norm…………. 46<br />

Figure 3.3 Contoured X-Y coordinate slices through resolution matrix to emphasize L P -norm.. 47<br />

Figure 3.4 Increasingly complicated starting model used for experimental validation………… 48<br />

Figure 3.5 Recovered model from Figure 3.4 using bound constraints and p=1………………. 49<br />

Figure 4.1 Starting model for resolution matrix studies………………………………………... 69<br />

Figure 4.2 Discretization for resolution matrix studies…………………………………………. 70<br />

Figure 4.3 Four resolution matrices as a function <strong>of</strong> L P -norm…………………......................... 71<br />

Figure 4.4 Histogram <strong>of</strong> resolution matrix amplitudes as function <strong>of</strong> L P -norm………………... 72<br />

Figure 4.5 Skewness index <strong>of</strong> resolution matrix as function <strong>of</strong> L P -norm………........................ 73<br />

Figure 4.6 X-coordinate resolution in model space for j th model cell………………………….. 74<br />

Figure 4.7 Eigenvalues <strong>of</strong> resolution matrix as function <strong>of</strong> L P -norm…………………………... 75<br />

Figure 5.1 Planview <strong>of</strong> the underdetermined system…………………………………………… 90<br />

Figure 5.2 Planview <strong>of</strong> the determined system…………………………………........................ 91<br />

Figure 5.3 Planview <strong>of</strong> the overdetermined system……………………………………………. 92<br />

Figure 5.4 Model discretization and Type-1 model……………………………………………. 93<br />

Figure 5.5 Model discretization and Type-2 model……………………………………………. 94<br />

Figure 5.6 Recovered model for the type-1 underdetermined problem for L 1 -norm and L 2 -<br />

norm…………………………………………………………………………………<br />

Figure 5.7 Recovered model for the type-1 determined problem for L 1 -norm and L 2 -norm…… 96<br />

95<br />

Figure 5.8 Recovered model for the type-1 overdetermined problem for L 1 -norm and L 2 -norm 97<br />

Figure 5.9<br />

Figure 5.10<br />

Linear distribution plots from resolution matrix <strong>of</strong> type-1 underdetermined<br />

problem……………………………………………………………………………….<br />

Log distribution plots from resolution matrix <strong>of</strong> type-1 underdetermined<br />

Figure 5.11 Linear distribution plots from resolution matrix <strong>of</strong> type-1 determined problem…… 100<br />

Figure 5.12 Log distribution plots from resolution matrix <strong>of</strong> type-1 determined problem……… 101<br />

Figure 5.13<br />

Figure 5.14<br />

Linear distribution plots from resolution matrix <strong>of</strong> type-1 overdetermined<br />

Log distribution plots from resolution matrix <strong>of</strong> type-1 overdetermined<br />

Figure 5.15 Mass integration for type-1 problem………………………………………………… 104<br />

Figure 5.16 Mass integration for type-2 problem………………………………………………… 105<br />

Figure 5.17 Tikhonov curve for the type-1 overdetermined problem…………............................. 106<br />

Figure 5.18 Comparison <strong>of</strong> model and data for type-1 underdetermined problem for L 1 -norm… 107<br />

Figure 5.19 Comparison <strong>of</strong> model and data for type-1 underdetermined problem for L 2 -norm… 108<br />

Figure 5.20 Plot <strong>of</strong> required values <strong>of</strong> q in type-1 GGD modeling………………………………. 109<br />

Figure 5.21 Plot <strong>of</strong> required values <strong>of</strong> in type-1 GGD modeling……………….......................... 110<br />

Figure 5.22 Plot <strong>of</strong> required amplitude correction in type-1 GGD modeling……......................... 111<br />

Figure 5.23 Plot <strong>of</strong> required values <strong>of</strong> q in type-2 GGD modeling………………………………. 112<br />

Figure 5.24 Plot <strong>of</strong> required values <strong>of</strong> in type-2 GGD modeling……………….......................... 113<br />

Figure 5.25 Plot <strong>of</strong> required amplitude correction in type-2 GGD modeling……......................... 114<br />

Figure 5.26 3-dimensional extension <strong>of</strong> 2-dimensional problem – geometry and data………….. 115<br />

Figure 5.27 Discretization <strong>of</strong> the three-dimensional extension problem…………………………. 116<br />

Figure 5.28<br />

Figure 5.29<br />

Figure 5.30<br />

Figure 5.31<br />

Comparison between the two-dimensional and three-dimensional horizontal<br />

modeling, L 1 -norm…………………………………………………………………...<br />

modeling, L 2 -norm…………………………………………………………………<br />

Comparison between the two-dimensional and three-dimensional vertical<br />

modeling, L 2 -norm…………………………………………………………………..<br />

Figure 6.1 Computation time as a function <strong>of</strong> L P -norm for all three systems ….......................... 126<br />

Figure 6.2 Linear distribution through j th cell from the j th column <strong>of</strong> R as a function <strong>of</strong> L P -<br />

norm…………………………………………………..................................................<br />

Figure 6.3 Log distribution through j th cell from the j th column <strong>of</strong> R as a function <strong>of</strong> L P -<br />

Figure 6.4 Mass integration curves showing equivalence <strong>of</strong> L 1.1 -norm and L 1.0 -norm………… 129<br />

98<br />

99<br />

102<br />

103<br />

117<br />

118<br />

119<br />

120<br />

127<br />

128<br />

LIST OF TABLES<br />

Table 4.1 RMS comparison <strong>of</strong> resolution matrices with different discretization quantities…... 63<br />

Table 4.2 Condition number for several resolution matrices as a function <strong>of</strong> L P -norm……….. 65<br />

Table 7.1 Estimation <strong>of</strong> speed-up as function <strong>of</strong> number or processors using Amdahl’s law…. 135<br />

Table 7.2 Risk analysis for gravity gradiometry imaging system……………………………... 136<br />

Table 7.3 Engineering flowchart for gravity gradiometry imaging system……………………. 138<br />

Table 7.4 Computations flowchart for gravity gradiometry imaging system…………………. 138<br />

Table 7.5 Operations flowchart for gravity gradiometry imaging system…………………….. 139<br />

ACKNOWLEDGEMENTS<br />

Throughout my <strong>Ph</strong>.D. study at the <strong>Colorado</strong> <strong>School</strong> <strong>of</strong> <strong>Mines</strong> (CSM), I have also<br />

maintained my position as a physicist at the Lawrence Livermore National Laboratory<br />

(LLNL) in a half-time capacity <strong>of</strong> 20 hours per week. The LLNL Advanced Study<br />

Program awarded me the leniency to study outside California as well as financially cover<br />

my tuition and fees, for which I am deeply appreciative. Although working while<br />

studying required more time, it also allowed me to maintain perspective and have access<br />

to the many brilliant minds at LLNL and Lawrence Berkeley National Laboratory for<br />

discussions. However, without certain individuals, I wouldn’t have been able to create or<br />

maintain this arrangement.<br />

<strong>Ph</strong>ilip Harben has been my group leader and mentor since I started at LLNL in 1998<br />

and has supported me both logistically and scientifically while I was studying in<br />

<strong>Colorado</strong>. <strong>Ph</strong>il helped me maintain my funding during heavy load periods such as my<br />

qualifying exams, smoothed over blown deadlines with sponsors, always kept looking for<br />

new proposals for me to write, and was a great friend and guide throughout. Without<br />

<strong>Ph</strong>il, I would have had to take a leave <strong>of</strong> absence from LLNL during my <strong>Ph</strong>.D. study. Pat<br />

Berge and Norm Burkhard at LLNL also were instrumental in receiving the Advanced<br />

Study Program. The early days <strong>of</strong> Fall, 2004, were the most difficult to balance work and<br />

study and I’m grateful to my past secretary Floralei Eckert, Adrienne Ridolfi, Arleen<br />

Allsup, Liz Garrett, and Barbara Gonzales in EODD for solving a huge amount <strong>of</strong><br />

logistical issues.<br />

Although I came back to study under my M.Sc. advisor, Pr<strong>of</strong>essor Gary Olhoeft, I<br />

switched into a dual-advisor mode in 2005 with Pr<strong>of</strong>essor Yaoguo Li. Gary allowed to<br />

me teach his EM course in 2004 and provided direction, encouragement, and<br />

opportunities for which I am deeply grateful. All the engineering research in this thesis<br />

was advised by Gary. Yaoguo Li is the rare individual who conducts brilliant research,<br />

maintains the coolest research group in geophysics (you know it’s true, RCP and A-<br />

team), deeply cares about his students’ progress and learning, is a machine for creating<br />

luminous ideas, all while maintaining a quiet integrity and reflective character. I’ve been<br />

seriously fortunate to study under Yaoguo Li who advised Chapters two through five.<br />

I’m also grateful to my committee members: Jason Liu, my mathematics minor advisor<br />

who taught me parallel computing which I use <strong>of</strong>ten, Tom Davis, who has advised me as<br />

far back as 1995 and is solely responsible for my falsely stereotyping the Canadian as<br />

eternally cool, Dag Nummedal, my committee chair who thought <strong>of</strong> some shockingly<br />

accurate questions in preparing me for my first qualifying exam, Paul Sava, who is a<br />

great person to discuss new ideas with, and David Simons at LLNL, who taught me that<br />

retirement is far more dangerous than working. Sara Summers in <strong>Geophysics</strong> has also<br />

helped me with little things such as correspondence with LLNL to big things such as<br />

helping me efficiently advance to candidacy. If Sara had gone into a growth industry,<br />

amazon.com would probably have biographic books written about her resourcefulness<br />

and organization about now. The department chair, Terry Young, has also helped me<br />

study efficiently and I’m also grateful for him not making a big deal <strong>of</strong> me leaving for a<br />

month <strong>of</strong> travel in 2006.<br />

My friends and colleagues aren’t half bad either. I met my fiancée, Whitney Goodrich,<br />

when she laughed at my apple joke during class in 2004, and she has since made my life<br />

far more pr<strong>of</strong>ound and meaningful than I could have ever known had I not met her.<br />

Whitney’s dog, The Pikus, has somehow provided inspiration by sheer wanton<br />

obliteration <strong>of</strong> anything made <strong>of</strong> paper. The Pikus has recently forayed her tastes into<br />

aluminum and plastics. My good friends such as Mike, H-Lin, and Pablo for letting me<br />

stay at their place during California visits, Ed and Lucy Jenner with little Graham, Ian,<br />

and the new kid, Kasper and Mila, the notorious JOT, mcasey, Rich, Eju, scrappy,<br />

Special K, Jeongmin and his lingering credit trail, V-dinero, TLC, Kurang, Xiaoxia who<br />

confused me into using her name to thank people in China, Misac who will someday<br />

admit his best memories aren’t actually from Berkeley but from CSM, Adel Zohdy who<br />

makes you feel <strong>of</strong> seeing an old friend during afternoon conversations, the stone-coldest<br />

Azerbaijan Mafia Trio west <strong>of</strong> Baku, the Brazilian contingency who don’t share love for<br />

Argentina fútbol, and the waning Dutch CSM-geophysics empire; chunks.<br />

Chapter 1<br />

INTRODUCTION<br />

It is well recognized that halting the production and transport <strong>of</strong> nuclear materials<br />

is the most important step in limiting the proliferation <strong>of</strong> nuclear devices. Whether<br />

nuclear materials are transported before or after assembly is inconsequential. Nuclear<br />

weapons either use fusion or fission as the primary method <strong>of</strong> energy release. Fission<br />

devices use Actinide Series metals, and their isotopes, such as Uranium as the entire<br />

source <strong>of</strong> energy release. Fusion devices use similar Actinide Series metals such as<br />

Plutonium in order to provide sufficient activation energy to fuse light nuclei together<br />

and release high energy neutrons. In both cases, the Actinide Series metal required is<br />

referred to as fissile material. Such fissile materials have an important feature I propose<br />

to use for their detection; an extremely high density, as compared to other materials, and<br />

thus a high gravitational signature contrast.<br />

In Chapter two, I propose an inspection technique with the ability to passively<br />

image these density signature contrasts. The image is formed with measurements made<br />

with the gradient <strong>of</strong> the gravity field, a quantity far easier to measure than the traditional<br />

gravity field using newly available commercial hardware. I acknowledge that items<br />

within a cargo container have realistic shapes; sharp edges and complex geometries with<br />

low-density air gaps separating items <strong>of</strong> higher density. Therefore, I develop a method to<br />

favor the recovery <strong>of</strong> sharp edges within images, which I call the Huber norm. It is also<br />

important to remember that negative mass has not yet been physically observed, even<br />

though its properties have been speculated (1.1). This means that items within a cargo<br />

container are assumed to have positive mass, and therefore a positive density. I therefore<br />

use a mathematical technique in Chapter two which forces the recovered densities to be<br />

constrained between zero and a realistic upper limit <strong>of</strong> densities commonly found on<br />

earth, approximately 20 g/cm 3 .<br />

Chapter three is the most critical in addressing the accuracy <strong>of</strong> the results <strong>of</strong><br />

Chapter two. Supposing an image were recovered which indicated an abnormally high<br />

density region, possibly indicative <strong>of</strong> fissile material. The operator would be required to<br />

accurately know the likelihood that fissile material is present and the precise location <strong>of</strong><br />

the material to decrease the time required for additional inspection and decrease false<br />

positive results. I propose and develop error analysis solutions for these requirements in<br />

Chapter three. These solutions are the resolution matrix, for the study <strong>of</strong> the precise<br />

location, and funnel analysis, for the study that the anomaly is truly fissile material.<br />

These two tools are developed under the subject area <strong>of</strong> nonlinear model appraisal, which<br />

is its own area <strong>of</strong> active research within the geophysical inversion community. Finally,<br />

two synthetic examples are generated which demonstrate the ability provide to error<br />

analysis in the cargo container images. A flowchart in Chapter seven contains the entire<br />

process <strong>of</strong> successfully developing a prototype system and applying the nonlinear model<br />

appraisal techniques developed in this thesis.<br />

Chapters four and five are increasingly theoretical. In Chapter four, I study<br />

several algebraic and distributional properties <strong>of</strong> the linear and nonlinear resolution<br />

matrix. Although these attractive mathematical results do not readily relate to the<br />

inspection technique described above, they could be used to allow an equivalent error<br />

analysis using only a partial construction <strong>of</strong> the resolution matrix, potentially saving<br />

significant time in error analysis. In particular, I examine the symmetry <strong>of</strong> the resolution<br />

matrix as a function <strong>of</strong> the model sharpness. I also look at the stability <strong>of</strong> the resolution<br />

matrix; its sensitivity to changes in the model discretization, its condition number, and<br />

associated eigenvalues.<br />

One <strong>of</strong> the foundations <strong>of</strong> Chapter two is the mathematical work to favor recovery<br />

<strong>of</strong> the sharp density contrasts typical <strong>of</strong> a realistic cargo container. Without this effort,<br />

the recovered images tend to be diffused and characterized by a lack <strong>of</strong> sharpness. There<br />

are, as one should expect in any performance gain, considerable increases in computation<br />

time involved with increasing the sharpness <strong>of</strong> the recovered image. Therefore, I seek to<br />

find a relation between the faster calculated model characterized by diffused edges and<br />

the more computationally intensive model characteristic by more realistic sharp edges.<br />

The idea is that after determining this relationship, I can predict the cost intensive sharpmodel<br />

response from the computationally efficient diffused-model at no additional cost<br />

for multiple classes <strong>of</strong> problems. To determine the relationship, I use an intriguing<br />

mathematical relationship known as the Generalized Gaussian Distribution to establish<br />

empirical relationships between the model. One other note about the research in Chapter<br />

five; it’s done in two-dimensions so that the solution is unique. Ostensibly, this provides<br />

a strong platform for extending this work to other physics such as diffusion<br />

electromagnetics. However, I also apply the results back to the first three dimensional<br />

problem introduced in Chapter three to validate the empirical results and to maintain the<br />

focus on the physics <strong>of</strong> the three-dimensional gravity gradient problem.<br />

This project has several broad impacts. First and foremost, this research generates<br />

an efficient and safe passive inspection technique for the detection and location <strong>of</strong> fissile<br />

materials in cargo containers. Secondly, the nonlinear inversion methodology and model<br />

appraisal developed is applicable to a variety <strong>of</strong> geophysical data arising from exploration<br />

problems, engineering problems, and other applications. Thirdly, investigation <strong>of</strong> the<br />

distributional, symmetry, and stability properties <strong>of</strong> the resolution matrix contributes to<br />

an active research field on several levels. Although the work on nonlinear model<br />

appraisal can be extended to other physics, the use <strong>of</strong> gravity gradiometry provides a<br />

stable platform for this research. As density inversion using gravity gradiometry data is<br />

physically linear, we can understand the resolution matrix without the complication <strong>of</strong><br />

nonlinearity. Yet, the presence <strong>of</strong> density bound constraints and the recovery <strong>of</strong> sharp<br />

density contrasts provides significant nonlinearity and insight into the structure and<br />

distributional nature <strong>of</strong> the nonlinear resolution matrix.<br />

This thesis can be viewed as two research efforts culminating in one solution; a<br />

proposed system to image fissile material within cargo containers and the development<br />

and study <strong>of</strong> a toolbox for generalized nonlinear model appraisal which provides critical<br />

error analysis for the recovered images.<br />

1.1 References<br />

(1.1) Bondi, H., 1957, Negative Mass in General Relativity, Reviews <strong>of</strong> Modern <strong>Ph</strong>ysics, Vol. 29, No.3,<br />

pp. 423-428<br />

Chapter 2<br />

IMAGING CARGO CONTAINERS USING GRAVITY GRADIOMETRY<br />

Identifying fissile materials inside cargo shipping containers is a current national<br />

security need. I propose using the geophysical technique <strong>of</strong> gravity gradiometry to image<br />

cargo shipping containers for the purpose <strong>of</strong> detecting high-density materials. I focus on<br />

developing the necessary numerical algorithms and carrying out feasibility study without<br />

being concerned with engineering, instrumentation, and application issues. To obtain<br />

realistic images with sharp boundaries, robust estimators are applied to the model<br />

objective function <strong>of</strong> the inversion operator and coupled with a Huber norm to provide<br />

stable numerical computation. Assuming a realistic data acquisition pattern requiring a<br />

reasonable amount <strong>of</strong> time, I show it is possible to identify high-density materials with a<br />

minimum volume <strong>of</strong> 15 cm x 15 cm x 15 cm. Finally, I provide a recovered density<br />

threshold to suggest the presence <strong>of</strong> high-density materials from an arbitrary recovered<br />

density model and apply this to two examples <strong>of</strong> recovering concealed fissile material<br />

from a cargo container.<br />

This chapter has been accepted for publication:<br />

Kirkendall, B., Li, Y., Oldenburg, D., 2007, Imaging cargo containers using gravity<br />

gradiometry, IEEE Transactions Geoscience and Remote Sensing, 15 p.<br />

2.1 Introduction<br />

Although the technique <strong>of</strong> gravity gradiometry (2.1) is close to one hundred years old,<br />

applications have dramatically increased partly due to recent advances in electronics and<br />

microprocessors. Such applications include airborne based remote sensing (2.2) (2.3),<br />

basin analysis (2.4), marine geophysical surveys (2.5), mining geophysics (2.6), and<br />

borehole geophysics (2.7). These applications rely on the large density contrast <strong>of</strong><br />

geologic targets and the improved accuracy <strong>of</strong> modern gravity gradiometers for sensing<br />

the gradients <strong>of</strong> gravity fields. Because <strong>of</strong> the density variation <strong>of</strong> cargo contents, the<br />

same technology should also be applicable to imaging the cargo containers. The<br />

application <strong>of</strong> gravity gradiometry towards imaging cargo inside metallic shipping<br />

containers has clear advantages over other traditional remote sensing techniques but has<br />

not been studied in scientific literature. The impetus for this research is the current<br />

domestic and international need to develop rapid, non-invasive imaging techniques to<br />

detect fissile material and export controlled items within cargo shipping containers.<br />

The metallic cargo container shell is constructed from a derivative <strong>of</strong> carbon steel,<br />

which precludes the use <strong>of</strong> electric and magnetic techniques due to the high electrical<br />

conductivity, magnetic susceptibility, and variable wall thickness. Low frequency<br />

electromagnetic time- and frequency-domain fields can penetrate the container shell and<br />

remain focused, but the usable frequency must be below 300 Hz (2.8), which does not<br />

allow sufficient electromagnetic induction or resolution. Seismic techniques are also not<br />

applicable as the items inside a cargo container have poor mechanical coupling with the<br />

container. Neutron and gamma imaging have been widely studied, but they generate<br />

radiation that could be problematic in the presence <strong>of</strong> biological material or sensitive<br />

integrated circuits (2.9). The high density <strong>of</strong> fissile materials in contrast to common<br />

commercial goods suggests that precise measurement <strong>of</strong> the gravity field produced by<br />

cargo contents may provide an alternative inspection technique. For example, Plutonium,<br />

a fissile material, has a density <strong>of</strong> 19.8 grams/cm 3 , or g/cm 3 , whereas the density <strong>of</strong> water<br />

and aluminum are, respectively, 1.0 g/cm 3 and 2.7 g/cm 3 . Detection <strong>of</strong> these density<br />

contrasts can be made with either traditional gravimeters or gravity gradiometers. The<br />

former measures the vertical component <strong>of</strong> the gravity field, and the latter senses the<br />

spatial gradient <strong>of</strong> gravitational acceleration produced by a mass distribution. Modern<br />

gravity gradiometers typically measure with identical pairs <strong>of</strong> accelerometers rotating at a<br />

constant angular velocity (2.6) but can also measure by precisely quantifying the<br />

deflection, or scissoring, <strong>of</strong> orthogonal bars mounted inside a cryogenic container.<br />

I propose an inspection technique Fig. 2.1 using gravity gradiometry to identify the<br />

presence <strong>of</strong> fissile materials in cargo containers, and conduct numerical simulations to<br />

ascertain the feasibility <strong>of</strong> the proposed technique. Since this is a feasibility study<br />

focusing on theoretical and numerical aspects, issues connected with development <strong>of</strong> a<br />

prototype are left for future research. The method first reconstructs a 3D density<br />

distribution within a synthetic cargo container by performing a generalized inversion <strong>of</strong><br />

gravity gradient data measured from an array <strong>of</strong> gradiometry sensors as a cargo container<br />

is passed between them. The total mass within the cargo container, configuration <strong>of</strong> mass<br />

distribution and lower and upper bounds <strong>of</strong> identified high-density regions are then<br />

examined to infer the possible presence <strong>of</strong> fissile materials. In this Chapter, I review the<br />

gravity gradiometry technique, the inversion algorithm and associated techniques<br />

developed and implemented by the authors used in constructing 3D density distributions,<br />

and methods developed to estimate the resolution and uncertainty <strong>of</strong> the inverted density<br />

distribution. A synthetic example is shown to illustrate the feasibility <strong>of</strong> the proposed<br />

technique.<br />

Finally, a note on standardizing nomenclature. The vector norm commonly referenced<br />

in literature as the L P -norm, l P -norm, or p-value are all equivalent despite obvious<br />

differences in appearance. The concept originates within the Lebesgue measure <strong>of</strong><br />

mathematics, and I henceforth refer to this measure as the L P -norm ( 1 ≤ p < ∞) . Henri<br />

Léon Lebesgue (c. 1875 – 1941) was a considerable French mathematician whose work<br />

spanned vast areas covered by measure theory and integration spaces. The Lebesgue<br />

measure, or LP-norm, is the standard way <strong>of</strong> assigning a length, area or volume to subsets<br />

<strong>of</strong> Euclidean space.<br />

2.2 Gravity Gradiometry Technique<br />

The technique <strong>of</strong> gravity gradiometry (2.10) is based on multiple point measurements<br />

<strong>of</strong> the gravity field and calculating the local gradient from those data. Figures 2.8 and 2.9<br />

show the manner in which one commercial instrument measures the gravity gradient.<br />

Several advantages from specifically measuring the gravity field gradient are increased<br />

measurement stability, rejection <strong>of</strong> common mode and vibrational noise, increased<br />

resolution due to a higher decay rate <strong>of</strong> the gradient field, and higher spatial sampling.<br />

Whereas gravity is measured in units <strong>of</strong> acceleration, m/s 2 , the gradient <strong>of</strong> gravity is<br />

measured in 1/s 2 . A unit reflecting the commonly encountered magnitude is eötvös:<br />

−9<br />

10<br />

1 eötvös =<br />

second<br />

2<br />

−4<br />

10 mGal<br />

=<br />

meter<br />

Current gravity gradiometers can have an instrument noise level <strong>of</strong> less than 1 eötvös<br />

during stationary data acquisition (2.11). One measurement can include gradients <strong>of</strong> all<br />

three Cartesian components <strong>of</strong> the gravity field to form a second order tensor whose<br />

elements are the second partial derivatives <strong>of</strong> the gravity potential, Φ ,<br />

⎛ ⎡∂<br />

Φ ⎤<br />

⎜<br />

⎢ 2 ⎥<br />

⎜ ⎣ ∂x<br />

⎦<br />

⎜ 2<br />

∂ Φ<br />

T = ∇∇Φ = ⎜<br />

⎜ ∂y∂x<br />

⎝<br />

∂z∂x<br />

⎡ ∂ Φ ⎤<br />

⎢ ⎥<br />

⎣∂x∂y<br />

⎡∂<br />

⎣ ∂y<br />

∂z∂y<br />

⎡ ∂ Φ ⎤⎞<br />

⎟<br />

⎣∂x∂z<br />

⎦⎟<br />

⎢ ⎥ ⎟<br />

⎣∂y∂z<br />

⎦ ⎟<br />

∂ Φ ⎟<br />

∂z<br />

⎠<br />

2.1.<br />

The gravity potential is harmonic and well behaved outside source regions.<br />

Consequently, T is symmetric and traceless. Thus, only the five components indicated<br />

by brackets are independent. Furthermore, a recovered model can be constructed through<br />

the inversion process with any one component <strong>of</strong> T. Additional components both<br />

increase the signal-to-noise ratio and provide further independent spatial information on<br />

the source density. T produced by a point source is related to the mass by<br />

1<br />

T = γm∇∇<br />

r r = γmΓ<br />

, 2.2<br />

−<br />

0<br />

where γ is the gravitational constant = 6.672x10 -8 m 3 /g/s 2 , Γ is the dyadic Green’s tensor,<br />

v<br />

r 0<br />

is the sensor location, and r is the source location. The gravity gradient due to<br />

distributed mass characterized by a density function can be derived using Equation 2.2.<br />

2.3 Inversion Algorithm to Construct Density Distribution<br />

The cargo container is divided into a set <strong>of</strong> prismatic cells by using a 3D orthogonal<br />

mesh and assuming a constant density within each cell (Fig. 2.2). Given this<br />

discretization, a particular component <strong>of</strong> the gradient tensor at a given observation<br />

location, denoted as the i’th datum,<br />

d i<br />

, can be written as,<br />

d<br />

i<br />

= T<br />

KL<br />

M<br />

∑<br />

j=<br />

ρ<br />

j<br />

⎪⎧<br />

⎨<br />

⎪⎩<br />

∫∫∫<br />

V<br />

∂<br />

∂x<br />

K<br />

L<br />

r r<br />

⎪⎫<br />

dV ⎬ =<br />

⎪⎭<br />

ρ G<br />

ij<br />

2.3<br />

In Equation 2.3, ρ j and V j are the density and volume <strong>of</strong> the j th cell, respectively, and<br />

G ij<br />

defined by the expression in braces, quantifies the contribution <strong>of</strong> the j<br />

th model cell to<br />

the i th datum. M is the number <strong>of</strong> model cells and K and L are the indices referring to the<br />

axis directions in the Cartesian coordinate system. Expressed in matrix notation, the<br />

gravity gradient data consisting <strong>of</strong> N observations are given by<br />

v v<br />

d obs = Gρ<br />

+ ε<br />

2.4<br />

where d v<br />

obs<br />

is the measured data vector, ε are the measurement errors, G is the sensitivity<br />

matrix whose elements are<br />

Gij<br />

, Equation 2.3, and<br />

v ρ is a model vector <strong>of</strong> spatially<br />

distributed density values. G contains the physics and geometry <strong>of</strong> the problem and<br />

represents the mapping from model space to data space. One seeks to minimize<br />

r r Gρ<br />

− d<br />

realistic.<br />

by finding<br />

v that predicts important aspects <strong>of</strong> the data and is physically<br />

The standard approach to solving this problem uses the L 2 -norm with some degree <strong>of</strong><br />

regularization (2.12). Anscombe (2.13) discussed the idea behind regularization as a<br />

measured sacrifice <strong>of</strong> model performance for stabilization caused by reasonable<br />

deviations from such model. One chooses to set up the inversion problem with a<br />

Tikhonov regularization approach (2.14) by constructing a model objective function for<br />

the recovered model v ρ , using a data misfit to measure the fit <strong>of</strong> the predicted data to the<br />

measured data, and choosing an optimal regularization parameter that combines the two<br />

quantities. Li and Oldenburg (2.15), (2.16) and Li (2.17) discuss the merits <strong>of</strong> a<br />

particular model objective function in potential field theory applications, which I<br />

generalize to the following form for this research,<br />

r<br />

r r p<br />

r ∂ρ<br />

(<br />

)<br />

φm<br />

( ρ)<br />

= α S ∫∫∫w(<br />

) ρ(<br />

) dV + α x ∫∫∫ w(<br />

V ∂x<br />

r p<br />

α y ∫∫∫ w(<br />

) dV + α z ∫∫∫ w(<br />

) dV<br />

∂y<br />

p<br />

dV +<br />

2.5<br />

In Equation 2.5,<br />

w(r)<br />

is a model cell-specific weighting term. The α parameters allow<br />

the user to choose the type <strong>of</strong> model. For example, increasing values <strong>of</strong> αx, α y , and α z<br />

provide smoother recovered models in respective dimensions, whereas increased α s<br />

attempts to minimize the amplitude <strong>of</strong> the model. I also develop cell weighting in G<br />

from Equation 2.4 which is used to compensate model cells with different distances from<br />

observation locations (2.18). Since the gravity gradiometric field decays with the inverse<br />

<strong>of</strong> the distance cubed (2.18), if distance from the source were not compensated, cells<br />

closest to the observation location would dominate in reproducing data through Equation<br />

2.3. In this scenario, the recovered model would have all the density in the model cells<br />

closest to the surface <strong>of</strong> the container.<br />

Also, whereas Equation 2.5 does not explicitly state that there may be a reference<br />

model, such a model, v ρ 0(<br />

rr ) , can simply be subtracted from v ρ (r r ) within the model<br />

objective function (2.15). Different choices <strong>of</strong> exponent p ∈[ 1, ∞)<br />

in Equation 2.5 define<br />

different measures for the complexity <strong>of</strong> the model. When p=2, Equation 2.5 is the mean<br />

square estimator, or L 2 -norm. If 1≤ p ≤ 2 , Equation 2.5 is characterized as a robust<br />

estimator and I examine the details in a later section.<br />

The additional component for an inversion using the formalism <strong>of</strong> Tikhonov<br />

regularization is a measure <strong>of</strong> difference between observed and predicted data, the data<br />

misfit,<br />

φ −<br />

2.6<br />

d = W d (G ρ d obs)<br />

where d is the measured data and W<br />

d a diagonal matrix whose i th element is 1/σ i ,<br />

where σ i is the standard deviation <strong>of</strong> the i th datum. The assumption that noise in d v<br />

is<br />

uncorrelated allows only diagonal terms in W d . I choose to use uncorrelated Gaussian<br />

noise for simplicity. The appropriate exponent in Equation 2.6 is p=2. The results<br />

presented here hold true when different noise models and corresponding statistics are<br />

used in the simulation. Combining Eqns. 2.5 and 2.6 with a regularization parameter, µ ,<br />

provides a global objective function,<br />

φ = φ d + µφ m<br />

. 2.7<br />

The regularization parameter controls the relative importance <strong>of</strong> data misfit to the<br />

model objective function (2.19).<br />

φ d is a chi-squared random variable distributed with N<br />

degrees <strong>of</strong> freedom, where N is the number <strong>of</strong> observation data. The expected value for<br />

the data misfit is then N, which defines a target misfit to be achieved in the inversion<br />

(2.15).<br />

The inverse solution for this problem is then obtained by finding a model, v ρ (r r ), that<br />

*<br />

minimizes φ m in Equation 2.7 and misfits the data by φ (2.20). The specific algorithm<br />

for carrying out the minimization depends on the value <strong>of</strong> p and other constraints I may<br />

desire to impose on the problem (2.21).<br />

The most common approach in geophysical inversion is to use a value <strong>of</strong><br />

p = 2<br />

in<br />

Equation 2.5, which yields a mean-squared estimator. For a numerical solution, I<br />

discretize Equation 2.5 using the same mesh as the forward modeling in Equation 2.3,<br />

and by a finite difference approximation to produce the following matrix form,<br />

φ<br />

m<br />

vT<br />

T v vT<br />

T<br />

( ρ ) ρ W W ρ + ρ ( W W + W W + W W )<br />

= S S<br />

X X Y Y Z Z ρ<br />

2.8<br />

T v<br />

≡ ρ W Wρ<br />

The constructed model will then be characterized by a smooth transition between regions<br />

with different density values.<br />

There is an important distinction between applying a L P -norm to the data misfit in<br />

Equation 2.6 versus applying the same norm to the model objective function in Equation<br />

2.5. Applied to the data misfit, solutions reflect the relative importance <strong>of</strong> each datum<br />

that is fundamentally determined by the distribution <strong>of</strong> the specific L P -norm. However,<br />

applied to the model objective function, solutions reflect the ability <strong>of</strong> a recovered model<br />

to contain significantly different parameter values in adjacent model cells, which is<br />

fundamentally determined by the distribution <strong>of</strong> the specific L P -norm. Thus, varying p in<br />

Equation 2.6 affects the weighting <strong>of</strong> outliers in data space, but varying p in Eqn 2.5<br />

determines the ability <strong>of</strong> adjacent cells to incorporate large jumps in model space. As we<br />

are not concerned with data outliers in this study, p = 2 in Eqn 2.6 for computational<br />

simplicity.<br />

2.3.1 Bound Constrained Inversion with Mean-Square Estimator<br />

In order to recover a realistic density distribution, I choose to impose bound constraints<br />

that density values be positive and have an upper bound. Fig. 2.3 shows the chosen<br />

model <strong>of</strong> a Plutonium (ρ=19 g/cm 3 ) pit with volume equal to one model cell (15 cm 3 for<br />

this example) is surrounded by an outer lead (ρ=11 g/cm 3 ) annulus also <strong>of</strong> one model cell<br />

thickness, which is surrounded by packaging material (ρ=0.6 g/cm 3 ) <strong>of</strong> thickness 1 model<br />

cell resulting in an average density <strong>of</strong> approximately 6 g/cm 3 . The lower and upper<br />

bounds are thus set to 0.0 g/cm 3 and 6.0 g/cm 3 , respectively. These bound constraints can<br />

be enforced during inversion and optimization using transformation methods (2.22),<br />

interior point methods (2.23), (2.24), and several quadratic programming methods (2.25).<br />

In this chapter, I use a primal logarithmic barrier technique (2.23), which is a class <strong>of</strong><br />

interior point methods. In this method, the bound constraints are enforced through a<br />

logarithmic term that acts as a barrier to prevent the solution from reaching over to the<br />

infeasible domain (i.e., negative or above the upper bound). The objective function then<br />

assumes the following form,<br />

min<br />

max<br />

⎡ ρ − ρ ρ − ρ ⎤<br />

φ ( λ) = φd<br />

+ µφm<br />

− 2λ∑<br />

⎢ln<br />

+ ln<br />

, 2.9<br />

max min max min ⎥<br />

1⎣<br />

ρ − ρ ρ − ρ ⎦<br />

min max<br />

where ρ and ρ are the lower and upper bounds respectively and λ is referred to as<br />

the barrier parameter.<br />

The first two terms have a quadratic relationship to the model parameters since the<br />

relationship between gravity gradient and density values in the cells is linear. However,<br />

the logarithm term <strong>of</strong> Equation 2.9 causes the total objective function to be non-<br />

quadratic. In addition, the logarithmic barrier method requires that a sequence <strong>of</strong><br />

minimization problems with decreasing λ be solved and the final solution is given<br />

whenλ<br />

→ 0. For these reasons, Equation 2.9 is solved iteratively. I start with a large λ<br />

and take a Newton step at each iteration while simultaneously decreasing λ in<br />

subsequent iterations. Further details <strong>of</strong> this optimization and derivative terms <strong>of</strong><br />

Equation 2.9 can be found in (2.18) and (2.19). When carrying out the logarithmic barrier<br />

solution, µ is held constant in Equation 2.9. A complete inverse solution typically is<br />

preceded by a line search for optimal µ through several trial values.<br />

To illustrate our construction algorithm, I refer again to the synthetic model shown in<br />

Fig. 2.3, which simulates a container with packaged Plutonium pit and a packaged<br />

depleted Uranium rod. This Plutonium and Uranium model is used to produce the<br />

simulated data set for our study. Since the gravity gradient signal has a range <strong>of</strong> more<br />

than 100 eötvös Fig. 2.4, and the noise level <strong>of</strong> stationary gravity gradiometers is stated<br />

to be below 1 eötvös (2.11), 2% Gaussian noise applied in this model is a reasonable<br />

estimate. As an illustration, Fig. 2.4 displays one component (T YZ ) <strong>of</strong> the gravity<br />

gradiometry response. Throughout this study, I have used all five independent<br />

components <strong>of</strong> the gradient tensor. I note that the gradient data are sampled discretely<br />

over limited areas in 3D space, so each component does bring additional independent<br />

information. A single component <strong>of</strong> data will produce good results, but multiple<br />

components are generally superior. I apply our inversion algorithms presented in this<br />

paper to these data to produce different density models (Fig. 2.5 and 2.7).<br />

Fig. 2.5 is the recovered model from using a mean-square estimator and bound<br />

constraints. Although this image identifies the high density zones within the cargo<br />

container within a misfit <strong>of</strong> 2%, the boundaries are blurred, which causes the amplitude<br />

<strong>of</strong> the density anomaly to be rather small. This blurring effect, well known in geophysical<br />

inversion (2.26) and the image processing community (2.27), arises because the<br />

constructed model from a mean-square estimator approximates sharp boundaries by a<br />

sequence <strong>of</strong> small steps spread over an interval. It is the mean-squared estimator that,<br />

when applied to the model derivatives, acts to suppress large differences between<br />

adjacent cells. To construct models with larger differences and therefore sharper<br />

boundaries, I next investigate robust estimators.<br />

2.3.2 Bound Constrained Inversion with Robust Estimator<br />

The proposed gradiometry system is stationary, which creates low instrument noise<br />

levels and effectively prevents data outliers. I therefore retain the mean-square estimator<br />

for data misfit Equation 2.6 and concentrate on the application <strong>of</strong> robust estimators for<br />

the model objective function. Robust estimators are based on the median <strong>of</strong> the model<br />

differences (2.28), whereas the mean-square estimator is based on the mean <strong>of</strong> the model<br />

differences (2.29). As previously stated, the median-based approach will preserve the<br />

large model differences crucial for recovering sharp boundaries.<br />

An attempt to apply the chosen solution method 1 ≤ p < 2 can be made at this point, but<br />

a numerical difficulty quickly appears. When p ≠ 2 , the model objective function is non-<br />

p−2<br />

quadratic. More specifically, the solution involves quantities such as δρ , where δρ<br />

is the difference between adjacent cells, thus creating singularities when the model<br />

differences approach zero during the optimization.<br />

The origination <strong>of</strong> the singularities can be shown with a one-dimensional minimization,<br />

r⎡<br />

∇x<br />

Ax − b<br />

⎢⎣<br />

+ µ Wx<br />

⎤<br />

= 0<br />

2.10<br />

⎥⎦<br />

which produces a generalized form <strong>of</strong> the normal equation,<br />

( A R A W R W ) x = A R b<br />

+ µ , 2.11<br />

where R<br />

r d ii<br />

and<br />

R = . If we focus on , the difference in the parameter<br />

r m ii<br />

R m<br />

values <strong>of</strong> two cells in model space,<br />

r , it is clear that when 1 ≤ p < 2 and is small<br />

m ii<br />

enough, a singularity will arise. It is worth noting 1 ≤ p < 2 is used primarily to<br />

concentrate the recovered mass into a well defined spatial area which decreases energy<br />

from other areas which in turn creates more singularities.<br />

These singularities can be addressed using one <strong>of</strong> several methods (2.30), (2.31).<br />

Strictly for p = 1, the most appropriate <strong>of</strong> these might be to recast the problem into an<br />

equivalent linear programming problem. Alternatively, iteratively re-weighted least<br />

squares, which solves a sequence <strong>of</strong> least squares problems with recursively computed<br />

weighting matrices, also provides an approximation to the L 1 -solution (2.30).<br />

However, the solution to the problem <strong>of</strong> singularities arising when1 ≤ p < 2, requires a<br />

more general approach. I choose to define a threshold, θ, which establishes a minimal<br />

acceptable value for the difference without causing numerical instability. θ is determined<br />

experimentally and is platform and problem specific. If the model difference is between<br />

zero and the defined threshold, a mean-squared estimator (p=2) is used. If the model<br />

gradient residual is greater than the threshold, the robust estimator is used ( 1 ≤ p < 2).<br />

The Huber norm (2.19)(2.28) is such a measure that satisfies our needs:<br />

R<br />

H<br />

⎧<br />

⎪<br />

= ⎨<br />

( δρ)<br />

,<br />

θ<br />

θ δρ − ,<br />

δρ ≤ θ<br />

δρ > θ<br />

2.12<br />

With the derivatives <strong>of</strong> Equation 2.10 defined as a series <strong>of</strong> weights,<br />

w<br />

1,<br />

( ri<br />

) = ⎨<br />

⎪⎩ θ δρ<br />

−1<br />

r − δρ ≤ θ<br />

r − δρ > θ<br />

2.13<br />

The weights, , then modify the model objective function by operating between W and<br />

w H<br />

W in Equation 2.8.<br />

A conceptual explanation <strong>of</strong> the Huber norm for p=1 is illustrated in Fig. 2.6. Note that<br />

the Huber norm is not a mathematical norm (2.32), but a mathematical function operating<br />

on a distribution. Also note that both sides <strong>of</strong> the threshold are defined in Equation 2.12<br />

so that the measure and its derivative in Equation 2.5 are now continuous. Although the<br />

second derivative <strong>of</strong> Equation 2.12 is discontinuous, this does not generally result in<br />

stability concerns.<br />

The Huber norm provides two advantages; it removes the singularities caused by the<br />

use <strong>of</strong> a robust estimator and maintains the large model differences required for sharp<br />

density discontinuities in the recovered model. Fig. 2.7 is the inverted image with a<br />

robust estimator, p=1, applied to the model objective function, with applied bound<br />

constraints, and the use <strong>of</strong> the Huber norm. The recovered density model has noticeably<br />

sharper boundaries.<br />

2.4 A Note on Non-Uniqueness and Global Minima<br />

Non-uniqueness is a term widely used and certainly applies to three-dimensional<br />

potential field solution. It is well known that the inverse gravity problem is extremely<br />

non-unique, but the majorities <strong>of</strong> such problems fall into the category <strong>of</strong> mathematical<br />

solutions and have little relevance to geological or engineering problems. I have<br />

formulated the inversion to incorporate constraints designed to obtained solutions that are<br />

plausible within the context <strong>of</strong> cargo inspection. Based on the existing literature and case<br />

applications, I am confident that non-uniqueness is not an issue in this application.<br />

It is also reasonable to question whether a global minimum has been reached, as there<br />

is no known method to assess it directly for general nonlinear problems. Monte Carlo<br />

simulations are <strong>of</strong>ten used to obtain an approximate evaluation, but they are ineffective<br />

for large-scale problems involving tens <strong>of</strong> thousands <strong>of</strong> parameters. Having said that, I<br />

have dealt with this aspect in our problem by the following: for p=2, I have a quadratic<br />

objective function and simple bound constraints which have a well defined minimum in a<br />

non-degenerative case. By invoking the method <strong>of</strong> continuation (varying p from 2 to 1<br />

with each resulting model shown to be consistent), we can confidently state that we have<br />

a global minimum for p=1 in the objective function.<br />

2.5 Conclusion<br />

The purpose <strong>of</strong> this research is to examine the feasibility <strong>of</strong> inferring the presence <strong>of</strong><br />

fissile materials in a cargo container. Given the total recovered mass <strong>of</strong> the cargo<br />

container from the inversion process, the mass distribution, and the lower and upper<br />

bounds <strong>of</strong> the identified high density regions, I seek to establish a threshold above which<br />

fissile material is likely present. This research attempts to optimize the variance and<br />

resolution <strong>of</strong> the gravity gradient imaging problem through the use <strong>of</strong> robust estimators to<br />

recover sharp boundaries and estimations for the variance and resolution <strong>of</strong> the recovered<br />

model, yet there still is a great deal <strong>of</strong> non-uniqueness inherent in the recovered models.<br />

It should be noted that although the choice <strong>of</strong> p in Equation 2.5 and the application <strong>of</strong> log<br />

barrier terms were based on problem geometry, recovered models still suffer from such<br />

non-uniqueness. Thus, the rationale behind forming the resolution matrix and performing<br />

funnel analysis is in direct response to this non-uniqueness: I seek to measure the quality<br />

<strong>of</strong> recovered models using the tools developed in the manuscript.<br />

Based on the results <strong>of</strong> this research, a future application <strong>of</strong> gravity gradient data<br />

towards cargo container imaging could best be used as a first estimation for recovering<br />

densities unexpected from the mandatory packing list <strong>of</strong> every cargo container. It is also<br />

worthwhile to consider other additional constraints applied to the inversion such as an<br />

absolute weight measurement <strong>of</strong> the cargo container before inversion, a moment <strong>of</strong><br />

inertia measurement for each <strong>of</strong> the container axes to constrain the inversion axes, and a<br />

maximum trailer density which is calculated from structural integrity limits <strong>of</strong> Corten<br />

steel. Since cargo container mass is conserved in the recovered models, this value could<br />

be used to place an additional upper bounds on the maximum recovered density.<br />

2.6 Acknowledgements<br />

Aside from my co-authors acknowledged at the beginning <strong>of</strong> this Chapter, I wish to<br />

thank Roman Shekhtman at the University <strong>of</strong> British Colombia for providing a Huber<br />

norm template and James Berryman at Lawrence Berkeley National Laboratory for useful<br />

discussions on robust estimators. I also thank Dr. Manik Talwani and three anonymous<br />

IEEE reviewers for their helpful suggestions that have significantly improved the<br />

manuscript.<br />

2.7 References<br />

(2.1) Bell, R.E., Gravity gradiometry, Scientific American, vol. 278, Issue 6, pp 74-80, 1998<br />

(2.2) Kusche, J., Klees, R., Regularization <strong>of</strong> gravity field estimation from satellite gravity gradients,<br />

Journal <strong>of</strong> Geodesy, vol. 76, no. 6-7, pp.359-368, 2002<br />

(2.3) Vasco, D.W., Taylor, C., Inversion <strong>of</strong> airborne gravity gradiometry data, southwestern Oklahoma,<br />

1991, <strong>Geophysics</strong>, v. 56, 1, pp. 90-101<br />

(2.4) Bell, R E., Pratson, L F., Anderson, R., Biegert, E.K., Gravity gradiometry; applications to basin<br />

analysis, AGU 1995 fall meeting, Eos, Transactions, American Geophysical Union, vol. 76, no. 46,<br />

Suppl., 1995, pp.143, 1995<br />

(2.5) Pratson, L F., Bell, R., Anderson, R., Dosch, D., White, J., Affleck, C, Grierson, A.,Korn, B., <strong>Ph</strong>air,<br />

R., Biegert, E., Gale, P, Results from a high-resolution, 3-D marine gravity gradiometry survey<br />

over a buried salt structure, Mississippi Canyon area, Gulf <strong>of</strong> Mexico, AGU 1995 fall meeting,<br />

Eos, Transactions, American Geophysical Union, vol. 76, no. 46, Suppl., pp.144, 1995<br />

(2.6) Dransfield, M,H., Lee, J.B., The Falcon airborne gravity gradiometer survey system, Australian<br />

Society <strong>of</strong> Exploration Geophysicists-PESA Airborne Gravity Workshop, Sydney, Australia, 2004<br />

(2.7) Nekut, A. G., Borehole gravity gradiometry, <strong>Geophysics</strong>, vol. 54, no. 2, pp. 225-334, 1989<br />

(2.8) Kirkendall, B.A., Lewis, J.P., Harben, P.E., Advances <strong>of</strong> crosswell electromagnetics in steel casing,<br />

1999 Society <strong>of</strong> Exploration Geophysicists Annual Meeting, Extended Abstracts, Dallas, TX, 4 pp.,<br />

1999<br />

(2.9) SPIE Defense and Security Symposium, Kissimmee, Florida, April 16 – 20, 2006, www.spie.org<br />

(2.10) H<strong>of</strong>meyer, G.M., Affleck, C.A., Rotating accelerometer gradiometer, United States Patent 5,357,802<br />

; www.uspto.gov, 1994<br />

(2.11) GEDEX, Mississauga, Ontario, Canada, http://www.gedex.ca/<br />

(2.12) Tikhonov, A.N., Arsenin, V.Y., Solutions <strong>of</strong> ill posed problems, New York, John Wiley and Sons,<br />

1977<br />

(2.13) Anscombe, F.J., Rejection <strong>of</strong> outliers, Technometrics, 2, pp. 123 – 147, 1960<br />

(2.14) Li, Y., Oldenburg, D.W., 3-D inversion <strong>of</strong> gravity data, <strong>Geophysics</strong>, vol. 63, 1, pp. 109 – 119, 1998<br />

(2.15) Li, Y., Oldenburg, D.W., Fast inversion <strong>of</strong> large-scale magnetic data using wavelet transforms and a<br />

logarithmic barrier method, Geophysical Journal International, vol. 152, pp. 251 – 265, 2003<br />

(2.16) Li, Y., Oldenburg, D.W., Joint inversion <strong>of</strong> surface and three-component borehole magnetic data,<br />

<strong>Geophysics</strong>, vol. 65, 2, pp. 540 – 552, 2000<br />

(2.17) Li, Y., 2001, 3D inversion <strong>of</strong> gravity gradiometry data, Society Exploration Geophysicists Annual<br />

Meeting Expanded Abstracts.<br />

(2.18) Li, Y., Oldenburg, D.W., 3-D Inversion <strong>of</strong> magnetic data, <strong>Geophysics</strong>, vol. 61, 2, pp. 394-408,<br />

1996<br />

(2.19) Farquharson, C.G., Oldenburg, Non-linear inversion using general measures <strong>of</strong> data misfit and<br />

model structure, Royal Ast. Soc. Geophysical Journal Intl., vol. 134, pp.213 – 227, 1998<br />

(2.20) Haber, E., Numerical strategies for the solution <strong>of</strong> inverse problems, <strong>Ph</strong>.D. <strong>Thesis</strong>, University <strong>of</strong><br />

British Columbia, Canada, 1996<br />

(2.21) Shewchuk, J.R., An introduction to the conjugate gradient method without the agonizing pain,<br />

Edition 1.25, <strong>School</strong> <strong>of</strong> Computer Science, Carnegie Mellon, Pittsburg, 1994<br />

(2.22) Oldenburg, D.W., Li, Y., Subspace linear inverse method, Inverse Theory, vol. 10, pp. 915 –<br />

935, 1994<br />

(2.23) Wright, S.J., Primal-dual interior point methods, Society for Industrial and Applied<br />

Mathmatics, <strong>Ph</strong>iladelphia, 1997, ISBN 0-89871-382-X<br />

(2.24) Dantzig, G.B., Linear programming and extensions, Princeton University Press, Princeton, New<br />

Jersey, 1963<br />

(2.25) Nocedal, J. and Wright, S.J., Numerical optimization, Springer-Verlag, New York, ISBN 0-387-<br />

98793-2, 1999<br />

(2.26) Portniaguine, O., Zhdanov, M.S., Focusing geophysical inversion images, <strong>Geophysics</strong>, vol. 64, 3,<br />

pp. 874 – 887, 1999<br />

(2.27) Bowyer, K. W. Ahuja, N., Advances in image understanding: A festschrift for Azriel Rosenfeld,<br />

Wiley-IEEE Computer Society, 1996, 358 pp.<br />

(2.28) Huber, P.J., Robust statistical procedures: Second Edition, SIAM, 68, <strong>Ph</strong>iladelphia, 67 pp., 1996<br />

(2.29) Scales, J.A., Gersztenkorn, A., Robust methods in inverse theory, Inverse Problems, vol. 4, pp.<br />

1071 – 1091, 1998<br />

(2.30) Scales, J.A., Gersztenkorn, A., Treitel, S., Fast lp Solution <strong>of</strong> large, sparse, linear systems:<br />

application to seismic travel time tomography, Journal <strong>of</strong> Computational <strong>Ph</strong>ysics, 75, pp. 314 –<br />

333, 1998<br />

(2.31) Gauss, C.F., Theoria motus corporum coelestium in sectionibus conicis solem ambientium,<br />

Hamburg, Germany (Original English trans. Charles Henry Davis, Little, Brown, and Company,<br />

Boston, 1857), 1809 orig.<br />

(2.32) Li, W. and Swetits, J.J., The linear L 1 estimator and the Huber M-estimator, SIAM J. Optim., vol.<br />

8, 2, pp. 457 – 475, 1998<br />

3.0 m<br />

Sensor Gate<br />

X<br />

3.3 m<br />

Cargo Container<br />

Y<br />

Z<br />

6.2 m<br />

Fig. 2.1 Illustration <strong>of</strong> proposed technique and axis coordinates. The cargo container is passed through a<br />

gate <strong>of</strong> sensors on the top and on both sides. Stationary sensors decrease noise levels to 1 Eötvös.<br />

In practice, this manner <strong>of</strong> acquisition can provide extremely dense data coverage, although this<br />

research will assume lower density coverage in intervals <strong>of</strong> 0.3 meters. These intervals are seen as<br />

the dotted black lines over the discretized model space in Fig. 2.2.<br />

+0.30 m<br />

-0.71 m<br />

-1.43 m<br />

-2.14 m<br />

-3.00 m<br />

0.00 m<br />

1.50 m<br />

3.00 m<br />

4.50 m<br />

6.00 m<br />

Fig. 2.2 Mesh <strong>of</strong> the cargo container with the projections <strong>of</strong> gravity gradiometry sensor gate locations onto<br />

the container indicated by dark black lines. The sensor gate is constructed from an array <strong>of</strong><br />

sensors stacked on top <strong>of</strong> each other (on the sides) and next to each other (on the top). On the top<br />

and sides, the sensors are separated by 0.60 meters which was chosen based on the size <strong>of</strong> the<br />

commercially-based sensors. As the container is pushed through the gate, we propose acquiring<br />

data every 0.30 meters, although the lengthwise data spacing can be increased at the cost <strong>of</strong><br />

additional acquisition time.<br />

0.30<br />

-0.71<br />

-1.43<br />

-2.14<br />

-3.00<br />

0.00<br />

1.50<br />

3.00<br />

g/cm 3<br />

4.50<br />

6.00<br />

Fig. 2.3 Model used to produce the dataset inverted in this paper. 2% Gaussian noise at a minimum <strong>of</strong> 1<br />

eötvös added to the data, prior to inversion. The left block is a Plutonium (ρ=19 g/cm 3 ) pit with<br />

volume equal to 1 model cell (chosen to be 15 cm 3 for this example), surrounded by an outer lead<br />

(ρ=11 g/cm 3 ) annulus <strong>of</strong> 1 model cell thickness, surrounded by packaging material (ρ=0.6 g/cm 3 )<br />

<strong>of</strong> thickness 1 model cell results in an average density <strong>of</strong> approximately 6 g/cm 3 . The horizontal<br />

bar on the right is depleted Uranium in low density packaging with average density <strong>of</strong> 4.0 g/cm 3 .<br />

The density units are g/cm 3 .<br />

3.0<br />

2.0<br />

1.0<br />

z (m) y (m) z (m)<br />

eötvös<br />

170<br />

050<br />

-130<br />

-210<br />

-3-10<br />

-4-30<br />

x (m)<br />

-5<br />

1.0 2.0 3.0 4.0 5.0 6.0<br />

Fig. 2.4 T YZ component <strong>of</strong> synthetic gradiometry data computed with Eqn (2.4) using the true model in<br />

Fig. 2.3. To interpret, start with an aerial view (XY-plane) <strong>of</strong> Fig. 2.2 from the vertical axis.<br />

Upward fold the two sides <strong>of</strong> the cargo container so that they are now co-planar to the XY-plane.<br />

The top frame is therefore the data from the sensors on the far end <strong>of</strong> the sensor gate as shown in<br />

Fig. 2.1, the middle frame is the data acquires from the horizontal top bar <strong>of</strong> sensors, and the<br />

bottom frame data from the near-side sensors. The colorbar units are in eötvös.<br />

Fig. 2.5 Density model recovered from true model in Fig. 2.3 using p=2. Bound constraints are enforced in<br />

this example in the interval, 0.0 g/cm 3 – 6.0 g/cm 3 . The lowest 2% <strong>of</strong> recovered density values are<br />

not plotted in this figure.<br />

R H<br />

L p<br />

-norm<br />

L p -norm<br />

L 2<br />

r i<br />

-θ<br />

Fig. 2.6 Distribution <strong>of</strong> recovered models and their respective norms from an arbitrary example. The<br />

purpose <strong>of</strong> a Huber norm is to condition a distribution with the potential for singularities to one that<br />

is computationally stable. A threshold θ is defined such that models having a residual less than θ<br />

are estimated by the mean-square estimator (p=2), whereas all models with a residual greater than θ<br />

are estimated with a robust estimator (p=1). Thus, as we approach a singularity (the vertical axis)<br />

and r i →∞, we switch values <strong>of</strong> r i in (16). θ is a function <strong>of</strong> data quality, degree <strong>of</strong> sensor coverage,<br />

expectation <strong>of</strong> sharply recovered boundaries, and estimation <strong>of</strong> resolution.<br />

Fig. 2.7 Density model recovered from the true model in Fig. 2.3 using p=1 and θ=1.0 x 10 -8 . Bound<br />

constraints are enforced in this example in the interval 0.0 g/cm 3 – 6.0 g/cm 3 . The lowest 2% <strong>of</strong><br />

recovered density values are not plotted in this figure. Note the higher recovered density values<br />

with the bound constraints and p=1. In a more realistic situation, we would expect more mass in the<br />

trailer, which will result in higher recovered densities.<br />

Fig. 2.8 The gradient <strong>of</strong> gravity can be measured with accelerometers. The yellow mass compresses a<br />

piezoelectric crystal such that the crystal produces an electric potential approximately one-half <strong>of</strong><br />

its dynamic range. Thus, if an external mass is located below this figure, the yellow mass will<br />

compress though gravitational attraction and create an increased electric potential. However, if an<br />

external mass is present above this figure, the yellow mass will decompress the piezoelectric crystal<br />

and reduce the amount <strong>of</strong> electric potential. This accelerometer thus forms the basis <strong>of</strong> one type <strong>of</strong><br />

gravity gradient measurement.<br />

Fig. 2.9 The foundation <strong>of</strong> the Lockheed-Martin gravity gradiometer. Two pairs <strong>of</strong> accelerometers<br />

mounted on a spinning plate (approximately 15 RPM) produce a gradient measurement based on<br />

the known distance between the accelerometers. There are typically three plates azimuthally<br />

located 120˚ apart and tilted inward 35˚; each plate samples all three dimensions. The<br />

instantaneous total gradient is therefore the sum <strong>of</strong> all three plates projected into that spatial<br />

dimension. This configuration is beneficial by providing a stable platform to measure gravity,<br />

common mode rejection <strong>of</strong> instrument and vibrational noise, and increased resolution because <strong>of</strong><br />

the rotation speed. A different design which measures the gravity gradient is <strong>of</strong>fered by GEDEX,<br />

Inc., but is not discussed here.<br />

Chapter 3<br />

APPRAISAL OF RECOVERED MODELS<br />

A critical link in the geophysical inversion process is model appraisal. Linear model<br />

appraisal is well-characterized whereas nonlinear model appraisal, as a more difficult<br />

task primarily because a change in each model parameter fundamentally changes the<br />

model, is not well-characterized. In Chapter two it was shown that including bound<br />

constraints and robust estimators such as the Huber Norm can introduce significant<br />

nonlinearity in the inversion process. A method is developed which forms the resolution<br />

matrix efficiently and incorporates all first-order nonlinear behavior. In addition, the<br />

variance is characterized through an adaptation <strong>of</strong> funnel analysis. Both these<br />

techniques are applied to the model results shown in Chapter 2 and another example is<br />

discussed for added clarity in more complicated container loads..<br />

3.1 Introduction<br />

Nonlinear model appraisal in the geoscience community (3.1) primarily focuses on the<br />

variance and resolution <strong>of</strong> recovered models. Variance analysis quantifies how errors in<br />

the measured data are mapped into the recovered model, while resolution analysis<br />

quantifies the ability <strong>of</strong> the recovered model to successfully identify separate features or<br />

to quantify individual features. The resolution is studied through the formation <strong>of</strong> both<br />

linear and nonlinear model resolution matrices to determine the spatial precision to which<br />

individual model parameters can be recovered. Variance analysis for non-linear model<br />

appraisal can be accomplished through several methods, including the covariance matrix<br />

(3.2)(3.3), the Cramer-Rao (CR) bound (3.4)(3.5), and funnel analysis. The covariance<br />

matrix indicates how measured data errors are correlated between model parameters,<br />

while the CR bound calculates the lower bound for any estimate <strong>of</strong> a nonrandom<br />

parameter. The CR bound is an intriguing subject for future study, in part, because the<br />

requisite second derivative <strong>of</strong> the log likelihood function is already explicitly calculated<br />

through the Hessian matrix in the optimization <strong>of</strong> Equation 2.7. However, as the critical<br />

focus in this nonlinear model appraisal is detection, funnel analysis is chosen because it<br />

<strong>of</strong>fers absolute maximum and minimum bounds <strong>of</strong> a model parameter as a function <strong>of</strong><br />

volume.<br />

3.2 Funnel Analysis<br />

A primary interest is to determine whether a high density volume recovered from<br />

inversion is likely to indicate fissile material. This section uses a type <strong>of</strong> bound analysis,<br />

called funnel analysis, to characterize the uncertainty in the recovered inversion models<br />

(3.6). The results <strong>of</strong> such an analysis are a function <strong>of</strong> the quality <strong>of</strong> sensor coverage,<br />

mass distribution <strong>of</strong> the container, and presence <strong>of</strong> sharp density contrasts within the<br />

container.<br />

Given a dataset, d v ( i = 1,<br />

L,<br />

N ), I perform an initial bound-constrained inversion. It is<br />

necessary to next identify the region <strong>of</strong> highest recovered density with the assumption<br />

that if fissile materials are present, they will have the highest density in the container.<br />

This region, defined as VSI, is the starting point for funnel analysis and is defined by<br />

discarding the lowest 98% <strong>of</strong> recovered model cell density values; the density threshold<br />

value having been determined experimentally. In the example <strong>of</strong> the Plutonium pit<br />

shown in Fig. 2.3, this starting region contains 27 (3x3x3) cells.<br />

In funnel analysis, one computes the lower and upper bound on the average density in a<br />

given region within the model domain. Each lower and upper bound is defined as the<br />

minimum and maximum mean density <strong>of</strong> all models that fit the data to the same degree as<br />

determined by the data errors. Each bound is calculated by carrying out an inversion to<br />

generate an extreme model that either minimizes or maximizes the density in the selected<br />

region while ignoring the complexity <strong>of</strong> the model in other regions. Within the region,<br />

V SI , this is described in (3.7). For the lower bound, I solve,<br />

min φ<br />

= ∫ ρ dv , such that φd<br />

= φ . 3.1<br />

Vsi<br />

For the upper bound, I solve a maximization problem,<br />

max φ<br />

= ∫ ρ dv,<br />

such that φd<br />

= φ , 3.2<br />

which can be solved by an equivalent minimization problem,<br />

= ∫ ρ − ρ<br />

dv , such that φd<br />

= φ ,<br />

and when ρ is large(e.g.,100)<br />

3.3<br />

φ is the same misfit expectation value discussed in the previous section. Equations 3.1<br />

and 3.3 are subject to density bound constraints <strong>of</strong> 0.0 g/cm 3 and 6.0 g/cm 3 applied in<br />

order to recover a reasonable model. Calculation <strong>of</strong> the first set <strong>of</strong> bounds is<br />

accomplished by defining V S(1) as a single cube at the center <strong>of</strong> the region <strong>of</strong> high density.<br />

The next set <strong>of</strong> bounds result from defining V S(2) as a larger symmetrical cube centered on<br />

V S(1). V S(n) is the largest cube in the study. The curves in Fig. 3.1 represent the size <strong>of</strong><br />

this region as a function <strong>of</strong> characteristic volume and the abscissa equals V S(n) normalized<br />

by the total volume <strong>of</strong> interest.<br />

As defined in Eqns. 3.1-3.3, only within V SI is the model objective function defined;<br />

the volume outside V S1 only contributes to the data misfit. In the limit as V SI approaches<br />

the size <strong>of</strong> the entire model, the minimum and maximum mean density values converge<br />

to the total model density. Once each pair <strong>of</strong> optimization problems is solved, one<br />

computes the average densities within V SI and use them as the upper and lower density<br />

bounds. Chapter seven discusses the role <strong>of</strong> funnel analysis in the cargo container<br />

inspection process. For a given sensor geometry and gate configuration, the funnel<br />

analysis should be calculated many times to develop a catalog <strong>of</strong> variance analysis as a<br />

function <strong>of</strong> volume. Therefore, during cargo inspection, no time is required for funnel<br />

analysis calculation.<br />

Fig. 3.1 plots the results, in two different axis configurations, for the synthetic model<br />

shown in Fig. 2.3. Given a volume <strong>of</strong> interest in the recovered model, the true density <strong>of</strong><br />

that volume can be any value between the corresponding upper and lower bounds in Fig.<br />

3.1. Whether we consider total mass or average density <strong>of</strong> the recovered plutonium pit as<br />

a function <strong>of</strong> volume, the analysis is unaffected. If one interprets the plutonium to be<br />

highly resolved within one cell in the recovered model, the far left <strong>of</strong> each plot in Fig. 3.1<br />

shows the true density <strong>of</strong> that model cell could vary between less than 1.0 x 10 -2 g/cm 3<br />

and 19.0 g/cm 3 . However, if one interprets the plutonium location as less compact,<br />

perhaps spreading into 125 model cells, the variance is reduced, thus illustrating the trade<br />

<strong>of</strong>f between resolution and variance in model appraisal. In the cargo container imaging<br />

problem, we seek to detect the presence <strong>of</strong> high-density spatially-compact materials such<br />

as Plutonium, which would ostensibly occupy less than 125 model cells in discretization<br />

<strong>of</strong> Fig. 2.3. Yet for small volumes, Fig. 3.1 shows a vast density range in which the true<br />

density can lie. This leads directly to a fundamental limitation in imaging cargo<br />

containers with the gravity gradiometry technique; nonlinear inversion can recover areas<br />

<strong>of</strong> high density likely to be indicative <strong>of</strong> spatially compact fissile materials, but can<br />

provide no certainty on the recovered density <strong>of</strong> such materials. Complementary<br />

inspection techniques must be then used for confirmation <strong>of</strong> fissile material.<br />

3.3 Construction <strong>of</strong> Unconstrained (Linear) and Bound-Constrained (Non-Linear)<br />

Resolution Matrices<br />

Inversion <strong>of</strong> a gravity gradiometry dataset,<br />

, attributes a set <strong>of</strong> gravity gradient<br />

density measurements to a distribution <strong>of</strong> mass, which best reproduce the dataset<br />

according to the error tolerance. This recovered density distribution,<br />

v ρ , can never<br />

perfectly resolve the true model due to non-uniqueness, data noise, prior assumptions,<br />

and round-<strong>of</strong>f error (3.8). Assumptions, even the least obvious, such as discretization,<br />

can also contribute to the difference between the recovered and true models. The primary<br />

effect <strong>of</strong> these assumptions and limitations on the recovered model is the edge, or<br />

boundaries, <strong>of</strong> recovered density tend to be a diffused zone <strong>of</strong> transition. The proposed<br />

use <strong>of</strong> the Huber norm in the previous section limits the spreading effect through the use<br />

<strong>of</strong> robust estimators, but it will not eliminate the spreading completely. The attempt in<br />

the previous section to limit the spreading effect through the use <strong>of</strong> robust estimators is<br />

now followed by studying the spreading effect through the use <strong>of</strong> the resolution matrix.<br />

The underlying physics and geometry <strong>of</strong> the imaging problem determine the resolution<br />

matrix, as does the choice <strong>of</strong> model regularization, µ in Equation 2.9, due to data noise<br />

levels and sensor coverage.<br />

Alumbaugh and Newman (3.9) apply linearized model covariance and resolution<br />

matrices to determine resolution and parameter estimation accuracy for non-linear<br />

inversions. Alumbaugh (3.10) uses covariance estimation techniques to understand the<br />

inherent differences between a linearized solution estimation and a full non-linear<br />

solution estimation. In addition, Alumbaugh and Newman (3.9) discuss resolution on<br />

spatial location estimated with model resolution and model covariance matrices. Routh<br />

(3.11) forms the resolution matrix for crosswell tomography applications in order to<br />

appraise the results <strong>of</strong> optimizing sensor placement. This prior research is significant<br />

because, for realistic large problems, it is not practical to execute the inversion with a<br />

direct method such as SVD (3.12) where the resolution matrix is explicitly formed.<br />

However, SVD has been successfully used on smaller problems to form the resolution<br />

matrix (3.3). For this reason, conjugate gradient is one alternate solution method used<br />

widely. The conjugate gradient method has the advantage <strong>of</strong> being able to solve large<br />

problems, since the required matrix-vector multiplications are obtained implicitly, and in<br />

turn leads to the disadvantage <strong>of</strong> not being able to explicitly form the model resolution<br />

matrix.<br />

The model resolution matrix, R, relates the true model to the recovered model:<br />

v v v<br />

ρ R = R ρT<br />

+ ∆ρ<br />

3.4<br />

where v ρ R and v ρT<br />

are the recovered and true model, respectively, and ∆ v ρ is a model<br />

bias and noise term. Inclusion <strong>of</strong> the last term in Equation 3.4 is necessary for<br />

consistency because, while v ρ R is a random variable, R and v ρT<br />

are not. R is a square<br />

matrix with dimensions equal to the number <strong>of</strong> model cells. R is also asymmetric, which<br />

leads to a conceptual difference between the rows and columns (3.7). The rows are<br />

averaging functions such that each cell in the recovered model is a weighted average <strong>of</strong><br />

the true model, whereas the columns are the point spread functions that quantify the<br />

manner in which an impulse in the true model spreads to other regions in the recovered<br />

model. A quantitative analysis <strong>of</strong> the differences between rows and columns, or<br />

correspondence analysis (3.13), should be a valuable tool in resolution appraisal and is<br />

the subject <strong>of</strong> a separate investigation.<br />

As the conjugate gradient method is used for the solution, one must form R<br />

accordingly. To accomplish this, I form R through a series <strong>of</strong> single inversions in the<br />

following manner. Below, I examine the resolution matrix in the case <strong>of</strong> the<br />

unconstrained inversion with a quadratic model objective function. For the quadratic and<br />

unconstrained problem, the recovered model can be written as,<br />

−1 T T<br />

= H G Wd<br />

Wd<br />

3.5<br />

where H -1 T<br />

is inverse <strong>of</strong> Hessian matrix without the logarithmic terms: H = G G + µ W W .<br />

Substituting the data equation<br />

d obs<br />

= Gρ<br />

+ ε into Equation 3.5 yields the definition <strong>of</strong> the<br />

resolution matrix for this simple case,<br />

T r<br />

ρ = H G Wd<br />

WdGρ<br />

+ H<br />

≡ Rρ<br />

T −1<br />

T T r<br />

G Wd<br />

n<br />

. 3.6<br />

This equation also provides the means to construct the resolution matrix without<br />

forming the inverse <strong>of</strong> Hessian,<br />

H , explicitly. Suppose we have a true model that<br />

consists <strong>of</strong> only one cell corresponding to the j th model cell,<br />

v ρ =<br />

3.7<br />

( 0,<br />

L,0,1,0,<br />

) T<br />

Substituting<br />

v j<br />

ρT<br />

to Equation 3.6 results in a recovered model<br />

v ρR<br />

that is the corresponding<br />

j th column <strong>of</strong> the model resolution matrix. Note that the noise term n v is no longer<br />

present. Although Equation 3.5 cannot be evaluated explicitly since there is no analytic<br />

explicit expression for H<br />

-1 , it can be obtained by performing one inversion to the data<br />

produced by the impulsive model<br />

v ρ ,<br />

= G<br />

v ρ , 3.8<br />

according to 3.5. Performing M inversion with M difference impulsive models therefore<br />

completes the resolution matrix; again, there are M discretized model cells.<br />

The formation <strong>of</strong> R to non-quadratic and bound constrained problems can be<br />

accomplished using the same approach. However, there is no explicit inverse operator<br />

since it is defined by the inversion process that incorporates nonlinear parts such as<br />

bound-constraints and non-quadratic model objective function. The advantage is that the<br />

resolution matrix can be constructed whenever we perform the inversion with minimal<br />

additional computation cost. This method applies whether the inversion is carried out by<br />

an explicit method such as SVD or by an implicit and iterative approach such as by<br />

conjugate gradient method. In this current problem, I note that the Hessian matrix in<br />

Equation 3.5 becomes model dependent due to the logarithmic terms at each iteration and<br />

that each inversion must be carried out by going through the entire logarithmic barrier<br />

iteration. This is the manner in which bound constraints are incorporated into the<br />

resolution matrix. In the non-quadratic R construction, I also use a robust estimator,<br />

which is accounted through the changing model weighting matrix for each iteration. In<br />

other words, since the constrained inversion allows us to obtain each column <strong>of</strong> the<br />

resolution matrix, the effect <strong>of</strong> the robust estimator on the resolution matrix is accounted<br />

for automatically. To summarize the formation <strong>of</strong> the resolution matrix, for any given<br />

data set, the chosen estimator, bound constraints, and optimal regularization parameters<br />

collectively define the inverse operator, which is mathematically represented explicitly or<br />

implicitly. Application <strong>of</strong> this inverse operator to the data yields the recovered model.<br />

This same inverse operator can then be applied to data sets produced by an impulse<br />

model, described in Equation 3.7, to obtain the model resolution matrix.<br />

In the example used in the funnel analysis, a shielded plutonium pit (the left model<br />

block in Fig. 2.3, I construct both linear and non-linear R matrices. Each row or column<br />

<strong>of</strong> the R corresponds to a model in three dimensions. I display each row or column in the<br />

format <strong>of</strong> a model either by volume rendering or by slices. Three spatially-orthogonal<br />

slices <strong>of</strong> the column intersecting the center <strong>of</strong> the plutonium pit are shown in Fig. 3.2 for<br />

the constrained resolution matrices when p=1 and p=2. More detailed plots <strong>of</strong> the<br />

differences between p=1 and p=2 are shown in Fig. 3.3. In Fig. 3.2,Iplot only the<br />

recovered model cell densities above 1.0 standard deviation <strong>of</strong> the values in model space.<br />

The choice <strong>of</strong> using standard deviation as a measure, although arbitrary, arises from the<br />

need to quantify the relative, not absolute, amplitudes <strong>of</strong> a slice through R. In Fig. 3.2,<br />

the recovered density above the threshold is plotted as the black region whereas the white<br />

box is the true model <strong>of</strong> the Plutonium pit. Recovered models tend to have skewed<br />

depth resolution but higher resolution in the Y-horizontal plane which result from uneven<br />

sensor configuration. The non-linear R is characterized by a higher resolution than the<br />

linear R due to the realistic bound constraints and robust estimator. The asymmetry in<br />

Fig. 3.2 (A),(C), and (E) will be discussed in a future manuscript.<br />

Density inversion using gravity gradiometry data is a linear process. One can thus<br />

understand the resolution matrix without the complication <strong>of</strong> nonlinearity. Yet, by<br />

including the presence <strong>of</strong> nonlinear bound constraints and modifying the distribution <strong>of</strong><br />

the model objective function to achieve sharp edge recovery, we can provide insight into<br />

the structure and statistical nature <strong>of</strong> the non-linear resolution matrix. Furthermore,<br />

resolution matrices resulting from a mean-squared estimator based inversion appear to<br />

have a distinctly different distribution from resolution matrices resulting from robust<br />

estimators such as the Huber Norm. I relate the distribution <strong>of</strong> the model objective<br />

function to the estimator distribution in future research.<br />

3.4 Analysis <strong>of</strong> Model Appraisal<br />

The funnel analysis clarifies the trade<strong>of</strong>f between resolution and variance (3.14). A<br />

smaller recovered anomaly average volume implies a larger variation <strong>of</strong> density. Larger<br />

recovered average anomalies have improved variance but decreased resolution. Whereas<br />

the example in this paper focuses on a small fissile body, the variance and resolution are<br />

increased for larger trailer masses with smaller density contrasts.<br />

Funnel analysis on the Plutonium pit example and others not discussed in this paper<br />

suggest we are unlikely to detect fissile material smaller than about 15 cm 3 . Relying on<br />

robust estimators and bound constraints, we should expect the resolution <strong>of</strong> a 15 cm 3<br />

Plutonium pit to be spread over a volume <strong>of</strong> at least 45 cm 3 in the Y-axis and at least 60<br />

cm 3 in the X- and Z-axes. In addition, resolution analysis suggests the Plutonium pit<br />

would be located about 30 cm below its true depth location.<br />

Based on the example presented and several other models analyzed, this threshold, E, is<br />

approximated as,<br />

Ε ≈ ρ avg<br />

3.9<br />

IQR(.25)<br />

where ρ max is the maximum recovered density, ρ IQR(.25) is the first quantile (3.15) <strong>of</strong> the<br />

recovered density assuming upper and non-negative bound constraints and a robust<br />

estimator <strong>of</strong> p=1, and ρ avg is the average density <strong>of</strong> the container. In Fig. 7, Equation 3.9<br />

estimates a threshold value <strong>of</strong> E=1.05 g/cm 3 . If there are multiple high density regions,<br />

Equation 3.9 estimates a threshold for only the region with the highest recovered density.<br />

Whereas we infer the presence <strong>of</strong> fissile material, we are not able to quantify how many<br />

instances <strong>of</strong> fissile material are likely.<br />

One other discrimination technique recently proposed (3.17) appears promising in<br />

initial testing. Consideration <strong>of</strong> the volume recovered in an anomaly can provide more<br />

information than just the amplitude or distribution <strong>of</strong> an anomaly. Future research is<br />

likely to include the volume <strong>of</strong> the anomaly as a discrimination tool.<br />

3.5 Experimental Validation<br />

A model with increased complexity is shown in Fig. 3.4 to further experimentally<br />

validate the inversion methodology discussed above. The logarithmic barrier term is<br />

again used to constrain the recovered density values and p=1.0 is used to recover sharp<br />

boundaries. This example is different from Fig. 2.3 in two ways: increased clutter is<br />

added to the container and non-Gaussian (i.e. uniform) noise is added to the data. All<br />

other parameters between the two models are equal, and because the regularization<br />

parameter in Equation 2.7 was not changed for non-Gaussian noise, the resolution<br />

matrices and the funnel analysis are identical.<br />

The recovered image <strong>of</strong> Fig. 3.5 does not display model cells with recovered values<br />

less than 2% <strong>of</strong> the maximum recovered density and is sliced diagonally for clarity. The<br />

maximum recovered density <strong>of</strong> 2.78 g/cm 3 occupies 15 model cells in the same<br />

approximate area as the original plutonium’s 27 model cells. The threshold <strong>of</strong> this<br />

recovered model from Equation 3.9 is 1.65 g/cm 3 , thus, this container would be flagged<br />

for possible presence <strong>of</strong> fissile material. The effect <strong>of</strong> noise type on the recovered model<br />

is also examined. While Fig. 3.5 is the result <strong>of</strong> inverting data corrupted with 2%<br />

uniform noise, inversion <strong>of</strong> the same data corrupted with 2% Gaussian noise produces<br />

essentially identical models.<br />

It is clear from Fig. 3.5 that gravity gradiometry has recovered the area <strong>of</strong> high density,<br />

but the areas <strong>of</strong> lower density are not well resolved. This is primarily due to the lack <strong>of</strong><br />

inherent depth resolution in gravity gradiometry data, regularization, and the p-value<br />

specifically chosen to recover localized, high-contrast targets.<br />

3.6 Conclusions<br />

Funnel analysis provides a lower and upper bounds for volumes <strong>of</strong> recovered bodies. It<br />

was shown that the lower bound is less diagnostic than the upper bound. Given a<br />

recovered anomaly, the upper bound <strong>of</strong> funnel analysis can be used to determine if the<br />

material has a density high enough to be fissile material. Funnel analysis shows that for<br />

the Plutonium and Uranium synthetic model, there can be no certainty on the recovered<br />

density value until the volume exceeds about 125 model cells. Furthermore, the<br />

esolution matrix is used to quantify errors in the location <strong>of</strong> a recovered anomaly. It is<br />

noted that recovered anomalies are pushed too deep in the downward Z-axis, but are<br />

centered in the X- and Y-axis. These results suggest that gravity gradiometry can be<br />

successful at identifying suspect high density areas <strong>of</strong> cargo containers, but since the<br />

volume <strong>of</strong> fissile materials is expected to be small, any certain determination would<br />

require a complementary technique such as Neutron detection or manual inspection. It is<br />

also important to note that other techniques can be used in place <strong>of</strong> funnel analysis in<br />

addition to those previously mentioned (3.16).<br />

Sensor array optimization and increased sampling density could further decrease the<br />

variance and increase resolution. An additional way to increase the resolution is to<br />

optimize the α parameters in Equation 2.5 which are initially set toα α = α = 1. 0 .<br />

y z<br />

Based on results in the previous section which found the resolution in the Y-dimension<br />

greater than the resolution in the X-dimension, we could modify Equation 2.5 by<br />

increasing α with respect toα . Furthermore, the previous section found recovered<br />

y<br />

models biased in the vertical Z-dimension. This artifact can be compensated by<br />

decreasing the static component in the cell weighting factors discussed in Chapter 2.<br />

be used to place an additional upper bounds on the maximum recovered density. Finally,<br />

results <strong>of</strong> this chapter suggest that gravity gradiometry imaging might best be used as a<br />

first inspection <strong>of</strong> all cargo containers. Complementary techniques such as using 14<br />

MeV neutron bombardment or photon fluoroscopy could then be used in containers that<br />

violate thresholds such as that in Equation 3.9.<br />

3.7 Acknowledgements<br />

Aside from the acknowledgements at the beginning <strong>of</strong> this chapter, I thanks Roman<br />

Shekhtman at the University <strong>of</strong> British Colombia for providing a Huber norm template<br />

and James Berryman at Lawrence Berkeley National Laboratory for useful discussions on<br />

robust estimators. I also thank Dr. Manik Talwani, three anonymous reviewers, and the<br />

Associate Editor <strong>of</strong> IEEE Transactions <strong>of</strong> Geoscience and Remote Sensing for their<br />

helpful suggestions that have significantly improved this chapter.<br />

3.8 References<br />

(3.1) Snieder, R. 1998, The role <strong>of</strong> nonlinearity in inverse problems, Inverse Problems, vol. 14, pp. 387 –<br />

404<br />

(3.2) Sambridge, M., C. Beghein, F. Simons, and R. Snieder, 2006, How do we understand and visualize<br />

uncertainty?, The Leading Edge, 25, pp. 542-546<br />

(3.3) Vasco, D.W., Resolution and variance operators <strong>of</strong> gravity and gravity gradiometry, 1989,<br />

<strong>Geophysics</strong>, v. 54, 7, pp. 889-899<br />

(3.4) Hero, A., Fessler, J.A., 1994, A recursive algorithm for computing Cramer-Rao-type bounds on<br />

estimator covariance, IEEE Trans. Information Theory, vol. 40, 4, pp. 1205-1210<br />

(3.5) Van Trees, H.L., Detection, estimation, and modulation theory, Part I, 2001, 720 p., ISBN<br />

0471095176<br />

(3.6) Oldenburg, D.W., Funnel functions in linear and nonlinear appraisal, Journal <strong>of</strong> Geophysical<br />

Research, vol. 88, B9, pp. 7387-7398, 1983<br />

(3.7) Oldenburg, D., Li, Y., Near-surface geophysics, Society <strong>of</strong> Exploration <strong>Geophysics</strong> Investigations in<br />

<strong>Geophysics</strong>, vol. 13, 2005<br />

(3.8) Wilkinson, J.H., Rounding errors in algebraic processes, Courier Dover Publications, 1994, 161 pp.,<br />

ISBN 0486679993<br />

(3.9) Alumbaugh, D.L., Newman, G.A., Image appraisal for 2-D and 3-D electromagnetic inversion,<br />

<strong>Geophysics</strong>, vol. 65, 5, pp. 1455 – 1467, 2000<br />

(3.10) Alumbaugh, D.L., Linearized and nonlinear parameter variance estimation for two-dimensional<br />

electromagnetic induction inversion, Inverse Problems, 16, pp. 1323 – 1341, 2000<br />

(3.11) Routh, P.S., Oldenborger, G.A., Oldenburg, D.W., 2005, Optimal survey design using the point<br />

spread function measure <strong>of</strong> resolution, Society Exploration Geophysicists Annual Meeting<br />

Expanded Abstracts, vol. 24, pp. 1033<br />

(3.12) Parker, R., Geophysical inverse theory, Princeton University Press, 400 pp., ISBN 0691036349,<br />

1994<br />

(3.13) Greenacre, M., Multiple correspondence analysis and related methods, Chapman & Hall/CRC, 2006,<br />

608 p., ISBN 1584886285<br />

(3.14) Menke, W., Geophysical data analysis: discrete inverse theory, International Geophysical Series,<br />

vol. 45, 289 pp., 1989<br />

(3.15) Vardeman, S.B., Jobe, J.M., Basic engineering data collection and analysis, Duxbury Thomson<br />

learning, Pacific Grove, California, 2001, 832 pp., ISBN 0-534-36957-X<br />

(3.16) Stephens, P.J., and A.S. Jones, Bounds on the variance in the pattern matching criteria, IEEE Trans.<br />

Geoscience Remote Sensing, vol. 9, pp. 2514-2522, 2006<br />

(3.17) Snieder, R., 2006, Personal communication, <strong>Colorado</strong> <strong>School</strong> <strong>of</strong> <strong>Mines</strong>, Department <strong>of</strong> <strong>Geophysics</strong><br />

Total Mass (g)<br />

1.0e5<br />

1.0e2<br />

1.0e0<br />

1.0e-2<br />

Lower bound<br />

Upper bound<br />

1.0e-4<br />

1.0e0 1.0e1 1.0e2 1.0e3<br />

1/3<br />

V SI<br />

Average Density (g/cm3)<br />

Fig. 3.1 Results <strong>of</strong> funnel analysis on a plutonium (ρ=19 g/cm 3 ) pit with volume equal to 1 model cell,<br />

surrounded by an outer lead (ρ=11 g/cm 3 ) annulus <strong>of</strong> 1 model cell thickness, surrounded by<br />

packaging material (ρ=0.6 g/cm 3 ) <strong>of</strong> thickness 1 model cell. The average density <strong>of</strong> this model is<br />

approximately 6.0 g/cm 3 . The analysis considers a maximum volume <strong>of</strong> V SI =2182 cells out <strong>of</strong><br />

the total number <strong>of</strong> model cells, 15200.<br />

The smallest volume contains 27 cells. The two plots<br />

result from density bounds enforced in inversion; bounded between 0.0 g/cm 3 and 19.0 g/cm 3 . In<br />

each plot is the upper limit <strong>of</strong> V SI from (19) and the lower limit <strong>of</strong> V SI from (17). The left plot<br />

shows total mass within V SI while the right shows the average density within V SI . Clearly, the<br />

variance <strong>of</strong> the true average density increases with decreasing volume size. For this reason, a<br />

plutonium pit can be detected with gravity gradiometric imaging, but nothing certain can be<br />

ascertained regarding the exact value <strong>of</strong> the recovered density. Larger bodies produce less<br />

variance and more can be said about their recovered densities.<br />

(A)<br />

(B)<br />

X-axis (m)<br />

Y-axis (m)<br />

(C)<br />

(D)<br />

(E)<br />

(F)<br />

Fig. 3.2 Three orthogonal slices through the column <strong>of</strong> the resolution matrix, R, corresponding to the<br />

center <strong>of</strong> the Plutonium pit shown in Fig. 2.3. All dimensions are in meters. Each sub-plot has a<br />

black area which contains the recovered density within 1.0 standard deviation <strong>of</strong> the maximum<br />

recovered density value. The white square in each figure is the location <strong>of</strong> the original<br />

Plutonium cube in each dimension. Each axis is the cargo container dimension <strong>of</strong> the plane in<br />

meters. Note the X-plane (A), Y-plane (C), and Z-plane (E) slices for the non-linear inversion<br />

when p=1 and bound constraints <strong>of</strong> 0.0 g/cm 3 (lower) and 6.0 g/cm 3 (upper) are applied. Also<br />

note the X-plane (B), Y-plane (D), Z-plane (F) slices for the linear inversion when p=2 and no<br />

bound constraints are used. For p=2, the recovered density appears to be centered in the X- and<br />

Y-planes, but biased towards greater depth in the Z-plane. The resolution image for p=1 is<br />

improved, but is asymmetric.<br />

Fig. 3.3 Contour X-Y slices through the column <strong>of</strong> the resolution matrix, R, corresponding to the center <strong>of</strong><br />

the Plutonium pit in Fig. 2.3. All dimensions are in meters. The upper contour (A) is the X-Y<br />

model plane when p=1 and bound constraints (0.0 g/cm 3 – 6.0 g/cm 3 ). The lower contour (B) is<br />

the X-Y model plane when p=2 and no bound constraints are applied. Note the effect <strong>of</strong> setting<br />

p=1 on recovering sharp boundaries. Contour values are not shown in order to accentuate on<br />

the contour shape.<br />

Fig. 3.4 Experimental validation <strong>of</strong> the inversion and model appraisal methods discussed in this paper<br />

using a more complicated example. This model has the same geometry, sensor coverage, and<br />

noise levels as in Fig. 2.3, yet has more clutter and uniform, instead <strong>of</strong> Gaussian, noise added to<br />

the forward solution. The packaged plutonium (ρ=6.00 g/cm 3 ), colored in black on the front right,<br />

is concealed in one <strong>of</strong> eight barrels <strong>of</strong> metallic scrap (ρ=3.20 g/cm 3 ) separated by 0.15 meters,<br />

alternately stacked aluminum rods (ρ=2.20 g/cm 3 ) are on the left side <strong>of</strong> the model, and a wooden<br />

construction form (ρ=0.75 g/cm 3 ) is in the rear center <strong>of</strong> the container.<br />

Fig. 3.5 Recovered model from Fig. 3.4. This image does not include model cells with density values less<br />

than 2% <strong>of</strong> the maximum recovered value. This image is also sliced diagonally in the front right<br />

for clarity. Comparing this figure with Fig. 3.4, the plutonium is mostly recovered in the correct<br />

location and the threshold calculated by Equation (3.9) correctly flags the presence <strong>of</strong> high<br />

density, possibly fissile, material.<br />

Chapter 4<br />

SYMMETRY AND STABILITY OF RESOLUTION MATRICES IN<br />

GEOPHYSICAL INVERSION<br />

The linear and nonlinear resolution matrices for a synthetic gravity gradiometry problem<br />

are studied within the context <strong>of</strong> the synthetic problem introduced in Chapter two. While<br />

gravity gradiometry is inherently linear, nonlinearity occurs from the use <strong>of</strong> a<br />

logarithmic barrier term and non-least squares L P -norm, thus allowing separate study <strong>of</strong><br />

nonlinear effects. Two properties <strong>of</strong> the resulting resolution matrices are examined:<br />

symmetry and stability. Since a strongly correlated column and row within the resolution<br />

matrix suggest high confidence in the interpretation <strong>of</strong> the corresponding model<br />

parameter, symmetry can be a powerful tool in model appraisal. Increasing asymmetry<br />

is shown to be proportional to both increasing regularization and increasing nonlinearity<br />

for underdetermined systems. Overdetermined systems are characterized by symmetric<br />

resolution matrices that do not allow recovery <strong>of</strong> the true model. Changes in the quantity<br />

<strong>of</strong> discretization are shown to not significantly affect the resolution matrix, and the<br />

condition number and eigenvalues illustrate the singular nature <strong>of</strong> the resolution matrix.<br />

Finally, a method is introduced that transforms the distributions within the resolution<br />

matrix into quantifiable images <strong>of</strong> the resolution within model space; one image for each<br />

dimension in model space.<br />

This chapter will be submitted to the Journal <strong>of</strong> Geophysical Research – Solid Earth for<br />

publication after <strong>Thesis</strong> Defense<br />

4.1 Introduction<br />

Model appraisal in geophysical inversion is, in essence, an attempt at<br />

characterizing the uncertainty <strong>of</strong> a recovered model. Understanding model uncertainty<br />

generally occurs as two distinctive analysis; error <strong>of</strong> the recovered model value and error<br />

in the location <strong>of</strong> the recovered parameter. The former, although not considered here, is a<br />

fascinating area <strong>of</strong> research in nonlinear model appraisal and can be quantified though<br />

several methods, including, but not limited to, the covariance matrix (4.1)(4.2), Cramer-<br />

Rao Bound (4.3), and funnel analysis (4.4) discussed in Chapter three. The latter,<br />

generally referred to as resolution, is the focus <strong>of</strong> this thesis for nonlinear problems.<br />

Associated with the idea <strong>of</strong> resolution is an operator identified as a resolution matrix,<br />

which relates a true model to a recovered model within the context <strong>of</strong> inverse theory.<br />

The concept <strong>of</strong> resolution applied to a recovered model has been gradually studied<br />

since the seminal work <strong>of</strong> Backus and Gilbert (4.5),(4.6). Berryman (4.7),(4.8) showed<br />

how to economically compute linear resolution matrices using standard methods such as<br />

singular value decomposition and using iterative methods such as conjugate gradient.<br />

The partial linear resolution matrix has also been computed; Alumbaugh and Newman<br />

(4.9) for diffusion electromagnetics and Routh (4.10) for use in optimizing survey sensor<br />

placement. However, if mathematical or physical nonlinearity is present and honored,<br />

construction <strong>of</strong> the resolution matrix is more complicated. In general, nonlinear model<br />

appraisal is more complicated since the model parameters themselves affect the<br />

relationship between data and model (4.10).<br />

Strong correlation, or balance, between a column and row within the resolution<br />

matrix suggests confidence in the interpretation <strong>of</strong> the corresponding model parameter.<br />

Therefore, resolution matrix symmetry could be used in model appraisal. The<br />

eigenvalues and condition number <strong>of</strong> resolution matrices are also examined to provide an<br />

understanding <strong>of</strong> stability in both underdetermined and overdetermined systems. In<br />

addition, sensitivity to changes in mesh discretization is studied. Thus, the stability and<br />

symmetry is studied for both linear and nonlinear resolution matrices constructed from a<br />

three-dimensional gravity gradiometry synthetic problem.<br />

4.2 Geophysical Technique and Model<br />

The potential-field technique <strong>of</strong> gravity gradiometry is the physical basis for this<br />

study in resolution matrices. While resolution matrices could be calculated for inverse<br />

problems based on any diffusion or propagation based physics, gravity gradiometry has<br />

the advantage <strong>of</strong> linearity. Nonlinearity can then be introduced mathematically with<br />

discretion.<br />

The model shown in Fig. 4.1 consists <strong>of</strong> a zero density background with a target<br />

volume <strong>of</strong> .0911 m 3 , or 27 model cells, placed near the grid center with density 6.0 g/cm 3 .<br />

A structured cubic grid with overall dimensions 30 m x 33 m x 60 m and discretization <strong>of</strong><br />

1.5 m x 1.5 m x 1.5 m is used to produce 15200 model cells. The model discretization is<br />

shown in Fig. 4.2. 2% Gaussian uncorrelated noise is added to the synthetic data. Data<br />

consists <strong>of</strong> five independent tensor components <strong>of</strong> the gravity gradiometry;<br />

T , T , T , T , T<br />

XX<br />

XY<br />

XZ<br />

YY<br />

YZ<br />

for a total <strong>of</strong> N=185 data locations. The resolution matrix can be<br />

formed with only one tensor component, but additional components contain unique<br />

information and decrease the signal-to-noise ratio. (4.12) provides background on<br />

gravity gradiometry acquisition and (4.13),(4.14) describe the physics and mathematics<br />

<strong>of</strong> the technique.<br />

4.3 Inversion Technique<br />

The Tikhonov deterministic inversion has had wide success in potential-field<br />

problems (4.14)(4.16). The Tikhonov approach fundamentally consists <strong>of</strong> a misfit in data<br />

space, φ<br />

, a regularization parameter, µ , and a smoothing three-dimensional objective<br />

function in model space, φ<br />

, and the problem is stated as minimizing<br />

. 4.1<br />

Where<br />

φ m ( ρ)<br />

= α S ∫∫∫ w(<br />

) ρ (<br />

) dV + ∑α<br />

j ∫∫∫ w j (<br />

) dV , 4.2<br />

v 2<br />

W (G d v<br />

φ = ρ − ) . 4.3<br />

, the data misfit in data space, is measured by a Euclidean L 2 -norm because data<br />

outliers are not <strong>of</strong> concern in this study. However, φ<br />

, the objective function in model<br />

space, is measured by an L P -norm which allows sharp contrasts in the recovered model<br />

for 1 ≤ p < 2 and a smooth solution for p = 2 . As discussed in Chapter two,<br />

mathematical singularities arising for 1 ≤ p < 2 are eliminated through incorporating a<br />

hybrid, or Huber, norm (4.14). The inverse solution for this problem is obtained by<br />

finding a model, v ρ (r r ) , that minimizes φ m and misfits the data by φ ∗ (4.15). w(r r ) in<br />

Equation 4.2 is a model specific cell-weighting term while the α parameter in the<br />

recovered model <strong>of</strong> Equation 4.2 allows adjustments to smoothness. Nonlinearity from<br />

the L P -norm and logarithmic barrier function requires Equation 4.1 be solved iteratively;<br />

an interior-point method Newton step (4.17) is chosen for this study. Further details <strong>of</strong><br />

Tikhonov inversion can be found in (4.16) and (4.18).<br />

4.4 Formation <strong>of</strong> the Resolution Matrix<br />

The resolution matrix is defined as relating the true model to the recovered model<br />

(4.20),<br />

≡ R ρT<br />

4.4<br />

where<br />

v ρ<br />

and v ρT<br />

bias and noise term. ∆ v ρ represents the stochastic component; while v ρ R<br />

is a random<br />

variable, R and<br />

v ρT<br />

are not. R is a square matrix with dimensions equal to the number<br />

<strong>of</strong> model parameters, M. It is critical to note that construction <strong>of</strong> the resolution matrix is<br />

computationally demanding. R is therefore formed column-wise through a series <strong>of</strong><br />

single inversions, where the j th inversion corresponds to the j th model cell and the j th<br />

column <strong>of</strong> the resolution matrix (4.19).<br />

4.4.1 Overdetermined and Determined Linear Cases with No Regularization<br />

In the overdetermined case with a least-squares solution, there is no regularization<br />

nor bound constraints, which are also a source <strong>of</strong> regularization. We can thus write,<br />

T r r<br />

( G G) ρ<br />

= G d<br />

4.5<br />

T T<br />

ρ = H G W W d . 4.6<br />

( G ) 1<br />

− = G<br />

1 −<br />

the standard deviation <strong>of</strong> the j th datum.<br />

and Wd is a diagonal matrix whose j th element is 1/σ j , where σ j is<br />

It should be noted that overdetermined systems can benefit from regularization in<br />

the form <strong>of</strong> increased numerical stability and a decrease in the vulnerability to errors in<br />

the data (4.22). If regularization is added to an overdetermined system, the resulting<br />

resolution matrix should be considered in an underdetermined sense as discussed in the<br />

next section.<br />

v r<br />

into Equation 4.6 yields the<br />

definition <strong>of</strong> the resolution matrix for this simple case,<br />

∆ρ<br />

. 4.7<br />

Thus, the resolution matrix for the linear overdetermined case is,<br />

overdetermined<br />

T −1 T T<br />

( G G) W W G G<br />

= 4.8<br />

Equation 4.8 reduces to the symmetric identity matrix and can be rewritten in a more<br />

familiar mathematical notation in the absence <strong>of</strong> consideration <strong>of</strong> the data errors,<br />

⊥<br />

R = M M<br />

4.9<br />

M is the Moore-Penrose pseudo-inverse (4.21). Section 4.8 provides additional<br />

details in the symmetry <strong>of</strong> the overdetermined resolution matrix.<br />

Although the overdetermined resolution matrix is the identity matrix, perfect<br />

resolution does not indicate the recovery <strong>of</strong> the true model. The reason for this<br />

discrepancy is that variance must be considered along with resolution in model appraisal.<br />

The discussion in Chapter three on the balance between the resolution and variance, and<br />

Fig. 3.1 in particular, shows that as resolution decreases, variance must increase. Thus, in<br />

the overdetermined case, the true model is never recovered due to the manifestation <strong>of</strong><br />

the data errors in the variance.<br />

The above discussion provides the means to construct the resolution matrix<br />

without forming H explicitly. Suppose a true model exists that consists <strong>of</strong> only one cell<br />

corresponding to the j th model cell,<br />

) 4.10<br />

into Equation 4.7 results in a recovered model,<br />

at the j th j<br />

model cell. In order to remain consistent with Equation 4.4,<br />

ρR<br />

, based on an impulse<br />

must be<br />

positioned at the j th column <strong>of</strong> the model resolution matrix. Note that the noise term<br />

no longer contributes to the resolution matrix due to the substitution <strong>of</strong> a noise-free<br />

impulse at the j th model cell. Thus, the j th column <strong>of</strong> the resolution matrix can be<br />

calculated by performing one inversion on the data produced by the impulsive model<br />

∆<br />

r ρ<br />

v ρ , 4.11<br />

according to Equation 4.6. Performing M inversions with M impulsive models therefore<br />

completes the resolution matrix.<br />

4.4.2 Underdetermined Linear Case<br />

The resolution matrix is a function <strong>of</strong> the sensor coverage and physics, but also <strong>of</strong><br />

sensor noise, which affects the choice <strong>of</strong> regularization that is required for<br />

underdetermined problems. The addition <strong>of</strong> regularization modifies Equation 4.8 to<br />

become,<br />

( H ) −1 T T<br />

W W G G<br />

R ≡ . 4.12<br />

* T<br />

T T T T<br />

where H = G G + µ ( α w w + α w w + α w w + α w w )<br />

s<br />

z<br />

from Equation 4.2. The<br />

superscript, (*), refers to the presence <strong>of</strong> regularization and all variables are defined in<br />

Chapter two. Section 4.7 proves the asymmetry <strong>of</strong> the underdetermined resolution matrix<br />

is proportional to the increase in degree <strong>of</strong> regularization.<br />

4.4.3 Underdetermined Non-Linear Case with Bound Constraints<br />

The underdetermined case will become nonlinear if Equation 4.1 is modified to<br />

include a logarithmic barrier term to impose bound constraints on the inversion solution,<br />

φ = φ + µφ − 2λ<br />

r min<br />

⎡ ρ − ρ<br />

⎣ ρ − ρ<br />

max r<br />

ρ − ρ ⎤<br />

max min ⎥<br />

ρ − ρ ⎦<br />

4.13<br />

where ρ is the lower bound and ρ is the upper bound for the model parameter<br />

r ρ .<br />

The logarithmic barrier method requires that a sequence <strong>of</strong> minimization problems with<br />

decreasing λ be solved and the final solution is given when λ → 0. Details <strong>of</strong> this<br />

minimization are discussed in Chapter 2.3.1. The resolution matrix corresponding to<br />

Equation 4.13 cannot be evaluated explicitly since there is no explicit analytic expression<br />

for the resulting inverse operation with bound constraints. The resolution matrix in this<br />

case would be expected to have significant asymmetry.<br />

The nonlinearity coming from the use <strong>of</strong> Equation 4.13 is <strong>of</strong> particular interest in<br />

this Chapter. Previous methods <strong>of</strong> forming the resolution matrix have not allowed the<br />

retention <strong>of</strong> nonlinear behavior, mostly due to the process <strong>of</strong> linearization. However, the<br />

method <strong>of</strong> column-wise forming the resolution matrix as described in Equation 4.6<br />

preserves all mathematical and physical nonlinearity in R, primarily due to using the<br />

same basis as for the calculation <strong>of</strong> the inversion. This formulation will, <strong>of</strong> course, also<br />

preserve the addition <strong>of</strong> nonlinearity from non-Euclidean norms as discussed in the next<br />

section.<br />

4.4.4 Underdetermined Non-Linear Case with Bound Constraints and L P -norm<br />

Application <strong>of</strong> a non-Euclidean L P -norm on the model objective function can indirectly<br />

create nonlinearity. As discussed in Chapter two, the use <strong>of</strong> the L P -norm coupled with<br />

the choice <strong>of</strong> an iterative solution will create mathematical singularities which I choose to<br />

condition through the use <strong>of</strong> the Huber norm. The resolution matrix in this case, as in the<br />

previous section, has no explicit (i.e. analytic) expression. Also, because <strong>of</strong> the presence<br />

<strong>of</strong> regularization and significant nonlinearity, the corresponding resolution matrix would<br />

again be asymmetric.<br />

4.4.5 Assumptions and Limitations in the Formation <strong>of</strong> the Resolution Matrix<br />

The resolution matrix described in this chapter is centrally characterized by<br />

Equation 4.11; a unit impulse model centered at the j th model cell produces the j th column<br />

<strong>of</strong> the resolution matrix. In the formulation <strong>of</strong> each column, all other model cells, ,<br />

have zero amplitude.<br />

i ≠ j<br />

One limitation in constructing the resolution matrix from a series <strong>of</strong> impulse<br />

models in a background <strong>of</strong> zero model parameters is the absence <strong>of</strong> higher order<br />

interactions between model cells. To compute the exact resolution matrix for the j th<br />

column, one should compute the general inversion, perturb the parameter value in the j th<br />

model cell <strong>of</strong> the recovered model by a small amount, calculate the resulting forward<br />

model, recalculate the inversion, and finally subtract the original and perturbed models to<br />

produce the j th column <strong>of</strong> the resolution matrix. This process is then repeated for each<br />

model parameter. The error resulting from forming R as described in Equation 4.11 and<br />

not using the perturbation method described above, however, is higher order. Not only<br />

would the perturbation approach incur severe computational costs, but more importantly,<br />

the result would be problem dependent. In the study <strong>of</strong> the resolution matrix, I choose to<br />

examine the general properties without limiting to a particular model.<br />

Another limitation might appear to be that since the formation <strong>of</strong> the resolution<br />

matrix is characterized by a series <strong>of</strong> impulse models, this would then give favor to the<br />

recovery <strong>of</strong> localized, rather than diffused, models. In other words, if the true model<br />

were diffusive in shape, would the resulting resolution matrix be accurately formed<br />

through the use <strong>of</strong> impulse models? The answer is yes. The impulsive-model approach<br />

only calculates the resolving function, or the spread <strong>of</strong> the j th model cell into adjacent<br />

model cells. In this approach, Equation 4.11 illustrates the data is exactly substituted<br />

with the j th impulse model. This substitution therefore does not depend on the nature <strong>of</strong><br />

the data, but rather serves to isolate the j th model cell.<br />

4.5 Symmetry and Scaling Properties <strong>of</strong> the Resolution Matrix<br />

The resolution matrices formed with the L P -norm, p=1.0, p=1.5, p=2.0, and p=3.0<br />

in Equation 4.2, and formed from the model in Figure 4.1, is shown in Fig. 4.3. It is<br />

important to note that any structure that appears in Fig. 4.3 aside from the diagonal is an<br />

artifact <strong>of</strong> the ordering system <strong>of</strong> the discretized model parameters. Fig. 4.4 plots a<br />

histogram <strong>of</strong> each resolution matrix in Fig. 4.3 to show the amplitude distribution. Note<br />

the predominance <strong>of</strong> near-zero values on the log 10 scale. The resolution matrix is the<br />

identity matrix for a perfectly resolved or over-determined model and, thus, any departure<br />

from unit diagonal values indicate a decrease <strong>of</strong> resolution for that model parameter.<br />

Indeed, recent research on resolution matrices has focused on the diagonal (4.23).<br />

However, R contains a rich amount <strong>of</strong> information and suggests a more thorough<br />

analysis <strong>of</strong> its properties. In particular, I look at the symmetry and scaling properties <strong>of</strong><br />

the resolution matrices as a function <strong>of</strong> nonlinearity and L P -norm.<br />

4.5.1 Numerical Evaluation <strong>of</strong> Asymmetry Versus p-value<br />

Realistic imaging problems with potential fields or electromagnetics will almost<br />

certainly be underdetermined. Thus, the inherent asymmetry <strong>of</strong> R leads to a conceptual<br />

difference between the rows and columns (4.19). The rows are averaging functions such<br />

that each cell in the recovered model is a weighted average <strong>of</strong> the true model, whereas the<br />

columns are the Backus-Gilbert point spread functions that quantify the manner in which<br />

an impulse in the true model spreads to other regions in the recovered model. The<br />

differences between rows and columns can also be applied to model appraisal. Well<br />

esolved model parameters are also those in which the corresponding row and column are<br />

balanced, or well-correlated. For this reason, the study <strong>of</strong> resolution matrix asymmetry<br />

can be a powerful tool in nonlinear model appraisal.<br />

The effect <strong>of</strong> nonlinearity on resolution matrix asymmetry is not understood, nor<br />

is it addressed in scientific literature to date. I therefore provide a study based on<br />

empirical relationships between the resolution matrix symmetry and the two sources <strong>of</strong><br />

nonlinearity; the L P -norm, and the presence or absence <strong>of</strong> bound constraints. First, I<br />

develop an index <strong>of</strong> the degree <strong>of</strong> symmetry which is referred herein as the skewness<br />

index, SI. Given a square resolution matrix, each element is compared with the<br />

corresponding opposite term with respect to the diagonal,<br />

SI =<br />

∑∑<br />

j= 1 k=<br />

jk<br />

− R<br />

kj<br />

4.14<br />

SI ≥ 0<br />

model parameters.<br />

is unbounded and equality is achieved only for a symmetric matrix with M<br />

SI can then be plotted as a function <strong>of</strong> the L P -norm and as a function <strong>of</strong> the<br />

inclusion or exclusion <strong>of</strong> bound constraints for the underdetermined problem (Fig. 4.5).<br />

In the absence <strong>of</strong> bound constraints, mathematical nonlinearity introduced through the<br />

Huber norm would still be present. In fact, the only linear datum would be with p=2 for<br />

unconstrained inversion. Each resolution matrix generated uses a fixed and optimal<br />

regularization which varies with the choice <strong>of</strong> L P -norm. Thus, according to the symmetry<br />

derivation for the underdetermined system in section 4.7 which relates increasing<br />

asymmetry with increasing regularization, one would expect the fluctuations in SI versus<br />

p-value illustrated in Fig. 4.5.<br />

In the constrained inversion <strong>of</strong> Fig. 4.5, maximum asymmetry occurs when p=1,<br />

with an unexpected increase in asymmetry between p=1.25 and p=2. p > 2 shows a<br />

gradual asymptotic decrease in asymmetry, suggesting that using a LP-norm beyond p=4<br />

may not significantly affect the recovered model. In the unconstrained inversion, the<br />

shape <strong>of</strong> the line is similar to the constrained case, but inflated. Maximum asymmetry<br />

occurs near p = 2.10 and minimum asymmetry near p = 1. 25 .<br />

Furthermore, there exists a relation between increasing asymmetry and increasing<br />

regularization thus predicting the unconstrained inversion to be more asymmetric than the<br />

constrained inversion; derivations <strong>of</strong> these results are shown in section 4.7. However,<br />

comparison between the two plotted lines in Fig. 4.5 shows opposing behavior for<br />

p < 1.5 . While the characteristic dip in asymmetry between p = 1 and p = 2 cannot<br />

currently be explained, it is clear that the choice <strong>of</strong> regularization significantly affects the<br />

asymmetry <strong>of</strong> the resolution matrix.<br />

4.5.2 Sensitivity <strong>of</strong> Resolution Matrix to Discretization<br />

In order to use the above results to improve understanding <strong>of</strong> the resolution<br />

matrix, it is important to examine the sensitivity to changes in the quantity <strong>of</strong><br />

discretization. Three resolution matrices, identical in all parameters apart from the<br />

number <strong>of</strong> model cells, are formed from the previous example. The total number <strong>of</strong><br />

model cells, M, for each increasingly refined resolution matrix are 2000, 6750, and<br />

16000. The first step is then to extract the column <strong>of</strong> each resolution matrix which<br />

corresponds to the geometrical center <strong>of</strong> the high density anomaly located at x = 1.65 m,<br />

y = 1.00 m, z = -1.80 m. I choose the column corresponding to the anomaly center<br />

because it should be the dominant component in the resolution matrix. Column lengths<br />

are then made equal through decimation.<br />

results:<br />

A cumulative Euclidean distance between each pair <strong>of</strong> columns has the following<br />

Columns <strong>of</strong> R to compare Max. amplitude in R<br />

ρ −<br />

ρ 2<br />

2000<br />

− ρ 6750<br />

2.3 x10 -1 1.30x10 -2<br />

ρ6750 − ρ 16000<br />

4.70 x10 -1 7.26x10 -2<br />

− ρ 16000<br />

9.8 x10 -1 3.10x10 -1<br />

Table 4.1. Root-mean-squared (RMS) comparison <strong>of</strong> resolution matrices with different discretization<br />

quantities.<br />

The maximum amplitude for each resolution matrix is approximately an order <strong>of</strong><br />

magnitude greater than the column differences. Therefore, to a first order approximation,<br />

and assuming no spatial aliasing present, the quantity <strong>of</strong> discretization does not<br />

significantly affect the resolution matrix.<br />

4.5.3 Quantifying the Resolution from R<br />

While R is a map between a true and a recovered model, R j represents the<br />

resolving ability for the j th model parameter. Since R j is computationally efficient,<br />

forming spatial images which quantify the resolving ability in each dimension for the j th<br />

parameter can be a useful diagnostic. One such method would be similar to that<br />

discussed in Parker (4.24); beginning with a δ function at the j th model parameter, invert<br />

the resulting forward data to achieve a resolving function <strong>of</strong> which the overall width<br />

indicates the resolution scale. Practically then, from our model, a 1-D slice from R j is<br />

extracted through the center <strong>of</strong> each model cell for each dimension and plot the width <strong>of</strong><br />

distribution. However, as model cells at the boundary will have a truncated distribution<br />

width, I have developed a measurement to compensate:<br />

( )<br />

dim ξ<br />

∆W ρ j = . 4.15<br />

Where ξ is the full width at half maximum for the j th model cell in the k th coordinate<br />

dimension, V the volume enclosed, and ∆W<br />

is the distribution metric. ∆ W approaches<br />

zero for a perfectly resolved model parameter and positively increases with decreasing<br />

resolution. Since each column <strong>of</strong> the resolution matrix corresponds to one cell in the<br />

model space, if this process were to continue for every column <strong>of</strong> R, the result would be<br />

a qualitative estimate <strong>of</strong> the resolving ability <strong>of</strong> each model parameter and for each<br />

spatial coordinate. In other words,<br />

∆W for each coordinate dimension can then be<br />

plotted into a 3-D image. Fig. 4.6 represents the X-coordinate resolution as calculated by<br />

Equation 4.14.<br />

4.6 Condition Number and Eigenvalues <strong>of</strong> Resolution Matrices<br />

The condition number <strong>of</strong> a matrix measures its sensitivity to small changes in the<br />

model parameters; generally, a lower condition number suggests lower sensitivity. The<br />

condition number,<br />

C R<br />

<strong>of</strong> a matrix, A, is defined as<br />

2 −1<br />

A A where the L<br />

2 -norm is the<br />

maximum eigenvalue attained from singular value decomposition. In the<br />

underdetermined linear case <strong>of</strong> Equation 4.12,<br />

H , is by definition, rank deficient.<br />

Therefore, the underdetermined linear resolution matrix can not be invertible and should,<br />

in theory, be infinite. The practical implication <strong>of</strong> this result is that the underdetermined<br />

resolution matrix can never be inverted to directly recover ρ in Equation 4.4.<br />

Nevertheless, Table 4.1 lists the condition numbers for the underdetermined<br />

resolution matrix as a function <strong>of</strong> L P -norm. Although one may study the trends <strong>of</strong><br />

as<br />

a function <strong>of</strong> LP-norm, the condition numbers are effectively infinite. The use <strong>of</strong> finite<br />

precision representing the logarithmic barrier terms <strong>of</strong> the bound constraints, finite<br />

tolerance within the conjugate gradient solver, and interior point method termination<br />

criteria all contribute in-part to a numerically finite<br />

infinite.<br />

representation that is effectively<br />

L P -norm C R for Bound Constrained R C R for Unconstrained R<br />

1.0 9.4542 x 10 6 1.2080 x 10 12<br />

1.1 8.7636 x 10 10 2.3776 x 10 9<br />

1.25 1.3995 x 10 7 1.2387 x 10 8<br />

1.5 8.7636 x 10 10 2.0827 x 10 7<br />

1.8 2.0191 x 10 7 1.8224 x 10 7<br />

2.0 3.4089 x 10 8 5.3784 x 10 11<br />

3.0 1.1142 x 10 7 1.6360 x 10 11<br />

4.0 6.5960 x 10 6 1.6909 x 10 11<br />

5.0 1.7505 x 10 7 4.3920 x 10 12<br />

Table 4.2 Condition numbers (C R ) for the resolution matrix as a function <strong>of</strong> L P -norm<br />

The eigenvalues for the same resolution matrix are plotted in Fig. 4.7. When p > 2 ,<br />

the eigenvalues are increasingly similar which suggest, based on earlier results in this<br />

chapter, that applying an LP-norm greater than approximately three is likely to result in<br />

marginal performance increases in the recovered model. Although the flat region for<br />

p = 1 at the lowest eigenvalues might suggest a sharp drop <strong>of</strong>f, this is an artifact <strong>of</strong> not<br />

ordering the eigenvalues in ascending order.<br />

4.7 Conclusions<br />

As the resolution matrix was intended to be a linear construct, and is generated for<br />

both linear and nonlinear conditions, I understand that the nonlinear resolution matrix<br />

might ultimately require a different name. Nevertheless, I have presented a methodology<br />

to column-wise form the complete resolution matrix for a potential field problem. This<br />

method incorporates all non-linearity inherent in the physics and mathematics except for<br />

the higher order effects that an impulse model with zero background introduces. Multiple<br />

resolution matrices were formed for 1 ≤ p ≤ 5 in the L P -norm. The results <strong>of</strong> which<br />

empirically show that the resolution matrices have a maximum skewness index for an L P -<br />

norm slightly above p=2 for both constrained and unconstrained inversions. The<br />

skewness index is also minimal near p=1.3; the relative locations <strong>of</strong> the maxima and<br />

minima <strong>of</strong> the skewness index are not affected by changes in regularization.<br />

The resolution matrix is examined for sensitivity to discretization. Three different<br />

choices <strong>of</strong> discretization quantity were used to construct independent resolution matrices.<br />

RMS comparisons <strong>of</strong> individual columns showed that the variations were at least an order<br />

<strong>of</strong> magnitude lower than the maximum.<br />

Since the resolution matrix is square, and each column or row refers to one<br />

corresponding model cell, taking slices through each column in the x-, y-, and z-<br />

directions produces three images for each resolution matrix showing the compactness, or<br />

degree <strong>of</strong> resolution, <strong>of</strong> each dimension in the final model space image. The<br />

distributional spread <strong>of</strong> each model parameter in each model coordinate is characterized<br />

by Equation 4.15.<br />

At first glance it might seem as if an extraordinary amount <strong>of</strong> time was spent<br />

analyzing the symmetry and scaling properties <strong>of</strong> R. However, aside from a<br />

mathematical interest, it is my vision that understanding the properties <strong>of</strong> the complete<br />

resolution matrix can eventually decrease the computational requirement <strong>of</strong> M inversions.<br />

For example, if a resolution matrix is known to be approximately symmetric, then one<br />

can assume the j th column <strong>of</strong> R equals the j th row, which could significantly decrease the<br />

number <strong>of</strong> inversions, and hence computation time. Also, if a decrease in discretization<br />

quantity is known to not significantly affect the resolution matrix, the computational<br />

requirements <strong>of</strong> formation could again be decreased.<br />

The symmetry <strong>of</strong> R can also be applied to model appraisal. It was shown that the<br />

j th model parameter directly corresponds to the j th row and the j th column. The degree to<br />

which the j th column and row are well-correlated reflects the degree to which confidence<br />

can be assigned to the j th model parameter. Since matrix symmetry is equivalent to<br />

correlation between rows and columns, symmetry can be a powerful tool in linear and<br />

nonlinear model appraisal.<br />

4.8 Acknowledgements<br />

The author is grateful to Pr<strong>of</strong>essor Yaoguo Li at the <strong>Colorado</strong> <strong>School</strong> <strong>of</strong> <strong>Mines</strong><br />

Department <strong>of</strong> <strong>Geophysics</strong> for indispensable theoretical and experimental advice in<br />

addition to advising this work. The author is also grateful to Jim Berryman at Lawrence<br />

Berkeley National Laboratory and Roel Snieder at <strong>Colorado</strong> <strong>School</strong> <strong>of</strong> <strong>Mines</strong> for valuable<br />

theoretical discussions. The visual s<strong>of</strong>tware MeshTools3D was developed at the<br />

University <strong>of</strong> British Columbia and was used to generate Figures 4.1, 4.2, and 4.6.<br />

4.9 References<br />

(4.1) Sambridge, M., Beghein, C., Simons, F.J., Snieder, R., 2006, How do we understand and visualize<br />

uncertainty?, The Leading Edge, Vol. 25, Issue 5, p. 542 – 546<br />

(4.2) Zhang, J., McMechan, G. A., 1995, Estimation <strong>of</strong> resolution and covariance for large matrix<br />

inversions, Geophysical Journal International, vol.121, no.2, pp.409-426<br />

(4.3) Van Trees, H.L., 2001, Detection, Estimation, and Modulation Theory, Part I, Wiley-Interscience,<br />

ISBN 0471095176, 720 p.<br />

(4.4) Oldenburg, D.W., 1983. Funnel functions in linear and nonlinear appraisal, Journal Geophys. Res.,<br />

v. 88, pp. 7387–7398<br />

(4.5) Backus G. E. and Gilbert J. F., 1968, The resolving power <strong>of</strong> gross earth data, Geophysical J. R.<br />

Astron. Soc., v. 16, pp. 169 – 205<br />

(4.6) Backus G. E. and Gilbert J. F., 1970, Uniqueness in the inversion <strong>of</strong> inaccurate earth data, <strong>Ph</strong>il.<br />

Trans. R. Soc. A, v. 266, pp. 123 - 92<br />

(4.7) Berryman, J.G., 2000, Analysis <strong>of</strong> approximate inverses in tomography I. Resolution analysis <strong>of</strong><br />

common inverses, Optimization and Engineering, v. 1, pp. 87 – 115<br />

(4.8) Berryman, J.G., 2000, Analysis <strong>of</strong> approximate inverses in tomography II. Iterative inverses,<br />

Optimization and Engineering, v. 1, pp. 437 – 473<br />

(4.9) Alumbaugh, D.L., Newman, G.A., 2000, Image appraisal for 2-D and 3-D electromagnetic<br />

inversion, <strong>Geophysics</strong>, vol. 65, 5, pp. 1455 – 1467<br />

(4.10) Routh, P.S., Oldenborger, G.A., Oldenburg, D.W., 2005, Optimal survey design using the point<br />

Expanded Abstracts,v. 24, pp. 1033<br />

(4.11) Snieder, R., 1998, The role <strong>of</strong> nonlinearity in inverse problems, Inverse Problems, v. 14, pp. 387-<br />

(4.12) H<strong>of</strong>meyer, G.M., Affleck, C.A., Rotating accelerometer gradiometer, United States Patent<br />

5,357,802 ; www.uspto.gov, 1994<br />

(4.13) Kirkendall, B., Li, Y., Oldenburg, D., 2006, Cargo container inspection using gravity gradiometry,<br />

SPIE Defense and Security Symposium, April 16 – 20, Kissimmee, Florida, 8 p.<br />

(4.14) Kirkendall, B., Li, Y., Oldenburg, D., 2006, Gravity gradiometry in imaging cargo containers,<br />

IEEE Trans. Geoscience and Remote Sensing, 16 p., accepted<br />

(4.15) Haber, E., 1997, Numerical strategies for the solution <strong>of</strong> inverse problems, <strong>Ph</strong>.D. <strong>Thesis</strong>,<br />

University <strong>of</strong> British Columbia<br />

(4.16) Li, Y., Oldenburg, D.W., 1996, 3-D Inversion <strong>of</strong> magnetic data, <strong>Geophysics</strong>, Vol. 61, 2, p. 394-<br />

408<br />

(4.17) Nocedal, J. and Wright, S.J., 1999, Numerical optimization, Springer-Verlag, New York, ISBN<br />

0387987932<br />

(4.18) Farquharson, C.G., Oldenburg, D., 1998, Non-linear inversion using general measures <strong>of</strong> data<br />

misfit and model structure, Royal Ast. Soc. Geophysical Journal Intl., v. 134, pp. 213 – 227<br />

(4.19) Oldenburg, D.W.,Li. Y., 2005, Near-surface geophysics, Society <strong>of</strong> Exploration <strong>Geophysics</strong><br />

Investigations in <strong>Geophysics</strong>, Vol. 13<br />

(4.20) Butler, D.K., ed., 2005, Near surface geophysics, SEG investigations in geophysics series no. 13,<br />

Chapter 5: Inversion for applied geophysics: a tutorial, Oldenburg, D.W., Li, Y.<br />

(4.21) Strang, G., 2005, Linear Algebra and Its Applications, Brooks Cole, ISBN 0030105676<br />

(4.22) Lawson, C.L.,Hanson, R.J., 1974, Solving least squares problems, Prentice Hall, ISBN<br />

0138225850<br />

(4.23) Friedel, S., 2003, Resolution, stability and efficiency <strong>of</strong> resistivity tomography estimated from a<br />

generalized inverse approach, Geophysical Journal Intl., v. 153, pp. 305 – 316<br />

(4.24) Parker, R.L., 1994, Geophysical Inverse Theory, Princeton University Press, 386 pp., ISBN<br />

0691036349<br />

Figure 4.1<br />

Starting model for resolution matrix studies. The <strong>of</strong>f-center block has density 6 g/cm 3 . Axis<br />

units are in meters.<br />

Z-axis<br />

X-axis<br />

Y-axis<br />

Figure 4.2 Discretization for resolution matrix studies. Axis units are in meters. There are M=2000<br />

model cells. Sensor locations are as follows: {67 locations in interval x=(0.0 m : 6.0 m),<br />

y=(0.0 m : 3.0 m), z=(0.0 m)},{67 locations in interval x=(0.0 m : 6.0 m), y=(-0.30 m),<br />

z=(0.0 m : -3.30 m)},{ 67 locations in interval x=(0.0 m : 6.0 m), y=(3.30 m), z=(0.0 m : -<br />

3.30 m)}<br />

L P<br />

-norm=1.0<br />

-norm=1.5<br />

500<br />

-10<br />

1000<br />

-20<br />

-15<br />

1500<br />

500 1000 1500 2000<br />

-30<br />

-25<br />

-norm=2.0<br />

-norm=3.0<br />

Fig. 4.3 Complete resolution matrices for the bound constrained gravity gradiometry problem in Equations<br />

(1) – (3) for the L P -norm p=1.0 (top left), p=1.5 (top right), p=2.0 (lower left), and p=3.0 (lower<br />

right). There are 2000 model cells and the scale is log 10 (g/cm 3 ). Note the range <strong>of</strong> values<br />

increases as p → 1.0 . The geometric patterns are solely an artifact <strong>of</strong> the how the models cells<br />

are numbered. The numerical double precision used to develop this matrix provides accuracy to<br />

only 10<br />

-16 , or –16 dB; Thus, the blue hues are close to zero and suffer from round-<strong>of</strong>f and<br />

truncation errors.<br />

15 x 104<br />

10 x 104 L P -norm=1.5<br />

Bin count<br />

5<br />

8<br />

6<br />

4<br />

2 x L 105 P -norm=2.0<br />

1.5<br />

0.5<br />

2 x L 105 P -norm=3.0<br />

-5 -10<br />

Log 10<br />

[R (i,j)<br />

]<br />

Fig. 4.4<br />

Histogram <strong>of</strong> resolution matrix values with each plot corresponding to the resolution matrix in<br />

Fig. 4.3. The x-axis is the log 10 amplitude <strong>of</strong> each element in the matrix and the y-axis is the<br />

number <strong>of</strong> occurrences in the corresponding bin. Note that in all matrices, the majority <strong>of</strong><br />

resolution matrix elements are close to zero, which is discussed from a different perspective in<br />

Table 4.1. Also, there appears to be two dominant modes in the amplitudes for p=1.5. The<br />

amplitude distribution for p > 2 appears to change minimally.<br />

Fig. 4.5 Skewness index <strong>of</strong> the resolution matrix for the underdetermined problem described in this paper<br />

with respect to the L P -norm applied to the objective smoothing function in model space. A<br />

symmetric matrix has a skewness index <strong>of</strong> zero. For the inversion constrained by the logarithmic<br />

barrier term, the resolution matrix is maximally asymmetric for p=1. However, maximum<br />

asymmetry for the unconstrained inversion is achieved for p=2.1. The symmetry <strong>of</strong> overdetermined<br />

resolution matrices will be studied in future work.<br />

Figure 4.6 X-coordinate resolution in model space. This image is cut away to show variation in the<br />

resolving capability <strong>of</strong> this particular problem. The scale is normalized to the model cell with<br />

the most resolved distribution (red) where blue represents the least resolved area <strong>of</strong> the model in<br />

the x-coordinate.<br />

10 0 Eigenvalues <strong>of</strong> Resolution Matrices for Gravity Gradiometry Container Problem<br />

10 -2<br />

Eigenvalue mode<br />

10 -4<br />

10 -6<br />

10 -8<br />

p=1<br />

p=1.25<br />

p=1.5<br />

p=2<br />

p=3<br />

p=4<br />

p=5<br />

0 200 400 600 800 1000 1200 1400 1600 1800 2000<br />

Ordered Eigenvalues<br />

Figure 4.7 Given the bound constrained resolution matrices in Figure 4.3, the eigenvalues are directly<br />

calculated through singular value decomposition as a function <strong>of</strong> L P -norm. Eigenvalues for<br />

p > 2 are similar.<br />

Appendix 4.A Determination <strong>of</strong> Symmetry for Underdetermined and Determined<br />

Systems<br />

I mathematically show the overdetermined resolution matrix to be symmetric using<br />

singular value decomposition and the underdetermined resolution matrix to be<br />

asymmetric using linear algebra. The degree to which the underdetermined resolution<br />

matrix is asymmetric is directly proportional to the degree <strong>of</strong> regularization.<br />

In the overdetermined case, we can write the resolution matrix as R ( G G) G G<br />

G<br />

T G<br />

∈ R<br />

[MxM<br />

symmetric. If R is symmetric, then<br />

Therefore, it is required to show that<br />

≡ ,<br />

is symmetric and given the inverse <strong>of</strong> a symmetric matrix is<br />

R = R . Let A = G G where A is orthonormal.<br />

AA<br />

− 1 −1<br />

= A A . The next step is decomposition <strong>of</strong> A<br />

into its singular values and eigenvectors, A = uλv<br />

and A = v λ u .<br />

inv<br />

Thus prove<br />

vλ<br />

u uλv<br />

invvinv<br />

= u λ v λ<br />

u<br />

. Since A is orthonormal,<br />

−1 T<br />

u u = 1 and v v = 1 and thus, vλ<br />

λv<br />

= u λ λ u . In general, λ − 1 λ ≠ I , but<br />

because matrix is full rank, λ − 1 T T<br />

λ = I . Therefore, vv = uu = 1, and R is symmetric in<br />

the overdetermined case. The equally determined case can be argued in the same manner<br />

to be symmetric.<br />

A<br />

In the underdetermined case, R ≡ ( A A) G G , where<br />

A G G + µ ( α w w + α w w + α w w + α w w )<br />

= . While A<br />

T A∈<br />

R and<br />

[MxM ]<br />

( A A)( G G)<br />

are both symmetric, the product <strong>of</strong> the two symmetric matrices,<br />

, is symmetric only if the two commute, or equivalently, share the same<br />

eigenspace. However, regularization, µ, clearly affects the eigenspace <strong>of</strong> ( ) −1<br />

G T G and ( A T A) −1<br />

do not, in general, commute unless µ is exceptionally weak.<br />

Therefore R is not, in general, symmetric in the underdetermined case.<br />

A T<br />

. Thus,<br />

Chapter 5<br />

DISTRIBUTIONAL MODELING OF THE L P -NORM RESOLUTION<br />

MATRIX<br />

The research in Chapter two focused on imaging cargo containers with the gravity<br />

gradiometry measurement coupled with two nonlinear mathematical operations. The<br />

corresponding nonlinear model appraisal in Chapter three was addressed with funnel<br />

analysis and resolution matrices, and in Chapter four, properties <strong>of</strong> the resolution matrix<br />

were studied. In this Chapter, I extend the resolution matrix to a lower dimension with a<br />

unique solution, so that the results can be more readily applied to other geophysical<br />

techniques such as diffusion electromagnetics. I then model the distribution and statistics<br />

<strong>of</strong> the resolution matrix as a function <strong>of</strong> the L P -norm using the Generalized Gaussian<br />

Distribution. In this manner, an empirical graphical relationship is developed between<br />

the distributions within the resolution matrix and the L P -norm. Finally, I show the<br />

empirical modeling results can be successfully applied to the three-dimensional cargo<br />

container problem from Chapter two and that the addition <strong>of</strong> theoretical non-uniqueness<br />

manifests as a decrease in resolution.<br />

5.1 Introduction<br />

If the curves, or distributions, within the resolution matrix created in Chapter four<br />

were directly extended to different physics, the results would certainly be clouded by the<br />

issue <strong>of</strong> non-uniqueness (5.1); an inherent and well known phenomena <strong>of</strong> the inverse<br />

three-dimensional gravity problem. A lower-dimensional gravity problem, however,<br />

does have a unique solution. Thus, I shift the resolution matrix into lower dimensions<br />

through the formation <strong>of</strong> two distinct classes <strong>of</strong> two-dimensional models, each<br />

characterized as underdetermined, determined, and overdetermined systems. The<br />

resulting distributions within the resolution matrix are then modeled as a function <strong>of</strong> L P -<br />

norm.<br />

One benefit <strong>of</strong> this approach is that the results can be extended to other kernels<br />

based on different physics without the complication <strong>of</strong> non-uniqueness. However, the<br />

primary benefit is from the distributional modeling, for which a L 2 solution can be<br />

extended to a L P<br />

( 1 ≤ p < 2)<br />

solution without requiring further computation. Since<br />

Chapter four illustrates the benefits in model performance for<br />

, and Chapter<br />

six explains that even slight decreases in the p-norm can result in massive computational<br />

increases, a computationally-free determination <strong>of</strong> the ( 1 ≤ p < 2)<br />

solution can be<br />

valuable. In essence, I study the relationship between classes <strong>of</strong> distributions as a<br />

function <strong>of</strong> p-norm applied to model space within the Tikhonov inversion. However, as<br />

uniqueness <strong>of</strong> the gravity gradiometry problem must first be established, I begin with the<br />

two-dimensional gravity response in the space-domain.<br />

5.2 Uniqueness <strong>of</strong> the Two-Dimensional Gravity Gradient Inverse<br />

Although a two-dimensional system can have multiple definitions within the<br />

scientific community, I define the two-dimensional problem as consisting <strong>of</strong> a<br />

distribution <strong>of</strong> masses confined to a two-coordinate horizontal plane, ρ ( x',<br />

y'<br />

) , and a<br />

collection <strong>of</strong> sensor locations also confined to a two coordinate horizontal plane,<br />

( x,<br />

y)<br />

. Although the two planes are not coincident, this does not affect the twodimensional<br />

characterization. Furthermore, the distance between the two planes is<br />

arbitrary and does not affect the forward problem in a theoretical study. Finally, to<br />

alleviate boundary conditions affecting the two-dimensional characterization, the mesh is<br />

extended far enough such that the energy from a localized source is not affected by a<br />

boundary.<br />

The space domain model description for this two-dimensional problem can<br />

therefore be written as,<br />

g<br />

∆z<br />

( ) ( )<br />

( h − z'<br />

x,<br />

y = − ∫∫∫ρ<br />

x',<br />

x' y' 0<br />

( x − x'<br />

) + ( y − y'<br />

) + ( h − z'<br />

γ dx'<br />

dy'<br />

5.1<br />

[ ]<br />

3<br />

Where ∆z is the vertical thickness <strong>of</strong> the plane <strong>of</strong> prism sources, h is the distance<br />

between the source plane and receiver plane, and γ is the universal gravitational constant<br />

defined in Chapter two. To prove Equation 5.1 unique, transformation into the Fourier<br />

domain will significantly reduce the complexity.<br />

Fundamental behavior within the Fourier domain is described by the Fourierconvolution<br />

theorem,<br />

[ g] F[ ρ] F[ ξ ]<br />

F = 5.2<br />

Where the Fourier transform <strong>of</strong> the gravity field, F [ g]<br />

, equals the Fourier transform <strong>of</strong><br />

the source distribution, F [ ρ]<br />

function, F [ ξ ].<br />

, multiplied by the Fourier transform <strong>of</strong> the Green’s<br />

Using Equation 5.2 to represent Equation 5.1 (5.2), the general relationships in the<br />

Fourier domain between a gravity signature measured on a horizontal surface,<br />

its source distribution located entirely below the surface can be shown as,<br />

F[ g]<br />

, and<br />

F<br />

k h<br />

[ g] = 2 e F[ ρ( z'<br />

)]<br />

∞<br />

∫<br />

h<br />

− k z'<br />

πγ e dz'<br />

5.3<br />

2πn<br />

k = where X is an interval and is the number <strong>of</strong> sinusoids,<br />

n F[ ρ ( z' )]<br />

represents the two-dimensional Fourier transform <strong>of</strong> the density on one horizontal slice<br />

through a body at depth z' .<br />

If the prism source in Eqn 5.1 is confined to a horizontal layer with top at depth ,<br />

bottom at , and density that varies only in the horizontal direction, Equation 5.3<br />

reduces to,<br />

z 2<br />

z 1<br />

πγ k h<br />

[ g ] = F[ ] e (<br />

2 − k z ⎪⎫<br />

1 − k z2<br />

ρ ⎨ e − e ) ⎬. 5.4<br />

⎪⎩ k<br />

Therefore, one can visibly conclude that the two-dimensional gravity problem described<br />

by the analytical representation in Equation 5.4 is therefore, along with its inverse,<br />

unique.<br />

Since the gravity response was shown to be unique, I now consider the uniqueness<br />

<strong>of</strong> the two-dimensional gravity gradiometry response. Since the integration <strong>of</strong> the gravity<br />

gradient response is equal to the gravity response, the resulting integration constant might<br />

at first glace appear to invalidate the uniqueness <strong>of</strong> the gravity gradient. However, if we<br />

assume that the model space is finite and all mass is enclosed within that model space,<br />

the integration constant is zero, and it therefore follows that the gravity gradiometry<br />

problem is also unique.<br />

5.3 Two-Dimensional Gravity Gradient Problem<br />

Figures 5.1, 5.2, and 5.3 illustrate the resulting two-dimensional geometry with<br />

underdetermined, determined, and overdetermined systems. All three systems have the<br />

same number <strong>of</strong> model parameters, M=625, and a variable number <strong>of</strong> data;<br />

N underdetermined =196, N determined =625, and N overdetermined =1024. An irregular discretization<br />

with 25 intervals in each spatial coordinate was chosen because, close to the anomalous<br />

body, we require a certain degree <strong>of</strong> resolution to accurately determine the distributional<br />

properties. At increasing distances from the source, discretization can be made<br />

increasingly coarse to decrease computation time. Other parameters <strong>of</strong> the inversion<br />

−14<br />

discussed in Chapter two are: θ = 1.0x10<br />

, L L = L = 1. 0 , = 0.10 , there is no<br />

depth or distance weighting, and no matrix compression. Bound constraints <strong>of</strong> (0 g/cm<br />

1.0 g/cm 3 ) are applied. Bound constraints incorporated to prevent distributions from<br />

having negative sidelobes, which would complicate the modeling effort and represent<br />

inconsistency with Chapter two, are discussed in more detail in section 5.6.<br />

L s<br />

3 ,<br />

The gravity gradiometric tensor in this toy problem is specified by the single T ZZ<br />

component. Mathematically, the 9 components <strong>of</strong> T are dependent, whereby only one<br />

component is required for successful inversion. In other words, T ZZ is linearly related to<br />

all the other components and uniquely relates the underlying data function. However, in<br />

practice, multiple components both increase the signal-to-noise ratio and contribute<br />

differently to a recovered model since each component is discretely sampled in space.<br />

Therefore, in determining whether or not a system is over- or underdetermined, multiple<br />

tensor components <strong>of</strong> one potential field measurement would count as multiple data at<br />

that location. Thus, to avoid confusion in this determination I include only the T ZZ<br />

component in our data.<br />

There are two classes <strong>of</strong> starting models in this example; type-1 and type-2. The<br />

type-1 model (Figure 5.4) consists <strong>of</strong> a 1.0 g/cm 3 impulse in the center <strong>of</strong> the model, cell<br />

313. The impulse is characterized by sharp boundaries and requires a p = 1 solution.<br />

The type-2 model (Figure 5.5) consists <strong>of</strong> a gradual density increase leading also to a 1.0<br />

g/cm 3 peak centered at cell 313. The type-2 model implies the need for a<br />

p = 2 solution.<br />

The 313 th columns <strong>of</strong> the resolution matrix in the type-1 model for each system<br />

and for p = 1 and p = 2 are plotted to illustrate the increase in resolution that can be<br />

achieved for<br />

p ≈ 1(Figures 5.6, 5.7, and 5.8). Note that the overdetermined results in<br />

Figure 5.8 show a small dependence on the choice <strong>of</strong> LP-norm which should not be the<br />

case if the model were purely overdetermined. In other words, the resolution matrix <strong>of</strong><br />

an overdetermined problem is the identity matrix.<br />

The reason for this inexact behavior originates in the weak regularization added to<br />

the overdetermined problem. The regularization in this case is not necessary, but<br />

provides computational stability and limit the effects <strong>of</strong> errors in the data (5.3). Another<br />

consideration in the overdetermined problem is that the fixed regularization for the<br />

overdetermined problem, µ = 1.0x10<br />

−20<br />

, may not necessarily be weak. Tikhonov curves<br />

are required to show that regularization is indeed weak. Note that in calculating the<br />

Tikhonov curve (Figure 5.17), a coarse mesh is used for the forward calculation and a<br />

finer mesh is used for the inversion. In this manner we can eliminate possible numerical<br />

“pigeon-holing” <strong>of</strong> the recovered model.<br />

In Figure 5.17, the location <strong>of</strong> operation outlined by the red box is consistent with<br />

an overdetermined problem (5.3). Note the limited range on the<br />

Φ d<br />

axis; the<br />

overdetermined problem cannot exactly fit the data. Also, note that for increasing<br />

regularization (i.e. decreasing Φ m ),<br />

asymptotically converge to zero.<br />

does not significantly change, and will not<br />

5.4 Mass Integration Within the Resolution Matrix<br />

A mathematical distribution is an object which generalizes functions and<br />

probability distributions and is fundamentally characterized by the area and geometric<br />

shape. Therefore, since the goal <strong>of</strong> this chapter is to model distributions within the<br />

resolution matrix, the total mass contained within the resolution matrices using numerical<br />

integration is examined in this section and referred to as mass integration studies.<br />

The j th column <strong>of</strong> the resolution matrix is calculated for both toy model classes;<br />

type-1 and type-2. Since the j th column <strong>of</strong> the resolution matrix illustrates the manner in<br />

which the energy <strong>of</strong> the j th cell is spread into adjacent model cells, horizontal slices are<br />

extracted from the j th column. It is from these slices that the area is calculated. Figure<br />

5.15 plots the area resulting from the trapezoidal integration <strong>of</strong> a one-dimensional slice<br />

through the type-1 toy problem for the three system types. Figure 5.16 plots the<br />

equivalently calculated area for the type-2 problem. Plots resulting from the integration<br />

<strong>of</strong> two-dimensional slices are identical and are not shown for brevity.<br />

The overdetermined system for type-1 and type-2 problems consistently estimates<br />

the mass accurately, although the error increases as p → 2.0 . In type-1 and type-2<br />

problems the mass is consistently underestimated for<br />

p > 1.4<br />

in the determined and<br />

underdetermined systems. Only for<br />

p = 1.0 is the mass accurately estimated in all three<br />

systems. Therefore, when modeling the distribution within the resolution matrix, these<br />

results show that one not need worry about preserving a unit mass.<br />

5.5 Distributions from Type-1 and Type-2 as Function <strong>of</strong> L P -norm<br />

Figures 5.9, 5.11, and 5.13 illustrate linear plots <strong>of</strong> each system type as function<br />

<strong>of</strong> L P -norm for the type-1 problem. Figures 5.10, 5.12, and 5.14 illustrate log plots <strong>of</strong><br />

each system type as function <strong>of</strong> L P -norm also for the type-1 problem. For brevity, the<br />

type-2 distributions are not plotted. The logarithmic scale accentuates the smaller<br />

distributional values and resulting artifacts. One such artifact are the sidelobe patterns on<br />

Figure 5.10 for p = 1, which are a result <strong>of</strong> the numerical process but not <strong>of</strong> randomness<br />

in the inversion process. Note that these sidelobes remain positive due to the bound<br />

constraints. Also note that noise applied to synthetic data is the only source <strong>of</strong><br />

randomness in this inversion code.<br />

5.6 The Generalized Gaussian Distribution (GGD)<br />

The distributions from the previous section coupled with the mass integration<br />

plots provide a basis for modeling. Wavelets (5.4) were initially considered as a<br />

foundation for the modeling, but the abrupt edges and cusps which characterize the<br />

distributions in Figures 5.9 – 5.14 result in severe oscillations at longer <strong>of</strong>fsets. Perhaps<br />

more appropriate as a foundation for modeling is the one-dimensional generalized<br />

Gaussian distribution (GGD) (5.5):<br />

( x)<br />

1−<br />

x−x0<br />

q<br />

q( σ ) q<br />

= C exp<br />

5.5<br />

⎛ 1 ⎞<br />

2σ<br />

qΓ⎜<br />

⎝ q ⎠<br />

Two parameters,<br />

q and σ , specify the distribution shape. The GGD generates a class <strong>of</strong><br />

stable functions such as boxcar, symmetric exponentials, and Gaussian. The familiar<br />

Gaussian function is but one particular case within this broad class <strong>of</strong> functions.<br />

The amplitude correction factor, C, in Equation 5.5 allows any distribution within<br />

any resolution matrix to be modeled as a function <strong>of</strong> L P -norm if the solution is positively<br />

bounded. Although this research restricts the values <strong>of</strong> L P -norm to 1 ≤ p ≤ 2, the ability<br />

<strong>of</strong> the GGD to provide all possible distributional shapes within a resolution matrix is a<br />

powerful empirical relationship. Furthermore, the fundamental Gaussian statistics<br />

inherent in the GGD provide an appealing foundation for near-future research. More<br />

specifically, statistical properties <strong>of</strong> distributions within the resolution matrix could be<br />

correlated with statistical properties <strong>of</strong> the GGD.<br />

The solution must be positively bounded in order to prevent the occurrence <strong>of</strong><br />

sidelobes, which would characteristically arise at the low-density values in the resolution<br />

matrix distributions, and which the GGD would not be able to model. If bound<br />

constraints were required to be relaxed, another basis for modeling would be required<br />

such as wavelets. Paradoxically, wavelets were studied and discarded in the earlier<br />

stages <strong>of</strong> research because <strong>of</strong> their ability to generate sidelobes.<br />

5.7 Distributional Modeling with GGD<br />

The relationship between model space and distributions within the resolution<br />

matrix is data specific. The reason for this is that regularization is at the heart <strong>of</strong> model<br />

space and is itself primarily determined by errors in the data. As discussed in Chapter<br />

four, the resolution matrix is computed with a fixed, optimized regularization parameter.<br />

Thus, a change in the data or model would affect any empirical relationships determined<br />

between the GGD and distributions within the resolution matrix. The distributional<br />

modeling in this chapter recognizes this inherent variability but also indicates that<br />

between certain classes <strong>of</strong> models, the variability will not be significant.<br />

Consider the type-1 and type-2 models discussed earlier in this Chapter as<br />

representing two distinct model classes. Applied to the cargo container example in<br />

Chapter 2, the type-1 impulse model is characteristic <strong>of</strong> a rapid change in density caused<br />

by the presence <strong>of</strong> fissile material, while the type-2 smooth model reflects the presence <strong>of</strong><br />

slowly varying low density materials. The data generated by these two classes can then<br />

be contaminated with noise, inverted using the formulation described in Chapter two.<br />

Then with the optimal regularization parameter from the inversion, the resolution matrix<br />

can then be developed as described in Chapter four. Slices through columns <strong>of</strong> the<br />

resolution matrix can then be modeled using the GGD discussed in the previous section<br />

as a function <strong>of</strong> L P -norm.<br />

It was noted also in the previous section that three parameters are required to fit<br />

the GGD to any distribution within the resolution matrix; q , σ , and C. Figures 5.18 and<br />

5.19 illustrate the ability <strong>of</strong> the GGD to generate equivalent curves for an<br />

underdetermined type-1 problem for p=1 and for p=2. The discrepancy between the<br />

GGD distribution and that within the resolution matrix is referred to as the misfit which is<br />

measured using the Euclidean norm. All misfits in this Chapter are less than 1%.<br />

Proceeding with the method outlined, Figures 5.20, 5.21, and 5.22 are plots <strong>of</strong> the<br />

required q , σ , and amplitude, respectively, in order to fit the type-1 underdetermined<br />

problem for<br />

1 ≤ p ≤<br />

2. Figures 5.23, 5.24, and 5.25 are plots <strong>of</strong> the same parameters<br />

adjusted to fit the type-2 underdetermined problem for 1 ≤ p ≤ 2.<br />

Although there are minimal differences in the GGD parameters between the type-<br />

1 and type-2 models, the trends are equivalent. Again, the only difference between the<br />

two model classes is a moderate change in regularization. The results in Figures 5.20<br />

through 5.25 illustrate that this change in regularization results in similar trends in GGD<br />

parameters.<br />

5.8 Application <strong>of</strong> 2-D Results to 3-D Gravity Gradiometry Imaging Problem<br />

GGD modeling provides the quantify the difference between a p = 2 solution and<br />

a<br />

1 ≤ p <<br />

solution without significant computation. In addition, the modeling<br />

generalizes the responses to a unique form so that it may be understood within the<br />

context <strong>of</strong> alternate physics such as diffusion electromagnetics. However, it is also<br />

important to link these unique two-dimensional results back into the three-dimensional<br />

gravity gradiometry problem discussed in Chapters two and three (5.6).<br />

The two-dimensional type-1 underdetermined problem developed in this chapter<br />

is then extended to three dimensions. Figures 5.26 and 5.27 illustrate the model space,<br />

starting model, and discretization are similar to the two-dimensional problem in this<br />

Chapter. In addition, all inversion parameters are similar. The one difference is the use<br />

<strong>of</strong> distance weighting in the three-dimensional example which creates a source <strong>of</strong> nonuniqueness.<br />

Figure 5.28 plots the resulting horizontal north-south slice from the three-dimensional<br />

type-1 underdetermined resolution matrix for p = 1and overlays the GGD distribution<br />

with the identical parameters developed in the previous section except for amplitude.<br />

Figure 5.29 plots the same horizontal north-south result except for<br />

p = 2 . Although C<br />

did not remain constant, the shape <strong>of</strong> the GGD distribution (i.e. the q and σ parameters)<br />

remained constant. The effect <strong>of</strong> non-uniqueness on the three-dimensional model is<br />

manifested as a decrease in the resolution from the two-dimensional unique model.<br />

The vertical resolution <strong>of</strong> the GGD model is also <strong>of</strong> interest and would be<br />

expected to be less than the horizontal resolution because the 2D problem was<br />

constrained to one depth. Figure 5.30 ( p = 1 ) and Figure 5.31 ( p = 2 ) illustrate the<br />

decreased resolution but for a vertical slice through the resolution matrix which<br />

corresponds to the center <strong>of</strong> the anomaly. It is clear that the vertical resolution suffers a<br />

sharp decrease at points away from the anomaly center. Again, the vertical resolution is<br />

lower in the GGD model because the parameters were determined using a twodimensional<br />

model region, while the vertical resolution is lower in the three-dimensional<br />

model because the sensors are located within a horizontal plane at a fixed vertical<br />

location.<br />

5.9 Conclusions<br />

There is an interest in extending the resolution matrix results in Chapter four to<br />

alternate physics such as diffusion electromagnetics. Modeling the shapes, or<br />

distributions, within the two-dimensional gravity gradiometry resolution matrix provides<br />

a basis for extension since the problem is now unique. The resulting distributions are<br />

also beneficial in estimating the computationally expensive 1 ≤ p < 2 resolution matrix<br />

responses from the significantly less expensive p = 2 resolution matrix responses.<br />

The Generalized Gaussian Distribution (GGD) is used to model the distributions<br />

within any resolution matrix for any L P -norm. It is shown that the GGD can accurately<br />

model any distribution within the resolution matrices corresponding to two distinct<br />

classes <strong>of</strong> two-dimensional models using three parameters; q , σ , and C. The only<br />

limitation is that the distributions within the resolution matrix must be positively<br />

constrained in order to prevent sidelobes, which the GGD can not model. A series <strong>of</strong><br />

plots were developed in the modeling effort which allow one distribution corresponding<br />

to a specific L P -norm to be transformed to a distribution corresponding to a different L P -<br />

The results <strong>of</strong> this two-dimensional modeling effort are also extended to a threedimensional<br />

problem similar to that developed in Chapter two with the cargo container<br />

imaging problem. The primary difference between these two models is the addition <strong>of</strong><br />

depth, or distance, weighting which creates a non-unique problem from a unique one. It<br />

is shown that the non-uniqueness in the three-dimensional problem creates an effective<br />

decrease in resolution from the two-dimensional problem.<br />

5.10 Acknowledgements<br />

addition to advising this work. The author also thanks Pr<strong>of</strong>essor Bill Navidi at the<br />

<strong>Colorado</strong> <strong>School</strong> <strong>of</strong> <strong>Mines</strong> Department <strong>of</strong> Mathematics for valuable assistance on<br />

empirical modeling.<br />

5.11 References<br />

(5.1) Kaufman, A.A., 1992, Geophysical Field Theory and Method: Gravitational, Electric and Magnetic<br />

Fields, Academic Press, 581 p., ISBN 0124020410<br />

(5.2) Blakley, R.J., 1996, Potential theory in gravity and magnetic applications, Cambridge University<br />

Press, ISBN 0521575478<br />

(5.3) Lawson, C.L., Hanson, R.J., 1974: Solving Least Squares Problems, Prentice-Hall series in<br />

Automatic Computation, 340 p., ISBN 0138225850<br />

(5.4) Chuang, G.C.-H. and Kuo, C.-C.J, 1996: Wavelet descriptor <strong>of</strong> planar curves: theory and<br />

applications, IEEE Transactions on Image Processing, v. 5, 1, pp 56 – 70<br />

(5.5) Tarantola, A., 1987: Inverse Problem Theory. Elsevier, 613 pp.<br />

(5.6) Kirkendall, B., Li, Y., Oldenburg, D., 2007, Gravity gradiometry in imaging cargo containers, IEEE<br />

Transactions on Geoscience and Remote Sensing, 16 pp., accepted.<br />

(meters)<br />

150<br />

Underdetermined system<br />

100<br />

50<br />

0 50 (meters) 100 150<br />

Fig. 5.1 Planview <strong>of</strong> the underdetermined system with data (black dot) overlaid with discretization (grid<br />

lines). Each point represents an independently measured T ZZ -component <strong>of</strong> the gravity gradient<br />

tensor. There are M=625 model parameter cells and N=196 for the type-1 and type-2<br />

underdetermined systems.<br />

Determined system<br />

0 50<br />

100 150<br />

Fig. 5.2 Planview <strong>of</strong> the determined system with data (black dot) overlaid with discretization (grid lines).<br />

Each point represents an independently measured T ZZ -component <strong>of</strong> the gravity gradient tensor.<br />

There are M=625 model parameter cells and N=625 for the type-1 and type-2 determined systems.<br />

Overdetermined system<br />

Fig. 5.3 Planview <strong>of</strong> the overdetermined system with data (black dot) overlaid with discretization (grid<br />

tensor. There are M=625 model parameter cells and N=1024 for the type-1 and type-2<br />

overdetermined systems.<br />

(g/cm 3 )<br />

Fig 5.4.<br />

Model discretization (left) and Type-1 model (right). The type-1 model is characteristic <strong>of</strong> a<br />

sharp impulse and thus an L P -norm <strong>of</strong> p=1. The heavily discretized central cells have dimension<br />

<strong>of</strong> 2.5 m x 2.5 m. Axis units are in meters. There are 625 total model cells.<br />

Fig 5.5.<br />

Model discretization (left) and Type-2 model (right). The type-2 model is characteristic <strong>of</strong> a<br />

gradual increase in mass and thus an L P -norm <strong>of</strong> p=2. The central cells have dimension <strong>of</strong> 2.5 m x<br />

2.5 m. Axis units are in meters. There are 625 total model cells.<br />

Figure 5.6 Recovered model for the type-1 toy underdetermined problem for L1-norm (above) and L2-<br />

norm (below). Axis are in meters and colorbar is in g/cm 3 . Compare true model in Figure 5.4<br />

Figure 5.7<br />

Recovered model for the type-1 toy determined problem for L1-norm (above) and L2-norm<br />

(below). Axis are in meters and colorbar is in g/cm 3 . Compare true model in Figure 5.4.<br />

Figure 5.8 Recovered model for the type-1 toy overdetermined problem for L1-norm (above) and L2-<br />

0.9<br />

0.8<br />

0.7<br />

p=1.0<br />

0.6<br />

Mass (g)<br />

0.4<br />

0.3<br />

0.2<br />

0.1<br />

p=1.1<br />

0 50 100 150<br />

X-coordinate (meters)<br />

Figure 5.9.<br />

Extraction <strong>of</strong> a 1-D cross section through cell 313 from the j th column <strong>of</strong> the resolution matrix<br />

as a function <strong>of</strong> L P -norm. This is the type-1 underdetermined problem. Note the amplitude<br />

decrease from p=1.0 to p=1.1. The Huber Norm threshold θ = 1.0x10<br />

in this chapter.<br />

for all calculations<br />

10 0 X-Coordinate (meters)<br />

p=1.5 - 2.0<br />

p=1.3<br />

10 -10<br />

10 -12<br />

as a function <strong>of</strong> L P -norm but plotted on a log 10 scale . This is the type-1 underdetermined<br />

problem. The side lobe oscillations for p=1 are significantly greater than increased p-norms.<br />

p=1.2<br />

Figure 5.11<br />

as a function <strong>of</strong> L P -norm. This is the type-1 determined problem. Note the amplitude<br />

10 0<br />

p=1.4 : p=2.0<br />

Figure 5.12<br />

as a function <strong>of</strong> L P -norm but plotted on a log 10 scale . This is the type-1 determined problem.<br />

The side lobe oscillations for p=1 are significantly greater than increased p-norms.<br />

p=1.0 : p=2.0<br />

Figure 5.13 Extraction <strong>of</strong> a 1-D cross section through cell 313 from the j th column <strong>of</strong> the resolution matrix<br />

as a function <strong>of</strong> L P -norm. This is the type-1 overdetermined problem. All curves for<br />

1 ≤ p < 2<br />

appear equal in a linear plot. The Huber Norm threshold θ = 1.0x10<br />

for all<br />

calculations in this chapter.<br />

10 0 X-coordinate (meters)<br />

p=2.0<br />

10 -14<br />

as a function <strong>of</strong> L P -norm but plotted on a log 10 scale . This is the type-1 overdetermined<br />

problem. The side lobe oscillations for p=1 are slightly greater than increased p-norms which<br />

indicates the weak regularization used in the overdetermined problem for stability issues.<br />

1.2<br />

1.1<br />

Total discrete-point mass for j th cell <strong>of</strong> R for Toy Problem - type 1<br />

underdetermined<br />

determined<br />

True value = 1.0 g<br />

p=1.34<br />

p=1.37<br />

1 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2<br />

Figure 5.15<br />

Mass integration for type-1 problem. With the exception <strong>of</strong> the overdetermined problem, the<br />

mass is underestimated for p > 1. 3<br />

1.05<br />

Total mass (g)<br />

0.95<br />

0.85<br />

True mass = 1g/cm 3<br />

0.75<br />

0.65<br />

Figure 5.16<br />

Mass integration for type-2 problem. The underdetermined and determined problems<br />

underestimate the true total mass for p ≥ 1.2 .<br />

4e3<br />

Tikhonov Curve Type-1 Overdetermined problem LP-inversion code<br />

3e3<br />

2e3<br />

1e3<br />

L 1<br />

1e-10 1e-5 1e0 1e3<br />

Φ m<br />

Figure 5.17 Tikhonov curve for the type-1 overdetermined problem p = 1. 0 formed from the L P -norm<br />

inversion code. Regularization is used in the overdetermined case for numerical stability,<br />

however, it is important that the regularization is weak to remain an overdetermined<br />

problem.<br />

The overdetermined problem operates in the area <strong>of</strong> the red box.<br />

GGD<br />

Data<br />

GGD Model<br />

q=1.0, σ=.3<br />

afact=2.16<br />

0 5 10 15 20 25<br />

X-coordinate (m)<br />

Figure 5.18<br />

Comparison between model and data for type-1 underdetermined problem for p=1. The<br />

−3<br />

Euclidean misfit is less than 1.0x10<br />

.<br />

9 x 10-3 GGD<br />

7<br />

q=2.7, σ=3.3<br />

afact=83<br />

Figure 5.19<br />

Comparison between model and data for type-1 underdetermined problem for p=2. The<br />

Type-1 Underdetermined<br />

Type-1 Determined<br />

Type-1 Overdetermined<br />

q value required for GGD model fit<br />

True L P<br />

Figure 5.20 Plot <strong>of</strong> required values <strong>of</strong> q in type-1 GGD modeling<br />

Required σ value for GGD fit<br />

Figure 5.21 Plot <strong>of</strong> required values <strong>of</strong> σ in type-1 GGD modeling<br />

Required amplitude correction for GGD fit<br />

250<br />

200<br />

True L p<br />

Figure 5.22 Plot <strong>of</strong> required amplitude correction in type-1 GGD modeling<br />

q value required for GGD fit<br />

11<br />

9<br />

Type-2 Underdetermined<br />

Type-2 Determined<br />

Type-2 Overdetermined<br />

Figure 5.23 Plot <strong>of</strong> required values <strong>of</strong> p in type-2 GGD modeling<br />

Value <strong>of</strong> σ required for GGD fit<br />

Figure 5.24 Plot <strong>of</strong> required values <strong>of</strong> σ in type-2 GGD modeling<br />

Amplitude factor required for GGD fir<br />

350<br />

300<br />

Figure 5.25 Plot <strong>of</strong> required amplitude factor in type-2 GGD modeling<br />

Figure 5.26<br />

3-dimensional extension <strong>of</strong> 2-dimensional problem. The geometry is the same the cargo<br />

container problem described in Chapter two. The T ZZ dataset is projected on the top <strong>of</strong> the<br />

model space. Axis units are in meters and colorbar units are in g/cm 3 . As in the twodimensional<br />

problem, the data is restricted to a horizontal plane fully above the ground. The<br />

emphasis in this problem is to maintain the underdetermined two-dimensional parameters<br />

except for the addition <strong>of</strong> the depth-dimension. In this manner the resulting non-uniqueness<br />

can be studied.<br />

Figure 5.27<br />

Discretization <strong>of</strong> the three-dimensional extension problem. The variable mesh density is the<br />

same as the two-dimensional toy problem except extended into the depth dimension. This<br />

extension is the source <strong>of</strong> non-uniqueness.<br />

Comparison between the two-dimensional GGD modeling and the horizontal north-south<br />

three-dimensional resolution matrix. The blue line represents the actual threedimensional<br />

results and the black line is the prediction generated from the twodimensional<br />

modeling results. The only discrepancy in mapping the 2D results is the<br />

amplitude.<br />

Comparison between the two-dimensional GGD modeling and a horizontal slice through the<br />

north-south three-dimensional resolution matrix. The blue line represents the actual threedimensional<br />

results and the black line is the prediction generated from the two-dimensional<br />

modeling results. The only discrepancy in mapping the 2D results is the amplitude.<br />

Comparison between the two-dimensional GGD modeling and the three-dimensional<br />

resolution matrix for a vertical slice through the resolution matrix. The blue line<br />

represents the actual three-dimensional results and the black line is the prediction<br />

generated from the two-dimensional modeling results. The only discrepancy in mapping<br />

the 2D results is the amplitude.<br />

Comparison between the two-dimensional GGD modeling and a vertical slice through the<br />

three-dimensional resolution matrix. The blue line represents the actual three-dimensional<br />

results and the black line is the prediction generated from the two-dimensional modeling<br />

results. The only discrepancy in mapping the 2D results is the amplitude.<br />

Chapter 6<br />

PRACTICAL ASPECTS OF LARGE-SCALE 3-D Lp-NORM<br />

COMPUTATIONS<br />

When considering the application <strong>of</strong> a non-least squared L P -norm, p ≠ 2 , to the model<br />

objective function, one should also consider the balance between expected model<br />

performance and computation time. I show that using the<br />

p = 1.1 norm requires less<br />

than half the computation time and suffers only slightly in model resolution. As a result,<br />

if<br />

is inappropriate for an anticipated target geometry, one should maintain an LPnorm<br />

<strong>of</strong> 1 ≤ p ≤ 4. However, only when p = 1. 0 is the true mass consistently recovered.<br />

When<br />

p ≈> 1.3 , the total mass is always underestimated for the underdetermined and<br />

determined problems. As would be expected in the overdetermined problem, the mass is<br />

accurately estimated for all values <strong>of</strong> p. I also argue that round-<strong>of</strong>f error does not exist<br />

in the conjugate gradient or interior point method solutions and <strong>of</strong>fer a method to<br />

determine when round-<strong>of</strong>f error would affect the accuracy <strong>of</strong> the conjugate gradient<br />

solution. Finally I suggest ways to increase the runtime <strong>of</strong> the inversion algorithms<br />

developed in this research such as a wavelet compression technique developed and<br />

employed by Yaoguo Li at the <strong>Colorado</strong> <strong>School</strong> <strong>of</strong> <strong>Mines</strong>.<br />

6.1 Computation Time as a Function <strong>of</strong> L P -norm<br />

Given the type-1 toy problem in Chapter 5, <strong>of</strong> obvious interest would be the<br />

determination <strong>of</strong> the computation times involved for the underdetermined, determined,<br />

and overdetermined systems. Based on the development <strong>of</strong> the resolution matrix in<br />

Chapter 3, the cost <strong>of</strong> computing one column <strong>of</strong> the resolution matrix is equivalent to the<br />

cost <strong>of</strong> computing one inversion. Therefore, Figure 6.1 shows the results <strong>of</strong> CPU time as<br />

a function <strong>of</strong> L P -norm for one inversion but is also accurate for one column <strong>of</strong> the<br />

resolution matrix. The computation times are normalized by N, the number <strong>of</strong> data and<br />

were run on a Windows PC Xeon 3.80 GHz Workstation with 4.0 GB <strong>of</strong> random-access<br />

memory. Although Figure 6.1 assumes a great deal <strong>of</strong> specific computer architecture and<br />

code efficiency, the computation costs <strong>of</strong> each system should be interpreted as relative to<br />

one another.<br />

The computation times for p = 2 are comparable for all three systems types.<br />

However, a large jump in computation time for the underdetermined and determined<br />

systems for<br />

p < 1.8 begins to incur increasing computation costs. In the underdetermined<br />

problem, foe example, the choice <strong>of</strong> using<br />

p = 1 rather than p = 2 results in a stunning<br />

200-fold increase in CPU time. However, if p = 1. 1 is acceptable, the increase is 70-<br />

fold. In the overdetermined case, the CPU time required remains relatively constant for<br />

p > 1.3 . The reason for the computational increase as a function <strong>of</strong> decreasing LP-norm<br />

is ill-conditioning <strong>of</strong> the Hessian matrix. Increasingly poor matrix conditioning as<br />

p → 1.0<br />

(Figure 4.4) which, in turn, results in increased time required for the conjugate<br />

gradient operation at each line search step.<br />

The choice <strong>of</strong> L P -norm is ultimately based on the geometry <strong>of</strong> the intended target<br />

and, in certain cases, an appropriate choice might well be p = 2 . However, a large class<br />

<strong>of</strong> problems including small-scale geophysical problems such as the one described in<br />

Chapter 2 would clearly benefit from the use <strong>of</strong> p = 1 as illustrated in Chapter 3. Based<br />

on the results <strong>of</strong> Figure 6.1 can a balance be achieved between model performance and<br />

CPU time?<br />

6.2 Model Performance as a Function <strong>of</strong> L P -norm<br />

Type-1 resolution matrix results for the underdetermined problem from Chapter 5<br />

are plotted on a linear scale in Figure 6.2 and the ordinate axis on log-scale in Figure 6.3.<br />

If the purpose <strong>of</strong> the inversion is the recovery <strong>of</strong> a true amplitude, then the user must<br />

apply an L P -norm <strong>of</strong> p = 1. However, if the purpose is determining the location <strong>of</strong> a<br />

target from measured data, the use <strong>of</strong><br />

p = 1.1 will provide comparable results with a<br />

three-fold CPU time decrease. For large problems, this will afford a significant decrease<br />

in computation time.<br />

1 .5 < p <<br />

Another result from Figure 6.3 is that use <strong>of</strong> an L P -norm in the interval<br />

provides only slight increases in model performance with a potential 10-<br />

fold computation time increase. Amplitude and resolution <strong>of</strong> the target is neither<br />

increased nor sharpened. The question <strong>of</strong> balance between LP-norm and computation<br />

time posed in the previous section should then assume the following prescription; if<br />

p = 2 is inappropriate for an anticipated target geometry, one should apply an LP-norm<br />

<strong>of</strong> p ~ 1 (for blockier models) or p ~ 4 (for impulsive models).<br />

6.3 Mass Integration in Resolution Matrix<br />

Figure 6.4 illustrates that true mass is only consistently conserved for p=1. This<br />

figure was formed from summation <strong>of</strong> the mass corresponding to a 1-D slice through the<br />

313 th column <strong>of</strong> the resolution matrix in the type-1 problem discussed in Chapter 5. The<br />

results are equivalent for 2-D slices integrated with the trapezoidal rule. Although the<br />

mass is initially overestimated between 1 .0 < p < ~ 1. 3 and underestimated for<br />

1 .5 < p < 2.0 , in all models the true mass is again estimated in the interval 1 .3 < p < 1.5 .<br />

However, this second crossing is inconsistent and fluctuates with starting model and<br />

noise. Mass conservation in the resolution matrix was not studied for p > 2 .<br />

6.4 Practical Error Considerations<br />

Double precision needs to be used in all calculations. The fundamental reason for<br />

this requirement is round-<strong>of</strong>f error, which can introduce error into the last several bits <strong>of</strong> a<br />

parameter value in substantial calculations. Double precision provides accuracy to 1.0 x<br />

10 -16 , while single precision provides accuracy only to 1.0 x 10 -8 . There are two areas<br />

within the inversion described in Chapter 2 in which round-<strong>of</strong>f error can build; the<br />

conjugate gradient (CG) solution and the interior point method. The CG method is<br />

applied to the Hessian and provides the direction for the next line step. The Newton step<br />

interior point method provides the remainder <strong>of</strong> the information leading to the next<br />

location in solution space.<br />

One interesting property <strong>of</strong> interior point methods is that numerical errors<br />

incurred in the calculation <strong>of</strong> each step in the hyper-dimensional solution space are<br />

independent from all other steps. One direction and one distance define an interior point<br />

method step which result in a new location in solution space. However, the subsequent<br />

step will only see a starting point and not interpret any error in that new location. The<br />

process <strong>of</strong> stepping along a line continues until a predetermined accuracy is achieved.<br />

Error will simply result in more required steps, but there is no accumulated error between<br />

steps. Thus it is not possible for round-<strong>of</strong>f error to occur in interior point methods<br />

defined by double precision.<br />

Conjugate gradient iterations continue until the system <strong>of</strong> equations is stable at<br />

1.0 x 10 -8 accuracy. Thus it is not possible, when using double precision, for round-<strong>of</strong>f<br />

error to occur in the conjugate gradient solution.<br />

If it were necessary to quantify the extent <strong>of</strong> round <strong>of</strong>f error in the CG algorithm,<br />

one could gradually decrease the termination accuracy, or tolerance, <strong>of</strong> the CG solution<br />

and plot the residual versus tolerance. The presence <strong>of</strong> round <strong>of</strong>f error will ostensibly not<br />

allow convergence to occur, even for the maximum amount <strong>of</strong> iterations in which<br />

convergence is guaranteed. Thus, provided convergence is met, round <strong>of</strong>f error is not<br />

present.<br />

6.5 Wavelet Compression to Create Sparse Matrices<br />

Using wavelet compression (6.2) can significantly reduce the computation time<br />

and memory requirements <strong>of</strong> the gravity gradiometry inversion process. This is<br />

accomplished through the sparse representation <strong>of</strong> the sensitivity matrix (Equation 2.3)<br />

using a wavelet transform based on compactly supported orthonormal wavelets. While<br />

this work has been coded and used frequently by the <strong>Colorado</strong> <strong>School</strong> <strong>of</strong> <strong>Mines</strong>, Golden,<br />

CO, and the University <strong>of</strong> British Colombia, Vancouver, Canada, wavelet compression<br />

was not applied in this research to alleviate the possibility <strong>of</strong> small artifacts appearing in<br />

the models and data.<br />

6.6 Acknowledgements<br />

The author gratefully thanks Pr<strong>of</strong>essor Paul Sava at the <strong>Colorado</strong> <strong>School</strong> <strong>of</strong> <strong>Mines</strong><br />

for discussions on round <strong>of</strong>f error.<br />

6.7 References<br />

(6.1) Li, Y. and Oldenburg, D. W., 1998, 3D inversion <strong>of</strong> gravity data, <strong>Geophysics</strong>, 63,<br />

109–119<br />

(6.2) Li Y. and Oldenburg, D.W., 2003, Fast inversion <strong>of</strong> large-scale magnetic data using<br />

wavelet transforms and a logarithmic barrier method, Geophysical Journal<br />

International, v. 152, 2, 251–265<br />

Figure 6.1<br />

Computation time as a function <strong>of</strong> L P -norm and for the underdetermined, determined, and<br />

overdetermined toy problems in Chapter 5. Note the ordinate axis is plotted on log-scale.<br />

All computation times were normalized by the number <strong>of</strong> data, N.<br />

Figure 6.2<br />

as a function <strong>of</strong> L P -norm. This is the underdetermined problem. Note the amplitude decrease<br />

from p=1.0 to p=1.1. The Huber Norm threshold θ = 1.0x10<br />

Figure 6.3.<br />

as a function <strong>of</strong> L P -norm but plotted on a log 10 scale . This is the underdetermined problem.<br />

Figure 6.4<br />

Given one column <strong>of</strong> the resolution matrix through the center <strong>of</strong> the Type-1 model developed<br />

in Chapter 5, the total mass should be 1.0 g/cm 3 . It is clear that when<br />

p = 1, the area is<br />

accurately recovered in all three system types. However, the underdetermined and<br />

determined systems overestimate the total mass for<br />

for<br />

currently shown to be<br />

p < 1.3 and underestimate the total mass<br />

1.4<br />

< p ≤ 2.0 . The curves remain the same for 2-D slices although the crossing points<br />

realizations.<br />

p = 1.34 and p = 1. 37 vary on model variation and noise<br />

Chapter 7<br />

ENGINEERING ISSUES ASSOCIATED WITH THE DEVELOPMENT<br />

OF A GRAVITY GRADIOMETRY IMAGING SYSTEM<br />

I list below four areas <strong>of</strong> engineering that will need to be addressed in any practical<br />

implementation <strong>of</strong> the imaging system described in Chapter two; sensor placement and<br />

requirements, noise requirements, sensor frequency response, and time required to fully<br />

image a cargo container. The proposed imaging system must be stationary in order to<br />

maintain noise levels below 1 eötvös and avoid time consuming recalibration procedures.<br />

Finally, I provide a risk assessment for a deployed system and a flowchart on the process<br />

<strong>of</strong> rapidly and accurately scanning cargo containers for fissile materials.<br />

7.1 Sensor Quantity and Location<br />

Gravity gradiometry sensor location currently depends on two factors; physical<br />

space and availability for purchase. The Lockheed-Martin sensors are approximately the<br />

size <strong>of</strong> a dishwasher which would limit a gate configuration as modeling in this research<br />

to a maximum <strong>of</strong> 16 sensors. The GEDEX system is smaller and would be able to form a<br />

gate configuration <strong>of</strong> 24 sensors. It should also be noted that the cost <strong>of</strong> 16 Lockheed-<br />

Martin sensors could extend into the $20 million USD range and it might require at least<br />

one year <strong>of</strong> time to have these units constructed. While there is no cost estimate to date<br />

<strong>of</strong> the GEDEX sensors, the cost would presumably be less and availability increased due<br />

to a simpler design.<br />

The modeling in this research used equally spaced sensors. However, irregularly<br />

spaced sensors might provide increased detection probability, for example, near the edges<br />

<strong>of</strong> the container. If fissile materials are placed near the corners <strong>of</strong> the cargo container,<br />

resolution is decreased at that location. An additional gate with sparse coverage<br />

primarily focused on the edges would provide increased resolution in those areas.<br />

Another possibility to increase the resolution at the container edges would be to extend<br />

the model space outside the cargo container.<br />

7.2 Noise<br />

It is the authors' experience that a stationary potential field sensor, properly<br />

isolated from coherent mechanical and acoustic vibration, can be effectively modeled<br />

with uncorrelated Gaussian noise. 2% <strong>of</strong> the maximum signal was chosen to be added as<br />

Gaussian noise in the data based on Fig. 2.4, which illustrates the range <strong>of</strong> gravity<br />

gradient signal from the forward model greater than 100 eötvös. GEDEX Inc. (7.1) can<br />

provide instrument noise levels below 0.20 eötvös in a stationary acquisition mode.<br />

Thus, it is certainly reasonable to expect instrument noise levels <strong>of</strong> less than 2% <strong>of</strong> the<br />

maximum signal. The use <strong>of</strong> non-Gaussian noise is also examined. Figs. 3.11 and 3.12<br />

are based on a synthetic dataset contaminated with uniform noise. For comparison, the<br />

same datasets were contaminated with Gaussian noise and inverted with the same<br />

parameters. The two recovered models show no significant difference.<br />

Correlated noise, however, can be problematic. One example, a whistle blast<br />

from a passing ship, would be the equivalent <strong>of</strong> an acoustic plane wave affecting all<br />

sensors coherently. The effects <strong>of</strong> correlated noise on gravity gradiometry inversion have<br />

shown that although singularities are likely to occur in forming the covariance matrix, the<br />

expectation value discussed in section 2.3 remains the same (7.2). The effect <strong>of</strong><br />

correlated noise on the inverted image, however, will result in coherent artifacts leading<br />

to false interpretation. It is therefore imperative that the sensor gate have an acoustically<br />

absorbent covering to remove such correlated effects. An additional benefit <strong>of</strong> this<br />

covering would be a shield from weather.<br />

The sensor gate proposed in this research would need to be physically isolated<br />

from all mechanical vibration. In addition, no moving object can be allowed in the area<br />

during scanning. Prior research on the sensitivity <strong>of</strong> borehole gravimeters to external<br />

masses posed the question in terms a priori measuring the effect <strong>of</strong>f a known mass at a<br />

known distance. In essence, a set <strong>of</strong> curves would be calculated after construction <strong>of</strong> the<br />

sensor gate which provide a minimum separation <strong>of</strong> a forklift or a human being, for<br />

example, to the sensor gate. If this separation minima is violated, scanning will need to<br />

be repeated.<br />

Common-mode noise is not a significant problem with the Lockheed-Martin<br />

gravity gradiometry sensors as each pair <strong>of</strong> sensors form a gradient measurement which<br />

inherently removes such noise. The GEDEX gravity gradiometer sensors, however,<br />

relate the deflection <strong>of</strong> two masses to the presence <strong>of</strong> external bodies. This deflection<br />

measurement does not involve a difference measurement per se and therefore does not<br />

inherently remove common-mode noise. The engineer using the GEDEX design would<br />

be required to maintain common-mode noise below approximately 1 eötvös.<br />

7.2.1 Noise from Weather-Related <strong>Ph</strong>enomena<br />

Changes in temperature and barometric pressure can affect the density <strong>of</strong> air. The<br />

formula for the density <strong>of</strong> dry air (7.4) is,<br />

P<br />

ρ =<br />

7.1<br />

RT<br />

Where ρ is the density <strong>of</strong> dry air, P is the air pressure in Pascals (Pa), R is the specific<br />

gas constant equal to<br />

dry<br />

J<br />

_ air<br />

= 287. 05 , and T is the air temperature in Kelvin. I<br />

K ⋅ kg<br />

study the air density without water vapor because the addition <strong>of</strong> water vapor reduces the<br />

density <strong>of</strong> the air. Thus sensitivity studies calculated with dry air represent the worst-<br />

case scenario. If the air temperature is -10 C, the density <strong>of</strong> air is ρ = 1.342x10<br />

g / cm<br />

compared to ρ = 1.165x10<br />

for a temperature <strong>of</strong> +30 C. The difference between<br />

these two extremes is<br />

diff<br />

1.77x10<br />

. Therefore, based on the results <strong>of</strong> funnel<br />

analysis in Chapter three, temperature would not be expected to affect gravity<br />

gradiometry measurements for this application.<br />

Changes in the barometric air pressure are linearly related to the density in Eqn.<br />

7.1. The highest atmospheric pressure recorded was in the year 2001 in Mongolia at<br />

108600 Pa, while the lowest pressure recorded was 88200 Pa within Hurricane Wilma in<br />

the year 2005. The difference between these extremes is 21600 Pa. Assuming +20 C<br />

temperature, the difference in dry air density is ρ = 1.29x10<br />

g cm -<br />

= .03x10<br />

g /<br />

/<br />

1 cm = 2.57x10<br />

g / cm , which is more than the difference<br />

originating from temperature, but less than is detectable in the gravity gradiometry<br />

system proposed in this research.<br />

7.3 Frequency Response <strong>of</strong> Sensor<br />

The transfer functions <strong>of</strong> both sensor designs are currently unknown to the author.<br />

The Lockheed-Martin transfer function would be characterized by the frequency response<br />

<strong>of</strong> the accelerometers, while that <strong>of</strong> the GEDEX design would likely be characterized by<br />

the geometry and rigidity <strong>of</strong> the two deflecting masses and the viscosity <strong>of</strong> the liquid<br />

helium coolant.<br />

7.4 Time Optimization<br />

Personal communication with the Port <strong>of</strong> Oakland in 2005 suggested that any<br />

inspection technique must require less than 30 seconds due to the heavy volume <strong>of</strong><br />

containers. Thus, the cargo container must maintain a constant velocity <strong>of</strong> 0.20 m/s or<br />

about 8 in/s.<br />

Regarding computation time, the serial code used in this research must be made<br />

parallel and likely implemented on a LINUX cluster. Including the MPI library would<br />

allow 1024 nodes to complete the inversion in a reasonable time. Amdahl’s Law (7.3)<br />

provides an upper bound <strong>of</strong> the speedup achievable with p processors,<br />

ψ ≤ . 7.1<br />

( 1−<br />

f )<br />

f +<br />

If we pessimistically assume the serial component <strong>of</strong> the code, f=0.10, Table 7.1<br />

states that 8 processors can provide a speedup <strong>of</strong> 4.70 times. 1024 processors can thus<br />

create a speedup <strong>of</strong> almost 10 times, which would allow any reasonable inversion to<br />

complete in less than 30 seconds.<br />

Table 7.1 Results <strong>of</strong> using 7.1 to predict speedup <strong>of</strong> inversion code, Ψ, from an increase<br />

in the number <strong>of</strong> microprocessors, p.<br />

The pipeline analogy in parallel processing is a good model for practical<br />

implementation; it describes overlapping operations by moving data or instructions into a<br />

conceptual pipe with all stages <strong>of</strong> the pipe processing simultaneously. In other words,<br />

while the n th cargo container is scanned, the computer is processing the inversion from<br />

the (n-1) th trailer. In this sense, although scanning would require 30 seconds and the<br />

inversion another 30 seconds, the net imaging time for a large collection <strong>of</strong> containers<br />

would be 30 seconds.<br />

7.5 Probabilistic Risk Assessment for Deployed Imaging System<br />

In conducting a risk analysis, three questions are posed;<br />

1. What can go wrong with the technology?<br />

2. What and how severe are the potential detriments?<br />

3. What are their probabilities that (1) occurs given (2)?<br />

Below is a risk analysis chart for eight adverse consequences with a risk analysis<br />

completed for each. The probabilities, ψ , are normalized so that ψ = 1. 0 is a certainty<br />

and ψ = 0. 0 is not possible. The first question is referenced in the left column and the<br />

second and third questions are referenced in the right column<br />

Sensor malfunction<br />

Platform or sensor<br />

gate is bumped<br />

Forklift drives or<br />

human walks nearby<br />

Decreased resolution and slightly increased variance in recovered<br />

model<br />

Probability=low<br />

Complete recalibration required for Lockheed-Martin (LM)<br />

system; unknown effects for GEDEX system. Recalibration <strong>of</strong><br />

the LM system will require at least one hour.<br />

Probability=1.0<br />

Correlated mass signature results in anomaly reconstructed within<br />

inversion. Total mass overestimated.<br />

Tidal variation<br />

affects sea level near<br />

sensors<br />

Surface waves from<br />

water<br />

Wind<br />

Trailer velocity not<br />

constant<br />

Insufficient liquid<br />

Helium/Nitrogen<br />

levels<br />

Electromagnetic<br />

interference /<br />

Radi<strong>of</strong>requency<br />

interference<br />

Probability=unknown<br />

Change in water mass results in respective change in net signal,<br />

and although this effect could be divided out using tide calendars,<br />

it still might result in an overestimation/underestimation <strong>of</strong> total<br />

mass<br />

Assuming the sensor gate is rigidly constructed, wave action will<br />

not result in correlated noise as all sensors and cargo container<br />

will be stationary relative to each other. The movement <strong>of</strong> the<br />

sensor gate will, however, result in the position <strong>of</strong> the water and<br />

nearby docks changed relative to the sensors. This is unlikely to<br />

significantly create noise.<br />

The sensor gate could be significantly affected by wind. As<br />

stated previously, the acoustic shielding <strong>of</strong> the sensor gate will<br />

also be required to block wind effects.<br />

If trailer location is not linked with data acquisition, this would<br />

result in error in the sensor locations which would result in<br />

decreased resolution and moderately increased variance in<br />

recovered model<br />

Increased noise levels lead to increased variance in data and a<br />

higher regularization parameter required. This leads to increased<br />

asymmetry <strong>of</strong> resolution matrix.<br />

High EMI/RFI energies can inductively couple to system wiring<br />

and create false images in the inversion. Grounded wire shielding<br />

would be required around all cables to decrease the probablility.<br />

Probability=0.10<br />

Table 7.2<br />

Risk analysis for cargo container imaging problem<br />

7.6 Technological Requirements for Successful Demonstration <strong>of</strong> Concept<br />

In order for the gravity gradiometry system be successfully demonstrated, an<br />

assortment <strong>of</strong> mature technologies are required. While only one gravity gradiometer<br />

needs to be purchased, the time required for data acquisition would be significantly<br />

increased. The cargo container could be moved through a limited sensor gate with the<br />

sensor gate locations updated after each pass to eventually provide all proposed sensor<br />

locations. Assuming the data were acquired at 24-bit A/D resolution on a National<br />

Instrument PXI chassis, a sampling rate <strong>of</strong> 0.10 KHz is low enough such that all eight<br />

PXI chassis slots, thus allowing 64 channels, could be used without straining the<br />

processor.<br />

7.7 Flowcharts<br />

Engineering System<br />

Build sensor gate with known<br />

configuration (7.1)<br />

Build vibrationally isolated<br />

platform (7.5)<br />

Build acoustic shielding (7.2)<br />

Engineer lowest environment<br />

noise levels possible (7.2)<br />

Optimize sensor placement<br />

(7.2)<br />

` Table 7.3 Engineering flowchart<br />

Computation System<br />

Parallelize code to MPI (6.1)<br />

Build PC cluster <strong>of</strong> 1024<br />

processors (6.1)<br />

Table 7.4<br />

Computation flowchart<br />

Define fixed geometry <strong>of</strong> cargo container (2.1)<br />

Optimize mesh discretization (2.3) - and don’t worry about it (4.52)<br />

Run cargo container through – acquire data (Ch. 2)<br />

Compute funnel analysis to find critical detection volume (3.2)<br />

Data check:<br />

*Is the checksum intact?<br />

*Are the statistics typical?<br />

NO<br />

YES<br />

Compute full resolution matrix for p=1.5 (3.3)<br />

Perform inversion with bound constraints (2.31) and p=1.5 (Ch. 6)<br />

NO YES<br />

Have any system risks<br />

described in Table 7.2<br />

occurred?<br />

Is there an absence <strong>of</strong> fissile material? (Eqn 3.9)<br />

YES NO<br />

CAN’T TELL<br />

Move cargo container aside for further<br />

inspection if Eqn. 3.9 is near 10% threshold<br />

Choose the j th model cell in center <strong>of</strong> anomaly Extract and view the j th column <strong>of</strong> R<br />

Is the distribution significantly different?<br />

Use Ch.5 modeling results to see p=1.X response<br />

Run cargo container<br />

through – acquire<br />

data (Ch. 2)<br />

Container passes<br />

– clear <strong>of</strong>f<br />

Alert operator fissile material likely at j th<br />

location +/- funnel analysis (3.2) – move<br />

container aside for further inspection<br />

Table 7.5 Operations flowchart<br />

Rerun inversion for p=1.X<br />

for new model with<br />

increased resolution<br />

7.8 Conclusions<br />

The implementation <strong>of</strong> the imaging system described in Chapter two will require<br />

significant engineering achievements, <strong>of</strong> which noise reduction will be the most critical.<br />

Variations in atmospheric conditions will not affect the data, although physical impulses<br />

to the system and vibrations will incur the largest errors. In the majority <strong>of</strong> cases where<br />

the imaging system was perturbed during data acquisition, the cargo container will need<br />

to be rescanned after confirming the system remains calibrated. The results in Chapter<br />

three are contingent on the imaging system maintaining a noise level below 1 Eötvös.<br />

The temptation to subtract noise from the sensors is ill-advised. For example, if an<br />

array <strong>of</strong> microphones were placed around the sensor gate and a boat whistle created an<br />

acoustic plane wave which created correlated noise on the sensor gate, one might wish to<br />

subtract that noise as modeled from the array. However, the gravity gradiometry sensors<br />

would acquire data approximately 0.50 Hz and it is necessary to sample at least 100 Hz in<br />

order to have sufficient data density to subtract acoustic waveforms in air. Therefore, as<br />

described in Table 7.5, the data should be checked for the checksum as well as the<br />

statistics which should be comparable to past experience. If the data is low quality,<br />

suggests the presence <strong>of</strong> abnormally high noise, or the testing system has undergone any<br />

<strong>of</strong> the risk factors discussed in Table 7.2, the cargo container must be run through the<br />

imaging system again.<br />

Finally, it may well be that Eqn. 3.9 will produce a threshold close to the value <strong>of</strong> the<br />

maximum recovered density. If this is the case, perhaps the threshold is within 20% <strong>of</strong><br />

the maximum recovered density, it might not be possible to determine the presence or<br />

absence <strong>of</strong> likely fissile material in the cargo container and alternate inspection<br />

techniques would be required such as high-energy neutron, photon fluoroscopy, or<br />

manual inspection.<br />

7.9 Acknowledgements<br />

The author is grateful to Pr<strong>of</strong>essor Gary Olhoeft at the <strong>Colorado</strong> <strong>School</strong> <strong>of</strong> <strong>Mines</strong> for<br />

advising the work in this chapter.<br />

7.10 References<br />

(7.1) GEDEX, Inc, personal communication, 2006, www.gedex.ca<br />

(7.2) Lee J., Effects <strong>of</strong> data filtering on inversion <strong>of</strong> gravity gradient data, M.Sc. <strong>Thesis</strong>, <strong>Colorado</strong> <strong>School</strong><br />

<strong>of</strong> <strong>Mines</strong>, 138 p., 2005<br />

(7.3) Wilkinson, B., Allen, M, 2005, Parallel programming, techniques and applications using networked<br />

workstations and parallel computers, 2 nd ed., Pearson Education, 467 p., ISBN 0131405632<br />

(7.4) Moran, J., 1984, An Introduction to Theoretical and Computational Aerodynamics, Dover, 480 p.,<br />

ISBN 0486428796<br />

Chapter 8<br />

GENERAL CONCLUSIONS AND NEAR-FUTURE RESEARCH<br />

Based on the results <strong>of</strong> Chapters two and three, it is clear that gravity gradiometry<br />

can be used to detect high density materials which would then be flagged as suspicious<br />

items for further inspection. Also discussed in Chapter two are suggestions for<br />

complementary techniques which could be used for further inspection. Chapter seven<br />

discusses the engineering issues required to construct and operate such a system. The<br />

quality <strong>of</strong> commercially available sensors, currently available, is sufficient for detecting<br />

fissile materials at least as small as 15 cm x 15 cm x 15 cm in volume. Detection <strong>of</strong><br />

smaller volumes can be accomplished with finer discretization and increased sensor<br />

locations. The reader should remember that models within this research were<br />

conservatively built and appraised.<br />

The results <strong>of</strong> Chapters four and five provide the mathematical study <strong>of</strong> a critical<br />

tool in nonlinear model appraisal; the resolution matrix. The resolution matrix was used<br />

in Chapter three to provide confidence in the locations <strong>of</strong> recovered anomalies. Through<br />

the study <strong>of</strong> its properties such as stability, symmetry, and distributions all as a function<br />

<strong>of</strong> L P -norm, a clearer understanding has emerged concerning the nature <strong>of</strong> the nonlinear<br />

resolution matrix. The variance for nonlinear model appraisal was accomplished through<br />

the use <strong>of</strong> funnel analysis; the second tool developed in the research and also applied in<br />

Chapter three to synthetic data. Although other techniques such as the Cramer-Rao<br />

bound and the covariance matrix can provide complementary information, funnel<br />

analysis provides the variance <strong>of</strong> a group <strong>of</strong> model cells as a function <strong>of</strong> volume. One<br />

cannot obtain the same information from simply summing up in quadrature the variance<br />

<strong>of</strong> individual model cells and computing 95% confidence ratios.<br />

Functionally, as the system is proposed in Chapter two, the resolution matrix need<br />

only be formed once for that fixed sensor geometry and stable noise levels. Although the<br />

resolution matrix is not directly dependent on the data, it is a function <strong>of</strong> the<br />

regularization parameter which is itself a reflection <strong>of</strong> the noise in the data as discussed in<br />

Chapter three. In addition, the funnel analysis need only be computed once if the model<br />

discretization remains fixed. In Chapter seven, a flow diagram is developed which<br />

suggests the appropriate time in the cargo container scanning and imaging process in<br />

which to conduct error analysis, or nonlinear model appraisal.<br />

Although the tools developed in this thesis for nonlinear model appraisal were<br />

formed for gravity gradiometry, they can be easily extended to any quasi-static electric or<br />

magnetic physics. In addition, they can be adapted to any iterative wave propagation<br />

solution, although the amount <strong>of</strong> effort required is not clear due to a lack <strong>of</strong> transparency<br />

in most in-house codes developed within the petroleum industry. The first extension <strong>of</strong><br />

this work will likely be to an existing frequency-domain finite-difference code able to<br />

model the single- and cross-borehole electromagnetic induction problem.<br />

Electromagnetic behavior is highly nonlinear and the code uses an iterative approach<br />

based on the Hessian matrix which strongly overlaps with the nonlinear gravity<br />

gradiometry problem solved in this research. The next extension <strong>of</strong> this work will be to<br />

physically build the prototype imaging system described in Chapter two, using only one<br />

sensor, to conceptually demonstrate the feasibility <strong>of</strong> this technique.<br />

Future additions to this nonlinear model appraisal toolset are likely to include the<br />

Cramer-Rao bound (CRB) as a second means to study variance. CRB provides an<br />

absolute lower bound for each model parameter based on an algebraic manipulation <strong>of</strong><br />

the Fisher information. The diagonal terms are then cast into 95% confidence intervals<br />

(with a small amount <strong>of</strong> work involved) and plotted. Interestingly, the Fisher information<br />

is traditionally defined as the “curvature <strong>of</strong> the cost function” in statistical literature, or<br />

simply as the Hessian in numerical optimization. Through the formulation developed in<br />

Chapter three, one can see that I am calculating the very same Hessian in a Krylov<br />

subspace which could be easily extracted from the code. In essence, the CRB is<br />

essentially additional, and complementary, variance information at little cost that would<br />

incorporate all nonlinear behavior and be valid for any L P -norm.<br />

• More documents
• Recommendations

CGEM <strong>Ph</strong>.D. <strong>Thesis</strong> <strong>Colorado</strong> <strong>School</strong> <strong>of</strong> <strong>Mines</strong> Center for Gravity, Electrical & Magnetic Studies Nonlinear model appraisal in gravity gradiometry imaging; properties and modeling <strong>of</strong> the resolution matrix Barry Kirkendall Department <strong>of</strong> <strong>Geophysics</strong> <strong>Colorado</strong> <strong>School</strong> <strong>of</strong> <strong>Mines</strong> Golden, CO 80401 http://www.geophysics.mines.edu/cgem

• Page 2 and 3: CGEM Ph.D. Thesis Colorado School o
• Page 4 and 5: Copyright by Barry Kirkendall 2007
• Page 6 and 7: ABSTRACT In order to study new meth
• Page 8 and 9: TABLE OF CONTENTS ABSTRACT………
• Page 10 and 11: 5.8 Application of 2-D Results to 3
• Page 12 and 13: Figure 5.8 Recovered model for the
• Page 14 and 15: ACKNOWLEDGEMENTS Throughout my Ph.D
• Page 16 and 17: Chapter 1 INTRODUCTION It is well r
• Page 18 and 19: are, as one should expect in any pe
• Page 20 and 21: Chapter 2 IMAGING CARGO CONTAINERS
• Page 22 and 23: former measures the vertical compon
• Page 24 and 25: increase the signal-to-noise ratio
• Page 26 and 27: closest to the observation location
• Page 28 and 29: are not concerned with data outlier
• Page 30 and 31: adjacent cells. To construct models
• Page 32 and 33: T The weights, , then modify the mo
• Page 34 and 35: absolute weight measurement of the
• Page 36 and 37: (2.27) Bowyer, K. W. Ahuja, N., Adv
• Page 38 and 39: +0.30 m -0.71 m -1.43 m -2.14 m -3.
• Page 40 and 41: 3.0 2.0 1.0 3.0 2.0 1.0 1.0 2.0 3.0
• Page 42 and 43: R H L p -norm L p -norm L 2 -norm r
• Page 44 and 45: Fig. 2.8 The gradient of gravity ca
• Page 46 and 47: Chapter 3 APPRAISAL OF RECOVERED MO
• Page 48 and 49: Given a dataset, d v ( i = 1, L, N
• Page 50 and 51: as Plutonium, which would ostensibl

As the conjugate gradient method is

differences between p=1 and p=2 are

again used to constrain the recover

MeV neutron bombardment or photon f

Total Mass (g) 1.0e5 1.0e2 1.0e0 1.

(A) (B) Fig. 3.3 Contour X-Y slices

g/cm 3 Fig. 3.5 Recovered model fro

4.1 Introduction Model appraisal in

φ = φ d + µφ m . 4.1 Where r p

−1 T T r ρ R = H G Wd WdGρ + H

4.4.3 Underdetermined Non-Linear Ca

only calculates the resolving funct

may not significantly affect the re

Where ξ is the full width at half

empirically show that the resolutio

(4.10) Routh, P.S., Oldenborger, G.

Z-axis X-axis Y-axis Figure 4.2 Dis

15 x 104 L P -norm=1.0 10 x 104 L P

Figure 4.6 X-coordinate resolution

Appendix 4.A Determination of Symme

5.1 Introduction If the curves, or

Using Equation 5.2 to represent Equ

There are two classes of starting m

Figures 5.9, 5.11, and 5.13 illustr

Then with the optimal regularizatio

5.9 Conclusions There is an interes

(meters) 150 Underdetermined system

(meters) 150 Overdetermined system

(meters) (g/cm 3 ) (meters) Fig 5.5

(meters) (g/cm 3 ) (meters) (g/cm 3

1 0.9 0.8 0.7 p=1.0 0.6 Mass (g) 0.

1 0.9 0.8 0.7 p=1.0 : p=2.0 0.6 Mas

1.2 1.1 Total discrete-point mass f

4e3 Tikhonov Curve Type-1 Overdeter

9 x 10-3 GGD 8 7 6 Data p=2.0 GGD M

4 3.5 Required σ value for GGD fit

q value required for GGD fit 11 10

Amplitude factor required for GGD f

(meters) (meters) Figure 5.27 Discr

Figure 5.29 Comparison between the

Figure 5.31 Comparison between the

6.1 Computation Time as a Function

1 .5 < p < 2.0 , in all models the

Figure 6.1 Computation time as a fu

10 0 X-Coordinate (meters) 10 -2 p=

Chapter 7 ENGINEERING ISSUES ASSOCI

are based on a synthetic dataset co

7.3 Frequency Response of Sensor Th

Tidal variation affects sea level n

Table 7.4 Computation flowchart Def

7.8 Conclusions The implementation

Chapter 8 GENERAL CONCLUSIONS AND N

essentially additional, and complem

Extended embed settings

Inappropriate

You have already flagged this document. Thank you, for helping us keep this platform clean. The editors will have a look at it as soon as possible.

Mail this publication

Delete template.

Are you sure you want to delete your template?

DOWNLOAD ePAPER

This ePaper is currently not available for download. You can find similar magazines on this topic below under ‘Recommendations’.

Save as template?

• Help & Support
• tuxbrain.com
• ooomacros.org
• nubuntu.org
• Terms of service
• Privacy policy
• Cookie policy
• Cookie settings

Choose your language

Main languages

Further languages

• Bahasa Indonesia

Performing this action will revert the following features to their default settings:

Hooray! Your file is uploaded and ready to be published.

Saved successfully!

Ooh no, something went wrong!

• My UCalgary
• Class Schedule
• UCalgary Directory
• Continuing Education
• Active Living
• Academic Calendar
• UCalgary Maps
• Close Faculty Websites List Viewing: Faculty Websites
• Cumming School of Medicine
• Faculty of Arts
• Faculty of Graduate Studies
• Faculty of Kinesiology
• Faculty of Law
• Faculty of Nursing
• Faculty of Nursing (Qatar)

Faculty of Science

• Faculty of Social Work
• Faculty of Veterinary Medicine
• Haskayne School of Business
• School of Architecture, Planning and Landscape
• School of Public Policy
• Schulich School of Engineering
• Werklund School of Education
• Future Students
• Explore programs
• How to apply
• Understanding graduate studies
• Indigenous graduate students
• Financing grad school
• International students
• Graduate Student life
• Current Students
• Indigenous Graduate Students
• Newly Admitted
• Graduate Orientation
• Pre-arrival
• Registration
• Annual Registration
• Concurrent Registration
• Flexible Grading Option (CG Grade)
• Confirmation of registration
• Course registration
• Leave of absence
• Registration status
• Studying at another university
• Updating personal information (included preferred name)
• Thesis-based students

Fees and funding

• Understanding your fees
• Paying your fees
• Funding options
• Payment plan
• Supervision
• Best practices and guidelines
• Conflict of interest
• Changing supervision
• Academic integrity
• Annual progress report
• Intellectual property
• Building a thesis
• Submit your thesis
• Conducting oral exams remotely
• Thesis defence
• Course-based Students
• Academic Integrity
• Sources of funding
• Payment Plan
• NEW: Term-Based Registration
• Completing my degree
• Important dates and resources
• Forms and documents
• Graduate Calendar
• Service Requests and eForms
• News, updates and events
• Find your Graduate Program Administrator
• Calendar Archives
• Award Opportunities
• Graduate Awards Database
• Award opportunities
• Doctoral Recruitment Scholarships
• Award Guide
• Step 1: Applying
• Looking for awards
• Eligibility
• Preparing your application
• Step 2: Receiving
• Accept/Decline your award
• Getting paid
• Step 3: Managing your award
• Renewing your award
• Award interruption
• Award Termination
• Policies and Regulations
• Regulations
• Contact the Scholarship Office
• My GradSkills
• Academic Success
• My GradSkills Partners
• Communication Skills
• Research Communications Feedback Sessions
• Oral communication
• Visual communication
• Written communication
• Experiential Learning
• Internships
• For employers
• For graduate students
• Finding an internship
• Making your internship a TTI
• Applying for a TTI
• For graduate supervisors
• Images of Research
• Three Minute Thesis
• 2024 UCalgary 3MT Finalists
• 2024 3MT Finals' Hosts and Judges
• Past Three Minute Thesis Videos
• Workshops and Resources
• Career planning and professional development resources
• My GradSkills Calendar
• My GradSkills Workshop Matrix
• Online/Virtual Training
• UCalgary Alumni Mentorship Program
• Exceptional scholars
• Graduate Mental Health Survey
• Test metrics
• Demographics
• Circumstances
• Mental Health
• What I wish I knew
• FGS Services
• Supervisory Renewal
• Supports for graduate students
• Graduate Academic and International Specialists
• Graduate supervisors
• Thesis and candidacy exams
• Supervisor resources
• Maintaining your supervisor profile
• Supervisory privileges
• Leadership team
• FGS Council
• Committees of Council
• Minutes and meetings
• Website Feedback

Doctor of Philosophy (PhD)

Thesis-based program

Program overview.

Formed in 1963, the Department of Geoscience - Canada's largest - is a vibrant cornerstone of the University of Calgary. The program is a wellspring of Canada's geoscience research and industry professionals, with close ties to the resource industry that has established Alberta's reputation as a global energy leader. Many students participate in field schools during their program, and benefit from working on the doorstep of a fantastic geological laboratory: the Rocky Mountains. Our vision is an improved understanding of Earth systems through innovative and impactful geoscience research, interdisciplinary learning and discovery, empowered and inspired teaching, and effective communication that not only raises our profile as a geoscience centre of excellence, but also creates a brighter future for our world.

Completing this program

• Core Courses: Geology and Geophysics of Western Canada and either an Advanced Independent Study course or Readings in Geology or Geophysics.
• Thesis: Students will be required to submit and defend an original research thesis.
• Candidacy: Students will complete both oral and written candidacy exams.
• Field Schools : Many students participate in field schools for 12-16 days in late summer or early spring. Activities include orienteering, mapping surficial deposts, measuring sections in sedimentary rocks, and mapping geologic structures in places like the Canadian Shield, Alberta prairies, Rocky Mountains and deserts of southwest USA.

Post-Secondary Teaching and Research, Oil and gas, Resource exploration, Resource Management, Environmental Consulting, Geo Hazards, Renewable Energy, Policy and Regulation.

A PhD in geoscience is usually considered a final degree.

Students are required to prepare a thesis and successfully defend in an open oral defense.

Four courses; some courses may be waived for students with MSc degrees

Learn more about program requirements in the Academic Calendar

Classroom delivery

Time commitment.

Three years full-time; six years maximum

A supervisor is required; potential supervisors must be listed when applying to the program.

See the Graduate Calendar for information on  fees and fee regulations,  and for information on  awards and financial assistance .

Virtual Tour

Explore the University of Calgary (UCalgary) from anywhere. Experience all that UCalgary has to offer for your graduate student journey without physically being on campus. Discover the buildings, student services and available programs all from your preferred device.

Supervisors

Learn about faculty available to supervise this degree. Please note: additional supervisors may be available. Contact the program for more information.

Jan Dettmer

David Eaton

Eva Enkelmann

Rob Ferguson

Charles Henderson

Stephen Hubbard

Steve Larter

Bernhard Mayer

Julio Mercader Florin

Admission requirements

A minimum of 3.0 GPA on a 4.0 point system, over the past two years of full-time study (a minimum of 10 full-course equivalents or 60 units) of the undergraduate degree.

Minimum education

MSc or equivalent in geology or geophysics, or a related field such as physics or mathematics from a recognized institution.

Work samples

A concise statement outlining the applicant’s research interests and reasons for wishing to attend the University of Calgary

Reference letters

Test scores, english language proficiency.

An applicant whose primary language is not English may fulfill the English language proficiency requirement in one of the following ways:

• Test of English as a Foreign Language (TOEFL ibt)  score of 97.
• International English Language Testing System (IELTS)  score of 7.0 (minimum of 6.5 in each section).
• Pearson Test of English (PTE)   score of 68, or higher (Academic version).
• Canadian Academic English Language test (CAEL)  score of 70 (70 in some sections – up to the program, 60 in all other).  
• Academic Communication Certificate (ACC)  score of A- in one or two courses (up to the program), “B+” on all other courses.  
• Cambridge C1 Advanced or Cambridge C2 Proficiency  minimum score of 191.
• Duolingo English Test  and obtaining a minimum score of 135* (with no sub-score below 115*). ( temporary until Fall 2024 intake ).

*Please contact your program of interest if you have any questions about ELP requirements

For admission on September 1:

• Canadians and permanent residents: Jan. 15 application deadline
• International students: Jan. 15 application deadline

If you're not a Canadian or permanent resident, or if you have international credentials, make sure to learn about international requirements

Are you ready to apply?

Learn more about this program, department of geoscience.

Earth Sciences Building Room 118 2500 University Drive NW Calgary, ABT2N 1N4 403.220-3254

Contact the Graduate Program Administrator

Visit the departmental website

University of Calgary 2500 University Drive NW Calgary, AB, T2N 1N4

Visit their website

Learn more about UCalgary by taking a virtual tour

Related programs

If you're interested in this program, you might want to explore other UCalgary programs.

Thesis-based MSc

Course-based MSc

Chemical and Petroleum Engineering

Thesis-based MEng

Course-based MEng

Course-based MEng (Petroleum only)

Civil Engineering

Course-based MEng

Thesis-based MEng

Thesis-based MSc

Physics and Astronomy

Curious about the university of calgary.

Located in the nation's most enterprising city, we are a living, growing and youthful institution that embraces change and opportunity with a can-do attitude.

Geophysics (GP)

Interested in applying to our MS or PhD programs? View presentations from this year's info sessions .

Students in the Geophysics (GP) graduate program study Earth and other planets to advance our fundamental understanding of their origin, composition, and evolution, and explore the implications for life, for the environment, and for society.

The graduate program provides a broad education in the fundamentals of geophysics, alongside research and coursework spanning multiple specializations. Our flexible curriculum and multidisciplinary researchers enable us to welcome graduate students from a diverse range of backgrounds in science and engineering, producing graduates who are well prepared for future careers in academia, industry, or public service.

Our multidisciplinary program offers graduate students a unique hands-on, collaborative learning environment. A core academic curriculum provides the foundation for working on research projects that emphasize observational techniques and the collection of novel datasets linked to testing new theoretical and computational approaches. GP students participate extensively in field experiments, instrument development, laboratory investigations, and shipboard expeditions.

Research in Geophysics

For an overview of the latest geophysics research at Scripps, please see the Institute of Geophysics and Planetary Physics annual report .

For a broader view of Earth Sciences research at Scripps, see the Earth Section annual report .

Faculty and Researchers

• Yehuda Bock
• Adrian Borsa
• Catherine Constable
• Steven Constable
• Wenyuan Fan
• Yuri Fialko
• Helen Amanda Fricker
• Alice Gabriel
• Jeffrey Gee
• Peter Gerstoft
• Jamin Greenbaum
• Jennifer Haase
• Matti Morzfeld
• Ross Parnell-Turner
• David Sandwell
• Peter Shearer
• Dave Stegman
• Vashan Wright

Is our Geophysics graduate program for you?

At Scripps you can enroll for either a PhD or Masters (MS) degree. Many PhD students complete an MS en route to the PhD by completing sufficient units of coursework.

If you missed our annual Pre-Application Virtual Open House on November 16th, you can access the information that was presented that may help you decide what areas of research interest you and answer questions about the application process. Please register  here  and access the presentation  here .

Potential Advisors and Projects for Fall 2024 Admission

The following faculty and research scientists are interested in seeking new students for Fall 2024 intake. If you wish to find out more about their research, please email them individually. If you are not sure what specific area of research you wish to pursue, or have any questions, please email the admissions coordinators, Jennifer Haase at [email protected] for help and guidance.

Yehuda Bock   [email protected] Geodesy, Natural Hazards. Our SOPAC group is application oriented with several research projects that can support students. These include (1) tsunami early warning systems with U.S. and Chilean agencies, (2) machine learning models for detecting transient crustal and atmospheric processes using 30-year GPS displacement and atmospheric delay time series, (3) Integration of radar interferometry and GPS for surface mapping of plate boundary deformation and subsidence due to groundwater extraction (4) Development of a dynamic reference frame for the U.S. National Spatial Reference System maintained by the National Geodetic Survey (NGS). Projects (3) and (4) are supported by NASA, California Department of Transportation (Caltrans) and California Department of Water Resources (DWR), and are in collaboration with Prof. David Sandwell’s research group.

Cathy Constable   [email protected]
 Geomagnetism and Paleomagnetism. Projects could include 1) making time varying paleomagnetic field models on time scales from millennia to millions of years; 2) Building stochastic models for geomagnetic  paleosecular variation; 3) Using paleomagnetic observables to improve realism in products of numerical  geodynamo simulations. Website:  igppweb.ucsd.edu/~cathy

Steven Constable [email protected] Marine electromagnetic methods. Projects include the study of offshore groundwater, marine gas hydrate, tectonic plate boundaries, and pretty well any other geological feature found offshore. We collect and interpret our own field data, but the lab is also interested in developing algorithms and software needed for data processing and modeling/inversion of EM data. Website: marineemlab.ucsd.edu c

Wenyuan Fan [email protected] Observational seismology. We focus on seismic sources and use onshore and offshore, dense array seismic observations to investigate earthquakes, slow earthquakes, subduction zone processes, environmental processes, and their interaction and triggering. Website: igppweb.ucsd.edu/~wenyuanfan

Yuri Fialko   [email protected] Space geodesy (InSAR/GNSS), earthquake and volcano deformation, active tectonics, numerical modeling, theoretical and experimental rock mechanics. Potential projects include studies of time-dependent deformation in California, Tibet, and Turkey.  Website:  igppweb.ucsd.edu/~fialko

Alice Gabriel [email protected]  Computational and theoretical seismology. Projects are available which use high-performance computing and physics-based modeling constrained by a multitude of observations. Application areas range from the seismic cycle in subduction zones and tsunami genesis, to strong ground motion scenarios in complicated settings, to induced seismicity. Projects may involve utilising new methods in terms of numerical discretisation, uncertainty quantification, imaging and monitoring. Website: algabriel.scrippsprofiles.ucsd.edu

Gabi Laske   [email protected] Observational seismology. Research projects typically cover aspects of structural seismology. Primary targets are the measurement and tomographic modeling of surface wave dispersion in combination with other seismic observables. Our research projects often involve the collection and analysis of ocean bottom seismic data in the Pacific ocean. A new project is the OHANA project that focuses on the seismic imaging of 4-50 Myr old Pacific lithosphere halfway between Hawaii and California. Website:  igppweb.ucsd.edu/~gabi

Ross Parnell-Turner   [email protected] Marine geophysics. Projects include 1) studying how the Iceland mantle plume controls seafloor uplift and oceanic circulation using reflection seismic and deep sea drilling data; 2) investigating volcanic eruption cycles on fast-spreading mid-ocean ridges; and 3) exploring how oceanic plate spreading is accommodated by slip on low-angle detachment faults. We collect data at sea and develop numerical models; methods include passive microearthquake monitoring, reflection seismology, and seafloor mapping using autonomous robots. Website:  rosspt.weebly.com

David Sandwell [email protected] Geodynamics, space geodesy, global seafloor mapping. We are improving the accuracy and spatial resolution of the marine gravity field using data from satellite radar altimeters inclusing the new SWOT altimeter. The improved marine gravity is important for exploring unknown tectonics in the deep oceans as well as revealing thousands of uncharted seamounts. In addition, we are developing methods to combine the high accuracy of point GPS time series with the high spatial resolution from radar interferometry to measure interseismic velocity along the San Andreas Fault system associated with earthquake hazard.  Several faculty at IGPP were recently funded by the National Geodetic Survey to train graduate students in the  broad field of Geodesy.  These fellowships are open to both U.S. citizens and permanent resident aliens. Website: https://topex.ucsd.edu

Peter Shearer [email protected] Seismology. Peter Shearer may have funding to support a student to study earthquakes and/or Earth structure. Website: https://igppweb.ucsd.edu/~shearer/mahi

Adam Young   [email protected] Coastal hazards, processes, and geomorphology. We use field based and remote sensing instrumentation to quantify coastal processes and change, and evaluate how coastal change impacts society. Example research topics include coastal erosion, coastal cliffs, beach morphology, coastal sediment, sediment budgets, and anthropogenic influences on the coastal system. Website: https://adyoung.scrippsprofiles.ucsd.edu

Requirements for GRADUATE Admission

In addition to the general requirements for admission to the PhD program , a major in physics, mathematics, or earth sciences is recommended. GRE scores are not required for Fall 2024 admission.

There are various application fee waiver programs offered by the UC San Diego Graduate Division . Please inquire with [email protected] .

GP Applicant evaluation Criteria

Factors which we use to evaluate applicants include, but are not limited to, (1) Academic Preparation; (2) Scholarly potential; (3) Diversity, equity, and inclusion contributions; (4) Alignment with the program; (5) Realistic self-appraisal; and (6) Long-term goals.

Applicants should ensure that they represent themselves accurately with the best possible information in all of the above areas . The admissions committee will consider all aspects of the application including the statement of purpose, transcripts, balance of coursework, letters of recommendation, and responses to optional questions about additional experiences. GRE scores may be included if you wish, and may serve as part of our holistic review, but they are not required. Please inquire with [email protected] .

For full consideration, please submit applications by December 6, 2023 . Applications submitted after the deadline may be considered on a case-by-case basis.

Financial Support

All PhD applicants are considered for financial support. Student support during the first year may come from a variety of sources including external or departmental fellowships and research grants. More information about funding can be found here .

Additional Information

• A list of current GP graduate students .
• Graduate student handbooks .

Program of Study for PhD

Students are admitted to the GP curricular group within the Geosciences of the Earth, Oceans, and Planets (GEO) Program based on their interests and the affiliations of their adviser. Each student is assigned a first year advisory committee, comprising their primary advisor and the three person GP departmental committee. Although students may change curricular groups in the course of the year, they must choose which departmental exam they will take. Departmental exams have similar structures among the curricular groups within GEO (a written exam at the end of spring quarter of their first year and an oral exam before the beginning of fall quarter of their second year).

Students are encouraged to begin a research project from the beginning and typically do not hold teaching assistant positions during their first year. Students may change advisers during their first year, but it is important for them to find an adviser by the end of the first year so that they are ready to work on research over the summer and develop a thesis proposal during their second and third years. Students are normally expected to present this proposal at their qualifying exam by the end of their third year.

No single course of study is appropriate to every student in the geophysics curricular group: instead, there is a sequence of foundational classes that each student is expected to complete successfully during the first year, together with a three-quarter seminar sequence on Geophysical Research Skills.

The foundational classes include:

Additional graduate class electives or research units (SIO299) under the guidance of a specific instructor provide a minimum of 12 units/quarter required for full-time study. Electives should be chosen from the broad range of available topics in consultation with the first-year guidance committee and the student’s advisor to provide breadth of expertise and to support the individual interests of the student. Some students will find it useful to take courses offered by other curricular groups across Scripps or by other departments on UCSD General campus.

The content of the foundational courses combined with the research skills acquired during the first year seminar forms the basis for the written departmental examination. A list of graduate classes offered by the GP faculty is provided below.

Students are also encouraged to attend Geophysics and Earth Section seminars for exposure to a broad range of geophysical research topics.

Program of Study for MS

The geophysics master’s degree provides a solid grounding in the fundamentals of geophysics for students intending to pursue professional positions in government, industry, or nonprofit organizations or to apply to PhD programs. Two different degree options are available:

MS Plan—Thesis

This plan combines course work and research, culminating in the preparation of a thesis. A minimum of thirty-six units of credit is required: twenty-two units are expected from Foundational Courses (see below); and twelve units of research work (SIO299) lead to the thesis. Students should contact a thesis adviser and co-adviser prior to, or as part of, the application process. Students are rarely accepted into the program without this prior consultation. This two-member faculty committee, in consultation with the student and the Geophysics Curriculum Advisor, will select the courses and research topic to be completed in two years or less.

Foundational classes:

• SIOG 200 A/B/C Geophysics Research Skills: Geophysics 1 st year seminar (2 units/ quarter)
• SIOG 223A Geophysical Data Analysis I (4 units)
• SIOG 223B. Geophysical Data Analysis II (4 units)
• SIOG 225. Physics of Earth Materials (4 units)
• SIOG 234. Geodynamics (4 units)
• SIOG 221. Plate Tectonics in Practice (4 units)
• SIOG 222. Introduction to Industry Reflection Seismic Methods (4 units)
• SIOG 224. Internal Constitution of the Earth (4 units)
• SIOG 227A. Introduction to Seismology (4 units)
• SIOG 227B. Structural Seismology (4 units)
• SIOG 227C. Seismological Sources (4 units)
• SIOG 228. MS Research Seminar for students in contiguous BS/MS programs
• SIOG 229. Fundamentals of Gravity and Geodesy (4 units)
• SIOG 230. Introduction to Inverse Theory (4 units)
• SIOG 231. Geomagnetism and Electromagnetism (4 units)
• SIOG 232. Ethical and Professional Science (2 units)
• SIOG 233. Introduction to Computing (4 units)
• SIOG 236. Satellite Remote Sensing (4 units)
• SIOG 238. Numerical Methods for PDEs (4 units)
• SIOG 239. Special Topics in Geophysics (4 units)
• SIOG 240. Marine Geology (4 units)
• SIOG 247. Rock Magnetism and Paleomagnetism (4 units)

Potential Upper Division UG Electives (if appropriate):

• SIO 105. Sedimentology and Stratigraphy (4 units)
• SIO 110. Introduction to GIS and GPS for Scientists (4 units)
• SIO 113. Introduction to Computational Earth Science (4 units)
• SIO 160. Introduction to Tectonics (4 units)
• SIO 161. Seismology (4 units)
• SIO 162. Structural Geology (4 units)
• SIO 182A. Environmental and Exploration Geophysics (4 units)

Emeritus Faculty and Researchers

• Duncan Agnew
• Catherine Degroot-Hedlin
• Leroy Dorman
• Alistair Harding
• Michael Hedlin
• Guy Masters
• Jean-Bernard Minster
• John Orcutt
• Hubert Staudigel
• Frank Vernon
• Mark Zumberge

• Graduate School
• Prospective Students
• Graduate Degree Programs

Doctor of Philosophy in Geophysics (PhD)

Canadian immigration updates.

Applicants to Master’s and Doctoral degrees are not affected by the recently announced cap on study permits. Review more details

Go to programs search

Theoretically, experimentally, and observationally oriented Master of Science (M.Sc.), Master of Applied Science (M.A.Sc.), and Doctor of Philosophy (Ph.D.) programs are offered in a number of key areas of geophysics. Current interests include topics in observational and theoretical glaciology; climate variability; geodynamics of the crust, mantle, and core of Earth and other planets; geological fluid mechanics; volcanic processes; surface processes on Earth and other planets; origin and structure of planetary magnetic fields; inversion methodologies with application to reflection seismology, mineral exploration, and environmental studies; computational electrodynamics; seismology with observational programs in crustal and upper mantle studies; earthquake studies focused on understanding past and current tectonic processes in Western Canada, and data science including applications of machine learning to Earth scientific problems.

For specific program requirements, please refer to the departmental program website

What makes the program unique?

Geophysics at UBC was originally a subprogram within the Department of Physics until 1963 when the Department of Geophysics was formed. In 1972 the Department of Geophysics changed its name to the Department of Geophysics & Astronomy reflecting increased activity in astronomical research and teaching. This department was dissolved in 1996, and geophysics faculty were merged with colleagues from geology, oceanography and, later, atmospheric sciences to become the Department of Earth, Ocean and Atmospheric Sciences (EOAS). EOAS is the largest and most diverse department of its kind in Canada and, accordingly, geophysics graduate students have unparalleled opportunities for engaging in cutting-edge pure and applied research in both traditional geophysical topics and those that cross disciplinary boundaries. 

Modern and interdisciplinary courses offered at UBC really aim to train the next generation of leaders in the transition to a sustainable society, and give young researchers the opportunity to break out of their silos and collaborate with other disciplines.

Quick Facts

Program enquiries, admission information & requirements, 1) check eligibility, minimum academic requirements.

The Faculty of Graduate and Postdoctoral Studies establishes the minimum admission requirements common to all applicants, usually a minimum overall average in the B+ range (76% at UBC). The graduate program that you are applying to may have additional requirements. Please review the specific requirements for applicants with credentials from institutions in:

• Canada or the United States
• International countries other than the United States

Each program may set higher academic minimum requirements. Please review the program website carefully to understand the program requirements. Meeting the minimum requirements does not guarantee admission as it is a competitive process.

English Language Test

Applicants from a university outside Canada in which English is not the primary language of instruction must provide results of an English language proficiency examination as part of their application. Tests must have been taken within the last 24 months at the time of submission of your application.

Minimum requirements for the two most common English language proficiency tests to apply to this program are listed below:

TOEFL: Test of English as a Foreign Language - internet-based

Overall score requirement : 100

IELTS: International English Language Testing System

Overall score requirement : 7.0

Other Test Scores

Some programs require additional test scores such as the Graduate Record Examination (GRE) or the Graduate Management Test (GMAT). The requirements for this program are:

The GRE is not required.

2) Meet Deadlines

January 2025 intake, application open date, canadian applicants, international applicants, september 2025 intake, january 2026 intake, deadline explanations.

Deadline to submit online application. No changes can be made to the application after submission.

Deadline to upload scans of official transcripts through the applicant portal in support of a submitted application. Information for accessing the applicant portal will be provided after submitting an online application for admission.

Deadline for the referees identified in the application for admission to submit references. See Letters of Reference for more information.

3) Prepare Application

Transcripts.

All applicants have to submit transcripts from all past post-secondary study. Document submission requirements depend on whether your institution of study is within Canada or outside of Canada.

Letters of Reference

A minimum of three references are required for application to graduate programs at UBC. References should be requested from individuals who are prepared to provide a report on your academic ability and qualifications.

Statement of Interest

Many programs require a statement of interest , sometimes called a "statement of intent", "description of research interests" or something similar.

Supervision

Students in research-based programs usually require a faculty member to function as their thesis supervisor. Please follow the instructions provided by each program whether applicants should contact faculty members.

Instructions regarding thesis supervisor contact for Doctor of Philosophy in Geophysics (PhD)

Citizenship verification.

Permanent Residents of Canada must provide a clear photocopy of both sides of the Permanent Resident card.

4) Apply Online

All applicants must complete an online application form and pay the application fee to be considered for admission to UBC.

Research Information

Research facilities.

In 2012 the new Earth Sciences Building was completed. The $75 million facility was designed to inspire collaboration and creativity across disciplines.

Tuition & Financial Support

Financial support.

Applicants to UBC have access to a variety of funding options, including merit-based (i.e. based on your academic performance) and need-based (i.e. based on your financial situation) opportunities.

Program Funding Packages

PhD students are guaranteed a minimum salary of CAN$ 25,500 (plus tuition) per year for the first four years, which can consist of research assistantships (RAs) to help professors with their grants and contracts, teaching assistantships (TAs) to help teach courses and labs and grade assignments, scholarships and prizes, and combinations of all the above. 

Average Funding

• 6 students received Teaching Assistantships. Average TA funding based on 6 students was $4,230.
• 8 students received Research Assistantships. Average RA funding based on 8 students was $8,567.
• 3 students received Academic Assistantships. Average AA funding based on 3 students was $3,739.
• 8 students received internal awards. Average internal award funding based on 8 students was $14,161.
• 4 students received external awards. Average external award funding based on 4 students was $20,500.

Scholarships & awards (merit-based funding)

All applicants are encouraged to review the awards listing to identify potential opportunities to fund their graduate education. The database lists merit-based scholarships and awards and allows for filtering by various criteria, such as domestic vs. international or degree level.

Graduate Research Assistantships (GRA)

Many professors are able to provide Research Assistantships (GRA) from their research grants to support full-time graduate students studying under their supervision. The duties constitute part of the student's graduate degree requirements. A Graduate Research Assistantship is considered a form of fellowship for a period of graduate study and is therefore not covered by a collective agreement. Stipends vary widely, and are dependent on the field of study and the type of research grant from which the assistantship is being funded.

Graduate Teaching Assistantships (GTA)

Graduate programs may have Teaching Assistantships available for registered full-time graduate students. Full teaching assistantships involve 12 hours work per week in preparation, lecturing, or laboratory instruction although many graduate programs offer partial TA appointments at less than 12 hours per week. Teaching assistantship rates are set by collective bargaining between the University and the Teaching Assistants' Union .

Graduate Academic Assistantships (GAA)

Academic Assistantships are employment opportunities to perform work that is relevant to the university or to an individual faculty member, but not to support the student’s graduate research and thesis. Wages are considered regular earnings and when paid monthly, include vacation pay.

Financial aid (need-based funding)

Canadian and US applicants may qualify for governmental loans to finance their studies. Please review eligibility and types of loans .

All students may be able to access private sector or bank loans.

Foreign government scholarships

Many foreign governments provide support to their citizens in pursuing education abroad. International applicants should check the various governmental resources in their home country, such as the Department of Education, for available scholarships.

Working while studying

The possibility to pursue work to supplement income may depend on the demands the program has on students. It should be carefully weighed if work leads to prolonged program durations or whether work placements can be meaningfully embedded into a program.

International students enrolled as full-time students with a valid study permit can work on campus for unlimited hours and work off-campus for no more than 20 hours a week.

A good starting point to explore student jobs is the UBC Work Learn program or a Co-Op placement .

Tax credits and RRSP withdrawals

Students with taxable income in Canada may be able to claim federal or provincial tax credits.

Canadian residents with RRSP accounts may be able to use the Lifelong Learning Plan (LLP) which allows students to withdraw amounts from their registered retirement savings plan (RRSPs) to finance full-time training or education for themselves or their partner.

Please review Filing taxes in Canada on the student services website for more information.

Cost Estimator

Applicants have access to the cost estimator to develop a financial plan that takes into account various income sources and expenses.

Career Outcomes

18 students graduated between 2005 and 2013. Of these, career information was obtained for 18 alumni (based on research conducted between Feb-May 2016):

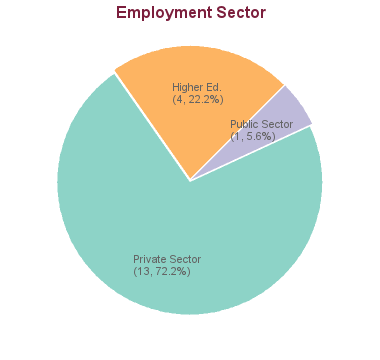
Sample Employers in Higher Education

Sample employers outside higher education, sample job titles outside higher education, phd career outcome survey, career options.

Geophysics graduate programs prepare students for work in a wide range of Earth science disciplines. The programs afford students with strong critical thinking, analytical problem solving, communication, statistical, computational and research skills, and the ability to work effectively in teams.These skills are highly sought after and are transferable to many workplaces. Recent graduates have found employment in academia (universities in Canada, United States, Europe and Australia), government (Geological Survey of Canada), environmental monitoring and mineral exploration industries, hydrocarbon exploration, software engineering (Google) and elsewhere in the technology sector (Tesla).

Enrolment, Duration & Other Stats

These statistics show data for the Doctor of Philosophy in Geophysics (PhD). Data are separated for each degree program combination. You may view data for other degree options in the respective program profile.

ENROLMENT DATA

Completion rates & times, upcoming doctoral exams, thursday, 18 april 2024 - 12:30pm - 5104, earth sciences building, 2207 main mall.

• Research Supervisors

Advice and insights from UBC Faculty on reaching out to supervisors

These videos contain some general advice from faculty across UBC on finding and reaching out to a supervisor. They are not program specific.

This list shows faculty members with full supervisory privileges who are affiliated with this program. It is not a comprehensive list of all potential supervisors as faculty from other programs or faculty members without full supervisory privileges can request approvals to supervise graduate students in this program.

• Bostock, Michael (structure of the Canadian upper mantle, Geophysics, formation and evolution of the first continental landmasses, the structure and dynamics of subduction zones)
• Haber, Eldad (Scientific computing and its application to geophysical and medical imaging)
• Heagy, Lindsey (Geoelectrics and geoelectromagnetics; Magnetism and paleomagnetism; Gravimetry; Environmental monitoring; Numerical computation; Machine learning; Geophysics; Inverse theory; data science; Machine Learning; Electromagnetics; Carbon sequestration; Groundwater; Environmental geophysics; Resource exploration)
• Jellinek, Mark (Volcanology, Geodynamics, Planetary Science, Geological Fluid Mechanics)
• Johnson, Catherine (Lunar geophysics, Evolution of Mars' Magnetic Field and Atmosphere)
• Orsi, Anais (Atmospheric measurement techniques; Physics of snow and ice; Cryosphere processes, n.e.c.; Isotope geochemistry; Geochronology; Environmental geochemistry; Quantitative methods for environmental sciences; Earth system sciences; Climate change impacts and adaptation; climate change; Polar climate; Data analysis, inverse modeling; Paleoclimate)
• Radic, Valentina (Atmospheric sciences; Geophysics; Climate Changes and Impacts; Climate Science; Glaciology; Meteorology)
• Schoof, Christian (Geophysics; Ice and Snow; Transformation and Evolution of the Earth Surface; Fluid mechanics; Hydraulic; Asymptotic and Classical Applied Analysis; Differential Equation; applied mathematics; glacier hydrology; Glaciology; ice sheet dynamics)

Doctoral Citations

Sample thesis submissions.

• How to descend a rocky slope : numerical techniques for the solution of noisy optimization problems
• Shallow subaqueous and subglacial explosive eruptions : quantifying controls on the dynamics, stability, evolution, and stratospheric injection of water-rich eruption columns : [supplementary material]
• Modelling the propagation of crevasses and calving in ice shelves
• Inverse modelling of subglacial hydraulic processes
• Shallow subaqueous and subglacial explosive eruptions : quantifying controls on the dynamics, stability, evolution, and stratospheric injection of water-rich eruption columns
• Studies of forearc seismicity and structure in British Columbia and Washington State
• Mountain glaciers as modifiers of streamflow in Western Canada : insights from data analysis and machine learning

Related Programs

Same specialization.

• Master of Applied Science in Geophysics (MASc)
• Master of Science in Geophysics (MSc)

Same Academic Unit

• Doctor of Philosophy in Atmospheric Science (PhD)
• Doctor of Philosophy in Geological Engineering (PhD)
• Doctor of Philosophy in Geological Sciences (PhD)
• Doctor of Philosophy in Oceanography (PhD)
• Graduate Certificate in Applied Geological Engineering (GCAGE)
• Master of Applied Science in Geological Engineering (MASc)
• Master of Engineering in Geological Engineering (MEng)
• Master of Science in Atmospheric Science (MSc)
• Master of Science in Geological Sciences (MSc)
• Master of Science in Oceanography (MSc)

Further Information

Specialization.

Current interests include topics in observational and theoretical glaciology; climate variability; geodynamics of the crust, mantle, and core of Earth and other planets; geological fluid mechanics; volcanic processes; origin and structure of planetary magnetic fields; reflection seismology; time-series analysis and wavelet processing; inversion methodologies with application to reflection seismology, mineral exploration, and environmental studies; computational electrodynamics; seismology with observational programs in crustal and upper mantle studies; earthquake studies focused on understanding past and current tectonic processes in Western Canada; and theoretical model studies to investigate wave propagation in laterally heterogeneous media.

UBC Calendar

Program website, faculty overview, academic unit, program identifier, classification, social media channels, supervisor search.

Departments/Programs may update graduate degree program details through the Faculty & Staff portal. To update contact details for application inquiries, please use this form .

Reid Merrill

The research project. There is no replacement for studying subduction and seismogenesis than in Vancouver, some 60 km above the descending Juan de Fuca plate.

Sam Anderson

I came to UBC to work with my supervisor, Dr. Valentina Radic. I was drawn to work in an environment that encouraged interdisciplinary research and where people are interested in asking big questions. Dr. Radic's experience and curiosity have encouraged me to pursue interdisciplinary research...

Curious about life in Vancouver?

Find out how Vancouver enhances your graduate student experience—from the beautiful mountains and city landscapes, to the arts and culture scene, we have it all. Study-life balance at its best!

• Why Grad School at UBC?
• Application & Admission
• Info Sessions
• Research Projects
• Indigenous Students
• International Students
• Tuition, Fees & Cost of Living
• Newly Admitted
• Student Status & Classification
• Student Responsibilities
• Supervision & Advising
• Managing your Program
• Health, Wellbeing and Safety
• Professional Development
• Dissertation & Thesis Preparation
• Final Doctoral Exam
• Final Dissertation & Thesis Submission
• Life in Vancouver
• Vancouver Campus
• Graduate Student Spaces
• Graduate Life Centre
• Life as a Grad Student
• Graduate Student Ambassadors
• Meet our Students
• Award Opportunities
• Award Guidelines
• Minimum Funding Policy for PhD Students
• Killam Awards & Fellowships
• Policies & Procedures
• Information for Supervisors
• Dean's Message
• Leadership Team
• Strategic Plan & Priorities
• Vision & Mission
• Equity, Diversity & Inclusion
• Initiatives, Plans & Reports
• Graduate Education Analysis & Research
• Media Enquiries
• Newsletters
• Giving to Graduate Studies

Strategic Priorities

• Strategic Plan 2019-2024
• Improving Student Funding
• Promoting Excellence in Graduate Programs
• Enhancing Graduate Supervision
• Advancing Indigenous Inclusion
• Supporting Student Development and Success
• Reimagining Graduate Education
• Enriching the Student Experience

Initiatives

• Public Scholars Initiative
• 3 Minute Thesis (3MT)
• PhD Career Outcomes
• Great Supervisor Week

PhD thesis projects offered

All partner institutes in the Solar System School (Institute for Astrophysics and Geophysics, Geoscience Center, and Max Planck Institute for Solar System Research) may offer and support PhD projects in the Solar System School. The PhD topics are as diverse as the research fields of the participating partner institutions. The topics include all areas of our own Solar system (the Sun and its planets and minor bodies), embedded in the wider geo- and astrophysical context, and extend to other stars and their planetary systems. Correspondingly, the following disciplines in geo- and astrophysics are represented in the Solar System School: Earth and planetary sciences, Solar and stellar physics, helioseismology, asteroseismology, and to some extent extra-solar planets. Since the methods of research comprise instrumentation development, calibration and improvement , ground- and space-based observations, remote-sensing or in-situ measurements in space exploration missions, data analysis and interpretation, numerical simulations and theoretical modeling, some projects may additionally require good skills in programming, in mathematics, or in engineering.

Supervising scientists without a universitiy affiliation share the supervision with faculty members. A Thesis Advisory Committee guides the student through the preparation period and monitors her/his work. The committee consists of the thesis advisor and two other faculty or senior staff members of the institutes involved in the Solar System School. At least one of the members must be a full professor at the University of Göttingen, or at another university at which the student is enrolled.

The following list gives an overview of the variety of research topics, but is not necessarily complete. Further projects may yet become available: This list still is updated from time to time. Please check the list again before submitting your application. Applications may be submitted between 1 August and 1 October.

Open PhD Projects

• Planetary Science
• Sun and Heliosphere
• Solar and Stellar Interiors

Sulfur on Mercury and on reduced protoplanets

Analytical geo-/cosmochemistry applied to BepiColombo-Mission to Mercury data more

Open PhD Project: Data Analysis

The magnetic field in the solar atmosphere exceeds the geomagnetic field strength by four orders of magnitude. It greatly influences the processes of energy transport within the solar atmosphere, and dominates the morphology of the solar chromosphere and corona. Kinetic energy from convective motions in the Sun can be efficiently stored in magnetic fields and subsequently released - to heat the solar corona to several million degrees or to blast off coronal mass ejections. more

Open PhD Project: Instrumentation

The MPS is one of the leading institutes worldwide in building instruments for solar research, both for ground based observatories as well as for balloon and space-borne missions. Scientists and engineers of MPS conceive new observing methods and develop novel instruments of highest technological complexity. These instruments are built in house, tested, calibrated, and used at the best solar observatories in the world, or delivered to NASA and ESA to be launched to space. more

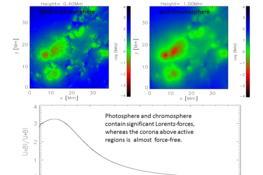
Study time series of solar active regions with sequences of magneto-hydro-static equilibria

Interaction of sound waves with Solar granulation

Hydrodynamic simulations of near surface convection and waves in the Sun and stars more

Solar accretion disk dynamics – the record from chondrites

“Space sediments” hold isotopic clues for reconstructing early solar system evolution more

The genetic heritage of late accretion to the Earth-Moon system

Isotopic investigation of the materials impacting the terrestrial planets after their formation more

"Other" and "Own" PhD projects

For PhD students whose project is already funded and who are applying for admission to the IMPRS, or for applicants who want to bring their own funding and their own project idea to the IMPRS. more

Open PhD Projects in the SLAM Group

The Solar Lower Atmosphere and Magnetism (SLAM) group covers many exciting subjects in solar physics, focussing on the development and testing of highly novel solar instrumentation, reduction and analysis of highest quality solar observations, or improving and developing advanced techniques for the analysis of solar observations. more

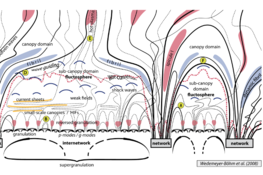
Deciphering the solar spectrum

Inversion codes are used to aid the detailed interpretation of solar spectro-polarimetric data. This computer code attempts to find the atmospheric structure that produced an observed spectrum by minimizing the difference between the observed spectrum and a Stokes spectrum. more

Open PhD Projects: Solar and Stellar Interiors

In the "Solar and Stellar Interiors" department, Laurent Gizon, Jesper Schou, Aaron Birch, Robert Cameron and others offer PhD projects in solar physics and astrophysics. Helioseismology and asteroseismology are used as important tools to study the oscillating Sun and stars. more

Other Interesting Articles

Scientific data analysis models for SWI onboard the JUICE mission to Jupiter

Understanding the JUICE/SWI instrument characteristics and the radiation intensity that the SWI instrument will receive from Jupiter’s icy moons

Solar System School PhD Positions 2025

Application deadline 1 October 2024. PhD projects in planetary science, solar and stellar physics, solar magnetism, heliophysics, helioseismology, asteroseismology, ...

Volatile element delivery to the terrestrial planets – constraints from isotope anomalies

Cosmochemical investigations on the heritage of volatiles in Earth, Mars, and the Moon

Frequently asked questions about PhD application

FAQ for applications to PhD positions in astrophysics at IMPRS Solar System Science Goettingen

Long-period oscillations control the Sun’s differential rotation

High-latitude long-period oscillations provide a feedback mechanism that limits the Sun’s pole-to-equator differential rotation.

Historical Sunspots: One, two, three … and Counting

In analyzing solar observations from the 19th century, scientists are turning to amateur researchers for help. The project will allow to better understand the history of our star.

Student funding

Doctoral candidates joining the Solar System School are offered attractive funding, clear prospects and optimal career conditions. IMPRS-funded students receive a three-year doctoral support contract at 65% pay level. Additional funds are available for travel to international conferences. Following their PhD period, graduates are offered postdoc wrap-up funding.

Award for MPS Director

Two scientific associations have awarded Prof. Dr. Thorsten Kleine the title "Geochemistry Fellow" for his contributions to the understanding of how the Solar System was formed.

IMPRS "Solar System School" Retreat 2023

01 - 06 October 2023

The impact of Earth’s mantle on geomagnetic field reversals

Numerical simulations to better understand the complete reversals of the geodynamo dipole

IMPRS students Löschl, Albert and Sinjan co-author joint SO/PHI-HR and SDO publication

Astronomical teamwork: By combining data from Solar Orbiter and SDO, a group of researchers has unambiguously determined the magnetic field at the solar surface.

International Awards for Yuto Bekki

With the help of computer simulations, the MPS researcher described the properties of the long-period oscillations of the Sun.

College of Natural Sciences and Mathematics    > Department of Earth and Atmospheric Sciences    > Geophysics, MS

The Department of Earth and Atmospheric Sciences (EAS) offers a wide range of courses leading to the Master of Science in Geophysics degree. Required core courses ensure a breadth of knowledge in the discipline including rock physics, seismic wave propagation, geophysical data analysis, and potential field methods. A wide variety of electives allows concentration in areas such as exploration, geotechnical, or environmental geophysics, solid earth geophysics, petroleum exploration, marine geophysics, earthquake seismology, and geodynamics. The typical student pursuing this degree is interested in geophysics and has a good background in the geosciences, mathematics, physics, and computing. Graduates will typically pursue careers with resource companies; geophysical service companies; various federal, state, and local government agencies; in the financial sector; in education; or will continue study to pursue a doctorate.

For more information, please see http://www.uh.edu/nsm/earth-atmospheric/graduate/degree-programs/ms-geophysics/ .

Admission Requirements

Admission to our graduate program is based on a competitive selection process. Meeting the minimum requirements published does not guarantee admission to our program. Applicants for the Master’s of Science in Geophysics are required to have

• Successfully completed a Bachelor’s of Science in Geophysics equivalent to one at the University of Houston.
• A complete graduate school application (link: www.uh.edu/graduate-school/admissions/how-to-apply ) must be submitted.
• Scores from the General GRE examination taken in the last 5 years are optional.
• Individuals with a lower cumulative GPA may be admitted conditionally.
• Letters of recommendation are also given considerable weight in the evaluation process.
• Students who did not earn a prior degree from a U.S. institution or a country where English is the medium of instruction (see list in the General Admission Policy   ) must meet minimum test scores to demonstrate English language proficiency. Visit  http://www.uh.edu/graduate-school/international-students/ to learn more.

 The admissions committee and the department chair will evaluate the credentials of each applicant for the MS program, considering a broad range of criteria, including:

• Content of the undergraduate program and, if applicable, graduate programs and grades earned, particularly in the areas of Geosciences, Mathematics, Physics, and Chemistry.
• A cumulative GPA of 3.00 or better in the last 60 hours of course work.
• Letters of recommendation from three (3) individuals (preferably faculty members), who are able to judge the candidate’s academic abilities and potential for scholarly research.
• GRE scores, if submitted (verbal, quantitative, and analytical writing: advanced GRE is recommended but optional)
• English proficiency test scores, if applicable.

In addition to these requirements, graduate admission may also be contingent upon a faculty advisor agreeing to supervise the applicant’s research. Therefore, prospective students are strongly encouraged to contact faculty members in the applicant’s field of interest prior to the application deadline.

Part-time students (6.0 Credit Hours per term or less) will be only admitted into the MS non-thesis track.

Prerequisites

Candidates are expected to have the necessary science and mathematics background and should have successfully completed coursework deemed equivalent to courses in the B.S. in Geophysics degree at the University of Houston.

The department will determine what deficiencies - if any - are present, and the acceptable means of removing those deficiencies (e.g. course work within and/or outside the department, directed study, research papers). Waivers of requirements will be considered on an individual basis. Applicants with a few deficiencies can satisfy those requirements while also taking graduate courses at the University of Houston.  It is normally recommended that a student with 6 or more deficiency courses, e.g., those whose Bachelor’s degree is in another discipline, consider working toward a second Bachelor’s degree in Geophysics prior to graduate work.

Degree Requirements

The Master of Science (MS) degree will be awarded after students have successfully completed requirements specified in one of the two following plans:

Plan I: Thesis Option

All students completing the thesis option must complete and defend a thesis acceptable to the department.

This option requires a  minimum of 30.0 approved Credit Hours , to include

• Formal Earth and Atmospheric Science courses (GEOL) at the 6000 level or higher  Credit Hours: 15.0

Letter-graded thesis courses (GEOL 6399 & GEOL 7399)&nbsp; Credit Hours: 6.0 

• Courses can be selected from approved courses outside the area of Earth and Atmospheric Science (GEOL), but relevant to the degree program, with prior permission of the Geophysics Graduate Faculty Advisor.
• No more than 6.0 Credit Hours of special problems courses can be counted towards the required 30.0 Credit Hours minimum.

Plan II: Non-Thesis Option

Completing a thesis is not required, but students must take additional course work and have the option of completing a capstone research project.

Students may satisfy the MS Plan II degree requirements by satisfactorily completing a  minimum of 36.0 approved Credit Hour s, to include

• Formal Earth & Atmospheric Science courses (GEOL) at the 6000 level or higher  Credit Hours: 30.0
• Selections should be courses at the 6000 level, or above, and can be selected from approved courses outside the area of Earth and Atmospheric Science, but relevant to the degree program, with prior permission from the Geophysics Graduate Faculty Advisor.
• Students can petition to have a 3-hour elective course substituted for a capstone project (GEOL 7301 - Capstone Project)

Note: Research hours do not count toward this degree.

After completion of 18 hours, students with a cumulative GPA of 3.40 or above and demonstrated abilities to conduct research may petition to switch to a thesis-based degree. In order to do this, the student must have an advisor and committee members willing to supervise them. The thesis research advisor, Geophysics Graduate Faculty Advisor, and Department Chair must sign a petition indicating approval of the change to a thesis-based MS degree and it must be filed with the department academic advisor. The student must successfully defend their thesis proposal (as outlined below) after they have completed their core course requirements and prior to completion of 27.0 Credit Hours of course credit. This change will not extend the 5-year limit to complete the MS degree.

Core Course Requirements

Upon completion of their program, students are expected to have breadth and a fundamental background in the essential elements Geophysics. To provide a fundamental background in the essential elements of geophysics, all MS students are required to take the courses listed below. Students are encouraged to consult with the Geophysics Graduate Faculty Advisor to make their selections of the remaining graduate courses.

• GEOL 7330 - Potntl Fld Mtds-Geophys Credit Hours: 3.0
• GEOL 7341 - Geophysical Data Processing Credit Hours: 3
• GEOL 7333 - Seismic Wave & Ray Theory Credit Hours: 3.0
• GEOL 7324 - Rock Physics Credit Hours: 3.0

Academic Policies

• University Academic Policies    
• Academic Policies: College of Natural Sciences and Mathematics    
• Department/Program Academic Policies:

Scholastic Requirements

Graduate students must maintain a minimum grade point average of 3.00 in all course work to be considered in good standing. Students not in good standing cannot receive a graduate degree and can be declared ineligible for support with a graduate assistantship (IA, TA or RA).

Research (Thesis) Advisor/Committee

• A formal thesis topic and thesis advisor must be chosen prior to the completion of 15.0 Credit Hours.
• The 30 required hours are a minimum and, for a specific area of interest, it may be necessary for the student to complete additional course work.
• The student may change his/her thesis advisor pending approval by the Geophysics Graduate Faculty Advisor, but it is the responsibility of the student to review his/her degree plan and prepare for potential changes in the department and/or faculty support with the new advisor.
• In addition, if the student has already formally proposed their project, they may have to present another thesis proposal of their new project(s).
• Students must specify a thesis committee and have the names on file in the NSM Office of Academic Affairs at least one term prior to their graduation.
• a minimum of two faculty members who have their primary appointment within EAS and
• one approved external member, outside of EAS, from industry, or other academia, who is acceptable to the department and approved by the College.
• A faculty member with a joint appointment in the major department is considered as an outside member unless he/she chairs the committee. In this case, an additional external member outside the major department is required.
• After these minimum requirements for committee members are satisfied, additional committee members may be approved from industry or academia, but at least 50% of the committee must be tenured/tenure‐track faculty at the University of Houston.
• Research faculty or instructional faculty may serve on thesis committees, but not chair the committees. However, a research professor may serve as a co‐advisor with a tenured/tenured‐track faculty.

Thesis Proposal

Students must present a thesis proposal.

• All full-time students and students financially supported by the University must propose prior to the end of their second term in the program.
• Scheduling of the thesis proposal is done by each applicant through the department academic advisor.
• Proposals (and re-proposals) can be scheduled Monday‐Friday, with starting times between 8:00 a.m. and 4:00 p.m., during the Fall and Spring terms.The proposal must be presented by the last day of the semester. Teaching Assistants must present by the first Monday in November in the Fall term, or the first Monday in July in the Summer term.
• Proposals cannot be presented during, vacations, weekends, or over spring break or inter‐semester breaks.
• Sumner p proposals can be scheduled pending approval of the entire committee.
• Two hours should be allocated for the thesis proposal presentation and questions.
• Proposals are preceded by the distribution of a 5 to 10 page (10 page suggested maximum for text) written description of the thesis project to the thesis committee.
• A one page abstract must be posted and distributed to all EAS faculty members at least seven calendar days prior to presentation, and a digital copy of the full proposal in the final form filed with the department academic advisor and committee members at that time.
• The proposal abstract must contain the title, time, place of the proposal, link for a video conference and the names of the committee members.
• The thesis advisor and at least one other member of the committee must initial the abstract prior to posting, indicating that they approve of the presentation of the proposal.
• Upon successful presentation of the proposal, a copy of the complete proposal with the thesis advisor’s signature indicating approval must be placed in the student’s permanent academic file.

Thesis Defense

Upon completion of the research and the writing of a thesis deemed acceptable by the thesis committee, a defense of the thesis is scheduled by the student.

• A public defense of the complete thesis research will be presented to the faculty-at-large and may be attended by any other interested parties.
• An abstract, which lists the time and place of the defense, must be distributed to the department faculty and posted publicly at least seven calendar days prior to the scheduled date.
• The thesis advisor and a least one other departmental committee member must initial the notice of defense, thus indicating that they approve of the defense.
• A digital copy or hard copy of the thesis in final form be submitted at least seven calendar days prior to presentation to the committee members and advising staff that can be provided to EAS faculty upon request.
• MS defenses can be scheduled Monday‐Friday during the Spring, Summer, and Fall terms with starting times between 8:00 a.m. and 4:00 p.m.
• Defenses cannot be given during vacations, weekends, or over spring break or inter‐semester breaks.
• Scheduling of defenses is done through the department academic advisor.
• A vote to pass by a majority of the thesis committee is required for successful defense of the thesis.

I work with the same writer every time. He knows my preferences and always delivers as promised. It’s like having a 24/7 tutor who is willing to help you no matter what. My grades improved thanks to him. That’s the story.

Do my essay with us and meet all your requirements.

We give maximum priority to customer satisfaction and thus, we are completely dedicated to catering to your requirements related to the essay. The given topic can be effectively unfolded by our experts but at the same time, you may have some exclusive things to be included in your writing too. Keeping that in mind, we take both your ideas and our data together to make a brilliant draft for you, which is sure to get you good grades.

Estelle Gallagher

To describe something in great detail to the readers, the writers will do my essay to appeal to the senses of the readers and try their best to give them a live experience of the given subject.

Customer Reviews

How can I be sure you will write my paper, and it is not a scam?

Geophysics Students Win Research and Knowledge Competitions

Apr 10, 2024 | SP24Newsletter

Geophysics students won top honors for research and knowledge this spring.

Among the contenders, four teams emerged from Mines and University of Colorado-Boulder, setting the stage for a spirited contest. The initial round served as a warm-up, engaging the audience and hinting at the challenging nature of the multiple-choice questions to come. Through three successive rounds, competition was fierce, with the scores remaining tight. However, as the contest progressed, Pablo Chang Huang and Ethan Deal, Mines Geophysics seniors, managed to pull ahead, ultimately taking the victory in the Challenge Bowl. They are now looking forward to representing Mines at the larger geophysics challenge bowl at the IMAGE conference jointly sponsored by the American Association of Petroleum Engineers and Society of Exploration Geophysicists’ this August in Houston, TX.