homework 9 parallel and perpendicular lines

Parallel and Perpendicular Lines: Worksheets with Answers

Whether you want a homework, some cover work, or a lovely bit of extra practise, this is the place for you. And best of all they all (well, most!) come with answers.

Mathster keyboard_arrow_up Back to Top

Mathster is a fantastic resource for creating online and paper-based assessments and homeworks. They have kindly allowed me to create 3 editable versions of each worksheet, complete with answers.

Corbett Maths keyboard_arrow_up Back to Top

Corbett Maths offers outstanding, original exam style questions on any topic, as well as videos, past papers and 5-a-day. It really is one of the very best websites around.

Parallel and Perpendicular Lines

How to use Algebra to find parallel and perpendicular lines

Parallel Lines

How do we know when two lines are parallel ?

Their slopes are the same!

Find the equation of the line that is:

• parallel to y = 2x + 1
• and passes though the point (5,4)

The slope of y = 2x + 1 is 2

The parallel line needs to have the same slope of 2.

We can solve it by using the "point-slope" equation of a line :

y − y 1 = 2(x − x 1 )

And then put in the point (5,4):

y − 4 = 2(x − 5)

That is an answer!

But it might look better in y = mx + b form. Let's expand 2(x − 5) and then rearrange:

y − 4 = 2x − 10

Vertical Lines

But this does not work for vertical lines ... I explain why at the end.

Not The Same Line

Be careful! They may be the same line (but with a different equation), and so are not parallel .

How do we know if they are really the same line? Check their y-intercepts (where they cross the y-axis) as well as their slope:

Example: is y = 3x + 2 parallel to y − 2 = 3x ?

For y = 3x + 2 : the slope is 3, and y-intercept is 2

For y − 2 = 3x : the slope is 3, and y-intercept is 2

So they are the same line and so are not parallel

Perpendicular Lines

Two lines are perpendicular when they meet at a right angle (90°).

To find a perpendicular slope:

When one line has a slope of m , a perpendicular line has a slope of −1 m

In other words the negative reciprocal

Find the equation of the line that is

• perpendicular to y = −4x + 10
• and passes though the point (7,2)

The slope of y = −4x + 10 is −4

The negative reciprocal of that slope is:

m = −1 −4 = 1 4

So the perpendicular line will have a slope of 1/4:

y − y 1 = (1/4)(x − x 1 )

And now we put in the point (7,2):

y − 2 = (1/4)(x − 7)

That answer is OK, but let's also put it in "y=mx+b" form:

y − 2 = x/4 − 7/4

y = x/4 + 1/4

Quick Check of Perpendicular

When we multiply a slope m by its perpendicular slope −1 m we get simply −1 .

So to quickly check if two lines are perpendicular:

When we multiply their slopes, we get −1

Are these two lines perpendicular?

When we multiply the two slopes we get:

2 × (−0.5) = −1

Yes, we got −1, so they are perpendicular.

The previous methods work nicely except for a vertical line :

In this case the gradient is undefined (as we cannot divide by 0 ):

m = y A − y B x A − x B = 4 − 1 2 − 2 = 3 0 = undefined

So just rely on the fact that:

• a vertical line is parallel to another vertical line.
• a vertical line is perpendicular to a horizontal line (and vice versa).
• parallel lines: same slope
• perpendicular lines: negative reciprocal slope (−1/m)

Parallel and Perpendicular Lines

Related Topics: Lesson Plans and Worksheets for Geometry Lesson Plans and Worksheets for all Grades More Lessons for Geometry Common Core For Geometry

New York State Common Core Math Geometry, Module 4, Lesson 8

Worksheets for Geometry

Student Outcomes

• Students recognize parallel and perpendicular lines from slope.
• Students create equations for lines satisfying criteria of the kind: “Contains a given point and is parallel/perpendicular to a given line.”

Opening Exercise

• a. Write an equation of the line that passes through the origin that intersects the line 2𝑥 + 5𝑦 = 7 to form a right angle. b. Determine whether the lines given by the equations 2𝑥 +3𝑦 = 6 and 𝑦 = 3/2 𝑥 + 4 are perpendicular. Support your answer. c. Two lines having the same 𝑦-intercept are perpendicular. If the equation of one of these lines is 𝑦 = −4/5 𝑥 + 6, what is the equation of the second line?

a. What is the relationship between two coplanar lines that are perpendicular to the same line? b. Given two lines, 𝑙1 and 𝑙2, with equal slopes and a line 𝑘 that is perpendicular to one of these two parallel lines, 𝑙1: i. What is the relationship between line 𝑘 and the other line, 𝑙2? ii. What is the relationship between 𝑙1 and 𝑙2?

Exercises 2–7

• Given a point (−3,6) and a line 𝑦 = 2𝑥 − 8: a. What is the slope of the line? b. What is the slope of any line parallel to the given line? c. Write an equation of a line through the point and parallel to the line. d. What is the slope of any line perpendicular to the given line? Explain.
• Find an equation of a line through (0,−7) and parallel to the line 𝑦 = 1/2𝑥 + 5. a. What is the slope of any line parallel to the given line? Explain your answer. b. Write an equation of a line through the point and parallel to the line. c. If a line is perpendicular to 𝑦 = 1/2 𝑥 + 5, will it be perpendicular to 𝑥 −2𝑦 = 14? Explain.
• Find an equation of a line through (√3,1/2) parallel to the line: a. 𝑥 = −9 b. 𝑦 = −√7 c. What can you conclude about your answer in parts (a) and (b)?
• Find an equation of a line through (−√2, 𝜋) parallel to the line 𝑥 − 7𝑦 = √5.
• Recall that our search robot is moving along the line 𝑦 = 3𝑥 − 600 and wishes to make a right turn at the point (400,600). Find an equation for the perpendicular line on which the robot is to move. Verify that your line intersects the 𝑥-axis at (2200,0).
• A robot, always moving at a constant speed of 2 units per second, starts at position (20,50) on the coordinate plane and heads in a southeast direction along the line 3𝑥 + 4𝑦 = 260. After 15 seconds, it turns clockwise 90° and travels in a straight line in this new direction. a. What are the coordinates of the point at which the robot made the turn? What might be a relatively straightforward way of determining this point? b. Find an equation for the second line on which the robot traveled. c. If, after turning, the robot travels for 20 seconds along this line and then stops, how far will it be from its starting position? d. What is the equation of the line the robot needs to travel along in order to now return to its starting position? How long will it take for the robot to get there?

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

Home » Worksheets » 9 Comprehensive Parallel And Perpendicular Lines Worksheets

9 Comprehensive Parallel And Perpendicular Lines Worksheets

It can be tough to figure out how to teach concepts that are completely ingrained in your own mind to students who are hearing about the idea for the first time. Understanding the difference between parallel and perpendicular lines can be tough for students who are just beginning to understand geometry, and as an instructor, it can be hard to figure out how to give students the practice that they need to solidify the concept. Choosing the right parallel and perpendicular lines worksheets can help your students begin to understand the difference between the two, and help them work toward understanding these concepts automatically. 

Table of Contents

What to look for in a parallel and perpendicular lines worksheet, free vs. paid worksheets, why teach simple.

Searching for the right parallel and perpendicular lines worksheet for your students? A few things you’ll want to keep an eye out for: 

• Clear explanations: Look for worksheets that clearly explain the difference between the two types of lines–it may be especially helpful to look for worksheets that explain the concepts differently than the way you explain them in class
• Required differentiation: You don’t want a worksheet that just provides an explanation: you’ll also want to clearly see whether your students can differentiate between the two types of lines
• Drawing: Worksheets that ask students to draw parallel and perpendicular line instead of just identifying them can help solidify understanding

The Best Parallel And Perpendicular Lines Worksheets

• Parallel And Perpendicular Line Guided Notes By ThreeFourthsMe

This guided notes set will allow you to help your students through each step of differentiating between parallel and perpendicular lines. Your students won’t just learn the difference between the two–they’ll also learn how the different line types affect equations, and will be able to understand how the information they’re learning fits into the problem solving you’re doing in class. 

• Parallel And Perpendicular Lines Notes And Homework Set By Eddie McCarthy

This notes and homework pack gives you everything you need for a full lesson of teaching your students the difference between perpendicular and parallel lines, and allows students to see how these types of lines will appear on a graphing calculator.

• Parallel And Perpendicular Line Differentiation Worksheet From Liveworksheets

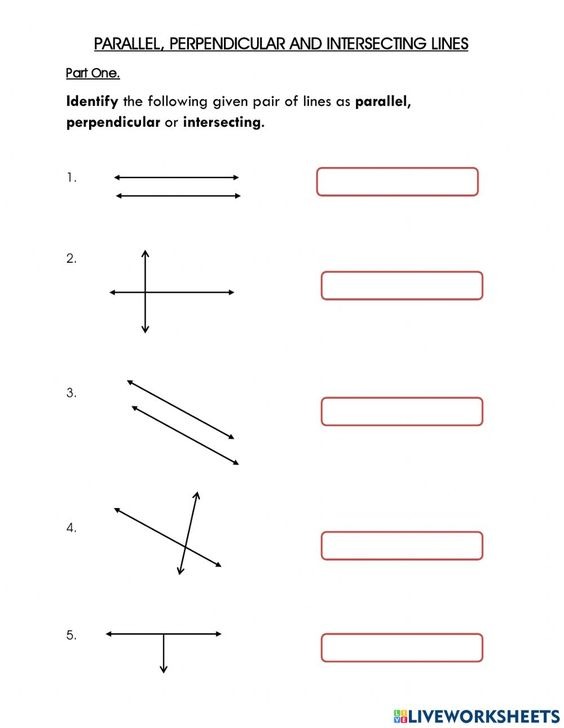
This simple worksheet allows students to begin understanding the difference between perpendicular and parallel lines. Students will also need to be able to identify intersecting lines. This worksheet can be a solid way to start a unit, allowing you to learn more about your students’ previous knowledge of parallel, perpendicular, and intersecting lines.

• Identification And Drawing Of Parallel, Perpendicular, And Intersecting Lines From K5 Learning

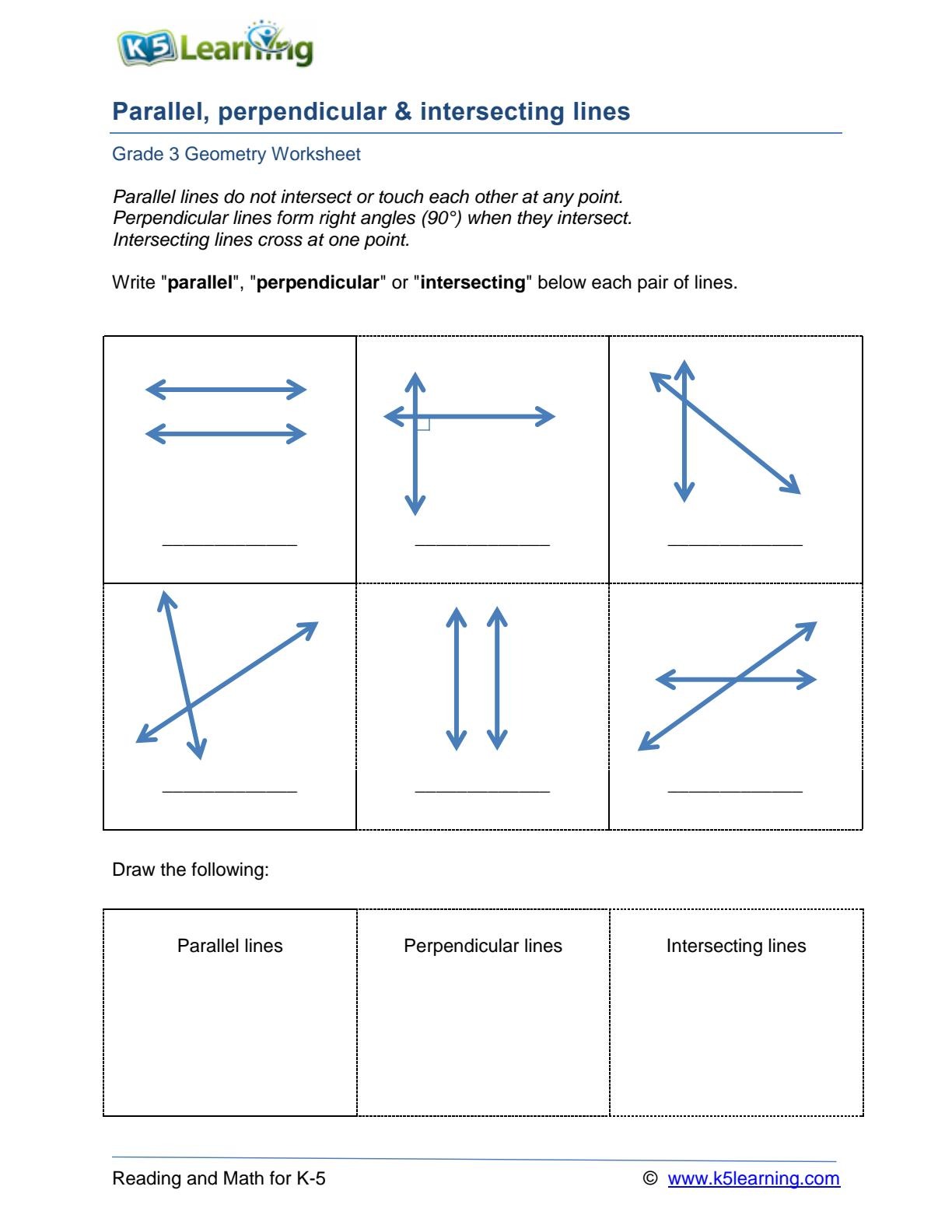
This worksheet asks students to both differentiate between parallel, perpendicular, and intersecting lines, as well as draw an example of each type of line. This can be a good way to get an idea of where your students are at in the process, as asking them to create the lines on their own can create a new challenge from just having students identify different types of lines.

• Parallel And Perpendicular Lines Worksheet Pack From Liveworksheets

Looking for a way to ease the burden of creating resources for your parallel and perpendicular lines unit? This complete worksheet pack will make it easy for your students to get the in class practice and homework that they need to solidify new concepts.

• Using Slope To Create Parallel And Perpendicular Lines By Lindsay Bowden

Perfect for higher level students who already know how to differentiate between parallel and perpendicular lines, this worksheet helps students incorporate their graphing calculators to determine what type of lines each slope will create. 

• Draw Perpendicular And Parallel Lines From All Kids Network

This simple worksheet is a great introduction to parallel and perpendicular lines. Whether you use this as a quick assessment for prior knowledge or as a warm up for a slope lesson, this is the perfect reminder of the difference between parallel and perpendicular lines.

• Slope Equation Practice From Scribd

This worksheet is for advanced students who are able to use tough formulas to determine whether they will form a parallel or perpendicular line.

•  Graph And Parallel/Perpendicular Lines From Education.com

This worksheet is perfect for students who are beginning to learn more about the idea of graphing equations. No graphing calculator is needed–to complete this activity, students simply need to determine which lines on the axes create perpendicular and parallel lines.

Where to Find Parallel and Perpendicular Lines Worksheets Online By

Struggling to find the perfect parallel and perpendicular lines worksheet for your students? 

Check out some great resources below:

• Education.com
• K5 Learning
• Live Worksheets

When you’re working hard to meet the needs of your students, it can be tough to figure out how to get them everything they need without breaking the bank (especially if your school doesn’t have the budget for paying for online resources). Free worksheets can be a great way for your students to get practice on a certain topic, and can work well for homework and extra credit work. Paid worksheets are often easier to customize, allowing you to meet the needs of your students as they explore a new topic. 

At Teach Simple, we’re proud to support teachers. We know how much time you put into your lessons, and we’re here to provide you with the resources you need to help your students thrive. Whether you’re looking for full unit plans or practice worksheets to help your students nail a new concept, we’ve got your back. We invite you to create a free account today so you can take a look at all we have to offer. 

Teaching math is tough, and you’re doing a great job for your classroom by taking the time necessary to find the right resources for your students. Your students will get the hang of parallel and perpendicular lines quickly–as long as they have the right practice materials. Be sure to browse our library to find the perfect parallel and perpendicular lines worksheet for your students.

Share Article:

Download unlimited teaching resources, join free today.

Amanda B. taught for 8 years after starting her career as a Teach for America corps member. She has a certification in Urban Education and an M.Ed. in School Counseling from UPenn.

We have a lot of interesting articles and educational resources from a wide variety of authors and teaching professionals.

The Best Teacher-Approved Solving Inequalities Worksheets

Weight value guide examples.

Last Updated on September 10, 2023 by Teach Simple

• HW Guidelines
• Study Skills Quiz
• Find Local Tutors
• Demo MathHelp.com
• Join MathHelp.com

Select a Course Below

• ACCUPLACER Math
• Math Placement Test
• PRAXIS Math
• + more tests
• 5th Grade Math
• 6th Grade Math
• Pre-Algebra
• College Pre-Algebra
• Introductory Algebra
• Intermediate Algebra
• College Algebra

Parallel & Perpendicular Lines

Slope & Formula Hor. & Vert. Lines Par. & Perp. Lines

Parallel lines and their slopes are easy. Since slope is a measure of the angle of a line from the horizontal, and since parallel lines must have the same angle, then parallel lines have the same slope — and lines with the same slope are parallel.

Perpendicular lines are a bit more complicated.

If you visualize a line with positive slope (so it's an increasing line), then the perpendicular line must have negative slope (because it will have to be a decreasing line). So perpendicular lines have slopes which have opposite signs.

Content Continues Below

MathHelp.com

Parallel and Perpendicular Lines

The other "opposite" thing with perpendicular slopes is that their values are reciprocals; that is, you take the one slope value, and flip it upside down. (This is the non -obvious thing about the slopes of perpendicular lines.) Put this together with the sign change, and you get that the slope of a perpendicular line is the "negative reciprocal" of the slope of the original line — and two lines with slopes that are negative reciprocals of each other are perpendicular to each other.

In your homework, you will probably be given some pairs of points, and be asked to state whether the lines through the pairs of points are "parallel, perpendicular, or neither". To answer the question, you'll have to calculate the slopes and compare them. Here's how that works:

One line passes through the points (−1, −2) and (1, 2) ; another line passes through the points (−2, 0) and (0, 4) . Are these lines parallel, perpendicular, or neither?

To answer this question, I'll find the two slopes. So I can keep things straight and tell the difference between the two slopes, I'll use subscripts.

Since these two lines have identical slopes, then:

these lines are parallel.

One line passes through the points (0, −4) and (−1, −7) ; another line passes through the points (3, 0) and (−3, 2) . Are these lines parallel, perpendicular, or neither?

I'll find the values of the slopes.

the lines are perpendicular.

One line passes through the points (−4, 2) and (0, 3) ; another line passes through the points (−3, −2) and (3, 2) . Are these lines parallel, perpendicular, or neither?

I'll find the slopes.

These slope values are not the same, so the lines are not parallel. The slope values are also not negative reciprocals, so the lines are not perpendicular. Then the answer is:

these lines are neither.

Find the slope of a line perpendicular to the line y = −4 x + 9 .

They've given me the original line's equation, and it's in " y = " form, so it's easy to find the slope. I can just read the value off the equation: m = −4 .

This slope can be turned into a fraction by putting it over 1 , so this slope can be restated as:

m = −4 / 1

To get the negative reciprocal, I need to flip this fraction, and change the sign. Then the slope of any line perpendicular to the given line is:

Warning: When asked a question of this type ("are these lines parallel or perpendicular?"), do not start drawing pictures. If the lines are close to being parallel or close to being perpendicular (or if you draw the lines messily), you can very-easily get the wrong answer from your picture.

Besides, they're not asking if the lines look parallel or perpendicular; they're asking if the lines actually are parallel or perpendicular. The only way to be sure of your answer is to do the algebra.

URL: https://www.purplemath.com/modules/slope3.htm

Page 1 Page 2 Page 3

Standardized Test Prep

College math, homeschool math, share this page.

• Terms of Use
• About Purplemath
• About the Author
• Tutoring from PM
• Advertising
• Linking to PM
• Site licencing

Visit Our Profiles

Parallel and Perpendicular Lines

Parallel and perpendicular lines are an important part of geometry and they have distinct characteristics that help to identify them easily. Two lines are termed as parallel if they lie in the same plane, are the same distance apart, and never meet each other. Perpendicular lines are intersecting lines that always meet at an angle of 90°. Let us learn more about parallel and perpendicular lines in this article.

What are Parallel and Perpendicular Lines?

If two straight lines lie in the same plane, and if they never intersect each other, they are called parallel lines . They are always the same distance apart and are equidistant lines. The symbol || is used to represent parallel lines. For example, AB || CD means line AB is parallel to line CD. On the other hand, when two lines intersect each other at an angle of 90°, they are known as perpendicular lines. Perpendicular lines are denoted by the symbol ⊥. For example, PQ ⊥ RS means line PQ is perpendicular to line RS. Observe the following figure and the properties of parallel and perpendicular lines to identify them and differentiate between them.

Properties of Parallel Lines

• Parallel lines are always equidistant from each other.
• They never meet at any common point.
• They lie in the same plane.

Properties of Perpendicular Lines

• Perpendicular lines always intersect at 90°.
• All perpendicular lines can be termed as intersecting lines , but all intersecting lines cannot be called perpendicular because they need to intersect at right angles .

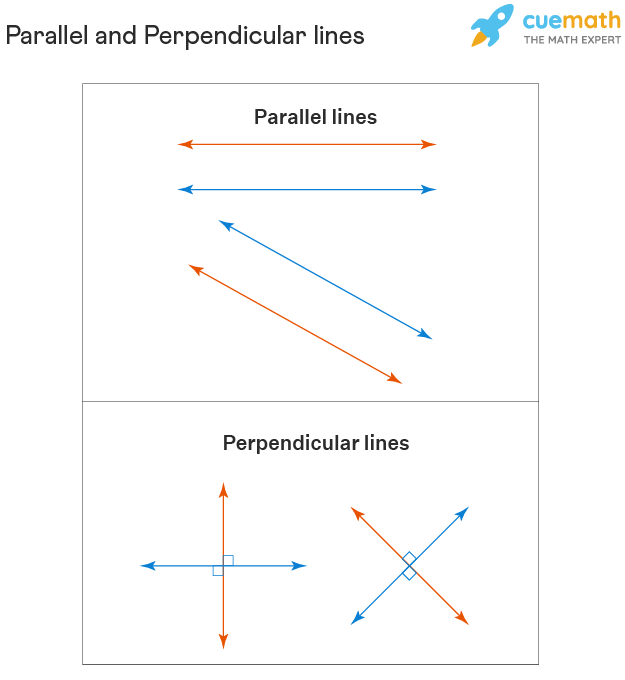
Difference Between Parallel and Perpendicular Lines

Although parallel and perpendicular lines are the two basic and most commonly used lines in geometry , they are quite different from each other. The following table shows the difference between parallel and perpendicular lines.

Equations of Parallel and Perpendicular Lines

The equation of a straight line is represented as y = ax + b which defines the slope and the y-intercept. Here 'a' represents the slope of the line. Since two parallel lines never intersect each other and they have the same steepness, their slopes are always equal. For example, if the equations of two lines are given as, y = -3x + 6 and y = -3x - 4, we can see that the slope of both the lines is the same (-3). Therefore, they are parallel lines. Mathematically, this can be expressed as m 1 = m 2 , where m 1 and m 2 are the slopes of two lines that are parallel.

Perpendicular lines do not have the same slope. The slope of one line is the negative reciprocal of the other line. This can be expressed mathematically as m 1 × m 2 = -1, where m 1 and m 2 are the slopes of two lines that are perpendicular. For example, if the equations of two lines are given as: y = 1/4x + 3 and y = - 4x + 2, we can see that the slope of one line is the negative reciprocal of the other. Therefore, they are perpendicular lines. In this case, the negative reciprocal of -4 is 1/4 and vice versa. Negative reciprocal means, if m 1 and m 2 are negative reciprocals of each other, their product will be -1.

Hence, it can be said that if the slope of two lines is the same, they are identified as parallel lines, whereas, if the slope of two given lines are negative reciprocals of each other, they are identified as perpendicular lines.

☛ Related Articles

Check out the following pages related to parallel and perpendicular lines.

• Points and Lines
• Line Segment
• Difference Between Line and Line Segment
• Lines and Angles
• Parallel and Perpendicular Lines Worksheets

Parallel and Perpendicular Lines Examples

Example 1: Observe the blue highlighted lines in the following examples and identify them as parallel or perpendicular lines.

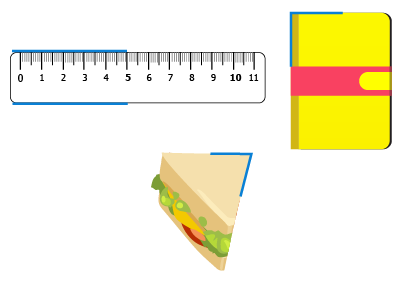
Solution: We need to know the properties of parallel and perpendicular lines to identify them.

a.) Ruler: The highlighted lines in the scale (ruler) do not intersect or meet each other directly, and are the same distance apart, therefore, they are parallel lines.

b.) Sandwich: The highlighted lines in the sandwich are neither parallel nor perpendicular lines. They are not parallel because they are intersecting each other. They are not perpendicular because they are not intersecting at 90°.

c.) Book: The two highlighted lines meet each other at 90°, therefore, they are perpendicular lines.

Example 2: State true or false using the properties of parallel and perpendicular lines.

a.) The letter A has a set of perpendicular lines.

b.) The opposite sides of a rectangle are parallel lines.

c.) Parallel lines intersect each other at 90°.

Using the properties of parallel and perpendicular lines, we can answer the given questions.

a.) False, the letter A does not have a set of perpendicular lines because the intersecting lines do not meet each other at right angles.

b.) True, the opposite sides of a rectangle are parallel lines.

c.) False, parallel lines do not intersect each other at all, only perpendicular lines intersect at 90°.

Example 3: Fill in the blanks using the properties of parallel and perpendicular lines.

a.) _____ lines are always equidistant from each other.

b.) If the slope of two given lines are negative reciprocals of each other, they are identified as ______ lines.

a.) Parallel lines are always equidistant from each other.

b.) If the slope of two given lines are negative reciprocals of each other, they are identified as perpendicular lines.

go to slide go to slide go to slide

Book a Free Trial Class

Practice Questions on Parallel and Perpendicular Lines

go to slide go to slide

FAQs on Parallel and Perpendicular Lines

Parallel lines are those lines that do not intersect at all and are always the same distance apart. Perpendicular lines are those lines that always intersect each other at right angles.

What Letters have Parallel and Perpendicular Lines?

There are some letters in the English alphabet that have parallel and perpendicular lines in them. Observe the horizontal lines in E and Z and the vertical lines in H, M and N to notice the parallel lines. Similarly, observe the intersecting lines in the letters L and T that have perpendicular lines in them.

What Shape has Parallel and Perpendicular Lines?

There are many shapes around us that have parallel and perpendicular lines in them. For example, the opposite sides of a square and a rectangle have parallel lines in them, and the adjacent lines in the same shapes are perpendicular lines. If we see a few real-world examples, we can notice parallel lines in them, like the opposite sides of a notebook or a laptop, represent parallel lines, and the intersecting sides of a notebook represent perpendicular lines.

How many Parallel and Perpendicular lines are there in a Square?

In a square, there are two pairs of parallel lines and four pairs of perpendicular lines. The opposite sides are parallel and the intersecting lines are perpendicular.

What Letter has both Parallel and Perpendicular Lines?

There are some letters in the English alphabet that have both parallel and perpendicular lines. For example, the letter H, in which the vertical lines are parallel and the horizontal line is perpendicular to both the vertical lines. Similarly, in the letter E, the horizontal lines are parallel, while the single vertical line is perpendicular to all the three horizontal lines.

How to Identify Parallel and Perpendicular Lines?

Parallel and perpendicular lines can be identified on the basis of the following properties:

Properties of Parallel Lines:

• Parallel lines are coplanar lines.
• They are always equidistant from each other.
• They do not meet at any common point.

Properties of Perpendicular Lines:

• Perpendicular lines always intersect at right angles.
• All perpendicular lines can be termed as intersecting lines, but all intersecting lines cannot be called perpendicular because they need to intersect at right angles.

What are the Slopes of Parallel and Perpendicular Lines?

If the slope of two given lines is equal, they are considered to be parallel lines. For example, if the equation of two lines is given as, y = 4x + 3 and y = 4x - 5, we can see that their slope is equal (4). These lines can be identified as parallel lines. Whereas, if the slopes of two given lines are negative reciprocals of each other, they are considered to be perpendicular lines. For example, if the equation of two lines is given as, y = 1/5x + 3 and y = - 5x + 2, we can see that the slope of one line is the negative reciprocal of the other. In this case, the negative reciprocal of 1/5 is -5. Therefore, these lines can be identified as perpendicular lines.

How are Parallel and Perpendicular Lines Similar?

Parallel and perpendicular lines have one common characteristic between them. They both consist of straight lines.

One to one maths interventions built for KS4 success

Weekly online one to one GCSE maths revision lessons now available

In order to access this I need to be confident with:

This topic is relevant for:

Parallel And Perpendicular Lines

Here we will learn about parallel and perpendicular lines including how to show when two lines are parallel or perpendicular, how to calculate the gradient of parallel and perpendicular lines and use this knowledge to calculate the gradient of tangents to circles.

There are also parallel and perpendicular worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

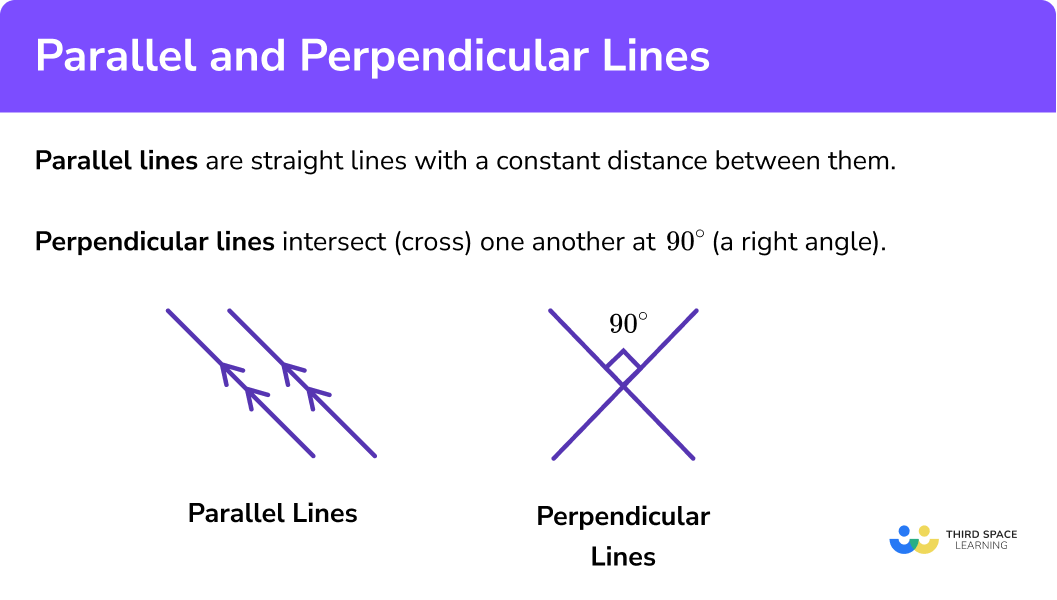
What are parallel and perpendicular lines?

Parallel lines are straight lines with a constant distance between them. Perpendicular lines intersect one another at a 90 degree angle (a right angle)

E.g. A table has 4 legs. Each leg is parallel to the other legs, but perpendicular to the table top that they are attached to:

Straight line graphs can be parallel, perpendicular or have 1 point of intersection. It is not possible for 1 straight line to intersect another line at two coordinates or be parallel and perpendicular at the same time. We therefore need to understand each property so that we can start to visualise when lines are parallel or perpendicular.

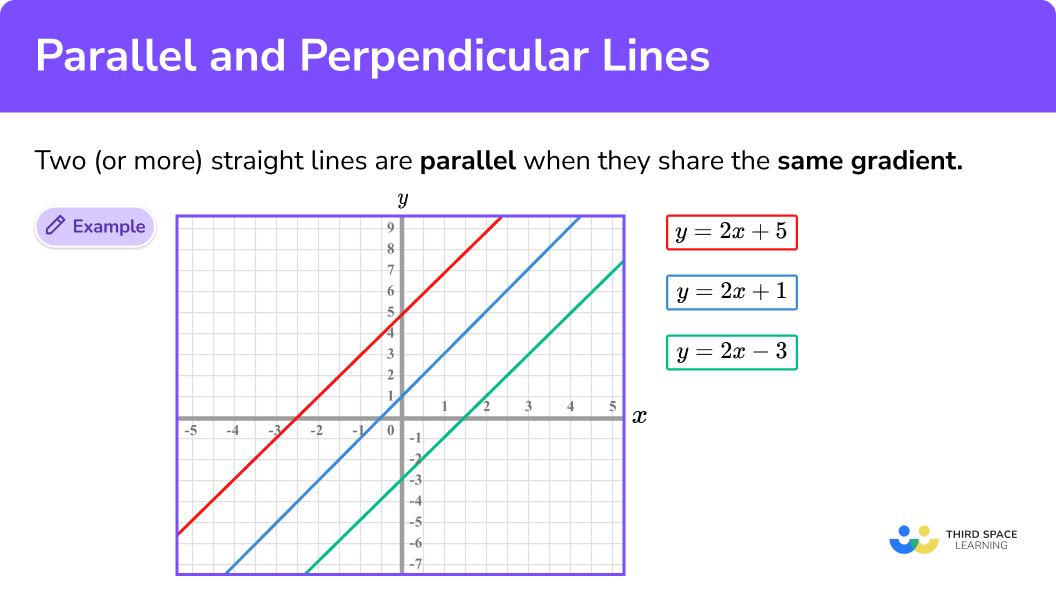
Parallel lines

Two (or more) straight lines are parallel when they share the same gradient . 

E.g. Let’s look at the three lines y = 2x + 1 , y = 2x + 5 and y = 2x − 3 :

Each straight line has the same gradient (here, m = 2 ) and the distance between any two lines remains constant in both directions. This means that all 3 lines are parallel.

We can therefore state that the equation of a line parallel to a line with the gradient 2 can be written in the form y = 2x + c , for any value of c that represents where the graph intercepts the y-axis.

Top Tip: All vertical lines are parallel to the line x = 0 and all horizontal lines are parallel to the line y = 0 .

What are parallel lines?

Equations of parallel lines

Parallel lines can be recognised by their equations by checking if their gradients are the same. This may require some rearranging.

Show that y=-2x+4 and 4x+2y=9 are parallel.

The gradient of the first line is -2 . We need to rearrange the second equation so that it is in the form y=mx+c so we can find the gradient.

The gradient of the second line is also -2. The gradients of the two lines are the same, so the lines are parallel.

Perpendicular lines

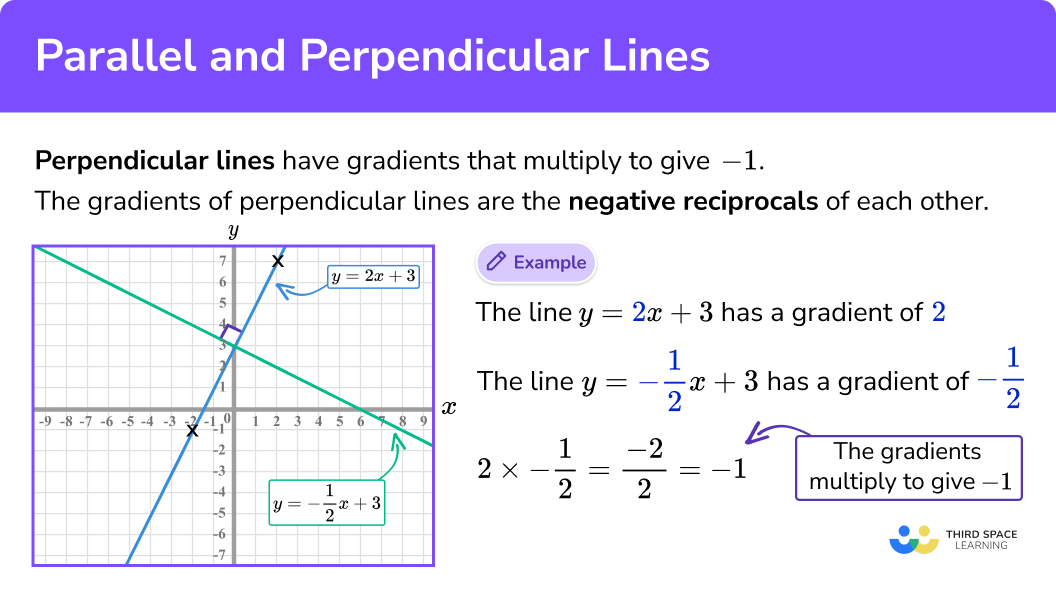
Perpendicular lines have gradients that multiply to give −1 . In other words, the gradients of two lines that are perpendicular to each other are the negative reciprocals of each other.

E.g. To see why let’s look at the line y = x :

The gradient of the line y = x is m = 1 as for each unit square we move right along the x-axis, we move 1 unit square up the y-axis.

Let’s now construct a line that is perpendicular to the line y = x ; we can do this by finding the perpendicular bisector for the line between the points (-3, -3) and (3, 3) :

The equation of a straight line that is perpendicular to the line y = x is the line y = −x .

We can see that the gradient of each line has a different sign (one has a positive gradient whilst the other has a negative gradient). To find out what is going on here let’s look at a second example.

E.g. Take the line y = 2x + 3 .

Let’s construct a perpendicular to the line y = 2x + 3 at the point ( 0,3 )

Here the equation of the line that is perpendicular to y = 2x + 3  at the point (0, 3) is y=−\frac{1}{2}x+3

We can still state that the gradients change from being positive to negative but we now have the gradient of -\frac{1}{2} which is the negative reciprocal of 2 .

Let us look at the previous two examples together in the table below:

Here we can see that the product of the gradients of each line is equal to −1 .  

We can therefore state that for any two perpendicular lines y = mx + c and y = nx + c ,

If we divide both sides of the formula by m , we get the formula for the gradient of the perpendicular line n to be: n=\frac{−1}{m} .

The value of n is called the negative reciprocal of m as we divide − 1 by m .

What are perpendicular lines?

Gradients of parallel and and perpendicular lines

The gradients of parallel lines are the same.

The gradients of perpendicular lines multiply together to make -1.

Here is a brief summary.

For any two lines to be parallel , the gradient is the same for each line.

E.g. y = 5x + 3 and y = 5x − 9 are parallel as the gradient for each line is 5 .

For any two lines to be perpendicular , the product of their gradients must equal − 1 .

E.g. y=4x+7 and y=-\frac{1}{4}x+9 are perpendicular as 4\times-\frac{1}{4}=-1

How to find the equation of a parallel line

In order to find the equation of a parallel line:

• State/calculate the gradient of the original straight line.
• Substitute the value for m into the equation of a new straight line.

Parallel and perpendicular lines worksheet

Get your free parallel and perpendicular lines worksheet of 20+ questions and answers. Includes reasoning and applied questions.

Related lessons on straight line graphs

Parallel and perpendicular lines  is part of our series of lessons to support revision on  straight line graphs . You may find it helpful to start with the main straight line graphs lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:

• Straight line graphs
• Gradient of a line
• Equation of a line
• Coordinates maths
• How to find the y intercept and the x intercept
• How to find the midpoint
• Intersecting lines
• Linear graph
• Distance formula

Parallel lines examples

Example 1: write the equation of a parallel line (algebraically).

The equation of a line A is given as 5y = x − 10 . Write the equation of a line that is parallel to A .

State/calculate the gradient of the original straight line .

As 5y=x-10 .

Here, the gradient of the line is \frac{1}{5}

2 Substitute the value for m into the equation of a new straight line .

Substituting m=\frac{1}{5} into a new equation, we get y=\frac{1}{5}x+c

3 State/calculate the value of the y-intercept .

Here we are asked to state a parallel line so any value of c , except for the value stated in the original equation (− 2 ), would satisfy this question.

An example of an equation of the line parallel to line A is y=\frac{1}{5}x+3

Example 2: write the equation of a parallel line (graphically)

The line B is drawn on a set of axes. Write the equation of a line that is parallel to B.

Substitute the value for m into the equation of a new straight line .

We now have y = −x + c

State/calculate the value of the y-intercept .

Here we are asked to state a parallel line so any value of c , except for the value stated in the original equation ( 3 ), would satisfy this question.

A possible solution would be y = −x − 4 .

Example 3: given 1 coordinate and the gradient

Two lines, D and E are written in the form y = mx + c . The gradient of the line D is equal to 0.4 and intersects the y-axis at the point ( 0,5 ). The line E is parallel to D and goes through the point ( 10,12 ). Work out the equation of line E.

We know from the question that the gradient of line D is 0.4 .

We now have y = 0.4x + c .

We need to calculate the value of c as it is stated that the line E goes through the point ( 10,12 ). We therefore substitute x = 10 and y = 12 into the equation to find the value of c .

The equation of line E is y = 0.4x + 8

How to calculate the equation of perpendicular lines

In order to find the equation of a perpendicular line:

Calculate the negative reciprocal of the gradient .

Substitute the negative reciprocal into the equation of a new straight line .

• State/calculate the value of the \textbf{y} -intercept .

Perpendicular lines examples

Example 1: write the equation of a perpendicular line (algebraically).

The equation of a line A is given as 2y + 7 = 8x . Write the equation of a line that is perpendicular to A.

First we need to rearrange the equation to make y the subject. This in turn will give us the value for the gradient m .

Now we can see that m = 4 .

The gradient of the line perpendicular to A is equal to

We now have the equation y=-\frac{1}{4}x+c for the line perpendicular to A.

Here, we are asked to state a perpendicular line so any value of c would satisfy this question. 

An example of an equation of the line perpendicular to line A is y=-\frac{1}{4}x+1

Example 2: write the equation of a perpendicular line (graphically)

The line B is drawn on a set of axes. Write the equation of a line that is perpendicular to B at the point ( 1,4 ).

The gradient of the line perpendicular to B is equal to

We now have the equation y=\frac{1}{2}x+c  for the line perpendicular to B.

Here we have to substitute the coordinate ( 1,4 ) into the new equation for our straight line to find the value of c .

The equation of the line that is perpendicular to the line B is y=\frac{1}{2}x+3\frac{1}{2} or 2y=x+7 .

Two lines, D and E are written in the form y = mx + c . The gradient of the line D is equal to -\frac{2}{5} and intersects the y-axis at the origin. The line E is perpendicular to D. Work out the equation of line E.

The gradient of line D is -\frac{2}{5} as stated in the question.

Here, we have

Substituting m=\frac{5}{2} into y=mx+c we get y=\frac{5}{2}x+c

Here we have to substitute the coordinate ( 0,0 ) into the new equation for our straight line to find the value of c .

The equation of line E is therefore y=\frac{5}{2}x

Common misconceptions

• Using the y-intercept instead of the coefficient of x (parallel lines)

E.g. Take example 1 : “The equation of a line A is given as 5y = x − 10 . Write the equation of a line that is parallel to A.” After making y the subject so we have the equation y=\frac{1}{5}x−2 the value for the gradient could be incorrectly taken as – 2 . This will generate a new equation that looks like y = mx − 2 which is incorrect as it is the coefficient of x that remains the same, and the y-intercept changes.

• Not/incorrectly rearranging to the form y = mx + c

The gradient is the coefficient of x , labelled as m . If the equation of a straight line is not written with y as the subject, the gradient may not be correct so it is important to be confident with rearranging equations. E.g. Take example 1 again: “The equation of a line A is given as 5y = x − 10 . Write the equation of a line that is parallel to A.” Here, the value of the gradient could be incorrectly stated as 1 as the coefficient of x is 1 . This is wrong because the equation is not in the form y = mx + c .

• The reciprocal vs the negative reciprocal

A common mistake is to state the gradient of the perpendicular to a line to be the reciprocal of the original gradient, and not the negative reciprocal. If the negative reciprocal was not used his would mean that both lines would have a positive gradient, or they would both have a negative gradient. This would mean that although the two lines may intersect they will not intersect at 90 °.

Practice parallel and perpendicular lines questions

1. Which equation is parallel to the line y=4x+3 ?

Any equation of the form y=4x+c for any value of c .

2. Which of the following equations is parallel to the line 2y-5=3x ?

Both have the gradient of 1.5 (or m=\frac{3}{2} )

3. Calculate the gradient of the line that is perpendicular to the line y=-0.4x+3 .

The product of the two gradients must equal -1 . Here, -1\div-0.4 = 1\div0.4 = 2.5

4. Calculate the gradient of the line that is perpendicular to the line y=-\frac{7}{10}x+4

The product of the two gradients must equal -1 .

Here, \frac{-7}{10}\times\frac{10}{7}=\frac{-70}{70}=-1

5. State the equation of the line that is parallel to the line y=2x+7 at the point ( 3,8 )

The line must have a gradient of 2 so y=2x+c . At the point ( 3,8 ), 8=2\times3+c , so c=2

Hence, y=2x+2

6. Calculate the equation of the line that is perpendicular to the line y=-\frac{1}{3}x+1 that intersects at the point ( 6,-1 )

New gradient = -1\div{-\frac{1}{3}}=-1\times{-3}=3 y=3x+c at the point ( 6,-1 ) means -1=(3\times6)+c c=-19

Parallel and perpendicular lines GCSE questions

1. Two straight lines A and B are shown below. Prove that the lines are parallel.

Gradient of line A = \frac{2−1}{2−0}=\frac{1}{2}

Gradient of line B = \frac{0−−2}{4−0}=\frac{2}{4}=\frac{1}{2}

Gradients are the same, therefore parallel

2. (a) Circle the equation of the line that is parallel to the y-axis.

(b) Use the straight line graph L below to write the equation of a parallel line passing through the coordinate ( 3,4 )

b) Gradient of line L is equal to − 1

4 = −3 + c so c = 7 or y = −x + 7

3. (a) The line P has the equation y=6−\frac{3}{5}x . Circle the gradient of a line that is perpendicular to P.

(b) Point C ( 3,6 ) lies on a circle, centre O. The tangent at C intersects the axes at points A and B. Show that the gradient of the tangent is -\frac{1}{2}

a) \frac{5}{3}

b) Gradient of OC= \frac{6}{3}=2

Gradient of perpendicular (tangent): AB=−1\div2 AB=−\frac{1}{2}

4. Use the graph below to show that the two lines are parallel. Clearly state any conclusions.

m=-\frac{6}{5} for both lines

The gradients are the same so the lines are parallel

Learning checklist

You have now learned how to:

• Identify horizontal and vertical lines and pairs of perpendicular and parallel lines.
• Use the form y = mx + c to identify parallel {and perpendicular} lines; find the equation of the line through 2 given points, or through 1 point with a given gradient.

The next lessons are

• Maths formulas
• Interpreting graphs
• Inequalities

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.

Privacy Overview

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Chapter 3: Graphing

3.6 Perpendicular and Parallel Lines

Perpendicular, parallel, horizontal, and vertical lines are special lines that have properties unique to each type. Parallel lines, for instance, have the same slope, whereas perpendicular lines are the opposite and have negative reciprocal slopes. Vertical lines have a constant [latex]x[/latex]-value, and horizontal lines have a constant [latex]y[/latex]-value.

Two equations govern perpendicular and parallel lines:

For parallel lines, the slope of the first line is the same as the slope for the second line. If the slopes of these two lines are called [latex]m_1[/latex] and [latex]m_2[/latex], then [latex]m_1 = m_2[/latex].

[latex]\text{The rule for parallel lines is } m_1 = m_2[/latex]

Perpendicular lines are slightly more difficult to understand. If one line is rising, then the other must be falling, so both lines have slopes going in opposite directions. Thus, the slopes will always be negative to one another. The other feature is that the slope at which one is rising or falling will be exactly flipped for the other one. This means that the slopes will always be negative reciprocals to each other. If the slopes of these two lines are called [latex]m_1[/latex] and [latex]m_2[/latex], then [latex]m_1 = \dfrac{-1}{m_2}[/latex].

[latex]\text{The rule for perpendicular lines is } m_1=\dfrac{-1}{m_2}[/latex]

Example 3.6.1

Find the slopes of the lines that are parallel and perpendicular to [latex]y = 3x + 5.[/latex]

The parallel line has the identical slope, so its slope is also 3.

The perpendicular line has the negative reciprocal to the other slope, so it is [latex]-\dfrac{1}{3}.[/latex]

Example 3.6.2

Find the slopes of the lines that are parallel and perpendicular to [latex]y = -\dfrac{2}{3}x -4.[/latex]

The parallel line has the identical slope, so its slope is also [latex]-\dfrac{2}{3}.[/latex]

The perpendicular line has the negative reciprocal to the other slope, so it is [latex]\dfrac{3}{2}.[/latex]

Typically, questions that are asked of students in this topic are written in the form of “Find the equation of a line passing through point [latex](x, y)[/latex] that is perpendicular/parallel to [latex]y = mx + b[/latex].” The first step is to identify the slope that is to be used to solve this equation, and the second is to use the described methods to arrive at the solution like previously done. For instance:

Example 3.6.3

Find the equation of the line passing through the point [latex](2,4)[/latex] that is parallel to the line [latex]y=2x-3.[/latex]

The first step is to identify the slope, which here is the same as in the given equation, [latex]m=2[/latex].

Now, simply use the methods from before:

[latex]\begin{array}{rrl} m&=&\dfrac{y-y_1}{x-x_1} \\ \\ 2&=&\dfrac{y-4}{x-2} \end{array}[/latex]

Clearing the fraction by multiplying both sides by [latex](x-2)[/latex] leaves:

[latex]2(x-2)=y-4 \text{ or } 2x-4=y-4[/latex]

Now put this equation in one of the three forms. For this example, use the standard form:

[latex]\begin{array}{rrrrrrr} 2x&-&4&=&y&-&4 \\ -y&+&4&&-y&+&4 \\ \hline 2x&-&y&=&0&& \end{array}[/latex]

Example 3.6.4

Find the equation of the line passing through the point [latex](1, 3)[/latex] that is perpendicular to the line [latex]y = \dfrac{3}{2}x + 4.[/latex]

The first step is to identify the slope, which here is the negative reciprocal to the one in the given equation, so [latex]m = -\dfrac{2}{3}.[/latex]

[latex]\begin{array}{rrl} m&=&\dfrac{y-y_1}{x-x_1} \\ \\ -\dfrac{2}{3}&=&\dfrac{y-3}{x-1} \end{array}[/latex]

First, clear the fraction by multiplying both sides by [latex]3(x - 1)[/latex]. This leaves:

[latex]-2(x - 1) = 3(y - 3)[/latex]

which reduces to:

[latex]-2x + 2 = 3y - 9[/latex]

Now put this equation in one of the three forms. For this example, choose the general form:

[latex]\begin{array}{rrrrrrrrr} -2x&&&+&2&=&3y&-&9 \\ &&-3y&+&9&&-3y&+&9 \\ \hline -2x&-&3y&+&11&=&0&& \end{array}[/latex]

For the general form, the coefficient in front of the [latex]x[/latex] must be positive. So for this equation, multiply the entire equation by −1 to make [latex]-2x[/latex] positive.

[latex](-2x -3y + 11 = 0)(-1)[/latex]

[latex]2x + 3y - 11 = 0[/latex]

Questions that are looking for the vertical or horizontal line through a given point are the easiest to do and the most commonly confused.

Vertical lines always have a single [latex]x[/latex]-value, yielding an equation like [latex]x = \text{constant.}[/latex]

Horizontal lines always have a single [latex]y[/latex]-value, yielding an equation like [latex]y = \text{constant.}[/latex]

Example 3.6.5

Find the equation of the vertical and horizontal lines through the point [latex](-2, 4).[/latex]

The vertical line has the same [latex]x[/latex]-value, so the equation is [latex]x = -2[/latex].

The horizontal line has the same [latex]y[/latex]-value, so the equation is [latex]y = 4[/latex].

For questions 1 to 6, find the slope of any line that would be parallel to each given line.

• [latex]y = 2x + 4[/latex]
• [latex]y = -\dfrac{2}{3}x + 5[/latex]
• [latex]y = 4x - 5[/latex]
• [latex]y = -10x - 5[/latex]
• [latex]x - y = 4[/latex]
• [latex]6x - 5y = 20[/latex]

For questions 7 to 12, find the slope of any line that would be perpendicular to each given line.

• [latex]y = \dfrac{1}{3}x[/latex]
• [latex]y = -\dfrac{1}{2}x - 1[/latex]
• [latex]y = -\dfrac{1}{3}x[/latex]
• [latex]y = \dfrac{4}{5}x[/latex]
• [latex]x - 3y = -6[/latex]
• [latex]3x - y = -3[/latex]

For questions 13 to 18, write the slope-intercept form of the equation of each line using the given point and line.

• (1, 4) and parallel to [latex]y = \dfrac{2}{5}x + 2[/latex]
• (5, 2) and perpendicular to [latex]y = \dfrac{1}{3}x + 4[/latex]
• (3, 4) and parallel to [latex]y = \dfrac{1}{2}x - 5[/latex]
• (1, −1) and perpendicular to [latex]y = -\dfrac{3}{4}x + 3[/latex]
• (2, 3) and parallel to [latex]y = -\dfrac{3}{5}x + 4[/latex]
• (−1, 3) and perpendicular to [latex]y = -3x - 1[/latex]

For questions 19 to 24, write the general form of the equation of each line using the given point and line.

• (1, −5) and parallel to [latex]-x + y = 1[/latex]
• (1, −2) and perpendicular to [latex]-x + 2y = 2[/latex]
• (5, 2) and parallel to [latex]5x + y = -3[/latex]
• (1, 3) and perpendicular to [latex]-x + y = 1[/latex]
• (4, 2) and parallel to [latex]-4x + y = 0[/latex]
• (3, −5) and perpendicular to [latex]3x + 7y = 0[/latex]

For questions 25 to 36, write the equation of either the horizontal or the vertical line that runs through each point.

• Horizontal line through (4, −3)
• Vertical line through (−5, 2)
• Vertical line through (−3,1)
• Horizontal line through (−4, 0)
• Horizontal line through (−4, −1)
• Vertical line through (2, 3)
• Vertical line through (−2, −1)
• Horizontal line through (−5, −4)
• Horizontal line through (4, 3)
• Vertical line through (−3, −5)
• Vertical line through (5, 2)
• Horizontal line through (5, −1)

Answer Key 3.6

Intermediate Algebra Copyright © 2020 by Terrance Berg is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Share This Book

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

4.6: Parallel and Perpendicular Lines

• Last updated
• Save as PDF
• Page ID 61388

Learning Objectives

• Determine the slopes of parallel and perpendicular lines.
• Find equations of parallel and perpendicular lines

Definition of Parallel and Perpendicular

Parallel lines are lines in the same plane that never intersect. Two nonvertical lines in the same plane, with slopes \(m_{1}\) and \(m_{2}\), are parallel if their slopes are the same, \(m_{1}=m_{2}\). Consider the following two lines:

Consider their corresponding graphs:

Figure \(\PageIndex{1}\)

Both lines have a slope \(m=\frac{3}{4}\) and thus are parallel.

Perpendicular lines are lines in the same plane that intersect at right angles (\(90\) degrees). Two nonvertical lines in the same plane, with slopes \(m_{1}\) and \(m_{2}\), are perpendicular if the product of their slopes is \(−1: m1⋅m2=−1\). We can solve for \(m_{1}\) and obtain \(m_{1}=\frac{−1}{m_{2}}\). In this form, we see that perpendicular lines have slopes that are negative reciprocals , or opposite reciprocals. For example, if given a slope

\(m=-\frac{5}{8}\)

then the slope of a perpendicular line is the opposite reciprocal:

\(m_{\perp}=\frac{8}{5}\)

The mathematical notation \(m_{⊥}\) reads “\(m\) perpendicular.” We can verify that two slopes produce perpendicular lines if their product is \(−1\).

\(m\cdot m_{\perp}=-\frac{5}{8}\cdot\frac{8}{5}=-\frac{40}{40}=-1\quad\color{Cerulean}{\checkmark}\)

Geometrically, we note that if a line has a positive slope, then any perpendicular line will have a negative slope. Furthermore, the rise and run between two perpendicular lines are interchanged.

Figure \(\PageIndex{2}\)

Perpendicular lines have slopes that are opposite reciprocals, so remember to find the reciprocal and change the sign. In other words,

If \(m=\frac{a}{b}\), then \(m_{\perp}=-\frac{b}{a}\)

Determining the slope of a perpendicular line can be performed mentally. Some examples follow

Example \(\PageIndex{1}\)

Determine the slope of a line parallel to \(y=−5x+3\).

Since the given line is in slope-intercept form, we can see that its slope is \(m=−5\). Thus the slope of any line parallel to the given line must be the same, \(m_{∥}=−5\). The mathematical notation \(m_{∥}\) reads “\(m\) parallel.”

\(m_{∥}=−5\)

Example \(\PageIndex{2}\)

Determine the slope of a line perpendicular to \(3x−7y=21\).

First, solve for \(y\) and express the line in slope-intercept form.

In this form, we can see that the slope of the given line is \(m=\frac{3}{7}\), and thus \(m_{⊥}=−\frac{7}{3}\).

\(m_{⊥}=−\frac{7}{3}\)

Exercise \(\PageIndex{1}\)

Find the slope of the line perpendicular to \(15x+5y=20\).

\(m_{\perp}=\frac{1}{3}\)

Finding Equations of Parallel and Perpendicular Lines

We have seen that the graph of a line is completely determined by two points or one point and its slope. Often you will be asked to find the equation of a line given some geometric relationship—for instance, whether the line is parallel or perpendicular to another line.

Example \(\PageIndex{3}\)

Find the equation of the line passing through \((6, −1)\) and parallel to \(y=\frac{1}{2}x+2\)

Here the given line has slope \(m=\frac{1}{2}\), and the slope of a line parallel is \(m_{∥}=\frac{1}{2}\). Since you are given a point and the slope, use the point-slope form of a line to determine the equation.

\(\begin{array}{cc}{\color{Cerulean}{Point}}&{\color{Cerulean}{Slope}}\\{(6,-1)}&{m_{\parallel}=\frac{1}{2}} \end{array}\)

\(y=\frac{1}{2}x-4\)

It is important to have a geometric understanding of this question. We were asked to find the equation of a line parallel to another line passing through a certain point.

Figure \(\PageIndex{3}\)

Through the point \((6, −1)\) we found a parallel line, \(y=\frac{1}{2}x−4\), shown dashed. Notice that the slope is the same as the given line, but the \(y\)-intercept is different. If we keep in mind the geometric interpretation, then it will be easier to remember the process needed to solve the problem.

Example \(\PageIndex{4}\)

Find the equation of the line passing through \((−1, −5)\) and perpendicular to \(y=−\frac{1}{4}x+2\).

The given line has slope \(m=−\frac{1}{4}\), and thus \(m_{⊥}=+\frac{4}{1}=4\). Substitute this slope and the given point into point-slope form.

\(\begin{array}{cc} {\color{Cerulean}{Point}}&{\color{Cerulean}{Slope}}\\{(-1,-5)}&{m_{\perp}=4}\end{array}\)

Geometrically, we see that the line \(y=4x−1\), shown dashed below, passes through \((−1, −5)\) and is perpendicular to the given line.

Figure \(\PageIndex{4}\)

It is not always the case that the given line is in slope-intercept form. Often you have to perform additional steps to determine the slope. The general steps for finding the equation of a line are outlined in the following example.

Example \(\PageIndex{5}\)

Find the equation of the line passing through \((8, −2)\) and perpendicular to \(6x+3y=1\).

Step 1 : Find the slope \(m\). First, find the slope of the given line. To do this, solve for \(y\) to change standard form to slope-intercept form, \(y=mx+b\).

\(\begin{aligned} 6x+3y&=1 \\ 6x+3y\color{Cerulean}{-6x}&=1\color{Cerulean}{-6x} \\ 3y&=-6x+1 \\ \frac{3y}{\color{Cerulean}{3}}&=\frac{-6x+1}{\color{Cerulean}{3}} \\ y&=\frac{-6x}{3}+\frac{1}{3}\\y&=-2x+\frac{1}{3} \end{aligned}\)

In this form, you can see that the slope is \(m=−2=−\frac{2}{1}\), and thus \(m_{⊥}=\frac{−1}{−2}=+\frac{1}{2}\).

Step 2 : Substitute the slope you found and the given point into the point-slope form of an equation for a line. In this case, the slope is \(m_{⊥}=\frac{1}{2}\) and the given point is \((8, −2)\).

\(\begin{aligned} y-y_{1}&=m(x-x_{1}) \\ y-(-2)&=\frac{1}{2}(x-8) \end{aligned}\)

Step 3 : Solve for \(y\).

\(y=\frac{1}{2}x−6\)

Example \(\PageIndex{6}\)

Find the equation of the line passing through \((\frac{7}{2}, 1)\) and parallel to \(2x+14y=7\).

Find the slope \(m\) by solving for \(y\).

\(\begin{aligned} 2x+14y&=7 \\ 2x+14y\color{Cerulean}{-2x}&=7\color{Cerulean}{-2x} \\ 14y&=-2x+7 \\ \frac{14y}{\color{Cerulean}{14}}&=\frac{-2x+7}{\color{Cerulean}{14}} \\ y&=\frac{-2x}{14}+\frac{7}{14} \\ y&=-\frac{1}{7}x+\frac{1}{2} \end{aligned}\)

The given line has the slope \(m=−\frac{1}{7}\), and so \(m_{∥}=−\frac{1}{7}\). We use this and the point \((\frac{7}{2}, 1)\) in point-slope form.

\(\begin{aligned} y-y_{1}&=m(x-x_{1}) \\ y-1&=-\frac{1}{7}\left(x-\frac{7}{2} \right) \\ y-1&=-\frac{1}{7}x+\frac{1}{2} \\ y-1\color{Cerulean}{+1}&=-\frac{1}{7}x+\frac{1}{2}\color{Cerulean}{+1} \\ y&=-\frac{1}{7}x+\frac{1}{2}+\color{Cerulean}{\frac{2}{2}} \\ y&=-\frac{1}{7}x+\frac{3}{2} \end{aligned}\)

\(y=-\frac{1}{7}x+\frac{3}{2}\)

Exercise \(\PageIndex{2}\)

Find the equation of the line perpendicular to \(x−3y=9\) and passing through \((−\frac{1}{2}, 2)\).

\(y=-3x+\frac{1}{2}\)

When finding an equation of a line perpendicular to a horizontal or vertical line, it is best to consider the geometric interpretation.

Example \(\PageIndex{7}\)

Find the equation of the line passing through \((−3, −2)\) and perpendicular to \(y=4\).

We recognize that \(y=4\) is a horizontal line and we want to find a perpendicular line passing through \((−3, −2)\).

Figure \(\PageIndex{5}\)

If we draw the line perpendicular to the given horizontal line, the result is a vertical line.

Figure \(\PageIndex{6}\)

Equations of vertical lines look like \(x=k\). Since it must pass through \((−3, −2)\), we conclude that \(x=−3\) is the equation. All ordered pair solutions of a vertical line must share the same \(x\)-coordinate.

\(x=−3\)

We can rewrite the equation of any horizontal line, \(y=k\), in slope-intercept form as follows:

Written in this form, we see that the slope is \(m=0=\frac{0}{1}\). If we try to find the slope of a perpendicular line by finding the opposite reciprocal, we run into a problem: \(m_{⊥}=−\frac{1}{0}\), which is undefined. This is why we took care to restrict the definition to two nonvertical lines. Remember that horizontal lines are perpendicular to vertical lines.

Key Takeaways

• Parallel lines have the same slope.
• Perpendicular lines have slopes that are opposite reciprocals. In other words, if \(m=\frac{a}{b}\), then \(m_{⊥}=−\frac{b}{a}\).
• To find an equation of a line, first use the given information to determine the slope. Then use the slope and a point on the line to find the equation using point-slope form.
• Horizontal and vertical lines are perpendicular to each other.

Exercise \(\PageIndex{3}\) Parallel and Perpendicular Lines

Determine the slope of parallel lines and perpendicular lines.

• \(y=−\frac{3}{4}x+8\)
• \(y=\frac{1}{2}x−3\)
• \(y=−3x+7\)
• \(y=−\frac{5}{8}x−12\)
• \(y=\frac{7}{3}x+\frac{3}{2}\)
• \(y=9x−25\)
• \(y=−10x+15\)
• \(x=−12\)
• \(x−y=0\)
• \(4x+3y=0\)
• \(3x−5y=10\)
• \(−2x+7y=14\)
• \(−x−y=\frac{1}{5}\)
• \(\frac{1}{2}x−\frac{1}{3}y=−1\)
• \(−\frac{2}{3}x+\frac{4}{5}y=8\)
• \(2x−\frac{1}{5}y=\frac{1}{10}\)
• \(−\frac{4}{5}x−2y=7\)

1. \(m_{∥}=−\frac{3}{4}\) and \(m_{⊥}=\frac{4}{3}\)

3. \(m_{∥}=4\) and \(m_{⊥}=−\frac{1}{4}\)

5. \(m_{∥}=−\frac{5}{8}\) and \(m_{⊥}=\frac{8}{5}\)

7. \(m_{∥}=9\) and \(m_{⊥}=−\frac{1}{9}\)

9. \(m_{∥}=0\) and \(m_{⊥}\) undefined

11. \(m_{∥}=1\) and \(m_{⊥}=−1\)

13. \(m_{∥}=−\frac{4}{3}\) and \(m_{⊥}=\frac{3}{4}\)

15. \(m_{∥}=\frac{2}{7}\) and \(m_{⊥}=−\frac{7}{2}\)

17. \(m_{∥}=\frac{3}{2}\) and \(m_{⊥}=−\frac{2}{3}\)

19. \(m_{∥}=10\) and \(m_{⊥}=−\frac{1}{10}\)

Exercise \(\PageIndex{4}\) Parallel and Perpendicular Lines

Determine if the lines are parallel, perpendicular, or neither.

• \(\left\{\begin{aligned}y&=\frac{2}{3}x+3\\y&=\frac{2}{3}x−3\end{aligned}\right.\)
• \(\left\{\begin{aligned}y&=\frac{3}{4}x−1\\y&=\frac{4}{3}x+3\end{aligned}\right.\)
• \(\left\{\begin{aligned}y&=−2x+1\\ y&=\frac{1}{2}x+8\end{aligned}\right.\)
• \(\left\{\begin{aligned}y&=3x−\frac{1}{2}\\ y&=3x+2\end{aligned}\right.\)
• \(\left\{\begin{aligned}y&=5\\x&=−2\end{aligned}\right.\)
• \(\left\{\begin{aligned}y&=7\\y&=−\frac{1}{7}\end{aligned}\right.\)
• \(\left\{\begin{aligned}3x−5y&=15\\ 5x+3y&=9\end{aligned}\right.\)
• \(\left\{\begin{aligned}x−y&=7\\3x+3y&=2\end{aligned}\right.\)
• \(\left\{\begin{aligned}2x−6y&=4\\−x+3y&=−2 \end{aligned}\right.\)
• \(\left\{\begin{aligned}−4x+2y&=3\\6x−3y&=−3 \end{aligned}\right.\)
• \(\left\{\begin{aligned}x+3y&=9\\2x+3y&=6 \end{aligned}\right.\)
• \(\left\{\begin{aligned}y−10&=0\\x−10&=0 \end{aligned}\right.\)
• \(\left\{\begin{aligned}y+2&=0\\2y−10&=0 \end{aligned}\right.\)
• \(\left\{\begin{aligned}3x+2y&=6\\2x+3y&=6 \end{aligned}\right.\)
• \(\left\{\begin{aligned}−5x+4y&=20\\10x−8y&=16 \end{aligned}\right.\)
• \(\left\{\begin{aligned}\frac{1}{2}x−\frac{1}{3}y&=1\\\frac{1}{6}x+\frac{1}{4}y&=−2\end{aligned}\right.\)

1. Parallel

3. Perpendicular

5. Perpendicular

7. Perpendicular

9. Parallel

11. Neither

13. Parallel

15. Parallel

Exercise \(\PageIndex{5}\) Equations in Point-Slope Form

Find the equation of the line

• Parallel to \(y=\frac{1}{2}x+2\) and passing through \((6, −1)\).
• Parallel to \(y=−\frac{3}{4}x−3\) and passing through \((−8, 2)\).
• Perpendicular to \(y=3x−1\) and passing through \((−3, 2)\).
• Perpendicular to \(y=−\frac{1}{3}x+2\) and passing through \((4, −3)\).
• Perpendicular to \(y=−2\) and passing through \((−1, 5)\).
• Perpendicular to \(x=\frac{1}{5}\) and passing through \((5, −3)\).
• Parallel to \(y=3\) and passing through \((2, 4)\).
• Parallel to \(x=2\) and passing through (7, −3)\).
• Perpendicular to \(y=x\) and passing through \((7, −13)\).
• Perpendicular to \(y=2x+9\) and passing through \((3, −1)\).
• Parallel to \(y=\frac{1}{4}x−5\) and passing through \((−2, 1)\).
• Parallel to \(y=−\frac{3}{4}x+1\) and passing through \((4, \frac{1}{4})\).
• Parallel to \(2x−3y=6\) and passing through \((6, −2)\).
• Parallel to \(−x+y=4\) and passing through \((9, 7)\).
• Perpendicular to \(5x−3y=18\) and passing through \((−9, 10)\).
• Perpendicular to \(x−y=11\) and passing through \((6, −8)\).
• Parallel to \(\frac{1}{5}x−\frac{1}{3}y=2\) and passing through \((−15, 6)\).
• Parallel to \(−10x−\frac{5}{7}y=12\) and passing through \((−1, \frac{1}{2})\).
• Perpendicular to \(\frac{1}{2}x−\frac{1}{3}y=1\) and passing through \((−10, 3)\).
• Perpendicular to \(−5x+y=−1\) and passing through \((−4, 0)\).
• Parallel to \(x+4y=8\) and passing through \((−1, −2)\).
• Parallel to \(7x−5y=35\) and passing through \((2, −3)\).
• Perpendicular to \(6x+3y=1\) and passing through \((8, −2)\).
• Perpendicular to \(−4x−5y=1\) and passing through \((−1, −1)\).
• Parallel to \(−5x−2y=4\) and passing through \((\frac{1}{5}, −\frac{1}{4})\).
• Parallel to \(6x−\frac{3}{2}y=9\) and passing through \((\frac{1}{3}, \frac{2}{3})\).
• Perpendicular to \(y−3=0\) and passing through \((−6, 12)\).
• Perpendicular to \(x+7=0\) and passing through \((5, −10)\).

1. \(y=\frac{1}{2}x−4\)

3. \(y=−\frac{1}{3}x+1\)

5. \(x=−1\)

9. \(y=−x−6\)

11. \(y=\frac{1}{4}x+\frac{3}{2}\)

13. \(y=\frac{2}{3}x−6\)

15. \(y=−\frac{3}{5}x+\frac{23}{5}\)

17. \(y=\frac{3}{5}x+15\)

19. \(y=−\frac{2}{3}x−\frac{11}{3}\)

21. \(y=−\frac{1}{4}x−\frac{9}{4}\)

23. \(y=\frac{1}{2}x−6\)

25. \(y=−\frac{5}{2}x+\frac{1}{4}\)

27. \(x=−6\)

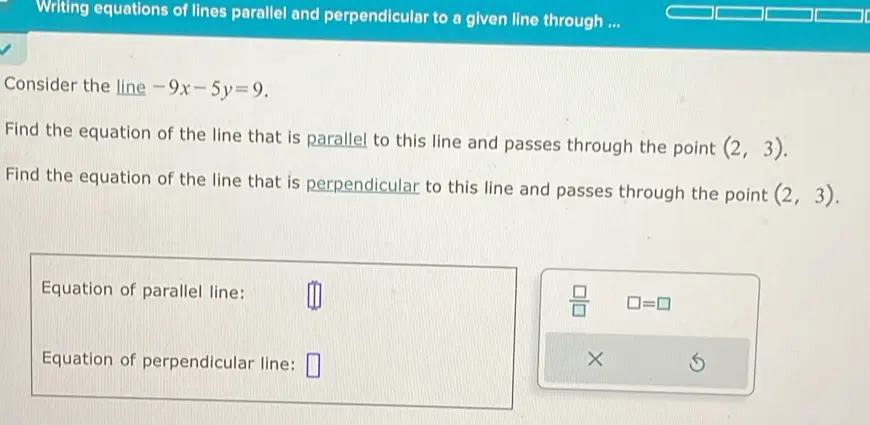
Writing equations of lines parallel and perpendicular to a given line through ... Consider the line -9x-5y=9. Find the equation of the line that is parallel to this line and passes through the point (2,3). Find the equation of the line that is perpendicular to this line and passes through the point (2,3). Equation of parallel line: □ /□ □ =□ Equation of perpendicular line: ×

Expert verified solution.