hypothesis test for normal distribution

Find Study Materials for

• Business Studies
• Combined Science
• Computer Science
• Engineering
• English Literature
• Environmental Science
• Human Geography
• Macroeconomics
• Microeconomics
• Social Studies
• Browse all subjects
• Read our Magazine

Create Study Materials

Hypothesis tests for the normal distribution can be conducted in a very similar way to binomial distribution , e xcept this time we switch our test statistic.  These tests are useful as again they help us test claims of normally distributed items.

Explore our app and discover over 50 million learning materials for free.

• Normal Distribution Hypothesis Test
• Explanations
• StudySmarter AI
• Textbook Solutions
• Applied Mathematics
• Decision Maths
• Discrete Mathematics
• Logic and Functions
• Mechanics Maths
• Probability and Statistics
• Bayesian Statistics
• Bias in Experiments
• Binomial Distribution
• Binomial Hypothesis Test
• Biostatistics
• Bivariate Data
• Categorical Data Analysis
• Categorical Variables
• Causal Inference
• Central Limit Theorem
• Chi Square Test for Goodness of Fit
• Chi Square Test for Homogeneity
• Chi Square Test for Independence
• Chi-Square Distribution
• Cluster Analysis
• Combining Random Variables
• Comparing Data
• Comparing Two Means Hypothesis Testing
• Conditional Probability
• Conducting A Study
• Conducting a Survey
• Conducting an Experiment
• Confidence Interval for Population Mean
• Confidence Interval for Population Proportion
• Confidence Interval for Slope of Regression Line
• Confidence Interval for the Difference of Two Means
• Confidence Intervals
• Correlation Math
• Cox Regression
• Cumulative Distribution Function
• Cumulative Frequency
• Data Analysis
• Data Interpretation
• Decision Theory
• Degrees of Freedom
• Discrete Random Variable
• Discriminant Analysis
• Distributions
• Empirical Bayes Methods
• Empirical Rule
• Errors In Hypothesis Testing
• Estimation Theory
• Estimator Bias
• Events (Probability)
• Experimental Design
• Factor Analysis
• Frequency Polygons
• Generalization and Conclusions
• Geometric Distribution
• Geostatistics
• Hierarchical Modeling
• Hypothesis Test for Correlation
• Hypothesis Test for Regression Slope
• Hypothesis Test of Two Population Proportions
• Hypothesis Testing
• Inference For Distributions Of Categorical Data
• Inferences in Statistics
• Item Response Theory
• Kaplan-Meier Estimate
• Kernel Density Estimation
• Large Data Set
• Lasso Regression
• Latent Variable Models
• Least Squares Linear Regression
• Linear Interpolation
• Linear Regression
• Logistic Regression
• Machine Learning
• Mann-Whitney Test
• Markov Chains
• Mean and Variance of Poisson Distributions
• Measures of Central Tendency
• Methods of Data Collection
• Mixed Models
• Multilevel Modeling
• Multivariate Analysis
• Neyman-Pearson Lemma
• Non-parametric Methods
• Normal Distribution
• Normal Distribution Percentile
• Ordinal Regression
• Paired T-Test
• Parametric Methods
• Path Analysis
• Point Estimation
• Poisson Regression
• Principle Components Analysis
• Probability
• Probability Calculations
• Probability Density Function
• Probability Distribution
• Probability Generating Function
• Product Moment Correlation Coefficient
• Quantile Regression
• Quantitative Variables
• Random Effects Model
• Random Variables
• Randomized Block Design
• Regression Analysis
• Residual Sum of Squares
• Robust Statistics
• Sample Mean
• Sample Proportion
• Sampling Distribution
• Sampling Theory
• Scatter Graphs
• Sequential Analysis
• Single Variable Data
• Spearman's Rank Correlation
• Spearman's Rank Correlation Coefficient
• Standard Deviation
• Standard Error
• Standard Normal Distribution
• Statistical Graphs
• Statistical Inference
• Statistical Measures
• Stem and Leaf Graph
• Stochastic Processes
• Structural Equation Modeling
• Sum of Independent Random Variables
• Survey Bias
• Survival Analysis
• Survivor Function
• T-distribution
• The Power Function
• Time Series Analysis
• Transforming Random Variables
• Tree Diagram
• Two Categorical Variables
• Two Quantitative Variables
• Type I Error
• Type II Error
• Types of Data in Statistics
• Variance for Binomial Distribution
• Venn Diagrams
• Wilcoxon Test
• Zero-Inflated Models
• Theoretical and Mathematical Physics

Lerne mit deinen Freunden und bleibe auf dem richtigen Kurs mit deinen persönlichen Lernstatistiken

Nie wieder prokastinieren mit unseren Lernerinnerungen.

Hypothesis tests for the normal distribution can be conducted in a very similar way to binomial distribution , e xcept this time we switch our test statistic. These tests are useful as again they help us test claims of normally distributed items.

How do we carry out a hypothesis test for normal distribution?

When we hypothesis test for the mean of a normal distribution we think about looking at the mean of a sample from a population.

So for a random sample of size n of a population, taken from the random variable \(X \sim N(\mu, \sigma^2)\) , the sample mean \(\bar{X}\) can be normally distributed by \(\bar{X} \sim N(\mu, \frac{\sigma^2}{n})\) .

Let's look at an example.

The weight of crisps is each packet is normally distributed with a standard deviation of 2.5g.

The crisp company claims that the crisp packets have a mean weight of 28g. There were numerous complaints that each crisp packet weighs less than this. Therefore a trading inspector investigated this and found in a sample of 50 crisp packets, the mean weight was 27.2g.

Using a 5% significance level and stating the hypothesis, clearly test whether or not the evidence upholds the complaints.

This is an example of a one tailed test. Let's look at an example of a two tailed test.

A machine produces circular discs with a radius R, where R is normally distributed with a mean of 2cm and a standard deviation of 0.3cm.

The machine is serviced and after the service, a random sample of 40 discs is taken to see if the mean has changed from 2cm. The radius is still normally distributed with a standard deviation of 0.3 cm.

The mean is found to be 1.9cm.

Has the mean changed? Test this to a 5% significance level.

Step 5 may be confusing – do we carry out the calculation with \(P(\bar{X} \leq \bar{x})\) or \(P(\bar{X} \geq \bar{x})\)? As a general rule of thumb if the value is between 0 and the mean, then we use \(P(\bar{X} \leq \bar{x})\) . If it is greater than the mean then we use \(P(\bar{X} \geq \bar{x})\) .

How about finding critical values and critical regions?

This is the same idea as in binomial distribution . However, in normal distribution, a calculator can make our lives easier.

The distributions menu has an option called inverse normal.

Here, we enter the significance level (Area), the mean (\(\mu\) ) and the standard deviation (\(\sigma\) ).

The calculator will give us an answer. Let's have a look at an example below.

Wheels are made to measure for a bike. The diameter of the wheel is normally distributed with a mean of 40cm and a standard deviation of 5cm. Some people think that their wheels are too small. Find the critical value of this to a 5% significance level.

In our calculator, in the inverse normal function, we need to enter:

If we perform the inverse normal function we get 31.775732 .

So that is our critical value and our critical region is \(X \leq 31.775732\) .

Let's look at an example with two tails.

Hypothesis Test for Normal Distribution - Key takeaways

• When we hypothesis test for a normal distribution we are trying to see if the mean is different from the mean stated in the null hypothesis.
• We use the sample mean which is \(\bar{X} \sim N(\mu, \frac{\sigma^2}{n})\) .
• In two-tailed tests we divide the significance level by two and test on both tails.
• When finding critical values we use the calculator inverse normal function entering the area as the significance level.
• For two-tailed tests we need to find two critical values on either end of the distribution.

Frequently Asked Questions about Normal Distribution Hypothesis Test

--> how do you test a hypothesis for a normal distribution, --> is hypothesis testing only for a normal distribution.

No, pretty much any distribution can be used when testing a hypothesis. The two distributions that you learn at A-Level are Normal and Binomial.

--> What statistical hypothesis can be tested in the means of a normal distribution?

We test whether or not the data can support the value of a mean being too low or too high.

What is our test statistic with normal distribution?

What calculator tool do we use to work backwards with normal distribution?

The Inverse Normal

A coach thinks his athletes will achieve less than 12 seconds in their 100 metre race. His assistant thinks they won't be this fast. If this claim was tested is this a one or two-tailed test?

One-tailed test

How do we find the critical region of a normal distribution?

By using the calculator inverse normal setting.

Learn with 4 Normal Distribution Hypothesis Test flashcards in the free StudySmarter app

Already have an account? Log in

of the users don't pass the Normal Distribution Hypothesis Test quiz! Will you pass the quiz?

How would you like to learn this content?

Free math cheat sheet!

Everything you need to know on . A perfect summary so you can easily remember everything.

Join over 22 million students in learning with our StudySmarter App

The first learning app that truly has everything you need to ace your exams in one place

• Flashcards & Quizzes
• AI Study Assistant
• Study Planner
• Smart Note-Taking

Sign up to highlight and take notes. It’s 100% free.

This is still free to read, it's not a paywall.

You need to register to keep reading, create a free account to save this explanation..

Save explanations to your personalised space and access them anytime, anywhere!

By signing up, you agree to the Terms and Conditions and the Privacy Policy of StudySmarter.

Entdecke Lernmaterial in der StudySmarter-App

7.4.1 - Hypothesis Testing

Five step hypothesis testing procedure.

In the remaining lessons, we will use the following five step hypothesis testing procedure. This is slightly different from the five step procedure that we used when conducting randomization tests. 

• Check assumptions and write hypotheses.  The assumptions will vary depending on the test. In this lesson we'll be confirming that the sampling distribution is approximately normal by visually examining the randomization distribution. In later lessons you'll learn more objective assumptions. The null and alternative hypotheses will always be written in terms of population parameters; the null hypothesis will always contain the equality (i.e., \(=\)).
• Calculate the test statistic.  Here, we'll be using the formula below for the general form of the test statistic.
• Determine the p-value.  The p-value is the area under the standard normal distribution that is more extreme than the test statistic in the direction of the alternative hypothesis.
• Make a decision.  If \(p \leq \alpha\) reject the null hypothesis. If \(p>\alpha\) fail to reject the null hypothesis.
• State a "real world" conclusion.  Based on your decision in step 4, write a conclusion in terms of the original research question.

General Form of a Test Statistic

When using a standard normal distribution (i.e., z distribution), the test statistic is the standardized value that is the boundary of the p-value. Recall the formula for a z score: \(z=\frac{x-\overline x}{s}\). The formula for a test statistic will be similar. When conducting a hypothesis test the sampling distribution will be centered on the null parameter and the standard deviation is known as the standard error.

This formula puts our observed sample statistic on a standard scale (e.g., z distribution). A z score tells us where a score lies on a normal distribution in standard deviation units. The test statistic tells us where our sample statistic falls on the sampling distribution in standard error units.

7.4.1.1 - Video Example: Mean Body Temperature

Research question:  Is the mean body temperature in the population different from 98.6° Fahrenheit?

7.4.1.2 - Video Example: Correlation Between Printer Price and PPM

Research question:  Is there a positive correlation in the population between the price of an ink jet printer and how many pages per minute (ppm) it prints?

7.4.1.3 - Example: Proportion NFL Coin Toss Wins

Research question:  Is the proportion of NFL overtime coin tosses that are won different from 0.50?

StatKey was used to construct a randomization distribution:

Step 1: Check assumptions and write hypotheses

From the given StatKey output, the randomization distribution is approximately normal.

\(H_0\colon p=0.50\)

\(H_a\colon p \ne 0.50\)

Step 2: Calculate the test statistic

\(test\;statistic=\dfrac{sample\;statistic-null\;parameter}{standard\;error}\)

The sample statistic is the proportion in the original sample, 0.561. The null parameter is 0.50. And, the standard error is 0.024.

\(test\;statistic=\dfrac{0.561-0.50}{0.024}=\dfrac{0.061}{0.024}=2.542\)

Step 3: Determine the p value

The p value will be the area on the z distribution that is more extreme than the test statistic of 2.542, in the direction of the alternative hypothesis. This is a two-tailed test:

The p value is the area in the left and right tails combined: \(p=0.0055110+0.0055110=0.011022\)

Step 4: Make a decision

The p value (0.011022) is less than the standard 0.05 alpha level, therefore we reject the null hypothesis.

Step 5: State a "real world" conclusion

There is evidence that the proportion of all NFL overtime coin tosses that are won is different from 0.50

7.4.1.4 - Example: Proportion of Women Students

Research question : Are more than 50% of all World Campus STAT 200 students women?

Data were collected from a representative sample of 501 World Campus STAT 200 students. In that sample, 284 students were women and 217 were not women. 

StatKey was used to construct a sampling distribution using randomization methods:

Because this randomization distribution is approximately normal, we can find the p value by computing a standardized test statistic and using the z distribution.

The assumption here is that the sampling distribution is approximately normal. From the given StatKey output, the randomization distribution is approximately normal. 

\(H_0\colon p=0.50\) \(H_a\colon p>0.50\)

2. Calculate the test statistic

\(test\;statistic=\dfrac{sample\;statistic-hypothesized\;parameter}{standard\;error}\)

The sample statistic is \(\widehat p = 284/501 = 0.567\).

The hypothesized parameter is the value from the hypotheses: \(p_0=0.50\).

The standard error on the randomization distribution above is 0.022.

\(test\;statistic=\dfrac{0.567-0.50}{0.022}=3.045\)

3. Determine the p value

We can find the p value by constructing a standard normal distribution and finding the area under the curve that is more extreme than our observed test statistic of 3.045, in the direction of the alternative hypothesis. In other words, \(P(z>3.045)\):

Our p value is 0.0011634

4. Make a decision

Our p value is less than or equal to the standard 0.05 alpha level, therefore we reject the null hypothesis.

5. State a "real world" conclusion

There is evidence that the proportion of all World Campus STAT 200 students who are women is greater than 0.50.

7.4.1.5 - Example: Mean Quiz Score

Research question:  Is the mean quiz score different from 14 in the population?

\(H_0\colon \mu = 14\)

\(H_a\colon \mu \ne 14\)

The sample statistic is the mean in the original sample, 13.746 points. The null parameter is 14 points. And, the standard error, 0.142, can be found on the StatKey output.

\(test\;statistic=\dfrac{13.746-14}{0.142}=\dfrac{-0.254}{0.142}=-1.789\)

The p value will be the area on the z distribution that is more extreme than the test statistic of -1.789, in the direction of the alternative hypothesis:

This was a two-tailed test. The p value is the area in the left and right tails combined: \(p=0.0368074+0.0368074=0.0736148\)

The p value (0.0736148) is greater than the standard 0.05 alpha level, therefore we fail to reject the null hypothesis.

There is not enough evidence to state that the mean quiz score in the population is different from 14 points. 

7.4.1.6 - Example: Difference in Mean Commute Times

Research question:  Do the mean commute times in Atlanta and St. Louis differ in the population? 

 From the given StatKey output, the randomization distribution is approximately normal.

\(H_0: \mu_1-\mu_2=0\)

\(H_a: \mu_1 - \mu_2 \ne 0\)

Step 2: Compute the test statistic

\(test\;statistic=\dfrac{sample\;statistic - null \; parameter}{standard \;error}\)

The observed sample statistic is \(\overline x _1 - \overline x _2 = 7.14\). The null parameter is 0. And, the standard error, from the StatKey output, is 1.136.

\(test\;statistic=\dfrac{7.14-0}{1.136}=6.285\)

The p value will be the area on the z distribution that is more extreme than the test statistic of 6.285, in the direction of the alternative hypothesis:

This was a two-tailed test. The area in the two tailed combined is 0.000000. Theoretically, the p value cannot be 0 because there is always some chance that a Type I error was committed. This p value would be written as p < 0.001.

The p value is smaller than the standard 0.05 alpha level, therefore we reject the null hypothesis. 

There is evidence that the mean commute times in Atlanta and St. Louis are different in the population. 

9.3 Probability Distribution Needed for Hypothesis Testing

Earlier in the course, we discussed sampling distributions. Particular distributions are associated with various types of hypothesis testing.

The following table summarizes various hypothesis tests and corresponding probability distributions that will be used to conduct the test (based on the assumptions shown below):

Assumptions

When you perform a hypothesis test of a single population mean μ using a normal distribution (often called a z-test), you take a simple random sample from the population. The population you are testing is normally distributed , or your sample size is sufficiently large. You know the value of the population standard deviation , which, in reality, is rarely known.

When you perform a hypothesis test of a single population mean μ using a Student's t-distribution (often called a t -test), there are fundamental assumptions that need to be met in order for the test to work properly. Your data should be a simple random sample that comes from a population that is approximately normally distributed. You use the sample standard deviation to approximate the population standard deviation. (Note that if the sample size is sufficiently large, a t -test will work even if the population is not approximately normally distributed).

When you perform a hypothesis test of a single population proportion p , you take a simple random sample from the population. You must meet the conditions for a binomial distribution : there are a certain number n of independent trials, the outcomes of any trial are success or failure, and each trial has the same probability of a success p . The shape of the binomial distribution needs to be similar to the shape of the normal distribution. To ensure this, the quantities np and nq must both be greater than five ( n p > 5   n p > 5   and n q > 5   n q > 5   ). Then the binomial distribution of a sample (estimated) proportion can be approximated by the normal distribution with μ = p   μ = p   and σ = p q n σ = p q n . Remember that q = 1 - p q q = 1 - p q .

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/introductory-statistics-2e/pages/1-introduction

• Authors: Barbara Illowsky, Susan Dean
• Publisher/website: OpenStax
• Book title: Introductory Statistics 2e
• Publication date: Dec 13, 2023
• Location: Houston, Texas
• Book URL: https://openstax.org/books/introductory-statistics-2e/pages/1-introduction
• Section URL: https://openstax.org/books/introductory-statistics-2e/pages/9-3-probability-distribution-needed-for-hypothesis-testing

© Dec 6, 2023 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Hypothesis Testing with the Normal Distribution

Contents Toggle Main Menu 1 Introduction 2 Test for Population Mean 3 Worked Example 3.1 Video Example 4 Approximation to the Binomial Distribution 5 Worked Example 6 Comparing Two Means 7 Workbooks 8 See Also

Introduction

When constructing a confidence interval with the standard normal distribution, these are the most important values that will be needed.

Distribution of Sample Means

where $\mu$ is the true mean and $\mu_0$ is the current accepted population mean. Draw samples of size $n$ from the population. When $n$ is large enough and the null hypothesis is true the sample means often follow a normal distribution with mean $\mu_0$ and standard deviation $\frac{\sigma}{\sqrt{n}}$. This is called the distribution of sample means and can be denoted by $\bar{X} \sim \mathrm{N}\left(\mu_0, \frac{\sigma}{\sqrt{n}}\right)$. This follows from the central limit theorem .

The $z$-score will this time be obtained with the formula \[Z = \dfrac{\bar{X} - \mu_0}{\frac{\sigma}{\sqrt{n}}}.\]

So if $\mu = \mu_0, X \sim \mathrm{N}\left(\mu_0, \frac{\sigma}{\sqrt{n}}\right)$ and $ Z \sim \mathrm{N}(0,1)$.

The alternative hypothesis will then take one of the following forms: depending on what we are testing.

Worked Example

An automobile company is looking for fuel additives that might increase gas mileage. Without additives, their cars are known to average $25$ mpg (miles per gallons) with a standard deviation of $2.4$ mpg on a road trip from London to Edinburgh. The company now asks whether a particular new additive increases this value. In a study, thirty cars are sent on a road trip from London to Edinburgh. Suppose it turns out that the thirty cars averaged $\overline{x}=25.5$ mpg with the additive. Can we conclude from this result that the additive is effective?

We are asked to show if the new additive increases the mean miles per gallon. The current mean $\mu = 25$ so the null hypothesis will be that nothing changes. The alternative hypothesis will be that $\mu > 25$ because this is what we have been asked to test.

\begin{align} &H_0:\mu=25. \\ &H_1:\mu>25. \end{align}

Now we need to calculate the test statistic. We start with the assumption the normal distribution is still valid. This is because the null hypothesis states there is no change in $\mu$. Thus, as the value $\sigma=2.4$ mpg is known, we perform a hypothesis test with the standard normal distribution. So the test statistic will be a $z$ score. We compute the $z$ score using the formula \[z=\frac{\bar{x}-\mu}{\frac{\sigma}{\sqrt{n} } }.\] So \begin{align} z&=\frac{\overline{x}-25}{\frac{2.4}{\sqrt{30} } }\\ &=1.14 \end{align}

We are using a $5$% significance level and a (right-sided) one-tailed test, so $\alpha=0.05$ so from the tables we obtain $z_{1-\alpha} = 1.645$ is our test statistic.

As $1.14<1.645$, the test statistic is not in the critical region so we cannot reject $H_0$. Thus, the observed sample mean $\overline{x}=25.5$ is consistent with the hypothesis $H_0:\mu=25$ on a $5$% significance level.

Video Example

In this video, Dr Lee Fawcett explains how to conduct a hypothesis test for the mean of a single distribution whose variance is known, using a one-sample z-test.

Approximation to the Binomial Distribution

A supermarket has come under scrutiny after a number of complaints that its carrier bags fall apart when the load they carry is $5$kg. Out of a random sample of $200$ bags, $185$ do not tear when carrying a load of $5$kg. Can the supermarket claim at a $5$% significance level that more that $90$% of the bags will not fall apart?

Let $X$ represent the number of carrier bags which can hold a load of $5$kg. Then $X \sim \mathrm{Bin}(200,p)$ and \begin{align}H_0&: p = 0.9 \\ H_1&: p > 0.9 \end{align}

We need to calculate the mean $\mu$ and variance $\sigma ^2$.

\[\mu = np = 200 \times 0.9 = 180\text{.}\] \[\sigma ^2= np(1-p) = 18\text{.}\]

Using the normal approximation to the binomial distribution we obtain $Y \sim \mathrm{N}(180, 18)$.

\[\mathrm{P}[X \geq 185] = \mathrm{P}\left[Z \geq \dfrac{184.5 - 180}{4.2426} \right] = \mathrm{P}\left[Z \geq 1.0607\right] \text{.}\]

Because we are using a one-tailed test at a $5$% significance level, we obtain the critical value $Z=1.645$. Now $1.0607 < 1.645$ so we cannot accept the alternative hypothesis. It is not true that over $90$% of the supermarket's carrier bags are capable of withstanding a load of $5$kg.

Comparing Two Means

When we test hypotheses with two means, we will look at the difference $\mu_1 - \mu_2$. The null hypothesis will be of the form

where $a$ is a constant. Often $a=0$ is used to test if the two means are the same. Given two continuous random variables $X_1$ and $X_2$ with means $\mu_1$ and $\mu_2$ and variances $\frac{\sigma_1^2}{n_1}$ and $\frac{\sigma_2^2}{n_2}$ respectively \[\mathrm{E} [\bar{X_1} - \bar{X_2} ] = \mathrm{E} [\bar{X_1}] - \mathrm{E} [\bar{X_2}] = \mu_1 - \mu_2\] and \[\mathrm{Var}[\bar{X_1} - \bar{X_2}] = \mathrm{Var}[\bar{X_1}] - \mathrm{Var}[\bar{X_2}]=\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}\text{.}\] Note this last result, the difference of the variances is calculated by summing the variances.

We then obtain the $z$-score using the formula \[Z = \frac{(\bar{X_1}-\bar{X_2})-(\mu_1 - \mu_2)}{\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}\text{.}\]

These workbooks produced by HELM are good revision aids, containing key points for revision and many worked examples.

• Tests concerning a single sample
• Tests concerning two samples

Selecting a Hypothesis Test

An Introduction to Bayesian Thinking

Chapter 5 hypothesis testing with normal populations.

In Section 3.5 , we described how the Bayes factors can be used for hypothesis testing. Now we will use the Bayes factors to compare normal means, i.e., test whether the mean of a population is zero or compare the means of two groups of normally-distributed populations. We divide this mission into three cases: known variance for a single population, unknown variance for a single population using paired data, and unknown variance using two independent groups.

Also note that some of the examples in this section use an updated version of the bayes_inference function. If your local output is different from what is seen in this chapter, or the provided code fails to run for you please make sure that you have the most recent version of the package.

5.1 Bayes Factors for Testing a Normal Mean: variance known

Now we show how to obtain Bayes factors for testing hypothesis about a normal mean, where the variance is known . To start, let’s consider a random sample of observations from a normal population with mean \(\mu\) and pre-specified variance \(\sigma^2\) . We consider testing whether the population mean \(\mu\) is equal to \(m_0\) or not.

Therefore, we can formulate the data and hypotheses as below:

Data \[Y_1, \cdots, Y_n \mathrel{\mathop{\sim}\limits^{\rm iid}}\textsf{Normal}(\mu, \sigma^2)\]

• \(H_1: \mu = m_0\)
• \(H_2: \mu \neq m_0\)

We also need to specify priors for \(\mu\) under both hypotheses. Under \(H_1\) , we assume that \(\mu\) is exactly \(m_0\) , so this occurs with probability 1 under \(H_1\) . Now under \(H_2\) , \(\mu\) is unspecified, so we describe our prior uncertainty with the conjugate normal distribution centered at \(m_0\) and with a variance \(\sigma^2/\mathbf{n_0}\) . This is centered at the hypothesized value \(m_0\) , and it seems that the mean is equally likely to be larger or smaller than \(m_0\) , so a dividing factor \(n_0\) is given to the variance. The hyper parameter \(n_0\) controls the precision of the prior as before.

In mathematical terms, the priors are:

• \(H_1: \mu = m_0 \text{ with probability 1}\)
• \(H_2: \mu \sim \textsf{Normal}(m_0, \sigma^2/\mathbf{n_0})\)

Bayes Factor

Now the Bayes factor for comparing \(H_1\) to \(H_2\) is the ratio of the distribution, the data under the assumption that \(\mu = m_0\) to the distribution of the data under \(H_2\) .

\[\begin{aligned} \textit{BF}[H_1 : H_2] &= \frac{p(\text{data}\mid \mu = m_0, \sigma^2 )} {\int p(\text{data}\mid \mu, \sigma^2) p(\mu \mid m_0, \mathbf{n_0}, \sigma^2)\, d \mu} \\ \textit{BF}[H_1 : H_2] &=\left(\frac{n + \mathbf{n_0}}{\mathbf{n_0}} \right)^{1/2} \exp\left\{-\frac 1 2 \frac{n }{n + \mathbf{n_0}} Z^2 \right\} \\ Z &= \frac{(\bar{Y} - m_0)}{\sigma/\sqrt{n}} \end{aligned}\]

The term in the denominator requires integration to account for the uncertainty in \(\mu\) under \(H_2\) . And it can be shown that the Bayes factor is a function of the observed sampled size, the prior sample size \(n_0\) and a \(Z\) score.

Let’s explore how the hyperparameters in \(n_0\) influences the Bayes factor in Equation (5.1) . For illustration we will use the sample size of 100. Recall that for estimation, we interpreted \(n_0\) as a prior sample size and considered the limiting case where \(n_0\) goes to zero as a non-informative or reference prior.

\[\begin{equation} \textsf{BF}[H_1 : H_2] = \left(\frac{n + \mathbf{n_0}}{\mathbf{n_0}}\right)^{1/2} \exp\left\{-\frac{1}{2} \frac{n }{n + \mathbf{n_0}} Z^2 \right\} \tag{5.1} \end{equation}\]

Figure 5.1 shows the Bayes factor for comparing \(H_1\) to \(H_2\) on the y-axis as \(n_0\) changes on the x-axis. The different lines correspond to different values of the \(Z\) score or how many standard errors \(\bar{y}\) is from the hypothesized mean. As expected, larger values of the \(Z\) score favor \(H_2\) .

Figure 5.1: Vague prior for mu: n=100

But as \(n_0\) becomes smaller and approaches 0, the first term in the Bayes factor goes to infinity, while the exponential term involving the data goes to a constant and is ignored. In the limit as \(n_0 \rightarrow 0\) under this noninformative prior, the Bayes factor paradoxically ends up favoring \(H_1\) regardless of the value of \(\bar{y}\) .

The takeaway from this is that we cannot use improper priors with \(n_0 = 0\) , if we are going to test our hypothesis that \(\mu = n_0\) . Similarly, vague priors that use a small value of \(n_0\) are not recommended due to the sensitivity of the results to the choice of an arbitrarily small value of \(n_0\) .

This problem arises with vague priors – the Bayes factor favors the null model \(H_1\) even when the data are far away from the value under the null – are known as the Bartlett’s paradox or the Jeffrey’s-Lindleys paradox.

Now, one way to understand the effect of prior is through the standard effect size

\[\delta = \frac{\mu - m_0}{\sigma}.\] The prior of the standard effect size is

\[\delta \mid H_2 \sim \textsf{Normal}(0, \frac{1}{\mathbf{n_0}})\]

This allows us to think about a standardized effect independent of the units of the problem. One default choice is using the unit information prior, where the prior sample size \(n_0\) is 1, leading to a standard normal for the standardized effect size. This is depicted with the blue normal density in Figure 5.2 . This suggested that we expect that the mean will be within \(\pm 1.96\) standard deviations of the hypothesized mean with probability 0.95 . (Note that we can say this only under a Bayesian setting.)

In many fields we expect that the effect will be small relative to \(\sigma\) . If we do not expect to see large effects, then we may want to use a more informative prior on the effect size as the density in orange with \(n_0 = 4\) . So they expected the mean to be within \(\pm 1/\sqrt{n_0}\) or five standard deviations of the prior mean.

Figure 5.2: Prior on standard effect size

Example 1.1 To illustrate, we give an example from parapsychological research. The case involved the test of the subject’s claim to affect a series of randomly generated 0’s and 1’s by means of extra sensory perception (ESP). The random sequence of 0’s and 1’s are generated by a machine with probability of generating 1 being 0.5. The subject claims that his ESP would make the sample mean differ significantly from 0.5.

Therefore, we are testing \(H_1: \mu = 0.5\) versus \(H_2: \mu \neq 0.5\) . Let’s use a prior that suggests we do not expect a large effect which leads the following solution for \(n_0\) . Assume we want a standard effect of 0.03, there is a 95% chance that it is between \((-0.03/\sigma, 0.03/\sigma)\) , with \(n_0 = (1.96\sigma/0.03)^2 = 32.7^2\) .

Figure 5.3 shows our informative prior in blue, while the unit information prior is in orange. On this scale, the unit information prior needs to be almost uniform for the range that we are interested.

Figure 5.3: Prior effect in the extra sensory perception test

A very large data set with over 104 million trials was collected to test this hypothesis, so we use a normal distribution to approximate the distribution the sample mean.

• Sample size: \(n = 1.0449 \times 10^8\)
• Sample mean: \(\bar{y} = 0.500177\) , standard deviation \(\sigma = 0.5\)
• \(Z\) -score: 3.61

Now using our prior in the data, the Bayes factor for \(H_1\) to \(H_2\) was 0.46, implying evidence against the hypothesis \(H_1\) that \(\mu = 0.5\) .

• Informative \(\textit{BF}[H_1:H_2] = 0.46\)
• \(\textit{BF}[H_2:H_1] = 1/\textit{BF}[H_1:H_2] = 2.19\)

Now, this can be inverted to provide the evidence in favor of \(H_2\) . The evidence suggests that the hypothesis that the machine operates with a probability that is not 0.5, is 2.19 times more likely than the hypothesis the probability is 0.5. Based on the interpretation of Bayes factors from Table 3.5 , this is in the range of “not worth the bare mention”.

To recap, we present expressions for calculating Bayes factors for a normal model with a specified variance. We show that the improper reference priors for \(\mu\) when \(n_0 = 0\) , or vague priors where \(n_0\) is arbitrarily small, lead to Bayes factors that favor the null hypothesis regardless of the data, and thus should not be used for hypothesis testing.

Bayes factors with normal priors can be sensitive to the choice of the \(n_0\) . While the default value of \(n_0 = 1\) is reasonable in many cases, this may be too non-informative if one expects more effects. Wherever possible, think about how large an effect you expect and use that information to help select the \(n_0\) .

All the ESP examples suggest weak evidence and favored the machine generating random 0’s and 1’s with a probability that is different from 0.5. Note that ESP is not the only explanation – a deviation from 0.5 can also occur if the random number generator is biased. Bias in the stream of random numbers in our pseudorandom numbers has huge implications for numerous fields that depend on simulation. If the context had been about detecting a small bias in random numbers what prior would you use and how would it change the outcome? You can experiment it in R or other software packages that generate random Bernoulli trials.

Next, we will look at Bayes factors in normal models with unknown variances using the Cauchy prior so that results are less sensitive to the choice of \(n_0\) .

5.2 Comparing Two Paired Means using Bayes Factors

We previously learned that we can use a paired t-test to compare means from two paired samples. In this section, we will show how Bayes factors can be expressed as a function of the t-statistic for comparing the means and provide posterior probabilities of the hypothesis that whether the means are equal or different.

Example 5.1 Trace metals in drinking water affect the flavor, and unusually high concentrations can pose a health hazard. Ten pairs of data were taken measuring the zinc concentration in bottom and surface water at ten randomly sampled locations, as listed in Table 5.1 .

Water samples collected at the the same location, on the surface and the bottom, cannot be assumed to be independent of each other. However, it may be reasonable to assume that the differences in the concentration at the bottom and the surface in randomly sampled locations are independent of each other.

To start modeling, we will treat the ten differences as a random sample from a normal population where the parameter of interest is the difference between the average zinc concentration at the bottom and the average zinc concentration at the surface, or the main difference, \(\mu\) .

In mathematical terms, we have

• Random sample of \(n= 10\) differences \(Y_1, \ldots, Y_n\)
• Normal population with mean \(\mu \equiv \mu_B - \mu_S\)

In this case, we have no information about the variability in the data, and we will treat the variance, \(\sigma^2\) , as unknown.

The hypothesis of the main concentration at the surface and bottom are the same is equivalent to saying \(\mu = 0\) . The second hypothesis is that the difference between the mean bottom and surface concentrations, or equivalently that the mean difference \(\mu \neq 0\) .

In other words, we are going to compare the following hypotheses:

• \(H_1: \mu_B = \mu_S \Leftrightarrow \mu = 0\)
• \(H_2: \mu_B \neq \mu_S \Leftrightarrow \mu \neq 0\)

The Bayes factor is the ratio between the distributions of the data under each hypothesis, which does not depend on any unknown parameters.

\[\textit{BF}[H_1 : H_2] = \frac{p(\text{data}\mid H_1)} {p(\text{data}\mid H_2)}\]

To obtain the Bayes factor, we need to use integration over the prior distributions under each hypothesis to obtain those distributions of the data.

\[\textit{BF}[H_1 : H_2] = \iint p(\text{data}\mid \mu, \sigma^2) p(\mu \mid \sigma^2) p(\sigma^2 \mid H_2)\, d \mu \, d\sigma^2\]

This requires specifying the following priors:

• \(\mu \mid \sigma^2, H_2 \sim \textsf{Normal}(0, \sigma^2/n_0)\)
• \(p(\sigma^2) \propto 1/\sigma^2\) for both \(H_1\) and \(H_2\)

\(\mu\) is exactly zero under the hypothesis \(H_1\) . For \(\mu\) in \(H_2\) , we start with the same conjugate normal prior as we used in Section 5.1 – testing the normal mean with known variance. Since we assume that \(\sigma^2\) is known, we model \(\mu \mid \sigma^2\) instead of \(\mu\) itself.

The \(\sigma^2\) appears in both the numerator and denominator of the Bayes factor. For default or reference case, we use the Jeffreys prior (a.k.a. reference prior) on \(\sigma^2\) . As long as we have more than two observations, this (improper) prior will lead to a proper posterior.

After integration and rearranging, one can derive a simple expression for the Bayes factor:

\[\textit{BF}[H_1 : H_2] = \left(\frac{n + n_0}{n_0} \right)^{1/2} \left( \frac{ t^2 \frac{n_0}{n + n_0} + \nu } { t^2 + \nu} \right)^{\frac{\nu + 1}{2}}\]

This is a function of the t-statistic

\[t = \frac{|\bar{Y}|}{s/\sqrt{n}},\]

where \(s\) is the sample standard deviation and the degrees of freedom \(\nu = n-1\) (sample size minus one).

As we saw in the case of Bayes factors with known variance, we cannot use the improper prior on \(\mu\) because when \(n_0 \to 0\) , then \(\textit{BF}[H1:H_2] \to \infty\) favoring \(H_1\) regardless of the magnitude of the t-statistic. Arbitrary, vague small choices for \(n_0\) also lead to arbitrary large Bayes factors in favor of \(H_1\) . Another example of the Barlett’s or Jeffreys-Lindley paradox.

Sir Herald Jeffrey discovered another paradox testing using the conjugant normal prior, known as the information paradox . His thought experiment assumed that our sample size \(n\) and the prior sample size \(n_0\) . He then considered what would happen to the Bayes factor as the sample mean moved further and further away from the hypothesized mean, measured in terms standard errors with the t-statistic, i.e., \(|t| \to \infty\) . As the t-statistic or information about the mean moved further and further from zero, the Bayes factor goes to a constant depending on \(n, n_0\) rather than providing overwhelming support for \(H_2\) .

The bounded Bayes factor is

\[\textit{BF}[H_1 : H_2] \to \left( \frac{n_0}{n_0 + n} \right)^{\frac{n - 1}{2}}\]

Jeffrey wanted a prior with \(\textit{BF}[H_1 : H_2] \to 0\) (or equivalently, \(\textit{BF}[H_2 : H_1] \to \infty\) ), as the information from the t-statistic grows, indicating the sample mean is as far as from the hypothesized mean and should favor \(H_2\) .

To resolve the paradox when the information the t-statistic favors \(H_2\) but the Bayes factor does not, Jeffreys showed that no normal prior could resolve the paradox .

But a Cauchy prior on \(\mu\) , would resolve it. In this way, \(\textit{BF}[H_2 : H_1]\) goes to infinity as the sample mean becomes further away from the hypothesized mean. Recall that the Cauchy prior is written as \(\textsf{C}(0, r^2 \sigma^2)\) . While Jeffreys used a default of \(r = 1\) , smaller values of \(r\) can be used if smaller effects are expected.

The combination of the Jeffrey’s prior on \(\sigma^2\) and this Cauchy prior on \(\mu\) under \(H_2\) is sometimes referred to as the Jeffrey-Zellener-Siow prior .

However, there is no closed form expressions for the Bayes factor under the Cauchy distribution. To obtain the Bayes factor, we must use the numerical integration or simulation methods.

We will use the function from the package to test whether the mean difference is zero in Example 5.1 (zinc), using the JZS (Jeffreys-Zellener-Siow) prior.

With equal prior probabilities on the two hypothesis, the Bayes factor is the posterior odds. From the output, we see this indicates that the hypothesis \(H_2\) , the mean difference is different from 0, is almost 51 times more likely than the hypothesis \(H_1\) that the average concentration is the same at the surface and the bottom.

To sum up, we have used the Cauchy prior as a default prior testing hypothesis about a normal mean when variances are unknown. This does require numerical integration, but it is available in the function from the package. If you expect that the effect sizes will be small, smaller values of \(r\) are recommended.

It is often important to quantify the magnitude of the difference in addition to testing. The Cauchy Prior provides a default prior for both testing and inference; it avoids problems that arise with choosing a value of \(n_0\) (prior sample size) in both cases. In the next section, we will illustrate using the Cauchy prior for comparing two means from independent normal samples.

5.3 Comparing Independent Means: Hypothesis Testing

In the previous section, we described Bayes factors for testing whether the mean difference of paired samples was zero. In this section, we will consider a slightly different problem – we have two independent samples, and we would like to test the hypothesis that the means are different or equal.

Example 5.2 We illustrate the testing of independent groups with data from a 2004 survey of birth records from North Carolina, which are available in the package.

The variable of interest is – the weight gain of mothers during pregnancy. We have two groups defined by the categorical variable, , with levels, younger mom and older mom.

Question of interest : Do the data provide convincing evidence of a difference between the average weight gain of older moms and the average weight gain of younger moms?

We will view the data as a random sample from two populations, older and younger moms. The two groups are modeled as:

\[\begin{equation} \begin{aligned} Y_{O,i} & \mathrel{\mathop{\sim}\limits^{\rm iid}} \textsf{N}(\mu + \alpha/2, \sigma^2) \\ Y_{Y,i} & \mathrel{\mathop{\sim}\limits^{\rm iid}} \textsf{N}(\mu - \alpha/2, \sigma^2) \end{aligned} \tag{5.2} \end{equation}\]

The model for weight gain for older moms using the subscript \(O\) , and it assumes that the observations are independent and identically distributed, with a mean \(\mu+\alpha/2\) and variance \(\sigma^2\) .

For the younger women, the observations with the subscript \(Y\) are independent and identically distributed with a mean \(\mu-\alpha/2\) and variance \(\sigma^2\) .

Using this representation of the means in the two groups, the difference in means simplifies to \(\alpha\) – the parameter of interest.

\[(\mu + \alpha/2) - (\mu - \alpha/2) = \alpha\]

You may ask, “Why don’t we set the average weight gain of older women to \(\mu+\alpha\) , and the average weight gain of younger women to \(\mu\) ?” We need the parameter \(\alpha\) to be present in both \(Y_{O,i}\) (the group of older women) and \(Y_{Y,i}\) (the group of younger women).

We have the following competing hypotheses:

• \(H_1: \alpha = 0 \Leftrightarrow\) The means are not different.
• \(H_2: \alpha \neq 0 \Leftrightarrow\) The means are different.

In this representation, \(\mu\) represents the overall weight gain for all women. (Does the model in Equation (5.2) make more sense now?) To test the hypothesis, we need to specify prior distributions for \(\alpha\) under \(H_2\) (c.f. \(\alpha = 0\) under \(H_1\) ) and priors for \(\mu,\sigma^2\) under both hypotheses.

Recall that the Bayes factor is the ratio of the distribution of the data under the two hypotheses.

\[\begin{aligned} \textit{BF}[H_1 : H_2] &= \frac{p(\text{data}\mid H_1)} {p(\text{data}\mid H_2)} \\ &= \frac{\iint p(\text{data}\mid \alpha = 0,\mu, \sigma^2 )p(\mu, \sigma^2 \mid H_1) \, d\mu \,d\sigma^2} {\int \iint p(\text{data}\mid \alpha, \mu, \sigma^2) p(\alpha \mid \sigma^2) p(\mu, \sigma^2 \mid H_2) \, d \mu \, d\sigma^2 \, d \alpha} \end{aligned}\]

As before, we need to average over uncertainty and the parameters to obtain the unconditional distribution of the data. Now, as in the test about a single mean, we cannot use improper or non-informative priors for \(\alpha\) for testing.

Under \(H_2\) , we use the Cauchy prior for \(\alpha\) , or equivalently, the Cauchy prior on the standardized effect \(\delta\) with the scale of \(r\) :

\[\delta = \alpha/\sigma^2 \sim \textsf{C}(0, r^2)\]

Now, under both \(H_1\) and \(H_2\) , we use the Jeffrey’s reference prior on \(\mu\) and \(\sigma^2\) :

\[p(\mu, \sigma^2) \propto 1/\sigma^2\]

While this is an improper prior on \(\mu\) , this does not suffer from the Bartlett’s-Lindley’s-Jeffreys’ paradox as \(\mu\) is a common parameter in the model in \(H_1\) and \(H_2\) . This is another example of the Jeffreys-Zellner-Siow prior.

As in the single mean case, we will need numerical algorithms to obtain the Bayes factor. Now the following output illustrates testing of Bayes factors, using the Bayes inference function from the package.

We see that the Bayes factor for \(H_1\) to \(H_2\) is about 5.7, with positive support for \(H_1\) that there is no difference in average weight gain between younger and older women. Using equal prior probabilities, the probability that there is a difference in average weight gain between the two groups is about 0.15 given the data. Based on the interpretation of Bayes factors from Table 3.5 , this is in the range of “positive” (between 3 and 20).

To recap, we have illustrated testing hypotheses about population means with two independent samples, using a Cauchy prior on the difference in the means. One assumption that we have made is that the variances are equal in both groups . The case where the variances are unequal is referred to as the Behren-Fisher problem, and this is beyond the scope for this course. In the next section, we will look at another example to put everything together with testing and discuss summarizing results.

5.4 Inference after Testing

In this section, we will work through another example for comparing two means using both hypothesis tests and interval estimates, with an informative prior. We will also illustrate how to adjust the credible interval after testing.

Example 5.3 We will use the North Carolina survey data to examine the relationship between infant birth weight and whether the mother smoked during pregnancy. The response variable, , is the birth weight of the baby in pounds. The categorical variable provides the status of the mother as a smoker or non-smoker.

We would like to answer two questions:

Is there a difference in average birth weight between the two groups?

If there is a difference, how large is the effect?

As before, we need to specify models for the data and priors. We treat the data as a random sample for the two populations, smokers and non-smokers.

The birth weights of babies born to non-smokers, designated by a subgroup \(N\) , are assumed to be independent and identically distributed from a normal distribution with mean \(\mu + \alpha/2\) , as in Section 5.3 .

\[Y_{N,i} \mathrel{\mathop{\sim}\limits^{\rm iid}}\textsf{Normal}(\mu + \alpha/2, \sigma^2)\]

While the birth weights of the babies born to smokers, designated by the subgroup \(S\) , are also assumed to have a normal distribution, but with mean \(\mu - \alpha/2\) .

\[Y_{S,i} \mathrel{\mathop{\sim}\limits^{\rm iid}}\textsf{Normal}(\mu - \alpha/2, \sigma^2)\]

The difference in the average birth weights is the parameter \(\alpha\) , because

\[(\mu + \alpha/2) - (\mu - \alpha/2) = \alpha\] .

The hypotheses that we will test are \(H_1: \alpha = 0\) versus \(H_2: \alpha \ne 0\) .

We will still use the Jeffreys-Zellner-Siow Cauchy prior. However, since we may expect the standardized effect size to not be as strong, we will use a scale of \(r = 0.5\) rather than 1.

Therefore, under \(H_2\) , we have \[\delta = \alpha/\sigma \sim \textsf{C}(0, r^2), \text{ with } r = 0.5.\]

Under both \(H_1\) and \(H_2\) , we will use the reference priors on \(\mu\) and \(\sigma^2\) :

\[\begin{aligned} p(\mu) &\propto 1 \\ p(\sigma^2) &\propto 1/\sigma^2 \end{aligned}\]

The input to the base inference function is similar, but now we will specify that \(r = 0.5\) .

We see that the Bayes factor is 1.44, which weakly favors there being a difference in average birth weights for babies whose mothers are smokers versus mothers who did not smoke. Converting this to a probability, we find that there is about a 60% chance of the average birth weights are different.

While looking at evidence of there being a difference is useful, Bayes factors and posterior probabilities do not convey any information about the magnitude of the effect. Reporting a credible interval or the complete posterior distribution is more relevant for quantifying the magnitude of the effect.

Using the function, we can generate samples from the posterior distribution under \(H_2\) using the option.

The 2.5 and 97.5 percentiles for the difference in the means provide a 95% credible interval of 0.023 to 0.57 pounds for the difference in average birth weight. The MCMC output shows not only summaries about the difference in the mean \(\alpha\) , but the other parameters in the model.

In particular, the Cauchy prior arises by placing a gamma prior on \(n_0\) and the conjugate normal prior. This provides quantiles about \(n_0\) after updating with the current data.

The row labeled effect size is the standardized effect size \(\delta\) , indicating that the effects are indeed small relative to the noise in the data.

Figure 5.4: Estimates of effect under H2

Figure 5.4 shows the posterior density for the difference in means, with the 95% credible interval indicated by the shaded area. Under \(H_2\) , there is a 95% chance that the average birth weight of babies born to non-smokers is 0.023 to 0.57 pounds higher than that of babies born to smokers.

The previous statement assumes that \(H_2\) is true and is a conditional probability statement. In mathematical terms, the statement is equivalent to

\[P(0.023 < \alpha < 0.57 \mid \text{data}, H_2) = 0.95\]

However, we still have quite a bit of uncertainty based on the current data, because given the data, the probability of \(H_2\) being true is 0.59.

\[P(H_2 \mid \text{data}) = 0.59\]

Using the law of total probability, we can compute the probability that \(\mu\) is between 0.023 and 0.57 as below:

\[\begin{aligned} & P(0.023 < \alpha < 0.57 \mid \text{data}) \\ = & P(0.023 < \alpha < 0.57 \mid \text{data}, H_1)P(H_1 \mid \text{data}) + P(0.023 < \alpha < 0.57 \mid \text{data}, H_2)P(H_2 \mid \text{data}) \\ = & I( 0 \text{ in CI }) P(H_1 \mid \text{data}) + 0.95 \times P(H_2 \mid \text{data}) \\ = & 0 \times 0.41 + 0.95 \times 0.59 = 0.5605 \end{aligned}\]

Finally, we get that the probability that \(\alpha\) is in the interval, given the data, averaging over both hypotheses, is roughly 0.56. The unconditional statement is the average birth weight of babies born to nonsmokers is 0.023 to 0.57 pounds higher than that of babies born to smokers with probability 0.56. This adjustment addresses the posterior uncertainty and how likely \(H_2\) is.

To recap, we have illustrated testing, followed by reporting credible intervals, and using a Cauchy prior distribution that assumed smaller standardized effects. After testing, it is common to report credible intervals conditional on \(H_2\) . We also have shown how to adjust the probability of the interval to reflect our posterior uncertainty about \(H_2\) . In the next chapter, we will turn to regression models to incorporate continuous explanatory variables.

Teach yourself statistics

How to Test for Normality: Three Simple Tests

Many statistical techniques (regression, ANOVA, t-tests, etc.) rely on the assumption that data is normally distributed. For these techniques, it is good practice to examine the data to confirm that the assumption of normality is tenable.

With that in mind, here are three simple ways to test interval-scale data or ratio-scale data for normality.

• Check descriptive statistics.
• Generate a histogram.
• Conduct a chi-square test.

Each option is easy to implement with Excel, as long as you have Excel's Analysis ToolPak.

The Analysis ToolPak

To conduct the tests for normality described below, you need a free Microsoft add-in called the Analysis ToolPak, which may or may not be already installed on your copy of Excel.

To determine whether you have the Analysis ToolPak, click the Data tab in the main Excel menu. If you see Data Analysis in the Analysis section, you're good. You have the ToolPak.

If you don't have the ToolPak, you need to get it. Go to: How to Install the Data Analysis ToolPak in Excel .

Descriptive Statistics

Perhaps, the easiest way to test for normality is to examine several common descriptive statistics. Here's what to look for:

• Central tendency. The mean and the median are summary measures used to describe central tendency - the most "typical" value in a set of values. With a normal distribution, the mean is equal to the median.
• Skewness. Skewness is a measure of the asymmetry of a probability distribution. If observations are equally distributed around the mean, the skewness value is zero; otherwise, the skewness value is positive or negative. As a rule of thumb, skewness between -2 and +2 is consistent with a normal distribution.
• Kurtosis. Kurtosis is a measure of whether observations cluster around the mean of the distribution or in the tails of the distribution. The normal distribution has a kurtosis value of zero. As a rule of thumb, kurtosis between -2 and +2 is consistent with a normal distribution.

Together, these descriptive measures provide a useful basis for judging whether a data set satisfies the assumption of normality.

To see how to compute descriptive statistics in Excel, consider the following data set:

Begin by entering data in a column or row of an Excel spreadsheet:

Next, from the navigation menu in Excel, click Data / Data analysis . That displays the Data Analysis dialog box. From the Data Analysis dialog box, select Descriptive Statistics and click the OK button:

Then, in the Descriptive Statistics dialog box, enter the input range, and click the Summary Statistics check box. The dialog box, with entries, should look like this:

And finally, to display summary statistics, click the OK button on the Descriptive Statistics dialog box. Among other outputs, you should see the following:

The mean is nearly equal to the median. And both skewness and kurtosis are between -2 and +2.

Conclusion: These descriptive statistics are consistent with a normal distribution.

Another easy way to test for normality is to plot data in a histogram , and see if the histogram reveals the bell-shaped pattern characteristic of a normal distribution. With Excel, this is a a four-step process:

• Enter data. This means entering data values in an Excel spreadsheet. The column, row, or range of cells that holds data is the input range .
• Define bins. In Excel, bins are category ranges. To define a bin, you enter the upper range of each bin in a column, row, or range of cells. The block of cells that holds upper-range entries is called the bin range .
• Plot the data in a histogram. In Excel, access the histogram function through: Data / Data analysis / Histogram .
• In the Histogram dialog box, enter the input range and the bin range ; and check the Chart Output box. Then, click OK.

If the resulting histogram looks like a bell-shaped curve, your work is done. The data set is normal or nearly normal. If the curve is not bell-shaped, the data may not be normal.

To see how to plot data for normality with a histogram in Excel, we'll use the same data set (shown below) that we used in Example 1.

Begin by entering data to define an input range and a bin range. Here is what data entry looks like in an Excel spreadsheet:

Next, from the navigation menu in Excel, click Data / Data analysis . That displays the Data Analysis dialog box. From the Data Analysis dialog box, select Histogram and click the OK button:

Then, in the Histogram dialog box, enter the input range, enter the bin range, and click the Chart Output check box. The dialog box, with entries, should look like this:

And finally, to display the histogram, click the OK button on the Histogram dialog box. Here is what you should see:

The plot is fairly bell-shaped - an almost-symmetric pattern with one peak in the middle. Given this result, it would be safe to assume that the data were drawn from a normal distribution. On the other hand, if the plot were not bell-shaped, you might suspect the data were not from a normal distribution.

Chi-Square Test

The chi-square test for normality is another good option for determining whether a set of data was sampled from a normal distribution.

Note: All chi-square tests assume that the data under investigation was sampled randomly.

Hypothesis Testing

The chi-square test for normality is an actual hypothesis test , where we examine observed data to choose between two statistical hypotheses:

• Null hypothesis: Data is sampled from a normal distribution.
• Alternative hypothesis: Data is not sampled from a normal distribution.

Like many other techniques for testing hypotheses, the chi-square test for normality involves computing a test-statistic and finding the P-value for the test statistic, given degrees of freedom and significance level . If the P-value is bigger than the significance level, we accept the null hypothesis; if it is smaller, we reject the null hypothesis.

How to Conduct the Chi-Square Test

The steps required to conduct a chi-square test of normality are listed below:

• Specify the significance level.
• Find the mean, standard deviation, sample size for the sample.
• Define non-overlapping bins.
• Count observations in each bin, based on actual dependent variable scores.
• Find the cumulative probability for each bin endpoint.
• Find the probability that an observation would land in each bin, assuming a normal distribution.
• Find the expected number of observations in each bin, assuming a normal distribution.
• Compute a chi-square statistic.
• Find the degrees of freedom, based on the number of bins.
• Find the P-value for the chi-square statistic, based on degrees of freedom.
• Accept or reject the null hypothesis, based on P-value and significance level.

So you will understand how to accomplish each step, let's work through an example, one step at a time.

To demonstrate how to conduct a chi-square test for normality in Excel, we'll use the same data set (shown below) that we've used for the previous two examples. Here it is again:

Now, using this data, let's check for normality.

Specify Significance Level

The significance level is the probability of rejecting the null hypothesis when it is true. Researchers often choose 0.05 or 0.01 for a significance level. For the purpose of this exercise, let's choose 0.05.

Find the Mean, Standard Deviation, and Sample Size

To compute a chi-square test statistic, we need to know the mean, standared deviation, and sample size. Excel can provide this information. Here's how:

Define Bins

To conduct a chi-square analysis, we need to define bins, based on dependent variable scores. Each bin is defined by a non-overlapping range of values.

For the chi-square test to be valid, each bin should hold at least five observations. With that in mind, we'll define four bins for this example, as shown below:

Bin 1 will hold dependent variable scores that are less than 4; Bin 2, scores between 4 and 5; Bin 3, scores between 5.1 and 6; and and Bin 4, scores greater than 6.

Note: The number of bins is an arbitrary decision made by the experimenter, as long as the experimenter chooses at least four bins and at least five observations per bin. With fewer than four bins, there are not enough degrees of freedom for the analysis. For this example, we chose to define only four bins. Given the small sample, if we used more bins, at least one bin would have fewer than five observations per bin.

Count Observed Data Points in Each Bin

The next step is to count the observed data points in each bin. The figure below shows sample observations allocated to bins, with a frequency count for each bin in the final row.

Note: We have five observed data points in each bin - the minimum required for a valid chi-square test of normality.

Find Cumulative Probability

A cumulative probability refers to the probability that a random variable is less than or equal to a specific value. In Excel, the NORMDIST function computes cumulative probabilities from a normal distribution.

Assuming our data follows a normal distribution, we can use the NORMDIST function to find cumulative probabilities for the upper endpoints in each bin. Here is the formula we use:

P j = NORMDIST (MAX j , X , s, TRUE)

where P j is the cumulative probability for the upper endpoint in Bin j , MAX j is the upper endpoint for Bin j , X is the mean of the data set, and s is the standard deviation of the data set.

When we execute the formula in Excel, we get the following results:

P 1 = NORMDIST (4, 5.1, 2.0, TRUE) = 0.29

P 2 = NORMDIST (5, 5.1, 2.0, TRUE) = 0.48

P 3 = NORMDIST (6, 5.1, 2.0, TRUE) = 0.67

P 4 = NORMDIST (999999999, 5.1, 2.0, TRUE) = 1.00

Note: For Bin 4, the upper endpoint is positive infinity (∞), a quantity that is too large to be represented in an Excel function. To estimate cumulative probability for Bin 4 (P 4 ) with excel, you can use a very large number (e.g., 999999999) in place of positive infinity (as shown above). Or you can recognize that the probability that any random variable is less than or equal to positive infinity is 1.00.

Find Bin Probability

Given the cumulative probabilities shown above, it is possible to find the probability that a randomly selected observation would fall in each bin, using the following formulas:

P( Bin = 1 ) = P 1 = 0.29

P( Bin = 2 ) = P 2 - P 1 = 0.48 - 0.29 = 0.19

P( Bin = 3 ) = P 3 - P 2 = 0.67 - 0.48 = 0.19

P( Bin = 4 ) = P 4 - P 3 = 1.000 - 0.67 = 0.33

Find Expected Number of Observations

Assuming a normal distribution, the expected number of observations in each bin can be found by using the following formula:

Exp j = P( Bin = j ) * n

where Exp j is the expected number of observations in Bin j , P( Bin = j ) is the probability that a randomly selected observation would fall in Bin j , and n is the sample size

Applying the above formula to each bin, we get the following:

Exp 1 = P( Bin = 1 ) * 20 = 0.29 * 20 = 5.8

Exp 2 = P( Bin = 2 ) * 20 = 0.19 * 20 = 3.8

Exp 3 = P( Bin = 3 ) * 20 = 0.19 * 20 = 3.8

Exp 3 = P( Bin = 4 ) * 20 = 0.33 * 20 = 6.6

Compute Chi-Square Statistic

Finally, we can compute the chi-square statistic ( χ 2 ), using the following formula:

χ 2 = Σ [ ( Obs j - Exp j ) 2 / Exp j ]

where Obs j is the observed number of observations in Bin j , and Exp j is the expected number of observations in Bin j .

Find Degrees of Freedom

Assuming a normal distribution, the degrees of freedom (df) for a chi-square test of normality equals the number of bins (n b ) minus the number of estimated parameters (n p ) minus one. We used four bins, so n b equals four. And to conduct this analysis, we estimated two parameters (the mean and the standard deviation), so n p equals two. Therefore,

df = n b - n p - 1 = 4 - 2 - 1 = 1

Find P-Value

The P-value is the probability of seeing a chi-square test statistic that is more extreme (bigger) than the observed chi-square statistic. For this problem, we found that the observed chi-square statistic was 1.26. Therefore, we want to know the probability of seeing a chi-square test statistic bigger than 1.26, given one degree of freedom.

Use Stat Trek's Chi-Square Calculator to find that probability. Enter the degrees of freedom (1) and the observed chi-square statistic (1.26) into the calculator; then, click the Calculate button.

From the calculator, we see that P( X 2 > 1.26 ) equals 0.26.

Test Null Hypothesis

When the P-Value is bigger than the significance level, we cannot reject the null hypothesis. Here, the P-Value (0.26) is bigger than the significance level (0.05), so we cannot reject the null hypothesis that the data tested follows a normal distribution.

Module 9: Hypothesis Testing With One Sample

Distribution needed for hypothesis testing, learning outcomes.

• Conduct and interpret hypothesis tests for a single population mean, population standard deviation known
• Conduct and interpret hypothesis tests for a single population mean, population standard deviation unknown

Earlier in the course, we discussed sampling distributions.  Particular distributions are associated with hypothesis testing. Perform tests of a population mean using a normal distribution or a Student’s t- distribution . (Remember, use a Student’s t -distribution when the population standard deviation is unknown and the distribution of the sample mean is approximately normal.) We perform tests of a population proportion using a normal distribution (usually n is large or the sample size is large).

If you are testing a  single population mean , the distribution for the test is for means :

[latex]\displaystyle\overline{{X}}\text{~}{N}{\left(\mu_{{X}}\text{ , }\frac{{\sigma_{{X}}}}{\sqrt{{n}}}\right)}{\quad\text{or}\quad}{t}_{{{d}{f}}}[/latex]

The population parameter is [latex]\mu[/latex]. The estimated value (point estimate) for [latex]\mu[/latex] is [latex]\displaystyle\overline{{x}}[/latex], the sample mean.

If you are testing a  single population proportion , the distribution for the test is for proportions or percentages:

[latex]\displaystyle{P}^{\prime}\text{~}{N}{\left({p}\text{ , }\sqrt{{\frac{{{p}{q}}}{{n}}}}\right)}[/latex]

The population parameter is [latex]p[/latex]. The estimated value (point estimate) for [latex]p[/latex] is p′ . [latex]\displaystyle{p}\prime=\frac{{x}}{{n}}[/latex] where [latex]x[/latex] is the number of successes and [latex]n[/latex] is the sample size.

Assumptions

When you perform a  hypothesis test of a single population mean μ using a Student’s t -distribution (often called a t-test), there are fundamental assumptions that need to be met in order for the test to work properly. Your data should be a simple random sample that comes from a population that is approximately normally distributed . You use the sample standard deviation to approximate the population standard deviation. (Note that if the sample size is sufficiently large, a t-test will work even if the population is not approximately normally distributed).

When you perform a  hypothesis test of a single population mean μ using a normal distribution (often called a z -test), you take a simple random sample from the population. The population you are testing is normally distributed or your sample size is sufficiently large. You know the value of the population standard deviation which, in reality, is rarely known.

When you perform a  hypothesis test of a single population proportion p , you take a simple random sample from the population. You must meet the conditions for a binomial distribution which are as follows: there are a certain number n of independent trials, the outcomes of any trial are success or failure, and each trial has the same probability of a success p . The shape of the binomial distribution needs to be similar to the shape of the normal distribution. To ensure this, the quantities np  and nq must both be greater than five ( np > 5 and nq > 5). Then the binomial distribution of a sample (estimated) proportion can be approximated by the normal distribution with μ = p and [latex]\displaystyle\sigma=\sqrt{{\frac{{{p}{q}}}{{n}}}}[/latex] . Remember that q = 1 – p .

Concept Review

In order for a hypothesis test’s results to be generalized to a population, certain requirements must be satisfied.

When testing for a single population mean:

• A Student’s t -test should be used if the data come from a simple, random sample and the population is approximately normally distributed, or the sample size is large, with an unknown standard deviation.
• The normal test will work if the data come from a simple, random sample and the population is approximately normally distributed, or the sample size is large, with a known standard deviation.

When testing a single population proportion use a normal test for a single population proportion if the data comes from a simple, random sample, fill the requirements for a binomial distribution, and the mean number of success and the mean number of failures satisfy the conditions:  np > 5 and nq > n where n is the sample size, p is the probability of a success, and q is the probability of a failure.

Formula Review

If there is no given preconceived  α , then use α = 0.05.

Types of Hypothesis Tests

• Single population mean, known population variance (or standard deviation): Normal test .
• Single population mean, unknown population variance (or standard deviation): Student’s t -test .
• Single population proportion: Normal test .
• For a single population mean , we may use a normal distribution with the following mean and standard deviation. Means: [latex]\displaystyle\mu=\mu_{{\overline{{x}}}}{\quad\text{and}\quad}\sigma_{{\overline{{x}}}}=\frac{{\sigma_{{x}}}}{\sqrt{{n}}}[/latex]
• A single population proportion , we may use a normal distribution with the following mean and standard deviation. Proportions: [latex]\displaystyle\mu={p}{\quad\text{and}\quad}\sigma=\sqrt{{\frac{{{p}{q}}}{{n}}}}[/latex].
• Distribution Needed for Hypothesis Testing. Provided by : OpenStax. Located at : . License : CC BY: Attribution
• Introductory Statistics . Authored by : Barbara Illowski, Susan Dean. Provided by : Open Stax. Located at : http://cnx.org/contents/[email protected] . License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

9.3: A Single Population Mean using the Normal Distribution

• Last updated
• Save as PDF
• Page ID 20074

All hypotheses tests have the same basic steps:

• The alternative hypothesis, \(H_{a}\), never has a symbol that contains an equal sign.
• The alternative hypothesis, \(H_{a}\), tells you if the test is left, right, or two-tailed. It is the key to conducting the appropriate test.
• In a hypothesis test problem, you may see words such as "the level of significance is 1%." The "1%" is the preconceived or preset \(\alpha\). The statistician setting up the hypothesis test selects the value of α to use before collecting the sample data. If no level of significance is given, a common standard to use is \(\alpha = 0.05\).
• When you calculate the \(p\)-value and draw the picture, the \(p\)-value is the area in the left tail, the right tail, or split evenly between the two tails. For this reason, we call the hypothesis test left, right, or two tailed.
• Never, ever, Accept the Null Hypothesis.
• Thinking about the meaning of the \(p\)-value: A data analyst (and anyone else) should have more confidence that he made the correct decision to reject the null hypothesis with a smaller \(p\)-value (for example, 0.001 as opposed to 0.04) even if using the 0.05 level for alpha. Similarly, for a large p -value such as 0.4, as opposed to a \(p\)-value of 0.056 (\(\alpha = 0.05\) is less than either number), a data analyst should have more confidence that she made the correct decision in not rejecting the null hypothesis. This makes the data analyst use judgment rather than mindlessly applying rules.
• Determine the conclusion : What does the decision mean in terms of the problem given?

Direction of Tail

Example \(\pageindex{1}\).

\(H_{0}: \mu \geq 5, H_{a}: \mu < 5\)

Test of a single population mean. \(H_{a}\) tells you the test is left-tailed. The picture of the \(p\)-value is as follows:

Exercise \(\PageIndex{1}\)

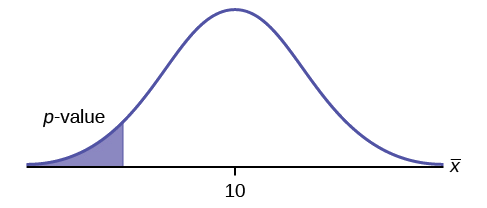
\(H_{0}: \mu \geq 10, H_{a}: \mu < 10\)

Assume the \(p\)-value is 0.0935. What type of test is this? Draw the picture of the \(p\)-value.

left-tailed test

Example \(\PageIndex{2}\)

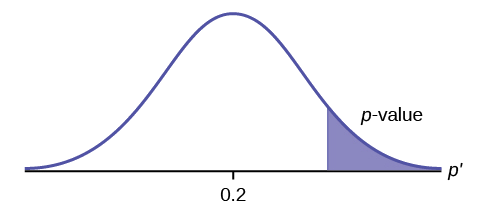
\(H_{0}: \mu \leq 0.2, H_{a}: \mu > 0.2\)

This is a test of a single population proportion. \(H_{a}\) tells you the test is right-tailed . The picture of the p -value is as follows:

Exercise \(\PageIndex{2}\)

\(H_{0}: \mu \leq 1, H_{a}: \mu > 1\)

Assume the \(p\)-value is 0.1243. What type of test is this? Draw the picture of the \(p\)-value.

right-tailed test

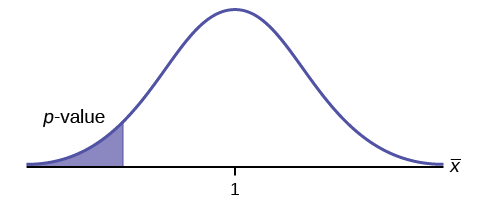
Example \(\PageIndex{3}\)

\(H_{0}: \mu = 50, H_{a}: \mu \neq 50\)

This is a test of a single population mean. \(H_{a}\) tells you the test is two-tailed . The picture of the \(p\)-value is as follows.

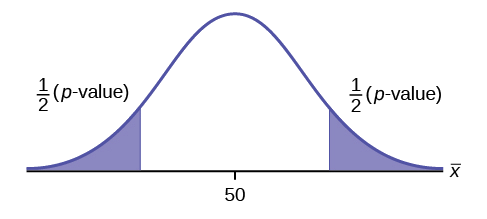
Exercise \(\PageIndex{3}\)

\(H_{0}: \mu = 0.5, H_{a}: \mu \neq 0.5\)

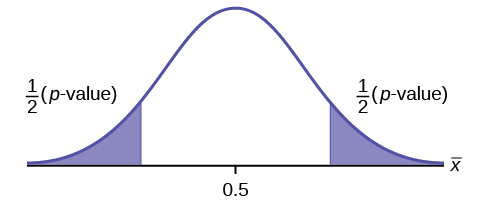
Assume the p -value is 0.2564. What type of test is this? Draw the picture of the \(p\)-value.

two-tailed test

Full Hypothesis Test Examples

Example \(\pageindex{4}\).

Jeffrey, as an eight-year old, established a mean time of 16.43 seconds for swimming the 25-yard freestyle, with a standard deviation of 0.8 seconds. His dad, Frank, thought that Jeffrey could swim the 25-yard freestyle faster using goggles. Frank bought Jeffrey a new pair of expensive goggles and timed Jeffrey for 15 25-yard freestyle swims. For the 15 swims, Jeffrey's mean time was 16 seconds. Frank thought that the goggles helped Jeffrey to swim faster than the 16.43 seconds. Conduct a hypothesis test using a preset α = 0.05. Assume that the swim times for the 25-yard freestyle are normal.

\(P\)-value Solution

Determine the hypothesis :

Since the problem is about a mean, this is a test of a single population mean.

For Jeffrey to swim faster, his time will be less than 16.43 seconds. So the claim will be that he can swim it in less time than 16.43 seconds.

\(H_{0}: \mu \geq 16.43\)

\(H_{a}: \mu < 16.43\) (claim)

The "\(<\)" in the alternative hypothesis tells you this is left-tailed.

Calculate the evidence :

Use the Standard Normal Distribution since the population standard deviation is given.

Calculate the test statistic using the same formula as a \(z\)-score using the Central Limit Theorem.

\[z=\frac{\bar{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\nonumber\]

\(\mu = 16.43\) comes from \(H_{0}\) and not the data. \(\sigma = 0.8\) and \(n = 15\). Which gives

\[z=\frac{16-16.43}{\frac{0.8}{\sqrt{15}}}=\frac{-0.43}{\frac{0.8}{3.87298}}=\frac{-0.43}{0.20656}=-2.0817\nonumber\]

Now calculate the p-value based on the test statistic found.

This is a left-tailed test, so use the Excel formula \(=\text{NORM.S.DIST}(z,\text{true})\).

In this case, we found \(z\), which is the test statistic, to be \(z=-2.0817\).

Use the Excel formula \(=\text{NORM.S.DIST}(-2.0817,\text{true})=0.0187\).

So the \(p\text{-value} = 0.0187\). This is the area to the left of the sample mean, which is given as 16.

Make a decision:

Interpretation of the \(p-\text{value}\): If \(H_{0}\) is true, there is a 0.0187 probability (1.87%) that Jeffrey's mean time to swim the 25-yard freestyle is 16 seconds or less. Because a 1.87% chance is small, the mean time of 16 seconds or less is unlikely to have happened randomly. It is a rare event.

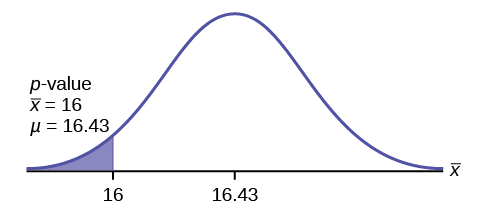
\(\mu = 16.43\) comes from \(H_{0}\). Our assumption gives \(\mu = 16.43\).

\(\alpha\) is the minimum area that could be considered to make our result significant.

Compare \(\alpha\) and the \(p\text{-value}\)

• If \(p\text{-value}\) is less than the \(\alpha\) then we will Reject \(H_0\).
• If \(\alpha\) is less than the \(p\text{-value}\) then we will Fail to Reject \(H_0\).

\(\alpha = 0.05\) and \(p\text{-value} = 0.0187\), so \(p\text{-value}<\alpha\)

Since \(p\text{-value}<\alpha\), reject \(H_{0}\).

Conclusion:

This means that you reject \(\mu \geq 16.43\).

There is sufficient evidence to support the claim that Jeffrey's mean swim time for the 25-yard freestyle is less than 16.43 seconds.

Critical Value Solution

Determine the hypothesis (Same as the \(P\)-value solution) :

Calculate the critical value. Use the Standard Normal Distribution, Critical Value, Right-tail Excel formula: \(=\text{NORM.S.INV}(\alpha)\).

In this problem, the \(\alpha=0.05\), so use \(=\text{NORM.S.INV}(0.05)=-1.64485\)

Graph the critical value and the test statistic along the number line of the Standard Normal Distribution graph.

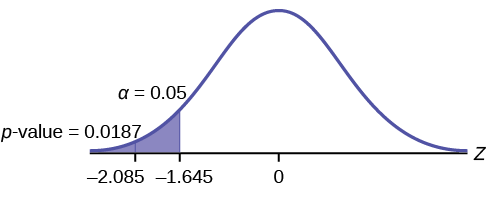
Since this is left-tailed, everything less than the critical value, \(\text{CV}=-1.64485\) will be the rejection region.

Since the test statistic, \(z=-2.0817\) is less than the critical value, \(\text{CV}=-1.64485, the decision will be to Reject the Null Hypothesis.

Conclusion (Same as the \(P\)-value solution):

The Type I and Type II errors for this problem are as follows :

The Type I error is to conclude that Jeffrey swims the 25-yard freestyle, on average, in less than 16.43 seconds when, in fact, he actually swims the 25-yard freestyle, on average, in 16.43 seconds. (Reject the null hypothesis when the null hypothesis is true.)

The Type II error is that there is not evidence to conclude that Jeffrey swims the 25-yard free-style, on average, in less than 16.43 seconds when, in fact, he actually does swim the 25-yard free-style, on average, in less than 16.43 seconds. (Do not reject the null hypothesis when the null hypothesis is false.)

Exercise \(\PageIndex{4}\)

The mean throwing distance of a football for a Marco, a high school freshman quarterback, is 40 yards, with a standard deviation of two yards. The team coach tells Marco to adjust his grip to get more distance. The coach records the distances for 20 throws. For the 20 throws, Marco’s mean distance was 45 yards. The coach thought the different grip helped Marco throw farther than 40 yards. Conduct a hypothesis test using a preset \(\alpha = 0.01\). Assume the throw distances for footballs are normal. Use the critical value method.

For Marco to throw farther, his distance will be greater than 40 yards. So the claim will be that he can throw farther than 40 yards.

\(H_{0}: \mu \leq 40\)

\(H_{a}: \mu > 40\) (claim)

The "\(>\)" in the alternative hypothesis tells you this is right-tailed.

Calculate the critical value. Use the Standard Normal Distribution, Critical Value, Right-tail Excel formula: \(=\text{NORM.S.INV}(1-\alpha)\).

In this problem, the \(\alpha=0.01\), so use \(=\text{NORM.S.INV}(1-0.01)=2.3263\)

\(\mu = 40\) comes from \(H_{0}\) and not the data. \(\sigma = 2\) and \(n = 20\). Which gives

\[z=\frac{45-40}{\frac{2}{\sqrt{20}}}=\frac{5}{\frac{2}{4.4721}}=\frac{5}{0.4472}=11.1803\nonumber\]

Since this is right-tailed, everything greater than the critical value, \(\text{CV}=2.3263\) will be the rejection region.

Since the test statistic, \(z=11.1803\) is greater than the critical value, \(\text{CV}=2.3263\), the decision will be to Reject the Null Hypothesis.

This means that you reject \(\mu \leq 40\).

There is sufficient evidence to support the claim that the change in Marco's grip improved his throwing distance to give a mean throw distance is greater than 40 yards.

Example \(\PageIndex{5}\)

A college football coach thought that his players could bench press a mean weight of 275 pounds. It is known that the standard deviation is 55 pounds. Three of his players thought that the mean weight was great than that amount. They asked 30 of their teammates for their estimated maximum lift on the bench press exercise. The data ranged from 205 pounds to 385 pounds. The actual different weights are given below

Conduct a \(p\)-value hypothesis test using a 2.5% level of significance to determine if the bench press mean is more than 275 pounds.

Since the problem is about a mean weight, this is a test of a single population mean.

\(H_{0}: \mu \leq 275\)

\(H_{a}: \mu > 275\) (claim)

The "\(>\)" in the alternative hypothesis tells you this is a right-tailed test.

Calculate the test statistic using the same formula as the \(z\)-score using the Central Limit Theorem.

\(\mu = 275\) comes from \(H_{0}\) and not the data. \(\sigma=55\) and \(n=30\). The problem does not give the sample mean, so that will need to be calculated using the data.

Enter the data into Excel, and use the Excel formula \(=\text{AVERAGE}()\) to find \(\bar{x}=286.2\).

\[z=\frac{286.2-275}{\frac{55}{\sqrt{30}}}=\frac{11.2}{\frac{2}{5.4772}}=\frac{11.2}{10.04}=1.11536\nonumber\]

Now calculate the \(p\)-value based on the test statistic found.

This is a right-tailed test, so use the Excel formula \(=1-\text{NORM.S.DIST}(z,\text{true})\).

In this case, we found \(z\), which is the test statistic, to be \(z=1.11536\).

Use the Excel formula \(=1-\text{NORM.S.DIST}(1.11536,\text{true})=0.132348\).

So the \(p\text{-value} = 0.132348\).

Interpretation of the p -value: If \(H_{0}\) is true, then there is a 0.1331 probability (13.23%) that the football players can lift a mean weight of 286.2 pounds or more. Because a 13.23% chance is large enough, a mean weight lift of 286.2 pounds or more is not a rare event.

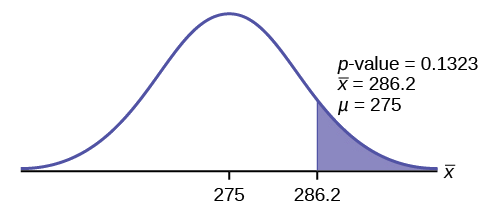
Make a decision :

\(\alpha = 0.025\) and \(p\)-value \(= 0.1323\)

Since \(\alpha < p\text{-value}\), do not reject \(H_{0}\).

Conclusion: At the 2.5% level of significance, from the sample data, there is not sufficient evidence to conclude that the true mean weight lifted is more than 275 pounds.

The hypothesis test itself has an established process. This can be summarized as follows:

• Determine \(H_{0}\) and \(H_{a}\). Remember, they are contradictory.
• Find the evidence: Draw a graph, calculate the test statistic, and use the test statistic to calculate the \(p\text{-value}\). (A z -score and a t -score are examples of test statistics.)
• Compare the preconceived α with the p -value, make a decision (reject or do not reject H 0 ).
• Write a clear conclusion using English sentences.

Notice that in performing the hypothesis test, you use \(\alpha\) and not \(\beta\). \(\beta\) is needed to help determine the sample size of the data that is used in calculating the \(p\text{-value}\). Remember that the quantity \(1 – \beta\) is called the Power of the Test . A high power is desirable. If the power is too low, statisticians typically increase the sample size while keeping α the same.If the power is low, the null hypothesis might not be rejected when it should be.

Exercise \(\PageIndex{5}\)

Assume \(H_{0}: \mu = 9\) and \(H_{a}: \mu < 9\). Is this a left-tailed, right-tailed, or two-tailed test?

This is a left-tailed test.

Exercise \(\PageIndex{6}\)

Assume \(H_{0}: \mu \leq 6\) and \(H_{a}: \mu > 6\). Is this a left-tailed, right-tailed, or two-tailed test?

Exercise \(\PageIndex{7}\)

Assume \(H_{0}: p = 0.25\) and \(H_{a}: p \neq 0.25\). Is this a left-tailed, right-tailed, or two-tailed test?

This is a two-tailed test.

Exercise \(\PageIndex{8}\)

Draw the general graph of a left-tailed test.

Exercise \(\PageIndex{9}\)

Draw the graph of a two-tailed test.

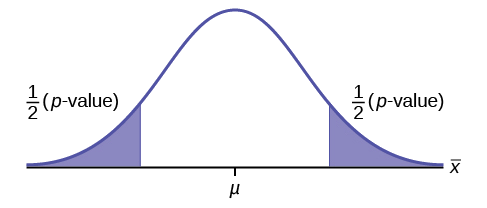
Exercise \(\PageIndex{10}\)

A bottle of water is labeled as containing 16 fluid ounces of water. You believe it is less than that. What type of test would you use?

Exercise \(\PageIndex{11}\)

Your friend claims that his mean golf score is 63. You want to show that it is higher than that. What type of test would you use?

a right-tailed test

Exercise \(\PageIndex{12}\)

A bathroom scale claims to be able to identify correctly any weight within a pound. You think that it cannot be that accurate. What type of test would you use?

Exercise \(\PageIndex{13}\)

You flip a coin and record whether it shows heads or tails. You know the probability of getting heads is 50%, but you think it is less for this particular coin. What type of test would you use?

a left-tailed test

Exercise \(\PageIndex{14}\)

If the alternative hypothesis has a not equals ( \(\neq\) ) symbol, you know to use which type of test?

Exercise \(\PageIndex{15}\)

Assume the null hypothesis states that the mean is at least 18. Is this a left-tailed, right-tailed, or two-tailed test?

Exercise \(\PageIndex{16}\)

Assume the null hypothesis states that the mean is at most 12. Is this a left-tailed, right-tailed, or two-tailed test?

Exercise \(\PageIndex{17}\)

Assume the null hypothesis states that the mean is equal to 88. The alternative hypothesis states that the mean is not equal to 88. Is this a left-tailed, right-tailed, or two-tailed test?

• Data from Amit Schitai. Director of Instructional Technology and Distance Learning. LBCC.
• Data from Bloomberg Businessweek . Available online at www.businessweek.com/news/2011- 09-15/nyc-smoking-rate-falls-to-record-low-of-14-bloomberg-says.html.
• Data from energy.gov. Available online at http://energy.gov (accessed June 27. 2013).
• Data from Gallup®. Available online at www.gallup.com (accessed June 27, 2013).
• Data from Growing by Degrees by Allen and Seaman.
• Data from La Leche League International. Available online at www.lalecheleague.org/Law/BAFeb01.html.
• Data from the American Automobile Association. Available online at www.aaa.com (accessed June 27, 2013).
• Data from the American Library Association. Available online at www.ala.org (accessed June 27, 2013).
• Data from the Bureau of Labor Statistics. Available online at http://www.bls.gov/oes/current/oes291111.htm .
• Data from the Centers for Disease Control and Prevention. Available online at www.cdc.gov (accessed June 27, 2013)
• Data from the U.S. Census Bureau, available online at quickfacts.census.gov/qfd/states/00000.html (accessed June 27, 2013).
• Data from the United States Census Bureau. Available online at www.census.gov/hhes/socdemo/language/.
• Data from Toastmasters International. Available online at http://toastmasters.org/artisan/deta...eID=429&Page=1 .
• Data from Weather Underground. Available online at www.wunderground.com (accessed June 27, 2013).
• Federal Bureau of Investigations. “Uniform Crime Reports and Index of Crime in Daviess in the State of Kentucky enforced by Daviess County from 1985 to 2005.” Available online at http://www.disastercenter.com/kentucky/crime/3868.htm (accessed June 27, 2013).
• “Foothill-De Anza Community College District.” De Anza College, Winter 2006. Available online at research.fhda.edu/factbook/DA...t_da_2006w.pdf.
• Johansen, C., J. Boice, Jr., J. McLaughlin, J. Olsen. “Cellular Telephones and Cancer—a Nationwide Cohort Study in Denmark.” Institute of Cancer Epidemiology and the Danish Cancer Society, 93(3):203-7. Available online at http://www.ncbi.nlm.nih.gov/pubmed/11158188 (accessed June 27, 2013).
• Rape, Abuse & Incest National Network. “How often does sexual assault occur?” RAINN, 2009. Available online at www.rainn.org/get-information...sexual-assault (accessed June 27, 2013).

Contributors and Attributions

Barbara Illowsky and Susan Dean (De Anza College) with many other contributing authors. Content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/[email protected] .

An open portfolio of interoperable, industry leading products

The Dotmatics digital science platform provides the first true end-to-end solution for scientific R&D, combining an enterprise data platform with the most widely used applications for data analysis, biologics, flow cytometry, chemicals innovation, and more.

Statistical analysis and graphing software for scientists

Bioinformatics, cloning, and antibody discovery software

Plan, visualize, & document core molecular biology procedures

Electronic Lab Notebook to organize, search and share data

Proteomics software for analysis of mass spec data

Modern cytometry analysis platform

Analysis, statistics, graphing and reporting of flow cytometry data

Software to optimize designs of clinical trials

How do I know if my data have a normal distribution?

You can test the hypothesis that your data were sampled from a Normal (Gaussian) distribution visually (with QQ-plots and histograms) or statistically (with tests such as D'Agostino-Pearson and Kolmogorov-Smirnov). However, it’s rare to need to test if your data are normal. Most likely you’re fitting some type of statistical model to your data such as ANOVA , linear regression , and nonlinear regression . In these cases, the assumption is that the residuals, the deviations between the model predictions and the observed data, are sampled from a normally distribution. The residuals need to be approximately normally distributed to get valid statistical inference such as confidence intervals , coefficient estimates , and p values .

This means that the data don’t necessarily need to be normally distributed, but the residuals do. 

In this article, we will take a deeper dive into the subject of normality testing, including:

Statistical test for normality with common statistical models

How to determine if data is normally distributed using visual and statistical tests

Normally distributed data examples

What to do if the residuals are not normal

How to test for normality with common statistical models

Linear and nonlinear regression.

With simple linear regression, the residuals are the vertical distance from the observed data to the line. In this case, the tests for normality should be performed on the residuals, not the raw data. 

The same idea applies to nonlinear regression, where the model fits a curve instead of a straight line. The p-values and confidence intervals are based on the assumption that the residuals are normally distributed. 

Discover the easiest way to test your data using linear regression with a free 30 day trial of Prism.

Note the language. The shorthand (used above) is to test the assumption that the residuals are normally distributed. What this really means is testing the assumption that the residuals are sampled from a normal distribution, or are sampled from a population that follows a normal distribution.

T tests (paired and unpaired)

With t tests and ANOVA models, it appears a little different, but it’s actually the same process of testing the model residuals. 

With paired t tests, which are used when two measurements are taken on the same data point (for example, before and after measurements for each test subject), the model assumption is that the differences between the two measurements are normally distributed. So in that case, simply test the difference for normality. A common mistake is to test each group as being normally distributed. 

With unpaired t tests, when comparing if the means between two different independent groups (such as male vs female heights), both columns of data are assumed to be normal, and both should be tested either individually or jointly if you assume equal variance and test the residuals, the difference of each column value minus its respective estimated mean, not the raw data. 

Are your residuals for t tests clearly deviating a little from normality? Note that t tests are robust to non-normal data with large sample sizes, meaning that as long as you have enough data, only substantial violations of normality need to be addressed.

Perform a t test in Prism today.

ANOVA with fixed effects

In two-way ANOVA with fixed effects, where there are two experimental factors such as fertilizer type and soil type, the assumption is that data within each factor combination are normally distributed. It’s easiest to test this by looking at all of the residuals at once. In this case, the residuals are the difference of each observation from the group mean of its respective factor combination. 

A common mistake is to test for normality across only one factor. Using the fertilizer and soil type example, the assumption is that each group (fertilizer A with soil type 1, fertilizer A with soil type 2, …) is normally distributed. It’s not the same thing to test if fertilizer A data are normally distributed, and in fact, if the soil type is a significant factor, then they wouldn’t be.

As long as you’re assuming equal variance among the different treatment groups, then you can test for normality across all residuals at once. This is useful in cases when you have only a few observations in any given factorial combination.

Test the normality of your data before conducting an ANOVA in Prism.

How to test for normality

There are both visual and formal statistical tests that can help you check if your model residuals meet the assumption of normality. In Prism , most models (ANOVA, Linear Regression, etc.) include tests and plots for evaluating normality, and you can also test a column of data directly .

The most common graphical tool for assessing normality is the Q-Q plot . In these plots, the observed data is plotted against the expected quantiles of a normal distribution . It takes practice to read these plots. In theory, sampled data from a normal distribution would fall along the dotted line. In reality, even data sampled from a normal distribution, such as the example QQ plot below, can exhibit some deviation from the line. 

Frequency distribution

You may also visually check normality by plotting a frequency distribution , also called a histogram, of the data and visually comparing it to a normal distribution (overlaid in red). In a frequency distribution, each data point is put into a discrete bin, for example (-10,-5], (-5, 0], (0, 5], etc. The plot shows the proportion of data points in each bin.

While this is a useful tool to visually summarize your data, a major drawback is that the bin size can greatly affect how the data look. The following histogram is the same data as above but using smaller bin sizes.

With statistical tests

There are many statistical tests to evaluate normality, although we don’t recommend relying on them blindly . Prism offers four normality test options : D'Agostino-Pearson, Anderson-Darling, Shapiro-Wilk and Kolmogorov-Smirnov. Each of the tests produces a p-value that tests the null hypothesis that the values (the sample) were sampled from a Normal (Gaussian) distribution (or population). :

If the p-value is not significant, the normality test was “passed”. While it’s true we can never say for certain that the data came from a normal distribution, there is not evidence to suggest otherwise.

If the p-value is significant, the normality test was “failed”. There is evidence that the data may not be normally distributed after all. 

If that does not fit with your intuition, remember that the null hypothesis for these tests is that your sample came from a normally distributed population of data. So as with any significant test result, you are rejecting the idea that the data was normally distributed. See our guide for more specific information and background on interpreting normality test p-values . 

Which is better: visual or statistical tests?

We recommend both. It’s always a good idea to plot your data, because, while helpful, statistical tests have limitations. This is especially true with medium to large sample sizes (over 70 observations), because in these cases, the normality tests can detect very slight deviations from normality. Therefore, if your data “fail” a normality test, a visual check might tell you that even if the data are statistically not normal, they are practically normal. 

Get started in Prism with your free 30 day trial today.

What if my residuals aren’t normally distributed?

If there is evidence your data are significantly different from the expected normal distribution, what can you do?

Some models are robust to deviations from normality

Depending on the model you are using, it may still provide accurate results despite some degree of non-normality. 1-Way ANOVA, for example, is often robust even if the data are not very close to normal. 

Transformations

In some situations, you can transform your data and re-test for normality. For example,  log transformations are common, because l ognormal distributions are common (especially in biology)

Non-Parametric Tests

If your data truly are not normal, many analyses have non-parametric alternatives, such as the one-way ANOVA analog, Kruskal-Wallis , and the two-sample t test analog, Mann-Whitney . These methods don’t rely on an assumption of normality. The downside is that they generally also have less power , so it’s harder to detect statistical differences. Here are some recommendations to determine when to use nonparametric tests .

Explore the Knowledgebase

Analyze, graph and present your scientific work easily with GraphPad Prism. No coding required.

scipy.stats.normaltest #

Test whether a sample differs from a normal distribution.

This function tests the null hypothesis that a sample comes from a normal distribution. It is based on D’Agostino and Pearson’s [1] , [2] test that combines skew and kurtosis to produce an omnibus test of normality.

The array containing the sample to be tested.

If an int, the axis of the input along which to compute the statistic. The statistic of each axis-slice (e.g. row) of the input will appear in a corresponding element of the output. If None , the input will be raveled before computing the statistic.

Defines how to handle input NaNs.

propagate : if a NaN is present in the axis slice (e.g. row) along which the statistic is computed, the corresponding entry of the output will be NaN.

omit : NaNs will be omitted when performing the calculation. If insufficient data remains in the axis slice along which the statistic is computed, the corresponding entry of the output will be NaN.

raise : if a NaN is present, a ValueError will be raised.

If this is set to True, the axes which are reduced are left in the result as dimensions with size one. With this option, the result will broadcast correctly against the input array.

s^2 + k^2 , where s is the z-score returned by skewtest and k is the z-score returned by kurtosistest .

A 2-sided chi squared probability for the hypothesis test.

Beginning in SciPy 1.9, np.matrix inputs (not recommended for new code) are converted to np.ndarray before the calculation is performed. In this case, the output will be a scalar or np.ndarray of appropriate shape rather than a 2D np.matrix . Similarly, while masked elements of masked arrays are ignored, the output will be a scalar or np.ndarray rather than a masked array with mask=False .

D’Agostino, R. B. (1971), “An omnibus test of normality for moderate and large sample size”, Biometrika, 58, 341-348

D’Agostino, R. and Pearson, E. S. (1973), “Tests for departure from normality”, Biometrika, 60, 613-622

Shapiro, S. S., & Wilk, M. B. (1965). An analysis of variance test for normality (complete samples). Biometrika, 52(3/4), 591-611.

B. Phipson and G. K. Smyth. “Permutation P-values Should Never Be Zero: Calculating Exact P-values When Permutations Are Randomly Drawn.” Statistical Applications in Genetics and Molecular Biology 9.1 (2010).

Panagiotakos, D. B. (2008). The value of p-value in biomedical research. The open cardiovascular medicine journal, 2, 97.

Suppose we wish to infer from measurements whether the weights of adult human males in a medical study are not normally distributed [3] . The weights (lbs) are recorded in the array x below.

The normality test of [1] and [2] begins by computing a statistic based on the sample skewness and kurtosis.

(The test warns that our sample has too few observations to perform the test. We’ll return to this at the end of the example.) Because the normal distribution has zero skewness and zero (“excess” or “Fisher”) kurtosis, the value of this statistic tends to be low for samples drawn from a normal distribution.

The test is performed by comparing the observed value of the statistic against the null distribution: the distribution of statistic values derived under the null hypothesis that the weights were drawn from a normal distribution. For this normality test, the null distribution for very large samples is the chi-squared distribution with two degrees of freedom.

The comparison is quantified by the p-value: the proportion of values in the null distribution greater than or equal to the observed value of the statistic.

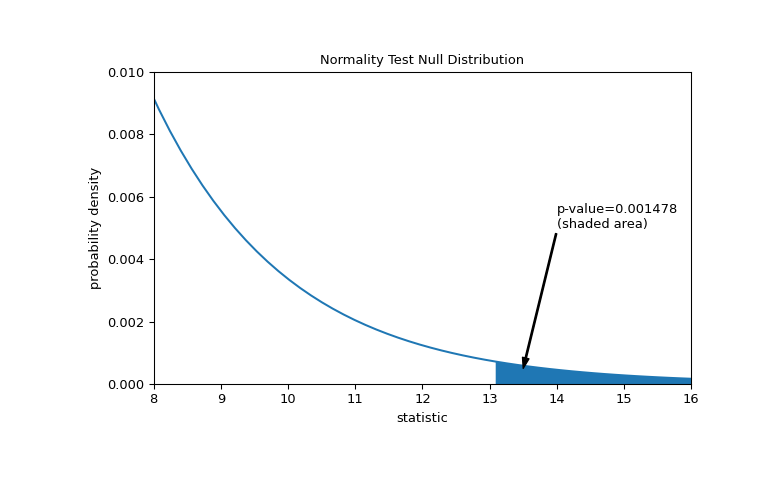
If the p-value is “small” - that is, if there is a low probability of sampling data from a normally distributed population that produces such an extreme value of the statistic - this may be taken as evidence against the null hypothesis in favor of the alternative: the weights were not drawn from a normal distribution. Note that:

The inverse is not true; that is, the test is not used to provide evidence for the null hypothesis.

The threshold for values that will be considered “small” is a choice that should be made before the data is analyzed [4] with consideration of the risks of both false positives (incorrectly rejecting the null hypothesis) and false negatives (failure to reject a false null hypothesis).

Note that the chi-squared distribution provides an asymptotic approximation of the null distribution; it is only accurate for samples with many observations. This is the reason we received a warning at the beginning of the example; our sample is quite small. In this case, scipy.stats.monte_carlo_test may provide a more accurate, albeit stochastic, approximation of the exact p-value.

Furthermore, despite their stochastic nature, p-values computed in this way can be used to exactly control the rate of false rejections of the null hypothesis [5] .