

17 Biggest Advantages and Disadvantages of Advertising
Advertising is the profession or activity of producing consumer marketing messages for commercial products or services. Although there are times when companies can advertise for free, this tactic typically involves paying another agency for space to promote something specific. The goal of this investment is to reach as many people as possible who are likely to pay for the items suggested in the ads.
When businesses start advertising, then it is essential for each firm to find their ideal customer. It is cheaper to create ads that work with a specific population group instead of working with generalized data. Companies can look at gender, age, education, income, and a person’s geographic location to determine if there is a strong likelihood that someone will become a customer.
Advertising can occur in a variety of ways. Outlets include television, radio, newspapers, and magazines. Some companies use billboards, the sides of buildings, or product packaging. Internet options continue to expand.
That’s why the advantages and disadvantages of advertising require a careful review. It could be a way to expand the influence of a brand, but this investment could also be a waste of money if not approached correctly.
List of the Advantages of Advertising
1. Advertising is what sets companies apart from each other. Advertising is the fastest way for an organization to prove the expertise it offers in its industry. This marketing approach allows a company to look at the specific pain points its goods or services address so that customers can independently decide if there is value available to consider. The free-market system allows consumers to make choices based on their needs for innovation, so the advantage here is that improved communication occurs from the business to the consumer.
2. Companies can reach multiple markets and population groups simultaneously. Advertising is one of the most straightforward ways to contact multiple demographics simultaneously. This investment helps a company to discover who their primary consumers are in better ways, along with the demographics to which they belong. Marketing through paid and unpaid platforms contributes to data that enables prospect duplication.
Advertising also allows a company to reach out to multiple new markets to judge how influential their marketing messages can be in the future.
3. Businesses can concentrate their advertising on a single population group. Advertising enables a company to target one population group specifically. We see this benefit daily through direct mail efforts, email marketing blasts, and television commercials. When you can time these messages to correspond with times or circumstances where a consumer feels a pain point, then a successful conversion is more likely to happen. It forms a natural networking opportunity that helps prospects engage with a brand message because they can acknowledge the created value proposition.
4. Advertising creates economic benefits at every level. The advertising economy in the United States is responsible for almost 20 million jobs. It is available in every market at each level, from ultra-local to international campaigns. This industry provides opportunities for almost every skill, ranging from sales-based approaches to creative careers like graphic design or writing. When successful outreach efforts occur, then businesses increase revenues. That creates even more jobs that support other companies at every level.
This cycle repeats itself every time a new advertising campaign occurs. Although there are no guarantees for success, a company must make itself known to its community for customers to become aware of its goods or services. That means there’s always a place for it.
5. The advertising industry creates a global culture. Every global event that involves participation, goods, or services requires advertising content to increase exposure. The budget for the Olympic Games in each cycle is several billion dollars. Companies use sponsorships, naming rights, and other strategies to increase brand awareness in a variety of ways. It gives us an opportunity to work together to support the common good at every level.
Even a group of businesses that support a youth soccer league get to take advantage of this benefit. Although the benefits are more localized with that support, it’s still creating a global culture within that community.
6. It gives an opportunity to create niche expertise presentations. The prevalence of PDF downloads, ebooks, whitepapers, and similar written content is a form of advertising that businesses use to prove their expertise. Advertising is moving toward a place where the value to the consumer is the priority instead of what the customer can do for the business. This benefit works for B2B and B2C firms because it shows people what can be done for them instead of telling them what can happen.
That’s why this form of advertising is so effective. It builds loyalty by focusing on relationships instead of relying on logo recognition or a tagline to stay at the top of the mind of possible consumers.
7. Advertising helps a customer make positive choices. Each customer has a different preference for specific products or services based on the pain points they encounter in life. Some choices are going to be more appealing than others, which is why businesses promote what they offer proactively. If someone can compare value propositions in real-time situations to determine what options provide the best value, then that ability increases the likelihood of a transaction taking place.
Businesses can provide specific or broad data about their goods or services to each demographic in unique ways to encourage this advantage. It is a benefit that can lead to tremendous growth opportunities when handled appropriate.
8. It is a straightforward way to support moral or social issues. Companies can support the public good by producing advertising campaigns that can bring more awareness to specific societal issues. Homelessness, cyberbullying, and similar concerns receive exposure in ways that wouldn’t be available to consumers without this marketing effort. Even though there are production costs to consider with this advantage, the value that occurs through increased revenues and economic activities from helping others more than makes up for the initial investment.
List of the Disadvantages of Advertising
1. Everyone is advertising. The average person gets exposed to over 2,000 brand messages every day because of advertising. That makes this marketing effort less effective unless there is a way for a company to rise above all of that noise. This disadvantage is the reason why you see businesses like Geico take unique approaches to this investment, using a mix of humor and character development to create something memorable.
Most people spend less than five seconds to determine if an advertisement is worth their attention. If that content fails, then the remainder of the ad gets forgotten.
2. Advertising cannot produce guaranteed results. Businesses take a gamble when they pay for advertising. This marketing effort doesn’t come with a guarantee. The companies that purchased TV spots during the 2020 Super Bowl were paying over $5 million for a segment. That’s a massive investment in something that may not produce additional revenues.
Although there is value in brand recognition, that outcome only translates to investment when it creates an eventual conversion. Having someone know that Flo represents Progressive isn’t beneficial if that person always uses public transportation. That’s why most small businesses focused on targeted, localized ads as a way to create results.
3. The cost of advertising can be a disadvantage to small businesses. The cost of TV advertising at local television stations is at least $5 for every 1,000 viewers during a 30-second commercial. Then you have the cost of creative development when taking this marketing approach to consider. By the time the first spot hits the air, a company has likely spent at least $10,000 to create the materials and purchase the airtime.
National spots are much more expensive. Businesses that purchase a 30-second television ad on a national broadcast spent an average of $115,000 per slot in 2019.
4. Potential customers may be on multiple platforms. If brand recognition is the goal of an advertising effort, then a business may need to invest in multiple platforms to gain the levels of familiarity they require. You can advertise in printed publications, online blogs, television, radio, Internet ad services, and all of the other traditional methods. A company might find over 100 different ways to reach their customers. When an advertising budget is financially limited, then finding out where most people are consistently becomes a top priority.
5. Advertising requires interesting materials to be useful. The best advertising efforts create memorable experiences for targeted consumers. If you’re a science-fiction fan, then you probably remember all of the exposure Taco Bell paid for itself in the movie Demolition Man. If you’re a fan of older superhero movies, then you may remember the giant Coca-Cola billboard blowing up in Superman. If a business can’t create such an experience, then the entire message gets forgotten.
This disadvantage means that every business must continuously invest in innovative marketing approaches to stay relevant. It’s also the reason why you see brands trying to copy the success that others find in this arena.
6. The “Fake News” movement tarnishes the reputation of advertisers. Politics in the United States has become a fractured, cantankerous space where anyone who doesn’t agree becomes an enemy. If a business advertises through a traditional media outlet that promotes a political agenda or news stories that someone finds to be disagreeable, then that company’s brand becomes directly tied to that experience. Although the people who agree will be more likely to purchase goods or services, those who don’t will boycott the agency indefinitely.
7. Advertising increases the risk of a brand message getting tarnished. Advertising can be memorable for all of the wrong reasons sometimes, leaving viewers to wonder what a business was thinking when putting a spot together. Qiaobi often receives credit for putting together one of the most racist commercials in history by having a Chinese woman forcing a black man into her washing machine after he whistles at her. Once the washing cycle is finished, a winking Asian man emerges.
Miracle Mattress put together a local advertising spot that mocked the events of 9/11, including having two stacks of mattresses fall on workers. Burger King unleashed a regional spot for their Texican Whopper that had the tagline of “The taste of Texas with a little spicy Mexican” – and the add featured a tall American cowboy and a short Mexican wrestler.
8. Most people consider advertising to be a nuisance. Extravagant advertising may have a positive effect on the economy. Still, it tends to harm consumers when the same promotions happen repetitively. This disadvantage occurs in the United States every two years during the election cycles when political ads take over the television and radio. It can also happen when spots frequently occur within the same broadcast or publication.
Hundreds of millions of dollars in advertising may get spent on a single election, exposing populations to competing messages that get monotonous and bothersome when they air several times per hour.
9. The targeted consumers may not see the marketing message from an advertising effort. New technologies make it easier than ever before for consumers to proactively opt-out of viewing advertisements. Popup blockers for Internet browsers can eliminate almost every ad that might display when users are online. Families can fast-forward through ads on broadcast networks when they record shows to watch. Some providers even offer tech that eliminates this marketing effort automatically.
Even if someone is watching live TV, an advertisement break creates an opportunity to walk away from the television. Companies can pay millions without ever knowing if their intended audience is available to watch what they’ve put together.
Advertising messages are an effort to persuade people to purchase specific goods or services. This outcome is also the goal of B2B transactions. A person must become convinced that one item is better over another. That’s why each ad offers a headline, subheading, body copy, image, and a call-to-action. It’s like a 30-second speech that shows how much value something has to a potential client.
Advertising isn’t the only way to get a message seen or heard. It can be more expensive to utilize than other marketing opportunities. That’s why it tends to be more popular with large corporations than sole proprietors and other small businesses.
The advantages and disadvantages of advertising balance cost with the opportunity to increase revenues and consumer awareness. Although there are no guarantees for success, this marketing option can produce immediate and memorable results.

Advantages and Disadvantages of Advertising

Advantages and Disadvantages of Advertising – Introduction
Advertising is a marketing strategy that aims to promote a specific product, cause, or service. The term “advertising” comes from the Latin word “adventure,” which means to turn someone’s attention towards something. A business, company, or organization tries to reach a large audience through advertising. Print media, digital campaigns, and social media are used for advertising today. Though advertisement has its advantages at the same time, it also has its disadvantages. This article aims to cover the advantages and disadvantages of advertising.
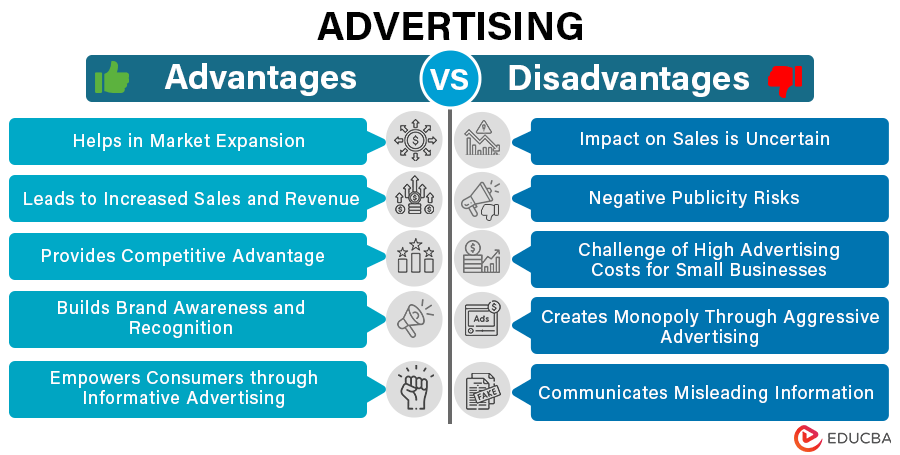
Advantages of Advertising
With advertising, a business or an organization needs a new product. It is the best method for communicating any information to old and new prospective customers. Here are the advantages of advertising:
Watch our Demo Courses and Videos
Valuation, Hadoop, Excel, Mobile Apps, Web Development & many more.
1. Helps in Market Expansion
Through advertising, businesses can reach new markets and demographics, expanding their customer base. This is especially true when you diversify your advertising channels and expand into all types of mediums such as social media, email, and even SMS via an SMS broadcast app .
2. Leads to Increased Sales and Revenue
One of the primary goals of advertising is to drive sales and boost revenue for businesses. Effective advertising campaigns can create awareness and generate interest, increasing sales.
3. Provides Competitive Advantage
Effective advertising can differentiate a product or service from competitors, giving a company a competitive edge.
4. Builds Brand Awareness and Recognition
Advertising helps create and maintain brand awareness. Consistent exposure to a brand through various channels increases the likelihood that consumers will remember and recognize the brand.
5. Empowers Consumers through Informative Advertising
Advertising provides a platform for businesses to educate consumers about their products or services. Detailed information helps consumers make informed decisions.
6. Offers Innovative Promotion
Advertising encourages businesses to innovate and improve their products or services to stay competitive. Companies often highlight new features or advancements in their advertising campaigns.
7. Powerful for Social Welfare Campaigns
Advertising is a powerful tool for promoting social causes and public awareness campaigns. It can gather support and resources for health, education, and environmental conservation issues.
8. Helps Differentiate Product in a Competitive Market
Advertising allows companies to highlight their products’ unique features and benefits, aiding product differentiation in a competitive market.
Disadvantages of Advertising
As we have seen the advantages, now let us look at some of the disadvantages of advertising:
1. Impact on Sales is Uncertain
Advertising, despite its significant costs, does not guarantee sales. Various factors, including market conditions, consumer preferences, and the competitive landscape, can influence an advertisement’s effectiveness in driving actual purchases.
2. Negative Publicity Risks
Advertising campaigns can backfire and lead to negative publicity, especially if the content is controversial, offensive, or misinterpreted by the audience. Negative publicity can harm a brand’s reputation and impact consumer perception.
3. Challenge of High Advertising Costs for Small Businesses
Advertising campaigns, especially on popular platforms or during prime time on television, can be extremely expensive, making it challenging for small businesses to compete.
4. Creates Monopoly Through Aggressive Advertising
In some cases, aggressive advertising by a dominant player in the market can create a monopoly , limiting consumer choice and stifling competition.
5. Communicates Misleading Information
Some advertisements may exaggerate or misrepresent product features, leading to consumer confusion and dissatisfaction.
6. Leads to Overconsumption and Greediness
Excessive advertising can contribute to a culture of overconsumption and greediness, encouraging people to buy more than they need.
7. Increase in Intrusiveness and Privacy Concerns
Advertisements often invade personal spaces, appearing on websites, social media, and emails, raising privacy concerns.
8. Cultural and Social Impact
Advertisements can reinforce stereotypes or promote unrealistic body images, contributing to societal pressures and expectations.
Final Thoughts
Advertising is a great weapon to stay ahead of your competitors and also helps create monopolies over products and services, but at the same time, there is no set of rules that can tell if an advertisement will work or not. Thus, advertising is a risk companies and manufacturers must take to stay relevant in this competitive market. Thus, there are advantages and disadvantages of advertising.
Recommended Articles
We hope this EDUCBA information on “Advantages and Disadvantages of Advertising” benefits you. You can view EDUCBA’s recommended articles for more information,
- Advantages and Disadvantages of Globalization
- What are the Advantages and Disadvantages of the Internet?
- Advantages and Disadvantages of Mobile Phones
- Advantages And Disadvantages of Budgeting

*Please provide your correct email id. Login details for this Free course will be emailed to you
By signing up, you agree to our Terms of Use and Privacy Policy .
Valuation, Hadoop, Excel, Web Development & many more.
Forgot Password?
This website or its third-party tools use cookies, which are necessary to its functioning and required to achieve the purposes illustrated in the cookie policy. By closing this banner, scrolling this page, clicking a link or continuing to browse otherwise, you agree to our Privacy Policy

Explore 1000+ varieties of Mock tests View more
Submit Next Question
🚀 Limited Time Offer! - 🎁 ENROLL NOW
Essay On Advertisement
500 words essay on advertisement.
We all are living in the age of advertisements. When you step out, just take a quick look around and you will lay eyes upon at least one advertisement in whichever form. In today’s modern world of trade and business, advertisement plays an essential role. All traders, big and small, make use of it to advertise their goods and services. Through essay on advertisement, we will go through the advantages and ways of advertisements.

The Various Ways Of Advertisement
Advertisements help people become aware of any product or service through the use of commercial methods. This kind of publicity helps to endorse a specific interest of a person for product sale.
As the world is becoming more competitive now, everyone wants to be ahead in the competition. Thus, the advertisement also comes under the same category. Advertising is done in a lot of ways.
There is an employment column which lists down job vacancies that is beneficial for unemployed candidates. Similarly, matrimonial advertisement help people find a bride or groom for marriageable prospects.
Further, advertising also happens to find lost people, shops, plots, good and more. Through this, people get to know about a nearby shop is on sale or the availability of a new tutor or coaching centre.
Nowadays, advertisements have evolved from newspapers to the internet. Earlier there were advertisements in movie theatres, magazines, building walls. But now, we have the television and internet which advertises goods and services.
As a large section of society spends a lot of time on the internet, people are targeting their ads towards it. A single ad posting on the internet reaches to millions of people within a matter of few seconds. Thus, advertising in any form is effective.
Benefits of Advertisements
As advertisements are everywhere, for some magazines and newspapers, it is their main source of income generation. It not only benefit the producer but also the consumer. It is because producers get sales and consumer gets the right product.
Moreover, the models who act in the advertisements also earn a handsome amount of money . When we look at technology, we learn that advertising is critical for establishing contact between seller and buyer.
This medium helps the customers to learn about the existence and use of such goods which are ready to avail in the market. Moreover, advertisement manages to reach the nooks and corners of the world to target their potential customers.
Therefore, it benefits a lot of people. Through advertising, people also become aware of the price difference and quality in the market. This allows them to make good choices and not fall to scams.
Get the huge list of more than 500 Essay Topics and Ideas
Conclusion of Essay On Advertisement
All in all, advertisements are very useful but they can also be damaging. Thus, it is upon us to use them with sense and ensure they are entertaining and educative. None of us can escape advertisements as we are already at this age. But, what we can do is use our intelligence for weeding out the bad ones and benefitting from the right ones.
FAQ on Essay On Advertisement
Question 1: What is the importance of advertisement in our life?
Answer 1: Advertising is the best way to communicate with customers. It helps informs the customers about the brands available in the market and the variety of products which can be useful to them.
Question 2: What are the advantages of advertising?
Answer 2: The advantages of advertising are that firstly, it introduces a new product in the market. Thus, it helps in expanding the market. As a result, sales also increase. Consumers become aware of and receive better quality products.
Customize your course in 30 seconds
Which class are you in.

- Travelling Essay
- Picnic Essay
- Our Country Essay
- My Parents Essay
- Essay on Favourite Personality
- Essay on Memorable Day of My Life
- Essay on Knowledge is Power
- Essay on Gurpurab
- Essay on My Favourite Season
- Essay on Types of Sports
Leave a Reply Cancel reply
Your email address will not be published. Required fields are marked *
Download the App


- Study Abroad Get upto 50% discount on Visa Fees
- Top Universities & Colleges
- Abroad Exams
- Top Courses
- Read College Reviews
- Admission Alerts 2024
- Education Loan
- Institute (Counselling, Coaching and More)
- Ask a Question
- College Predictor
- Test Series
- Practice Questions
- Course Finder
- Scholarship
- All Courses
- B.Sc (Nursing)

Sayantani Barman
Study Abroad Expert
Advantages and Disadvantages Of Advertisements IELTS Writing Task 2 consists of three sample answers provided below. The task requires the candidates to provide a tentative and argumentative answer for the question. The sample answers comprises two parts: Introduction and body. The introduction is a brief description about the topic. The body contains argumentative statements and tentative answers to support the test-taker's perspective. IELTS writing task 2 evaluates candidates based on the knowledge and views they have expressed. The areas that candidates are assessed on are grammar, vocabulary, and style. IELTS writing score is marked based on band scores. The band scores range from 0 to 9. Since the topics are very diverse, candidates must go through IELTS Writing practice papers to become familiar with a lot of topics.
Check: Get 10 Free IELTS Sample Papers Check: Register for IELTS Coaching - Join for Free Trial Class Now
Topic: Discuss the advantages and disadvantages of advertisements.
Band 6.5 IELTS Essay
Recently, it has become clear that advertising is growing in popularity across all industries. With the evolution of technology, there has been a significant global tendency toward brand publicity. Even though advertising has many benefits, there are some negatives as well. Both viewpoints will be discussed in detail along with a conclusion in this essay.
It is clear that advertising is growing in importance in the news industry. For publicity, a variety of resources, including social media and television, are useful. One advantage of advertising is that it aids in more effective business sales. For instance, tourism benefits from positive and appealing publicity. More people are aware of the product. The fact that advertisements provide consumers additional choices is another draw. This is also a great method to save time. One can choose from a wider range of computers, for instance, even without rummaging through markets. Thus, it appears that both the supplier and the customer have gained from advertising.
Commercial advertisements have the potential to target certain demographics. Such as children or the illiterate, who may be duped by deceptive marketing strategies. According to a recent story in Al-Ahram Weekly, ten agencies that marketed illegal drugs were shut down by the Egyptian government. Of these agencies' clients, 95% were ignorant locals living in underdeveloped areas. Another unfavorable effect is that some families could experience stress as a result of having to meet the high expectations of their dependents.
However, there are also certain drawbacks to advertising. This might lead to competition among various trades. For instance, some companies can spend more money to draw customers to their subpar goods. In this approach, consumers can be duped by false advertising. Second, excessive advertising makes it difficult for consumers to choose products. People occasionally purchase unnecessary items. Money is wasted in this way. Therefore, some people believe that advertising has a greater detrimental impact on business.
In conclusion, despite growing in popularity, advertising still has issues. It is advised that sincere advertising will produce better results and be more advantageous for all parties involved.
Band 7.5 IELTS Essay
The use of advertising in the promotion of goods and services is growing. Even if they are thought to be beneficial, ads can have a lot of harmful effects.
There are unquestionably a number of advantages to advertising. Due to the massive expansion of advertising across practically all mass media and almost all hoardings. This industry is anticipated to create a variety of job opportunities. In other words, it gives jobs to copywriters, painters, and designers who create logos, contents, and concepts for commercials.
Another benefit is that marketing may make it possible for communications about goods and services to contact potential consumers. This would enhance business sales. Additionally, clients may only be kept in the loop about recently announced products by advertising. As a result, individuals have more options when it comes to their favorite things, which raises their comfort level and living standards.
Advertising, though, can have a few drawbacks for consumers. Customers may feel confused about products as soon as corporations or businesses exaggerate. Even alter the facts about them for commercial gain, making it difficult for them to choose the ones that suit their tastes.
Facts also support the notion that product prices rise in direct proportion to increases in advertising costs. The reason might be that the massive price of advertisements is covered by the sales price of the promoted goods. As a consequence, the advertised goods may be more expensive than necessary. Finally, there is a good chance that customers may buy items that are unneeded. If they are unable to resist the attraction of things that are offered beyond what buyers expect. One would consider this tendency to be a monetary waste.
In summary, based on the aforementioned justifications. People may experience a variety of advantages as well as disadvantages from the expanding use of advertisements.
Band 8.5 IELTS Essay
In recent times, advertising has ingrained itself deeply into our daily lives. Almost every item is promoted through a variety of media, including YouTube, television, and websites. While some people favor this development, others are typically opposed to it. This is due to a number of factors. I will address various points of view and offer my stance on the subject in this essay.
People who think advertising is not particularly helpful are on one side of the debate. The primary justification for this opinion is that viewers of these advertising have a propensity to make unneeded purchases. Another factor is that some products do not perform as promised in advertisements. For instance, several coding boot programs these days provide a 100% guaranteed income for each graduate of their boot camp. But after careful research, it was discovered that a job may be a full-time employment, a part-time job, or an internship. It is clear why this argument has got momentum as a result.
A huge number of consumers will be impacted if there are reasons that contributed to the industry's volume being reduced. The ability to introduce new goods and opportunities to consumers is another advantage of advertisements. Despite the pointless place cards and posters, customers might end up consuming more affordable goods or purchasing their ideal house. So it seems to make sense that advertising has become a necessary component of modern business.
However, some people are in favor of advertisements. The market is currently incredibly competitive, which is the main explanation. It is better to publicize a business so as to increase its appeal among the general public rather than allowing it to go unnoticed. Marketing, for instance, has a significant impact on the proportion of sales of two goods that top companies release on the same day. According to a recent poll, properly promoted products increase sales by 40%. Even though some people or businesses like to use false advertising to sell their items, the buyer ultimately has the final say.
Check- IELTS Writing Samples
- General Increase in Anti Social Behaviours IELTS Writing Task 2
- Many People Go To University For Academic Study IELTS Writing Task 2
- Whether Or Not Someone Achieves Their Aims Is Mostly By A Question Of Luck IELTS Writing Task 2
- Copying Famous Personalities IELTS Writing Task 2
- Businesses Also Have Social Responsibility IELTS Writing Task 2
- Students Today can Access Information Online IELTS Writing Task 2
- Some people think that young people should be required to do unpaid work IELTS Task 2
- Walking Is a Good Exercise For Health IELTS Writing Task 2
- Children Are Facing More Pressures Nowadays from Academic, Social and Commercial Perspectives IELTS Writing Task 2
- People Should Follow The Customs And Traditions IELTS Writing Task 2
- Too Much Emphasis Is Placed On Testing These Days IELTS Writing Task 2
- Government and Individuals are Spending Too Much Money IELTS Writing Task 2
- Consumption of the World's Resources IELTS Writing Task 2
- Is it Right to Exclude Males or Females from Certain Professions IELTS Writing Task 2
- Ambition IELTS Writing Task 2
- People Today do not Feel Safe either at Home or when they are Out IELTS Writing Task 2
- Social Networking Sites have a Huge Negative Impact IELTS Writing Task 2
- Most Countries Believe That International Tourism Has Harmful Effects IELTS Writing Task 2
- Natural Resources IELTS Writing Task 2
- There is a General Increase in Anti-Social Behaviours IELTS Writing Task 2
IELTS IELTS Practice Papers
IELTS General Training Papers
IELTS IELTS Solved Papers
IELTS Overview
IELTS IELTS Exam Dates
IELTS IELTS Results
IELTS IELTS Writing Task 2
IELTS IELTS Reading
IELTS IELTS Speaking Topics
IELTS IELTS Preparation
IELTS IELTS Listening
IELTS IELTS Exam Pattern
IELTS IELTS Coaching in India
IELTS IELTS Cutoff
 (6).png?h=160&w=320&mode=stretch)
The Importance of Vitamins Reading Answers...
 (5).png?h=160&w=320&mode=stretch)
Vietnam Vets may have Cancer causing Parasites Reading Answers...
 (4).png?h=160&w=320&mode=stretch)
The Supermoon Reading Answers
 (3).png?h=160&w=320&mode=stretch)
You Mistakenly Bought the Wrong Medicine from a Pharmacy IELTS Writing Task 1...
Want to know more?
Ask questions to our experts
SUBSCRIBE TO OUR NEWS LETTER


IELTS Essay: Effects of Advertisements
by Dave | General Training | 0 Comment
This is an IELTS writing task 2 sample answer essay on the topic of the effects of advertising from the real IELTS exam.
Please consider supporting me on Patreon.com/howtodoielts to receive my exclusive IELTS Ebooks – you can even sign up for private live lessons with me!
People are annoyed or entertained by advertising but they are not affected by advertisements when making shopping decisions.
To what extent you agree or disagree?
Many believe that advertising does not influence actual buying decisions. In my opinion, though this may be true in the majority of instances, advertising is nonetheless extremely effective.
Those who feel that advertising serves little useful purpose can point to the most typical response from consumers. Whether they are on the internet, on television, or in real life, most individuals endeavor to skip or ignore ads. There are only isolated cases when a shopper will see an ad and as a direct result make a purchase. For example, YouTube advertisements have included a feature to “skip ads” that has become an automatic response from nearly every viewer. Even when forced to watch ads, such as in the cinema before a film starts, consumers are unlikely to remember the products or services and there is a strong chance they will take out their phones to completely shut out distracting commercials.
Nonetheless, advertisements have a limited yet powerful efficacy. The strongest evidence for this comes from the enduring health of the advertising industry. This flourishing is because advertisements only need to yield results occasionally in order to be successful. For example, a fast food company such as McDonald’s or KFC might run an advertisement with the profitable expectation of only converting 1% of viewers, accepting the 99% failure rate as part of the business. Moreover, the 1% who make an immediate purchase are only one piece of the overall strategy. Advertising raises brand awareness and may lead to later consumption and even have a subliminal effect that is difficult to trace.
In conclusion, advertising is not designed to effective at all times but instead to slowly influence and achieve the occasional success. In the aggregate, it is worthwhile for corporations to advertise even if the most common outcome is to be ignored.
1. Many believe that advertising does not influence actual buying decisions. 2. In my opinion, though this may be true in the majority of instances, advertising is nonetheless extremely effective.
- Paraphrase the overall essay topic.
- Write a clear opinion. Read more about introductions here .
1. Those who feel that advertising serves little useful purpose can point to the most typical response from consumers. 2. Whether they are on the internet, on television, or in real life, most individuals endeavor to skip or ignore ads. 3. There are only isolated cases when a shopper will see an ad and as a direct result make a purchase. 4. For example, YouTube advertisements have included a feature to “skip ads” that has become an automatic response from nearly every viewer. 5. Even when forced to watch ads, such as in the cinema before a film starts, consumers are unlikely to remember the products or services and there is a strong chance they will take out their phones to completely shut out distracting commercials.
- Write a topic sentence with a clear main idea at the end.
- Explain your main idea.
- Develop it with specific examples.
- Keep developing it fully.
- You can have some long sentences like this to really argue your point.
1. Nonetheless, advertisements have a limited yet powerful efficacy. 2. The strongest evidence for this comes from the enduring health of the advertising industry. 3. This flourishing is because advertisements only need to yield results occasionally in order to be successful. 4. For example, a fast food company such as McDonald’s or KFC might run an advertisement with the profitable expectation of only converting 1% of viewers, accepting the 99% failure rate as part of the business. 5. Moreover, the 1% who make an immediate purchase are only one piece of the overall strategy. 6. Advertising raises brand awareness and may lead to later consumption and even have a subliminal effect that is difficult to trace.
- Write a new topic sentence with a new main idea at the end.
- Explain your new main idea.
- Include specific details and examples.
- Continue developing it…
- as fully as possible!
- This paragraph can be slightly longer since you agree with it.
1. In conclusion, advertising is not designed to effective at all times but instead to slowly influence and achieve the occasional success. 2. In the aggregate, it is worthwhile for corporations to advertise even if the most common outcome is to be ignored.
- Summarise your main ideas.
- Include a final thought. Read more about conclusions here .
What do the words in bold below mean? Make some notes on paper to aid memory and then check below.
Many believe that advertising does not influence actual buying decisions . In my opinion, though this may be true in the majority of instances , advertising is nonetheless extremely effective .
Those who feel that advertising serves little useful purpose can point to the most typical response from consumers . Whether they are on the internet, on television, or in real life, most individuals endeavor to skip or ignore ads. There are only isolated cases when a shopper will see an ad and as a direct result make a purchase . For example, YouTube advertisements have included a feature to “skip ads” that has become an automatic response from nearly every viewer . Even when forced to watch ads, such as in the cinema before a film starts, consumers are unlikely to remember the products or services and there is a strong chance they will take out their phones to completely shut out distracting commercials .
Nonetheless, advertisements have a limited yet powerful efficacy . The strongest evidence for this comes from the enduring health of the advertising industry . This flourishing is because advertisements only need to yield results occasionally in order to be successful. For example, a fast food company such as McDonald’s or KFC might run an advertisement with the profitable expectation of only converting 1% of viewers, accepting the 99% failure rate as part of the business. Moreover , the 1% who make an immediate purchase are only one piece of the overall strategy . Advertising raises brand awareness and may lead to later consumption and even have a subliminal effect that is difficult to trace .
In conclusion, advertising is not designed to effective at all times but instead to slowly influence and achieve the occasional success. In the aggregate , it is worthwhile for corporations to advertise even if the most common outcome is to be ignored .
For extra practice, write an antonym (opposite word) on a piece of paper to help you remember the new vocabulary:
advertising commercials, banner ads, pop-ups, etc.
influence impact, affect
actual real
buying decisions consumer choices
though this may be true in the majority of instances this might be the case most of the time
nonetheless regardless of
extremely effective very impactful
serves little useful purpose doesn’t have much impact
most typical response most common action
consumers people who buy things
endeavor try hard
skip go past
ignore not pay attention to
isolated cases individual situations
shopper buyer
as a direct result the clear effect
purchase buying something
included also has
feature an element of a product
automatic response without thinking action
nearly every viewer almost everyone watching
forced made to
unlikely probably not going to happen
services such as delivery, taxis, online streaming, etc.
strong chance lots of likelihood
completely shut out distracting commercials ignore 100% annoying ads
limited not wide and complete
powerful efficacy real effect
strongest evidence greatest support
comes from results from
enduring health continue to work
industry field or area
flourishing doing really well
yield results are successful
occasionally sometimes
run an advertisement play or make a commercial, ad
profitable expectation think they will make money from it
converting making successful acquisitions
accepting being content with
failure rate as part of not being successful as a piece of
moreover also
immediate purchase buying right away
overall strategy whole aim
raises brand awareness make people know more about your company/product
subliminal effect unconscious impact
trace follow back
at all times never stopping
slowly influence impact lightly
achieve affect
in the aggregate altogether
worthwhile worth the time
even if despite
most common outcome likely result
ignored not paid attention to
Pronunciation
Practice saying the vocabulary below and use this tip about Google voice search :
ˈædvətaɪzɪŋ ˈɪnflʊəns ˈækʧʊəl ˈbaɪɪŋ dɪˈsɪʒənz ðəʊ ðɪs meɪ biː truː ɪn ðə məˈʤɒrɪti ɒv ˈɪnstənsɪz ˌnʌnðəˈlɛs ɪksˈtriːmli ɪˈfɛktɪv sɜːvz ˈlɪtl ˈjuːsfʊl ˈpɜːpəs məʊst ˈtɪpɪk(ə)l rɪsˈpɒns kənˈsjuːməz ɪnˈdɛvə skɪp ɪgˈnɔː ˈaɪsəleɪtɪd ˈkeɪsɪz ˈʃɒpə æz ə dɪˈrɛkt rɪˈzʌlt ˈpɜːʧəs ɪnˈkluːdɪd ˈfiːʧə ˌɔːtəˈmætɪk rɪsˈpɒns ˈnɪəli ˈɛvri ˈvjuːə fɔːst ʌnˈlaɪkli ˈsɜːvɪsɪz strɒŋ ʧɑːns kəmˈpliːtli ʃʌt aʊt dɪsˈtræktɪŋ kəˈmɜːʃəlz ˈlɪmɪtɪd ˈpaʊəfʊl ˈɛfɪkəsi ˈstrɒŋgɪst ˈɛvɪdəns kʌmz frɒm ɪnˈdjʊərɪŋ hɛlθ ˈɪndəstri ˈflʌrɪʃɪŋ jiːld rɪˈzʌlts əˈkeɪʒnəli rʌn ən ədˈvɜːtɪsmənt ˈprɒfɪtəbl ˌɛkspɛkˈteɪʃən kənˈvɜːtɪŋ əkˈsɛptɪŋ ˈfeɪljə reɪt æz pɑːt ɒv mɔːˈrəʊvə ɪˈmiːdiət ˈpɜːʧəs piːs ˈəʊvərɔːl ˈstrætɪʤi ˈreɪzɪz brænd əˈweənəs sʌbˈlɪmɪnl ɪˈfɛkt treɪs æt ɔːl taɪmz ˈsləʊli ˈɪnflʊəns əˈʧiːv ɪn ði ˈægrɪgɪt ˈwɜːθˈwaɪl ˈiːvən ɪf məʊst ˈkɒmən ˈaʊtkʌm ɪgˈnɔːd
Vocabulary Practice
I recommend getting a pencil and piece of paper because that aids memory. Then write down the missing vocabulary from my sample answer in your notebook:
Many believe that a_____________g does not i_______________________________s . In my opinion, t__________________________________________________s , advertising is n______________s e_____________________e .
Those who feel that advertising s_________________________e can point to the m_____________________e from c______________s . Whether they are on the internet, on television, or in real life, most individuals e____________r to s_____p or i__________e ads. There are only i______________s when a s____________r will see an ad and a___________________t make a p___________e . For example, YouTube advertisements have i___________d a f__________e to “skip ads” that has become an a______________________e from n____________________r . Even when f________d to watch ads, such as in the cinema before a film starts, consumers are u___________y to remember the products or s_________s and there is a s_______________e they will take out their phones to c____________________________________________s .
Nonetheless, advertisements have a l__________d yet p_________________y . The s_____________________e for this c____________m the e_________________h of the advertising i___________y . This f_______________g is because advertisements only need to y_____________s o___________y in order to be successful. For example, a fast food company such as McDonald’s or KFC might r_______________________t with the p______________________n of only c____________g 1% of viewers, a__________g the 99% f____________e a_____________f the business. M____________r , the 1% who make an i_____________________e are only one p______e of the o________________y . Advertising r____________________s and may lead to later consumption and even have a s___________________t that is difficult to t________e .
In conclusion, advertising is not designed to effective a_____________s but instead to s_______________e and a__________e the occasional success. I_____________________e , it is w_______________e for corporations to advertise e________f the m________________________e is to be i_________d .
Listening Practice
Learn more about this topic in the video below and practice with these activities :
Reading Practice
Read more about this topic and use these ideas to practice :
https://www.nytimes.com/2021/04/18/business/media/subscriptions-advertising-media.html
Speaking Practice
Practice with the following speaking questions from the real IELTS speaking exam :
- Do people in your country shop at malls or street markets?
- Is online shopping common?
- Is it better to shop alone or with friends?
- Why is online shopping becoming more popular?
- Is shopping a waste of time?
Writing Practice
Practice with the related IELTS essay topic below:
Some believe that people will purchase a product based on their needs and advertising is not needed.
To what extent do you agree or disagree?
IELTS Writing Task 2 Sample Answer Essay: Advertisements & Needs (Real Past IELTS Exam/Test)
Recommended For You

Latest IELTS Writing Task 1 2024 (Graphs, Charts, Maps, Processes)
by Dave | Sample Answers | 147 Comments
These are the most recent/latest IELTS Writing Task 1 Task topics and questions starting in 2019, 2020, 2021, 2022, 2023, and continuing into 2024. ...

Recent IELTS Writing Topics and Questions 2024
by Dave | Sample Answers | 342 Comments
Read here all the newest IELTS questions and topics from 2024 and previous years with sample answers/essays. Be sure to check out my ...

Find my Newest IELTS Post Here – Updated Daily!
by Dave | IELTS FAQ | 18 Comments

IELTS Cambridge 16 Essay: Advertising New Products
by Dave | Cambridge 16 | 9 Comments
This is an IELTS writing task 2 sample answer essay from the newly released Cambridge 16 on the topic of businesses nowadays emphasising that their products ...
IELTS Cambridge 16 Essay Task 1: Sugar Cane
by Dave | IELTS Cambridge 16 | 6 Comments
This is an IELTS writing task 1 sample answer essay on the topic of the process of how sugar cane is produced. Be ...

IELTS Cambridge 16 Essay: History of a House or Building
by Dave | Cambridge 16 | 17 Comments
This is an IELTS writing task 2 sample answer essay on the topic of the history of a house or building and why people are interested ...
Submit a Comment Cancel reply
You must be logged in to post a comment.
Exclusive Ebooks, PDFs and more from me!
Sign up for patreon.
Don't miss out!
"The highest quality materials anywhere on the internet! Dave improved my writing and vocabulary so much. Really affordable options you don't want to miss out on!"
Minh, Vietnam
Hi, I’m Dave! Welcome to my IELTS exclusive resources! Before you commit I want to explain very clearly why there’s no one better to help you learn about IELTS and improve your English at the same time... Read more
Patreon Exclusive Ebooks Available Now!
BUS615: International Marketing
Marketing Communication Methods
Should we use traditional marketing or digital marketing? This question is top-of-mind for all marketers. The decision to use one platform or outlet can mean the difference between success or failure. Evaluating each option is time-consuming but essential for forming a cohesive, meaningful marketing effort. This section looks at a variety of traditional media activities, including advertising, public relations, sales promotions, and direct marketing. It also explores digital marketing, including websites, interactive tools, content marketing, SEO (search engine optimization), and other strategies. As you read, consider the criteria you might need to use when determining which strategies are right for your organization and offerings.
Advertising: Pay to Play
Advantages and disadvantages of advertising.
The primary disadvantage of advertising is cost. Marketers question whether this communication method is really cost-effective at reaching large groups. Of course, costs vary depending on the medium, with television ads being very expensive to produce and place. In contrast, print and digital ads tend to be much less expensive. Along with cost is the question of how many people an advertisement actually reaches. Ads are easily tuned out in today's crowded media marketplace. Even ads that initially grab attention can grow stale over time. While digital ads are clickable and interactive, traditional advertising media are not. In the bricks-and-mortar world, it is difficult for marketers to measure the success of advertising and link it directly to changes in consumer perceptions or behavior. Because advertising is a one-way medium, there is usually little direct opportunity for consumer feedback and interaction, particularly from consumers who often feel overwhelmed by competing market messages.
Ultimate Guide to IELTS Advantages Disadvantages Essays
11 min read
Updated On Jun 12, 2024
Share on Whatsapp
Share on Email
Share on Linkedin

IELTS Writing Prediction Questions & Answers : Free PDF
We have all made a list of pros and cons when faced with a difficult decision. An advantages disadvantages essay in IELTS Writing is kind of like an organized pros and cons list.
In this article, we will go over the structure of Task 2 advantages and disadvantages, how to write an advantages and disadvantages essay and go over a few IELTS sample essays of this type.
Understanding the Question and Structure of the IELTS Advantages Disadvantages Essay
The IELTS advantages disadvantages essay is a question type you will come across in IELTS Writing Task 2 .
You will be asked to write about the benefits and drawbacks of the topic given. It can be worded in different ways. Let’s see some examples.
- At the present time, the population of some countries includes a relatively large number of young adults, compared with the number of older people. Do the advantages of this situation outweigh the disadvantages?
- Discuss the advantages and disadvantages of mobile phones in our daily lives.
- Some companies and organizations require their employees to wear uniforms. What are the advantages and disadvantages of wearing a uniform?
- A lot of places in the world rely on tourism as a main source of income. Unfortunately, tourism can also be a source of problems if it is not managed correctly. Describe the advantages and disadvantages of tourism in the modern world. Do you think that the benefits of tourism outweigh its drawbacks?
- What are the pros and cons for children watching television? Give reasons for your answer and include any relevant example from your knowledge or experience.
- Globalization has both advantages and disadvantages. Discuss both and give your opinion.
Discussing the Question of Advantages and Disadvantages Essay IELTS
In some questions of Task 2 Advantages and Disadvantages essay, you will be asked to share your opinion. However, in most cases, discussing the pros and cons/benefits and drawbacks/advantages and disadvantages is enough.

The first part of the question for advantage and disadvantage essays in IELTS Writing Task 2 will always be a statement. In the second part, you will get to know whether you have to discuss only the benefits and drawbacks or add your opinion along with it. So, no need to worry!
As you can see in the image above, the first question asks you to share your opinion, whereas in the second, you will have to discuss the advantages and disadvantages.
Structure of the IELTS Advantages Disadvantages Essay
The IELTS Essay writing task is quite challenging as it requires you to write an essay on an unseen topic from any walk of life – it can range from social issues to environmental discourse. To make it easy, you can practice advantage and disadvantage essay topics based on the following structure breakdown.
- Paraphrase the question statement.
- State what the following paragraphs will discuss.
- Mention your viewpoint (if asked in the question)
- Discuss the advantages.
- Explain the benefits with examples in 2-3 sentences.
- Discuss the disadvantages.
- Explain the drawbacks with examples in 2-3 sentences.
- Summarize the benefits and drawbacks discussed in the essay.
Remember that there is no right or wrong structure for advantages and disadvantages writing task 2 . However, if you use this, it will enable you to plan your essay in no time during the exam.
Join us in our IELTS webinars to learn tricks to handle IELTS Writing Task 2 essays! Explore Now!
How to Plan Your Task 2 Advantages and Disadvantages Essay?
The planning for writing any essay type in IELTS Writing Task 2 requires around 5 minutes.
The process covers essential aspects such as analysis of the question, organization of the points to be included, identifying relevant vocabulary, and understanding the marking criteria to obtain a good band score .
The following points will provide a concise guide on how to plan your answer for the advantages and disadvantages of essays in IELTS academic writing task 2 and save some time to revise your response.
- To answer the advantages disadvantages essay questions in IELTS Writing Task 2, first you have to identify the keywords and instructions in the question to discuss the positives and negatives of the statement.
- Plan your structure, including your main arguments, advantages, and disadvantages, to present your answer in a well-structured manner.
- Take at least 10 minutes to analyze and understand the given statement and evaluate its pros and cons.
- Organize your thoughts and provide a clear and concise response.
- Using appropriate writing task 2 vocabulary and phrases (lexical resource) is important. But avoid stuffing too many words into irrelevant places.
- Ensure that your response remains relevant to the given topic.
- Understand the IELTS writing band descriptors like Task Response, Coherence and cohesion, Lexical resource, Grammatical range and accuracy to obtain a high band score .
How to Write an Advantages Disadvantages Essay for IELTS Writing Task 2?
Once you have planned your advantage and disadvantage essay for Writing Task 2, it is time to write down your answer.
Writing The Essay Introduction
The first thing that you have to do is to write an introduction for an advantages disadvantages essay.
- Your introduction should paraphrase the topic of the essay and try to use different vocabulary/synonyms for the words in the topic, wherever possible.
- Then, give a brief idea about what could be expected in the essay, i.e. the advantages and the disadvantages of the concerned topic.
- Finally, state which side you think weighs the most (when asked for an opinion.)
Body Paragraphs for Advantages And Disadvantages Essay IELTS
Although there is no strict rule about the number of paragraphs forIELTS essays, it is better to limit the number to two. It will not only help you to follow the word count but also keep your essay concise.
Body Paragraph 1
- It should state the advantage/s of the topic.
- This should be backed by practical points, and the examples would be even better.
- Day-to-day incidents and instances can be brought to notice.
Body Paragraph 2
- It should state the disadvantage/s of the topic.
- This as well should be supported by valid points, and the daily incidents and examples can be highlighted to back your points.
How To Write An Essay Conclusion?
You should conclude the topic by providing a summary of the points put forth in the entire essay and how the advantages or disadvantages of the topic outweigh the other (if applicable).
- Make sure to end the essay with a well rounded conclusion.
- Link your ideas discussed in the essay to ensure cohesion and coherence.
- The question/s along with the essay statement should be answered.
To help you to understand this type of essay better, given below are some essential essay vocabulary you must know as well as a sample essay with a detailed outline. We’ve provided you with ample IELTS advantages and disadvantages essay topics to help you hone your essay writing skills.
IELTS Essay Vocabulary
A strong command of vocabulary is crucial for writing an effective advantages disadvantages essay in IELTS Writing Task 2.
Your proficiency in English language vocabulary will be evident in how expertly you can select the most suitable expressions to convey precise meanings. Diversifying your vocabulary will enable you to incorporate a greater variety of words in your essays. However, it is important to note that overusing uncommon words and phrases can reduce the relevance of your answer.
Wondering the Trick to Score a Band 8 in Writing Task 2? Know the Secret!
Tips for Mastering Advantages and Disadvantages Essay
Writing an essay on IELTS advantage disadvantage essay topics needs careful preparation and planning. Here are some tips that you can use to write a high quality essay:
- Understand the Question: Make sure you understand the question and what is expected of you before you begin writing. Decide which advantages and disadvantages you need to talk about and if you need to share your opinion.
- Generate Ideas: Spend a few minutes identifying the benefits and drawbacks of the selected subject. List the main ideas and instances you’ll utilize to support your claims.
- Structure Your Essay: Write your essay with a logical and obvious structure. Begin with an introduction that briefly summarizes your key points and states the subject. After that, give each benefit and drawback a paragraph of its own, and then wrap up by summarizing your points in the conclusion.
- Use Linking Words: To connect your thoughts and create a smooth writing flow, use a range of linking words and phrases, like “furthermore,” “however,” “on the other hand,” and “in conclusion.”
- Support Your Points: Give particular instances, figures, or anecdotes to back up each benefit and drawback you discuss. This will improve the persuasiveness of your arguments and raise your score.
- Plan your Time Effectively: During the exam, manage your time well. Plan your essay for a few minutes, then concentrate on creating paragraphs that are precise and to the point. At the conclusion, give yourself some time to review and make any required changes.
- Practice is the Key to Success: It is the ultimate truth. The more you practice, the more you will become efficient in planning, organizing and structuring your advantages disadvantages essay for IELTS Writing Task 2. So, take up more writing practice tests and make the best use of them.
Ensure you’re using the right structure for IELTS Advantages and Disadvantages Essays!
Get Evaluated for Free!
Advantages and Disadvantages IELTS Essay Questions and Sample Answers
Given below are some sample questions for the advantages and disadvantages type of essay and band 9 methodologies of answering them.
Sample Question 1
Sample answer.
Foreign education has become one of the most sought-after ventures in this day and age. A majority of students plan on pursuing higher education in a foreign nation, especially when it comes to a master’s degree. One of the reasons why studying abroad has become such a popular phenomenon is the relaxation of travel laws and procedures across the world. However, there are pros and cons to studying abroad and the following paragraphs will explore the topic and elaborate on why the advantages outweigh the disadvantages.
One of the primary reasons for studying abroad is the presence of a more refined and sophisticated education system in several first-world countries. It is common for students from underdeveloped or developing countries like Brazil, China, India, Argentina and other countries to look for better opportunities than the ones available in their native country in terms of academics. Also, residing in a foreign country helps individuals to gain international exposure and also helps them develop social and interpersonal skills, which are extremely important for being eligible for lucrative job opportunities.
Nevertheless, there are numerous drawbacks to travelling abroad for education. First of all, from the beginning of applying to a foreign university to staying in the host country for the entire duration of your degree, it is an exorbitant affair. Such a costly endeavour is often unaffordable for the household of many people. That being said, becoming accustomed to the norms and conventions of an unfamiliar country can be a tough ordeal for many due to differences in culture and social traditions.
Finally, I would like to conclude by saying that foreign education can be a blessing if it is financially feasible for aspiring students. That being said, the benefits of studying abroad surpass the drawbacks for the same.
Check Out – How to Plan an IELTS Writing Task 2 Essay (Best Strategy)
Sample Question 2
Globalization has been one of the most significant phenomena in the last few decades, and it has changed several aspects of human society both economically and socially. There has been remarkable progress in terms of economic and financial development for developing countries due to the expansion of global organizations. However, there are several drawbacks to this rapid progress that need to be addressed. Evidently, globalization has more advantages than disadvantages and the following paragraphs will elaborate on the topic and justify these views.
First of all, the most advantageous aspect of globalization is the advent of numerous international companies and franchises in developing countries. Ever since global brands and corporations have expanded their operations in countries such as India, China, Sri Lanka and many more, there has been a notable increase in employment in these countries. Additionally, due to the remarkable rise in the number of imports and exports, people from third world countries now have access to a vast catalogue of products and services that were previously unattainable.
That being said, there are drawbacks to globalization that create concerning issues for a sizable portion of the global population. One of the most disturbing consequences faced is the exploitation of labour. Many corporations are known to outsource their operations to developing countries due to cheap labour costs. This enables them to accomplish their manufacturing operations without having to provide proper remuneration. Also, due to the use of inexpensive labour, the quality of products is diminished, and customers receive inferior products.
In conclusion, there is no doubt that the effects of globalization are not entirely positive or negative. Nonetheless, the benefits brought by this occupation outweigh the drawbacks.
Practice Advantages Disadvantages Essays IELTS with IELTSMaterial
There is no doubt that you are preparing for the IELTS Writing Task 2. So, we would recommend you to take up advantage and disadvantage essay topics regularly. The more you practice, the better you will become at solving the IELTS Writing test and answers within the dedicated timeframe.
Check out our well-reviewed IELTS Writing study guide , which includes self-explanatory lessons and sample answers. If you need more guidance, don’t hesitate to contact our IELTS specialists . Make the necessary preparations to improve your score on the IELTS Speaking test and get a Band 8+.
More Related IELTS Advantages Disadvantages Essay Topics:
- Advantages and disadvantages of online shopping essay
- Globalization advantages and disadvantages essay
- Advantages and disadvantages of online education essay
- Advertisement advantages and disadvantages ielts essay
- IELTS Writing Actual Test & Band 8.0 Advantage/Disadvantage Essay – Topic: Travel
- IELTS Writing Actual Test In 2016 & Band 8.0 Sample Advantage/Disadvantage Essays
- IELTS Advantage/Disadvantage Essay Of Band 8.5 – Topic: Traffic & Accommodation
- IELTS Writing Actual Test & Band 9.0 Advantage/Disadvantage Essay – Topic: Gap Year
- IELTS Writing Actual Test In April 2016 – Band 8.5 Advantage/Disadvantage Essay
- Academic IELTS Writing Task 2 Topic & Band 8.5 Advantage/Disadvantage Essay
- IELTS Writing Task 2 Advantage/Disadvantage Essay Of Band 8.0– Topic: Youth & Community
- Advantage/Disadvantage Essay – Topic: Students
- Increase your Speaking & Writing Score with Synonyms and Antonyms
- Useful Structures to Help You Get Band 7.5+ in IELTS Writing
- IELTS Band 9 Essay Samples: Writing Task 2 Insights for IELTS Learners
- IELTS Writing Task 2 Advantage/Disadvantage Essay Topic: Differences between countries become less evident each year
- Children Are Often Told that They Can Achieve Anything if They Try Hard Enough
- Advantages and Disadvantages of Government Providing Free Healthcare – IELTS Writing Task 2
- People now have the Freedom to Work and live Anywhere in the World- IELTS Writing Task 2
Frequently Asked Questions
What is an advantage/disadvantage essay? How do you identify that the essay falls under this category?
Is it mandatory to put advantages and disadvantages separately in two paragraphs or can I club them?
In case of questions where advantages outweigh disadvantages, I might have to write disadvantages first. Will it affect my score?
Do I have to write more than one point for advantages and disadvantages essays for IELTS Writing?
When can I note down the voc
What will happen if I write the exact question statement of the advantages disadvantages essay topic?
What is the importance of the topic sentence of an advantages disadvantages essay?
Is it mandatory to follow the word limit given with the IELTS advantages and disadvantages essay?
What can I do if my IELTS advantages and disadvantages essay is less than 250 words?
Is there any upper limit for word count for IELTS advantages and disadvantages essay?
Explore IELTS Writing

Start Preparing for IELTS: Get Your 10-Day Study Plan Today!
Kasturika Samanta
Kasturika is a professional Content Writer with over three years of experience as an English language teacher. Her understanding of English language requirements, as set by foreign universities, is enriched by her interactions with students and educators. Her work is a fusion of extensive knowledge of SEO practices and up-to-date guidelines. This enables her to produce content that not only informs but also engages IELTS aspirants. Her passion for exploring new horizons has driven her to achieve new heights in her learning journey.
Explore other Advantage Disadvantage Essays

Raajdeep Saha

Nehasri Ravishenbagam

Janice Thompson
Post your Comments
10 comments.

Ashlin Devi
Posted on Oct 5, 2023
Nowdays, technologies are in high demand. People are possessed with their own computers and cell phones, so it is quite easy for them to do their job at home. Even though it is acknowledged with several points that working from home is quite easier, the essay will argue that the drawbacks of working from home will outweigh its strength. The main disadvantages are ineffective communication and the relationship amongst people becoming distant. First of all, people need internet to communicate. The internet connectivity is very poor at times, especially in the remote areas. Furthermore, during virtual meetings, discussion gets difficult due to connection issues where meeting is not worthwhile since no voice or no video. Moreover, working from home gives distance amongst people where you will not be able to have interact with colleague. Face-to-face discussion is very important where you get to work more effectively and efficiently. On the other hand, working from home is indeed benefit. People do not have to travel to reach work. The time which are spend on travelling, can be utilized on other activities such as house cores, leisure activities or even can work extra hours to meet the given deadline. Furthermore, people get flexibility in working hours, since there are no superior workers supervising employee. To conclude, there are some strengths on working from home but drawbacks overweigh strengths since working from home is not as easy task as people think since ineffective communication and people interaction is very important.
ria mahajan
Posted on Oct 6, 2023
Overall Band 5.5 Main ideas are relevant, but some are insufficiently developed and lack clarity, while some supporting arguments and evidences are missing for the question.Simple vocabulary is used accurately but the range does not permit much variation in expression.A mix of simple and complex sentence forms is used but flexibility is limited. For detailed analysis,you can avail a Free trial class Find the link below: https://ieltsmaterial.com/signup-1/ or you may reach out to us: +91 8929053019
Posted on May 15, 2023
More students prefer foreign colleges and universities. Although studying abroad is costly, a concerning drawback, the global exposure a student gets is the primary benefit that outweighs any disadvantage. On the one hand, pursuing education abroad is quite expensive, which is the primary concern. The tuition fee in the universities of developed countries is relatively high, and it is challenging for a student from an average financial background to afford it. Furthermore, people need to find part-time jobs to handle their daily expenditures. For example, a study by the University of Dubai revealed a drop of 25% in the enrolment of international students in the year 2023 compared to 2022 among the Gulf nations due to an increase in college fees. However, many universities provide scholarships to merit students, and youth can get global exposure which is of considerable significance. The primary benefit of choosing foreign universities is that the pupils get excellent global exposure. In many developed nations, the education system is quite advanced and leans towards practical knowledge than textbook learning. Moreover, people can build a strong network with locals which helps them in their professional careers. For instance, one of my friends, Ravi, who runs a garment business, is able to expand his work abroad due to the exposure he got while pursuing his master’s in abroad and the network he built during his education period. This is why youth prefer foreign universities. In conclusion, although studying abroad is quite expensive, the undisputed benefit of getting global exposure surpasses any hindrance.
Posted on Dec 3, 2022
“Nowadays online shopping becomes more popular than in-store shopping. Is it a positive or a negative development? Give your reasons and examples.” Isn’t this an opinion question though you have categorized it under advantages and disadvantages? I believe we have to describe only one aspect in our body paragraphs rather than describing both positive and negative aspects?
Posted on May 29, 2022
Nowadays, studying abroad is a new trend among students. Undoubtedly, there are positive and negative aspects of studying in a foreign country. However, the benefits of attending colleges and universities in a foreign country outweigh the drawbacks. The next couple of paragraphs will explain the topic and justify these viewpoints.
To begin with, studying abroad has several advantages for students. For instance, a student who is studying in a foreign country will probably improve language skills better than others. Learning a foreign language is extremely significant in a global environment. Moreover, living outside of a home country will enhance students’ worldview thanks to the culture of the host country. Therefore, it can be said that studying abroad paws the way for great career options.
However, there are undesired sides to education in a foreign state. One of them is education expenditure. Studying abroad might be expensive. Thus, it might lead to a huge economic burden for both student and his family. When a student moves to another country for education, he must face several challenges caused by living alone. For instance, some students might have some psychological problems during the first couple of weeks following their move. It can be claimed that being homesick is a common problem among young students.
In conclusion, having a graduate degree from a foreign country has both negative and positive sides. Although there are significant advantages, the benefits of studying abroad surpass the drawbacks for the same.
Posted on May 30, 2022
Band Score – 6
Concentrate on the correct usage of quantifiers and subject-verb agreement.
In some places words are used incorrectly, pay attention to them.
Use C2 level of words.
Purnima Koli
Posted on Oct 25, 2021
Parents tend to give the children better resources as compared to their own childhood. This way they also feel compensated in the process while bringing up their own child. While having a huge collection of toys to play with is not all that bad, at the same time can lead to some issues.
Firstly, having a diversity in the range of toys have multiple benefits. The child can learn how to manage or organize better. Varied exposure to different themes of toys makes one more aware.
Secondly, sharing can also develop social skills among the child’s friend circle. To get hands-on-experience with toys such as Rubix’s cube, puzzles hone mental capacity of the kid. Similarly, educational and infotainment toys help shape likes and dislikes, opinions, communication skills. Thus, caters to holistic development which is often a cause of worry for parents.
On the other hand, if the child is given more and more, this may result in losing the value of individual toy. Not only is this expenditure wasteful but also teaching consumerist tendencies to the child. Perhaps unconsciously the child stops valuing his toys and takes them for granted in desire for more.
To have enough needs to be inculcated rather than frivolous costs being incurred. The parents need to be also mindful of teaching holistic habits like outdoor games, reading, painting apart from playing with toys for all round development.
Having many toys is also burdensome when it comes to maintenance. If that could be sorted then it’s much easier to assemble and play as per the child’s convenience. Gifting once in a while is a good option to keep the spirits of the child happy.
Posted on Nov 13, 2021
If you would have presented this same as a 4 paragraph structure and added the conclusion you would have score 7 easily.
Overall band: 5
Coherence: It is better to follow a 4 paragraph structure so that it is easy for the examiner to mark you for coherence. Conclusion is missing in your essay. Conclusion is where you sum up and restate points.
Recent Articles

IELTSMaterial Master Program
1:1 Live Training with Band 9 Teachers
4.9 ( 3452 Reviews )
Our Offices
Gurgaon city scape, gurgaon bptp.
Step 1 of 3
Great going .
Get a free session from trainer
Have you taken test before?
Please select any option
Email test -->
Please enter Email ID
Mobile Band 9 trainer -->
Please enter phone number
Application
Please select any one
Already Registered?
Select a date
Please select a date
Select a time (IST Time Zone)
Please select a time
Mark Your Calendar: Free Session with Expert on
Which exam are you preparing?
Great Going!

Advertisements: Positive and Negative Consequences Essay
- To find inspiration for your paper and overcome writer’s block
- As a source of information (ensure proper referencing)
- As a template for you assignment
Advertising
The advantages and disadvantages of advertising, the impacts of advertising: the truth and lies, interviews on advertising, works cited.
Many companies and organizations around the world use marketing communication tools to create more awareness about the types of goods or services they offer to customers. This concept of marketing is viewed to be important as it helps the company achieve its marketing goals and objectives.
The tools of marketing communication that are commonly used by companies to market their products include sales promotions by offering coupons, samples and premium items, public relations by conducting media and press releases about the companies products, sponsorships, point of purchase communication and advertising which encompasses advertising through the media and through the Internet (Shimp 7).
All the marketing tools mentioned above make up the promotion component of the marketing mix which is composed of elements such as the product, price of the product, place and promotion.
Although many consumers view promotion as the most common term for conducting the communication and awareness of a product, marketing communication is the most preferable term for most researchers and practitioners in the marketing field.
The purpose of this study is to focus on the marketing communication tool of advertising and how this promotion tool might be viewed as means to distort the truth from the customer so as to sell more products or services.
Advertising as well as the other forms of marketing communication are seen as a vital means of communicating about the product or service on offer between the marketers and consumers. Advertising is defined as a paid form of communication from a source such as the TV, radio, magazine, newspaper or the Internet to inform and persuade the receiver of the information take action by purchasing the product or service that is on offer.
The term paid in the above definition differentiates advertising from public relations which is another form of marketing communication that involves using sources such as the media for unpaid space or time to market the product.Apart from the media, advertising can be conducted by word of mouth, face to face interaction between the marketer and the consumer and by personal selling.
The main purpose of conducting advertising campaigns is to influence and convince the targeted audience to take action and change their behavior towards the company’s products or services (Shimp 182).
The major functions of advertising include informing, influencing, adding value, assisting the company’s efforts and reminding consumers about the company’s products or services. Informing involves creating awareness about the company’s products as well as publicizing the company’s brands to target consumers in the market.
Advertising informs consumers about new products as well as educate them on how the products function as well as teach them how the products are used. This type of advertising is know as usage expansion advertising examples of which include Campbell’s soup advert which publicized the soup as suitable for both family dinners and breakfast occasions (Shimp 188).
Apart from informing, advertising acts as an influencing agent that motivates consumers to try out the new brands on offer by the company. Customers are influenced to make a purchasing decision by sampling the product and also listening to the marketer’s explanation about the usefulness of the product. The reminding part of an advert is meant to keep the product in the customer’s mind.
This becomes important in the event a consumer needs a product with similar features. The influence of adverts that recur in the present and past make it possible for the consumer to remember the product.
The aspect of adding value in advertising is done by innovating, altering the customer’s perception about the product and improving the brand, its features and product specifications. These three value addition components are interdependent of each other as explained by the quote below:
‘Innovation without quality is mere novelty. Consumer perception without quality or innovation is viewed to be mere puffery while innovation and quality, if not translated into consumer perceptions, are like the sound of the proverbial tree falling in the empty forest.’ (Shimp 190)
Adding value ensures that companies can be able to generate brands that will see higher sales volumes, more revenues and higher profits for the company. Advertising evokes different responses from the customers who are targeted by the promotion effort.
Some of the responses that consumers get after being exposed to advertising include a change of behavior where the customer is persuaded by the marketer to buy a new product or service, the consumer is educated on new product possibilities, the marketer creates an emotional response for the product that is being marketed by create positive brand association.
Advertising is seen as the most important tool of marketing a company’s products or services. Investing in advertising campaigns is therefore seen as an investment that will yield higher profits and higher returns as well as increase the number of customers a company has.
Some of the benefits of conducting advertising include improving the sale of the product since more people are now aware of the brand on offer, the attitudes and perceptions that customers have on the company’s products are changed in a positive way, there is an increase in employment as many people are needed in designing and developing the advert.
Advertising ensures that the company is able to progress economically by increasing the sales volumes and revenue of the company. It has also provided moral and religious benefits by creating adverts that communicate patriotic, faith and tolerance messages.
It also plays an important in contributing to the modern market economy by making sure the systems conform to the moral standards set by the society. Advertising is seen as a useful communication tool for sustaining honesty and ethical responsibility, integrity when it comes to dealing with competitors (Kapoor par. 1-8).
There have been critics who have viewed advertising as being negative especially with regards to the message that the advert is communicating to its intended audience. These critics have viewed advertising to have an impact on the viewers with regards to their state of mind and their past experiences with the company’s products or services.
Advertisements have been viewed to have a negative effect on young children and teenagers as this age group is more susceptible to the misleading information that is usually contained in some of the ads. Children are able to view whatever an ad relays as the truth and are convinced that the falsified information that is contained within the ad is the truth.
Pediatric research has shown that children who are younger than eight years are psychologically defenseless against adverts and advertising campaigns because they cannot understand the intention and purpose of the advert (Shifrin et al 2563).
Advertising has been viewed to be detrimental to children because their perceptions are easily manipulated. The Federal Trade Commission (FTC) conducted an investigation in 2000 the results of which showed that violent movies, games and music were marketed with a particular focus on young children and adolescents.
The FTC decided to issue a ban on R rated content by preventing movie theaters from playing violent movies, games or music before movies that were G rated. Children however continue to view this content through other forms of media. G-rated movies designed for children also have advertisements for alcoholic beverages and cigarettes before the movie is aired (Shifrin et al 2564).
For example Coca Cola partnered with Warner Bros by paying $150 million for the company’s ads to be aired before the airing of Harry Potter and the Sorcerer’s Stone.
There have also been the airings of tie in ads which have been viewed to be inappropriate to young children such as the World Wrestling Federation action figures which when pressed utter profanities. Such examples show that advertisers usually design their adverts to target children despite the contents of the advert bearing information for an older generation (Shifrin et al 2564).
Critics have argued that there has been an increase in cigarette and alcohol consumption after viewers have been exposed to ads that market these products (Platania par. 3 -4). Tobacco manufacturers spend about $30 million in a day which amounts to $11 billion in a year on tobacco advertisements and promotional campaigns while alcohol manufacturers spend close to $5.7 billion in a year on alcoholic advertisements.
FTC reports have shown that teenagers and children are exposed to 2,000 beer advertisements in one year. For example during prime time viewing hours, one alcoholic advertisement is aired after every four hours. Such large amounts of beer and wine adverts have been attributed to the increasing alcoholic consumption amongst teenagers.
Two longitudinal studies have attributed tobacco advertisements to one third of adolescents who smoke. Other studies have shown that young children who are exposed to cigarette adverts are likely to smoke in the later stages of their lives (Shifrin et al 2565).
In order to remain competitive, companies have had to reinvent their products and services to have an edge over their rivals. Many companies have designed adverts that promote their products to be more superior and better than those of the competitors by focusing on the functions of advertisements as well as on the aspect of appeal.
Each company has actively been involved in battling for the consumer’s attention which has seen the increase the scope of their advertising activities as well as cut throat competition when it comes to creating adverts that are more superior to those of competitors (Maitra par.2).
The cut throat competition has seen advertisers develop different measures that are used to attract the attention of the target audience. These measures at times might involve distorting the truth about the competitor’s products so that the company carrying the advertisement is seen to have more superior products and services.
The adverts might also distort the truth about the products features and what the product is capable of doing (Maitra par. 3). For example some automobile dealers have been known to distort the truth about some of the car models they sell in their auto marts by listing car specifications that are not present in the genuine car.
Most of these dealers who advertise their products through media such as the newspapers and the Internet list car features that are popular with consumers so that they can increase their sales and revenues. This misleads customers to buy their products based on the falsified information.
Most critics today view advertising to be deliberately misleading audiences by presenting information that is untrue. The issue of truth in advertisements is portrayed in a subtle way in that the contents of the advert do not portray false information but they basically distort the truth with factual information that is meant to discredit the competitor’s products (Berger et al 816).
For example a particular brand of bread in the US advertised that its bread had fewer calories per slice when compared to that of its competitors. While the information on the calories was true, the advert failed to inform the consumer that their bread slices were smaller than those of the competitor.
Apart from discrediting the competitor’s products, advertisements have been falsified so as to increase the sales volumes and improve profits. This is mostly common in industries that deal with the manufacture of food, cosmetics, and mobile network providers (Noland par. 6).
Most advertising campaigns lack information that is based on research and scientific studies. The content of the advert is usually based on the manufacturer’s instructions/ingredients or the features and qualities of the product. The advertiser therefore has to appeal to the consumer to change their perception and behavior towards the product.
Appeal is what is meant to influence the consumer to change their perception about the company’s product or services. Appeal can be in the form of rational and emotional appeal. Rational appeal focuses on presenting factual information about the products that are on offer by the organization.
The message in the advert contains truthful and factual information which is meant to appeal to the customer to purchase the product based on the information (Orwig par. 3-10).
Emotional appeal focuses on the feelings and responses of the target audience on the product or service that is being advertised. The message of the advert is focused on eliciting an emotional response from the consumer who is targeted.
For example British Airways has developed adverts for business and first class passengers by evoking a feeling of relaxation and comfort whenever they fly with British Airways. In order to appeal to customers on an emotional and rational level, advertisements have to incorporate information that is truthful and factual about the product or service that is on offer (Maira par.2).
Interviews were conducted on consumers and marketers to find out whether advertising distorted the truth about the type of products that were on offer by a company. Customers were asked whether they felt the adverts in the media and on the street distorted the truth about the brand that was on promotion. One interviewee remarked that adverts on TV generally contained information that was factually correct.
They also noted that for the information to be aired on TV or any other media outlet, it had to under go some verification procedures that would authenticate the truth of the advert’s content. The same interviewee also noted that advertisers conducted research on their target audience before they designed their adverts. He however noted that they preyed on people’ weaknesses but they did so in an honest and truthful way.
A second interviewee who worked for a marketing and advertising company remarked that the company had successfully conducted advertising promotions for products and services in the last 50 years of its operations without having to distort the truth about the brands in any way.
The interviewee noted that successful businesses such as the one he was working for did not need to distort the truth to increase their sales volumes and gain more customers. He noted that businesses needed to have a strong relationship marketing foundation that would see customers satisfied with the company’s brands and services while at the same time maintaining a loyalty with the company.
Also, customers who were satisfied with the products that a company offered were more than likely to tell their friends, families and colleagues about their experiences with these brands thereby increasing the company’s customer base. The third interviewee who was a general consumer also disagreed that advertisers distorted the truth to sell more products and services to the target market.
They termed such an action as false and deceptive advertising which would be bad for a business that wants to increase its sales and profits while at the same time increase its customer base. The interviewee noted that governments around the world had regulations that controlled falsified information and facts from being aired in media outlets.
To support these interviewee’s views Hansen and Law (3) talk about the “truth about advertising regulation” which arose from a movement that emerged in the early 20 th century.
These movement known as the “truth in advertising movement” was made up of reformers in the retail, manufacturing and publishing industry who lobbied governments around the world to formulate legislation that would reduce the number of falsified adverts in the media.
The enacted truth about advertising regulation was meant to regulate the type of information in commercials and adverts. This regulation basically set the foundation for other regulations in the United States that were meant to deal with false information posed by advertisers in the media.
The regulation was enacted to deal with the pressure that emerged from the negative consequences of misleading adverts as well as pressure from the truth in advertising movement.
The various stakeholders in this group noted that adverts and commercials contained untruthful information that imposed a negative perception on the targeted audience which was mostly made of the average consumer, young children, teenagers and young adults.
False advertising was therefore viewed to be harmful to not only the consumer but to the business that aired the misleading adverts. The regulation was seen to be a mechanism that would ensure marketing and advertising firms improved their credibility (Hansen and Law 3).
A fourth interviewee viewed advertisements to be a nuisance as they kept interrupting her viewership of television programs that were on air. She stated that in the event she watched a commercial that advertised food, she did not believe the information and contents of the advert.
On further inquiry, the interviewee intimated that they had tried out a food product that was advertised to have fewer calories and high fibers to realize that the calorie content was falsified and the food had no fiber whatsoever. This made her have a negative image of the company that was advertising the food product and dented her image about food advertisements in general.
Another interviewee agreed that some adverts were misleading in terms of the adverts contents and the message that was being relayed to the target audience. The fifth interviewee remarked that companies sometimes exaggerated the features that their products had so as to get more sales and more revenue.
They leave out the negative aspects of the product intentionally so as to mislead the consumer to purchase the product. This is mostly evident in mobile phone and automobile adverts. The creators of the Apple 4GS are still marketing the product despite the phone having several defects in its antennae reception (RealCool Biz par. 1-2).
The sixth interviewee noted that most adverts did not display any truthful information especially when it came to the real cost of the good. He remarked that most advertisers gave out prices for products or services that were not real.
They did this because they wanted to recover the costs of developing and running the advert from the price that the consumer was going to pay for the product/service. The consumers are unaware that they are paying for the costs of advertising incurred by the advertiser and the company (RealCool. Biz par. 1-2)
The above analysis has shown that advertisements have both positive and negative consequences on the consumer’s perception about the company and its products that are on offer. The research has shown that customers base their purchase decisions on the information that is contained in an advertisement. What the advertiser puts in an advert is the main factor that will compel customers to go out and buy the product.
Companies and advertisers are therefore charged with the role of ensuring the information contained in the advert is truthful and not misleading. While some companies have used falsified information to gain a competitive edge, the long run sees this strategy to be detrimental to the company’s image in the event customers are dissatisfied with the products and services that are on offer by the company.
Berger, Jonah, Alan T. Sorensen and Scott J. Rasmussen, Positive effects of negative publicity: can negative reviews increase sales? Marketing Science , 29(5) pp. 815-827, 2010.
Hansen, Zeynep and Marc Law, Advertising regulation during the progressive e ra, Working Paper 11927, Cambridge, Massachusetts: National Bureau of Economic Research, 2006.
Kapoor, C., Benefits of advertising . Web.
Maitra, Soumyamoy, Ethics in advertising , 2010, Web.
Noland, Jones, Marketing strategies . Web.
Platania, Vincent, The advantages and disadvantages of advertising . Web.
Orwig, Ken, Rational appeals vs. emotional appeals in advertising and marketing communication . Web.
Real Cool.Biz, The negative effects of advertising , 2008. Web.
Shimp, Terence A., Advertising promotion, and other aspects of integrated marketing communications , Mason US: South Western Cengage Learning, 2010.
Shifrin, Donald, Ari Brown, Bernard P. Dreyer, Kenneth R. Grinsburg, Regina M. Milteer, Kathleen G. Nelson and Deborah Ann Mulligan, Advertising regulation during the progressive era. Children, adolescents and television, Pediatrics Journal , 11(6): 2563-2569, 2006.
- Ethical Behavior Among Firms' Executives
- Target Corporation Security Breach and Legal Consequences
- Coca-Cola's The Super Bowl Advert
- Effective Advertising: Its Principles & Strategies
- Marketing Communications Mix: Apple vs. Samsung
- Wheat Fillets Company Marketing Plan
- Integrated Marketing Communications: Microsoft Retail Stores Marketing
- Integrated Marketing Communication
- Chicago (A-D)
- Chicago (N-B)
IvyPanda. (2019, June 7). Advertisements: Positive and Negative Consequences. https://ivypanda.com/essays/marketing-communication-3/
"Advertisements: Positive and Negative Consequences." IvyPanda , 7 June 2019, ivypanda.com/essays/marketing-communication-3/.
IvyPanda . (2019) 'Advertisements: Positive and Negative Consequences'. 7 June.
IvyPanda . 2019. "Advertisements: Positive and Negative Consequences." June 7, 2019. https://ivypanda.com/essays/marketing-communication-3/.
1. IvyPanda . "Advertisements: Positive and Negative Consequences." June 7, 2019. https://ivypanda.com/essays/marketing-communication-3/.
Bibliography
IvyPanda . "Advertisements: Positive and Negative Consequences." June 7, 2019. https://ivypanda.com/essays/marketing-communication-3/.

Advantages and Disadvantages of Advertisement
Looking for advantages and disadvantages of Advertisement?
We have collected some solid points that will help you understand the pros and cons of Advertisement in detail.
But first, let’s understand the topic:
What is Advertisement?
What are the advantages and disadvantages of advertisement.
The following are the advantages and disadvantages of Advertisement:
| Advantages | Disadvantages |
|---|---|
| Increased Awareness | Misleading Information |
| Targeted Audience | Increased Costs |
| Creative Freedom | Overexposure |
| Brand Recognition | Negative Association |
| Economic Benefit | Environmental Impact |

Advantages of Advertisement
Also check:
Disadvantages of Advertisement
You can view other “advantages and disadvantages of…” posts by clicking here .
If you have a related query, feel free to let us know in the comments below.
Also, kindly share the information with your friends who you think might be interested in reading it.
Leave a Reply Cancel reply
Save my name, email, and website in this browser for the next time I comment.

- Listening Tests
- Academic Tests
- General Tests
- IELTS Writing Checker
- IELTS Writing Samples
- Speaking Club
- IELTS AI Speaking Test Simulator
- Latest Topics
- Vocabularying
- 2024 © IELTS 69
ADVANTAGES AND DISADVANTAGES OF ADVERTISING
IELTS essay ADVANTAGES AND DISADVANTAGES OF ADVERTISING
- Structure your answers in logical paragraphs
- ? One main idea per paragraph
- Include an introduction and conclusion
- Support main points with an explanation and then an example
- Use cohesive linking words accurately and appropriately
- Vary your linking phrases using synonyms
- Try to vary your vocabulary using accurate synonyms
- Use less common question specific words that accurately convey meaning
- Check your work for spelling and word formation mistakes
- Use a variety of complex and simple sentences
- Check your writing for errors
- Answer all parts of the question
- ? Present relevant ideas
- Fully explain these ideas
- Support ideas with relevant, specific examples
- ? Currently is not available
- Meet the criteria
- Doesn't meet the criteria
- 6 band Nowadays some people think that parents teach there children about society good other think that school is the best place. discuss your openion. It is desire of all the parents their child become extraordinary and well educated. While there are those who think that the school is the place where kids acquire better knowledge, other hold that they try to prepare and get educate there kids by themselves. This essay analyze both these aspects an ...
- 8 band Children should care of an animal, it will be beneficial for them. It is frequently said that toddlers benefit from caring for domestic animals, especially in today’s technology-focused world. However, the issue is not entirely straightforward, and arguments can also be made against the idea. This essay will discuss the debate and give a concluding view. On the on ...
- One should not aim at being possible to understand but at being impossible to misunderstand. Marcus Fabius Quintilian
- 5.5 band Solar energy is getting more and more popularity these day. Discuss the advantages and disadvantages? Usage of Solar energy is increasing day by day as the most effective source around the globe however, there are merits and the demirts associated with the uses of solar energy. This essay will make an attempt to discuss both. Firstly, there are certain reasons why people switching to solar energy t ...
- 8 band It is advantageous if children take care of an animal. It is frequently said that toddlers benefit from caring for domestic animals, especially in today’s technology-focused world. However, the issue is not entirely straightforward, and arguments can also be made against the idea. This essay will discuss the debate and give a concluding view. On the on ...
- I love commuting between languages just like I love commuting between cultures and cities. Elif Safak
- 5.5 band There is an increasing trend to having smaller families. Is this a positive or negative development? In recent years, there are many people who think that there are positive effects on having a smaller family. I agree to some extent with this view, while there many are negative aspects to this opinion, it seems to be more likely to have beneficial impacts on the family. To begin with, it is true t ...
- 6.5 band Pros and cons of immigration As a matter of the fact, a considerable number of people leave their own countries for different reasons every year in particular the ones who live in either Third-World or underdeveloped countries. There is no denying that immigration can bring several advantages and disadvantages for immigrants as ...
- One who speaks only one language is one person, but one who speaks two languages is two people. Turkish proverb
- IELTS Twenty20 Course
- IELTS Model Answers
- Study Abroad NEW
- Visas & Citizenship NEW
IELTS Writing Task 2 Model Answer: Discussing the pros and cons of advertising.
feel free to call us +61.4.50973975 [email protected]
IELTS Writing Task 2 essay with model answer
You should spend about 40 minutes on this task. Write about the following topic
Advertising has become an inevitable part of our lives. Some people believe that it is a positive aspect of our lives while others are of opposite belief. Discuss both views and give your opinion.
Write at least 250 words.
Model Answer :
In the recent years, advertising has become an integral part of our daily life. Almost every product is advertised through several media sources like Youtube, television, websites. While some people support this trend, others tend to oppose it. There are several reasons for this. In this essay, I am going to discuss these viewpoints and give my opinion on the matter.
On one side of the argument, there are people who believe that advertising is not very beneficial. The main reason for this view is that people tend to buy unnecessary items because of watching these advertisements. Another reason is that several products fo not work the way they are claimed to work in the ads. For instance, these days several coding boot camps advertise a 100% job guarantee for every student who graduates from their boot camp. However, upon careful investigation, it was found that a job could be an internship, part-time position, or a full-time job! Thus, it is easy to see why this argument has gained weight.
On the other hand, there are people who support advertisements. The primary reason is that the market very competitive these days. Rather than letting a product go unnoticed, it is better to advertise the product so as to enhance its popularity among the masses. For example, the percentage of sales of two products released by top brands on the same day is greatly affected by marketing. A recent survey indicated that there is a 40% boost in sales if the product is rightly marketed. Althogh, some people or companies tend to promote the sales of their products through fake claims, it is left to the discretion of the buyer to decide.

In conclusion, advertising has its pros and cons as discussed. I feel that the benefits outweigh the drawbacks. People need to be very careful with falsce advertisements and decide on the usefulness of the product before buying it.
Total Words: 280
Task Achievement: 9
Coherence & cohesion: 9, lexical resources: 9, overall score: band 9.
For unlimited feedback with speaking and writing tasks sign up for IELTS Twenty20 Online Course today!
Study 20 minutes a day for 20 days and Ace the IELTS exam.
IELTS Score Calculators and Estimators:
- IELTS Overall Score Calculator
- Free IELTS Level Check
Useful FREE resources for IELTS preparation:
- Free IELTS preparation Course
- Free IELTS Model Answers for Academic and General Writing tasks
- Free IELTS Exam Day Cheat Sheet
Tutorials on Essay Writing
- How to identify the main topic and all parts of the IELTS writing task essay?
- How to brainstorm and organise ideas for writing task 2?
Finally, if you need ongoing feedback from an experienced IELTS teacher for your writing or speaking tasks, simply subscribe to one of our IELTS CORRECTION packs
Say "Hi" on our social media channels...
- Follow on Twitter: @IELTS_T20
- Like on Facebook
- Subscribe to our Youtube Channel
IELTS Writing Task 2 Model Answer: Many countries are currently witnessing an increase in criminal activity among young people
IELTS Writing Task 2 essay with model answer You should spend about 40 minutes on this task. Write about...
IELTS Model Essay: Government investment in the arts, such as music and theatre, is a waste of money.
Ielts writing task 2 model answer: big cities have become overcrowded, ielts writing task 2 model answer: some people think that it is unfair to have a set retirement age agree or disagree.
Submit Task For Review ($15) IELTS Score Calculators and Estimators: IELTS Overall Score Calculator Free IELTS Level Check Useful...
IELTS Writing Task 2 Model Answer: Students should study whatever they like.
Ielts model essay: telecommuting.
IELTS General Writing Task 2 with model answer You should spend about 40 minutes on this task. Write about the following...
IELTS Writing Task 2 Model Answer: Many people believe that free public transportation should be available in most major cities. Advantages and disadvantages?
Ielts writing task 2 model answer: the most important thing about a job is how much money you earn in that job. do you agree or disagree, free ielts level check.
Take our 5-minute IELTS level check and receive a detailed report highlighting the areas where you need to improve the most to achieve your target IELTS score.
IELTS CORRECTION PACKS

HOT BONUS 1:
Hot bonus 2:, hot bonus 3:, hot bonus 4:, hot bonus 5:, like us on facebook.
Tel: +61 450 973 975 Email: [email protected]
Recent Posts
- IELTS Model Answer: Countries must invest resources on the young population
- IELTS Model Answer: Living in big cities is bad for people’s health
- IELTS Model Answer: Technology makes life complex
- IELTS Model Essay: All people will choose to talk the same global language in the future
- IELTS Model Essay: Countries should invest resources on the young population
- IELTS Samples of Band 7, 8 & 9 Students
- Study Abroad
- Immigration Advice
- Code of Conduct for Australian RMAs
- Registered Migration Agent (Australia) MARN 2016128
©2012-2024 All prices are in USD. IELTS Online Practice is provided by Wisekangaroo Pty Ltd (ABN: 86 159 373 770)
Send us an email with any questions about our courses and we'll get back to you, asap.
Log in with your credentials
Forgot your details.
Discuss the advantages and disadvantages of advertisements
Recently it has been seen that advertising is getting very popular in all fields of trade. With the advent of technology, there is a huge trend of publicity of different brands all over the world. Although there are tremendous advantages of advertisement but there are some drawbacks too. This essay will elaborate both points of views with final conclusion. It is seen that advertisement is becoming an important part of setting news buisness. Many resources like social media and television are helpful for publicity. One of benefit of advertisement is that it helps for better selling of a trade . For example tourisam is effected with good and attractive publicity. People are more informed about the product. Another attraction of advertisement is that it provides more options for buyers. This is good way of saving time too. For example someone can make more choices to buy a computer even without wondering around in markets. Thus it seems that advertisement has benefited seller and buyer both. At the same time advertisement has some disadvantages too . This can cause a competition between different trades. For example some people can spend more money to attract buyers for their low quality products. This way people can be fooled with fake publicity. Secondly too much advertisement make confusions for buyer for selection of products. Sometimes people buy un necessary stuff . This way there is waste of money. So some people think that advertisement has more negative effects on buisness. In conclusion, although advertisement is getting popularity but it has its own problems. It is recommended that if an advertisement is done with real honesty it will show more better results and will be more beneficial for everyone.
| Post date | Users | Rates | Link to Content |
|---|---|---|---|
| 2022-04-14 | 10 | ||
| 2018-08-06 | 75 | ||
| 2018-08-06 | 75 | ||
| 2018-08-06 | 85 |
- Log in or register to post comments
- Some people believe that it is better to keep criminals in prison for longer while others disagree and say that we must find a different solution Discuss both views and give your own opinion 68
- some people think that government should provide education for free on all levels primary secondary and tertiary others believe that it is the responsibility of individual to pay for their own education discuss both views and give your opinion 49
- Most of the schools are planning to replace sports and exercise classes with more academic sessions What i s your opinion on this change How is this change will affect children s life in your view 28
- Discuss the advantages and disadvantages of advertisements 85
Essay evaluations by e-grader
Grammar and spelling errors: Line 1, column 1, Rule ID: WHITESPACE_RULE Message: Possible typo: you repeated a whitespace Suggestion: Recently it has been seen that advertisi... ^^ Line 2, column 1, Rule ID: WHITESPACE_RULE Message: Possible typo: you repeated a whitespace Suggestion: ...oints of views with final conclusion. It is seen that advertisement is becomin... ^^^^^ Line 2, column 245, Rule ID: COMMA_PARENTHESIS_WHITESPACE Message: Don't put a space before the full stop Suggestion: . ...t it helps for better selling of a trade . For example tourisam is effected with g... ^^ Line 2, column 582, Rule ID: SENT_START_CONJUNCTIVE_LINKING_ADVERB_COMMA[1] Message: Did you forget a comma after a conjunctive/linking adverb? Suggestion: Thus, ...en without wondering around in markets. Thus it seems that advertisement has benefit... ^^^^ Line 3, column 1, Rule ID: WHITESPACE_RULE Message: Possible typo: you repeated a whitespace Suggestion: ...t has benefited seller and buyer both. At the same time advertisement has some ... ^^^^ Line 3, column 62, Rule ID: COMMA_PARENTHESIS_WHITESPACE Message: Don't put a space before the full stop Suggestion: . ...advertisement has some disadvantages too . This can cause a competition between di... ^^ Line 3, column 389, Rule ID: COMMA_PARENTHESIS_WHITESPACE Message: Don't put a space before the full stop Suggestion: . ... Sometimes people buy un necessary stuff . This way there is waste of money. So so... ^^ Line 4, column 1, Rule ID: WHITESPACE_RULE Message: Possible typo: you repeated a whitespace Suggestion: ...as more negative effects on buisness. In conclusion, although advertisement is... ^^^^^ Line 4, column 155, Rule ID: WHITESPACE_RULE Message: Possible typo: you repeated a whitespace Suggestion: ...at if an advertisement is done with real honesty it will show more better results... ^^ Line 4, column 178, Rule ID: MOST_COMPARATIVE[2] Message: Use only 'better' (without 'more') when you use the comparative. Suggestion: better ...is done with real honesty it will show more better results and will be more beneficial for... ^^^^^^^^^^^
Transition Words or Phrases used: but, if, second, secondly, so, thus, for example, in conclusion
Attributes: Values AverageValues Percentages(Values/AverageValues)% => Comments
Performance on Part of Speech: To be verbs : 19.0 13.1623246493 144% => OK Auxiliary verbs: 7.0 7.85571142285 89% => OK Conjunction : 6.0 10.4138276553 58% => More conjunction wanted. Relative clauses : 7.0 7.30460921844 96% => OK Pronoun: 22.0 24.0651302605 91% => OK Preposition: 32.0 41.998997996 76% => OK Nominalization: 13.0 8.3376753507 156% => OK
Performance on vocabulary words: No of characters: 1460.0 1615.20841683 90% => OK No of words: 281.0 315.596192385 89% => More content wanted. Chars per words: 5.19572953737 5.12529762239 101% => OK Fourth root words length: 4.09427095027 4.20363070211 97% => OK Word Length SD: 2.96334982312 2.80592935109 106% => OK Unique words: 155.0 176.041082164 88% => More unique words wanted. Unique words percentage: 0.551601423488 0.561755894193 98% => OK syllable_count: 466.2 506.74238477 92% => OK avg_syllables_per_word: 1.7 1.60771543086 106% => OK
A sentence (or a clause, phrase) starts by: Pronoun: 7.0 5.43587174349 129% => OK Article: 0.0 2.52805611222 0% => OK Subordination: 2.0 2.10420841683 95% => OK Conjunction: 0.0 0.809619238477 0% => OK Preposition: 3.0 4.76152304609 63% => OK
Performance on sentences: How many sentences: 23.0 16.0721442886 143% => OK Sentence length: 12.0 20.2975951904 59% => The Avg. Sentence Length is relatively short. Sentence length SD: 25.1028131637 49.4020404114 51% => The essay contains lots of sentences with the similar length. More sentence varieties wanted. Chars per sentence: 63.4782608696 106.682146367 60% => More chars_per_sentence wanted. Words per sentence: 12.2173913043 20.7667163134 59% => More words per sentence wanted. Discourse Markers: 2.73913043478 7.06120827912 39% => More transition words/phrases wanted. Paragraphs: 4.0 4.38176352705 91% => OK Language errors: 10.0 5.01903807615 199% => OK Sentences with positive sentiment : 11.0 8.67935871743 127% => OK Sentences with negative sentiment : 6.0 3.9879759519 150% => OK Sentences with neutral sentiment: 6.0 3.4128256513 176% => OK What are sentences with positive/Negative/neutral sentiment?
Coherence and Cohesion: Essay topic to essay body coherence: 0.174724859814 0.244688304435 71% => OK Sentence topic coherence: 0.0558985997608 0.084324248473 66% => OK Sentence topic coherence SD: 0.0709850238967 0.0667982634062 106% => OK Paragraph topic coherence: 0.109998476097 0.151304729494 73% => OK Paragraph topic coherence SD: 0.0150734655646 0.056905535591 26% => Paragraphs are similar to each other. Some content may get duplicated or it is not exactly right on the topic.
Essay readability: automated_readability_index: 9.2 13.0946893788 70% => Automated_readability_index is low. flesch_reading_ease: 50.84 50.2224549098 101% => OK smog_index: 8.8 7.44779559118 118% => OK flesch_kincaid_grade: 9.2 11.3001002004 81% => OK coleman_liau_index: 11.99 12.4159519038 97% => OK dale_chall_readability_score: 7.94 8.58950901804 92% => OK difficult_words: 66.0 78.4519038076 84% => More difficult words wanted. linsear_write_formula: 7.5 9.78957915832 77% => OK gunning_fog: 6.8 10.1190380762 67% => OK text_standard: 9.0 10.7795591182 83% => OK What are above readability scores?
--------------------- Rates: 61.797752809 out of 100 Scores by essay e-grader: 5.5 Out of 9 --------------------- Note: the e-grader does NOT examine the meaning of words and ideas. VIP users will receive further evaluations by advanced module of e-grader and human graders.

IELTS advantage disadvantage essay
Model answer for an ielts advantage disadvantage (outweigh) essay..
Updated: February 2024
One of the most difficult essay types for many band 6 students is the ‘outweigh’ essay, which is an advantage disadvantage essay that is asking your opinion about which side you think is stronger.
The keyword in the task is ‘outweigh’. So you must cover the advantage and the disadvantage in this essay and clearly state your opinion. Do not only write about the advantages. you will need to cover both sides for a higher score in task response.
If you believe the advantage is stronger you must give your opinion on that in the thesis statement, but also make sure you show what a possible downside is. Have a look at the structures below for this type of essay.
Note that these are just guidelines. There is nothing mentioned in the marking criteria about the correct structure to use.

Check this blog post on the 3 types of advantage disadvantage essays.
Model answer.
People now have the freedom to work and live anywhere in the world due to the development of communication technology and transportation. Do the advantages of this development outweigh the disadvantages?
In recent times people have the choice of any location worldwide to live and work because of advances in communication technology and transport. Although there are downsides, this essay argues that the advantages are stronger as this has positively changed work life because people can work remotely via the internet from anywhere in the world.
One considerable advantage of technological innovation in transportation and communication is that it has revolutionised the way people work, bringing new opportunities and employment that did not exist before. In my view, this has had a positive impact on peoples lives due to the flexibility of combining work with travel. For instance, reliable Wi-fi networks and cloud computing, cheaper flights and high-speed trains allow people to live anywhere in the world while working online. Additionally, employees can participate in video conference calls and international forums, while entrepreneurs can run their businesses online from any location worldwide.
Admittedly, there are drawbacks in that some individuals have issues while living and working in different countries. In particular, culture shock and motivational problems while living outside their home country. This tends to lead to frustration for many remote workers who are relocated to offices in other countries. For example, multinational companies often neglect to train employees to deal with culture shock, as they assume that a positive experience on vacation in a new country will lead to easy cultural integration abroad. I believe communication technology has a positive role to play here, such as online coaching, which could help employees with motivation and cultural adjustment.
To conclude, despite the downsides, I believe that the benefits of communication technology and transport are greater because of new opportunities to travel and work online globally.
As you can see, I’m going with one advantage and one disadvantage here. This is ok for a Band 7+ but the essay must be well developed. If you have 2 advantages and 2 disadvantages, you may run out of time and end up with a very long essay at well over 300 words. Keep the essay concise.
You will notice in the thesis statement that I state:
‘Although there are downsides, this essay argues that the advantages are stronger as this has positively changed work life because people can work remotely via the internet from anywhere in the world.’
This shows balance as I have referred to the fact that there is a downside. In main body one, I cover the advantage and give my opinion on this. ‘ In my view, this has had a positive impact on people’s lives… .’
In main body two, I stated: ‘Admittedly, there are drawbacks….’ this shows the examiner that I’m covering the downsides now.
In the conclusion I refer to the disadvantages again briefly then restate my opinion… ‘ To conclude, despite the downsides, I believe that….’

Leave a Comment Cancel reply
21 Advantages & Disadvantages of New Media (College Essay Ideas)

Chris Drew (PhD)
Dr. Chris Drew is the founder of the Helpful Professor. He holds a PhD in education and has published over 20 articles in scholarly journals. He is the former editor of the Journal of Learning Development in Higher Education. [Image Descriptor: Photo of Chris]
Learn about our Editorial Process

When writing a college essay on new media, make sure you cover the following points. These points can help you add depth and detail to your essay.
To write a strong essay, I recommend paraphrasing the following points and turning each point into a full paragraph . Provide clear examples and reference a source for each paragraph. You can use the sources listed below, but remember to use your college’s referencing style when citing your sources.
There are both pros and cons of new media. So it’s important to give a well-rounded analysis that shows you have considered your essay from both old and new media perspectives.
Old Media vs New Media
Here’s the difference between old and new media:
- Old media are media that were owned and controlled by large companies and disseminated through one-way communication methods. Examples include newspapers, film and television.
- New media are media that can be produced and distributed digitally by anyone with an internet connection and generally involve two-way communication. Examples include blogs, social media (like Facebook and Twitter) and online forums.
My favorite definition is from Logan (2010, p. 4) :
“The term ‘new media’ will generally refer to those digital media that are interactive, will incorporate two-way communication, and involve some form of computing.”
New media like Facebook and Twitter have made communication, socialization, sharing and interacting easier for people with an internet connection. We can now not only be the consumers of information but also information producers . Sharing news, thoughts and opinions to a global audience is no longer something only the rich and powerful can do. Anyone with a Twitter handle how has global reach.
Advantages of Old Media
1. Old media have broad reach. Old media were designed as a form of mass communication that was to be broadcast to the masses. From the invention of the printing press in 1440 to the 1980s, print media such as newspapers, then radio, and finally television, followed this same broadcast formula. One message was broadcast to an entire population of a nation. People of all ages got their news from a small amount of publications that had extremely broad reach across a population.
2. Urgent information is broadly dispersed. A follow-up benefit of this broad reach of old media was that information of public importance was distributed rapidly. Still today, when a public disaster occurs, most people turn to old media of television and radio to get important information from authorities. This information is often controlled by, distributed by, and policed by the government so everyone gets the same information about how to protect themselves during times of emergency.
3. The people who control news dissemination are authorities and experts. Old media has important gatekeepers (Carr, 2012) to ensure the quality and authenticity of information. Published information is parsed by editors and producers to ensure it is true. People along the information supply train are trained and experienced journalists, and their editors provide checks and balances to what is distributed in newspaper, radio and television broadcasts. By contrast, new media can be produced and disseminated by anybody with an internet connection, leading to misinformation. This is one possible con of the internet .
4. Extreme views do not spread easily. Because of the control that gatekeepers exert over old media, unfettered media bias , extreme and radical opinions are curtailed. Untrue information can be prevented and filtered and offensive information can be bleeped out to protect children. Unfortunately with the rise of social media, our world has become increasingly polarized and radicalized (Thompson, 2011) . This is largely due to the fact those gatekeepers aren’t there to provide quality control for information anymore.
5. A sense of community and social cohesion develops. Benedict Anderson (1983) theorized that the emergence of the printing press led to the concept of the ‘nation’. He said that when people of a nation all started to read the same information each day, they began to see themselves as a community. Before then, our sense of community was to people in our villages. After that, we saw ourselves as an “imagined community” who share a common set of values and culture.
Related: Imagined Communities Pros and Cons
Disadvantages of Old Media
6. Minority views can be marginalized. There is extensive literature that shows that people of color, women, and other minorities have had their views curtailed and silenced in old media. Instead, dominant views are perpetuated by old media. Critical theory and post-structuralism (inspired in large part by Michel Foucault) have long stressed that media has produced unfair stereotypes and narratives about minorities. Old media were complicit in the reproduction and normalization of ‘dominant discourses’, and have long silenced minority or unpopular opinions.
7 The government and oligarchs often control the message. Throughout the 20th Century, the ability to share information was controlled by a small group of people. This helped them to maintain their power. In Manufacturing Consent , Herman and Chomsky (2010) highlight how corporate America and media oligarchs (such as Rupert Murdoch) have had a mutually beneficial relationship where they perpetuated untruths and propaganda in order to maintain their positions of power in society. To a greater extreme, in socialist nations, governments literally censor the ‘old’ press and only allow favorable media coverage.
8. Old media don’t get much instant feedback. Today, when you broadcast something on the internet, it gets comments and re-tweets to provide the writer with instantaneous feedback. This isn’t the case with traditional media like television , which broadcast information without an instantaneous response (one exception might be talk back radio). Interestingly, many major communication models in the 20th Century that had a linear structure (e.g. the Laswell model and the Shannon-Weaver model ) are largely outdated due to the two-way communication features of new media.
9. People don’t listen to or respect old media anymore. The declining trust in expertise and authority is widely a result of the emergence of new media. As previously marginalized and even extreme voices have been magnified by new media, people have started turning away from old media and considering it to be elitist and untrue. Whether these claims are accurate or not, the declining trust in old media means it doesn’t have the clout it once did.
Advantages of New Media
10. Information production is no longer just for the elites. In the era of blogs, social media , and instant communication, elites and the powerful no longer hold a monopoly on mass dissemination of information. Anyone with an internet connection can now have their beliefs and opinions broadcast to anyone around the world who wants to listen. This removal of gatekeepers has allowed us to become not just information consumers, but also information producers.
11. People can find their ‘tribe’. With the rise of the internet, people can connect to people who share their interests from around the world. This has led to the rise of a multitude of internet subcultures where people get together on forums and associate with their ‘tribe’. Now, subculture groups (goths, LGBTQI youth, punks, etc.) who feel out of place among their friends from school can go online and connect with people who share their experiences.
12. National borders are less of a barrier. In the 20th Century, our ability to communicate was often restricted to people in our local community. This limited who we could associate with. The rise of dispersed tribes could have the effect of undermining traditional cultural groups (based around national identities, etc.) and instead allow us to link up with our dispersed sub-cultural groups around the world.
13. Minority views and opinions can gain traction. People from minority groups that were traditionally excluded from old mass media platforms have found platforms to share their opinions online. Together, they have been able to form groups large enough to have their voices heard. Silenced voices have risen up – from the #metoo movement to the Arab Spring – to change our world for the better.
14. We can stay in touch. Prior to social media platforms like Facebook, we often lost touch with people form out past. But now, thanks to social media, we can watch people from a distance and share our major achievements, milestones and life changes to stay in touch with people on our distant periphery.
15. News is instantaneous. Thanks to news apps, Twitter, etc., news spreads faster than ever. We no longer need to wait until the 6pm news to access our news. As part of this instantaneous access to knowledge, we now have what’s known as the “24 hour news cycle”. Consumers have an insatiable appetite for news, so new media have to pump out an ongoing stream of ever more sensationalized news articles.
16. News producers get instant feedback. As soon as a piece of news is pumped out, tweets fling back and comments are provided to show feedback. Digital analytics software identifies which headlines get the most clicks and can show how long people spend reading each article . These qualitative and quantitative big data coalesce to help news producers to create content that best serves their consumers.
Disadvantages of New Media
17. Misinformation spreads like wildfire. Without traditional gatekeepers of knowledge such as editors and publishing houses, there is nobody controlling which information is disseminated. Misinformation has become widespread in the 21st Century thanks to social media (Allcott, Gentzkow & Yu, 2019). This causes fringe conspiracy theories and even doctored images to influence people’s political and social views.
18. We can live in an ideological bubble. New media often allow us to ‘subscribe’ to our own news networks and favorite information producers. Without the need to have widespread mass appeal, new media target dispersed niche and ideological markets. Conservatives begin to only consume conservative media; and liberals only consume liberal media. People begin to only reinforce their personal views, causing social polarization.
19. There is fierce media competition. While in the past there were three or four major news organizations, now there are diverse and numerous sources for news. Small news websites with fresh takes for niche audiences popped up, crowding the market with information. In this crowded media market, there is competition in all niches, and brands need to have a fresh take to get attention.
20. There is a wider customer base for companies large and small. While competition is more fierce than ever, there is also a bigger customer base than ever before. Websites target global audiences and have global reach. A savvy media producer or social media marketer can expand their market globally – beyond what traditional media was generally capable of.
21. Children can access inappropriate information more easily. New media gives on-demand access to information. While in the past adult content was broadcast late at night, today it can be accessed day and night. Scholars like Neil Postman (1985) argue that there is a “disappearance of childhood” as a result of how media is changing. As children have greater access to adult information, the innocence of childhood is being decayed earlier than ever.
For your essay you might have to take a position on whether new media has been a ‘positive’ or a ‘negative’ force in society. In reality, there is no clear answer here: it’s been both positive and negative, in different ways. But we can clearly see that it has changed society significantly. It plays a huge role in political campaigns and changing how companies communicate with potential consumers. By outlining all the different facets of the advantages and disadvantages of new media, you can show the person grading your paper your deep and nuanced knowledge of the impact of new media on society.

Allcott, H., Gentzkow, M., & Yu, C. (2019). Trends in the diffusion of misinformation on social media. Research & Politics , 6 (2).
Anderson, B. (2006). Imagined communities: Reflections on the origin and spread of nationalism . New York: Verso books.
Carr, J. (2012). No laughing matter: the power of cyberspace to subvert conventional media gatekeepers. International journal of communication , 6 , 21.
Herman, E. S., & Chomsky, N. (2010). Manufacturing consent: The political economy of the mass media . New York: Random House.
Kellner, D., Dines, G., & Humez, J. M. (2011). Gender, race, and class in media: A critical reader. New York: Sage.
Logan, R. K. (2010). Understanding new media: extending Marshall McLuhan . New York: Peter Lang.
Postman, N., (1985). The disappearance of childhood. Childhood Education , 61 (4), pp.286-293.
Thompson, R. (2011). Radicalization and the use of social media. Journal of strategic security , 4 (4), 167-190.

- Chris Drew (PhD) https://helpfulprofessor.com/author/chris-drew-phd/ 19 Top Cognitive Psychology Theories (Explained)
- Chris Drew (PhD) https://helpfulprofessor.com/author/chris-drew-phd/ 119 Bloom’s Taxonomy Examples
- Chris Drew (PhD) https://helpfulprofessor.com/author/chris-drew-phd/ All 6 Levels of Understanding (on Bloom’s Taxonomy)
- Chris Drew (PhD) https://helpfulprofessor.com/author/chris-drew-phd/ 15 Self-Actualization Examples (Maslow's Hierarchy)
Leave a Comment Cancel Reply
Your email address will not be published. Required fields are marked *
Sample details
Advertisement
- Views: 1,689
Related Topics
- Digital marketing
- Marketing Management
- Market Segmentation
- Marketing Research
- Market research
- Competitive Advantage
- Franchising
- Customer Satisfaction
- Global marketing
- Marketing Strategy
- Marketing Communications
- Customer service
- Marketing Mix
- Target market
- Pricing strategies
- Marketing Plan

Advertisements: Advantages and Disadvantages Argumentative Essay
Discuss the advantages and disadvantages of advertisements. Advertising is a communication whose purpose is to inform potential customers about various products and services and how to obtain and use them. Advertising is a multi-billion dollar business and its messages are conveyed to the farthest places on Earth. It uses every major medium to deliver these messages including television, movies, newspapers, radio, magazines, video games, the internet and billboards. Most advertisements are often placed by an advertising agency on behalf of a company.
An advertisement is a product and like every other product in the world, it has its pros and cons. Advertisements are used to sell products. Businesses advertise their products to potential consumers with the hope that they will buy these products. Businesses thrive through effective marketing and advertisement of their products. One good advertisement can make a product a household name and one bad advertisement can ruin the entire company. Advertisements generate awareness about various products and are essential to all businesses. After all, if you haven’t heard of it, you won’t buy it.
ready to help you now
Without paying upfront
One of the best known advantages of advertisements is their ability to raise awareness among the people about consumer products, varied opportunities and more. But raising awareness through advertisement is always done to sell a new car or new brand of soap. Advertisements have done a lot to raise awareness about many issues of local, national and international importance. These advertisements, also called public service announcements, help inform the people about many social issues such as blood donation programs, immunization programs, AIDS, cancer and many more.
Many NGOs, INGOs and other non-profit organizations raise awareness about various plights plaguing people through advertisements. These advertisements appeal to the people to help their fellow man. They send out a message with the hope that one or more of the billions of people in the world will answer their call for help. This is by far the biggest advantage of advertisements: their ability to make people do something. This ability of advertisements to make people do something can also be a disadvantage.
Advertisements can sometimes be so persuasive as to make the viewers buy something that they may not actually need or may in fact be harmful to them. They achieve this by creating false impressions about their products. A certain cigarette advertisement for example, may show that people who smoke a certain brand of cigarette are more successful than others. This not only creates a false impression upon the viewers about success but also encourages them to smoke. This creation of false impressions is very common in advertising.
In fact, this creation of false impressions is what makes advertisements so influential in shaping a consumer. Advertisements have also been known to play to certain stereotypes. They have, on occasions, downplayed people with certain physical attributes. Only ‘beautiful’ people are employed to appear in advertisements for various products. Advertisement agencies hardly ever employ people of ‘average beauty’. Food commercials never have malnourished people. Energy drink advertisements always have athletic models taking part in sports.
The Marlboro Man is always a ‘ruggedly handsome cowboy’. All these advertisements play to various stereotypes. These types of advertisement create the impression that being normal and ordinary isn’t good enough. Another disadvantage of advertisement is the sheer volume. There are advertisements almost everywhere one looks these days. Entire walls are plastered with posters about the new chocolate bars from Nestle. There are billboards on top of city buildings as far as the eye can see. Television shows are increasingly airing commercial after commercial.
Entire pages of newspapers and magazines have been taken up by advertisements. With the growth in popularity of the internet and E-mail, unsolicited bulk E-mail advertising, also known as spam has increased a lot. This large quantity of advertisements can ruin these media of communication. Television programs may lose their viewers if they take too many commercial breaks. Newspapers and magazines are sometimes unreadable when advertisements take more space than the articles. This large quantity of advertisements can make these media less appealing than before.
Advertising is a business and like any other business people profit from it. Advertising has both pros and cons. Advertisements influence us in many ways and this is both an advantage and a disadvantage. They can persuade us to choose a product that is good and a product that is bad. They influence us and they enlighten us. Businesses advertise products and services that can benefit the customers. They also advertise products and services that are potentially harmful to the customers.
Cite this page
https://graduateway.com/advertisements-advantages-and-disadvantages/
You can get a custom paper by one of our expert writers
Check more samples on your topics
Advantages and disadvantages: advertisements.
Why we advertise our products If we want our products to be well-known we should advertise them. Advertisements play an important role in the modern economy. They are useful to both consumers and producers. They help the consumers by giving them information about various products available on the market. Many readers appreciate advertising because it
Advantages and Disadvantages of Surrogacy Argumentative Essay
Human development
Surrogacy, according to Balen and Jacobs (1997), is the process where a surrogate mother carries a baby for a couple whose woman lacks the ability to carry one on her own or conceive. This process is performed by arrangements usually by companies that aid the intended couple by helping them pick a suitable candidate as
Advantages and Disadvantages of Living in a Countryside Argumentative Essay
Living in the countryside is a coveted aspiration for urban dwellers, encompassing both positive and negative elements. The advantages of country living are plentiful: proximity to nature's serenity, reduced pollution from fewer vehicles, and deeper personal connections fostered by a more relaxed lifestyle. Consequently, rural inhabitants often exhibit greater friendliness and willingness to lend a
Advantages and Disadvantages of Online Education Argumentative Essay
Advantages and disadvantages of online education Introduction It is basically credit-granting courses or education training delivered primarily via the Internet to students at remote locations, including their homes. The Online courses may or may not be delivered synchronously. An online course may need that students and teachers meet once or periodically in a physical setting
Advantages and Disadvantages of mobile phone Argumentative Essay
Cyberbullying
Mobile Phone
Cell phones are a great invention and a popular way to communicate---half of all Americans and Europeans use one. They allow us to work on the go and stay in touch. When put in the hands of a teenager, however, they can have some effects of which adults should be aware. It is a common sight
Essay – Used Cars Advantages and Disadvantages
If you have ever been discouraged by the expensive prices of new cars at a dealership, there is no need to worry. You can save thousands by buying a used car that still offers a reliable and attractive vehicle. Used cars provide some of the best deals possible.Undoubtedly, a pre-owned car can offer equal satisfaction
Essay- Advantages and Disadvantages of City School
Walking down the hall I get a sense of disbelief. Is this really me and am I really here or is it a dream. I just transferred to a new school. Though it does not sound that bad, in actually reality it has been a total turn around. My old high school (Hancock High) was
How the Advertisements Influence the Customers and Monitor Their Buying Behavior
Product placement
How the advertisements influence the customers and monitor their buying behavior. There is high impact of advertisements on customers’ motivation. Literature review: In the context of the research proposition, an extensive literature review has been done. The impact of advertisements on customers motivation has been reviewed in the light of research work already been carried
An Analysis of the Yum Chums Series of Advertisements Created by Mcdonalds
I will be examining McDonalds' advertisements and the strategies they employ to entice children, either by encouraging them to visit McDonalds or by delivering a message promoting health and physical activity. In response to significant media coverage in August 2004, McDonalds introduced a set of educational cartoon characters known as the Yum Chums, aimed at

Hi, my name is Amy 👋
In case you can't find a relevant example, our professional writers are ready to help you write a unique paper. Just talk to our smart assistant Amy and she'll connect you with the best match.
Advantages / Disadvantages Essay: IELTS Writing Task 2
Transport: ielts advantage/disadvantage essay sample.

IELTS Writing Task 2 advantage/disadvantage essay example that is a band score 8. The question is: Some people believe that using a bicycle as your main form of transport has a lot of advantages whereas others think it has many disadvantages. Discuss both views and give your opinion. Take a look at the sample answer
IELTS Writing Task 2 Question Types
Ielts advantage/disadvantage essay sample 4 – communication, ielts advantage/disadvantage essay sample 3 – transport, ielts advantage/disadvantage essay sample 2 – environment, ielts advantage/disadvantage essay sample 1 – work.
Home — Essay Samples — Life — Cat — Advantages and Disadvantages of Communication
Advantages and Disadvantages of Communication
- Categories: Cat
About this sample

Words: 592 |
Published: Jun 13, 2024
Words: 592 | Page: 1 | 3 min read
Introduction
Body paragraph.

Cite this Essay
Let us write you an essay from scratch
- 450+ experts on 30 subjects ready to help
- Custom essay delivered in as few as 3 hours
Get high-quality help

Prof Ernest (PhD)
Verified writer
- Expert in: Life

+ 120 experts online
By clicking “Check Writers’ Offers”, you agree to our terms of service and privacy policy . We’ll occasionally send you promo and account related email
No need to pay just yet!
Related Essays
1 pages / 564 words
2 pages / 895 words
2 pages / 994 words
3 pages / 1579 words
Remember! This is just a sample.
You can get your custom paper by one of our expert writers.
121 writers online
Still can’t find what you need?
Browse our vast selection of original essay samples, each expertly formatted and styled
Related Essays on Cat
Willa Cather's short story "Paul's Case," first published in 1905, provides a poignant exploration of a young man's struggle with his identity and his desperate quest for beauty and acceptance. At the heart of the narrative [...]
Immanuel Kant, an 18th-century German philosopher, revolutionized ethical theory with his deontological approach, which emphasizes duty over consequences in moral decision-making. Central to Kant's ethical framework are the [...]
The case of Arizona v. Gant, adjudicated by the United States Supreme Court in 2009, stands as a pivotal moment in the interpretation of the Fourth Amendment, which protects citizens against unreasonable searches and [...]
Frank Parsons, often hailed as the father of vocational guidance, developed the Career Matching Theory in the early 20th century. This theory represents a systematic approach to career decision-making, which was groundbreaking [...]
The most common question to be asked. A frequent conversation starter; are you a cat or dog person? There are numerous reasons for owning a pet, you can choose to buy one as your close companion or to simply buy it to consider [...]
While a few vermin regularly live on a feline's skin and hair follicles, numerous others are outcasts and potentially parasites. As little cat forms into an adult feline, their insusceptible framework holds the vermin populace [...]
Related Topics
By clicking “Send”, you agree to our Terms of service and Privacy statement . We will occasionally send you account related emails.
Where do you want us to send this sample?
By clicking “Continue”, you agree to our terms of service and privacy policy.
Be careful. This essay is not unique
This essay was donated by a student and is likely to have been used and submitted before
Download this Sample
Free samples may contain mistakes and not unique parts
Sorry, we could not paraphrase this essay. Our professional writers can rewrite it and get you a unique paper.
Please check your inbox.
We can write you a custom essay that will follow your exact instructions and meet the deadlines. Let's fix your grades together!
Get Your Personalized Essay in 3 Hours or Less!
We use cookies to personalyze your web-site experience. By continuing we’ll assume you board with our cookie policy .
- Instructions Followed To The Letter
- Deadlines Met At Every Stage
- Unique And Plagiarism Free
| / ✓ % width | Posts: |
Advantages and Disadvantages Essay about the value of Advertisements
Advertisements are becoming more and more common in everyday life.
| / / |

Advertising made simpler for you. Read about new Advertising Trends, Campaigns, and Strategies.
Below the Line Marketing Advantages and Disadvantages

Below-the-line (BTL) marketing targeting particular consumer categories with direct, tailored communication sets it apart from conventional Above-the-line (ATL) techniques. BTL marketing is a more sophisticated approach to advertising. In contrast to ATL techniques, which employ mass media channels like radio and television to cast a wide net, BTL marketing concentrates on intimate involvement through strategies like sponsorships, direct mail, and individually customized digital campaigns. The necessity for precise audience targeting to make sure that marketing messages are more deeply felt and result in quantifiable actions is what is driving this move in advertising toward more interactive content.
Developments in digital technology and data analytics have significantly increased the efficacy of BTL marketing by giving marketers access to comprehensive insights into customer behavior and enabling them to adjust their plans accordingly. Though BTL is great at reaching niche audiences and generating high conversion rates, its reach is inherently smaller than that of broad-spectrum ATL ads. BTL marketing, which strikes a balance between the depth and engagement of direct consumer interactions and the wider visibility of ATL, is nevertheless an
essential tactic for businesses looking to forge meaningful connections with their target audience and accomplish certain marketing objectives. But is this tailored approach always the best choice? While BTL marketing offers advantages such as precise targeting and measurable results, it also presents challenges such as higher costs and limited reach. Join us as we delve into the pros and cons of BTL marketing, assisting you in determining its suitability for your brand’s goals.
| 1. Targeted Audience: Uses data analytics to pinpoint the ideal consumers. 2. Cost-Effectiveness: Maximizes ROI by minimizing waste and focusing on a targeted audience. 3. Measurable Results: Allows monitoring and optimization of campaign effectiveness. 4. Personalization: Enables tailored interactions that cater to individual consumer preferences. 5. Customer Engagement: Facilitates direct interaction and emotional connections with customers. 6. Flexibility: Allows quick campaign adjustments based on feedback and market changes. | 1. Limited Reach: Targets smaller, specific groups and limiting market visibility. 2. Resource Intensive: Requires significant time, energy, and labor investment. 3. Scalability Issues: Difficult to scale without losing the personalized touch. 4. Short-Term Impact: Often focuses on immediate results rather than long-term brand building. 5. High Initial Costs for Some Tactics: Certain strategies can have substantial upfront expenses. 6. Limited Media Coverage: Lacks the extensive media attention that ATL marketing benefits from. |
Table of Contents
Advantages of BTL Marketing
One way that below-the-line marketing stands out is through focused, direct interactions that provide several strategic benefits, especially when it comes to connecting brands with their target audiences. The efficacy and efficiency of marketing efforts are improved by the unique advantages that each component of BTL marketing offers.
1. Targeted Audience
BTL marketing allows brands to pinpoint their ideal consumers using sophisticated segmentation and data analytics. This targeted approach ensures that marketing efforts are focused on individuals who are most likely to be interested in the product or service, thereby increasing the relevance and impact of the campaigns.
2. Cost-Effectiveness
BTL marketing maximizes return on investment while minimizing waste by interacting directly with a targeted audience. By avoiding the broad approach of mass media, this strategy lowers expenses and increases the efficacy of marketing expenditures through focused tactics.
3. Measurable Results
The capacity of BTL marketing to generate quantifiable results is one of its main advantages. Marketing professionals can monitor the efficacy of their tactics in real-time and make well-informed decisions to optimize their campaigns through direct answers, campaign analytics, or engagement data.
4. Personalization
5. customer engagement.
Direct mail, events, and demonstrations are examples of interactive strategies that enable one-on-one interaction with clients. BTL marketing is an effective strategy for meaningfully engaging customers because it fosters emotional connections and increases brand awareness through direct involvement.
6. Flexibility
BTL marketing’s tactical approach enables campaigns to be swiftly modified or redirected in response to customer input and shifting circumstances. This adaptability is essential in a changing market because it allows marketers to modify their tactics to increase their efficacy and responsiveness.
7. Higher Conversion Rates
When opposed to ATL advertising approaches, BTL marketing usually has higher conversion rates because of its targeted approach. Direct communication with a pre-selected audience that has expressed interest in the good or service results in shorter sales cycles and more successful conversions.
8. Local Market Penetration
Local markets are particularly well-suited for BTL marketing, as a thorough grasp of area preferences and subtleties can greatly improve consumer reaction. Local initiatives that are specifically designed for the community can effectively connect with them and increase local engagement and loyalty.
9. Consumer Trust
BTL marketing establishes and maintains customer trust through tailored interactions and straightforward communication. Building a devoted client base, improving brand reputation, and exhibiting a dedication to address the unique requirements and concerns of customers are all ways to build trust.
All of these benefits highlight the reasons that BTL marketing is still an essential part of the strategic marketing toolbox, particularly for campaigns that want to establish a tight relationship with particular market groups.
Disadvantages of BTL Marketing
1. limited reach.
BTL marketing’s limited reach is one of its fundamental drawbacks. BTL marketing targets more specific, smaller groups than Above the Line (ATL) marketing, which employs mass media outlets to reach a wider audience. This may hinder a company’s capacity to become well-known and visible in the marketplace, missing out on chances to interact with a wider audience.
2. Resource Intensive
BTL marketing frequently calls for a significant investment of time, energy, and labor. Developing customized marketing campaigns, planning events, and overseeing face-to-face customer contacts necessitate significant operational investment. This extensive use of resources might be a major disadvantage for companies looking for simpler marketing solutions or those with a small workforce.
3. Scalability Issues
It can be difficult to scale BTL initiatives to a larger audience without sacrificing the individualized touch. Even if these activities work well when conducted on a smaller scale, scaling them up to a bigger audience frequently entails exponentially increased expenses and complexity, which can reduce return on investment and put a burden on marketing budgets.
4. Short-Term Impact
While many BTL tactics, like promotional events or time-limited deals, aim to increase sales or recognition right away, they might only sometimes help develop a brand over the long run. This emphasis on quick profits might push businesses into a cycle of constant BTL activity spending to stay in the market, which may only be viable for some types of enterprises.
5. High Initial Costs for Some Tactics
Even while BTL marketing is typically less expensive, some strategies, such as elaborate events or cutting-edge direct marketing tools, may need a substantial upfront cost. These strategies can have unaffordable upfront expenses, particularly for startups or smaller businesses with limited funding.
6. Limited Media Coverage
BTL marketing does not rely on mass media channels and usually uses more direct and intimate connection techniques. Consequently, these efforts frequently attract little media attention, which limits their potential to raise public awareness in comparison to ATL techniques that reap the benefits of extensive media coverage.
These drawbacks emphasize how crucial it is to balance BTL marketing with other advertising tactics in order to create a holistic marketing strategy that takes advantage of both the breadth of ATL techniques and the depth of BTL involvement. Making judgments that align with their overall business objectives and resource capacities is made easier for marketers when they are aware of these obstacles.
In conclusion, Below the Line (BTL) marketing is essential in today’s marketing environment due to its individualized and targeted approach. Tailored interactions enable companies to interact directly with their target audiences, creating stronger bonds and increasing consumer loyalty. Though BTL marketing has many benefits, such as high conversion rates, cost-effectiveness, and quantifiable outcomes, it also has drawbacks, like restricted reach, scalability problems, and resource intensity. Businesses can considerably benefit from working with The Media Ant specialized Media buying and planning agency who have the know-how to carry out meticulous and successful BTL campaigns in order to navigate these complexities. These kinds of collaborations have the power to elevate standard marketing campaigns into remarkable, result-oriented ventures that let companies get the most out of their BTL marketing investments. By interacting with knowledgeable experts, one may maximize the benefits of BTL marketing while reducing its drawbacks, which promotes more fruitful marketing campaigns and long-term company expansion.
FAQs on Below-the-Line Marketing
What is below the line in marketing.
Below the Line (BTL) marketing refers to advertising strategies that involve direct and more personalized communication with specific target audiences. Unlike mass media campaigns, BTL marketing focuses on individualized interactions using tactics such as direct mail, telemarketing, promotions, and digital ads to directly engage with potential customers.
What are below-the-line ideas?
Below-the-line ideas encompass creative, innovative marketing strategies designed to engage directly with the target audience at a personal level. These ideas can include promotional events, direct mail campaigns, sponsorships, online marketing, and other tactics aimed at creating direct interaction and measurable responses from specific consumer segments.
What is ATL and BTL in marketing?
ATL (Above the Line) and BTL (Below the Line) marketing are two strategies used to target consumers. ATL marketing uses mass media methods like TV, radio, and print ads to reach a broad audience. In contrast, BTL marketing targets specific groups with more personalized and direct communication methods. These approaches are often used in combination to create comprehensive marketing campaigns.
What is BTL activity?
BTL activity includes various forms of direct marketing and promotional tactics that target individual consumers or specific consumer groups. These activities can range from in-store demonstrations, samples, events, roadshows, direct mail, and personalized online advertising. The key characteristic of BTL activity is its focus on direct engagement and measurable response from the audience.
What is BTL used for?
BTL is used to build personal relationships with customers, enhance brand loyalty, and drive immediate and measurable responses from targeted marketing initiatives. It is particularly effective in reaching specific demographic groups, introducing new products, providing detailed information, and encouraging direct interaction and engagement with the brand. BTL strategies are often utilized to supplement broader ATL campaigns, providing a deeper level of engagement where needed.
You may also like:

What is Roadshow Marketing? Types, Benefits and Examples

What is Personalization in Marketing? Strategies and Examples

What is Tween Marketing? Definition, Strategies and Examples

Influencer Marketing: Is It Right Fit For Your Brand
Leave a reply cancel reply.
Your email address will not be published. Required fields are marked *
Save my name, email, and website in this browser for the next time I comment.
This site uses Akismet to reduce spam. Learn how your comment data is processed .

IMAGES
VIDEO
COMMENTS
IELTS Writing Task 2 Sample Essay. Advertising is gaining more popularity in the marketing of products or services. While advertisements are considered to be advantageous, they can have numerous negative influences. It is unquestionable that there are several benefits of advertising.
3. The cost of advertising can be a disadvantage to small businesses. The cost of TV advertising at local television stations is at least $5 for every 1,000 viewers during a 30-second commercial. Then you have the cost of creative development when taking this marketing approach to consider.
On the one hand, the cost of advertising can increase the cost of consumer products. This is because companies and conglomerates spend billions of dollars in order to advertise a product. In the end, companies are forced to include these costs into their product which ultimately makes them expensive. For example, a beats headphone only costs 18 ...
It is the best method for communicating any information to old and new prospective customers. Here are the advantages of advertising: 1. Helps in Market Expansion. Through advertising, businesses can reach new markets and demographics, expanding their customer base. This is especially true when you diversify your advertising channels and expand ...
Answer 2: The advantages of advertising are that firstly, it introduces a new product in the market. Thus, it helps in expanding the market. As a result, sales also increase. Consumers become aware of and receive better quality products. Share with friends.
Topic: Discuss the advantages and disadvantages of advertisements. Band 6.5 IELTS Essay. Recently, it has become clear that advertising is growing in popularity across all industries. With the evolution of technology, there has been a significant global tendency toward brand publicity.
Benefits and Drawbacks of Types of Advertising. Media or banner advertising involves posting text or graphics on websites, forums, and portals. One of the main advantages of the banner is that it contains animation, which is usually an excellent eye-catcher for visitors (Schneider, 2017). In addition, the banner usually has a hyperlink to the ...
To conclude, while it is true that the market of popular consumer goods is booming because of the high sales, instead of the real needs of humans, capitalism and advertising are the key factors behind this prosperity. 1) Simon: "task 2 introductions should be short and direct". "Keep your introduction short.
5. Moreover, the 1% who make an immediate purchase are only one piece of the overall strategy. 6. Advertising raises brand awareness and may lead to later consumption and even have a subliminal effect that is difficult to trace. Write a new topic sentence with a new main idea at the end. Explain your new main idea.
Tell about its aim and target audience. Then describe the main points and how it impacts people, providing your opinion. Write about the influence of advertising and your own impression. To make it easier for you to decide on a topic for your advertising essay, our team has created a list of ideas for you.
The primary disadvantage of advertising is cost. Marketers question whether this communication method is really cost-effective at reaching large groups. Of course, costs vary depending on the medium, with television ads being very expensive to produce and place. In contrast, print and digital ads tend to be much less expensive.
IELTS Essay Vocabulary. A strong command of vocabulary is crucial for writing an effective advantages disadvantages essay in IELTS Writing Task 2. Your proficiency in English language vocabulary will be evident in how expertly you can select the most suitable expressions to convey precise meanings.
An advertisement is a product and like every other product in the world, it has its pros and cons. Advertisements are used to sell products. Businesses advertise their products to …show more content…. This ability of advertisements to make people do something can also be a disadvantage. Advertisements can sometimes be so persuasive as to ...
The Advantages and Disadvantages of Advertising. Advertising is seen as the most important tool of marketing a company's products or services. Investing in advertising campaigns is therefore seen as an investment that will yield higher profits and higher returns as well as increase the number of customers a company has.
Advertising is the non-personal communication of information usually paid for and usually persuasive in nature about products, services or ideas by identified sponsors through the various media. TYPES OF ADVERTISING. Newspaper advertising. Advantages. -Affordability - cheaper -Timeliness - fast and east to create your ads.
Advantages of Advertisement. Increased Awareness - Advertisements help to increase awareness of a product or service, by introducing it to a wider audience. This can lead to increased interest and sales. Targeted Audience - Advertisements can be targeted to a specific audience, based on factors such as age, gender, and interests. This helps to ensure that the right message is reaching the ...
ADVANTAGES AND DISADVANTAGES OF ADVERTISING. In the present times, promoting one's business gives focus to the unique new products. There are several positives of advertising such as more income and opportunities that improves the items that businesses sell. However, some companies and business owners turn to fallacy and false information ...
There are few disadvantages in personal selling. Firstly, this type of promotional tool is the most cost-effective way compared to others (advertising, sales promotion, direct marketing etc). Secondly, it cannot target several customers at a time compared to other promotional tool, which causes slow progress in generating sales.
IELTS Writing Task 2 essay with model answer. You should spend about 40 minutes on this task. Write about the following topic. Advertising has become an inevitable part of our lives. Some people believe that it is a positive aspect of our lives while others are of opposite belief. Discuss both views and give your opinion. Write at least 250 words.
Recently it has been seen that advertising is getting very popular in all fields of trade. With the advent of technology, there is a huge trend of publicity of different brands all over the world. Although there are tremendous advantages of advertisement but there are some drawbacks too. This essay will elaborate both points of views with final conclusion.
The keyword in the task is 'outweigh'. So you must cover the advantage and the disadvantage in this essay and clearly state your opinion. Do not only write about the advantages. you will need to cover both sides for a higher score in task response. If you believe the advantage is stronger you must give your opinion on that in the thesis ...
Consumers have an insatiable appetite for news, so new media have to pump out an ongoing stream of ever more sensationalized news articles. 16. News producers get instant feedback. As soon as a piece of news is pumped out, tweets fling back and comments are provided to show feedback.
Advertising is a business and like any other business people profit from it. Advertising has both pros and cons. Advertisements influence us in many ways and this is both an advantage and a disadvantage. They can persuade us to choose a product that is good and a product that is bad. They influence us and they enlighten us.
IELTS Advantage/Disadvantage Essay Sample 4 - Communication. IELTS Writing Task 2 advantage/disadvantage essay example that is a band score 8. The question is: Social media has replaced the traditional methods of communicating and people use more and more of social media in communicate and to follow news and events.
The rapid advancement of technology has significantly transformed communication methods, making it more accessible and efficient. However, despite its numerous benefits, communication also has its drawbacks. This essay explores the advantages and disadvantages of communication, providing a comprehensive understanding of its impact on society.
In addition, advertising increases sales, employment and profits. The overall effect of all this is economic progress for the nation, or more broadly for the world as a whole. On the other hand, it has some disadvantages. First of all, people are influenced by them badly especially children and teenagers.
The advantages and disadvantages of advertising. In the open- market economy, wars among companies or corporation are becoming sharper and sharper. Goods and services are available in the market, which makes customers puzzle to choose. At that time, advertising was born to do its duty in sale.It has both advantages and disadvantages.
The essay that has been written does not meet the discussion requirement. The current presentation uses an advantage V. disadvantage discussion when the requirement was to discuss (one of the 2) whether it is a positive or negative development. There is a clear lack of instruction comprehension/ understanding of how the essay was to be discussed.
2. Cost-Effectiveness. BTL marketing maximizes return on investment while minimizing waste by interacting directly with a targeted audience. By avoiding the broad approach of mass media, this strategy lowers expenses and increases the efficacy of marketing expenditures through focused tactics. 3.