hypothesis space in machine learning python

• Python for Machine Learning
• Machine Learning with R
• Machine Learning Algorithms
• Math for Machine Learning
• Machine Learning Interview Questions
• ML Projects
• Deep Learning
• Computer vision
• Data Science
• Artificial Intelligence

Hypothesis in Machine Learning

• Demystifying Machine Learning
• Bayes Theorem in Machine learning
• What is Machine Learning?
• Best IDEs For Machine Learning
• Learn Machine Learning in 45 Days
• Interpolation in Machine Learning
• How does Machine Learning Works?
• Machine Learning for Healthcare
• Applications of Machine Learning
• Machine Learning - Learning VS Designing
• Continual Learning in Machine Learning
• Meta-Learning in Machine Learning
• P-value in Machine Learning
• Why Machine Learning is The Future?
• How Does NASA Use Machine Learning?
• Few-shot learning in Machine Learning
• Machine Learning Jobs in Hyderabad

The concept of a hypothesis is fundamental in Machine Learning and data science endeavours. In the realm of machine learning, a hypothesis serves as an initial assumption made by data scientists and ML professionals when attempting to address a problem. Machine learning involves conducting experiments based on past experiences, and these hypotheses are crucial in formulating potential solutions.

It’s important to note that in machine learning discussions, the terms “hypothesis” and “model” are sometimes used interchangeably. However, a hypothesis represents an assumption, while a model is a mathematical representation employed to test that hypothesis. This section on “Hypothesis in Machine Learning” explores key aspects related to hypotheses in machine learning and their significance.

Table of Content

How does a Hypothesis work?

Hypothesis space and representation in machine learning, hypothesis in statistics, faqs on hypothesis in machine learning.

A hypothesis in machine learning is the model’s presumption regarding the connection between the input features and the result. It is an illustration of the mapping function that the algorithm is attempting to discover using the training set. To minimize the discrepancy between the expected and actual outputs, the learning process involves modifying the weights that parameterize the hypothesis. The objective is to optimize the model’s parameters to achieve the best predictive performance on new, unseen data, and a cost function is used to assess the hypothesis’ accuracy.

In most supervised machine learning algorithms, our main goal is to find a possible hypothesis from the hypothesis space that could map out the inputs to the proper outputs. The following figure shows the common method to find out the possible hypothesis from the Hypothesis space:

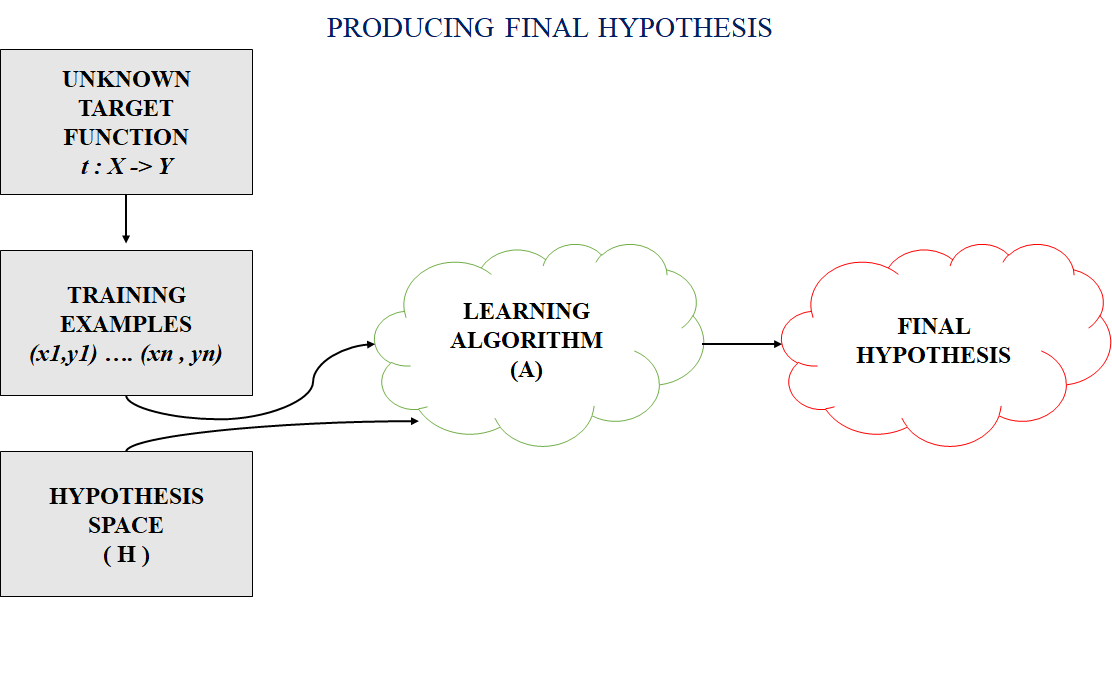
Hypothesis Space (H)

Hypothesis space is the set of all the possible legal hypothesis. This is the set from which the machine learning algorithm would determine the best possible (only one) which would best describe the target function or the outputs.

Hypothesis (h)

A hypothesis is a function that best describes the target in supervised machine learning. The hypothesis that an algorithm would come up depends upon the data and also depends upon the restrictions and bias that we have imposed on the data.

The Hypothesis can be calculated as:

[Tex]y = mx + b [/Tex]

• m = slope of the lines
• b = intercept

To better understand the Hypothesis Space and Hypothesis consider the following coordinate that shows the distribution of some data:

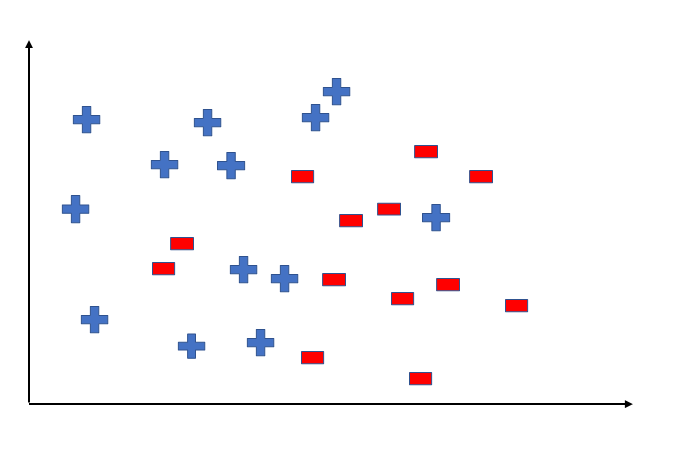
Say suppose we have test data for which we have to determine the outputs or results. The test data is as shown below:

We can predict the outcomes by dividing the coordinate as shown below:

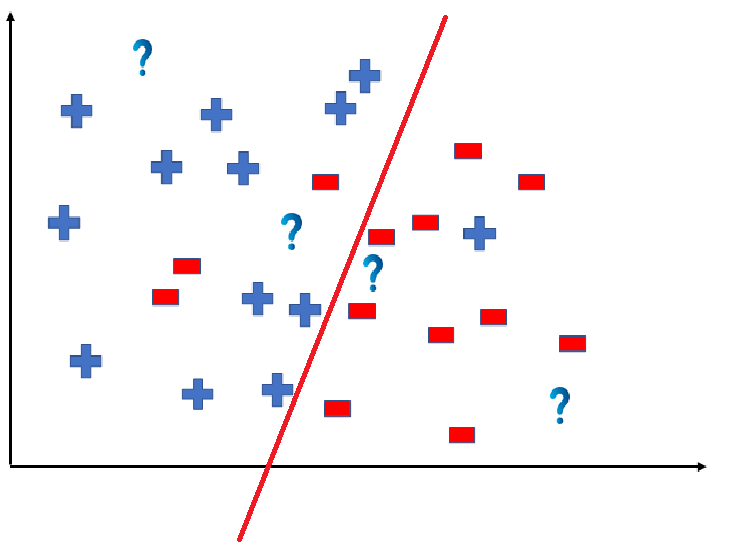
So the test data would yield the following result:

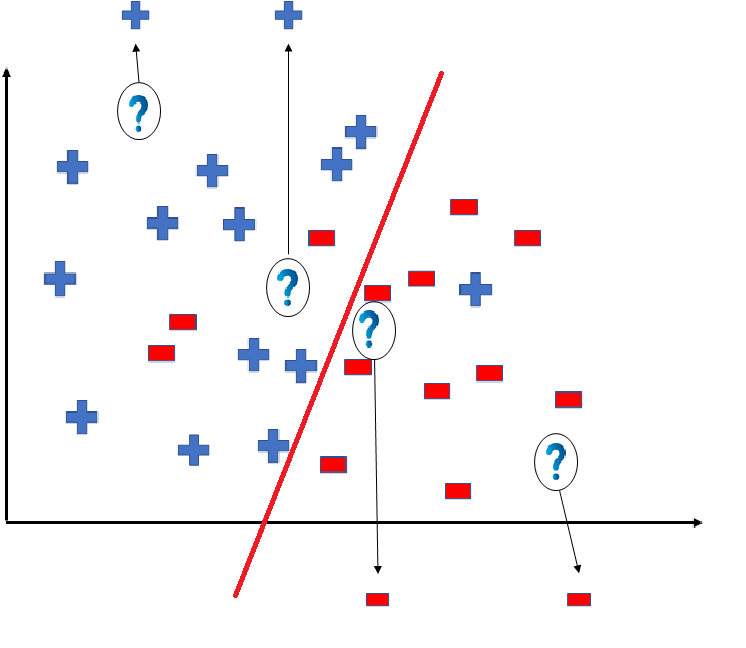
But note here that we could have divided the coordinate plane as:

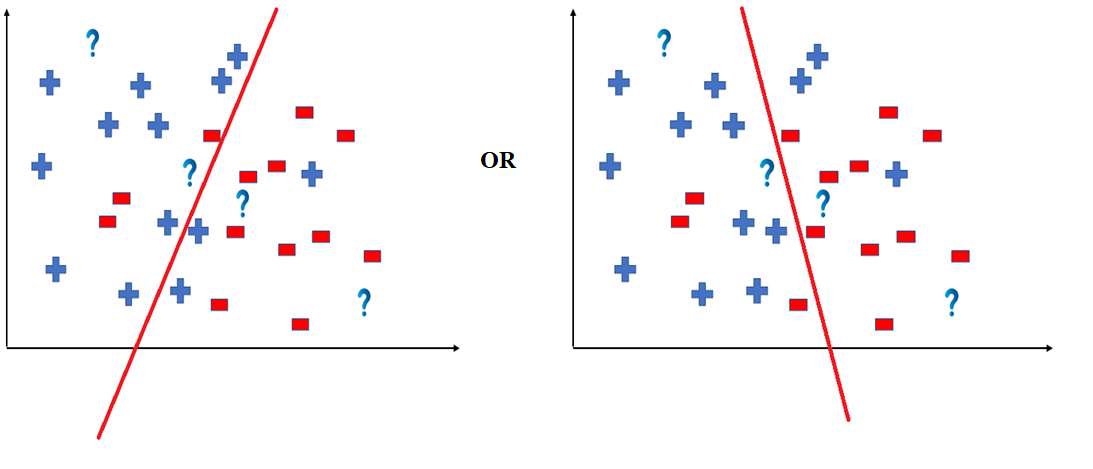
The way in which the coordinate would be divided depends on the data, algorithm and constraints.

• All these legal possible ways in which we can divide the coordinate plane to predict the outcome of the test data composes of the Hypothesis Space.
• Each individual possible way is known as the hypothesis.

Hence, in this example the hypothesis space would be like:

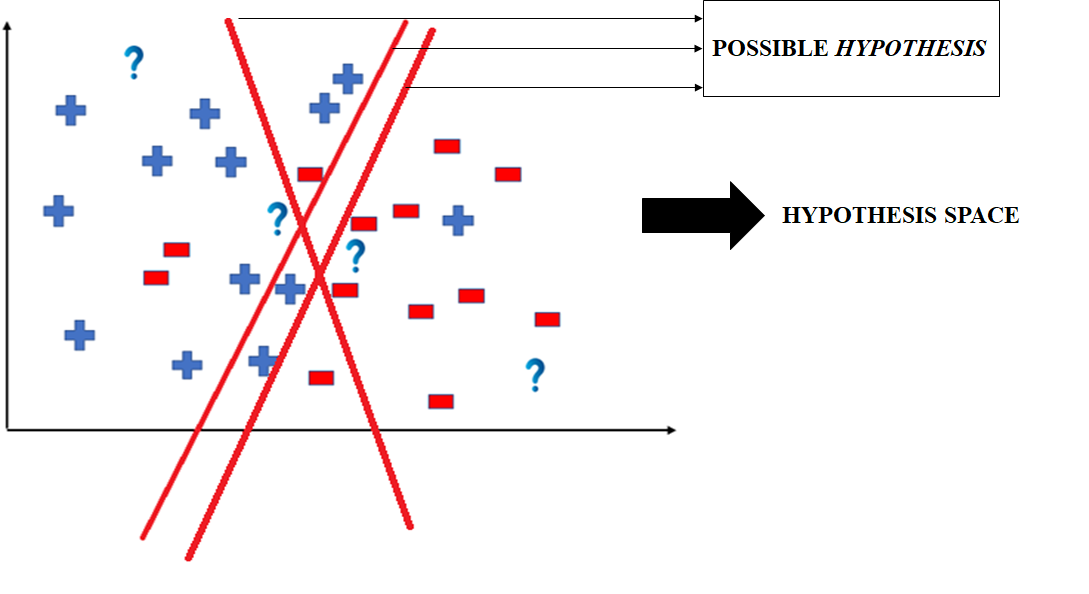
The hypothesis space comprises all possible legal hypotheses that a machine learning algorithm can consider. Hypotheses are formulated based on various algorithms and techniques, including linear regression, decision trees, and neural networks. These hypotheses capture the mapping function transforming input data into predictions.

Hypothesis Formulation and Representation in Machine Learning

Hypotheses in machine learning are formulated based on various algorithms and techniques, each with its representation. For example:

• Linear Regression : [Tex] h(X) = \theta_0 + \theta_1 X_1 + \theta_2 X_2 + … + \theta_n X_n[/Tex]
• Decision Trees : [Tex]h(X) = \text{Tree}(X)[/Tex]
• Neural Networks : [Tex]h(X) = \text{NN}(X)[/Tex]

In the case of complex models like neural networks, the hypothesis may involve multiple layers of interconnected nodes, each performing a specific computation.

Hypothesis Evaluation:

The process of machine learning involves not only formulating hypotheses but also evaluating their performance. This evaluation is typically done using a loss function or an evaluation metric that quantifies the disparity between predicted outputs and ground truth labels. Common evaluation metrics include mean squared error (MSE), accuracy, precision, recall, F1-score, and others. By comparing the predictions of the hypothesis with the actual outcomes on a validation or test dataset, one can assess the effectiveness of the model.

Hypothesis Testing and Generalization:

Once a hypothesis is formulated and evaluated, the next step is to test its generalization capabilities. Generalization refers to the ability of a model to make accurate predictions on unseen data. A hypothesis that performs well on the training dataset but fails to generalize to new instances is said to suffer from overfitting. Conversely, a hypothesis that generalizes well to unseen data is deemed robust and reliable.

The process of hypothesis formulation, evaluation, testing, and generalization is often iterative in nature. It involves refining the hypothesis based on insights gained from model performance, feature importance, and domain knowledge. Techniques such as hyperparameter tuning, feature engineering, and model selection play a crucial role in this iterative refinement process.

In statistics , a hypothesis refers to a statement or assumption about a population parameter. It is a proposition or educated guess that helps guide statistical analyses. There are two types of hypotheses: the null hypothesis (H0) and the alternative hypothesis (H1 or Ha).

• Null Hypothesis(H 0 ): This hypothesis suggests that there is no significant difference or effect, and any observed results are due to chance. It often represents the status quo or a baseline assumption.
• Aternative Hypothesis(H 1 or H a ): This hypothesis contradicts the null hypothesis, proposing that there is a significant difference or effect in the population. It is what researchers aim to support with evidence.

Q. How does the training process use the hypothesis?

The learning algorithm uses the hypothesis as a guide to minimise the discrepancy between expected and actual outputs by adjusting its parameters during training.

Q. How is the hypothesis’s accuracy assessed?

Usually, a cost function that calculates the difference between expected and actual values is used to assess accuracy. Optimising the model to reduce this expense is the aim.

Q. What is Hypothesis testing?

Hypothesis testing is a statistical method for determining whether or not a hypothesis is correct. The hypothesis can be about two variables in a dataset, about an association between two groups, or about a situation.

Q. What distinguishes the null hypothesis from the alternative hypothesis in machine learning experiments?

The null hypothesis (H0) assumes no significant effect, while the alternative hypothesis (H1 or Ha) contradicts H0, suggesting a meaningful impact. Statistical testing is employed to decide between these hypotheses.

Please Login to comment...

Similar reads.

• Machine Learning

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Machine Learning Theory - Part 2: Generalization Bounds

Last time we concluded by noticing that minimizing the empirical risk (or the training error) is not in itself a solution to the learning problem, it could only be considered a solution if we can guarantee that the difference between the training error and the generalization error (which is also called the generalization gap ) is small enough. We formalized such requirement using the probability:

That is if this probability is small, we can guarantee that the difference between the errors is not much, and hence the learning problem can be solved.

In this part we’ll start investigating that probability at depth and see if it indeed can be small, but before starting you should note that I skipped a lot of the mathematical proofs here. You’ll often see phrases like “It can be proved that …”, “One can prove …”, “It can be shown that …”, … etc without giving the actual proof. This is to make the post easier to read and to focus all the effort on the conceptual understanding of the subject. In case you wish to get your hands dirty with proofs, you can find all of them in the additional readings, or on the Internet of course!

Independently, and Identically Distributed

The world can be a very messy place! This is a problem that faces any theoretical analysis of a real world phenomenon; because usually we can’t really capture all the messiness in mathematical terms, and even if we’re able to; we usually don’t have the tools to get any results from such a messy mathematical model.

So in order for theoretical analysis to move forward, some assumptions must be made to simplify the situation at hand, we can then use the theoretical results from that simplification to infer about reality.

Assumptions are common practice in theoretical work. Assumptions are not bad in themselves, only bad assumptions are bad! As long as our assumptions are reasonable and not crazy, they’ll hold significant truth about reality.

A reasonable assumption we can make about the problem we have at hand is that our training dataset samples are independently, and identically distributed (or i.i.d. for short), that means that all the samples are drawn from the same probability distribution and that each sample is independent from the others.

This assumption is essential for us. We need it to start using the tools form probability theory to investigate our generalization probability, and it’s a very reasonable assumption because:

• It’s more likely for a dataset used for inferring about an underlying probability distribution to be all sampled for that same distribution. If this is not the case, then the statistics we get from the dataset will be noisy and won’t correctly reflect the target underlying distribution.
• It’s more likely that each sample in the dataset is chosen without considering any other sample that has been chosen before or will be chosen after. If that’s not the case and the samples are dependent, then the dataset will suffer from a bias towards a specific direction in the distribution, and hence will fail to reflect the underlying distribution correctly.

So we can build upon that assumption with no fear.

The Law of Large Numbers

Most of us, since we were kids, know that if we tossed a fair coin a large number of times, roughly half of the times we’re gonna get heads. This is an instance of wildly known fact about probability that if we retried an experiment for a sufficiency large amount of times, the average outcome of these experiments (or, more formally, the sample mean ) will be very close to the true mean of the underlying distribution. This fact is formally captured into what we call The law of large numbers :

If $x_1, x_2, …, x_m$ are $m$ i.i.d. samples of a random variable $X$ distributed by $P$. then for a small positive non-zero value $\epsilon$: \[\lim_{m \rightarrow \infty} \mathbb{P}\left[\left|\mathop{\mathbb{E}}_{X \sim P}[X] - \frac{1}{m}\sum_{i=1}^{m}x_i \right| > \epsilon\right] = 0\]

This version of the law is called the weak law of large numbers . It’s weak because it guarantees that as the sample size goes larger, the sample and true means will likely be very close to each other by a non-zero distance no greater than epsilon. On the other hand, the strong version says that with very large sample size, the sample mean is almost surely equal to the true mean.

The formulation of the weak law lends itself naturally to use with our generalization probability. By recalling that the empirical risk is actually the sample mean of the errors and the risk is the true mean, for a single hypothesis $h$ we can say that:

Well, that’s a progress, A pretty small one, but still a progress! Can we do any better?

Hoeffding’s inequality

The law of large numbers is like someone pointing the directions to you when you’re lost, they tell you that by following that road you’ll eventually reach your destination, but they provide no information about how fast you’re gonna reach your destination, what is the most convenient vehicle, should you walk or take a cab, and so on.

To our destination of ensuring that the training and generalization errors do not differ much, we need to know more info about the how the road down the law of large numbers look like. These info are provided by what we call the concentration inequalities . This is a set of inequalities that quantifies how much random variables (or function of them) deviate from their expected values (or, also, functions of them). One inequality of those is Heoffding’s inequality :

If $x_1, x_2, …, x_m$ are $m$ i.i.d. samples of a random variable $X$ distributed by $P$, and $a \leq x_i \leq b$ for every $i$, then for a small positive non-zero value $\epsilon$: \[\mathbb{P}\left[\left|\mathop{\mathbb{E}}_{X \sim P}[X] - \frac{1}{m}\sum_{i=0}^{m}x_i\right| > \epsilon\right] \leq 2\exp\left(\frac{-2m\epsilon^2}{(b -a)^2}\right)\]

You probably see why we specifically chose Heoffding’s inequality from among the others. We can naturally apply this inequality to our generalization probability, assuming that our errors are bounded between 0 and 1 (which is a reasonable assumption, as we can get that using a 0/1 loss function or by squashing any other loss between 0 and 1) and get for a single hypothesis $h$:

This means that the probability of the difference between the training and the generalization errors exceeding $\epsilon$ exponentially decays as the dataset size goes larger. This should align well with our practical experience that the bigger the dataset gets, the better the results become.

If you noticed, all our analysis up till now was focusing on a single hypothesis $h$. But the learning problem doesn’t know that single hypothesis beforehand, it needs to pick one out of an entire hypothesis space $\mathcal{H}$, so we need a generalization bound that reflects the challenge of choosing the right hypothesis.

Generalization Bound: 1st Attempt

In order for the entire hypothesis space to have a generalization gap bigger than $\epsilon$, at least one of its hypothesis: $h_1$ or $h_2$ or $h_3$ or … etc should have. This can be expressed formally by stating that:

Where $\bigcup$ denotes the union of the events, which also corresponds to the logical OR operator. Using the union bound inequality , we get:

We exactly know the bound on the probability under the summation from our analysis using the Heoffding’s inequality, so we end up with:

Where $|\mathcal{H}|$ is the size of the hypothesis space. By denoting the right hand side of the above inequality by $\delta$, we can say that with a confidence $1 - \delta$:

And with some basic algebra, we can express $\epsilon$ in terms of $\delta$ and get:

This is our first generalization bound, it states that the generalization error is bounded by the training error plus a function of the hypothesis space size and the dataset size. We can also see that the the bigger the hypothesis space gets, the bigger the generalization error becomes. This explains why the memorization hypothesis form last time, which theoretically has $|\mathcal{H}| = \infty$, fails miserably as a solution to the learning problem despite having $R_\text{emp} = 0$; because for the memorization hypothesis $h_\text{mem}$:

But wait a second! For a linear hypothesis of the form $h(x) = wx + b$, we also have $|\mathcal{H}| = \infty$ as there is infinitely many lines that can be drawn. So the generalization error of the linear hypothesis space should be unbounded just as the memorization hypothesis! If that’s true, why does perceptrons, logistic regression, support vector machines and essentially any ML model that uses a linear hypothesis work?

Our theoretical result was able to account for some phenomena (the memorization hypothesis, and any finite hypothesis space) but not for others (the linear hypothesis, or other infinite hypothesis spaces that empirically work). This means that there’s still something missing from our theoretical model, and it’s time for us to revise our steps. A good starting point is from the source of the problem itself, which is the infinity in $|\mathcal{H}|$.

Notice that the term $|\mathcal{H}|$ resulted from our use of the union bound. The basic idea of the union bound is that it bounds the probability by the worst case possible, which is when all the events under union are mutually independent. This bound gets more tight as the events under consideration get less dependent. In our case, for the bound to be tight and reasonable, we need the following to be true:

For every two hypothesis $h_1, h_2 \in \mathcal{H}$ the two events $|R(h_1) - R_\text{emp}(h_1)| > \epsilon$ and $|R(h_2) - R_\text{emp}(h_2)| > \epsilon$ are likely to be independent. This means that the event that $h_1$ has a generalization gap bigger than $\epsilon$ should be independent of the event that also $h_2$ has a generalization gap bigger than $\epsilon$, no matter how much $h_1$ and $h_2$ are close or related; the events should be coincidental.

But is that true?

Examining the Independence Assumption

The first question we need to ask here is why do we need to consider every possible hypothesis in $\mathcal{H}$? This may seem like a trivial question; as the answer is simply that because the learning algorithm can search the entire hypothesis space looking for its optimal solution. While this answer is correct, we need a more formal answer in light of the generalization inequality we’re studying.

The formulation of the generalization inequality reveals a main reason why we need to consider all the hypothesis in $\mathcal{H}$. It has to do with the existence of $\sup_{h \in \mathcal{H}}$. The supremum in the inequality guarantees that there’s a very little chance that the biggest generalization gap possible is greater than $\epsilon$; this is a strong claim and if we omit a single hypothesis out of $\mathcal{H}$, we might miss that “biggest generalization gap possible” and lose that strength, and that’s something we cannot afford to lose. We need to be able to make that claim to ensure that the learning algorithm would never land on a hypothesis with a bigger generalization gap than $\epsilon$.

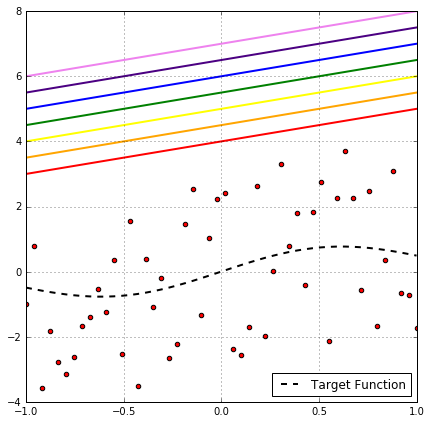
Looking at the above plot of binary classification problem, it’s clear that this rainbow of hypothesis produces the same classification on the data points, so all of them have the same empirical risk. So one might think, as they all have the same $R_\text{emp}$, why not choose one and omit the others?!

This would be a very good solution if we’re only interested in the empirical risk, but our inequality takes into its consideration the out-of-sample risk as well, which is expressed as:

This is an integration over every possible combination of the whole input and output spaces $\mathcal{X, Y}$. So in order to ensure our supremum claim, we need the hypothesis to cover the whole of $\mathcal{X \times Y}$, hence we need all the possible hypotheses in $\mathcal{H}$.

Now that we’ve established that we do need to consider every single hypothesis in $\mathcal{H}$, we can ask ourselves: are the events of each hypothesis having a big generalization gap are likely to be independent?

Well, Not even close! Take for example the rainbow of hypotheses in the above plot, it’s very clear that if the red hypothesis has a generalization gap greater than $\epsilon$, then, with 100% certainty, every hypothesis with the same slope in the region above it will also have that. The same argument can be made for many different regions in the $\mathcal{X \times Y}$ space with different degrees of certainty as in the following figure.

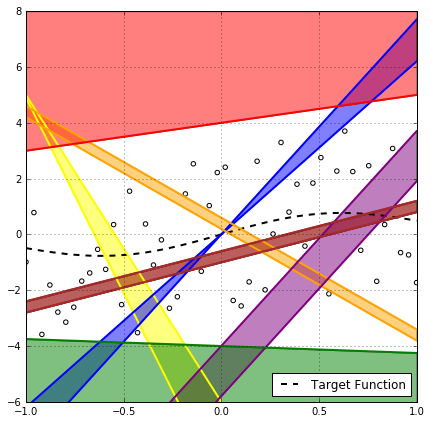
But this is not helpful for our mathematical analysis, as the regions seems to be dependent on the distribution of the sample points and there is no way we can precisely capture these dependencies mathematically, and we cannot make assumptions about them without risking to compromise the supremum claim.

So the union bound and the independence assumption seem like the best approximation we can make,but it highly overestimates the probability and makes the bound very loose, and very pessimistic!

However, what if somehow we can get a very good estimate of the risk $R(h)$ without needing to go over the whole of the $\mathcal{X \times Y}$ space, would there be any hope to get a better bound?

The Symmetrization Lemma

Let’s think for a moment about something we do usually in machine learning practice. In order to measure the accuracy of our model, we hold out a part of the training set to evaluate the model on after training, and we consider the model’s accuracy on this left out portion as an estimate for the generalization error. This works because we assume that this test set is drawn i.i.d. from the same distribution of the training set (this is why we usually shuffle the whole dataset beforehand to break any correlation between the samples).

It turns out that we can do a similar thing mathematically, but instead of taking out a portion of our dataset $S$, we imagine that we have another dataset $S’$ with also size $m$, we call this the ghost dataset . Note that this has no practical implications, we don’t need to have another dataset at training, it’s just a mathematical trick we’re gonna use to git rid of the restrictions of $R(h)$ in the inequality.

We’re not gonna go over the proof here, but using that ghost dataset one can actually prove that:

where $R_\text{emp}’(h)$ is the empirical risk of hypothesis $h$ on the ghost dataset. This means that the probability of the largest generalization gap being bigger than $\epsilon$ is at most twice the probability that the empirical risk difference between $S, S’$ is larger than $\frac{\epsilon}{2}$. Now that the right hand side in expressed only in terms of empirical risks, we can bound it without needing to consider the the whole of $\mathcal{X \times Y}$, and hence we can bound the term with the risk $R(h)$ without considering the whole of input and output spaces!

This, which is called the symmetrization lemma , was one of the two key parts in the work of Vapnik-Chervonenkis (1971).

The Growth Function

Now that we are bounding only the empirical risk, if we have many hypotheses that have the same empirical risk (a.k.a. producing the same labels/values on the data points), we can safely choose one of them as a representative of the whole group, we’ll call that an effective hypothesis, and discard all the others.

By only choosing the distinct effective hypotheses on the dataset $S$, we restrict the hypothesis space $\mathcal{H}$ to a smaller subspace that depends on the dataset $\mathcal{H}_{|S}$.

We can assume the independence of the hypotheses in $\mathcal{H}_{|S}$ like we did before with $\mathcal{H}$ (but it’s more plausible now), and use the union bound to get that:

Notice that the hypothesis space is restricted by $S \cup S’$ because we using the empirical risk on both the original dataset $S$ and the ghost $S’$. The question now is what is the maximum size of a restricted hypothesis space? The answer is very simple; we consider a hypothesis to be a new effective one if it produces new labels/values on the dataset samples, then the maximum number of distinct hypothesis (a.k.a the maximum number of the restricted space) is the maximum number of distinct labels/values the dataset points can take. A cool feature about that maximum size is that its a combinatorial measure, so we don’t need to worry about how the samples are distributed!

For simplicity, we’ll focus now on the case of binary classification, in which $\mathcal{Y}=\{-1, +1\}$. Later we’ll show that the same concepts can be extended to both multiclass classification and regression. In that case, for a dataset with $m$ samples, each of which can take one of two labels: either -1 or +1, the maximum number of distinct labellings is $2^m$.

We’ll define the maximum number of distinct labellings/values on a dataset $S$ of size $m$ by a hypothesis space $\mathcal{H}$ as the growth function of $\mathcal{H}$ given $m$, and we’ll denote that by $\Delta_\mathcal{H}(m)$. It’s called the growth function because it’s value for a single hypothesis space $\mathcal{H}$ (aka the size of the restricted subspace $\mathcal{H_{|S}}$) grows as the size of the dataset grows. Now we can say that:

Notice that we used $2m$ because we have two datasets $S,S’$ each with size $m$.

For the binary classification case, we can say that:

But $2^m$ is exponential in $m$ and would grow too fast for large datasets, which makes the odds in our inequality go too bad too fast! Is that the best bound we can get on that growth function?

The VC-Dimension

The $2^m$ bound is based on the fact that the hypothesis space $\mathcal{H}$ can produce all the possible labellings on the $m$ data points. If a hypothesis space can indeed produce all the possible labels on a set of data points, we say that the hypothesis space shatters that set.

But can any hypothesis space shatter any dataset of any size? Let’s investigate that with the binary classification case and the $\mathcal{H}$ of linear classifiers $\mathrm{sign}(wx + b)$. The following animation shows how many ways a linear classifier in 2D can label 3 points (on the left) and 4 points (on the right).

In the animation, the whole space of possible effective hypotheses is swept. For the the three points, the hypothesis shattered the set of points and produced all the possible $2^3 = 8$ labellings. However for the four points,the hypothesis couldn’t get more than 14 and never reached $2^4 = 16$, so it failed to shatter this set of points. Actually, no linear classifier in 2D can shatter any set of 4 points, not just that set; because there will always be two labellings that cannot be produced by a linear classifier which is depicted in the following figure.

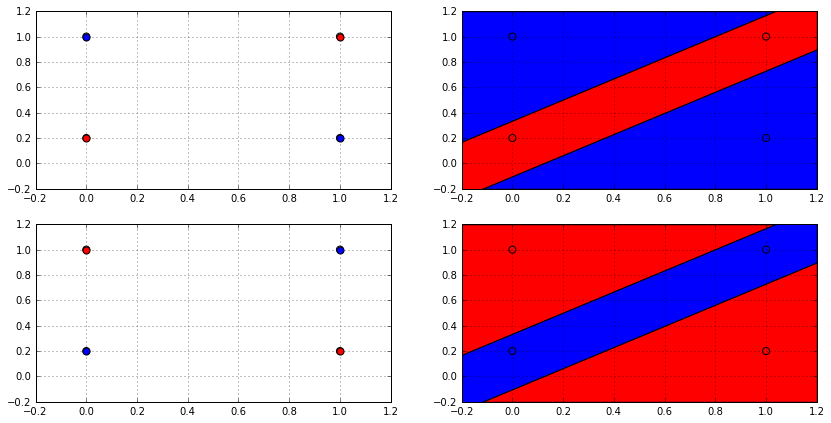
From the decision boundary plot (on the right), it’s clear why no linear classifier can produce such labellings; as no linear classifier can divide the space in this way. So it’s possible for a hypothesis space $\mathcal{H}$ to be unable to shatter all sizes. This fact can be used to get a better bound on the growth function, and this is done using Sauer’s lemma :

If a hypothesis space $\mathcal{H}$ cannot shatter any dataset with size more than $k$, then: \[\Delta_{\mathcal{H}}(m) \leq \sum_{i=0}^{k}\binom{m}{i}\]

This was the other key part of Vapnik-Chervonenkis work (1971), but it’s named after another mathematician, Norbert Sauer; because it was independently proved by him around the same time (1972). However, Vapnik and Chervonenkis weren’t completely left out from this contribution; as that $k$, which is the maximum number of points that can be shattered by $\mathcal{H}$, is now called the Vapnik-Chervonenkis-dimension or the VC-dimension $d_{\mathrm{vc}}$ of $\mathcal{H}$.

For the case of the linear classifier in 2D, $d_\mathrm{vc} = 3$. In general, it can be proved that hyperplane classifiers (the higher-dimensional generalization of line classifiers) in $\mathbb{R}^n$ space has $d_\mathrm{vc} = n + 1$.

The bound on the growth function provided by sauer’s lemma is indeed much better than the exponential one we already have, it’s actually polynomial! Using algebraic manipulation, we can prove that:

Where $O$ refers to the Big-O notation for functions asymptotic (near the limits) behavior, and $e$ is the mathematical constant.

Thus we can use the VC-dimension as a proxy for growth function and, hence, for the size of the restricted space $\mathcal{H_{|S}}$. In that case, $d_\mathrm{vc}$ would be a measure of the complexity or richness of the hypothesis space.

The VC Generalization Bound

With a little change in the constants, it can be shown that Heoffding’s inequality is applicable on the probability $\mathbb{P}\left[|R_\mathrm{emp}(h) - R_\mathrm{emp}’(h)| > \frac{\epsilon}{2}\right]$. With that, and by combining inequalities (1) and (2), the Vapnik-Chervonenkis theory follows:

This can be re-expressed as a bound on the generalization error, just as we did earlier with the previous bound, to get the VC generalization bound :

or, by using the bound on growth function in terms of $d_\mathrm{vc}$ as:

Professor Vapnik standing in front of a white board that has a form of the VC-bound and the phrase “All your bayes are belong to us”, which is a play on the broken english phrase found in the classic video game Zero Wing in a claim that the VC framework of inference is superior to that of Bayesian inference . [Courtesy of Yann LeCunn ].

This is a significant result! It’s a clear and concise mathematical statement that the learning problem is solvable, and that for infinite hypotheses spaces there is a finite bound on the their generalization error! Furthermore, this bound can be described in term of a quantity ($d_\mathrm{vc}$), that solely depends on the hypothesis space and not on the distribution of the data points!

Now, in light of these results, is there’s any hope for the memorization hypothesis?

It turns out that there’s still no hope! The memorization hypothesis can shatter any dataset no matter how big it is, that means that its $d_\mathrm{vc}$ is infinite, yielding an infinite bound on $R(h_\mathrm{mem})$ as before. However, the success of linear hypothesis can now be explained by the fact that they have a finite $d_\mathrm{vc} = n + 1$ in $\mathbb{R}^n$. The theory is now consistent with the empirical observations.

Distribution-Based Bounds

The fact that $d_\mathrm{vc}$ is distribution-free comes with a price: by not exploiting the structure and the distribution of the data samples, the bound tends to get loose. Consider for example the case of linear binary classifiers in a very higher n-dimensional feature space, using the distribution-free $d_\mathrm{vc} = n + 1$ means that the bound on the generalization error would be poor unless the size of the dataset $N$ is also very large to balance the effect of the large $d_\mathrm{vc}$. This is the good old curse of dimensionality we all know and endure.

However, a careful investigation into the distribution of the data samples can bring more hope to the situation. For example, For data points that are linearly separable, contained in a ball of radius $R$, with a margin $\rho$ between the closest points in the two classes, one can prove that for a hyperplane classifier:

It follows that the larger the margin, the lower the $d_\mathrm{vc}$ of the hypothesis. This is theoretical motivation behind Support Vector Machines (SVMs) which attempts to classify data using the maximum margin hyperplane. This was also proved by Vapnik and Chervonenkis.

One Inequality to Rule Them All

Up until this point, all our analysis was for the case of binary classification. And it’s indeed true that the form of the vc bound we arrived at here only works for the binary classification case. However, the conceptual framework of VC (that is: shattering, growth function and dimension) generalizes very well to both multi-class classification and regression.

Due to the work of Natarajan (1989), the Natarajan dimension is defined as a generalization of the VC-dimension for multiple classes classification, and a bound similar to the VC-Bound is derived in terms of it. Also, through the work of Pollard (1984), the pseudo-dimension generalizes the VC-dimension for the regression case with a bound on the generalization error also similar to VC’s.

There is also Rademacher’s complexity , which is a relatively new tool (devised in the 2000s) that measures the richness of a hypothesis space by measuring how well it can fit to random noise. The cool thing about Rademacher’s complexity is that it’s flexible enough to be adapted to any learning problem, and it yields very similar generalization bounds to the other methods mentioned.

However, no matter what the exact form of the bound produced by any of these methods is, it always takes the form:

where $C$ is a function of the hypothesis space complexity (or size, or richness), $N$ the size of the dataset, and the confidence $1 - \delta$ about the bound. This inequality basically says the generalization error can be decomposed into two parts: the empirical training error, and the complexity of the learning model.

This form of the inequality holds to any learning problem no matter the exact form of the bound, and this is the one we’re gonna use throughout the rest of the series to guide us through the process of machine learning.

References and Additional Readings

• Mohri, Mehryar, Afshin Rostamizadeh, and Ameet Talwalkar. Foundations of machine learning. MIT press, 2012.
• Shalev-Shwartz, Shai, and Shai Ben-David. Understanding machine learning: From theory to algorithms. Cambridge University Press, 2014.
• Abu-Mostafa, Y. S., Magdon-Ismail, M., & Lin, H. (2012). Learning from data: a short course.

Mostafa Samir

Wandering in a lifelong journey seeking after truth.

ID3 Algorithm and Hypothesis space in Decision Tree Learning

The collection of potential decision trees is the hypothesis space searched by ID3. ID3 searches this hypothesis space in a hill-climbing fashion, starting with the empty tree and moving on to increasingly detailed hypotheses in pursuit of a decision tree that properly classifies the training data.

In this blog, we’ll have a look at the Hypothesis space in Decision Trees and the ID3 Algorithm. 

ID3 Algorithm: 

The ID3 algorithm (Iterative Dichotomiser 3) is a classification technique that uses a greedy approach to create a decision tree by picking the optimal attribute that delivers the most Information Gain (IG) or the lowest Entropy (H).

What is Information Gain and Entropy?  

Information gain: .

The assessment of changes in entropy after segmenting a dataset based on a characteristic is known as information gain.

It establishes how much information a feature provides about a class.

We divided the node and built the decision tree based on the value of information gained.

The greatest information gain node/attribute is split first in a decision tree method, which always strives to maximize the value of information gain. 

The formula for Information Gain: 

Entropy is a metric for determining the degree of impurity in a particular property. It denotes the unpredictability of data. The following formula may be used to compute entropy:

S stands for “total number of samples.”

P(yes) denotes the likelihood of a yes answer.

P(no) denotes the likelihood of a negative outcome.

• Calculate the dataset’s entropy.
• For each feature/attribute.

Determine the entropy for each of the category values.

Calculate the feature’s information gain.

• Find the feature that provides the most information.
• Repeat it till we get the tree we want.

Characteristics of ID3: 

• ID3 takes a greedy approach, which means it might become caught in local optimums and hence cannot guarantee an optimal result.
• ID3 has the potential to overfit the training data (to avoid overfitting, smaller decision trees should be preferred over larger ones).
• This method creates tiny trees most of the time, however, it does not always yield the shortest tree feasible.
• On continuous data, ID3 is not easy to use (if the values of any given attribute are continuous, then there are many more places to split the data on this attribute, and searching for the best value to split by takes a lot of time).

Over Fitting:  

Good generalization is the desired property in our decision trees (and, indeed, in all classification problems), as we noted before. 

This implies we want the model fit on the labeled training data to generate predictions that are as accurate as they are on new, unseen observations.

Capabilities and Limitations of ID3:

• In relation to the given characteristics, ID3’s hypothesis space for all decision trees is a full set of finite discrete-valued functions.
• As it searches across the space of decision trees, ID3 keeps just one current hypothesis. This differs from the prior version space candidate Elimination approach, which keeps the set of all hypotheses compatible with the training instances provided.
• ID3 loses the capabilities that come with explicitly describing all consistent hypotheses by identifying only one hypothesis. It is unable to establish how many different decision trees are compatible with the supplied training data.
• One benefit of incorporating all of the instances’ statistical features (e.g., information gain) is that the final search is less vulnerable to faults in individual training examples.
• By altering its termination criterion to allow hypotheses that inadequately match the training data, ID3 may simply be modified to handle noisy training data.
• In its purest form, ID3 does not go backward in its search. It never goes back to evaluate a choice after it has chosen an attribute to test at a specific level in the tree. As a result, it is vulnerable to the standard dangers of hill-climbing search without backtracking, resulting in local optimum but not globally optimal solutions.
• At each stage of the search, ID3 uses all training instances to make statistically based judgments on how to refine its current hypothesis. This is in contrast to approaches that make incremental judgments based on individual training instances (e.g., FIND-S or CANDIDATE-ELIMINATION ).

Hypothesis Space Search by ID3: 

• ID3 climbs the hill of knowledge acquisition by searching the space of feasible decision trees.
• It looks for all finite discrete-valued functions in the whole space. Every function is represented by at least one tree.
• It only holds one theory (unlike Candidate-Elimination). It is unable to inform us how many more feasible options exist.
• It’s possible to get stranded in local optima.
• At each phase, all training examples are used. Errors have a lower impact on the outcome.

Help | Advanced Search

Statistics > Machine Learning

Title: hypothesis spaces for deep learning.

Abstract: This paper introduces a hypothesis space for deep learning that employs deep neural networks (DNNs). By treating a DNN as a function of two variables, the physical variable and parameter variable, we consider the primitive set of the DNNs for the parameter variable located in a set of the weight matrices and biases determined by a prescribed depth and widths of the DNNs. We then complete the linear span of the primitive DNN set in a weak* topology to construct a Banach space of functions of the physical variable. We prove that the Banach space so constructed is a reproducing kernel Banach space (RKBS) and construct its reproducing kernel. We investigate two learning models, regularized learning and minimum interpolation problem in the resulting RKBS, by establishing representer theorems for solutions of the learning models. The representer theorems unfold that solutions of these learning models can be expressed as linear combination of a finite number of kernel sessions determined by given data and the reproducing kernel.

Submission history

Access paper:.

• HTML (experimental)
• Other Formats

References & Citations

• Google Scholar
• Semantic Scholar

BibTeX formatted citation

Bibliographic and Citation Tools

Code, data and media associated with this article, recommenders and search tools.

• Institution

arXivLabs: experimental projects with community collaborators

arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website.

Both individuals and organizations that work with arXivLabs have embraced and accepted our values of openness, community, excellence, and user data privacy. arXiv is committed to these values and only works with partners that adhere to them.

Have an idea for a project that will add value for arXiv's community? Learn more about arXivLabs .

Candidate Elimination Algorithm Program in Python

What is candidate elimination algorithm in machine learning.

• Before Implementing the Candidate Elimination Algorithm in Python we Shall discuss about this briefly.
• The Candidate Elimination Algorithm is a Machine Learning Algorithm used for concept learning and hypothesis space search in the context of content Classification.
• This algorithm incrementally builds the version space given a hypothesis space H and a set E of examples.
• The examples are added one by one; each example possibly shrinks the version space by removing the hypotheses that are inconsistent with the example.
• It does this by updating the general and specific boundary for each new example.

The Primary Goal is to generate a set of hypothesis, known as the “Version Space” that represents a range of possible concepts based on observed training data.

Version Space: It is an intermediate of general hypothesis and Specific hypothesis. It not only just writes one hypothesis but a set of all possible hypotheses based on training dataset.

How It Updates the Version Space?

• Version Space Update: The version space represents the set of all hypotheses that are consistent with the training data encountered so far. It is the intersection of S and G. As more examples are processed, the version space narrows down to a smaller set of consistent hypotheses.
• Termination: The algorithm continues processing examples until convergence, meaning that the version space becomes a single hypothesis or remains unchanged. At this point, the algorithm terminates.
• The Candidate Elimination Algorithm is used in concept learning tasks where there is uncertainty about the true concept being learned. It efficiently explores the hypothesis space and helps maintain a range of potential concepts, making it a valuable tool in machine learning and artificial intelligence, particularly in the early days of concept learning research.

Steps to Follow for the Candidate Elimination Algorithm:

• Start with two hypotheses:
• The most specific hypothesis, denoted as S, initially assumes that no attribute value can be generalized (usually initialized with the most specific values, like ‘Φ’ for each attribute).
• The most general hypothesis, denoted as G, initially assumes that all attribute values can be generalized (initialized with the least specific values, like ‘?’for each attribute).
• For each training example:
• When a positive example is encountered, the algorithm refines both S and G as follows:
• If the attribute value in the example is different from the value in S, replace the value in S with ‘Φ’ (indicating uncertainty).
• If the attribute value in the example matches the value in G, keep it unchanged.
• If the attribute value in the example is different from the value in G, generalize the value in G to include the value in the example.
• This process makes S more specific and G more general.
• When a negative example is encountered, the algorithm only updates G
• If the attribute value in the example does not match the value in G, keep it unchanged.
• If the attribute value in the example matches the value in G, replace the value in G with ‘?’ (indicating uncertainty).
• This process makes G more general.
• Continue the iteration through all training examples until no more updates can be made to S and G , or a single set of Hypothesis with consistent space comes.
• The final hypothesis is a conjunction of the most specific S and the most general G is updated throughout the process.

The Candidate Elimination Algorithm maintains a set of hypotheses that are consistent with the training data seen so far. It gradually narrows down the set of possible hypotheses as it processes more examples.

The specific hypothesis S represents the current “best guess” of the target concept, while the general hypothesis G maintains a set of potential generalizations of the concept.

It’s important to note that the Candidate Elimination Algorithm works well for learning simple concepts, but it may struggle with more complex concepts or noisy data.

Step 1: Load the Data set. (Enjoysport dataset is taken from Kaggle website as .csv file) Step 2: Initialize General Hypothesis ‘G’ and Specific Hypothesis ‘S’. Step 3: For each training example, if example is positive example: Make specific hypothesis more general. if attribute_value == hypothesis_value: Do nothing else: replace attribute value with ‘?’ (Basically generalizing it) Step 4: If example is Negative example: Make generalize hypothesis more specific.

Step 1: Importing the dataset

The Dataset can be downloaded from the given link :

EnjoySport Dataset :

Step 2: Initialize the Given General Hypothesis ‘G’ and Specific Hypothesis ‘S’.

S={Φ,Φ,Φ,Φ,Φ,Φ} Because Six instance of enjoy sport are given in the dataset. G={?,?,?,?,?,?} Because Six instance of enjoy sport are given in the dataset.

Step 3: Python Source code

# import the packages import numpy as np import pandas as pd

# Loading Data from a CSV File data=pd.DataFrame(data=pd.read_csv(‘training data.csv’)) print(data)

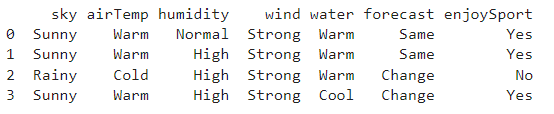
# Separating concept features from Target concepts = np.array(data.iloc[:,0:-1]) print(concepts)

# Isolating target into a separate DataFrame # copying last column to target array target = np.array(data.iloc[:,-1]) print(target)

[‘Yes’ ‘Yes’ ‘No’ ‘Yes’]

# building the algorithm

Step 4: The Final Hypothesis For S and G

G = [[‘sunny’, ?, ?, ?, ?, ?], [?, ‘warm’, ?, ?, ?, ?]] S = [‘sunny’,’warm’,?,’strong’, ?, ?]

Related Posts

The Rise of Generative AI: Unlocking Possibilities Across Industries

Top Machine Learning Projects for Final Year

Markov Decision Process in Machine Learning

30 thoughts on “candidate elimination algorithm program in python”.

Great Content

Hi would you mind sharing which blog platform you’re working with? I’m going to start my own blog soon but I’m having a hard time making a decision between BlogEngine/Wordpress/B2evolution and Drupal. The reason I ask is because your layout seems different then most blogs and I’m looking for something completely unique. P.S My apologies for getting off-topic but I had to ask!

could you please briefly explain what you are expecting?

Home | learnfreeblog

Every weekend i used to pay a visit this web site, because i wish for enjoyment, as this this web page conations in fact fastidious funny stuff too.

Every weekend i used to go to see this site, because i wish for enjoyment, since this this web page conations actually fastidious funny material too.

Nice post. I learn something totally new and challenging on websites I stumbleupon everyday. It’s always helpful to read through content from other writers and practice a little something from their web sites.

“Great read! The information provided is not only insightful but also practical. I appreciate the effort you’ve put into explaining Candidate Elimination Algorithm in such a clear and concise manner. It’s evident that you have a deep understanding of the subject, making it easy for readers like me to grasp the concepts. Looking forward to more valuable content from your blog!”

I, for my friends in the class, wish to express our own thanks for the truly wonderful secrets revealed through your article. Your own clear explanation helped bring comfort and optimism to all of us and would certainly really help us in a research we are at this time doing. I think if still come across web pages like yours, my own stay in college is an easy one. Thanks

Hello – I must say, I’m impressed with your site. I had no trouble navigating through all the tabs and information was very easy to access. I found what I wanted in no time at all. Pretty awesome. Would appreciate it if you add forums or something, it would be a perfect way for your clients to interact. Great job

Very good blog! Do you have any hints for aspiring writers? I’m planning to start my own site soon but I’m a little lost on everything. Would you suggest starting with a free platform like WordPress or go for a paid option? There are so many choices out there that I’m totally confused .. Any tips? Bless you!

hi Dear Monty! kindly contact us. I will help you!

Reading your post made me think. Mission accomplished I guess. I will write something about this on my blog. .

– Gulvafslibning | Kurt Gulvmand After research a few of the blog posts in your web site now, and I truly like your way of blogging. I bookmarked it to my bookmark website checklist and might be checking again soon. Pls try my website online as nicely and let me know what you think. Regards, Fine Teak Chair

I always was interested in this subject and still am, thankyou for posting .

Howdy sir” you have a really nice blog layout “    

Your blog is amazing dude, i love to visit it everyday. very nice layout and content “    

Thank you friend!

I will right away grasp your rss as I can not to find your email subscription link or newsletter service. Do you have any? Kindly allow me recognise in order that I may subscribe. Thanks.

It¡¦s actually a great and helpful piece of information. I¡¦m glad that you just shared this helpful information with us. Please stay us informed like this. Thank you for sharing.

Your blog never ceases to amaze me, it is very well written and organized.”\”*”-

Outstanding read, I just passed this onto a colleague who was doing a little research on that. And he actually bought me lunch because I discovered it for him smile So let me rephrase that: Thanks for lunch!

There is noticeably a bundle to learn about this. I assume you’ve made specific nice points in functions also.

I actually wanted to make a brief word to say thanks to you for all the superb guidelines you are writing on this website. My considerable internet investigation has now been paid with good quality facts to exchange with my family members. I ‘d express that most of us site visitors are extremely fortunate to be in a useful website with very many brilliant people with interesting pointers. I feel really fortunate to have discovered the site and look forward to many more entertaining moments reading here. Thanks once more for a lot of things.

Nice site, nice and easy on the eyes and great content too. How long have you been blogging for?

Just six months only friend!

What a lovely blog. I’ll surely be back again. Please preserve writing!

Leave a Comment Cancel Reply

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.

Machine Learning

Artificial Intelligence

Control System

Supervised Learning

Classification, miscellaneous, related tutorials.

Interview Questions

• Send your Feedback to [email protected]

Help Others, Please Share

Learn Latest Tutorials

Transact-SQL

Reinforcement Learning

R Programming

React Native

Python Design Patterns

Python Pillow

Python Turtle

Preparation

Verbal Ability

Company Questions

Trending Technologies

Cloud Computing

Data Science

B.Tech / MCA

Data Structures

Operating System

Computer Network

Compiler Design

Computer Organization

Discrete Mathematics

Ethical Hacking

Computer Graphics

Software Engineering

Web Technology

Cyber Security

C Programming

Data Mining

Data Warehouse

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

• View all journals
• My Account Login
• Explore content
• About the journal
• Publish with us
• Sign up for alerts
• Open access
• Published: 08 May 2024

Predicting equilibrium distributions for molecular systems with deep learning

• Shuxin Zheng   ORCID: orcid.org/0000-0001-7828-5374 1   na1 ,
• Jiyan He   ORCID: orcid.org/0009-0003-4539-1826 1 , 2   na1 ,
• Chang Liu   ORCID: orcid.org/0000-0001-5207-5440 1   na1 ,
• Yu Shi 1   na1 ,
• Ziheng Lu 1   na1 ,
• Weitao Feng 1 , 2 ,
• Fusong Ju   ORCID: orcid.org/0000-0002-0467-7858 1 ,
• Jiaxi Wang 1 ,
• Jianwei Zhu   ORCID: orcid.org/0000-0002-8272-9190 1 ,
• Yaosen Min 1 ,
• He Zhang 1 ,
• Shidi Tang   ORCID: orcid.org/0000-0001-5493-7411 1 ,
• Hongxia Hao   ORCID: orcid.org/0000-0002-4382-200X 1 ,
• Peiran Jin 1 ,
• Chi Chen   ORCID: orcid.org/0000-0001-8008-7043 3 ,
• Frank Noé 4 ,
• Haiguang Liu   ORCID: orcid.org/0000-0001-7324-6632 1 &
• Tie-Yan Liu   ORCID: orcid.org/0000-0002-0476-8020 1  

Nature Machine Intelligence ( 2024 ) Cite this article

1686 Accesses

24 Altmetric

Metrics details

• Computational methods
• Computational science
• Molecular modelling

Advances in deep learning have greatly improved structure prediction of molecules. However, many macroscopic observations that are important for real-world applications are not functions of a single molecular structure but rather determined from the equilibrium distribution of structures. Conventional methods for obtaining these distributions, such as molecular dynamics simulation, are computationally expensive and often intractable. Here we introduce a deep learning framework, called Distributional Graphormer (DiG), in an attempt to predict the equilibrium distribution of molecular systems. Inspired by the annealing process in thermodynamics, DiG uses deep neural networks to transform a simple distribution towards the equilibrium distribution, conditioned on a descriptor of a molecular system such as a chemical graph or a protein sequence. This framework enables the efficient generation of diverse conformations and provides estimations of state densities, orders of magnitude faster than conventional methods. We demonstrate applications of DiG on several molecular tasks, including protein conformation sampling, ligand structure sampling, catalyst–adsorbate sampling and property-guided structure generation. DiG presents a substantial advancement in methodology for statistically understanding molecular systems, opening up new research opportunities in the molecular sciences.

Similar content being viewed by others

Molecular Geometry Prediction using a Deep Generative Graph Neural Network

State-specific protein–ligand complex structure prediction with a multiscale deep generative model

Language models can learn complex molecular distributions

Deep learning methods excel at predicting molecular structures with high efficiency. For example, AlphaFold predicts protein structures with atomic accuracy 1 , enabling new structural biology applications 2 , 3 , 4 ; neural network-based docking methods predict ligand binding structures 5 , 6 , supporting drug discovery virtual screening 7 , 8 ; and deep learning models predict adsorbate structures on catalyst surfaces 9 , 10 , 11 , 12 . These developments demonstrate the potential of deep learning in modelling molecular structures and states.

However, predicting the most probable structure only reveals a fraction of the information about a molecular system in equilibrium. Molecules can be very flexible, and the equilibrium distribution is essential for the accurate calculation of macroscopic properties. For example, biomolecule functions can be inferred from structure probabilities to identify metastable states; and thermodynamic properties, such as entropy and free energies, can be computed from probabilistic densities in the structure space using statistical mechanics.

Figure 1a shows the difference between conventional structure prediction and distribution prediction of molecular systems. Adenylate kinase has two distinct functional conformations (open and closed states), both experimentally determined, but a predicted structure usually corresponds to a highly probable metastable state or an intermediate state (as shown in this figure). A method is desired to sample the equilibrium distribution of proteins with multiple functional states, such as adenylate kinase.

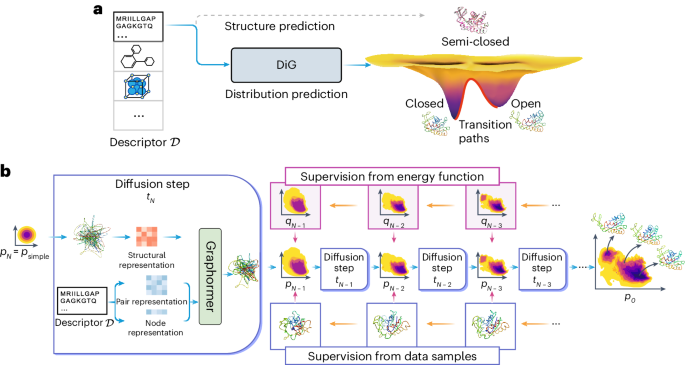
a , DiG takes the basic descriptor \({{{\mathcal{D}}}}\) of a target molecular system as input—for example, an amino acid sequence—to generate a probability distribution of structures that aims at approximating the equilibrium distribution and sampling different metastable or intermediate states. In contrast, static structure prediction methods, such as AlphaFold 1 , aim at predicting one single high-probability structure of a molecule. b , The DiG framework for predicting distributions of molecular structures. A deep learning model (Graphormer 10 ) is used as modules to predict a diffusion process (→) that gradually transforms a simple distribution towards the target distribution. The model is trained so that the derived distribution p i in each intermediate diffusion time step i matches the corresponding distribution q i in a predefined diffusion process (←) that is set to transform the target distribution to the simple distribution. Supervision can be obtained from both samples (workflow in the top row) and a molecular energy function (workflow shown in the bottom row).

Unlike single structure prediction, equilibrium distribution research still depends on classical and costly simulation methods, while deep learning methods are underdeveloped. Commonly, equilibrium distributions are sampled with molecular dynamics (MD) simulations, which are expensive or infeasible 13 . Enhanced sampling simulations 14 , 15 and Markov state modelling 16 can accelerate rare event sampling but need system-specific collective variables and are not easily generalized. Another approach is coarse-grained MD 17 , 18 , where deep learning approaches have been proposed 19 , 20 . These deep learning coarse-grained methods have worked well for individual molecular systems but have not yet demonstrated generalization. Boltzmann generators 21 are a deep learning approach to generate equilibrium distributions by creating a probability flow from a simple reference state, but this also hard to generalize to different molecules. Generalization has been demonstrated for flows generating simulations with longer time steps for small peptides but has not yet been scaled to large proteins 22 .

In this Article, we develop DiG, a deep learning approach to approximately predict the equilibrium distribution and efficiently sample diverse and function-relevant structures of molecular systems. We show that DiG can generalize across molecular systems and propose diverse structures that resemble observations in experiments. DiG draws inspiration from simulated annealing 23 , 24 , 25 , 26 , which transforms a uniform distribution to a complex one through a simulated annealing process. DiG simulates a diffusion process that gradually transforms a simple distribution to the target one, approximating the equilibrium distribution of the given molecular system 27 , 28 (Fig. 1b , right arrow symbol). As the simple distribution is chosen to enable independent sampling and have a closed-form density function, DiG enables independent sampling of the equilibrium distribution and also provides a density function for the distribution by tracking the process. The diffusion process can also be biased towards a desired property for inverse design and allows interpolation between structures that passes through high-probability regions. This diffusion process is implemented by a deep learning model based upon the Graphormer architecture 10 (Fig. 1b ), conditioned on a descriptor of the target molecule, such as a chemical graph or a protein sequence. DiG can be trained with structure data from experiments and MD simulations. For data-scarce cases, we develop a physics-informed diffusion pre-training (PIDP) method to train DiG with energy functions (such as force fields) of the systems. In both data-based or energy-supervised modes, the model gets a training signal in each diffusion step independently (Fig. 1b , left arrow symbol), enabling efficient training that avoids long-chain back-propagation.

We evaluate DiG on three predictive tasks: protein structure distribution, the ligand conformation distribution in binding pockets and the molecular adsorption distribution on catalyst surfaces. DiG generates realistic and diverse molecular structures in these tasks. For the proteins in this Article, DiG efficiently generated structures resembling major functional states. We further demonstrate that DiG can facilitate the inverse design of molecular structures by applying biased distributions that favour structures with desired properties. This capability can expand molecular design for properties that lack enough data. These results indicate that DiG advances deep learning for molecules from predicting a single structure towards predicting structure distributions, paving the way for efficient prediction of the thermodynamic properties of molecules.

Here, we demonstrate that DiG can be applied to study protein conformations, protein–ligand interactions and molecule adsorption on catalyst surfaces. In addition, we investigate the inverse design capability of DiG through its application to carbon allotrope generation for desired electronic band gaps.

Protein conformation sampling

At physiological conditions, most protein molecules exhibit multiple functional states that are linked via dynamical processes. Sampling of these conformations is crucial for the understanding of protein properties and their interactions with other molecules. Recently, it was reported that AlphaFold 1 can generate alternative conformations for certain proteins by manipulating input information such as multiple sequence alignments (MSAs) 29 . However, this approach is developed on the basis of varying the depth of MSAs, and it is hard to generalize to all proteins (especially those with a small number of homologous sequences). Therefore, it is highly desirable to develop advanced artificial intelligence (AI) models that can sample diverse structures consistent with the energy landscape in the conformational space 29 . Here, we show that DiG is capable of generating diverse and functionally relevant protein structures, which is a key capability for being able to efficiently sample equilibrium distributions.

Because the equilibrium distribution of protein conformations is difficult to obtain experimentally or computationally, there is a lack of high-quality data for training or benchmarking. To train this model, we collect experimental and simulated structures from public databases. To mitigate the data scarcity, we generated an MD simulation dataset and developed the PIDP training method (see Supplementary Information sections A.1.1 and D.1 for the training procedure and the dataset). The performance of DiG was assessed at two levels: (1) by comparing the conformational distributions against those obtained from extensive (millisecond timescale) atomistic MD simulations and (2) by validating on proteins with multiple conformations. As shown in Fig. 2a , the conformational distributions are obtained from MD simulations for two proteins from the SARS-CoV-2 virus 30 (the receptor-binding domain (RBD) of the spike protein and the main protease, also known as 3CL protease; see Supplementary Information section A.7 for details on the MD simulation data). These two proteins are the crucial components of the SARS-CoV-2 and key targets for drug development in treating COVID-19 31 , 32 . The millisecond-timescale MD simulations extensively sample conformation space, and we therefore regard the resulting distribution as a proxy for the equilibrium distribution.

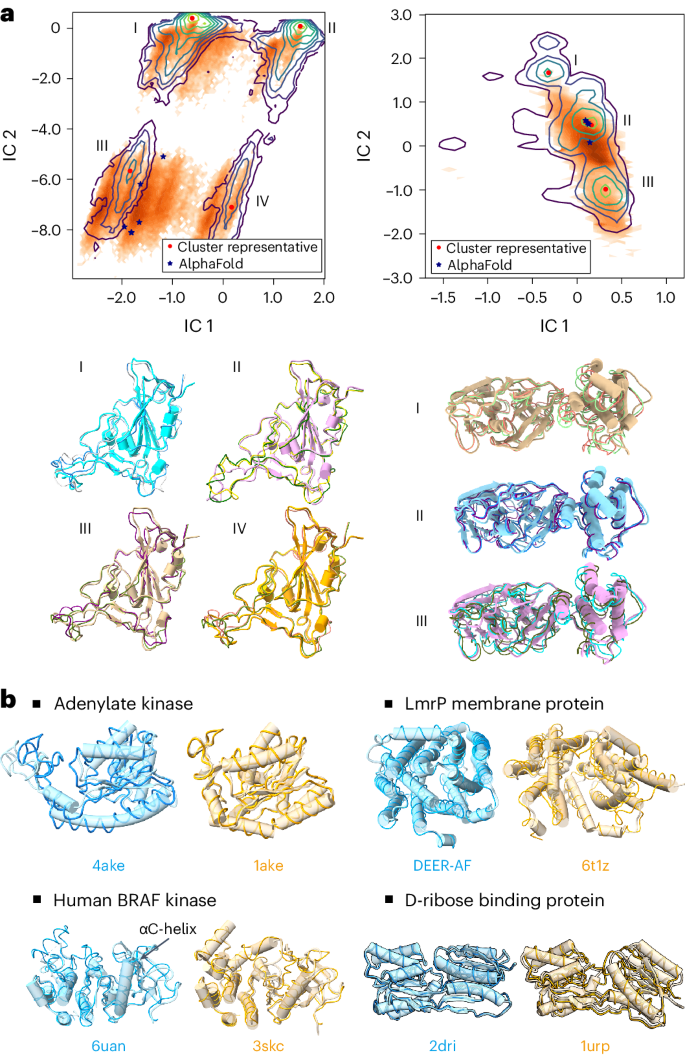
a , Structures generated by DiG resemble the diverse conformations of millisecond MD simulations. MD-simulated structures are projected onto the reduced space spanned by two time-lagged independent component analysis (TICA) coordinates (that is, independent component (IC) 1 and 2), and the probability densities are depicted using contour lines. Left: for the RBD protein, MD simulation reveals four highly populated regions in the 2D space spanned by TICA coordinates. DiG-generated structures are mapped to this 2D space (shown as orange dots), with a distribution reflected by the colour intensity. Under the distribution plot, structures generated by DiG (thin ribbons) are superposed on representative structures. AlphaFold-predicted structures (stars) are shown in the plot. Right: the results for the SARS-CoV-2 main protease, compared with MD simulation and AlphaFold prediction results. The contour map reveals three clusters, DiG-generated structures overlap with clusters II and III, whereas structures in cluster I are underrepresented. b , The performance of DiG on generating multiple conformations of proteins. Structures generated by DiG (thin ribbons) are compared with the experimentally determined structures (each structure is labelled by its PDB ID, except DEER-AF, which is an AlphaFold predicted model, shown as cylindrical cartoons). For the four proteins (adenylate kinase, LmrP membrane protein, human BRAF kinase and D-ribose binding protein), structures in two functional states (distinguished by cyan and brown) are well reproduced by DiG (ribbons).

Taking protein sequences as the descriptor inputs for DiG, structures were generated and compared with simulation data. Although simulation data of RBD and the main protease were not used for DiG training, generated structures resemble the conformational distributions (Fig. 2a ). In the two-dimensional (2D) projection space of RBD conformations, MD simulations populate four regions, which are all sampled by DiG (Fig. 2a , left). Four representative structures are well reproduced by DiG. Similarly, three representative structures from main protease simulations are predicted by DiG (Fig. 2a ). We noticed that conformations in cluster I are not well recovered by DiG, indicating room for improvement. In terms of conformational coverage, we compared the regions sampled by DiG with those from simulations in the 2D manifold (Fig. 2a ), observing that about 70% of the RBD conformations sampled by simulations can be covered with just 10,000 DiG-generated structures (Supplementary Fig. 1 ).

Atomistic MD simulations are computationally expensive, therefore millisecond-timescale simulations of proteins are rarely executed, except for simulations on special-purpose hardware such as the Anton supercomputer 13 or extensive distributed simulations combined in Markov state models 16 . To obtain an additional assessment on the diverse structures generated by DiG, we turn to proteins with multiple structures that have been experimentally determined. In Fig. 2b , we show the capability of DiG in generating multiple conformations for four proteins. Experimental structures are shown in cylinder cartoons, each aligned with two structures generated by DiG (thin ribbons). For example, DiG generated structures similar to either open or closed states of the adenylate kinase protein (for example, backbone root mean square difference (r.m.s.d.) < 1.0 Å to the closed state, 1ake). Similarly, for the drug transport protein LmrP, DiG generated structures covering both states (r.m.s.d. < 2.0 ): one structure is experimentally determined, and the other (denoted as DEER-AF) is the AlphaFold prediction 29 supported by double electron electron resonance (DEER) experiments 33 . For human BRAF kinase, the overall structural difference between the two states is less pronounced. The major difference is in the A-loop region and a nearby helix (the αC-helix, indicated in the figure) 34 . Structures generated by DiG accurately capture such regional structural differences. For D-ribose binding protein, the packing of two domains is the major source of structural difference. DiG correctly generates structures corresponding to both the straight-up conformation (cylinder cartoon) and the twisted or tilted conformation. If we align one domain of D-ribose binding protein, the other domain only partially matches the twisted conformation as an ‘intermediate’ state. Furthermore, DiG can generate plausible conformation transition pathways by latent space interpolations (see demonstration cases in Supplementary Videos 1 and 2 ). In summary, beyond static structure prediction for proteins, DiG generates diverse structures corresponding to different functional states.

Ligand structure sampling around binding sites

An immediate extension of protein conformational sampling is to predict ligand structures in druggable pockets. To model the interactions between proteins and ligands, we conducted MD simulations for 1,500 complexes to train the DiG model (see Supplementary Information section D.1 for the dataset). We evaluated the performance of DiG with 409 protein–ligand systems 35 , 36 that are not in the training dataset. The inputs of DiG include protein pocket information (atomic type and position) and the ligand descriptor (a SMILES string). We pad the input node and pair representations with zeros to handle the different number of atoms surrounding a pocket and the different length of SMILES strings. The predicted results are the atomic coordinate distributions of both the ligand and the protein pocket. For protein pockets, changes in atomic positions are up to 1.0 Å in terms of r.m.s.d. compared with the input values, reflecting pocket flexibility during ligand structure generation. For the ligand structures, the deviation comes from two sources: (1) the conformational difference between generated and experimental structures, and (2) the difference in the binding pose due to ligand translation and rotation. Among all the tested cases, the conformational differences are small, with an r.m.s.d. value of 1.74 Å on average, indicating that generated structures are highly similar to the ligands resolved in crystal structures (Fig. 3a ). When including the binding pose deviations, larger discrepancies are observed. Yet, the DiG predicts structures that are very similar to the experimental structure for each system. The best matched structure among 50 generated structures for each system is within 2.0 Å r.m.s.d. compared with the experimental data for nearly all 409 testing systems (see Fig. 3a for the r.m.s.d. distribution, with more cases shown in Supplementary Fig. 3 ). The accuracy of generated structures for ligand is related to the characteristics of the binding pocket. For example, in the case of the TYK2 kinase protein, the ligand shown in Fig. 3b (top) deviated from the crystal structure by 0.91 Å (r.m.s.d.) on average. For target P38, the ligand exhibited more diverse binding poses, probably owing to the relatively shallow binding pocket, making the most stable binding pose less dominant compared with other poses (Fig. 3b , bottom). MD simulations reveal similar trends as DiG-generated structures, with ligand binding to TYK2 more tightly than in the case of P38 (Supplementary Fig. 2 ). Overall, we observed that the generated structures resemble experimentally observed poses.

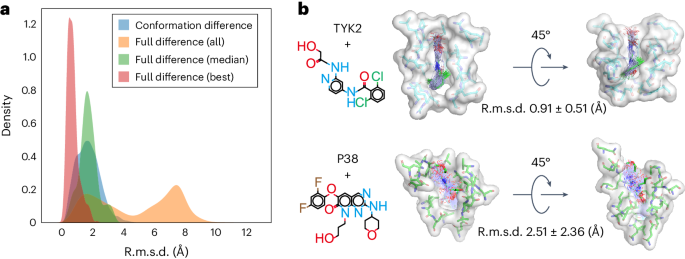
a , The results of DiG on poses of ligands bound to protein pockets. DiG generates ligand structures and binding poses with good accuracy compared with the crystal structures (reflected by the r.m.s.d. statistics shown in the red histogram for the best matching cases and the green histogram for the median r.m.s.d. statistics). When considering all 50 predicted structures for each system, diversity is observed, as reflected in the r.m.s.d. histogram (yellow colour, normalized). All r.m.s.d. values are calculated for ligands with respect to their coordinates in complex structures. b , Representative systems show diversity in ligand structures, and such predicted diversity is related to the properties of the binding pocket. For a deep and narrow binding pocket such as for the TYK2 protein (shown in the surface representation, top panel), DiG predicts highly similar binding poses for the ligand (in atom bond representations, top panel). For the P38 protein, the binding pocket is relatively flat and shallow and predicted ligand poses are more diverse and have large conformational flexibility (bottom panel, following the same representations as in the TYK2 case). The average r.m.s.d. values and the associated standard deviations are indicated next to the complex structures.

Catalyst–adsorbate sampling

Identifying active adsorption sites is a central task in heterogeneous catalysis. Owing to the complex surface–molecule interactions, such tasks rely heavily on a combination of quantum chemistry methods such as density functional theory (DFT) and sampling techniques such as MD simulations and grid search. These lead to large and sometimes intractable computational costs. We evaluate the capability of DiG for this task by training it on the MD trajectories of catalyst–adsorbate systems from the Open Catalyst Project and carrying out further evaluations on random combinations of adsorbates and surfaces that are not included in the training set 9 . DiG takes the atomic types, initial positions of atoms in substrate, and the lattice vectors of the substrate, with an initial structure of the molecular adsorbate, as joint inputs. Besides, we use a cross-attention sub-layer to handle the periodic boundary conditions, as detailed in Supplementary Information section B.5 . On feeding the model with a substrate and a molecular adsorbate, DiG can predict adsorption sites and stable adsorbate configurations, along with the probability for each configuration (see Supplementary Information sections A.4 and A.7 for training and evaluation details). Figure 4a,b shows the adsorption configurations of an acyl group on a stepped TiIr alloy surface. Multiple adsorption sites are predicted by DiG. To test the plausibility of these predicted configurations and evaluate the coverage of the predictions, we carry out a grid search using DFT methods. The results confirm that DiG predicts all stable sites found by the grid search and that the adsorption configurations are in close agreement, with an r.m.s.d. of 0.5–0.8 Å (Fig. 4b ). It should be noted that the combinations of substrate and adsorbate shown in Fig. 4b are not included in the training dataset. Therefore, the result demonstrates the cross-system generalization capability of DiG in catalyst adsorption predictions. Here we show only the top view. Supplementary Fig. 4 in addition shows the front view of the adsorption configurations.

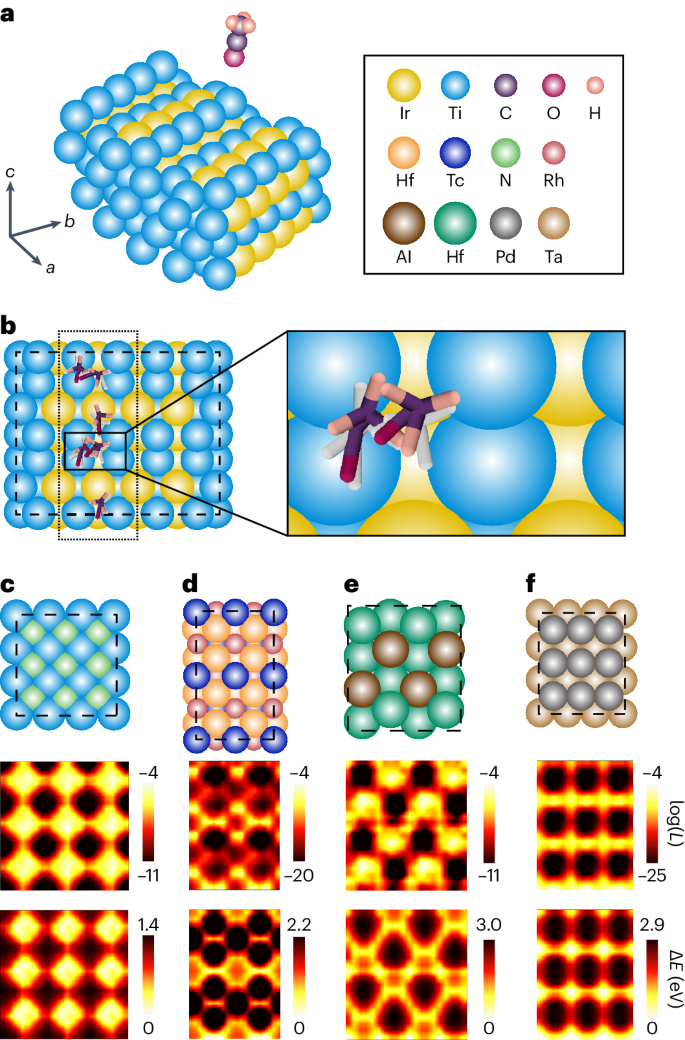
a , The problem setting: the prediction of the adsorption configuration distribution of an adsorbate on a catalyst surface. b , The adsorption sites and corresponding configurations of the adsorbate found by DiG (in colour) compared with DFT results (in white). DiG finds all adsorption sites, with adsorbate structures close to the DFT calculation results (see Supplementary Information for details of the adsorption sites and configurations). c – f , Adsorption prediction results of single N or O atoms on TiN ( c ), RhTcHf ( d ), AlHf ( e ) and TaPd ( f ) catalyst surfaces compared with DFT calculation results. Top: the catalyst surface. Middle: the probability distribution of adsorbate molecules on the corresponding catalyst surfaces on log scale. Bottom: the interaction energies between the adsorbate molecule and the catalyst calculated using DFT methods. The adsorption sites and predicted probabilities are highly consistent with the energy landscape obtained by DFT.

DiG not only predicts the adsorption sites with correct configurations but also provides a probability estimate for each adsorption configuration. This capability is illustrated in the systems with single-atom adsorbates (including H, N and O atoms) on ten randomly chosen metallic surfaces. For each combination of adsorbate and catalyst, DiG predicts the adsorption sites and the probability distributions. To validate the results, for the same systems, grid search DFT calculations are carried out to find adsorption sites and corresponding energies. Taking the adsorption sites identified by grid search as references, DiG achieved 81% site coverage for single-atom adsorbates on the ten metallic catalyst surfaces. Figure 4c–f shows closer examinations on adsorption predictions for four systems, namely single N or O atoms on TiN, RhTcHf, AlHf and TaPd metallic surfaces (top panels). The predicted adsorption probabilities projected on the plane in parallel with the catalyst surface are shown in the middle panels. The probabilities show excellent accordance with the adsorption energies calculated using DFT methods (bottom panels). It is worth noting that the speed of DiG is much faster compared with DFT; that is, it takes about 1 min to sample all adsorption sites for a catalyst–adsorbate system for DiG on a single modern graphics processing unit (GPU), but at least 2 hours for a single DFT relaxation with VASP, a number that will be further multiplied by a factor of >100 depending on the resolution of the searching grid 37 . Such fast and accurate prediction of adsorption sites and the corresponding distributional features can be useful in identifying catalytic mechanisms and guiding research on new catalysts.

Property-guided structure generation

While DiG by default generates structures following the learned training data distribution, the output distribution can be purposely biased to steer the structure generation to meet particular requirements. Here, we leverage this capability by using DiG for inverse design (described in ‘ Property-guided structure generation with DiG ’ section). As a proof of concept, we search for carbon allotropes with desired electronic band gaps. Similar tasks are critical to the design of novel photovoltaic and semi-conductive materials 38 . To train this model, we prepared a dataset composed of carbon materials by carrying out structure search based on energy profiles obtained from DFT calculations (L.Z., manuscript in preparation). The structures corresponding to energy minima form the dataset used to train DiG, which in turn are applied to generate carbon structures. We use a neural network model based on the M3GNet architecture 11 as the property predictor for the electronic band gap, which is fed to the property-guided structure generation of carbon structures.

Figure 5 shows the distributions of band gaps calculated from generated carbon structures. In the original training dataset, most structures have a band gap of around 0 eV (Fig. 5a ). When the target band gaps are supplied to DiG as an additional condition, carbon structures are generated with desired band gaps. Under the guidance of a band gap model in conditional generation, the distribution is biased towards the targets, showing pronounced peaks around the target band gaps. Representative structures are shown in Fig. 5 . For conditional generation with a target band gap of 4 eV, DiG generates stable carbon structures similar to diamond, which has large band gaps. In the case of the 0 eV band gap, we obtain graphite-like structures with small band gaps. In Fig. 5a , we show some structures obtained by unconditional generation. To evaluate the quality of carbon structures generated by DiG, we calculate the percentage of generated structures that match relaxed structures in the dataset by using the ‘StructureMatcher’ in the PyMatgen package 39 . For unconditional generation, the match rate is 99.87%, and the average matched normalized r.m.s.d. computed from fractional coordinates over all sampled structures is 0.16. For conditional generation, the match rate is 99.99%, but with a higher average normalized r.m.s.d. of 0.22. While increasing the possibility of generating structures with the target band gap, conditional generation can influence the quality of the structures (see Supplementary Information section F.1 for more discussion). This proof-of-concept study shows that DiG not only captures the probability distributions with complex features in a large configurational space but also can be applied for inverse design of materials, when combined with a property quantifier, such as a machine learning (ML) predictor. Since the property prediction model (for example, the M3GNet model for band gap prediction) and the diffusion model of DiG are fully decoupled, our approach can be readily extended to inverse design of materials targeting for other properties.

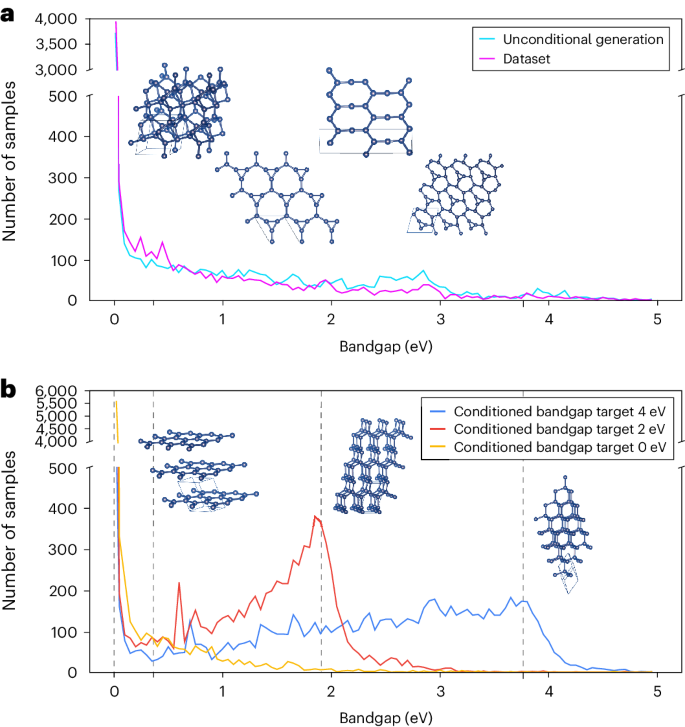
a , The electronic band gaps of generated structures from the trained DiG with no specification on the band gap. Generated structures do not show any obvious preference on band gaps, closely resembling the distribution of the training dataset. b , Structures generated for three band gaps (0, 2 and 4 eV). The distributions of band gaps for generated structures peak at the desired values. In particular, DiG generates graphite-like structures when the desired band gap is 0 eV, while for the 4 eV band gap, the generated structures are mostly similar to diamonds. The vertical dashed lines represent the band gaps of generated structures near to 0, 2 and 4 eV. Inset: representative structures.

Predicting the equilibrium distribution of molecular states is a formidable challenge in molecular sciences, with broad impacts for understanding structure–function relations, computing macroscopic properties and designing molecules and materials. Existing methods need numerous measurements or simulated samples of single molecules to characterize the equilibrium distribution. We introduce DiG, a deep generative framework towards predicting equilibrium probability distributions, enabling efficient sampling of diverse conformations and state densities across molecular systems. Inspired by the annealing process, DiG uses a sequence of deep neural networks to gradually transform state distributions from a simple form to the target ones. DiG can be trained to approximate the equilibrium distribution with suitable data.

We applied DiG to several molecular tasks, including protein conformation sampling, protein–ligand binding structure generation, molecular adsorption on catalyst surfaces and property-guided structure generation. DiG generates chemically realistic and diverse structures, and distributions that resemble MD simulations in low-dimensional projections in some cases. By leveraging advanced deep learning architectures, DiG learns the representation of molecular conformations from molecular descriptors such as sequences for proteins or formulas for compound molecules. Moreover, its capacity to model complex, multimodal distributions using diffusion models enables it to capture equilibrium distributions in high-dimensional space.

Consequently, the framework opens the door to a multitude of research opportunities and applications in molecular science. DiG can provide statistical understanding of molecules, enabling computation of macroscopic properties such as free energies and thermodynamic stability. These insights are critical for investigating physical and chemical phenomena of molecular systems.

Finally, with its ability to generate independent and identically distributed (i.i.d.) conformations from equilibrium distributions, DiG offers a substantial advantage over traditional sampling or simulation approaches, such as Markov chain Monte Carlo (MCMC) or MD simulations, which need rare events to cross energy barriers. DiG covers similar conformation space as millisecond-timescale MD simulations in the two tested protein cases. On the basis of the OpenMM performance benchmark, it would require about 7–10 GPU-years on NVIDIA A100s to simulate 1.8 ms for RBD of the spike protein, while generating 50k structures with DiG takes about 10 days on a single A100 GPU without inference acceleration (Supplementary Information section A.6 ). Similar or even better speed-up has been achieved for predicting the adsorbate distribution on a catalyst surface, as shown in Results . Combined with high-accuracy probability distributions, such order-of-magnitude speed-up will be transformative for molecular simulation and design.

Although the quantitative prediction of equilibrium distributions at given states will hinge upon data availability, the capacity of DiG to explore vast and diverse conformational spaces contributes to the discovery of novel and functional molecular structures, including protein structures, ligand conformers and adsorbate configurations. DiG can help to connect microscopic descriptors and macroscopic observations of molecular systems, with potential effect on various areas of molecular sciences, including but not limited to life sciences, drug design, catalysis research and materials sciences.

Deep neural networks have been demonstrated to predict accurate molecular structures from descriptors \({{{\mathcal{D}}}}\) for many molecular systems 1 , 5 , 6 , 9 , 10 , 11 , 12 . Here, DiG aims to take one step further to predict not only the most probable structure but also diverse structures with probabilities under the equilibrium distribution. To tackle this challenge, inspired by the heating–annealing paradigm, we break down the difficulty of this problem into a series of simpler problems. The heating–annealing paradigm can be viewed as a pair of reciprocal stochastic processes on the structure space that simulate the transformation between the system-specific equilibrium distribution and a system-independent simple distribution p simple . Following this idea, we use an explicit diffusion process (forward process; Fig. 1b , orange arrows) that gradually transforms the target distribution of the molecule \({q}_{{{{\mathcal{D}}}},0}\) , as the initial distribution, towards p simple through a time period τ . The corresponding reverse diffusion process then transforms p simple back to the target distribution \({q}_{{{{\mathcal{D}}}},0}\) . This is the generation process of DiG (Fig. 1b , blue arrows). The reverse process is performed by incorporating updates predicted by deep neural networks from the given \({{{\mathcal{D}}}}\) , which are trained to match the forward process. The descriptor \({{{\mathcal{D}}}}\) is processed into node representations \({{{\mathcal{V}}}}\) describing the feature of each system-specific individual element and a pair representation \({{{\mathcal{P}}}}\) describing inter-node features. The \(\{{{{\mathcal{V}}}},{{{\mathcal{P}}}}\}\) representation is the direct input from the descriptor part to the Graphormer model 10 , together with the geometric structure input R to produce a physically finer structure (Supplementary Information sections B.1 and B.3 ). Specifically, we choose \({p}_{{{\mbox{simple}}}}:= {{{\mathcal{N}}}}({{{\bf{0}}}},{{{\bf{I}}}})\) as the standard Gaussian distribution in the state space, and the forward diffusion process as the Langevin diffusion process targeting this p simple (Ornstein–Uhlenbeck process) 40 , 41 , 42 . A time dilation scheme β t (ref. 43 ) is introduced for approximate convergence to p simple after a finite time τ . The result is written as the following stochastic differential equation (SDE):

where B t is the standard Brownian motion (a.k.a. Wiener process). Choosing this forward process leads to a p simple that is more concentrated than a heated distribution, hence it is easier to draw high-density samples, and the form of the process enables efficient training and sampling.

Following stochastic process theory (see, for example, ref. 44 ), the reverse process is also a stochastic process, written as the following SDE:

where \(\bar{t}:= \tau -t\) is the reversed time, \({q}_{{{{\mathcal{D}}}},\bar{t}}:= {q}_{{{{\mathcal{D}}}},t = \tau -\bar{t}}\) is the forward process distribution at the corresponding time and \({{{{\bf{B}}}}}_{\bar{t}}\) is the Brownian motion in reversed time. Note that the forward and corresponding reverse processes, equations ( 1 ) and ( 2 ), are inspired from but not exactly the heating and annealing processes. In particular, there is no concept of temperature in the two processes. The temperature T mentioned in the PIDP loss below is the temperature of the real target system but is not related to the diffusion processes.

From equation ( 2 ), the only obstacle that impedes the simulation of the reverse process for recovering \({q}_{{{{\mathcal{D}}}},0}\) from p simple is the unknown \(\nabla \log {q}_{{{{\mathcal{D}}}},\bar{t}}({{{{\bf{R}}}}}_{\bar{t}})\) . Deep neural networks are then used to construct a score model \({{{{\bf{s}}}}}_{{{{\mathcal{D}}}},t}^{\theta }({{{\bf{R}}}})\) , which is trained to predict the true score function \(\nabla \log {q}_{{{{\mathcal{D}}}},t}({{{\bf{R}}}})\) of each instantaneous distribution \({q}_{{{{\mathcal{D}}}},t}\) from the forward process. This formulation is called a diffusion-based generative model and has been demonstrated to be able to generate high-quality samples of images and other content 27 , 28 , 45 , 46 , 47 . As our score model is defined in molecular conformational space, we use our previously developed Graphormer model 10 as the neural network architecture backbone of DiG, to leverage its capabilities in modelling molecular structures and to generalize to a range of molecular systems. Note that the score model aims to approximate a gradient, which is a set of vectors. As these are equivariant with respect to the input coordinates, we designed an equivariant vector output head for the Graphormer model (Supplementary Information section B.4 ).

With the \({{{{\bf{s}}}}}_{{{{\mathcal{D}}}},t}^{\theta }({{{\bf{R}}}})\) model, drawing a sample R 0 from the equilibrium distribution of a system \({{{\mathcal{D}}}}\) can be done by simulating the reverse process in equation ( 2 ) on N  + 1 steps that uniformly discretize [0,  τ ] with step size h  =  τ / N (Fig. 1b , blue arrows), thus

where the discrete step index i corresponds to time t  =  i h , and β i  :=  h β t = i h . Supplementary Information section A.1 provides the derivation. Note that the reverse process does not need to be ergodic. The way that DiG models the equilibrium distribution is to use the instantaneous distribution at the instant t  = 0 (or \(\bar{t}=\tau\) ) on the reverse process, but not using a time average. As R N samples can be drawn independently, DiG can generate statistically independent R 0 samples for the equilibrium distribution. In contrast to MD or MCMC simulations, the generation of DiG samples does not suffer from rare events that link different states and can thus be far more computationally efficient.

DiG can be trained by using conformation data sampled over a range of molecular systems. However, collecting sufficient experimental or simulation data to characterize the equilibrium distribution for various systems is extremely costly. To address this data scarcity issue, we propose a pre-training algorithm, called PIDP, which effectively optimizes DiG on an initial set of candidate structures that need not be sampled from the equilibrium distribution. The supervision comes from the energy function \({E}_{{{{\mathcal{D}}}}}\) of each system \({{{\mathcal{D}}}}\) , which defines the equilibrium distribution \({q}_{{{{\mathcal{D}}}},0}({{{\bf{R}}}})\propto \exp (-\frac{{E}_{{{{\mathcal{D}}}}}({{{\bf{R}}}})}{{k}_{{{{\rm{B}}}}}T})\) at the target temperature T .

The key idea is that the true score function \(\nabla \log {q}_{{{{\mathcal{D}}}},t}\) from the forward process in equation ( 1 ) obeys a partial differential equation, known as the Fokker–Planck equation (see, for example, ref. 48 ). We then pre-train the score model \({{{{\bf{s}}}}}_{{{{\mathcal{D}}}},t}^{\theta }\) by minimizing the following loss function that enforces the equation to hold:

Here, the second term, weighted by λ 1 , matches the score model at the final generation step to the score from the energy function, and the first term implicitly propagates the energy function supervision to intermediate time steps (Fig. 1b , upper row). The structures \({\{{{{{\bf{R}}}}}_{{{{\mathcal{D}}}},i}^{(m)}\}}_{m = 1}^{M}\) are points on a grid spanning the structure space. Since these structures are only used to evaluate the loss function on discretized points, they do not have to obey the equilibrium distribution (as is required by structures in the training dataset), therefore the cost of preparing these structures can be much lower. As structure spaces of molecular systems are often very high dimensional (for example, thousands for proteins), a regular grid would have intractably many points. Fortunately, the space of actual interest is only a low-dimensional manifold of physically reasonable structures (structures with low energy) relevant to the problem. This allows us to effectively train the model only on these relevant structures as R 0 samples. R i samples are produced by passing R 0 samples through the forward process. See Supplementary Information section C.1 for an example on acquiring relevant structures for protein systems.

We also leverage stochastic estimators, including Hutchinson’s estimator 49 , 50 , to reduce the complexity in calculating derivatives of high order and for high-dimensional vector-valued functions. Note that, for each step i , the corresponding model \({{{{\bf{s}}}}}_{{{{\mathcal{D}}}},i}^{\theta }\) receives a training loss independent of other steps and can be directly back-propagated. In this way, the supervision on each step can improve the optimizing efficiency.

Training DiG with data

In addition to using the energy function for information on the probability distribution of the molecular system, DiG can also be trained with molecular structure samples that can be obtained from experiments, MD or other simulation methods. See Supplementary Information section C for data collection details. Even when the simulation data are limited, they still provide information about the regions of interest and about the local shape of the distribution in these regions; hence, they are helpful to improve a pre-trained DiG. To train DiG on data, the score model \({{{{\bf{s}}}}}_{{{{\mathcal{D}}}},i}^{\theta }({{{{\bf{R}}}}}_{i})\) is matched to the corresponding score function \(\nabla \log {q}_{{{{\mathcal{D}}}},i}\) demonstrated by data samples. This can be done by minimizing \({{\mathbb{E}}}_{{q}_{{{{\mathcal{D}}}},i}({{{{\bf{R}}}}}_{i})}{\parallel {{{{\bf{s}}}}}_{{{{\mathcal{D}}}},i}^{\theta }({{{{\bf{R}}}}}_{i})-\nabla \log {q}_{{{{\mathcal{D}}}},i}({{{{\bf{R}}}}}_{i})\parallel }^{2}\) for each diffusion time step i . Although a precise calculation of \(\nabla \log {q}_{{{{\mathcal{D}}}},i}\) is impractical, the loss function can be equivalently reformulated into a denoising score-matching form 51 , 52

where \({\alpha }_{i}:= \mathop{\prod }\nolimits_{j = 1}^{i}\sqrt{1-{\beta }_{j}}\) , \({\sigma }_{i}:= \sqrt{1-{\alpha }_{i}^{2}}\) and p ( ϵ i ) is the standard Gaussian distribution. The expectation under \({q}_{{{{\mathcal{D}}}},0}\) can be estimated using the simulation dataset.

We remark that this score-predicting formulation is equivalent (Supplementary Information section A.1.2 ) to the noise-predicting formulation 28 in the diffusion model literature. Note that this function allows direct loss estimation and back-propagation for each i in constant (with respect to i ) cost, recovering the efficient step-specific supervision again (Fig. 1b , bottom).

Density estimation by DiG

The computation of many thermodynamic properties of a molecular system (for example, free energy or entropy) also requires the density function of the equilibrium distribution, which is another aspect of the distribution besides a sampling method. DiG allows for this by tracking the distribution change along the diffusion process 45 :

where D is the dimension of the state space and \({{{{\bf{R}}}}}_{{{{\mathcal{D}}}},t}^{\theta }({{{{\bf{R}}}}}_{0})\) is the solution to the ordinary differential equation (ODE)

with initial condition R 0 , which can be solved using standard ODE solvers or more efficient specific solvers (Supplementary Information section A.6 ).

Property-guided structure generation with DiG

There is a growing demand for the design of materials and molecules that possess desired properties, such as intrinsic electronic band gaps, elastic modulus and ionic conductivity, without going through a forward searching process. DiG provides a feature to enable such property-guided structure generation, by directly predicting the conditional structural distribution given a value c of a microscopic property.

To achieve this goal, regarding the data-generating process in equation ( 2 ), we only need to adapt the score function from \(\nabla \log {q}_{{{{\mathcal{D}}}},t}({{{\bf{R}}}})\) to \({\nabla }_{{{{\bf{R}}}}}\log {q}_{{{{\mathcal{D}}}},t}({{{\bf{R}}}}| c)\) . Using Bayes’ rule, the latter can be reformulated as \({\nabla }_{{{{\bf{R}}}}}\log {q}_{{{{\mathcal{D}}}},t}({{{\bf{R}}}}| c)=\nabla \log {q}_{{{{\mathcal{D}}}},t}({{{\bf{R}}}})+{\nabla }_{{{{\bf{R}}}}}\log {q}_{{{{\mathcal{D}}}}}(c| {{{\bf{R}}}})\) , where the first term can be approximated by the learned (unconditioned) score model; that is, the new score model is

Hence, only a \({q}_{{{{\mathcal{D}}}}}(c| {{{\bf{R}}}})\) model is additionally needed 45 , 46 , which is a property predictor or classifier that is much easier to train than a generative model.

In a normal workflow for ML inverse design, a dataset must be generated to meet the conditional distribution, then an ML model will be trained on this dataset for structure distribution predictions. The ability to generate structures for conditional distribution without requiring a conditional dataset places DiG in an advantageous position when compared with normal workflows in terms of both efficiency and computational cost.

Interpolation between states

Given two states, DiG can approximate a reaction path that corresponds to reaction coordinates or collective variables, and find intermediate states along the path. This is achieved through the fact that the distribution transformation process described in equation ( 1 ) is equivalent to the process in equation ( 3 ) if \({{{{\bf{s}}}}}_{{{{\mathcal{D}}}},i}^{\theta }\) is well learned, which is deterministic and invertible, hence establishing a correspondence between the structure and latent space. We can then uniquely map the two given states in the structure space to the latent space, approximate the path in the latent space by linear interpolation and then map the path back to the structure space. Since the distribution in the latent space is Gaussian, which has a convex contour, the linearly interpolated path goes through high-probability or low-energy regions, so it gives an intuitive guess of the real reaction path.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.

Data availability

Structures from the Protein Data Bank (PDB) were used for training and as templates ( https://www.wwpdb.org/ftp/pdb-ftp-sites ; for the associated sequence data and 100% sequence clustering see also https://ftp.wwpdb.org/pub/pdb/derived_data/ and https://cdn.rcsb.org/resources/sequence/clusters/clusters-by-entity-100.txt ). Training used a version of the PDB downloaded on 25 December 2020. The template search also used the PDB70 database, downloaded 13 May 2020 ( https://wwwuser.gwdg.de/~compbiol/data/hhsuite/databases/hhsuite_dbs/ ). For MSA lookup at both the training and prediction time, we used Uniclust30 v.2018_08 ( https://wwwuser.gwdg.de/~compbiol/uniclust/2018_08/ ). The milisecond MD simulation trajectories for the RBD and main protease of SARS-CoV-2 are downloaded from the coronavirus disease 2019 simulation database ( https://covid.molssi.org/simulations/ ). We collect 238 simulation trajectories from the GPCRmd dataset ( https://www.gpcrmd.org/dynadb/datasets/ ). Protein–ligand docked complexes are collected from CrossDocked2020 dataset v1.3 ( https://github.com/gnina/models/tree/master/data/CrossDocked2020 ). The MD simulation trajectories for 1,500 protein–ligand complexes and the generated carbon structures are available upon request from the corresponding authors (S.Z., C.L., H.L. or T.Y.-L.) owing to Microsoft’s data release policy.

The OC20 dataset used for catalyst–adsorption generation modelling is publicly available ( https://github.com/Open-Catalyst-Project/ocp/blob/main/DATASET.md ). Specifically, we use the IS2RS part and MD part. The carbon polymorphs dataset is generated using random structure search where random initial structures are relaxed together with the lattice using density functional theory with conjugated gradient. The generated carbon structures are available upon request from the corresponding authors (S.Z., C.L., H.L. or T.-Y.L.) owing to Microsoft’s data release policy.

Code availability

Source code for the Distributional Graphormer model, inference scripts, and model weights are available via Zenodo at https://doi.org/10.5281/zenodo.10911143 (ref. 53 ). An online demo page is available at https://DistributionalGraphormer.github.io .

The DiG models are primarily developed using Python, PyTorch, Numpy, fairseq, torch-geometric and rdkit. We used HHBlits and HHSearch from the hh-suite for MSA and PDB70 template searches, and Gromacs for MD simulations. OpenMM, pdbfixer and the amber14 force field were utilized for energy function training. DFT calculations for the carbon polymorphs dataset were performed with VASP. Both the carbon polymorphs and OC20 datasets were converted to PyG graphs using torch-geometric and stored in lmdb databases. For more detailed information, please refer to the code repository.

Data analysis for proteins and ligands was conducted using Python, PyTorch, Numpy, Matplotlib, MDTraj, seaborn, SciPy, scikit-learn, pandas and Biopython. Visualization and rendering were done with ChimeraX and Pymol. Analysis and visualization of catalyst–adsorption systems and carbon structures were performed with Python, PyTorch, Numpy, Matplotlib, Pandas and VESTA. Adsorption configurations were searched using density functional theory computations with VASP.

Jumper, J. et al. Highly accurate protein structure prediction with alphafold. Nature 596 , 583–589 (2021).

Article   Google Scholar  

Cramer, P. Alphafold2 and the future of structural biology. Nat. Struct. Mol. Biol. 28 , 704–705 (2021).

Akdel, M. et al. A structural biology community assessment of AlphaFold2 applications. Nat. Struct. Mol. Biol. 29 , 1056–1067 (2022).

Pereira, J. et al. High-accuracy protein structure prediction in casp14. Proteins Struct. Funct. Bioinf. 89 , 1687–1699 (2021).

Stärk, H., Ganea, O., Pattanaik, L., Barzilay, R. & Jaakkola, T. Equibind: geometric deep learning for drug binding structure prediction. In Proc. International Conference on Machine Learning 20503–20521 (PMLR, 2022).

Corso, G., Stärk, H., Jing, B., Barzilay, R. & Jaakkola, T. DiffDock: diffusion steps, twists, and turns for molecular docking. In Proc. International Conference on Learning Representations (2023).

Diaz-Rovira, A. M. et al. Are deep learning structural models sufficiently accurate for virtual screening? application of docking algorithms to AlphaFold2 predicted structures. J. Chem. Inf. Model. 63 , 1668–1674 (2023).

Scardino, V., Di Filippo, J. I. & Cavasotto, C. N. How good are AlphaFold models for docking-based virtual screening? iScience 26 , 105920 (2022).

Chanussot, L. et al. Open catalyst 2020 (OC20) dataset and community challenges. ACS Catal. 11 , 6059–6072 (2021).

Ying, C. et al. Do transformers really perform badly for graph representation? Adv. Neural Inf. Process. Syst. 34 , 28877–28888 (2021).

Google Scholar  

Chen, C. & Ong, S. P. A universal graph deep learning interatomic potential for the periodic table. Nat. Comput. Sci. 2 , 718–728 (2022).

Schaarschmidt, M. et al. Learned force fields are ready for ground state catalyst discovery. Preprint at https://arxiv.org/abs/2209.12466 (2022).

Lindorff-Larsen, K., Piana, S., Dror, R. O. & Shaw, D. E. How fast-folding proteins fold. Science 334 , 517–520 (2011).

Barducci, A., Bonomi, M. & Parrinello, M. Metadynamics. Wiley Interdisc. Rev. Comput. Mol. Sci. 1 , 826–843 (2011).

Kästner, J. Umbrella sampling. Wiley Interdisc. Rev. Comput. Mol. Sci. 1 , 932–942 (2011).

Chodera, J. D. & Noé, F. Markov state models of biomolecular conformational dynamics. Curr. Opin. Struct. Biol. 25 , 135–144 (2014).

Monticelli, L. et al. The Martini coarse-grained force field: extension to proteins. J. Chem. Theory Comput. 4 , 819–834 (2008).

Clementi, C. Coarse-grained models of protein folding: toy models or predictive tools? Curr. Opin. Struct. Biol. 18 , 10–15 (2008).

Wang, J. et al. Machine learning of coarse-grained molecular dynamics force fields. ACS Cent. Sci. 5 , 755–767 (2019).

Arts, M. et al. Two for one: diffusion models and force fields for coarse-grained molecular dynamics. J. Chem. Theory Comput. 19 , 6151–6159 (2023).

Noé, F., Olsson, S., Köhler, J. & Wu, H. Boltzmann generators: sampling equilibrium states of many-body systems with deep learning. Science 365 , 1147 (2019).

Klein, L. et al. Timewarp: transferable acceleration of molecular dynamics by learning time-coarsened dynamics. In Advances Neural Information Processing Systems Vol 36 (2024).

Kirkpatrick, S., Gelatt Jr, C. D. & Vecchi, M. P. Optimization by simulated annealing. Science 220 , 671–680 (1983).

Article   MathSciNet   Google Scholar  

Neal, R. M. Annealed importance sampling. Stat. Comput. 11 , 125–139 (2001).

Del Moral, P., Doucet, A. & Jasra, A. Sequential Monte Carlo samplers. J. R. Stat. Soc. B 68 , 411–436 (2006).

Doucet, A., Grathwohl, W.S., Matthews, A.G.d.G. & Strathmann, H. Annealed importance sampling meets score matching. In Proc. ICLR Workshop on Deep Generative Models for Highly Structured Data (2022).

Sohl-Dickstein, J., Weiss, E., Maheswaranathan, N. & Ganguli, S. Deep unsupervised learning using nonequilibrium thermodynamics. In Proc. International Conference on Machine Learning 2256–2265 (PMLR, 2015).

Ho, J., Jain, A. & Abbeel, P. Denoising diffusion probabilistic models. Adv. Neural Inf. Process. Syst. 33 , 6840–6851 (2020).

Del Alamo, D., Sala, D., Mchaourab, H. S. & Meiler, J. Sampling alternative conformational states of transporters and receptors with alphafold2. eLife 11 , 75751 (2022).

Zimmerman, M. I. et al. SARS-CoV-2 simulations go exascale to predict dramatic spike opening and cryptic pockets across the proteome. Nat. Chem. 13 , 651–659 (2021).

Zhang, L. et al. Crystal structure of SARS-CoV-2 main protease provides a basis for design of improved α -ketoamide inhibitors. Science 368 , 409–412 (2020).

Tai, W. et al. Characterization of the receptor-binding domain (rbd) of 2019 novel coronavirus: implication for development of rbd protein as a viral attachment inhibitor and vaccine. Cell. Mol. Immunol. 17 , 613–620 (2020).

Masureel, M. et al. Protonation drives the conformational switch in the multidrug transporter LmrP. Nat. Chem. Biol. 10 , 149–155 (2014).

Nussinov, R., Zhang, M., Liu, Y. & Jang, H. Alphafold, artificial intelligence (AI), and allostery. J. Phys. Chem. B 126 , 6372–6383 (2022).

Schindler, C. E. et al. Large-scale assessment of binding free energy calculations in active drug discovery projects. J. Chem. Inf. Model. 60 , 5457–5474 (2020).

Wang, L. et al. Accurate and reliable prediction of relative ligand binding potency in prospective drug discovery by way of a modern free-energy calculation protocol and force field. J. Am. Chem. Soc. 137 , 2695–2703 (2015).

Hafner, J. Ab-initio simulations of materials using VASP: density-functional theory and beyond. J. Comput. Chem. 29 , 2044–2078 (2008).

Lu, Z. Computational discovery of energy materials in the era of big data and machine learning: a critical review. Mater. Rep. Energy 1 , 100047 (2021).

Ong, S. P. et al. Python materials genomics (pymatgen): a robust, open-source python library for materials analysis. Comput. Mater. Sci. 68 , 314–319 (2013).

Langevin, P. Sur la théorie du mouvement brownien. Compt. Rendus 146 , 530–533 (1908).

Uhlenbeck, G. E. & Ornstein, L. S. On the theory of the Brownian motion. Phys. Rev. 36 , 823–841 (1930).

Roberts, G. O. et al. Exponential convergence of Langevin distributions and their discrete approximations. Bernoulli 2 , 341–363 (1996).

Wibisono, A., Wilson, A. C. & Jordan, M. I. A variational perspective on accelerated methods in optimization. Proc. Natl Acad. Sci. USA 113 , 7351–7358 (2016).

Anderson, B. D. Reverse-time diffusion equation models. Stoch. Process. Their Appl. 12 , 313–326 (1982).

Song, Y. et al. Score-based generative modeling through stochastic differential equations. In Proc. International Conference on Learning Representations (2021).

Dhariwal, P. & Nichol, A. Diffusion models beat GANs on image synthesis. Adv. Neural Inf. Process. Syst. 34 , 8780–8794 (2021).

Ramesh, A., Dhariwal, P., Nichol, A., Chu, C. & Chen, M. Hierarchical text-conditional image generation with clip latents. Preprint at https://arxiv.org/abs/2204.06125 (2022).

Risken, H. Fokker–Planck Equation (Springer, 1996).

Hutchinson, M. F. A stochastic estimator of the trace of the influence matrix for Laplacian smoothing splines. Commun. Stats. Simul. Comput. 18 , 1059–1076 (1989).

Grathwohl, W., Chen, R.T., Bettencourt, J., Sutskever, I. & Duvenaud, D. FFJORD: free-form continuous dynamics for scalable reversible generative models. In Proc. International Conference on Learning Representations (2019).

Vincent, P. A connection between score matching and denoising autoencoders. Neural Comput. 23 , 1661–1674 (2011).

Alain, G. & Bengio, Y. What regularized auto-encoders learn from the data-generating distribution. J. Mach. Learn. Res. 15 , 3563–3593 (2014).

MathSciNet   Google Scholar  

Zheng, L. et al. Towards predicting equilibrium distributions for molecular systems with deep learning. Zenodo https://doi.org/10.5281/zenodo.10911143 (2024).

Download references

Acknowledgements

This work has been supported by the Joint Funds of the National Natural Science Foundation of China (grant no. U20B2047). We thank N. A. Baker, L. Sun, B. Veeling, V. García Satorras, A. Foong and C. Lu for insightful discussions; S. Luo for helping with dataset preparations; J. Su for managing the project; J. Bai for helping with figure design; G. Guo for helping with cover design; and colleagues at Microsoft for their encouragement and support.

Author information

These authors contributed equally: Shuxin Zheng, Jiyan He, Chang Liu, Yu Shi, Ziheng Lu.

Authors and Affiliations

Microsoft Research AI4Science, Beijing, China

Shuxin Zheng, Jiyan He, Chang Liu, Yu Shi, Ziheng Lu, Weitao Feng, Fusong Ju, Jiaxi Wang, Jianwei Zhu, Yaosen Min, He Zhang, Shidi Tang, Hongxia Hao, Peiran Jin, Haiguang Liu & Tie-Yan Liu

University of Science and Technology of China, Hefei, China

Jiyan He & Weitao Feng

Microsoft Quantum, Redmond, WA, USA

Microsoft Research AI4Science, Berlin, Germany

You can also search for this author in PubMed   Google Scholar

Contributions

S.Z. and T.-Y.L. led the research. S.Z., J.H., C.L., Z.L. and H.L. conceived the project. J.H., C.L., Y.S., W.F., F.J. and J.Wang developed the diffusion model and training pipeline. J.H., Y.S., Z.L., J.Z., F.J., H.Z. and H.L. developed data and analytics systems. H.L., Y.S., Z.L., Y.M. and S.T. conducted simulations. H.H., P.J., C.C., and F.N. contributed technical advice and ideas. S.Z., J.H., C.L., Y.S., Z.L., F.N., H.Z. and H.L. wrote the paper with input from all authors.

Corresponding authors

Correspondence to Shuxin Zheng , Chang Liu , Haiguang Liu or Tie-Yan Liu .

Ethics declarations

Competing interests.

S.Z., C.L., Y.S., H.L. and T.-Y.L. are inventors of a pending patent application in the name of Microsoft Technology Licensing LLC concerning machine learning for predicting molecular systems as related to this paper. The other authors declare no competing interests.

Peer review

Peer review information.

Nature Machine Intelligence thanks Tiago Rodrigues, Dacheng Tao, and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary information.

Supplementary discussion, Figs. 1–9 and Tables 1–6.

Reporting Summary

Supplementary video 1.

DiG can generate plausible transition pathways that connect the two structures of adenylate kinase, corresponding to open and closed conformations. Using an interpolation approach, DiG generates pathways connecting open and closed states. The open and closed structures are shown as semi-transparent ribbons, and the structures along the predicted pathways are shown as cartoons (each secondary structure component is coloured differently for better visualization).

Supplementary Video 2

DiG can generate plausible transition pathways that connect the two structures of LmrP membrane protein, corresponding to open and closed conformations. Using an interpolation approach, DiG generates pathways connecting open and closed states. The open and closed structures are shown as semi-transparent ribbons, and the structures along the predicted pathways are shown as cartoons (each secondary structure component is coloured differently for better visualization).

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Cite this article.

Zheng, S., He, J., Liu, C. et al. Predicting equilibrium distributions for molecular systems with deep learning. Nat Mach Intell (2024). https://doi.org/10.1038/s42256-024-00837-3

Download citation

Received : 02 August 2023

Accepted : 10 April 2024

Published : 08 May 2024

DOI : https://doi.org/10.1038/s42256-024-00837-3

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

Quick links

• Explore articles by subject
• Guide to authors
• Editorial policies

Sign up for the Nature Briefing: AI and Robotics newsletter — what matters in AI and robotics research, free to your inbox weekly.

• Computer Vision
• Federated Learning
• Reinforcement Learning
• Natural Language Processing
• New Releases
• AI Dev Tools
• Advisory Board Members
• 🐝 Partnership and Promotion

Shobha Kakkar

Shobha is a data analyst with a proven track record of developing innovative machine-learning solutions that drive business value.

• Shobha Kakkar https://www.marktechpost.com/author/shobha-kakkar/ Top 50 AI Writing Tools To Try in 2024
• Shobha Kakkar https://www.marktechpost.com/author/shobha-kakkar/ Top Low/No Code AI Tools 2024
• Shobha Kakkar https://www.marktechpost.com/author/shobha-kakkar/ Top 40+ Generative AI Tools in 2024
• Shobha Kakkar https://www.marktechpost.com/author/shobha-kakkar/ Top Courses for Machine Learning with Python

RELATED ARTICLES MORE FROM AUTHOR

Aloe: a family of fine-tuned open healthcare llms that achieves state-of-the-art results through model merging and prompting strategies, innovating game design with gpt: a comprehensive scoping review, chuxin: a fully open-sourced language model with a size of 1.6 billion parameters, top 50 ai writing tools to try in 2024, nvidia ai releases the tensorrt model optimizer: a library to quantize and compress deep learning models for optimized inference on gpus, leveraging linguistic expertise in nlp: a deep dive into relies and its impact on large language models, aloe: a family of fine-tuned open healthcare llms that achieves state-of-the-art results through model..., nvidia ai releases the tensorrt model optimizer: a library to quantize and compress deep..., leveraging linguistic expertise in nlp: a deep dive into relies and its impact on..., ms marco web search: a large-scale information-rich web dataset featuring millions of real clicked..., top ai-powered seo tools in 2024, optimizing graph neural network training with diskgnn: a leap toward efficient large-scale learning, this ai paper by microsoft and tsinghua university introduces yoco: a decoder-decoder architectures for....

• AI Magazine
• Privacy & TC
• Cookie Policy

🐝 🐝 Join the Fastest Growing AI Research Newsletter Read by Researchers from Google + NVIDIA + Meta + Stanford + MIT + Microsoft and many others...

Thank You 🙌

Privacy Overview