linear programming is an appropriate problem solving technique

• School Guide
• Mathematics
• Number System and Arithmetic
• Trigonometry
• Probability
• Mensuration
• Maths Formulas
• Integration Formulas
• Differentiation Formulas
• Trigonometry Formulas
• Algebra Formulas
• Mensuration Formula
• Statistics Formulas
• Trigonometric Table
• CBSE Class 12 Maths Notes: Chapter Wise Notes PDF 2024

Chapter 1: Relations and Functions

• Types of Functions
• Composite functions - Relations and functions
• Invertible Functions
• Composition of Functions
• Inverse Functions
• Verifying Inverse Functions by Composition

Chapter 2: Inverse Trigonometric Functions

• Inverse Trigonometric Functions
• Graphs of Inverse Trigonometric Functions - Trigonometry | Class 12 Maths
• Properties of Inverse Trigonometric Functions
• Inverse Trigonometric Identities

Chapter 3: Matrices

• Types of Matrices
• Matrix Operations
• Matrix Addition
• Matrix Multiplication: How to Multiply Matrices, Methods, Examples
• Transpose of a Matrix
• Symmetric and Skew Symmetric Matrices
• Elementary Operations on Matrices
• Inverse of a Matrix by Elementary Operations - Matrices | Class 12 Maths
• Invertible Matrix

Chapter 4: Determinants

• Determinant of a Matrix with Solved Examples
• Properties of Determinants
• Area of a Triangle using Determinants
• Minors and Cofactors
• Adjoint of a Matrix
• Applications of Matrices and Determinants

Chapter 5: Continuity and Differentiability

• Continuity and Discontinuity in Calculus - Class 12 CBSE
• Differentiability of a Function | Class 12 Maths
• Derivatives of Inverse Functions
• Derivatives of Implicit Functions - Continuity and Differentiability | Class 12 Maths
• Derivatives of Composite Functions
• Derivatives of Inverse Trigonometric Functions | Class 12 Maths
• Derivative of Exponential Functions
• Logarithmic Differentiation - Continuity and Differentiability
• Proofs for the derivatives of eˣ and ln(x) - Advanced differentiation
• Rolle's Theorem and Lagrange's Mean Value Theorem
• Derivative of Functions in Parametric Forms
• Second Order Derivatives in Continuity and Differentiability | Class 12 Maths
• Mean Value Theorem
• Algebra of Continuous Functions - Continuity and Differentiability | Class 12 Maths

Chapter 6: Applications of Derivatives

• Critical Points
• Derivatives as Rate of Change
• Increasing and Decreasing Functions
• Increasing and Decreasing Intervals
• Tangents and Normals
• Equation of Tangents and Normals
• Relative Minima and Maxima
• Absolute Minima and Maxima
• Concave Function
• Inflection Point
• Curve Sketching
• Approximations & Maxima and Minima - Application of Derivatives | Class 12 Maths
• Higher Order Derivatives

Chapter 7: Integrals

• Integration by Substitution Method
• Integration by Partial Fractions
• Integration by Parts
• Integration of Trigonometric Functions
• Functions Defined by Integrals
• Definite Integral
• Computing Definite Integrals
• Fundamental Theorem of Calculus
• Finding Derivative with Fundamental Theorem of Calculus
• Evaluating Definite Integrals
• Properties of Definite Integrals
• Definite Integrals of Piecewise Functions
• Improper Integrals
• Riemann Sum
• Riemann Sums in Summation Notation
• Trapezoidal Rule
• Definite Integral as the Limit of a Riemann Sum
• Antiderivatives
• Indefinite Integrals
• Particular Solutions to Differential Equations
• Integration by U-substitution
• Reverse Chain Rule
• Partial Fraction Expansion
• Trigonometric Substitution: Method, Formula and Solved Examples

Chapter 8: Applications of Integrals

• Area under Simple Curves
• Area Between Two Curves - Calculus
• Area between Polar Curves
• Area as Definite Integral

Chapter 9: Differential Equations

• Differential Equations
• Homogeneous Differential Equations
• Separable Differential Equations
• Exact Equations and Integrating Factors
• Implicit Differentiation
• Implicit differentiation - Advanced Examples
• Advanced Differentiation
• Disguised Derivatives - Advanced differentiation | Class 12 Maths
• Derivative of Inverse Trig Functions
• Logarithmic Differentiation

Chapter 10: Vector Algebra

• Vector Algebra
• Dot and Cross Products on Vectors
• How to Find the Angle Between Two Vectors?
• Section Formula - Vector Algebra

Chapter 11: Three-dimensional Geometry

• Direction Cosines and Direction Ratios
• Equation of a Line in 3D
• Angles Between two Lines in 3D Space: Solved Examples
• Shortest Distance Between Two Lines in 3D Space | Class 12 Maths
• Points, Lines and Planes

Chapter 12: Linear Programming

Linear programming.

• Graphical Solution of Linear Programming Problems

Chapter 13: Probability

• Conditional Probability and Independence - Probability | Class 12 Maths
• Multiplication Theorem
• Dependent and Independent Events
• Bayes' Theorem
• Probability Distribution
• Binomial Distribution in Probability
• Binomial Mean and Standard Deviation - Probability | Class 12 Maths
• Bernoulli Trials and Binomial Distribution
• Discrete Random Variable
• Expected Value
• NCERT Solution for Class 12 Math PDF 2024-25
• RD Sharma Class 12 Solutions for Maths

Linear programming is a mathematical concept that is used to find the optimal solution of the linear function. This method uses simple assumptions for optimizing the given function. Linear Programming has a huge real-world application and it is used to solve various types of problems.

Linear programming is used in various industries such as shipping industries, manufacturing industries, transportation industries, telecommunications, and others.

Term “linear programming” consists of two words linear and programming, the word linear tells the relation between various types of variables of degree one used in a problem and the word programming tells us the step-by-step procedure to solve these problems.

In this article, we will learn about linear programming, its examples, formulas, and other concepts in detail.

Table of Content

What is Linear Programming? 

Components of linear programming, linear programming examples, linear programming problems, types of linear programming problems, linear programming formula, how to solve linear programming problems, linear programming methods, linear programming simplex method, linear programming graphical method, linear programming applications, importance of linear programming, up-to-date applications of linear programming, linear programming in operations research, simplex method.

Linear programming or Linear optimization is a technique that helps us to find the optimum solution for a given problem, an optimum solution is a solution that is the best possible outcome of a given particular problem.

In simple terms, it is the method to find out how to do something in the best possible way. With limited resources, you need to do the optimum utilization of resources and achieve the best possible result in a particular objective such as least cost, highest margin, or least time. 

The situation that requires a search for the best values of the variables subject to certain constraints is where we use linear programming problems. These situations cannot be handled by the usual calculus and numerical techniques.

Linear Programming Definition

Linear programming is the technique used for optimizing a particular scenario. Using linear programming provides us with the best possible outcome in a given situation. It uses all the available resources in a manner such that they produce the optimum result.

The basic components of a linear programming(LP) problem are:

• Decision Variables: Variables you want to determine to achieve the optimal solution.
• Objective Function: M athematical equation that represents the goal you want to achieve
• Constraints: Limitations or restrictions that your decision variables must follow.
• Non-Negativity Restrictions: In some real-world scenarios, decision variables cannot be negative

Additional Characteristics of Linear Programming

• Finiteness: The number of decision variables and constraints in an LP problem are finite.
• Linearity: The objective function and all constraints must be linear functions of the decision variables . It means the degree of variables should be one.

We can understand the situations in which Linear programming is applied with the help of the example discussed below,

Suppose a delivery man has to deliver 8 packets in a day to the different locations of a city. He has to pick all the packets from A and has to deliver them to points P, Q, R, S, T, U, V, and W. The distance between them is indicated using the lines as shown in the image below. The shortest path followed by the delivery man is calculated using the concept of Linear Programming.

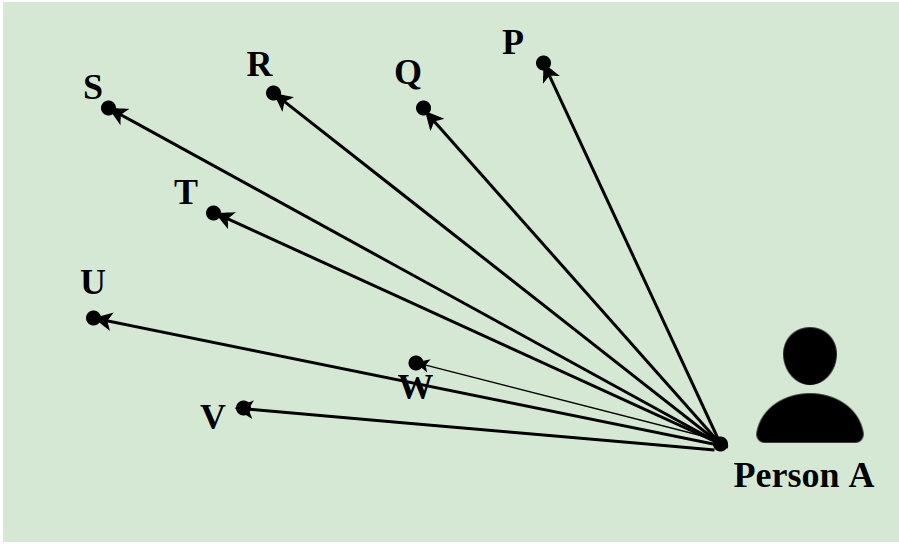
Linear Programming Problems (LPP) involve optimizing a linear function to find the optimal value solution for the function. The optimal value can be either the maximum value or the minimum value.

In LPP, the linear functions are called objective functions. An objective function can have multiple variables, which are subjected to conditions and have to satisfy the linear constraints .

There are many different linear programming problems(LPP) but we will deal with three major linear programming problems in this article.

Manufacturing Problems

Manufacturing problems are a problem that deals with the number of units that should be produced or sold to maximize profits when each product requires fixed manpower, machine hours, and raw materials.

Diet Problems

It is used to calculate the number of different kinds of constituents to be included in the diet to get the minimum cost, subject to the availability of food and their prices.

Transportation Problems

It is used to determine the transportation schedule to find the cheapest way of transporting a product from plants /factories situated at different locations to different markets.

A linear programming problem consists of,

• Decision variables
• Objective function
• Constraints
• Non-Negative restrictions

Decision variables are the variables x, and y, which decide the output of the linear programming problem and represent the final solution. 

The objective function , generally represented by Z, is the linear function that needs to be optimized according to the given condition to get the final solution. 

The restrictions imposed on decision variables that limit their values are called constraints.

Now, the general formula of a linear programming problem is,

Objective Function : Z = ax + by

Constraints: cx + dy ≥ e, px + qy ≤ r

Non-Negative restrictions: x ≥ 0, y ≥ 0

In the above condition x, and y are the decision variables.

Before solving the linear programming problems first we have to formulate the problems according to the standard parameters. The steps for solving linear programming problems are,

Step 1: Mark the decision variables in the problem. Step 2: Build the objective function of the problem and check if the function needs to be minimized or maximized. Step 3: Write down all the constraints of the linear problems. Step 4: Ensure non-negative restrictions of the decision variables. Step 5: Now solve the linear programming problem using any method generally we use either the simplex or graphical method.

We use various methods for solving linear programming problems. The two most common methods used are,

• Graphical Method

Let’s learn about these two methods in detail in this article,

One of the most common methods to solve the linear programming problem is the simplex method. In this method, we repeat a specific condition ‘n’ a number of times until an optimum solution is achieved.

The steps required to solve linear programming problems using the simplex method are,

Step 1: Formulate the linear programming problems based on the given constraints. Step 2: Convert all the given inequalities to equations or equalities of the linear programming problems by adding the slack variable to each inequality where ever required. Step 3: Construct the initial simplex table. By representing each constraint equation in a row and writing the objective function at the bottom row. The table so obtained is called the Simplex table. Step 4: Identify the greatest negative entry in the bottom row the column of the element with the highest negative entry is called the pivot column Step 5: Divide the entries of the right-most column with the entries of the respective pivot column, excluding the entries of the bottommost row. Now the row containing the least entry is called the pivot row. The pivot element is obtained by the intersection of the pivot row and the pivot column. Step 6: Using matrix operation and with the help of the pivot element make all the entries in the pivot column to be zero. Step 7: Check for the non-negative entries in the bottommost row if there are no negative entries in the bottom row, end the process else start the process again from step 4. Step 8: The final simplex table so obtained gives the solution to our problem.

Graphical Method is another method than the Simplex method which is used to solve linear programming problems. As the name suggests this method uses graphs to solve the given linear programming problems. This is the best method to solve linear programming problems and requires less effort than the simplex method. 

While using this method we plot all the inequalities that are subjected to constraints in the given linear programming problems. As soon as all the inequalities of the given LPP are plotted in the XY graph the common region of all the inequalities gives the optimum solution. All the corner points of the feasible region are calculated and the value of the objective function at all those points is calculated then comparing these values we get the optimum solution of the LPP.

Example: Find the maximal and minimal value of z = 6x + 9y when the constraint conditions are,

• 2x + 3y ≤ 12
• x and y ≥ 0

Step 1 : First convert the inequations into normal equations. Hence the equations will be 2x+3y = 0, x = 0, y = 0 and x + y = 5. Step 2 : Find the points at which 2x + 3y and x + y = 5 cut the x-axis and y-axis. To find the point of intersection of the x-axis put y = 0 in the respective equation and find the point. Similarly for y-axis intersection points put x = 0 in the respective equation. Step 3 : Draw the two lines cutting the x-axis and y-axis. We find that the two axes cut each other at (3,2). Step 4 : For x ≥ 0 and y ≥ 0, we find that both inequations are followed. Hence the region will include an area region enclosed by two axes and both lines including the origin. The plotted region is shown below in the figure. Step 5 : Find Z for each point and maxima and minima. Coordinates Z = 6x + 9y (0,5) Z = 45 (0,4) Z = 36 (5,0) Z = 30 (6,0) Z = 36 (3,2) Z = 36 Hence, we find that Z = 6x + 9y is maximum at (0,5) and minimum at (5,0).

Linear Programming has applications in various fields. It is used to find the minimum cost of a process when all the constraints of the problems are given. It is used to optimize the transportation cost of the vehicle, etc. Various applications of Linear Programming are

Engineering Industries

Engineering Industries use linear programming to solve design and manufacturing problems and to get the maximum output from a given condition.

Manufacturing Industries

Manufacturing Industries use linear programming to maximize the profit of the companies and to reduce the manufacturing cost.

Energy Industries

Energy companies use linear programming to optimize their production output.

Transportation Industries

Linear programming is also used in transportation industries to find the path to minimize the cost of transportation.

Linear Programming has huge importance in various industries it maximizes the output value while minimizing the input values according to various constraints.

LP is highly applicable when we have multiple conditions while solving a problem and we have to optimize the output of the problem i.e. either we have to find the minimum or the maximum value according to a given condition.

Linear Inequalities Algebraic Solution of Linear Inequalities

Problem 1: A company manufactures and sells two types of products and the cost of production of each unit a and b is rupees 200 and 150 respectively each unit of product yields a profit of 20 rupees and each unit of product b yields a profit of 15 rupees on selling. The company estimates the monthly demand of A and B to be at a maximum of the harvested unit in all the production budget for the month is set at rupees 50000. How many units should the company manufacture to earn maximum profit from its monthly sales from a and b?

Let x = number of units of type A y = Number of units of type B Maximize Z = 40x + 50y Subject to the constraints 3x + y ≤ 9 x + 2y ≤ 8 and x, y ≥ 0 Consider the equation, 3x + y = 9 x = 3 y = 0 and x + 2y = 8 x = 8 y = 0 Now, we can determine the maximum value of Z by evaluating the value of Z at the four points (vertices) is shown below Vertices Z = 40x + 50y (0, 0) Z = 40 × 0 + 50 × 0 = Rs. 0 (3, 0) Z = 40 × 3 + 50 × 0 = Rs. 120 (0, 4)  Z = 40 × 0 + 50 × 4 = Rs. 200 (2, 3) Z = 40 × 2 + 50 × 3 = Rs. 230 Maximum profit, Z = Rs. 230 ∴ Number of units of type A is 2 and the number of units of type B is 3.

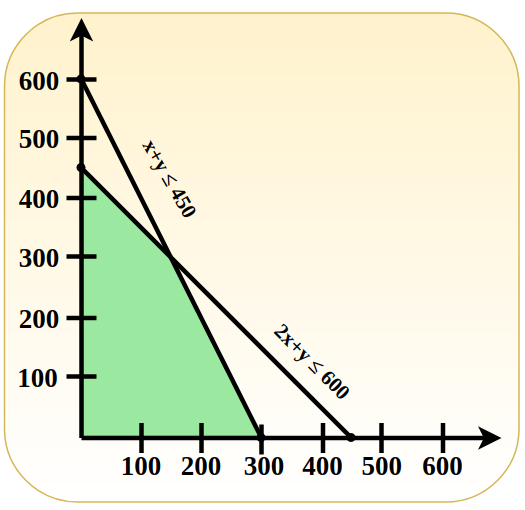
Problem 2: Maximize Z = 3x + 4y.

Subject to constraints , x + y ≤ 450, 2x + y ≤ 600 and x, y ≤ 0.

We have from the given Constraints (1) X + Y = 450 Putting x = 0, ⇒ 0 + y = 450 ⇒ y = 450 Putting y = 0, ⇒ x + 0 = 450 ⇒ x = 450 From, Constraints (2) 2x + y = 600 Putting x = 0, ⇒ 0 + y = 600 ⇒ y = 600 Putting  y = 0, ⇒ 2x + 0 = 600 ⇒ x = 300 Now, we have the points co-ordinate Z = 3x + 4y

Therefore, the optimal solution maximum Z = 1800 at co-ordinate x = 0 and y = 450. The graph is given below.

Linear programming, a powerful mathematical technique, is used to solve optimization problems in various industries. Here are some modern applications:

• Supply Chain Optimization : Linear programming helps companies minimize costs and maximize efficiency in their supply chains. It’s used for determining the most cost-effective transportation routes, warehouse operations, and inventory management strategies.
• Energy Management : In the energy sector, linear programming is utilized to optimize the mix of energy production methods. This includes balancing traditional energy sources with renewable ones to reduce costs and environmental impact while meeting demand.
• Telecommunications Network Design : Linear programming aids in designing efficient telecommunications networks. It helps in allocating bandwidth, designing network layouts, and optimizing the flow of data to ensure high-speed communication at lower costs.
• Financial Planning : Businesses and financial analysts use linear programming for portfolio optimization, risk management, and capital budgeting. It helps in making investment decisions that maximize returns while minimizing risk.
• Healthcare Logistics : In healthcare, linear programming is applied to optimize the allocation of resources, such as hospital beds, medical staff, and equipment. It’s crucial for improving patient care, reducing wait times, and managing costs effectively.
• Manufacturing Process Optimization : Linear programming is used to determine the optimal production levels for multiple products within a manufacturing facility, considering constraints like labor, materials, and machine availability.
• Agricultural Planning : Farmers and agricultural planners use linear programming to decide on crop selection, land use, and resource allocation to maximize yields and profits while conserving resources.
• Airline Crew Scheduling : Airlines employ linear programming to schedule crews efficiently, ensuring that flights are staffed in compliance with regulations and minimizing operational costs.

These applications demonstrate the versatility and power of linear programming in solving complex optimization problems across various sectors, showcasing its relevance in today’s data-driven world.

• Core Tool : Linear programming is a foundational tool in operations research for optimizing resources.
• Decision Making : Helps in making the best decisions regarding resource allocation, maximizing profits, or minimizing costs.
• Wide Applications : Used in various fields such as logistics, manufacturing, finance, and healthcare for solving complex problems.
• Modeling Real-World Problems : Transforms real-world problems into mathematical models to find the most efficient solutions.
• Optimization Algorithm : The Simplex Method is a powerful algorithm used in linear programming to find the optimal solution to linear inequalities.
• Step-by-Step Approach : It iteratively moves towards the best solution by navigating the edges of the feasible region defined by constraints.
• Efficiency : Known for its efficiency in solving large-scale linear programming problems.
• Versatility : Applicable in various domains like diet planning, network flows, production scheduling, and more, showcasing its versatility.

Linear Programming – FAQs

What is linear programming.

Linear programming is a mathematical concept which is used to optimize a given linear problem which has a variety of constraints. Using linear programming we the optimum output of the given problem

What are Linear Programming Problems?

Linear Programming Problems (LPP) are the problems which give the optimum solution to the given conditions.

What is Linear Programming Formula?

General Linear Programming Formulas are, Objective Function: Z = ax + by Constraints: px + qy ≤ r, sx + ty ≤ u Non-Negative Restrictions: x ≥ 0, y ≥ 0

What are the different types of Linear Programming?

Different types of linear programming methods are, Linear Programming by Simplex Method Linear Programming by R Method Linear Programming by Graphical Method

What are requirements of Linear Programming?

Various requirements of linear programming problems are, Linearity Objective Function Constraints Non-negativity

What are the advantages of Linear Programming?

Various advantages of linear programming are, It provides the optimal solution to any given linear problem. It is easy to use and always gives consistent results It helps to maximize profits and to reduce the input cost.

Please Login to comment...

Similar reads.

• Math-Concepts
• Maths-Class-12
• Technical Scripter 2020
• School Learning
• Technical Scripter

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Reset password New user? Sign up

Existing user? Log in

Linear Programming

Already have an account? Log in here.

• Andrew Hayes

Linear programming is an optimization technique for a system of linear constraints and a linear objective function. An objective function defines the quantity to be optimized, and the goal of linear programming is to find the values of the variables that maximize or minimize the objective function.

A factory manufactures doodads and whirligigs. It costs $2 and takes 3 hours to produce a doodad. It costs $4 and takes 2 hours to produce a whirligig. The factory has $220 and 150 hours this week to produce these products. If each doodad sells for $6 and each whirligig sells for $7, then how many of each product should be manufactured this week in order to maximize profit? This kind of problem is perfect to use linear programming techniques on. All of the quantifiable relationships in the problem are linear. The values of variables are constrained in some way. The goal is to find values of the variables that will maximize some quantity.

Linear programming is useful for many problems that require an optimization of resources. It could be applied to manufacturing, to calculate how to assign labor and machinery to minimize cost of operations. It could be applied in high-level business operations, to decide which products to sell and in what quantity in order to maximize profit. It could also be applied in logistics, to decide how to apply resources to get a job done in the minimum amount of time.

When to use Linear Programming

Linear programming in two variables, simplex algorithm, special cases of simplex algorithm, big-m method.

Linear programming can be used to solve a problem when the goal of the problem is to maximize some value and there is a linear system of inequalities that defines the constraints on the problem.

A constraint is an inequality that defines how the values of the variables in a problem are limited. In order for linear programming techniques to work, all constraints should be linear inequalities.

Returning to the example in the introduction:

Note that there is a cost associated with producing each part. Each doodad costs $2 to make and each whirligig costs $4 to make. The factory only has $220 available to spend on these costs, so the production is limited by cost. Let \(x\) be the number of doodads produced, and let \(y\) be the number of whirligigs produced. Then this constraint can be written as an inequality: \[2x+4y \le 220.\] There is also the limitation on how much time the factory has to produce these parts. Each doodad requires 3 hours to make and each whirligig requires 2 hours to make. The factory only has 150 hours available this week, so production is also limited by time. This constraint can be written as an inequality: \[3x+2y \le 150.\] In addition to these constraints, there is also a couple of "common sense" constraints. It's not possible to produce less than 0 of any part, so these constraints are also written: \[\begin{align} x &\ge 0 \\ y &\ge 0. \end{align}\] These are called non-negative constraints . Altogether, the constraints form a system of inequalities: \[\begin{cases}\begin{align} 2x+4y &\le 220 \\ 3x+2y &\le 150 \\ x &\ge 0 \\ y &\ge 0. \end{align}\end{cases}\]

Graphing these inequalities in the coordinate plane creates a polygon shape.

Graph the system of constraints \[\begin{cases}\begin{align} 2x+4y &\le 220 \\ 3x+2y &\le 150 \\ x &\ge 0 \\ y &\ge 0. \end{align}\end{cases}\]

The shaded region above is the feasible region of this problem.

The region that is bound by the system of constraints is called the feasible region . It represents the possible values of the variables that satisfy all of the constraints. In order for linear programming techniques to work, it should be a convex polytope (in 2 dimensions, a convex polygon; in 3 dimensions, a convex polyhedron; and so on).

Finding the feasible region is only sufficient to give the possible solutions of a problem. The goal of linear programming is to find the best solution to a problem. This is done by maximizing or minimizing the objective function .

The objective function is a function that defines some quantity that should be minimized or maximized. The arguments of the objective function are the same variables that are used in the constraints. In order for linear programming techniques to work, the objective function should be linear.

Each doodad costs $2 to make and sells for $6. This gives a profit of $4 per doodad. Each whirligig costs $4 to make and sells for $7. This gives a profit of $3 per whirligig. The profit function can be defined as \[p(x,y)=4x+3y.\] This is the objective function of this problem, and the goal is to maximize it.

It seems like the strategy now would be to test ordered pairs in the feasible region until a maximum profit is found. However, a more efficient method is available.

Let \(P\) be the maximum profit in the feasible region: \[P=4x+3y.\] Solve for y: \[y=-\frac{4}{3}x+\frac{P}{3}.\] This maximum profit gives an equation of a line, and whatever point in the feasible region passes through this line is the optimal solution. The \(y\)-intercept of this line is \(\frac{P}{3}.\) Since \(P\) is maximized, this \(y\)-intercept should be maximized as well. Graph several lines with the same slope of \(-\frac{4}{3}.\) The line that maximizes the \(y\)-intercept is the one that passes through the vertex at \((20,45),\) the intersection of the first two constraints. All other higher lines do not pass through the feasible region. All other lower lines pass through more than one point in the feasible region, and do not maximize the \(y\)-intercept of the line. Therefore, the factory should produce 20 doodads and 45 whirligigs. This will give a profit of \($215.\) \(_\square\)

In the previous example, it was shown that the optimal solution was on a vertex of the feasible region. This is true for all linear programming problems.

Given a convex polygonal feasible region and a linear objective function, the solution that maximizes or minimizes the objective function will be located on one of the vertices of the feasible region.

Let the objective function be \(f(x,y)=ax+by.\) Let the maximum value of this function be \(P,\) and let the minimum value of this function be \(Q.\) There exist lines which intersect each of the optimal solutions, \((x,y)\): \[\begin{align} ax+by &= P &&\qquad (1) \\ ax+by &= Q &&\qquad (2) \\\\ \Rightarrow y &= -\frac{a}{b}x + \frac{P}{b} &&\qquad (1) \\ y &= -\frac{a}{b}x + \frac{Q}{b}. &&\qquad (2) \end{align}\] Since \(P\) is the maximum value of the objective function, \((1)\) has the maximum \(y\)-intercept of a line with slope \(-\frac{a}{b}\) that passes through the feasible region. Likewise, \((2)\) has the minimum \(y\)-intercept of a line with slope \(-\frac{a}{b}\) that passes through the feasible region. Suppose that \((1)\) or \((2)\) passes through a point that is not one of the vertices of the feasible region. Case 1. The intersection point is on a side of the feasible region that is parallel to lines \((1)\) and \((2).\) If this is the case, then line \((1)\) or \((2)\) also contains a vertex of the feasible region, so this cannot be so. Case 2. The intersection point is somewhere else within the feasible region. The line will intersect more than one point in the feasible region. Then there will exist another point within the feasible region, either higher or lower, that a line with a parallel slope intersects. This cannot be true if line \((1)\) or \((2)\) has the maximum or minimum \(y\)-intercept of a line that passes through the feasible region. Hence, \((1)\) and \((2)\) must intersect a vertex of the feasible region. Each optimal solution is located at a vertex of the feasible region. \(_\square\)

This theorem gives a simple method for finding the optimal solution to a linear programming problem in two variables.

Process for finding the optimal solution of a linear programming problem in two variables Confirm that the feasible region is a convex polygon and the objective function is linear. Find the ordered pair of each vertex of the feasible region. Substitute each ordered pair into the objective function to find the solution that maximizes or minimizes the objective function.

A farmer feeds his cows a feed mix to supplement their foraging. The farmer uses two types of feed for the mix. Corn feed contains 100 g protein per kg and 750 g starch per kg. Wheat feed contains 150 g protein per kg and 700 g starch per kg. Each cow should be fed at most 7 kg of feed per day. The farmer would like each cow to receive at least 650 g protein and 4000 g starch per day. If corn feed costs $0.40/kg and wheat costs $0.45/kg, then what is the optimal feed mix that minimizes cost? Round your answers to the nearest gram. Let \(c\) be the kilograms of corn feed per cow per day, and let \(w\) be the kilograms of wheat feed per cow per day. The system of constraints can be written: \[\begin{cases} \begin{align} 0.1c+0.15w &\ge 0.65 \\ 0.75c+0.7w &\ge 4 \\ c+w &\le 7 \\ c &\ge 0 \\ w &\ge 0. \end{align} \end{cases}\] The objective function is \[\text{Minimize:} \ f(c,w)=0.40c+0.45w.\] Graphing the system of constraints gives an idea of where the vertices of the feasible region are, and which lines intersect to form them: Solve for each vertex of the feasible region by solving each pair of intersecting lines as a system of equations. For example, to solve for the vertex within the \(1^\text{st}\) quadrant, solve the system of equations \[\begin{cases} \begin{align} 0.1c+0.15w &= 0.65 \\ 0.75c +0.7w &= 4. \end{align} \end{cases}\] Solving this system gives \(c \approx 3.411\) and \(w \approx 2.059.\) These values can be substituted into the objective function to obtain the cost of this mix: \[f(3.411,2.059) = \$2.29.\] Note that it is not necessary to solve for every vertex. Since the problem requires a minimum and the objective function line has a negative slope, the optimal solution must be on the underside of the feasible region. Solve for these vertices: \[\begin{cases} \begin{align} 0.75c +0.7w &= 4 \\ c &= 0 \end{align} \end{cases} \implies c=0, w \approx 5.714 \implies f(0,5.714)=\$2.57 \] \[\begin{cases} \begin{align} 0.1c+0.15w &= 0.65 \\ w &= 0 \end{align} \end{cases} \implies c=6.5, w=0 \implies f(6.5,0)=\$2.60. \] The feed mix that minimizes cost contains 3411 g corn and 2059 g wheat. It costs $2.29 per cow. \(_\square\)

A manufacturer has 750 meters of cotton and 1000 meters of polyester. Production of a sweatshirt requires 1 meter of cotton and 2 meters of polyester, while production of a shirt requires 1.5 meters of cotton and 1 meter of polyester. The sale prices of a sweatshirt and a shirt are 30 € and 24 €, respectively. What are the number of sweatshirts \((S)\) and the number of shirts \((C)\) that maximize total sales?

Submit \(S + C.\)

Jordan has $100 to buy some comic books. He really likes the Star Wars books which cost $12 each, but he could also buy the Marvels books which cost $5 each. If he has to buy at least 12 books, what is the maximum number of the Star Wars books that he can buy?

An amateur bodybuilder is looking for supplement protein bars to build his muscle fast, and there are 2 available products: protein bar A and protein bar B.

Each protein bar A contains 15 g of protein and 30 g of carbohydrates and has total 200 calories. On the other hand, each protein bar B contains 30 g of protein and 20 g of carbohydrates and has total 240 calories.

According to his nutritional plan, this bodybuilder needs at least 20,000 calories from these supplements over the month, which must comprise of at least 1,800 g of protein and at least 2,200 g of carbohydrates.

If each protein bar A costs $3 and each protein bar B costs $4, what is the least possible amount of money (in $) he can spend to meet all his one-month requirements?

This kind of method would also work for linear optimization problems in more than two variables. However, these kinds of problems are more challenging to visualize with a coordinate graph, and there can be many more vertices to check for the optimal solution. The simplex algorithm was developed as an efficient method to solve these kinds of problems.

The simplex algorithm is a method to obtain the optimal solution of a linear system of constraints, given a linear objective function. It works by beginning at a basic vertex of the feasible region, and then iteratively moving to adjacent vertices, improving upon the solution each time until the optimal solution is found.

The simplex algorithm has many steps and rules, so it is helpful to understand the logic behind these steps and rules with a simple example before proceeding with the formal algorithm.

Given the system of constraints \[\begin{cases} \begin{align} 2x+3y &\le 90 \\ 3x+2y &\le 120 \\ x & \ge 0 \\ y & \ge 0, \end{align} \end{cases}\] maximize the objective function \[f(x,y)=7x+5y.\] The simplex algorithm begins by converting the constraints and objective functions into a system of equations. This is done by introducing new variables called slack variables . Slack variables represent the positive difference, or slack , between the left hand side of an inequality and the right hand side of that inequality. The inequality \[2x+3y \le 90\] becomes \[2x+3y+s_1=90.\] Likewise, the inequality \[3x+2y \le 120\] becomes \[3x+2y+s_2 = 120.\] In addition to the slack variables, a variable \(z\) is introduced to represent the value of the objective function. This gives the equation \[z-7x-5y=0.\] These equations give the system of equations \[\begin{cases} \begin{array}{cccccccccccc} z & - & 7x & - & 5y & & & & & = & 0 && (0) \\ & & 2x & + & 3y & + & s_1 & & & = & 90 && (1) \\ & & 3x & + & 2y & & & + & s_2 & = & 120. && (2) \end{array} \end{cases}\] In augmented matrix form, this is \[\left[\begin{array}{ccccc|c} 1 & -7 & -5 & 0 & 0 & 0 \\ 0 & 2 & 3 & 1 & 0 & 90 \\ 0 & 3 & 2 & 0 & 1 & 120 \end{array}\right]. \qquad \begin{array}{c} (0) \\ (1) \\ (2) \end{array}\] It is implied that all variables in this system (including \(s_1,\) \(s_2,\) and \(z\)) are greater than or equal to 0. The variables \(s_1\) and \(s_2\) have zero coefficients in row \((0)\) and are called basic variables . The variables \(x\) and \(y\) have non-zero coefficients in row \((0)\) and are called non-basic variables . At any point in this process, the basic solution is given by setting the non-basic variables to 0. Currently, the basic solution is \[x=0, \quad y=0, \quad s_1=90, \quad s_2=120, \quad z=0.\] Consider what effect increasing the values of the non-basic variables would have on the value of \(z.\) Increasing either \(x\) or \(y\) would cause \(z\) to also increase, because \(x\) and \(y\) have negative coefficients in row \((0).\) Thus, this is not the optimal solution. The iterations of the simplex algorithm involve exchanging basic variables and non-basic variables by using matrix row operations. At each step of the process, a non-basic variable in row \((0)\) is eliminated, leading another basic variable to take its place as a non-basic variable. This is called a pivot . Suppose \(x\) were to be eliminated in row \((0).\) This can be done with either row \((1)\) or row \((2).\) Case 1. Eliminating \(x\) in row \((0)\) with row \((1)\), \[\left[\begin{array}{ccccc|c} 1 & 0 & \frac{21}{2} & \frac{7}{2} & 0 & 315 \\ 0 & 2 & 3 & 1 & 0 & 90 \\ 0 & 3 & 2 & 0 & 1 & 120 \end{array}\right]. \qquad \begin{array}{c} (0)\vphantom{\frac{1}{2}} \\ (1) \\ (2) \end{array}\] During this pivot, the variable \(x\) entered as a basic variable, and the variable \(s_1\) left to become a non-basic variable. Now eliminate \(x\) in row \((2)\): \[\left[\begin{array}{ccccc|c} 1 & 0 & \frac{21}{2} & \frac{7}{2} & 0 & 315 \\ 0 & 2 & 3 & 1 & 0 & 90 \\ 0 & 0 & -\frac{5}{2} & -\frac{3}{2} & 1 & -15 \end{array}\right]. \qquad \begin{array}{c} (0)\vphantom{\frac{1}{2}} \\ (1) \\ (2)\vphantom{\frac{1}{2}} \end{array}\] This gives the basic solution \[x=45, \quad y=0, \quad s_1=0, \quad s_2=-15, \quad z=315.\] This solution is impossible, because it leads to one of the variables being negative. Case 2. Eliminating \(x\) in row \((0)\) with row \((2)\), \[\left[\begin{array}{ccccc|c} 1 & 0 & -\frac{1}{3} & 0 & \frac{7}{3} & 280 \\ 0 & 2 & 3 & 1 & 0 & 90 \\ 0 & 3 & 2 & 0 & 1 & 120 \end{array}\right]. \qquad \begin{array}{c} (0)\vphantom{\frac{1}{2}} \\ (1) \\ (2) \end{array}\] During this pivot, the variable \(x\) entered as a basic variable, and the variable \(s_2\) left to become a non-basic variable. Now eliminate \(x\) in row \((1)\): \[\left[\begin{array}{ccccc|c} 1 & 0 & -\frac{1}{3} & 0 & \frac{7}{3} & 280 \\ 0 & 0 & \frac{5}{3} & 1 & -\frac{2}{3} & 10 \\ 0 & 3 & 2 & 0 & 1 & 120 \end{array}\right]. \qquad \begin{array}{c} (0)\vphantom{\frac{1}{2}} \\ (1)\vphantom{\frac{1}{2}} \\ (2) \end{array}\] This gives the basic solution \[x=40, \quad y=0, \quad s_1=10, \quad s_2=0, \quad z=280.\] This solution is possible, but it is not optimal, because there is a negative coefficient in row \((0).\) This implies that \(z\) can be increased further by increasing \(y.\) Another pivot will be needed to find the optimal solution. It is a fair amount of work to perform a pivot, only to find that it gives an infeasible solution. Fortunately, one can anticipate which pivot will result in a feasible solution by observing the ratio of the element in the right part of the augmented matrix to the coefficient of the entering variable. Consider \(y\) as the entering variable, and calculate these ratios: \[\left[\begin{array}{ccccc|c} 1 & 0 & -\frac{1}{3} & 0 & \frac{7}{3} & 280 \\ 0 & 0 & {\color{red}\frac{5}{3}} & 1 & -\frac{2}{3} & {\color{red}10} \\ 0 & 3 & {\color{blue}2} & 0 & 1 & {\color{blue}120} \end{array}\right]. \qquad \begin{array}{c} (0)\vphantom{\frac{1}{2}} \\ (1)\vphantom{\frac{1}{2}} \\ (2) \end{array}\] For entering variable \(y,\) this ratio is \(10\div \frac{5}{3}=6\) for row \((1)\) and \(\frac{120}{2}=60\) for row \((2).\) Selecting the row that minimizes this ratio will ensure that the pivot results in a feasible solution. Thus, row \((1)\) should be selected as the pivot row. Eliminating \(y\) in row \((0)\) with row \((1)\), \[\left[\begin{array}{ccccc|c} 1 & 0 & 0 & \frac{1}{5} & \frac{11}{5} & 282 \\ 0 & 0 & \frac{5}{3} & 1 & -\frac{2}{3} & 10 \\ 0 & 3 & 2 & 0 & 1 & 120 \end{array}\right]. \qquad \begin{array}{c} (0)\vphantom{\frac{1}{2}} \\ (1)\vphantom{\frac{1}{2}} \\ (2) \end{array}\] Then eliminating \(y\) in row \((2)\), \[\left[\begin{array}{ccccc|c} 1 & 0 & 0 & \frac{1}{5} & \frac{11}{5} & 282 \\ 0 & 0 & \frac{5}{3} & 1 & -\frac{2}{3} & 10 \\ 0 & 3 & 0 & -\frac{6}{5} & \frac{9}{5} & 108 \end{array}\right]. \qquad \begin{array}{c} (0)\vphantom{\frac{1}{2}} \\ (1)\vphantom{\frac{1}{2}} \\ (2)\vphantom{\frac{1}{2}} \end{array}\] This gives the basic solution \[x=36, \quad y=6, \quad s_1=0, \quad s_2=0, \quad z=282.\] This solution must be optimal, because any increase in the non-basic variables \(s_1\) and \(s_2\) will cause a decrease in \(z.\) Thus, the maximum value of the objective function is \[f(36,6)=282.\ _\square\]

Simplex Algorithm for Maximization This version of the simplex algorithm is valid for a maximization problem with all constraints (except for the non-negative constraints) giving maximum values (using the \(\le\) symbol). In matrix form, the requirements are \[\begin{array}{ll} \text{Maximize:} & \textbf{c}^\text{T} \cdot \textbf{x} \\ \text{Subject to:} & \textbf{A}\textbf{x} \le \textbf{b}, \ \ x_i \ge 0, \end{array}\] where \(\textbf{c}\) is a vector containing the coefficients of the objective function, \(\textbf{x}\) is a vector containing the variables of the problem, \(\textbf{A}\) is a matrix containing the constraint coefficients, and \(\textbf{b}\) is a vector containing the maximum values of those constraints. Convert the constraints and objective function into a system of equations by introducing slack variables and the \(z\) variable. Put the system of equations into augmented matrix form. The objective function equation should go in row \((0).\) Select one of the non-basic variables to be the entering variable. Select the pivot row by computing the ratio \(\frac{\text{Element on right side of augmented matrix}}{\text{Coefficient of entering variable}}\) for each row. The correct pivot row minimizes this ratio. However, this ratio must be positive. If all coefficients of non-basic variables in row \((0)\) are positive, then you have the optimal solution. Otherwise, select a non-basic variable that has a negative coefficient in row \((0)\) to be the next entering variable, then pivot again to find another feasible solution. Continue pivoting until the optimal solution is found.

A toy factory manufactures three kinds of toys: cars, motorcycles, and boats. One toy car makes $20 profit, one toy motorcycle makes $15 profit, and one toy boat makes $25 profit. There are three departments of labour: casting, which has 8 workers; assembly, which has 12 workers; quality control, which has 10 workers.

Every day, the labour is allocated as follows: a toy car requires 2 casting, 2 assembly, 2 quality control; a toy motorcycles requires 1 casting, 2 assembly, 1 quality control; a toy boat requires 2 casting, 3 assembly, 3 quality control.

What is the maximum profit per day (in dollars) the toy company can achieve?

The simplex algorithm for minimization problems works by converting the problem to a maximization problem. This concept that every maximization problem has a corresponding minimization problem is formalized with the von Neumann duality principle .

Given the system of constraints \[\begin{cases}\begin{align} 4x+3y+5z &\ge 65 \\ x+3y+2z &\ge 38 \\ 2x+3y+4z &\ge 52 \\ x,y,z &\ge 0, \end{align}\end{cases}\] minimize the function \[f(x,y,z)=12x+3y+10z.\] This problem could be put into the form shown in the maximization examples above, but an issue would occur with finding the first basic solution: setting the \(x,\) \(y,\) and \(z,\) variables to \(0\) would give an infeasible solution with the slack variables taking on negative values. The simplex algorithm needs to start with a feasible solution, so this would not work. The Big-M method gives a workaround to this problem, but there is a much simpler method for this problem. A "dual" of this problem can be written by transposing the coefficients. Place the coefficients of the constraints into an augmented matrix. Place the coefficients of the objective function into the bottom row, with a 0 in the right part: \[\left[\begin{array}{ccc|c} \color{green}4 & \color{red}3 & \color{blue}5 & \color{orange}65 \\ \color{green}1 & \color{red}3 & \color{blue}2 & \color{orange}38 \\ \color{green}2 & \color{red}3 & \color{blue}4 & \color{orange}52 \\ \hline \color{green}12 & \color{red}3 & \color{blue}10 & \color{orange}0 \end{array}\right].\] Transpose the elements of the matrix: \[\left[\begin{array}{ccc|c} \color{green}4 & \color{green}1 & \color{green}2 & \color{green}12 \\ \color{red}3 & \color{red}3 & \color{red}3 & \color{red}3 \\ \color{blue}5 & \color{blue}2 & \color{blue}4 & \color{blue}10 \\ \hline \color{orange}65 & \color{orange}38 & \color{orange}52 & \color{orange}0 \end{array}\right].\] Note: It's tempting to divide out the 3 in the second row of this matrix, but this will break the symmetry that is required to return to the original problem. This gives a new system of constraints and an objective function to be maximized: Given the system of constraints \[\begin{cases}\begin{align} 4u+v+2w &\le 12 \\ 3u+3v+3w &\le 3 \\ 2u+3v+4w &\le 52 \\ u,v,w &\ge 0, \end{align}\end{cases}\] maximize the function \[g(u,v,w)=65u+38v+52w.\] Now the simplex algorithm can be applied to find the optimal solution \[\left[\begin{array}{ccccccc|c} 1 & -65 & -38 & -52 & 0 & 0 & 0 & 0 \\ 0 & 4 & 1 & 2 & 1 & 0 & 0 & 12 \\ 0 & 3 & 3 & 3 & 0 & 1 & 0 & 3 \\ 0 & 2 & 3 & 4 & 0 & 0 & 1 & 52 \end{array}\right]. \qquad \begin{array}{c} (0) \\ (1) \\ (2) \\ (3) \end{array}\] Enter \(u\) with row \((2)\): \[\left[\begin{array}{ccccccc|c} 1 & 0 & 27 & 13 & 0 & \frac{65}{3} & 0 & 65 \\ 0 & 0 & -3 & -2 & 1 & -4 & 0 & 8 \\ 0 & 1 & 1 & 1 & 0 & \frac{1}{3} & 0 & 1 \\ 0 & 0 & 1 & 2 & 0 & -2 & 1 & 50 \end{array}\right]. \qquad \begin{array}{c} (0)\vphantom{\frac{1}{2}} \\ (1) \\ (2)\vphantom{\frac{1}{2}} \\ (3) \end{array}\] All coefficients in row \((0)\) are positive, so this is the optimal solution. The maximum value in the top right of the matrix, \(65,\) is the same as the minimum value for the original problem. However, the variables \(u,\) \(v,\) and \(w\) are not the same as the variables in the original problem. Fortunately, the values of the variables that minimize the original problem correspond to the coefficients of the slack variables in row \((0).\) \[\left[\begin{array}{ccccccc|c} 1 & 0 & 27 & 13 & \color{red}0 & \color{red}\frac{65}{3} & \color{red}0 & 65 \\ 0 & 0 & -3 & -2 & 1 & -4 & 0 & 8 \\ 0 & 1 & 1 & 1 & 0 & \frac{1}{3} & 0 & 1 \\ 0 & 0 & 1 & 2 & 0 & -2 & 1 & 50 \end{array}\right]. \qquad \begin{array}{c} (0)\vphantom{\frac{1}{2}} \\ (1) \\ (2)\vphantom{\frac{1}{2}} \\ (3) \end{array}\] Thus, the values of the original problem that minimize the objective function are \[x=0, \quad y=\frac{65}{3}, \quad z=0.\ _\square\]

Simplex Algorithm for Minimization This version of the simplex algorithm is valid for a minimization problem with all constraints giving minimum values (using the \(\ge\) symbol). In matrix form, the requirements are: \[\begin{array}{ll} \text{Minimize:} & \textbf{c}^\text{T} \cdot \textbf{x} \\ \text{Subject to:} & \textbf{A}\textbf{x} \ge \textbf{b}\, \quad x_i \ge 0 \end{array}\] where \(\textbf{c}\) is a vector containing the coefficients of the objective function, \(\textbf{x}\) is a vector containing the variables of the problem, \(\textbf{A}\) is a matrix containing the constraint coefficients, and \(\textbf{b}\) is a vector containing the minimum values of those constraints. Place the coefficients of the constraints and objective function into an augmented matrix. The coefficients of the objective function should go into the bottom row. Transpose this matrix. This new matrix represents the dual maximization problem. Write the new system of constraints and objective function. This problem has different variables than the original problem. Use the simplex algorithm for maximization to obtain the maximum value. This maximum value is the same as the minimum value for the original problem. The coefficients of the slack variables in row \((0)\) correspond to the values of the variables in the original problem.

The simplex algorithm can sometimes lead to some surprising results. It is possible that a linear programming problem has infinite solutions or no solutions. These special cases are explored here.

As was stated earlier, a linear programming problem that has minimum constraints does not work with the simplex algorithm. The reason for this is that the initial basic solution is infeasible.

Given the system of constraints \[\begin{cases}\begin{align} 2x+3y &\ge 10 \\ 3x+y &\ge 8 \\ x &\ge 0 \\ y &\ge 0, \end{align}\end{cases}\] minimize the function \[f(x,y)=5x+10y.\] Show that this cannot be done using the normal simplex algorithm. This problem could be solved with a dual or by simply testing the vertices of the feasible region, but consider solving it with the simplex algorithm. Because the constraints are minimum constraints, the slack variables need to have negative coefficients. In addition, the objective function is a minimization. This can be accounted for by treating the problem as a maximization of \(-z.\) Applying the simplex algorithm, this gives the initial matrix \[\left[ \begin{array}{ccccc|c} -1 & 5 & 10 & 0 & 0 & 0 \\ 0 & 2 & 3 & -1 & 0 & 10 \\ 0 & 3 & 1 & 0 & -1 & 8 \\ \end{array}\right]. \qquad \begin{array}{c} (0) \\ (1) \\ (2) \end{array}\] This initial matrix implies an infeasible solution of \(s_1=-10,\ s_2=-8.\) The simplex algorithm will not produce a meaningful result if the initial basic solution is infeasible. \(_\square\)

It is sometimes possible to solve the problem with its dual, but this is not the case if a problem mixes minimum constraints with maximum constraints.

Given the system of constraints \[\begin{cases}\begin{align} -x+5y &\le 25 \\ 6x+5y &\le 60 \\ x+y &\ge 2 \\ x &\ge 0 \\ y &\ge 0, \end{align}\end{cases}\] minimize the function \[f(x,y)=x-10y.\] Show that this cannot be done using the normal simplex algorithm or the dual method. Putting this problem into a simplex matrix would give an initial basic solution that is infeasible: \[\left [ \begin{array}{cccccc|c} -1 & 1 & -10 & 0 & 0 & 0 & 0 \\ 0 & -1 & 5 & 1 & 0 & 0 & 25 \\ 0 & 6 & 5 & 0 & 1 & 0 & 60 \\ 0 & 1 & 1 & 0 & 0 & -1 & 2 \\ \end{array} \right ] \qquad \begin{array}{c} (0) \\ (1) \\ (2) \\ (3) \end{array}\] \[\begin{array}{ccc} s_1 = 25, & s_2 = 60, & s_3 = -2. \end{array}\] Putting the problem's dual into a simplex matrix would also yield an infeasible initial basic solution: \[\left [ \begin{array}{cccccc|c} 1 & -25 & -60 & 2 & 0 & 0 & 0\\ 0 & 1 & -6 & 1 & 1 & 0 & 1 \\ 0 & -5 & -5 & 1 & 0 & 1 & -10 \end{array} \right ] \qquad \begin{array}{c} (0) \\ (1) \\ (2) \end{array}\] \[\begin{array}{cc} s_1 = 1, & s_2 = -10.\ _\square \end{array}\]

The Big-M method can be used when an initial basic solution is infeasible. The idea behind this method is to introduce artificial variables to the problem in order to move the solution into the feasible region. Unlike slack variables, these artificial variables must have a value of zero in the final solution.

Given the system of constraints \[\begin{cases}\begin{align} -x+5y &\le 25 \\ 6x+5y &\le 60 \\ x+y &\ge 2 \\ x &\ge 0 \\ y &\ge 0, \end{align}\end{cases}\] minimize the function \[f(x,y)=x-10y.\] From the previous example, it is known that the third constraint produces an infeasible \(s_3=-2.\) To compensate for this, an artificial variable, \(a_1,\) is introduced to this constraint and the objective function. In the objective function, this variable has a coefficient of \(M.\) \(M\) represents an arbitrarily large constant amount. The new constraints and objective function are \[\begin{cases}\begin{array}{ccccccccccccccc} -z & + & x & - & 10y & & & & & & & + & Ma_1 & = & 0 \\ & - & x & + & 5y & + & s_1 & & & & & & & = & 25 \\ & & 6x & + & 5y & & & + & s_2 & & & & & = & 60 \\ & & x & + & y & & & & & - & s_3 & + & a_1 & = & 2. \end{array}\end{cases} \qquad \begin{array}{c} (0) \\ (1) \\ (2) \\ (3) \end{array}\] In matrix form, \[\left [ \begin{array}{ccccccc|c} -1 & 1 & -10 & 0 & 0 & 0 & M & 0 \\ 0 & -1 & 5 & 1 & 0 & 0 & 0 & 25 \\ 0 & 6 & 5 & 0 & 1 & 0 & 0 & 60 \\ 0 & 1 & 1 & 0 & 0 & -1 & 1 & 2 \end{array} \right ]. \qquad \begin{array}{c} (0) \\ (1) \\ (2) \\ (3) \end{array}\] The first goal with the Big-M method is to move the problem into the feasible region. Recall that the current basic solution has \(s_3=-2.\) This variable will be the leaving variable, with the artificial variable, \(a_1,\) being the entering variable: \[\left [ \begin{array}{ccccccc|c} -1 & 1-M & -10-M & 0 & 0 & M & 0 & -2M \\ 0 & -1 & 5 & 1 & 0 & 0 & 0 & 25 \\ 0 & 6 & 5 & 0 & 1 & 0 & 0 & 60 \\ 0 & 1 & 1 & 0 & 0 & -1 & 1 & 2 \\ \end{array} \right ]. \qquad \begin{array}{c} (0) \\ (1) \\ (2) \\ (3) \end{array}\] The current solution is now in the feasible region, with all basic variables positive: \[s_1 = 25, \quad s_2 = 60, \quad a_1 = 2.\] This solution is clearly not correct, because it contains a non-zero artificial variable in the solution. Furthermore, there are negative coefficients in row \((0)\). The Big-M method now proceeds just as the simplex algorithm. The new goal is to enter variables with negative coefficients in row \((0)\). Since \(y\) has the most negative coefficient in the row \((0)\), that variable will be entered first. The row that minimizes the ratio of the right hand side and the coefficient is \((3)\), so \(y\) will be entered through this row: \[\left [ \begin{array}{ccccccc|c} -1 & 11 & 0 & 0 & 0 & -10 & 10+M & 20 \\ 0 & -6 & 0 & 1 & 0 & 5 & -5 & 15 \\ 0 & 1 & 0 & 0 & 1 & 5 & -5 & 50 \\ 0 & 1 & 1 & 0 & 0 & -1 & 1 & 2 \\ \end{array} \right ] \qquad \begin{array}{c} (0) \\ (1) \\ (2) \\ (3) \end{array}\] \[y=2, \quad s_1=15, \quad s_2=50.\] This solution no longer contains the artificial variable, but it is not yet optimal due to the negative coefficient in row \((0).\) \(s_3\) must be the next variable to enter. The minimum positive ratio for this variable is in row \((1)\): \[\left [ \begin{array}{ccccccc|c} -1 & -1 & 0 & 2 & 0 & 0 & M & 50 \\ 0 & -6 & 0 & 1 & 0 & 5 & -5 & 15 \\ 0 & 7 & 0 & -1 & 1 & 0 & 0 & 35 \\ 0 & -1 & 5 & 1 & 0 & 0 & 0 & 25 \\ \end{array} \right ] \qquad \begin{array}{c} (0) \\ (1) \\ (2) \\ (3) \end{array}\] \[y = 5, \quad s_2 = 35, \quad s_3 = 3.\] Now \(x\) must be the entering variable, and the only row with a positive ratio is \((2)\): \[\left [ \begin{array}{ccccccc|c} -1 & 0 & 0 & \frac{15}{7} & \frac{1}{7} & 0 & M & 55 \\ 0 & 0 & 0 & \frac{1}{7} & \frac{6}{7} & 5 & -5 & 45 \\ 0 & 7 & 0 & -1 & 1 & 0 & 0 & 35 \\ 0 & 0 & 5 & \frac{6}{7} & \frac{1}{7} & 0 & 0 & 30 \\ \end{array} \right ]. \qquad \begin{array}{c} (0)\vphantom{\frac{1}{7}} \\ (1)\vphantom{\frac{1}{7}} \\ (2) \\ (3)\vphantom{\frac{1}{7}} \end{array}\] Now it is clear that this gives the optimal solution: \[x=5, y=6, s_3=9\implies f(5,6)=-55.\ _\square\]

Big M Simplex Method This method is viable for any linear programming problem that does not match the forms of the previous section . It is also required for problems which contain equality constraints. Assign slack variables and the \(z\) variable as with the basic simplex algorithm, and create a simplex matrix. For each slack variable that has a negative value in the initial basic solution, add a distinct artificial variable to that constraint. Also add a distinct artificial variable to each equality constraint. Artificial variables begin with a coefficient of \(1\) in each constraint row. In the objective function row, every artificial variable begins with the same coefficient, \(M.\) This represents an arbitrarily large positive constant amount. If the problem is a minimization, then the coefficients of the objective function row are negated, and the goal is to maximize \(-z.\) Move the solution into the feasible region by performing pivots with a negative slack variable as the leaving variable and an artificial variable as the entering variable. Once the basic solution is in the feasible region, proceed with the simplex algorithm as before. While performing the simplex algorithm, ensure that the elements in the right side of the matrix are positive. If an element in the right side is not positive, multiply that row by \(-1\) to make it positive. If an element in the right side of the matrix is \(0,\) then ensure that the coefficient of the basic variable in that row is positive. Choose the entering variable by observing the coefficient in row \((0)\) that is the most negative. Choose pivot rows by selecting the row that minimizes the ratio \(\frac{\text{Element on right side of augmented matrix}}{\text{Coefficient of entering variable}}.\) The ratio must be non-negative, and the coefficient of the entering variable in the pivot row must be positive. An optimal solution cannot contain any artificial variables. If row \((0)\) of the matrix contains no negative coefficients, and the solution contains an artificial variable, then the problem has no solution.

Vanessa is scheduling her employees for the upcoming week. When on the assembly line, Darren assembles 5 units per hour, and when on the packaging line, he packages 10 units per hour. Lori only works on the assembly line, and she assembles 4 units per hour. Darren's pay is $12 per hour and Lori's pay is $9 per hour Vanessa needs to have at least 200 units assembled and packaged by the end of the week. She can assign each worker a maximum of 40 hours. How should Vanessa schedule her employees to minimize payroll? This problem can be solved with simpler methods, but is solved here with the Big M method as a demonstration of how to deal with different types of constraints with the Big M method. Let \(m_d\) and \(m_l\) be the number of hours that Darren and Lori work on the assembly line, respectively. Let \(p_d\) be the number of hours that Darren and Lori work on the packaging line, respectively. Each worker can work a maximum of 40 hours. This gives the constraints \[\begin{align} m_d+p_d &\le 40 \\ m_l &\le 40. \end{align}\] Vanessa would not want to waste hours on packaging if there are no assembled units to package. Therefore, the number of units assembled should equal the number of units packaged. This can be expressed with the equation \[5m_d+4m_l=10p_d.\] The number of units assembled and packaged should be at least 200. This can be expressed with the constraint \[\begin{align} 10p_d &\ge 200 \\ p_d &\ge 20. \end{align}\] This gives the following system of constraints: \[\begin{cases} \begin{array}{ccccccc} m_d & & & + & p_d & \le & 40 \\ & & m_l & & & \le & 40 \\ & & & & p_d & \ge & 20 \\ 5m_d & + & 4m_l & - & 10p_d & = & 0 \\ m_d, & & m_l, & & p_d & \ge & 0. \end{array} \end{cases}\] The objective function is \[f(m_d,m_l,p_d)=12m_d+9m_l+12p_d.\] Converting the system of constraints and objective function to a simplex matrix, \[\left[\begin{array}{ccccccc|c} -1 & 12 & 9 & 12 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 1 & 1 & 0 & 0 & 40 \\ 0 & 0 & 1 & 0 & 0 & 1 & 0 & 40 \\ 0 & 0 & 0 & 1 & 0 & 0 & -1 & 20 \\ 0 & 5 & 4 & -10 & 0 & 0 & 0 & 0 \\ \end{array}\right]. \qquad \begin{array}{c} (0) \\ (1) \\ (2) \\ (3) \\ (4) \end{array}\] The basic solution is currently infeasible: \[m_d=0, \quad m_l=0, \quad p_d=0, \quad s_1 = 40, \quad s_2=40, \quad s_3=-20.\] Since \(s_3\) has an infeasible value, the row that contains it requires an artificial variable. The equality constraint row also requires an artificial variable. These artificial variables are given the coefficient \(M\) in row \((0):\) \[\left[\begin{array}{ccccccccc|c} -1 & 12 & 9 & 12 & 0 & 0 & 0 & M & M & 0 \\ 0 & 1 & 0 & 1 & 1 & 0 & 0 & 0 & 0 & 40 \\ 0 & 0 & 1 & 0 & 0 & 1 & 0 & 0 & 0 & 40 \\ 0 & 0 & 0 & 1 & 0 & 0 & -1 & 1 & 0 & 20 \\ 0 & 5 & 4 & -10 & 0 & 0 & 0 & 0 & 1 & 0 \end{array}\right]. \qquad \begin{array}{c} (0) \\ (1) \\ (2) \\ (3) \\ (4) \end{array}\] To move the solution into the feasible region, \(s_3\) will be the leaving variable and \(a_1\) will be the entering variable. The pivot will be performed with row \((3):\) \[\left[\begin{array}{ccccccccc|c} -1 & 12 & 9 & 12-M & 0 & 0 & M & 0 & M & -20M \\ 0 & 1 & 0 & 1 & 1 & 0 & 0 & 0 & 0 & 40 \\ 0 & 0 & 1 & 0 & 0 & 1 & 0 & 0 & 0 & 40 \\ 0 & 0 & 0 & 1 & 0 & 0 & -1 & 1 & 0 & 20 \\ 0 & 5 & 4 & -10 & 0 & 0 & 0 & 0 & 1 & 0 \end{array}\right]. \qquad \begin{array}{c} (0) \\ (1) \\ (2) \\ (3) \\ (4) \end{array}\] The other artificial variable must be moved into the basic solution as well: \[\left[\begin{array}{ccccccccc|c} -1 & 12-5M & 9-4M & 12+9M & 0 & 0 & M & 0 & 0 & -20M \\ 0 & 1 & 0 & 1 & 1 & 0 & 0 & 0 & 0 & 40 \\ 0 & 0 & 1 & 0 & 0 & 1 & 0 & 0 & 0 & 40 \\ 0 & 0 & 0 & 1 & 0 & 0 & -1 & 1 & 0 & 20 \\ 0 & 5 & 4 & -10 & 0 & 0 & 0 & 0 & 1 & 0 \end{array}\right]. \qquad \begin{array}{c} (0) \\ (1) \\ (2) \\ (3) \\ (4) \end{array}\] Now the algorithm proceeds as the usual simplex algorithm. The goal is to eliminate the negative coefficients in row \((0).\) Since \(M\) is an arbitrarily large positive constant value, \(12-5M\) is the most negative coefficient in row \((0).\) Therefore, \(m_d\) will be the entering variable. The selection of the pivot row is slightly more challenging than the usual simplex algorithm. Observe that every value in the right-hand side of the constraint rows is positive except for the value in row \((4).\) In this row, the right-hand side is \(0,\) and the basic variable contained in this row, \(a_2,\) has a positive coefficient. It is important to maintain these two things: values in the right-hand sides of the constraint rows are positive, or if the value in the right hand side is \(0,\) then the coefficient of the basic variable in that row is positive. Maintaining this will ensure the correct selection of the pivot row. The pivot row is selected by choosing the row that minimizes the ratio of \(\frac{\text{Element on right side of augmented matrix}}{\text{Coefficient of entering variable}},\) provided that the coefficient of the entering variable is positive . Thus, the minimum ratio for the entering variable is \(\frac{0}{5}\) from row \((4).\) This will be the pivot row: \[\left[\begin{array}{ccccccccc|c} -1 & 0 & -\frac{3}{5} & 36-M & 0 & 0 & M & 0 & M-\frac{12}{5} & -20M \\ 0 & 0 & -4 & 15 & 5 & 0 & 0 & 0 & -1 & 200 \\ 0 & 0 & 1 & 0 & 0 & 1 & 0 & 0 & 0 & 40 \\ 0 & 0 & 0 & 1 & 0 & 0 & -1 & 1 & 0 & 20 \\ 0 & 5 & 4 & -10 & 0 & 0 & 0 & 0 & 1 & 0 \end{array}\right]. \qquad \begin{array}{c} (0) \\ (1) \\ (2) \\ (3) \\ (4) \end{array}\] Now \(36-M\) is the most negative coefficient in row \((0).\) Thus, \(p_d\) will be the entering variable. Row \((4)\) will not be chosen as the pivot row again, as it has a negative coefficient for this variable. The row that minimizes the ratio is \(\frac{200}{15}\) from row \((1):\) \[\left[\begin{array}{ccccccccc|c} -1 & 0 & 9-\frac{4}{15}M & 0 & \frac{1}{3}M-12 & 0 & M & 0 & \frac{14}{15}M & -\frac{20}{3}M-480 \\ 0 & 0 & -4 & 15 & 5 & 0 & 0 & 0 & -1 & 200 \\ 0 & 0 & 1 & 0 & 0 & 1 & 0 & 0 & 0 & 40 \\ 0 & 0 & 4 & 0 & -5 & 0 & -15 & 15 & 1 & 100 \\ 0 & 15 & 4 & 0 & 10 & 0 & 0 & 0 & 1 & 400 \end{array}\right]. \qquad \begin{array}{c} (0) \\ (1) \\ (2) \\ (3) \\ (4) \end{array}\] Now \(9-\frac{4}{15}M\) is the most negative coefficient in row \((0).\) \(m_l\) will be the entering variable and the minimizing ratio is \(\frac{100}{4}\) in row \((3):\) \[\left[\begin{array}{ccccccccc|c} -1 & 0 & 0 & 0 & -\frac{3}{4} & 0 & \frac{135}{4} & M-\frac{135}{4} & M-\frac{9}{4} & -705 \\ 0 & 0 & 0 & 1 & 0 & 0 & -1 & 1 & 0 & 20 \\ 0 & 0 & 0 & 0 & 5 & 4 & 15 & -15 & -1 & 60 \\ 0 & 0 & 4 & 0 & -5 & 0 & -15 & 15 & 1 & 100 \\ 0 & 1 & 0 & 0 & 1 & 0 & 1 & -1 & 0 & 20 \end{array}\right]. \qquad \begin{array}{c} (0) \\ (1) \\ (2) \\ (3) \\ (4) \end{array}\] Now \(-\frac{3}{4}\) is the most negative coefficient in row \((0).\) \(s_1\) will be the entering variable and the minimizing ratio is \(\frac{60}{5}\) in row \((2):\) \[\left[\begin{array}{ccccccccc|c} -1 & 0 & 0 & 0 & 0 & \frac{3}{5} & 36 & M-36 & M-\frac{12}{5} & -696 \\ 0 & 0 & 0 & 1 & 0 & 0 & -1 & 1 & 0 & 20 \\ 0 & 0 & 0 & 0 & 5 & 4 & 15 & -15 & -1 & 60 \\ 0 & 0 & 1 & 0 & 0 & 1 & 0 & 0 & 0 & 40 \\ 0 & 5 & 0 & 0 & 0 & -4 & -10 & 10 & 1 & 40 \end{array}\right]. \qquad \begin{array}{c} (0) \\ (1) \\ (2) \\ (3) \\ (4) \end{array}\] With all coefficients in row \((0)\) positive and no artificial variables in the solution, the solution is optimal. The solution is \[m_d=8, \quad m_l=40, \quad p_d=20, \quad z=696.\] Vanessa should put Darren on the assembly line for 8 hours and on the packaging line for 20 hours. She should put Lori on the assembly line for 40 hours. This will put payroll at $696 for the week. \(_\square\)

Problem Loading...

Note Loading...

Set Loading...

5.11 Linear Programming

Learning objectives.

After completing this section, you should be able to:

• Compose an objective function to be minimized or maximized.
• Compose inequalities representing a system application.
• Apply linear programming to solve application problems.

Imagine you hear about some natural disaster striking a far-away country; it could be an earthquake, a fire, a tsunami, a tornado, a hurricane, or any other type of natural disaster. The survivors of this disaster need help—they especially need food, water, and medical supplies. You work for a company that has these supplies, and your company has decided to help by flying the needed supplies into the disaster area. They want to maximize the number of people they can help. However, there are practical constraints that need to be taken into consideration; the size of the airplanes, how much weight each airplane can carry, and so on. How do you solve this dilemma? This is where linear programming comes into play. Linear programming is a mathematical technique to solve problems involving finding maximums or minimums where a linear function is limited by various constraints.

As a field, linear programming began in the late 1930s and early 1940s. It was used by many countries during World War II; countries used linear programming to solve problems such as maximizing troop effectiveness, minimizing their own casualties, and maximizing the damage they could inflict upon the enemy. Later, businesses began to realize they could use the concept of linear programming to maximize output, minimize expenses, and so on. In short, linear programming is a method to solve problems that involve finding a maximum or minimum where a linear function is constrained by various factors.

A Mathematician Invents a “Tsunami Cannon”

On December 26, 2004, a massive earthquake occurred in the Indian Ocean. This earthquake, which scientists estimate had a magnitude of 9.0 or 9.1 on the Richter Scale, set off a wave of tsunamis across the Indian Ocean. The waves of the tsunami averaged over 30 feet (10 meters) high, and caused massive damage and loss of life across the coastal regions bordering the Indian Ocean.

Usama Kadri works as an applied mathematician at Cardiff University in Wales. His areas of research include fluid dynamics and non-linear phenomena. Lately, he has been focusing his research on the early detection and easing of the effects of tsunamis. One of his theories involves deploying a series of devices along coastlines which would fire acoustic-gravity waves (AGWs) into an oncoming tsunami, which in theory would lessen the force of the tsunami. Of course, this is all in theory, but Kadri believes it will work. There are issues with creating such a device: they would take a tremendous amount of electricity to generate an AGW, for instance, but if it would save lives, it may well be worth it.

Compose an Objective Function to Be Minimized or Maximized

An objective function is a linear function in two or more variables that describes the quantity that needs to be maximized or minimized.

Example 5.96

Composing an objective function for selling two products.

Miriam starts her own business, where she knits and sells scarves and sweaters out of high-quality wool. She can make a profit of $8 per scarf and $10 per sweater. Write an objective function that describes her profit.

Let x x represent the number of scarves sold, and let y y represent the number of sweaters sold. Let P P represent profit. Since each scarf has a profit of $8 and each sweater has a profit of $10, the objective function is P = 8 x + 10 y P = 8 x + 10 y .

Your Turn 5.96

Example 5.97, composing an objective function for production.

William’s factory produces two products, widgets and wadgets. It takes 24 minutes for his factory to make 1 widget, and 32 minutes for his factory to make 1 wadget. Write an objective function that describes the time it takes to make the products.

Let x x equal the number of widgets made; let y y equal the number of wadgets made; let T T represent total time. The objective function is T = 24 x + 32 y T = 24 x + 32 y .

Your Turn 5.97

Composing inequalities representing a system application.

For our two examples of profit and production, in an ideal world the profit a person makes and/or the number of products a company produces would have no restrictions. After all, who wouldn’t want to have an unrestricted profit? However in reality this is not the case; there are usually several variables that can restrict how much profit a person can make or how many products a company can produce. These restrictions are called constraints .

Many different variables can be constraints. When making or selling a product, the time available, the cost of manufacturing and the amount of raw materials are all constraints. In the opening scenario with the tsunami, the maximum weight on an airplane and the volume of cargo it can carry would be constraints. Constraints are expressed as linear inequalities; the list of constraints defined by the problem forms a system of linear inequalities that, along with the objective function, represent a system application.

Example 5.98

Representing the constraints for selling two products.

Two friends start their own business, where they knit and sell scarves and sweaters out of high-quality wool. They can make a profit of $8 per scarf and $10 per sweater. To make a scarf, 3 bags of knitting wool are needed; to make a sweater, 4 bags of knitting wool are needed. The friends can only make 8 items per day, and can use not more than 27 bags of knitting wool per day. Write the inequalities that represent the constraints. Then summarize what has been described thus far by writing the objective function for profit and the two constraints.

Let x x represent the number of scarves sold, and let y y represent the number of sweaters sold. There are two constraints: the number of items the business can make in a day (a maximum of 8) and the number of bags of knitting wool they can use per day (a maximum of 27). The first constraint (total number of items in a day) is written as:

Since each scarf takes 3 bags of knitting wool and each sweater takes 4 bags of knitting wool, the second constraint, total bags of knitting wool per day, is written as:

In summary, here are the equations that represent the new business:

P = 8 x + 10 y P = 8 x + 10 y ; This is the profit equation: The business makes $8 per scarf and $10 per sweater.

Your Turn 5.98

Example 5.99, representing constraints for production.

A factory produces two products, widgets and wadgets. It takes 24 minutes for the factory to make 1 widget, and 32 minutes for the factory to make 1 wadget. Research indicates that long-term demand for products from the factory will result in average sales of 12 widgets per day and 10 wadgets per day. Because of limitations on storage at the factory, no more than 20 widgets or 17 wadgets can be made each day. Write the inequalities that represent the constraints. Then summarize what has been described thus far by writing the objective function for time and the two constraints.

Let x x equal the number of widgets made; let y y equal the number of wadgets made. Based on the long-term demand, we know the factory must produce a minimum of 12 widgets and 10 wadgets per day. We also know because of storage limitations, the factory cannot produce more than 20 widgets per day or 17 wadgets per day. Writing those as inequalities, we have:

x ≥ 12 x ≥ 12

y ≥ 10 y ≥ 10

x ≤ 20 x ≤ 20

y ≤ 17 y ≤ 17

The number of widgets made per day must be between 12 and 20, and the number of wadgets made per day must be between 10 and 17. Therefore, we have:

12 ≤ x ≤ 20 12 ≤ x ≤ 20

10 ≤ y ≤ 17 10 ≤ y ≤ 17

The system is:

T = 24 x + 32 y T = 24 x + 32 y

T T is the variable for time; it takes 24 minutes to make a widget and 32 minutes to make a wadget.

Your Turn 5.99

Applying linear programming to solve application problems.

There are four steps that need to be completed when solving a problem using linear programming. They are as follows:

Step 1: Compose an objective function to be minimized or maximized.

Step 2: Compose inequalities representing the constraints of the system.

Step 3: Graph the system of inequalities representing the constraints.

Step 4: Find the value of the objective function at each corner point of the graphed region.

The first two steps you have already learned. Let’s continue to use the same examples to illustrate Steps 3 and 4.

Example 5.100

Solving a linear programming problem for two products.

Three friends start their own business, where they knit and sell scarves and sweaters out of high-quality wool. They can make a profit of $8 per scarf and $10 per sweater. To make a scarf, 3 bags of knitting wool are needed; to make a sweater, 4 bags of knitting wool are needed. The friends can only make 8 items per day, and can use not more than 27 bags of knitting wool per day. Determine the number of scarves and sweaters they should make each day to maximize their profit.

Step 1: Compose an objective function to be minimized or maximized. From Example 5.98 , the objective function is P = 8 x + 10 y P = 8 x + 10 y .

Step 2: Compose inequalities representing the constraints of the system. From Example 5.98 , the constraints are x + y ≤ 8 x + y ≤ 8 and 3 x + 4 y ≤ 27 3 x + 4 y ≤ 27 .

Step 3: Graph the system of inequalities representing the constraints. Using methods discussed in Graphing Linear Equations and Inequalities , the graphs of the constraints are shown below. Because the number of scarves ( x x ) and the number of sweaters ( y y ) both must be non-negative numbers (i.e., x ≥ 0 x ≥ 0 and y ≥ 0 y ≥ 0 ), we need to graph the system of inequalities in Quadrant I only. Figure 5.99 shows each constraint graphed on its own axes, while Figure 5.100 shows the graph of the system of inequalities (the two constraints graphed together). In Figure 5.100 , the large shaded region represents the area where the two constraints intersect. If you are unsure how to graph these regions, refer back to Graphing Linear Equations and Inequalities .

Step 4: Find the value of the objective function at each corner point of the graphed region. The “graphed region” is the area where both of the regions intersect; in Figure 5.101 , it is the large shaded area. The “corner points” refer to each vertex of the shaded area. Why the corner points? Because the maximum and minimum of every objective function will occur at one (or more) of the corner points. Figure 5.101 shows the location and coordinates of each corner point.

Three of the four points are readily found, as we used them to graph the regions; the fourth point, the intersection point of the two constraint lines, will have to be found using methods discussed in Systems of Linear Equations in Two Variables , either using substitution or elimination. As a reminder, set up the two equations of the constraint lines:

For this example, substitution will be used.

Substituting 8 - x 8 - x into the first equation for y y , we have

Now, substituting the 5 in for x x in either equation to solve for y y . Choosing the second equation, we have:

Therefore, x = 5 x = 5 , and y = 3 y = 3 .

To find the value of the objective function, P = 8 x + 10 y P = 8 x + 10 y , put the coordinates for each corner point into the equation and solve. The largest solution found when doing this will be the maximum value, and thus will be the answer to the question originally posed: determining the number of scarves and sweaters the new business should make each day to maximize their profit.

The maximum value for the profit P P occurs when x = 5 x = 5 and y = 3 y = 3 . This means that to maximize their profit, the new business should make 5 scarves and 3 sweaters every day.

Your Turn 5.100

People in mathematics, leonid kantorovich.

Leonid Vitalyevich Kantorovich was born January 19, 1912, in St. Petersburg, Russia. Two major events affected young Leonid’s life: when he was five, the Russian Revolution began, making life in St. Petersburg very difficult; so much so that Leonid’s family fled to Belarus for a year. When Leonid was 10, his father died, leaving his mother to raise five children on her own.

Despite the hardships, Leonid showed incredible mathematical ability at a young age. When he was only 14, he enrolled in Leningrad State University to study mathematics. Four years later, at age 18, he graduated with what would be equivalent to a Ph.D. in mathematics.

Although his primary interests were in pure mathematics, in 1938 he began working on problems in economics. Supposedly, he was approached by a local plywood manufacturer with the following question: how to come up with a work schedule for eight lathes to maximize output, given the five different kinds of plywood they had at the factory. By July 1939, Leonid had come up with a solution, not only to the lathe scheduling problem but to other areas as well, such as an optimal crop rotation schedule for farmers, minimizing waste material in manufacturing, and finding optimal routes for transporting goods. The technique he discovered to solve these problems eventually became known as linear programming. He continued to use this technique for solving many other problems involving optimization, which resulted in the book The Best Use of Economic Resources , which was published in 1959. His continued work in linear programming would ultimately result in him winning the Nobel Prize of Economics in 1975.

Check Your Understanding

• P = 20 t − 10 c
• P = 20 c + 10 t
• P = 20 t + 10 c
• P = 20 c − 10 t
• P = 150 w + 180 b
• P = 150 b + 180 w
• P = 180 w + 150 b
• P = 150 w − 180 b
• P = 2.50 f + 6.75 c
• P = 2.50 f + 6.75 t
• P = 2.50 t + 6.75 f
• None of these
• 20 t + 10 c ≤ 70
• 15 t + 4 c ≥ 70
• 15 t + 4 c ≤ 70
• 20 t + 10 c ≤ 12
• 20 t + 10 c ≥ 12
• w + b ≤ 945
• 10 w + 15 b ≥ 945
• 10 w + 15 b ≤ 945
• 150 w + 180 w ≤ 945
• 150 w + 180 b ≤ 1,635
• 25 w + 30 b ≤ 1,635
• w + b ≤ 1,635
• 30 w + 25 b ≤ 1,635
• ( 0 , 0 ) , ( 0 , 12 ) , ( 10 , 2 ) , ( 12 , 0 )
• ( 0 , 0 ) , ( 0 , 12 ) , ( 2 , 10 ) , ( 4 2 3 , 0 )
• ( 0 , 0 ) , ( 17.5 , 0 ) , ( 2 , 10 ) , ( 12 , 0 )

Section 5.11 Exercises

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/contemporary-mathematics/pages/1-introduction

• Authors: Donna Kirk
• Publisher/website: OpenStax
• Book title: Contemporary Mathematics
• Publication date: Mar 22, 2023
• Location: Houston, Texas
• Book URL: https://openstax.org/books/contemporary-mathematics/pages/1-introduction
• Section URL: https://openstax.org/books/contemporary-mathematics/pages/5-11-linear-programming

© Dec 21, 2023 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Linear Programming

Linear programming is a process that is used to determine the best outcome of a linear function. It is the best method to perform linear optimization by making a few simple assumptions. The linear function is known as the objective function. Real-world relationships can be extremely complicated. However, linear programming can be used to depict such relationships, thus, making it easier to analyze them.

Linear programming is used in many industries such as energy, telecommunication, transportation, and manufacturing. This article sheds light on the various aspects of linear programming such as the definition, formula, methods to solve problems using this technique, and associated linear programming examples.

What is Linear Programming?

Linear programming, also abbreviated as LP, is a simple method that is used to depict complicated real-world relationships by using a linear function . The elements in the mathematical model so obtained have a linear relationship with each other. Linear programming is used to perform linear optimization so as to achieve the best outcome.

Linear Programming Definition

Linear programming can be defined as a technique that is used for optimizing a linear function in order to reach the best outcome. This linear function or objective function consists of linear equality and inequality constraints. We obtain the best outcome by minimizing or maximizing the objective function .

Linear Programming Examples

Suppose a postman has to deliver 6 letters in a day from the post office (located at A) to different houses (U, V, W, Y, Z). The distance between the houses is indicated on the lines as given in the image. If the postman wants to find the shortest route that will enable him to deliver the letters as well as save on fuel then it becomes a linear programming problem. Thus, LP will be used to get the optimal solution which will be the shortest route in this example.

Linear Programming Formula

A linear programming problem will consist of decision variables , an objective function, constraints, and non-negative restrictions. The decision variables, x, and y, decide the output of the LP problem and represent the final solution. The objective function, Z, is the linear function that needs to be optimized (maximized or minimized) to get the solution. The constraints are the restrictions that are imposed on the decision variables to limit their value. The decision variables must always have a non-negative value which is given by the non-negative restrictions. The general formula of a linear programming problem is given below:

• Objective Function: Z = ax + by
• Constraints: cx + dy ≤ e, fx + gy ≤ h. The inequalities can also be "≥"
• Non-negative restrictions: x ≥ 0, y ≥ 0

How to Solve Linear Programming Problems?

The most important part of solving linear programming problem is to first formulate the problem using the given data. The steps to solve linear programming problems are given below:

• Step 1: Identify the decision variables.
• Step 2: Formulate the objective function. Check whether the function needs to be minimized or maximized.
• Step 3: Write down the constraints.
• Step 4: Ensure that the decision variables are greater than or equal to 0. (Non-negative restraint)
• Step 5: Solve the linear programming problem using either the simplex or graphical method.

Let us study about these methods in detail in the following sections.

Linear Programming Methods

There are two main methods available for solving linear programming problem. These are the simplex method and the graphical method. Given below are the steps to solve a linear programming problem using both methods.

Linear Programming by Simplex Method

The simplex method in lpp can be applied to problems with two or more decision variables. Suppose the objective function Z = 40\(x_{1}\) + 30\(x_{2}\) needs to be maximized and the constraints are given as follows:

\(x_{1}\) + \(x_{2}\) ≤ 12

2\(x_{1}\) + \(x_{2}\) ≤ 16

\(x_{1}\) ≥ 0, \(x_{2}\) ≥ 0

Step 1: Add another variable, known as the slack variable, to convert the inequalities into equations. Also, rewrite the objective function as an equation .

- 40\(x_{1}\) - 30\(x_{2}\) + Z = 0

\(x_{1}\) + \(x_{2}\) + \(y_{1}\) =12

2\(x_{1}\) + \(x_{2}\) + \(y_{2}\) =16

\(y_{1}\) and \(y_{2}\) are the slack variables.

Step 2: Construct the initial simplex matrix as follows:

\(\begin{bmatrix} x_{1} & x_{2} &y_{1} & y_{2} & Z & \\ 1&1 &1 &0 &0 &12 \\ 2& 1 & 0& 1 & 0 & 16 \\ -40&-30&0&0&1&0 \end{bmatrix}\)

Step 3: Identify the column with the highest negative entry. This is called the pivot column. As -40 is the highest negative entry, thus, column 1 will be the pivot column.

Step 4: Divide the entries in the rightmost column by the entries in the pivot column. We exclude the entries in the bottom-most row.

12 / 1 = 12

The row containing the smallest quotient is identified to get the pivot row. As 8 is the smaller quotient as compared to 12 thus, row 2 becomes the pivot row. The intersection of the pivot row and the pivot column gives the pivot element.

Thus, pivot element = 2.

Step 5: With the help of the pivot element perform pivoting, using matrix properties , to make all other entries in the pivot column 0.

Using the elementary operations divide row 2 by 2 (\(R_{2}\) / 2)

\(\begin{bmatrix} x_{1} & x_{2} &y_{1} & y_{2} & Z & \\ 1&1 &1 &0 &0 &12 \\ 1& 1/2 & 0& 1/2 & 0 & 8 \\ -40&-30&0&0&1&0 \end{bmatrix}\)

Now apply \(R_{1}\) = \(R_{1}\) - \(R_{2}\)

\(\begin{bmatrix} x_{1} & x_{2} &y_{1} & y_{2} & Z & \\ 0&1/2 &1 &-1/2 &0 &4 \\ 1& 1/2 & 0& 1/2 & 0 & 8 \\ -40&-30&0&0&1&0 \end{bmatrix}\)

Finally \(R_{3}\) = \(R_{3}\) + 40\(R_{2}\) to get the required matrix.

\(\begin{bmatrix} x_{1} & x_{2} &y_{1} & y_{2} & Z & \\ 0&1/2 &1 &-1/2 &0 &4 \\ 1& 1/2 & 0& 1/2 & 0 & 8 \\ 0&-10&0&20&1&320 \end{bmatrix}\)

Step 6: Check if the bottom-most row has negative entries. If no, then the optimal solution has been determined. If yes, then go back to step 3 and repeat the process. -10 is a negative entry in the matrix thus, the process needs to be repeated. We get the following matrix.

\(\begin{bmatrix} x_{1} & x_{2} &y_{1} & y_{2} & Z & \\ 0&1 &2 &-1 &0 &8 \\ 1& 0 & -1& 1 & 0 & 4 \\ 0&0&20&10&1&400 \end{bmatrix}\)

Writing the bottom row in the form of an equation we get Z = 400 - 20\(y_{1}\) - 10\(y_{2}\). Thus, 400 is the highest value that Z can achieve when both \(y_{1}\) and \(y_{2}\) are 0.

Also, when \(x_{1}\) = 4 and \(x_{2}\) = 8 then value of Z = 400

Thus, \(x_{1}\) = 4 and \(x_{2}\) = 8 are the optimal points and the solution to our linear programming problem.

Linear Programming by Graphical Method

If there are two decision variables in a linear programming problem then the graphical method can be used to solve such a problem easily.

Suppose we have to maximize Z = 2x + 5y.

The constraints are x + 4y ≤ 24, 3x + y ≤ 21 and x + y ≤ 9

where, x ≥ 0 and y ≥ 0.

To solve this problem using the graphical method the steps are as follows.

Step 1: Write all inequality constraints in the form of equations.

x + 4y = 24

3x + y = 21

Step 2: Plot these lines on a graph by identifying test points.

x + 4y = 24 is a line passing through (0, 6) and (24, 0). [By substituting x = 0 the point (0, 6) is obtained. Similarly, when y = 0 the point (24, 0) is determined.]

3x + y = 21 passes through (0, 21) and (7, 0).

x + y = 9 passes through (9, 0) and (0, 9).

Step 3: Identify the feasible region. The feasible region can be defined as the area that is bounded by a set of coordinates that can satisfy some particular system of inequalities.

Any point that lies on or below the line x + 4y = 24 will satisfy the constraint x + 4y ≤ 24.

Similarly, a point that lies on or below 3x + y = 21 satisfies 3x + y ≤ 21.

Also, a point lying on or below the line x + y = 9 satisfies x + y ≤ 9.

The feasible region is represented by OABCD as it satisfies all the above-mentioned three restrictions.

Step 4: Determine the coordinates of the corner points. The corner points are the vertices of the feasible region.

B = (6, 3). B is the intersection of the two lines 3x + y = 21 and x + y = 9. Thus, by substituting y = 9 - x in 3x + y = 21 we can determine the point of intersection.

C = (4, 5) formed by the intersection of x + 4y = 24 and x + y = 9

Step 5: Substitute each corner point in the objective function. The point that gives the greatest (maximizing) or smallest (minimizing) value of the objective function will be the optimal point.

33 is the maximum value of Z and it occurs at C. Thus, the solution is x = 4 and y = 5.

Applications of Linear Programming

Linear programming is used in several real-world applications. It is used as the basis for creating mathematical models to denote real-world relationships. Some applications of LP are listed below:

• Manufacturing companies make widespread use of linear programming to plan and schedule production.
• Delivery services use linear programming to decide the shortest route in order to minimize time and fuel consumption.
• Financial institutions use linear programming to determine the portfolio of financial products that can be offered to clients.

Related Articles:

• Introduction to Graphing
• Linear Equations in Two Variables
• Solutions of a Linear Equation
• Mathematical Induction

Important Notes on Linear Programming

• Linear programming is a technique that is used to determine the optimal solution of a linear objective function.
• The simplex method in lpp and the graphical method can be used to solve a linear programming problem.
• In a linear programming problem, the variables will always be greater than or equal to 0.

As the minimum value of Z is 127, thus, B (3, 28) gives the optimal solution. Answer: The minimum value of Z is 127 and the optimal solution is (3, 28)

• Example 3: Using the simplex method in lpp solve the linear programming problem Minimize Z = \(x_{1}\) + 2\(x_{2}\) + 3\(x_{3}\) \(x_{1}\) + \(x_{2}\) + \(x_{3}\) ≤ 12 2\(x_{1}\) + \(x_{2}\) + 3\(x_{3}\) ≤ 18 \(x_{1}\), \(x_{2}\), \(x_{3}\) ≥ 0 Solution: Convert all inequalities to equations by introducing slack variables. -\(x_{1}\) - 2\(x_{2}\) - 3\(x_{3}\) + Z = 0 \(x_{1}\) + \(x_{2}\) + \(x_{3}\) + \(y_{1}\) = 12 2\(x_{1}\) + \(x_{2}\) + 3\(x_{3}\) + \(y_{2}\) = 18 Expressing this as a matrix we get, \(\begin{bmatrix} x_{1} & x_{2} & x_{3} & y_{1} & y_{2} & Z & \\ 1 & 1 & 1 & 1 & 0 & 0 & 12\\ 2 & 1 & 3 & 0 & 1 & 0 & 18\\ -1 & -2 & -3 & 0 & 0 & 1 & 0 \end{bmatrix}\) As -3 is the greatest negative value thus, column 3 is the pivot column. 12 / 1 = 12 18 / 3 = 6 As 6 is the smaller quotient thus, row 2 is the pivot row and 3 is the pivot element. By applying matrix operations we get, \(\begin{bmatrix} x_{1} & x_{2} & x_{3} & y_{1} & y_{2} & Z & \\ 0.33 & 0.667 & 0 & 1 & -0.33 & 0 & 6\\ 0.667 & 0.33 & 1 & 0 & 0.33 & 0 & 6\\ 1 & -1 & 0 & 0 & 1 & 1 & 18 \end{bmatrix}\) Now -1 needs to be eliminated. Thus, by repreating the steps the matrix so obtained is as follows \(\begin{bmatrix} x_{1} & x_{2} & x_{3} & y_{1} & y_{2} & Z & \\ 0.5 & 1 & 0 & 1.5 & 0.5 & 0 & 9\\ 0.5 & 0 & 1 & -0.5 & 0.5 & 0 & 3\\ 1.5 & 0 & 0 & 1.5 & 0.5 & 1 & 27 \end{bmatrix}\) We get the maximum value of Z = 27 at \(x_{1}\) = 0, \(x_{2}\) = 9 \(x_{3}\) = 3 Answer: Maximum value of Z = 27 and optimal solution (0, 9, 3)

go to slide go to slide go to slide

Book a Free Trial Class

Practice Questions on Linear Programming

go to slide go to slide

FAQs on Linear Programming

What is meant by linear programming.

Linear programming is a technique that is used to identify the optimal solution of a function wherein the elements have a linear relationship.

What is Linear Programming Formula?

The general formula for a linear programming problem is given as follows:

What is the Objective Function in Linear Programming Problems?

The objective function is the linear function that needs to be maximized or minimized and is subject to certain constraints. It is of the form Z = ax + by.

How to Formulate a Linear Programming Model?

The steps to formulate a linear programming model are given as follows:

• Identify the decision variables.
• Formulate the objective function.
• Identify the constraints.
• Solve the obtained model using the simplex or the graphical method.

How to Find Optimal Solution in Linear Programming?

We can find the optimal solution in a linear programming problem by using either the simplex method or the graphical method. The simplex method in lpp can be applied to problems with two or more variables while the graphical method can be applied to problems containing 2 variables only.

How to Find Feasible Region in Linear Programming?

To find the feasible region in a linear programming problem the steps are as follows:

• Draw the straight lines of the linear inequalities of the constraints.
• Use the "≤" and "≥" signs to denote the feasible region of each constraint.
• The region common to all constraints will be the feasible region for the linear programming problem.

What are Linear Programming Uses?

Linear programming is widely used in many industries such as delivery services, transportation industries, manufacturing companies, and financial institutions. The linear program is solved through linear optimization method, and it is used to determine the best outcome in a given scenerio.

• Math Article

Linear Programming

In Mathematics, linear programming is a method of optimising operations with some constraints. The main objective of linear programming is to maximize or minimize the numerical value. It consists of linear functions which are subjected to the constraints in the form of linear equations or in the form of inequalities.  Linear programming is considered an important technique that is used to find the optimum resource utilisation. The term “linear programming” consists of two words as linear and programming. The word “linear” defines the relationship between multiple variables with degree one. The word “programming” defines the process of selecting the best solution from various alternatives.

Linear Programming is widely used in Mathematics and some other fields such as economics, business, telecommunication, and manufacturing fields. In this article, let us discuss the definition of linear programming, its components, and different methods to solve linear programming problems.

Table of Contents:

• Characteristics
• Linear programming Problems
• Simplex Method

Graphical Method

• Applications
• Practice Problems

What is Linear Programming?

Linear programming (LP)   or Linear Optimisation may be defined as the problem of maximizing or minimizing a linear function that is subjected to linear constraints. The constraints may be equalities or inequalities. The optimisation problems involve the calculation of profit and loss.   Linear programming problems  are an important class of optimisation problems, that helps to find the feasible region and optimise the solution in order to have the highest or lowest value of the function.

In other words, linear programming is considered as an optimization method to maximize or minimize the objective function of the given mathematical model with the set of some requirements which are represented in the linear relationship. The main aim of the linear programming problem is to find the optimal solution.

Linear programming is the method of considering different inequalities relevant to a situation and calculating the best value that is required to be obtained in those conditions.  Some of the assumptions taken while working with linear programming are:

• The number of constraints should be expressed in the quantitative terms
• The relationship between the constraints and the objective function should be linear
• The linear function (i.e., objective function) is to be optimised

Components of Linear Programming

The basic components of the LP are as follows:

• Decision Variables
• Constraints
• Objective Functions

Characteristics of Linear Programming

The following are the five characteristics of the linear programming problem:

Constraints – The limitations should be expressed in the mathematical form, regarding the resource.

Objective Function – In a problem, the objective function should be specified in a quantitative way.

Linearity – The relationship between two or more variables in the function must be linear. It means that the degree of the variable is one.

Finiteness –  There should be finite and infinite input and output numbers. In case, if the function has infinite factors, the optimal solution is not feasible. 

Non-negativity – The variable value should be positive or zero. It should not be a negative value.

Decision Variables – The decision variable will decide the output. It gives the ultimate solution of the problem. For any problem, the first step is to identify the decision variables.

Linear Programming Problems

The Linear Programming Problems (LPP) is a problem that is concerned with finding the optimal value of the given linear function. The optimal value can be either maximum value or minimum value. Here, the given linear function is considered an objective function. The objective function can contain several variables, which are subjected to the conditions and it has to satisfy the set of linear inequalities called linear constraints. The linear programming problems can be used to get the optimal solution for the following scenarios, such as manufacturing problems, diet problems, transportation problems, allocation problems and so on.

Methods to Solve Linear Programming Problems

The linear programming problem can be solved using different methods, such as the graphical method, simplex method, or by using tools such as R, open solver etc. Here, we will discuss the two most important techniques called the simplex method and graphical method in detail.

Linear Programming Simplex Method

The simplex method is one of the most popular methods to solve linear programming problems. It is an iterative process to get the feasible optimal solution. In this method, the value of the basic variable keeps transforming to obtain the maximum value for the objective function. The algorithm for linear programming simplex method is provided below:

Step 1 : Establish a given problem. (i.e.,) write the inequality constraints and objective function.

Step 2: Convert the given inequalities to equations by adding the slack variable to each inequality expression.

Step 3 : Create the initial simplex tableau. Write the objective function at the bottom row. Here, each inequality constraint appears in its own row. Now, we can represent the problem in the form of an augmented matrix, which is called the initial simplex tableau.

Step 4 : Identify the greatest negative entry in the bottom row, which helps to identify the pivot column. The greatest negative entry in the bottom row defines the largest coefficient in the objective function, which will help us to increase the value of the objective function as fastest as possible.

Step 5 : Compute the quotients. To calculate the quotient, we need to divide the entries in the far right column by the entries in the first column, excluding the bottom row. The smallest quotient identifies the row. The row identified in this step and the element identified in the step will be taken as the pivot element.

Step 6: Carry out pivoting to make all other entries in column is zero.

Step 7: If there are no negative entries in the bottom row, end the process. Otherwise, start from step 4.

Step 8: Finally, determine the solution associated with the final simplex tableau.

The graphical method is used to optimize the two-variable linear programming. If the problem has two decision variables, a graphical method is the best method to find the optimal solution. In this method, the set of inequalities are subjected to constraints. Then the inequalities are plotted in the XY plane. Once, all the inequalities are plotted in the XY graph, the intersecting region will help to decide the feasible region. The feasible region will provide the optimal solution as well as explains what all values our model can take.  Let us see an example here and understand the concept of linear programming in a better way.

Calculate the maximal and minimal value of z = 5x + 3y for the following constraints.

x + 2y ≤ 14

3x – y ≥ 0

x – y ≤ 2

The three inequalities indicate the constraints. The area of the plane that will be marked is the feasible region.

The optimisation equation (z) = 5x + 3y. You have to find the (x,y) corner points that give the largest and smallest values of z.

To begin with, first solve each inequality.

x + 2y ≤ 14 ⇒  y ≤ -(1/2)x + 7

3x – y ≥ 0 ⇒  y ≤ 3x

x – y ≤ 2 ⇒ y  ≥ x – 2

Here is the graph for the above equations.

Now pair the lines to form a system of linear equations to find the corner points.

y = -(½) x + 7

Solving the above equations, we get the corner points as (2, 6)

y = -1/2 x + 7

y = x – 2

Solving the above equations, we get the corner points as (6, 4)

Solving the above equations, we get the corner points as (-1, -3)

For linear systems, the maximum and minimum values of the optimisation equation lie on the corners of the feasibility region. Therefore, to find the optimum solution, you only need to plug these three points in z = 3x + 4y

z = 5(2) + 3(6) = 10 + 18 = 28

z = 5(6) + 3(4) = 30 + 12 = 42

z = 5(-1) + 3(-3) = -5 -9 = -14

Hence, the maximum of z = 42 lies at (6, 4) and the minimum of z = -14 lies at (-1, -3)

Linear Programming Applications

A real-time example would be considering the limitations of labours and materials and finding the best production levels for maximum profit in particular circumstances. It is part of a vital area of mathematics known as optimisation techniques. The applications of LP in some other fields are

• Engineering – It solves design and manufacturing problems as it is helpful for doing shape optimisation
• Efficient Manufacturing – To maximise profit, companies use linear expressions
• Energy Industry – It provides methods to optimise the electric power system.
• Transportation Optimisation – For cost and time efficiency.

Importance of Linear Programming

Linear programming is broadly applied in the field of optimisation for many reasons. Many functional problems in operations analysis can be represented as linear programming problems. Some special problems of linear programming are such as network flow queries and multi-commodity flow queries are deemed to be important to have produced much research on functional algorithms for their solution.

Linear Programming Video Lesson

Linear programming problem.

Linear Programming Practice Problems

Solve the following linear programming problems:

• A doctor wishes to mix two types of foods in such a way that the vitamin contents of the mixture contain at least 8 units of vitamin A and 10 units of vitamin C. Food ‘I’ contains 2 units/kg of vitamin A and 1 unit/kg of vitamin C. Food ‘II’ contains 1 unit/kg of vitamin A and 2 units/kg of vitamin C. It costs Rs 50 per kg to purchase Food ‘I’ and Rs 70 per kg to purchase Food ‘II’. Formulate this problem as a linear programming problem to minimise the cost of such a mixture
• One kind of cake requires 200g of flour and 25g of fat, and another kind of cake requires 100g of flour and 50g of fat.  Formulate this problem as a linear programming problem to find the maximum number of cakes that can be made from 5kg of flour and 1 kg of fat assuming that there is no shortage of the other ingredients used in making the cakes.

Frequently Asked Questions on Linear Programming

Linear programming is a process of optimising the problems which are subjected to certain constraints. It means that it is the process of maximising or minimizing the linear functions under linear inequality constraints. The problem of solving linear programs is considered as the easiest one.

Mention the different types of linear programming.

The different types of linear programming are: Solving linear programming by Simplex method Solving linear programming using R Solving linear programming by graphical method Solving linear programming with the use of an open solver.

What are the requirements of linear programming?

The five basic requirements of linear programming are: Objective function Constraints Linearity Non-negativity Finiteness

Mention the advantages of Linear programming

The advantages of linear programming are: Linear programming provides insights to the business problems It helps to solve multi-dimensional problems According to the condition change, LP helps in making the adjustments By calculating the cost and profit of various things, LP helps to take the best optimal solution

What is meant by linear programming problems?

The linear programming problems (LPP) helps to find the best optimal solution of a linear function (also, known as the objective function) which are placed under certain constraints (set of linear inequality constraints)

To learn all concepts in Maths in a more engaging way, register at BYJU’S. Also, watch interesting videos on various Maths topics by downloading BYJU’S– The Learning App.

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

Thank you so much for clearly explained notes. I benefited a lot from them

Thank you very much for this material.

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

Linear programming basics

A short explanation is given what Linear programming is and some basic knowledge you need to know.

A linear programming problem is mathematically formulated as follows:

• A linear function to be maximized or minimized
• Problem constraints of the following form
• Default lower bounds of zero on all variables.

The problem is usually expressed in matrix form, and then becomes:

So a linear programming model consists of one objective which is a linear equation that must be maximized or minimized. Then there are a number of linear inequalities or constraints.

c T , A and B are constant matrixes. x are the variables (unknowns). All of them are real, continue values.

Note the default lower bounds of zero on all variables x. People tend to forget this build-in default. If no negative (or negative infinite) lower bound is explicitely set on variables, they can and will take only positive (zero included) values.

The inequalities can be <=, >= or = Because all numbers are real values, <= is the same as < and >= is the same as >

Also note that both objective function and constraints must be linear equations. This means that no variables can be multiplied with each other.

This formulation is called the Standard form . It is the usual and most intuitive form of describing a linear programming problem.

Sometimes, these problems are formulated in the canonical form. All inequalities are converted to equalities by adding an extra variable where needed:

Above example can then be written as:

So everywhere an equality was specified, an extra variable is introduced and subtracted (if it was >) or added (if it was <) to the constraint. These variables also only take positive (or zero) values only. These extra variables are called slack or surplus variables.

lp_solve add's these variables automatically to its internal structure. The formulator doesn't have to do it and it is even better not to. There will be fewer variables in the model and thus quicker to solve.

See Formulation of an lp problem in lpsolve for a practical example.

The right hand side (RHS), the B-vector, must be a constant matrix. Some people see this as a problem, but it isn't The RHS can always be brought to the left by a simple operation:

Basic mathematics also states that if a constraint is multiplied by a negative constant, that the inequality changes from direction. For example:

If the objective is multiplied by -1, then maximization becomes minimization and the other way around. For example:

The result will be the same, but changed from sign.

Minima and maxima on single variables are special cases of restrictions. They are called bounds. The optimization algorithm can handle these bounds more effeciently than other restrictions. They consume less memory and the algorithm is faster with them. As already specified, there is by default an implicit lower bound of zero on each variable. Only when explicitly another lower bound is set, the default of 0 is overruled. This other bound can be negative also. There is no default upper bound on variables. Almost all solvers support bounds on variables. So does lp_solve.

Frequently, it happens that on the same equation a less than and a greater than restriction must be set. Instead of adding two extra restrictions to the model, it is more performant and less memory consument to only add one restiction with either the less than or greater than restriction and put the other inequality on that same constraint by means of a range. Not all solvers support this feature but lp_solve does.

Integer and binary variables

By default, all variables are real. Sometimes it is required that one or more variables must be integer. It is not possible to just solve the model as is and then round to the nearest solution. At best, this result will maybe furfill all constraints, but you cannot be sure of. As you cannot be sure of the fact that this is the most optimal solution. Problems with integer variables are called integer or descrete programming problems. If all variables are integer it is called a pure integer programming problem, else it is a mixed integer programming problem. A special case of integer variables are binary variables. These are variables that can only take 0 or 1 as value. They are used quite frequently to program discontinue conditions. lp_solve can handle integer and binary variables. Binary variables are defined as integer variables with a maximum (upper bound) of 1 on them. See integer variables for a description on them.

Semi-continuous variables

Semi-continuous variables are variables that must take a value between their minimum and maximum or zero. So these variables are treated the same as regular variables, except that a value of zero is also accepted, even if there is a minimum bigger than zero is set on the variable. See semi-continuous variables for a description on them.

Special ordered sets (SOS)

A specially ordered set of degree N is a collection of variables where at most N variables may be non-zero. The non-zero variables must be contiguous (neighbours) sorted by the ascending value of their respective unique weights. In lp_solve, specially ordered sets may be of any cardinal type 1, 2, and higher, and may be overlapping. The number of variables in the set must be equal to, or exceed the cardinal SOS order. See Special ordered sets (SOS) for a description on them.

lp_solve uses the simplex algorithm to solve these problems. To solve the integer restrictions, the branch and bound (B&B) method is used.

Other resources

Another very usefull and free paper about linear programming fundamentals and advanced features plus several problems being discussed and modeled is Applications of optimization with Xpress-MP . It describes linear programming and modeling with the commercial solver Xpress-MP, but is as usefull for other solvers like lp_solve. In case that this link would not work anymore, try this via google search.

• HW Guidelines
• Study Skills Quiz
• Find Local Tutors
• Demo MathHelp.com
• Join MathHelp.com

Select a Course Below

• ACCUPLACER Math
• Math Placement Test
• PRAXIS Math
• + more tests
• 5th Grade Math
• 6th Grade Math
• Pre-Algebra
• College Pre-Algebra
• Introductory Algebra
• Intermediate Algebra
• College Algebra

An Introduction to Linear Programming

Intro How-To Word Problems More Examples Four Variables

What is linear programming?

Linear programming is the process of taking various linear inequalities (called "constraints") relating to some situation, and finding the best value obtainable under those conditions. A typical example would be taking the limitations of materials and labor, and then determining the optimal production levels for maximal profits under those conditions.

Content Continues Below

MathHelp.com

Is linear programming useful in real life?

Advertisement

In real life, linear programming is part of a very important area of mathematics called "optimization techniques".

This field of study (or at least the applied results of it) are used every day in the organization and allocation of resources. These real life systems can have dozens of variables, or hundreds, or more. (For the curious, a history of linear programming: PDF )

In algebra, though, you'll only work with the simple (and graphable) two-variable linear case.

How do you solve a linear programming problem?

The general process for solving linear-programming exercises is as follows:

• Graph the system of linear inequalities. The area walled off by the various inequalities is called the "feasibility region".
• Taking the "equals" versions of the inequalities, solve pairs of lines to find the corner points (or "vertices") of the feasibility region.
• Plug the coordinates of each of the vertices into the model for the situation at hand (that is, into the optimization equation).
• If you're maximizing, take the corner that gives you the highest value; otherwise, take the one with the lowest value.

Why do you test only the corners?

Somebody figured out that, given a system of linear inequalities and an equation to be optimized (that is, to be maximized or minimized), the system's optimal solution will always be on a corner.

There are complicated explanations for this, but also intuitive ones (for the simple two-variable case that we'll be working with). Either way, the corners are where it's at.

The three inequalities in the curly braces are the constraints. The area of the plane that they mark off will be the feasibility region. The formula " z  = 3 x  + 4 y " is the optimization equation. I need to find the ( x ,  y ) corner points of the feasibility region that return the largest and smallest values of z .

My first step is to solve each inequality for the more-easily graphed equivalent forms:

It's easy to graph the system ; you take the "equals" version of each inequality (these "equals" versions being the lines forming the edges of the feasibility region), and solve the system of linear equations formed by each pair of lines:

To find the corner points — which aren't always clear from the graph — I'll pair the lines (thus forming a system of linear equations ) and solve:

− x + 14 = 6 x

y = 3(2) = 6

corner point at (2, 6)

y = x − 2

− x + 14 = 2 x − 4

y = (6) − 2 = 4

corner point at (6, 4)

3 x = x − 2

2 x = −2

x = −1

y = 3(−1) = −3

corner point at (−1, −3)

So the corner points — the points I'll be plugging into the optimization equation — are (2, 6) , (6, 4) , and (−1, −3) . To find the solution to this exercise, I only need to plug these three points into " z  = 3 x  + 4 y ".

(2, 6): z = 3(2) + 4(6) = 6 + 24 = 30 (6, 4): z = 3(6) + 4(4) = 18 + 16 = 34 (−1, −3): z = 3(−1) + 4(−3) = −3 −12 = −15

Then the maximum of z = 34 occurs at (6, 4) , and the minimum of z = −15 occurs at (−1, −3) .

As you can see, solving a linear-programming exercise can be a lengthly process, but each individual step is fairly straightforward. Just take your time, label clearly, and work neatly, and you'll get it!

URL: https://www.purplemath.com/modules/linprog.htm

Page 1 Page 2 Page 3 Page 4 Page 5

Standardized Test Prep

College math, homeschool math, share this page.

• Terms of Use
• Privacy / Cookies
• About Purplemath
• About the Author
• Tutoring from PM
• Advertising
• Linking to PM
• Site licencing

Visit Our Profiles