problem solving using search algorithm

Artificial Intelligence

Control System

• Interview Q

Intelligent Agent

Problem-solving, adversarial search, knowledge represent, uncertain knowledge r., subsets of ai, artificial intelligence mcq, related tutorials.

• Send your Feedback to [email protected]

Help Others, Please Share

Learn Latest Tutorials

Transact-SQL

Reinforcement Learning

R Programming

React Native

Python Design Patterns

Python Pillow

Python Turtle

Preparation

Verbal Ability

Interview Questions

Company Questions

Trending Technologies

Cloud Computing

Data Science

Machine Learning

B.Tech / MCA

Data Structures

Operating System

Computer Network

Compiler Design

Computer Organization

Discrete Mathematics

Ethical Hacking

Computer Graphics

Software Engineering

Web Technology

Cyber Security

C Programming

Data Mining

Data Warehouse

• Admiral “Amazing Grace” Hopper

Exploring the Intricacies of NP-Completeness in Computer Science

Understanding p vs np problems in computer science: a primer for beginners, understanding key theoretical frameworks in computer science: a beginner’s guide.

Learn Computer Science with Python

CS is a journey, not a destination

• Foundations

Understanding Algorithms: The Key to Problem-Solving Mastery

The world of computer science is a fascinating realm, where intricate concepts and technologies continuously shape the way we interact with machines. Among the vast array of ideas and principles, few are as fundamental and essential as algorithms. These powerful tools serve as the building blocks of computation, enabling computers to solve problems, make decisions, and process vast amounts of data efficiently.

An algorithm can be thought of as a step-by-step procedure or a set of instructions designed to solve a specific problem or accomplish a particular task. It represents a systematic approach to finding solutions and provides a structured way to tackle complex computational challenges. Algorithms are at the heart of various applications, from simple calculations to sophisticated machine learning models and complex data analysis.

Understanding algorithms and their inner workings is crucial for anyone interested in computer science. They serve as the backbone of software development, powering the creation of innovative applications across numerous domains. By comprehending the concept of algorithms, aspiring computer science enthusiasts gain a powerful toolset to approach problem-solving and gain insight into the efficiency and performance of different computational methods.

In this article, we aim to provide a clear and accessible introduction to algorithms, focusing on their importance in problem-solving and exploring common types such as searching, sorting, and recursion. By delving into these topics, readers will gain a solid foundation in algorithmic thinking and discover the underlying principles that drive the functioning of modern computing systems. Whether you’re a beginner in the world of computer science or seeking to deepen your understanding, this article will equip you with the knowledge to navigate the fascinating world of algorithms.

What are Algorithms?

At its core, an algorithm is a systematic, step-by-step procedure or set of rules designed to solve a problem or perform a specific task. It provides clear instructions that, when followed meticulously, lead to the desired outcome.

Consider an algorithm to be akin to a recipe for your favorite dish. When you decide to cook, the recipe is your go-to guide. It lists out the ingredients you need, their exact quantities, and a detailed, step-by-step explanation of the process, from how to prepare the ingredients to how to mix them, and finally, the cooking process. It even provides an order for adding the ingredients and specific times for cooking to ensure the dish turns out perfect.

In the same vein, an algorithm, within the realm of computer science, provides an explicit series of instructions to accomplish a goal. This could be a simple goal like sorting a list of numbers in ascending order, a more complex task such as searching for a specific data point in a massive dataset, or even a highly complicated task like determining the shortest path between two points on a map (think Google Maps). No matter the complexity of the problem at hand, there’s always an algorithm working tirelessly behind the scenes to solve it.

Furthermore, algorithms aren’t limited to specific programming languages. They are universal and can be implemented in any language. This is why understanding the fundamental concept of algorithms can empower you to solve problems across various programming languages.

The Importance of Algorithms

Algorithms are indisputably the backbone of all computational operations. They’re a fundamental part of the digital world that we interact with daily. When you search for something on the web, an algorithm is tirelessly working behind the scenes to sift through millions, possibly billions, of web pages to bring you the most relevant results. When you use a GPS to find the fastest route to a location, an algorithm is computing all possible paths, factoring in variables like traffic and road conditions, to provide you the optimal route.

Consider the world of social media, where algorithms curate personalized feeds based on our previous interactions, or in streaming platforms where they recommend shows and movies based on our viewing habits. Every click, every like, every search, and every interaction is processed by algorithms to serve you a seamless digital experience.

In the realm of computer science and beyond, everything revolves around problem-solving, and algorithms are our most reliable problem-solving tools. They provide a structured approach to problem-solving, breaking down complex problems into manageable steps and ensuring that every eventuality is accounted for.

Moreover, an algorithm’s efficiency is not just a matter of preference but a necessity. Given that computers have finite resources — time, memory, and computational power — the algorithms we use need to be optimized to make the best possible use of these resources. Efficient algorithms are the ones that can perform tasks more quickly, using less memory, and provide solutions to complex problems that might be infeasible with less efficient alternatives.

In the context of massive datasets (the likes of which are common in our data-driven world), the difference between a poorly designed algorithm and an efficient one could be the difference between a solution that takes years to compute and one that takes mere seconds. Therefore, understanding, designing, and implementing efficient algorithms is a critical skill for any computer scientist or software engineer.

Hence, as a computer science beginner, you are starting a journey where algorithms will be your best allies — universal keys capable of unlocking solutions to a myriad of problems, big or small.

Common Types of Algorithms: Searching and Sorting

Two of the most ubiquitous types of algorithms that beginners often encounter are searching and sorting algorithms.

Searching algorithms are designed to retrieve specific information from a data structure, like an array or a database. A simple example is the linear search, which works by checking each element in the array until it finds the one it’s looking for. Although easy to understand, this method isn’t efficient for large datasets, which is where more complex algorithms like binary search come in.

Binary search, on the other hand, is like looking up a word in the dictionary. Instead of checking each word from beginning to end, you open the dictionary in the middle and see if the word you’re looking for should be on the left or right side, thereby reducing the search space by half with each step.

Sorting algorithms, meanwhile, are designed to arrange elements in a particular order. A simple sorting algorithm is bubble sort, which works by repeatedly swapping adjacent elements if they’re in the wrong order. Again, while straightforward, it’s not efficient for larger datasets. More advanced sorting algorithms, such as quicksort or mergesort, have been designed to sort large data collections more efficiently.

Diving Deeper: Graph and Dynamic Programming Algorithms

Building upon our understanding of searching and sorting algorithms, let’s delve into two other families of algorithms often encountered in computer science: graph algorithms and dynamic programming algorithms.

A graph is a mathematical structure that models the relationship between pairs of objects. Graphs consist of vertices (or nodes) and edges (where each edge connects a pair of vertices). Graphs are commonly used to represent real-world systems such as social networks, web pages, biological networks, and more.

Graph algorithms are designed to solve problems centered around these structures. Some common graph algorithms include:

Dynamic programming is a powerful method used in optimization problems, where the main problem is broken down into simpler, overlapping subproblems. The solutions to these subproblems are stored and reused to build up the solution to the main problem, saving computational effort.

Here are two common dynamic programming problems:

Understanding these algorithm families — searching, sorting, graph, and dynamic programming algorithms — not only equips you with powerful tools to solve a variety of complex problems but also serves as a springboard to dive deeper into the rich ocean of algorithms and computer science.

Recursion: A Powerful Technique

While searching and sorting represent specific problem domains, recursion is a broad technique used in a wide range of algorithms. Recursion involves breaking down a problem into smaller, more manageable parts, and a function calling itself to solve these smaller parts.

To visualize recursion, consider the task of calculating factorial of a number. The factorial of a number n (denoted as n! ) is the product of all positive integers less than or equal to n . For instance, the factorial of 5 ( 5! ) is 5 x 4 x 3 x 2 x 1 = 120 . A recursive algorithm for finding factorial of n would involve multiplying n by the factorial of n-1 . The function keeps calling itself with a smaller value of n each time until it reaches a point where n is equal to 1, at which point it starts returning values back up the chain.

Algorithms are truly the heart of computer science, transforming raw data into valuable information and insight. Understanding their functionality and purpose is key to progressing in your computer science journey. As you continue your exploration, remember that each algorithm you encounter, no matter how complex it may seem, is simply a step-by-step procedure to solve a problem.

We’ve just scratched the surface of the fascinating world of algorithms. With time, patience, and practice, you will learn to create your own algorithms and start solving problems with confidence and efficiency.

Related Articles

Three Elegant Algorithms Every Computer Science Beginner Should Know

Smart. Open. Grounded. Inventive. Read our Ideas Made to Matter.

Which program is right for you?

Through intellectual rigor and experiential learning, this full-time, two-year MBA program develops leaders who make a difference in the world.

A rigorous, hands-on program that prepares adaptive problem solvers for premier finance careers.

A 12-month program focused on applying the tools of modern data science, optimization and machine learning to solve real-world business problems.

Earn your MBA and SM in engineering with this transformative two-year program.

Combine an international MBA with a deep dive into management science. A special opportunity for partner and affiliate schools only.

A doctoral program that produces outstanding scholars who are leading in their fields of research.

Bring a business perspective to your technical and quantitative expertise with a bachelor’s degree in management, business analytics, or finance.

A joint program for mid-career professionals that integrates engineering and systems thinking. Earn your master’s degree in engineering and management.

An interdisciplinary program that combines engineering, management, and design, leading to a master’s degree in engineering and management.

Executive Programs

A full-time MBA program for mid-career leaders eager to dedicate one year of discovery for a lifetime of impact.

This 20-month MBA program equips experienced executives to enhance their impact on their organizations and the world.

Non-degree programs for senior executives and high-potential managers.

A non-degree, customizable program for mid-career professionals.

Accelerated research about generative AI

Disciplined entrepreneurship: 6 questions for startup success

Startup tactics: How and when to hire technical talent

Credit: Alejandro Giraldo

Ideas Made to Matter

How to use algorithms to solve everyday problems

Kara Baskin

May 8, 2017

How can I navigate the grocery store quickly? Why doesn’t anyone like my Facebook status? How can I alphabetize my bookshelves in a hurry? Apple data visualizer and MIT System Design and Management graduate Ali Almossawi solves these common dilemmas and more in his new book, “ Bad Choices: How Algorithms Can Help You Think Smarter and Live Happier ,” a quirky, illustrated guide to algorithmic thinking. 

For the uninitiated: What is an algorithm? And how can algorithms help us to think smarter?

An algorithm is a process with unambiguous steps that has a beginning and an end, and does something useful.

Algorithmic thinking is taking a step back and asking, “If it’s the case that algorithms are so useful in computing to achieve predictability, might they also be useful in everyday life, when it comes to, say, deciding between alternative ways of solving a problem or completing a task?” In all cases, we optimize for efficiency: We care about time or space.

Note the mention of “deciding between.” Computer scientists do that all the time, and I was convinced that the tools they use to evaluate competing algorithms would be of interest to a broad audience.

Why did you write this book, and who can benefit from it?

All the books I came across that tried to introduce computer science involved coding. My approach to making algorithms compelling was focusing on comparisons. I take algorithms and put them in a scene from everyday life, such as matching socks from a pile, putting books on a shelf, remembering things, driving from one point to another, or cutting an onion. These activities can be mapped to one or more fundamental algorithms, which form the basis for the field of computing and have far-reaching applications and uses.

I wrote the book with two audiences in mind. One, anyone, be it a learner or an educator, who is interested in computer science and wants an engaging and lighthearted, but not a dumbed-down, introduction to the field. Two, anyone who is already familiar with the field and wants to experience a way of explaining some of the fundamental concepts in computer science differently than how they’re taught.

I’m going to the grocery store and only have 15 minutes. What do I do?

Do you know what the grocery store looks like ahead of time? If you know what it looks like, it determines your list. How do you prioritize things on your list? Order the items in a way that allows you to avoid walking down the same aisles twice.

For me, the intriguing thing is that the grocery store is a scene from everyday life that I can use as a launch pad to talk about various related topics, like priority queues and graphs and hashing. For instance, what is the most efficient way for a machine to store a prioritized list, and what happens when the equivalent of you scratching an item from a list happens in the machine’s list? How is a store analogous to a graph (an abstraction in computer science and mathematics that defines how things are connected), and how is navigating the aisles in a store analogous to traversing a graph?

Nobody follows me on Instagram. How do I get more followers?

The concept of links and networks, which I cover in Chapter 6, is relevant here. It’s much easier to get to people whom you might be interested in and who might be interested in you if you can start within the ball of links that connects those people, rather than starting at a random spot.

You mention Instagram: There, the hashtag is one way to enter that ball of links. Tag your photos, engage with users who tag their photos with the same hashtags, and you should be on your way to stardom.

What are the secret ingredients of a successful Facebook post?

I’ve posted things on social media that have died a sad death and then posted the same thing at a later date that somehow did great. Again, if we think of it in terms that are relevant to algorithms, we’d say that the challenge with making something go viral is really getting that first spark. And to get that first spark, a person who is connected to the largest number of people who are likely to engage with that post, needs to share it.

With [my first book], “Bad Arguments,” I spent a month pouring close to $5,000 into advertising for that project with moderate results. And then one science journalist with a large audience wrote about it, and the project took off and hasn’t stopped since.

What problems do you wish you could solve via algorithm but can’t?

When we care about efficiency, thinking in terms of algorithms is useful. There are cases when that’s not the quality we want to optimize for — for instance, learning or love. I walk for several miles every day, all throughout the city, as I find it relaxing. I’ve never asked myself, “What’s the most efficient way I can traverse the streets of San Francisco?” It’s not relevant to my objective.

Algorithms are a great way of thinking about efficiency, but the question has to be, “What approach can you optimize for that objective?” That’s what worries me about self-help: Books give you a silver bullet for doing everything “right” but leave out all the nuances that make us different. What works for you might not work for me.

Which companies use algorithms well?

When you read that the overwhelming majority of the shows that users of, say, Netflix, watch are due to Netflix’s recommendation engine, you know they’re doing something right.

Related Articles

• Runestone in social media: Follow @iRunestone Our Facebook Page
• Table of Contents
• Assignments
• Peer Instruction (Instructor)
• Peer Instruction (Student)
• Change Course
• Instructor's Page
• Progress Page
• Edit Profile
• Change Password
• Scratch ActiveCode
• Scratch Activecode
• Instructors Guide
• About Runestone
• Report A Problem
• 6.1 Objectives
• 6.2 Searching
• 6.3 The Sequential Search
• 6.4 The Binary Search
• 6.5 Hashing
• 6.6 Sorting
• 6.7 The Bubble Sort
• 6.8 The Selection Sort
• 6.9 The Insertion Sort
• 6.10 The Shell Sort
• 6.11 The Merge Sort
• 6.12 The Quick Sort
• 6.13 Summary
• 6.14 Key Terms
• 6.15 Discussion Questions
• 6.16 Programming Exercises
• 5.17. Programming Exercises" data-toggle="tooltip">
• 6.1. Objectives' data-toggle="tooltip" >

6. Sorting and Searching ¶

Sorting and Searching

• 6.1. Objectives
• 6.2. Searching
• 6.3.1. Analysis of Sequential Search
• 6.4.1. Analysis of Binary Search
• 6.5.1. Hash Functions
• 6.5.2. Collision Resolution
• 6.5.3. Implementing the Map Abstract Data Type
• 6.5.4. Analysis of Hashing
• 6.6. Sorting
• 6.7. The Bubble Sort
• 6.8. The Selection Sort
• 6.9. The Insertion Sort
• 6.10. The Shell Sort
• 6.11. The Merge Sort
• 6.12. The Quick Sort
• 6.13. Summary
• 6.14. Key Terms
• 6.15. Discussion Questions
• 6.16. Programming Exercises

Ensure that you are logged in and have the required permissions to access the test.

A server error has occurred. Please refresh the page or try after some time.

An error has occurred. Please refresh the page or try after some time.

Signup and get free access to 100+ Tutorials and Practice Problems Start Now

Linear Search

• Binary Search
• Ternary Search
• Bubble Sort
• Selection Sort
• Insertion Sort
• Counting Sort
• Bucket Sort
• Basics of Greedy Algorithms
• Graph Representation
• Breadth First Search
• Depth First Search
• Minimum Spanning Tree
• Shortest Path Algorithms
• Flood-fill Algorithm
• Articulation Points and Bridges
• Biconnected Components
• Strongly Connected Components
• Topological Sort
• Hamiltonian Path
• Maximum flow
• Minimum Cost Maximum Flow
• Basics of String Manipulation
• String Searching
• Z Algorithm
• Manachar’s Algorithm
• Introduction to Dynamic Programming 1
• 2 Dimensional
• State space reduction
• Dynamic Programming and Bit Masking

Solve Problems

ATTEMPTED BY: 1535 SUCCESS RATE: 67% LEVEL: Easy

• Participate

Equal Strings

ATTEMPTED BY: 714 SUCCESS RATE: 54% LEVEL: Medium

AND Subsequence

ATTEMPTED BY: 490 SUCCESS RATE: 42% LEVEL: Medium

Adjacent Sum Greater than K

ATTEMPTED BY: 887 SUCCESS RATE: 69% LEVEL: Medium

Equal Diverse Teams

ATTEMPTED BY: 1361 SUCCESS RATE: 29% LEVEL: Easy

Permutation Swaps

ATTEMPTED BY: 987 SUCCESS RATE: 35% LEVEL: Easy

Guess Permutation

ATTEMPTED BY: 587 SUCCESS RATE: 69% LEVEL: Hard

ATTEMPTED BY: 478 SUCCESS RATE: 75% LEVEL: Medium

Equal Parity Sum

ATTEMPTED BY: 667 SUCCESS RATE: 59% LEVEL: Medium

Employee rating

ATTEMPTED BY: 2363 SUCCESS RATE: 84% LEVEL: Easy

• An alphabet
• A special character
• Minimum 8 characters

A password reset link will be sent to the following email id

Help | Advanced Search

Computer Science > Neural and Evolutionary Computing

Title: learning from offline and online experiences: a hybrid adaptive operator selection framework.

Abstract: In many practical applications, usually, similar optimisation problems or scenarios repeatedly appear. Learning from previous problem-solving experiences can help adjust algorithm components of meta-heuristics, e.g., adaptively selecting promising search operators, to achieve better optimisation performance. However, those experiences obtained from previously solved problems, namely offline experiences, may sometimes provide misleading perceptions when solving a new problem, if the characteristics of previous problems and the new one are relatively different. Learning from online experiences obtained during the ongoing problem-solving process is more instructive but highly restricted by limited computational resources. This paper focuses on the effective combination of offline and online experiences. A novel hybrid framework that learns to dynamically and adaptively select promising search operators is proposed. Two adaptive operator selection modules with complementary paradigms cooperate in the framework to learn from offline and online experiences and make decisions. An adaptive decision policy is maintained to balance the use of those two modules in an online manner. Extensive experiments on 170 widely studied real-value benchmark optimisation problems and a benchmark set with 34 instances for combinatorial optimisation show that the proposed hybrid framework outperforms the state-of-the-art methods. Ablation study verifies the effectiveness of each component of the framework.

Submission history

Access paper:.

• HTML (experimental)
• Other Formats

References & Citations

• Google Scholar
• Semantic Scholar

BibTeX formatted citation

Bibliographic and Citation Tools

Code, data and media associated with this article, recommenders and search tools.

• Institution

arXivLabs: experimental projects with community collaborators

arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website.

Both individuals and organizations that work with arXivLabs have embraced and accepted our values of openness, community, excellence, and user data privacy. arXiv is committed to these values and only works with partners that adhere to them.

Have an idea for a project that will add value for arXiv's community? Learn more about arXivLabs .

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

• View all journals
• My Account Login
• Explore content
• About the journal
• Publish with us
• Sign up for alerts
• Open access
• Published: 10 April 2024

A hybrid particle swarm optimization algorithm for solving engineering problem

• Jinwei Qiao 1 , 2 ,
• Guangyuan Wang 1 , 2 ,
• Zhi Yang 1 , 2 ,
• Xiaochuan Luo 3 ,
• Jun Chen 1 , 2 ,
• Kan Li 4 &
• Pengbo Liu 1 , 2  

Scientific Reports volume  14 , Article number:  8357 ( 2024 ) Cite this article

344 Accesses

Metrics details

• Computational science
• Mechanical engineering

To overcome the disadvantages of premature convergence and easy trapping into local optimum solutions, this paper proposes an improved particle swarm optimization algorithm (named NDWPSO algorithm) based on multiple hybrid strategies. Firstly, the elite opposition-based learning method is utilized to initialize the particle position matrix. Secondly, the dynamic inertial weight parameters are given to improve the global search speed in the early iterative phase. Thirdly, a new local optimal jump-out strategy is proposed to overcome the "premature" problem. Finally, the algorithm applies the spiral shrinkage search strategy from the whale optimization algorithm (WOA) and the Differential Evolution (DE) mutation strategy in the later iteration to accelerate the convergence speed. The NDWPSO is further compared with other 8 well-known nature-inspired algorithms (3 PSO variants and 5 other intelligent algorithms) on 23 benchmark test functions and three practical engineering problems. Simulation results prove that the NDWPSO algorithm obtains better results for all 49 sets of data than the other 3 PSO variants. Compared with 5 other intelligent algorithms, the NDWPSO obtains 69.2%, 84.6%, and 84.6% of the best results for the benchmark function ( \({f}_{1}-{f}_{13}\) ) with 3 kinds of dimensional spaces (Dim = 30,50,100) and 80% of the best optimal solutions for 10 fixed-multimodal benchmark functions. Also, the best design solutions are obtained by NDWPSO for all 3 classical practical engineering problems.

Similar content being viewed by others

A clustering-based competitive particle swarm optimization with grid ranking for multi-objective optimization problems

Qianlin Ye, Zheng Wang, … Mengjiao Yu

A modified shuffled frog leaping algorithm with inertia weight

Zhuanzhe Zhao, Mengxian Wang, … Zhibo Liu

Appropriate noise addition to metaheuristic algorithms can enhance their performance

Kwok Pui Choi, Enzio Hai Hong Kam, … Weng Kee Wong

Introduction

In the ever-changing society, new optimization problems arise every moment, and they are distributed in various fields, such as automation control 1 , statistical physics 2 , security prevention and temperature prediction 3 , artificial intelligence 4 , and telecommunication technology 5 . Faced with a constant stream of practical engineering optimization problems, traditional solution methods gradually lose their efficiency and convenience, making it more and more expensive to solve the problems. Therefore, researchers have developed many metaheuristic algorithms and successfully applied them to the solution of optimization problems. Among them, Particle swarm optimization (PSO) algorithm 6 is one of the most widely used swarm intelligence algorithms.

However, the basic PSO has a simple operating principle and solves problems with high efficiency and good computational performance, but it suffers from the disadvantages of easily trapping in local optima and premature convergence. To improve the overall performance of the particle swarm algorithm, an improved particle swarm optimization algorithm is proposed by the multiple hybrid strategy in this paper. The improved PSO incorporates the search ideas of other intelligent algorithms (DE, WOA), so the improved algorithm proposed in this paper is named NDWPSO. The main improvement schemes are divided into the following 4 points: Firstly, a strategy of elite opposition-based learning is introduced into the particle population position initialization. A high-quality initialization matrix of population position can improve the convergence speed of the algorithm. Secondly, a dynamic weight methodology is adopted for the acceleration coefficients by combining the iterative map and linearly transformed method. This method utilizes the chaotic nature of the mapping function, the fast convergence capability of the dynamic weighting scheme, and the time-varying property of the acceleration coefficients. Thus, the global search and local search of the algorithm are balanced and the global search speed of the population is improved. Thirdly, a determination mechanism is set up to detect whether the algorithm falls into a local optimum. When the algorithm is “premature”, the population resets 40% of the position information to overcome the local optimum. Finally, the spiral shrinking mechanism combined with the DE/best/2 position mutation is used in the later iteration, which further improves the solution accuracy.

The structure of the paper is given as follows: Sect. “ Particle swarm optimization (PSO) ” describes the principle of the particle swarm algorithm. Section “ Improved particle swarm optimization algorithm ” shows the detailed improvement strategy and a comparison experiment of inertia weight is set up for the proposed NDWPSO. Section “ Experiment and discussion ” includes the experimental and result discussion sections on the performance of the improved algorithm. Section “ Conclusions and future works ” summarizes the main findings of this study.

Literature review

This section reviews some metaheuristic algorithms and other improved PSO algorithms. A simple discussion about recently proposed research studies is given.

Metaheuristic algorithms

A series of metaheuristic algorithms have been proposed in recent years by using various innovative approaches. For instance, Lin et al. 7 proposed a novel artificial bee colony algorithm (ABCLGII) in 2018 and compared ABCLGII with other outstanding ABC variants on 52 frequently used test functions. Abed-alguni et al. 8 proposed an exploratory cuckoo search (ECS) algorithm in 2021 and carried out several experiments to investigate the performance of ECS by 14 benchmark functions. Brajević 9 presented a novel shuffle-based artificial bee colony (SB-ABC) algorithm for solving integer programming and minimax problems in 2021. The experiments are tested on 7 integer programming problems and 10 minimax problems. In 2022, Khan et al. 10 proposed a non-deterministic meta-heuristic algorithm called Non-linear Activated Beetle Antennae Search (NABAS) for a non-convex tax-aware portfolio selection problem. Brajević et al. 11 proposed a hybridization of the sine cosine algorithm (HSCA) in 2022 to solve 15 complex structural and mechanical engineering design optimization problems. Abed-Alguni et al. 12 proposed an improved Salp Swarm Algorithm (ISSA) in 2022 for single-objective continuous optimization problems. A set of 14 standard benchmark functions was used to evaluate the performance of ISSA. In 2023, Nadimi et al. 13 proposed a binary starling murmuration optimization (BSMO) to select the effective features from different important diseases. In the same year, Nadimi et al. 14 systematically reviewed the last 5 years' developments of WOA and made a critical analysis of those WOA variants. In 2024, Fatahi et al. 15 proposed an Improved Binary Quantum-based Avian Navigation Optimizer Algorithm (IBQANA) for the Feature Subset Selection problem in the medical area. Experimental evaluation on 12 medical datasets demonstrates that IBQANA outperforms 7 established algorithms. Abed-alguni et al. 16 proposed an Improved Binary DJaya Algorithm (IBJA) to solve the Feature Selection problem in 2024. The IBJA’s performance was compared against 4 ML classifiers and 10 efficient optimization algorithms.

Improved PSO algorithms

Many researchers have constantly proposed some improved PSO algorithms to solve engineering problems in different fields. For instance, Yeh 17 proposed an improved particle swarm algorithm, which combines a new self-boundary search and a bivariate update mechanism, to solve the reliability redundancy allocation problem (RRAP) problem. Solomon et al. 18 designed a collaborative multi-group particle swarm algorithm with high parallelism that was used to test the adaptability of Graphics Processing Units (GPUs) in distributed computing environments. Mukhopadhyay and Banerjee 19 proposed a chaotic multi-group particle swarm optimization (CMS-PSO) to estimate the unknown parameters of an autonomous chaotic laser system. Duan et al. 20 designed an improved particle swarm algorithm with nonlinear adjustment of inertia weights to improve the coupling accuracy between laser diodes and single-mode fibers. Sun et al. 21 proposed a particle swarm optimization algorithm combined with non-Gaussian stochastic distribution for the optimal design of wind turbine blades. Based on a multiple swarm scheme, Liu et al. 22 proposed an improved particle swarm optimization algorithm to predict the temperatures of steel billets for the reheating furnace. In 2022, Gad 23 analyzed the existing 2140 papers on Swarm Intelligence between 2017 and 2019 and pointed out that the PSO algorithm still needs further research. In general, the improved methods can be classified into four categories:

Adjusting the distribution of algorithm parameters. Feng et al. 24 used a nonlinear adaptive method on inertia weights to balance local and global search and introduced asynchronously varying acceleration coefficients.

Changing the updating formula of the particle swarm position. Both papers 25 and 26 used chaotic mapping functions to update the inertia weight parameters and combined them with a dynamic weighting strategy to update the particle swarm positions. This improved approach enables the particle swarm algorithm to be equipped with fast convergence of performance.

The initialization of the swarm. Alsaidy and Abbood proposed 27 a hybrid task scheduling algorithm that replaced the random initialization of the meta-heuristic algorithm with the heuristic algorithms MCT-PSO and LJFP-PSO.

Combining with other intelligent algorithms: Liu et al. 28 introduced the differential evolution (DE) algorithm into PSO to increase the particle swarm as diversity and reduce the probability of the population falling into local optimum.

Particle swarm optimization (PSO)

The particle swarm optimization algorithm is a population intelligence algorithm for solving continuous and discrete optimization problems. It originated from the social behavior of individuals in bird and fish flocks 6 . The core of the PSO algorithm is that an individual particle identifies potential solutions by flight in a defined constraint space adjusts its exploration direction to approach the global optimal solution based on the shared information among the group, and finally solves the optimization problem. Each particle \(i\) includes two attributes: velocity vector \({V}_{i}=\left[{v}_{i1},{v}_{i2},{v}_{i3},{...,v}_{ij},{...,v}_{iD},\right]\) and position vector \({X}_{i}=[{x}_{i1},{x}_{i2},{x}_{i3},...,{x}_{ij},...,{x}_{iD}]\) . The velocity vector is used to modify the motion path of the swarm; the position vector represents a potential solution for the optimization problem. Here, \(j=\mathrm{1,2},\dots ,D\) , \(D\) represents the dimension of the constraint space. The equations for updating the velocity and position of the particle swarm are shown in Eqs. ( 1 ) and ( 2 ).

Here \({Pbest}_{i}^{k}\) represents the previous optimal position of the particle \(i\) , and \({Gbest}\) is the optimal position discovered by the whole population. \(i=\mathrm{1,2},\dots ,n\) , \(n\) denotes the size of the particle swarm. \({c}_{1}\) and \({c}_{2}\) are the acceleration constants, which are used to adjust the search step of the particle 29 . \({r}_{1}\) and \({r}_{2}\) are two random uniform values distributed in the range \([\mathrm{0,1}]\) , which are used to improve the randomness of the particle search. \(\omega\) inertia weight parameter, which is used to adjust the scale of the search range of the particle swarm 30 . The basic PSO sets the inertia weight parameter as a time-varying parameter to balance global exploration and local seeking. The updated equation of the inertia weight parameter is given as follows:

where \({\omega }_{max}\) and \({\omega }_{min}\) represent the upper and lower limits of the range of inertia weight parameter. \(k\) and \(Mk\) are the current iteration and maximum iteration.

Improved particle swarm optimization algorithm

According to the no free lunch theory 31 , it is known that no algorithm can solve every practical problem with high quality and efficiency for increasingly complex and diverse optimization problems. In this section, several improvement strategies are proposed to improve the search efficiency and overcome this shortcoming of the basic PSO algorithm.

Improvement strategies

The optimization strategies of the improved PSO algorithm are shown as follows:

The inertia weight parameter is updated by an improved chaotic variables method instead of a linear decreasing strategy. Chaotic mapping performs the whole search at a higher speed and is more resistant to falling into local optimal than the probability-dependent random search 32 . However, the population may result in that particles can easily fly out of the global optimum boundary. To ensure that the population can converge to the global optimum, an improved Iterative mapping is adopted and shown as follows:

Here \({\omega }_{k}\) is the inertia weight parameter in the iteration \(k\) , \(b\) is the control parameter in the range \([\mathrm{0,1}]\) .

The acceleration coefficients are updated by the linear transformation. \({c}_{1}\) and \({c}_{2}\) represent the influential coefficients of the particles by their own and population information, respectively. To improve the search performance of the population, \({c}_{1}\) and \({c}_{2}\) are changed from fixed values to time-varying parameter parameters, that are updated by linear transformation with the number of iterations:

where \({c}_{max}\) and \({c}_{min}\) are the maximum and minimum values of acceleration coefficients, respectively.

The initialization scheme is determined by elite opposition-based learning . The high-quality initial population will accelerate the solution speed of the algorithm and improve the accuracy of the optimal solution. Thus, the elite backward learning strategy 33 is introduced to generate the position matrix of the initial population. Suppose the elite individual of the population is \({X}=[{x}_{1},{x}_{2},{x}_{3},...,{x}_{j},...,{x}_{D}]\) , and the elite opposition-based solution of \(X\) is \({X}_{o}=[{x}_{{\text{o}}1},{x}_{{\text{o}}2},{x}_{{\text{o}}3},...,{x}_{oj},...,{x}_{oD}]\) . The formula for the elite opposition-based solution is as follows:

where \({k}_{r}\) is the random value in the range \((\mathrm{0,1})\) . \({ux}_{oij}\) and \({lx}_{oij}\) are dynamic boundaries of the elite opposition-based solution in \(j\) dimensional variables. The advantage of dynamic boundary is to reduce the exploration space of particles, which is beneficial to the convergence of the algorithm. When the elite opposition-based solution is out of bounds, the out-of-bounds processing is performed. The equation is given as follows:

After calculating the fitness function values of the elite solution and the elite opposition-based solution, respectively, \(n\) high quality solutions were selected to form a new initial population position matrix.

The position updating Eq. ( 2 ) is modified based on the strategy of dynamic weight. To improve the speed of the global search of the population, the strategy of dynamic weight from the artificial bee colony algorithm 34 is introduced to enhance the computational performance. The new position updating equation is shown as follows:

Here \(\rho\) is the random value in the range \((\mathrm{0,1})\) . \(\psi\) represents the acceleration coefficient and \({\omega }{\prime}\) is the dynamic weight coefficient. The updated equations of the above parameters are as follows:

where \(f(i)\) denotes the fitness function value of individual particle \(i\) and u is the average of the population fitness function values in the current iteration. The Eqs. ( 11 , 12 ) are introduced into the position updating equation. And they can attract the particle towards positions of the best-so-far solution in the search space.

New local optimal jump-out strategy is added for escaping from the local optimal. When the value of the fitness function for the population optimal particles does not change in M iterations, the algorithm determines that the population falls into a local optimal. The scheme in which the population jumps out of the local optimum is to reset the position information of the 40% of individuals within the population, in other words, to randomly generate the position vector in the search space. M is set to 5% of the maximum number of iterations.

New spiral update search strategy is added after the local optimal jump-out strategy. Since the whale optimization algorithm (WOA) was good at exploring the local search space 35 , the spiral update search strategy in the WOA 36 is introduced to update the position of the particles after the swarm jumps out of local optimal. The equation for the spiral update is as follows:

Here \(D=\left|{x}_{i}\left(k\right)-Gbest\right|\) denotes the distance between the particle itself and the global optimal solution so far. \(B\) is the constant that defines the shape of the logarithmic spiral. \(l\) is the random value in \([-\mathrm{1,1}]\) . \(l\) represents the distance between the newly generated particle and the global optimal position, \(l=-1\) means the closest distance, while \(l=1\) means the farthest distance, and the meaning of this parameter can be directly observed by Fig.  1 .

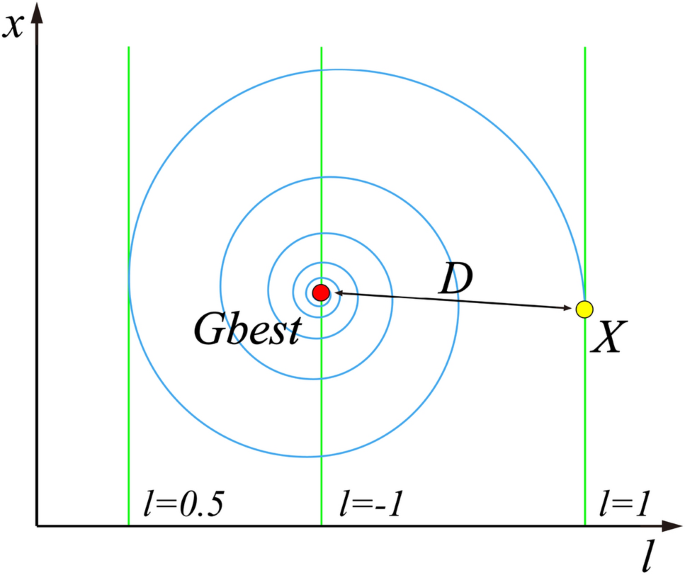
Spiral updating position.

The DE/best/2 mutation strategy is introduced to form the mutant particle. 4 individuals in the population are randomly selected that differ from the current particle, then the vector difference between them is rescaled, and the difference vector is combined with the global optimal position to form the mutant particle. The equation for mutation of particle position is shown as follows:

where \({x}^{*}\) is the mutated particle, \(F\) is the scale factor of mutation, \({r}_{1}\) , \({r}_{2}\) , \({r}_{3}\) , \({r}_{4}\) are random integer values in \((0,n]\) and not equal to \(i\) , respectively. Specific particles are selected for mutation with the screening conditions as follows:

where \(Cr\) represents the probability of mutation, \(rand\left(\mathrm{0,1}\right)\) is a random number in \(\left(\mathrm{0,1}\right)\) , and \({i}_{rand}\) is a random integer value in \((0,n]\) .

The improved PSO incorporates the search ideas of other intelligent algorithms (DE, WOA), so the improved algorithm proposed in this paper is named NDWPSO. The pseudo-code for the NDWPSO algorithm is given as follows:

The main procedure of NDWPSO.

Comparing the distribution of inertia weight parameters

There are several improved PSO algorithms (such as CDWPSO 25 , and SDWPSO 26 ) that adopt the dynamic weighted particle position update strategy as their improvement strategy. The updated equations of the CDWPSO and the SDWPSO algorithm for the inertia weight parameters are given as follows:

where \({\text{A}}\) is a value in \((\mathrm{0,1}]\) . \({r}_{max}\) and \({r}_{min}\) are the upper and lower limits of the fluctuation range of the inertia weight parameters, \(k\) is the current number of algorithm iterations, and \(Mk\) denotes the maximum number of iterations.

Considering that the update method of inertia weight parameters by our proposed NDWPSO is comparable to the CDWPSO, and SDWPSO, a comparison experiment for the distribution of inertia weight parameters is set up in this section. The maximum number of iterations in the experiment is \(Mk=500\) . The distributions of CDWPSO, SDWPSO, and NDWPSO inertia weights are shown sequentially in Fig.  2 .

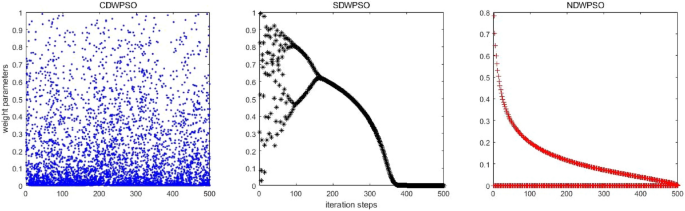
The inertial weight distribution of CDWPSO, SDWPSO, and NDWPSO.

In Fig.  2 , the inertia weight value of CDWPSO is a random value in (0,1]. It may make individual particles fly out of the range in the late iteration of the algorithm. Similarly, the inertia weight value of SDWPSO is a value that tends to zero infinitely, so that the swarm no longer can fly in the search space, making the algorithm extremely easy to fall into the local optimal value. On the other hand, the distribution of the inertia weights of the NDWPSO forms a gentle slope by two curves. Thus, the swarm can faster lock the global optimum range in the early iterations and locate the global optimal more precisely in the late iterations. The reason is that the inertia weight values between two adjacent iterations are inversely proportional to each other. Besides, the time-varying part of the inertial weight within NDWPSO is designed to reduce the chaos characteristic of the parameters. The inertia weight value of NDWPSO avoids the disadvantages of the above two schemes, so its design is more reasonable.

Experiment and discussion

In this section, three experiments are set up to evaluate the performance of NDWPSO: (1) the experiment of 23 classical functions 37 between NDWPSO and three particle swarm algorithms (PSO 6 , CDWPSO 25 , SDWPSO 26 ); (2) the experiment of benchmark test functions between NDWPSO and other intelligent algorithms (Whale Optimization Algorithm (WOA) 36 , Harris Hawk Algorithm (HHO) 38 , Gray Wolf Optimization Algorithm (GWO) 39 , Archimedes Algorithm (AOA) 40 , Equilibrium Optimizer (EO) 41 and Differential Evolution (DE) 42 ); (3) the experiment for solving three real engineering problems (welded beam design 43 , pressure vessel design 44 , and three-bar truss design 38 ). All experiments are run on a computer with Intel i5-11400F GPU, 2.60 GHz, 16 GB RAM, and the code is written with MATLAB R2017b.

The benchmark test functions are 23 classical functions, which consist of indefinite unimodal (F1–F7), indefinite dimensional multimodal functions (F8–F13), and fixed-dimensional multimodal functions (F14–F23). The unimodal benchmark function is used to evaluate the global search performance of different algorithms, while the multimodal benchmark function reflects the ability of the algorithm to escape from the local optimal. The mathematical equations of the benchmark functions are shown and found as Supplementary Tables S1 – S3 online.

Experiments on benchmark functions between NDWPSO, and other PSO variants

The purpose of the experiment is to show the performance advantages of the NDWPSO algorithm. Here, the dimensions and corresponding population sizes of 13 benchmark functions (7 unimodal and 6 multimodal) are set to (30, 40), (50, 70), and (100, 130). The population size of 10 fixed multimodal functions is set to 40. Each algorithm is repeated 30 times independently, and the maximum number of iterations is 200. The performance of the algorithm is measured by the mean and the standard deviation (SD) of the results for different benchmark functions. The parameters of the NDWPSO are set as: \({[{\omega }_{min},\omega }_{max}]=[\mathrm{0.4,0.9}]\) , \(\left[{c}_{max},{c}_{min}\right]=\left[\mathrm{2.5,1.5}\right],{V}_{max}=0.1,b={e}^{-50}, M=0.05\times Mk, B=1,F=0.7, Cr=0.9.\) And, \(A={\omega }_{max}\) for CDWPSO; \({[r}_{max},{r}_{min}]=[\mathrm{4,0}]\) for SDWPSO.

Besides, the experimental data are retained to two decimal places, but some experimental data will increase the number of retained data to pursue more accuracy in comparison. The best results in each group of experiments will be displayed in bold font. The experimental data is set to 0 if the value is below 10 –323 . The experimental parameter settings in this paper are different from the references (PSO 6 , CDWPSO 25 , SDWPSO 26 , so the final experimental data differ from the ones within the reference.

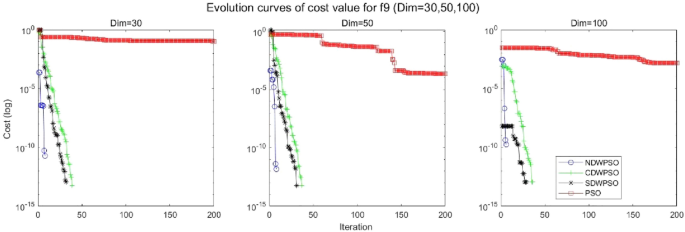
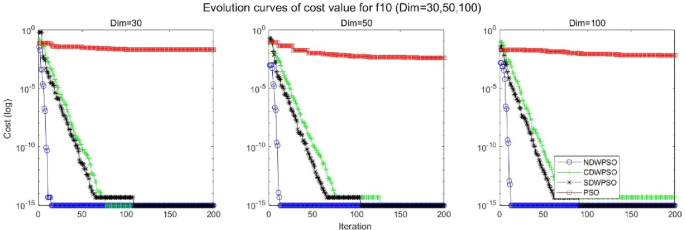
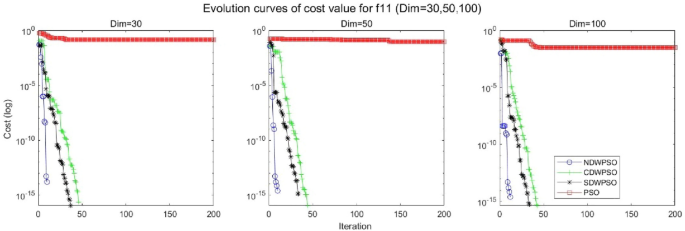
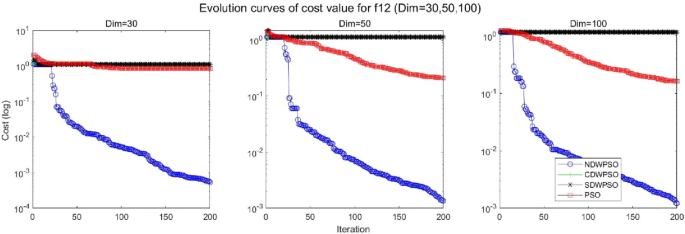
As shown in Tables 1 and 2 , the NDWPSO algorithm obtains better results for all 49 sets of data than other PSO variants, which include not only 13 indefinite-dimensional benchmark functions and 10 fixed-multimodal benchmark functions. Remarkably, the SDWPSO algorithm obtains the same accuracy of calculation as NDWPSO for both unimodal functions f 1 –f 4 and multimodal functions f 9 –f 11 . The solution accuracy of NDWPSO is higher than that of other PSO variants for fixed-multimodal benchmark functions f 14 -f 23 . The conclusion can be drawn that the NDWPSO has excellent global search capability, local search capability, and the capability for escaping the local optimal.

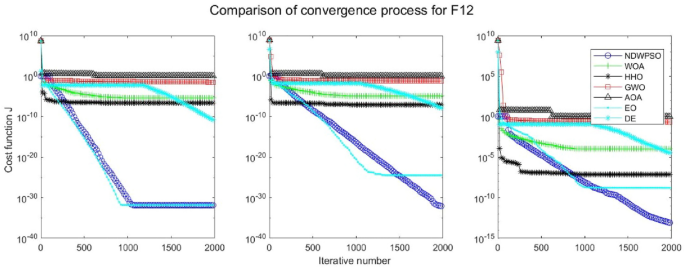
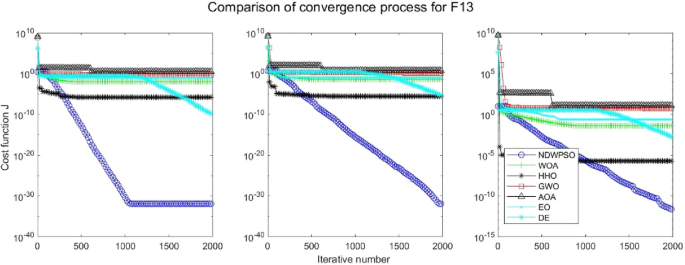
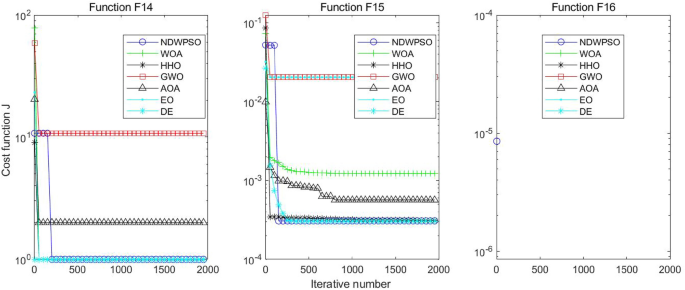
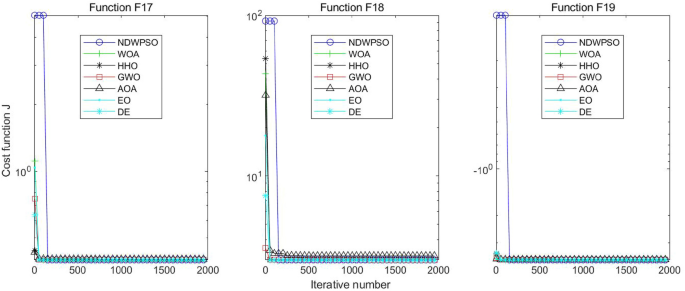
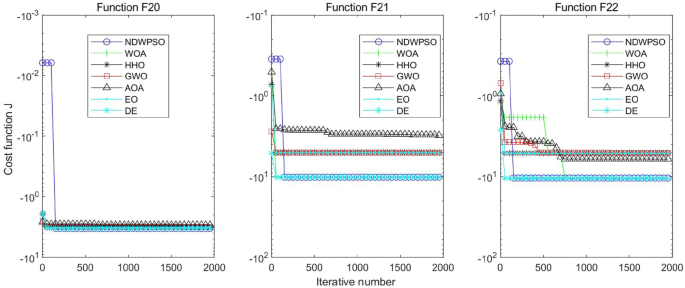
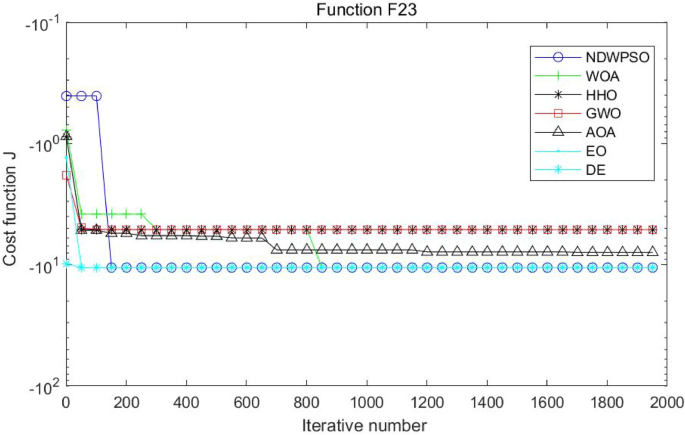
In addition, the convergence curves of the 23 benchmark functions are shown in Figs. 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15 , 16 , 17 , 18 and 19 . The NDWPSO algorithm has a faster convergence speed in the early stage of the search for processing functions f1-f6, f8-f14, f16, f17, and finds the global optimal solution with a smaller number of iterations. In the remaining benchmark function experiments, the NDWPSO algorithm shows no outstanding performance for convergence speed in the early iterations. There are two reasons of no outstanding performance in the early iterations. On one hand, the fixed-multimodal benchmark function has many disturbances and local optimal solutions in the whole search space. on the other hand, the initialization scheme based on elite opposition-based learning is still stochastic, which leads to the initial position far from the global optimal solution. The inertia weight based on chaotic mapping and the strategy of spiral updating can significantly improve the convergence speed and computational accuracy of the algorithm in the late search stage. Finally, the NDWPSO algorithm can find better solutions than other algorithms in the middle and late stages of the search.

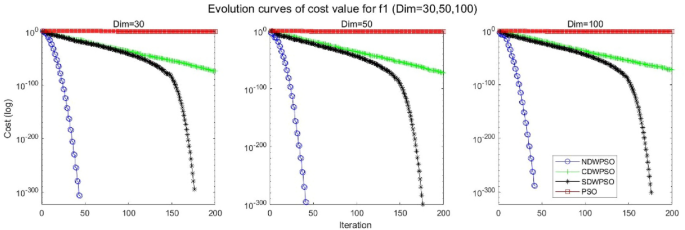
Evolution curve of NDWPSO and other PSO algorithms for f1 (Dim = 30,50,100).

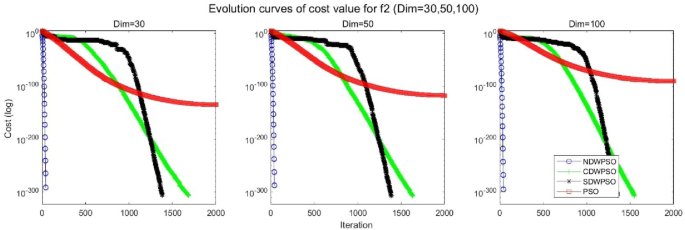
Evolution curve of NDWPSO and other PSO algorithms for f2 (Dim = 30,50,100).

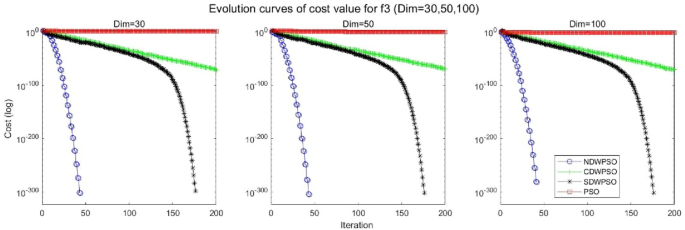
Evolution curve of NDWPSO and other PSO algorithms for f3 (Dim = 30,50,100).

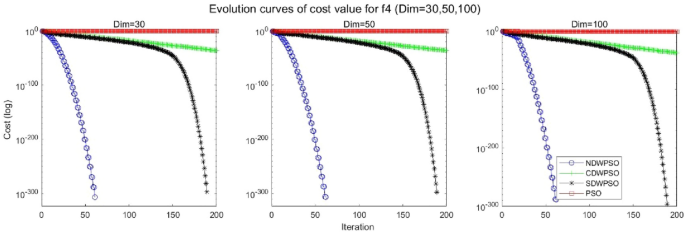
Evolution curve of NDWPSO and other PSO algorithms for f4 (Dim = 30,50,100).

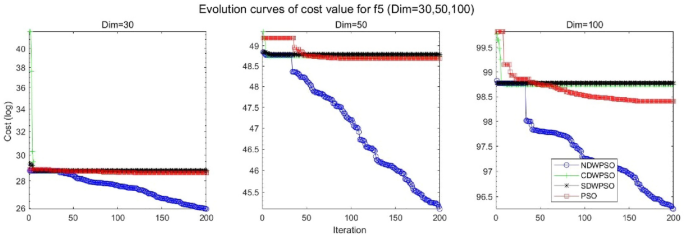
Evolution curve of NDWPSO and other PSO algorithms for f5 (Dim = 30,50,100).

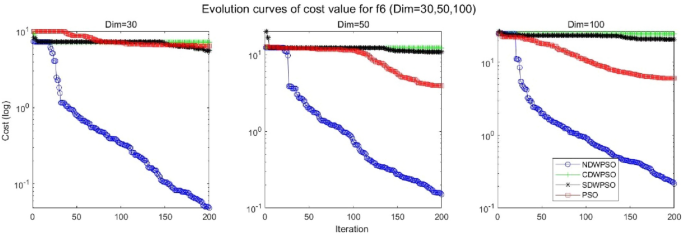
Evolution curve of NDWPSO and other PSO algorithms for f6 (Dim = 30,50,100).

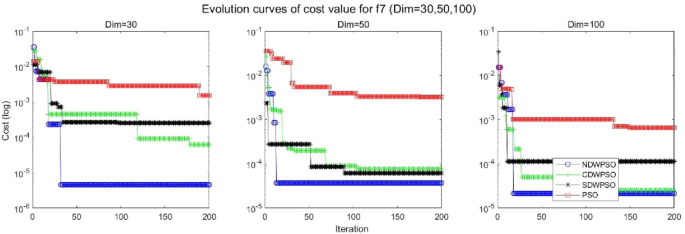
Evolution curve of NDWPSO and other PSO algorithms for f7 (Dim = 30,50,100).

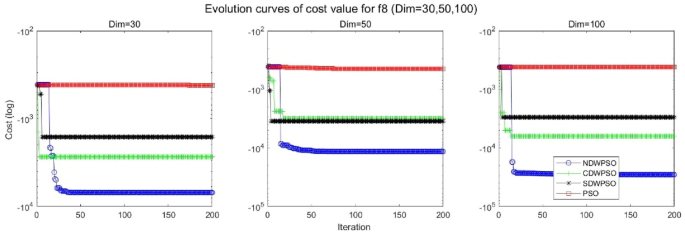
Evolution curve of NDWPSO and other PSO algorithms for f8 (Dim = 30,50,100).

Evolution curve of NDWPSO and other PSO algorithms for f9 (Dim = 30,50,100).

Evolution curve of NDWPSO and other PSO algorithms for f10 (Dim = 30,50,100).

Evolution curve of NDWPSO and other PSO algorithms for f11(Dim = 30,50,100).

Evolution curve of NDWPSO and other PSO algorithms for f12 (Dim = 30,50,100).

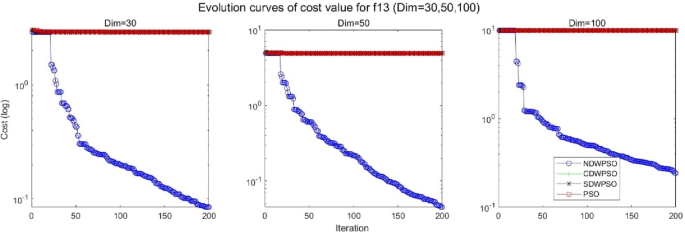
Evolution curve of NDWPSO and other PSO algorithms for f13 (Dim = 30,50,100).

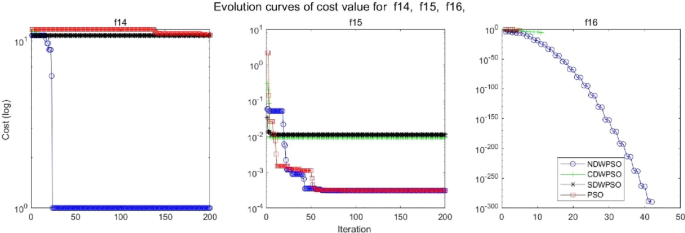
Evolution curve of NDWPSO and other PSO algorithms for f14, f15, f16.

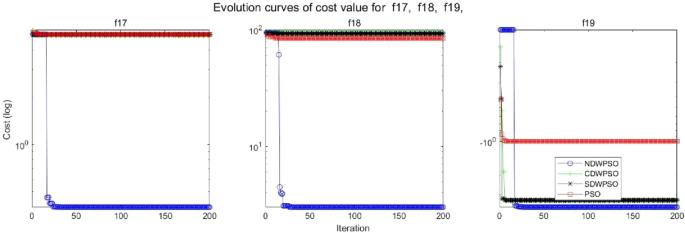
Evolution curve of NDWPSO and other PSO algorithms for f17, f18, f19.

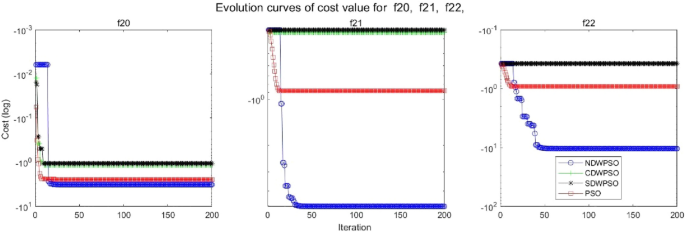
Evolution curve of NDWPSO and other PSO algorithms for f20, f21, f22.

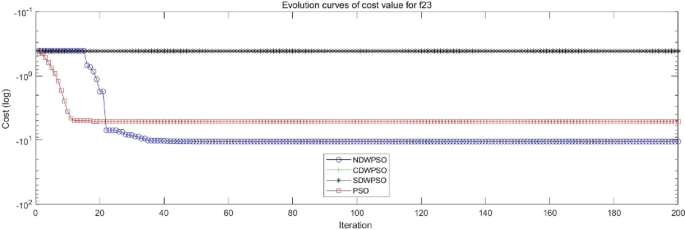
Evolution curve of NDWPSO and other PSO algorithms for f23.

To evaluate the performance of different PSO algorithms, a statistical test is conducted. Due to the stochastic nature of the meta-heuristics, it is not enough to compare algorithms based on only the mean and standard deviation values. The optimization results cannot be assumed to obey the normal distribution; thus, it is necessary to judge whether the results of the algorithms differ from each other in a statistically significant way. Here, the Wilcoxon non-parametric statistical test 45 is used to obtain a parameter called p -value to verify whether two sets of solutions are different to a statistically significant extent or not. Generally, it is considered that p  ≤ 0.5 can be considered as a statistically significant superiority of the results. The p -values calculated in Wilcoxon’s rank-sum test comparing NDWPSO and other PSO algorithms are listed in Table  3 for all benchmark functions. The p -values in Table  3 additionally present the superiority of the NDWPSO because all of the p -values are much smaller than 0.5.

In general, the NDWPSO has the fastest convergence rate when finding the global optimum from Figs. 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15 , 16 , 17 , 18 and 19 , and thus we can conclude that the NDWPSO is superior to the other PSO variants during the process of optimization.

Comparison experiments between NDWPSO and other intelligent algorithms

Experiments are conducted to compare NDWPSO with several other intelligent algorithms (WOA, HHO, GWO, AOA, EO and DE). The experimental object is 23 benchmark functions, and the experimental parameters of the NDWPSO algorithm are set the same as in Experiment 4.1. The maximum number of iterations of the experiment is increased to 2000 to fully demonstrate the performance of each algorithm. Each algorithm is repeated 30 times individually. The parameters of the relevant intelligent algorithms in the experiments are set as shown in Table 4 . To ensure the fairness of the algorithm comparison, all parameters are concerning the original parameters in the relevant algorithm literature. The experimental results are shown in Tables 5 , 6 , 7 and 8 and Figs. 20 , 21 , 22 , 23 , 24 , 25 , 26 , 27 , 28 , 29 , 30 , 31 , 32 , 33 , 34 , 35 and 36 .

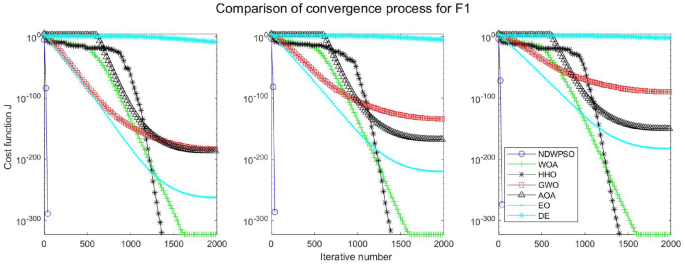
Evolution curve of NDWPSO and other algorithms for f1 (Dim = 30,50,100).

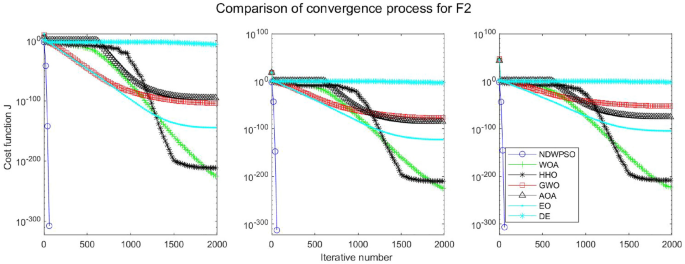
Evolution curve of NDWPSO and other algorithms for f2 (Dim = 30,50,100).

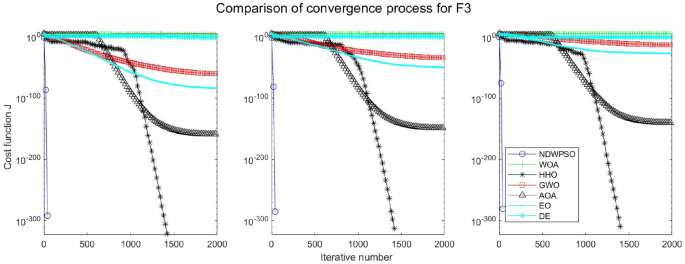
Evolution curve of NDWPSO and other algorithms for f3(Dim = 30,50,100).

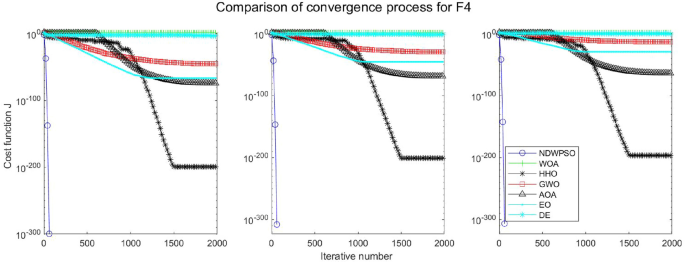
Evolution curve of NDWPSO and other algorithms for f4 (Dim = 30,50,100).

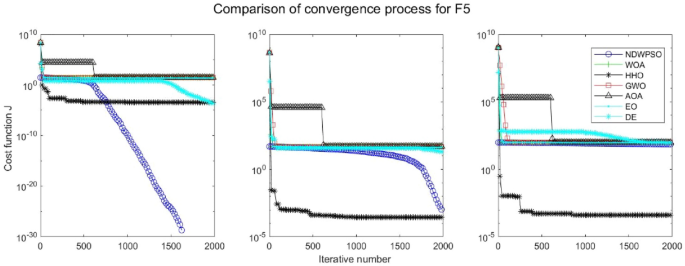
Evolution curve of NDWPSO and other algorithms for f5 (Dim = 30,50,100).

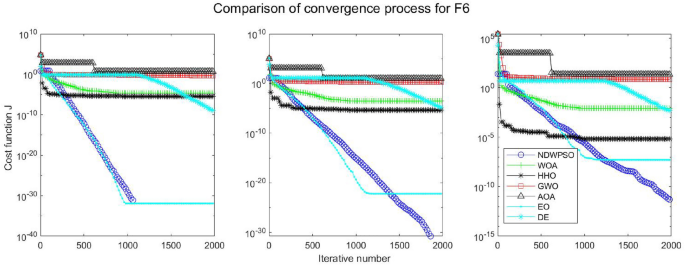
Evolution curve of NDWPSO and other algorithms for f6 (Dim = 30,50,100).

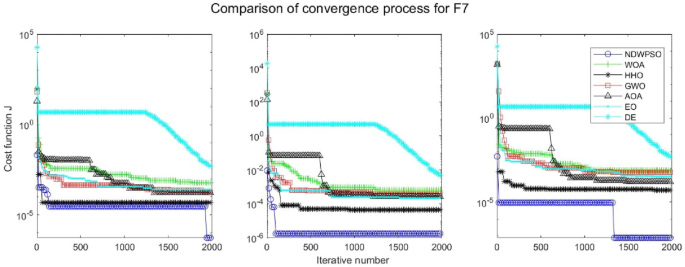
Evolution curve of NDWPSO and other algorithms for f7 (Dim = 30,50,100).

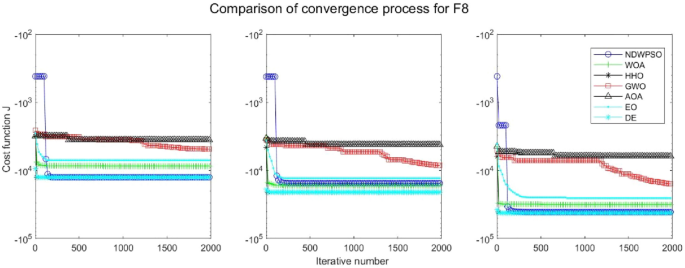
Evolution curve of NDWPSO and other algorithms for f8 (Dim = 30,50,100).

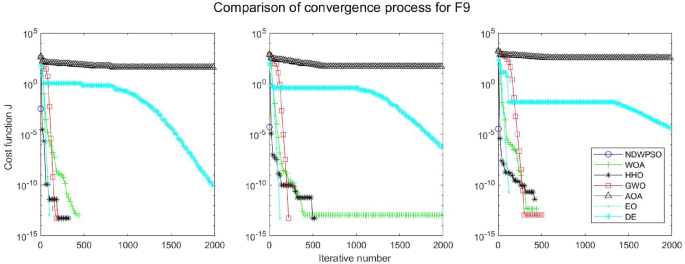
Evolution curve of NDWPSO and other algorithms for f9(Dim = 30,50,100).

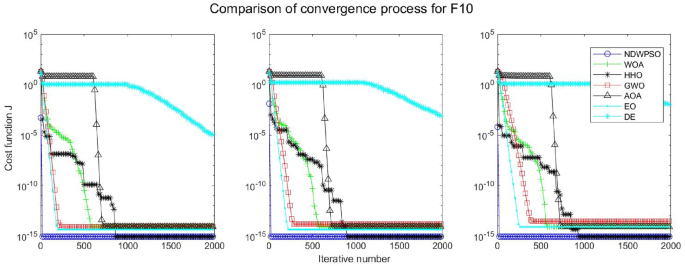
Evolution curve of NDWPSO and other algorithms for f10 (Dim = 30,50,100).

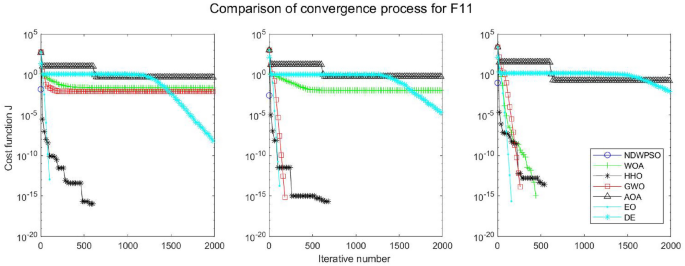
Evolution curve of NDWPSO and other algorithms for f11 (Dim = 30,50,100).

Evolution curve of NDWPSO and other algorithms for f12 (Dim = 30,50,100).

Evolution curve of NDWPSO and other algorithms for f13 (Dim = 30,50,100).

Evolution curve of NDWPSO and other algorithms for f14, f15, f16.

Evolution curve of NDWPSO and other algorithms for f17, f18, f19.

Evolution curve of NDWPSO and other algorithms for f20, f21, f22.

Evolution curve of NDWPSO and other algorithms for f23.

The experimental data of NDWPSO and other intelligent algorithms for handling 30, 50, and 100-dimensional benchmark functions ( \({f}_{1}-{f}_{13}\) ) are recorded in Tables 8 , 9 and 10 , respectively. The comparison data of fixed-multimodal benchmark tests ( \({f}_{14}-{f}_{23}\) ) are recorded in Table 11 . According to the data in Tables 5 , 6 and 7 , the NDWPSO algorithm obtains 69.2%, 84.6%, and 84.6% of the best results for the benchmark function ( \({f}_{1}-{f}_{13}\) ) in the search space of three dimensions (Dim = 30, 50, 100), respectively. In Table 8 , the NDWPSO algorithm obtains 80% of the optimal solutions in 10 fixed-multimodal benchmark functions.

The convergence curves of each algorithm are shown in Figs. 20 , 21 , 22 , 23 , 24 , 25 , 26 , 27 , 28 , 29 , 30 , 31 , 32 , 33 , 34 , 35 and 36 . The NDWPSO algorithm demonstrates two convergence behaviors when calculating the benchmark functions in 30, 50, and 100-dimensional search spaces. The first behavior is the fast convergence of NDWPSO with a small number of iterations at the beginning of the search. The reason is that the Iterative-mapping strategy and the position update scheme of dynamic weighting are used in the NDWPSO algorithm. This scheme can quickly target the region in the search space where the global optimum is located, and then precisely lock the optimal solution. When NDWPSO processes the functions \({f}_{1}-{f}_{4}\) , and \({f}_{9}-{f}_{11}\) , the behavior can be reflected in the convergence trend of their corresponding curves. The second behavior is that NDWPSO gradually improves the convergence accuracy and rapidly approaches the global optimal in the middle and late stages of the iteration. The NDWPSO algorithm fails to converge quickly in the early iterations, which is possible to prevent the swarm from falling into a local optimal. The behavior can be demonstrated by the convergence trend of the curves when NDWPSO handles the functions \({f}_{6}\) , \({f}_{12}\) , and \({f}_{13}\) , and it also shows that the NDWPSO algorithm has an excellent ability of local search.

Combining the experimental data with the convergence curves, it is concluded that the NDWPSO algorithm has a faster convergence speed, so the effectiveness and global convergence of the NDWPSO algorithm are more outstanding than other intelligent algorithms.

Experiments on classical engineering problems

Three constrained classical engineering design problems (welded beam design, pressure vessel design 43 , and three-bar truss design 38 ) are used to evaluate the NDWPSO algorithm. The experiments are the NDWPSO algorithm and 5 other intelligent algorithms (WOA 36 , HHO, GWO, AOA, EO 41 ). Each algorithm is provided with the maximum number of iterations and population size ( \({\text{Mk}}=500,\mathrm{ n}=40\) ), and then repeats 30 times, independently. The parameters of the algorithms are set the same as in Table 4 . The experimental results of three engineering design problems are recorded in Tables 9 , 10 and 11 in turn. The result data is the average value of the solved data.

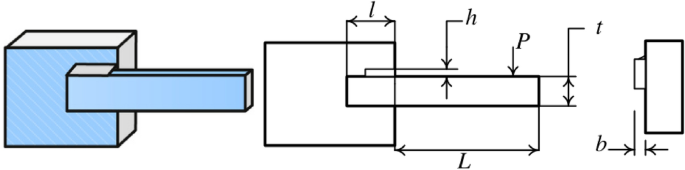
Welded beam design

The target of the welded beam design problem is to find the optimal manufacturing cost for the welded beam with the constraints, as shown in Fig.  37 . The constraints are the thickness of the weld seam ( \({\text{h}}\) ), the length of the clamped bar ( \({\text{l}}\) ), the height of the bar ( \({\text{t}}\) ) and the thickness of the bar ( \({\text{b}}\) ). The mathematical formulation of the optimization problem is given as follows:

Welded beam design.

In Table 9 , the NDWPSO, GWO, and EO algorithms obtain the best optimal cost. Besides, the standard deviation (SD) of t NDWPSO is the lowest, which means it has very good results in solving the welded beam design problem.

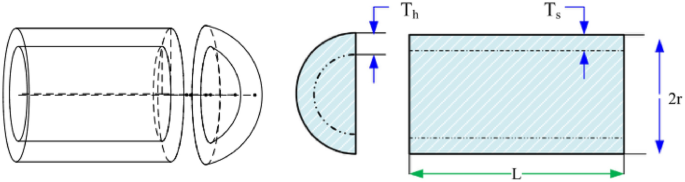
Pressure vessel design

Kannan and Kramer 43 proposed the pressure vessel design problem as shown in Fig.  38 to minimize the total cost, including the cost of material, forming, and welding. There are four design optimized objects: the thickness of the shell \({T}_{s}\) ; the thickness of the head \({T}_{h}\) ; the inner radius \({\text{R}}\) ; the length of the cylindrical section without considering the head \({\text{L}}\) . The problem includes the objective function and constraints as follows:

Pressure vessel design.

The results in Table 10 show that the NDWPSO algorithm obtains the lowest optimal cost with the same constraints and has the lowest standard deviation compared with other algorithms, which again proves the good performance of NDWPSO in terms of solution accuracy.

Three-bar truss design

This structural design problem 44 is one of the most widely-used case studies as shown in Fig.  39 . There are two main design parameters: the area of the bar1 and 3 ( \({A}_{1}={A}_{3}\) ) and area of bar 2 ( \({A}_{2}\) ). The objective is to minimize the weight of the truss. This problem is subject to several constraints as well: stress, deflection, and buckling constraints. The problem is formulated as follows:

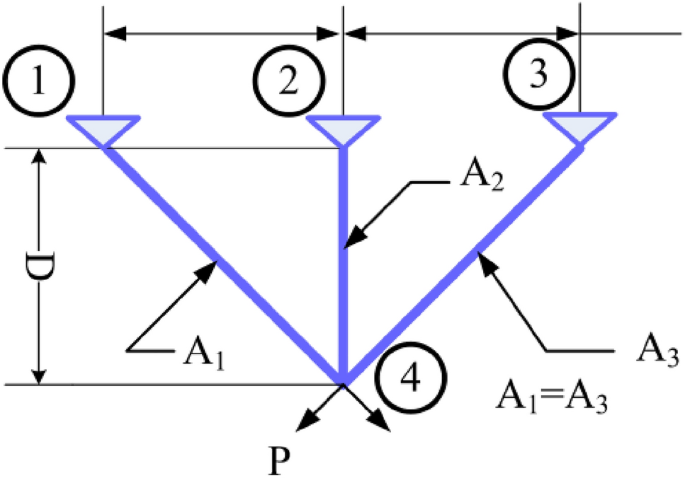
Three-bar truss design.

From Table 11 , NDWPSO obtains the best design solution in this engineering problem and has the smallest standard deviation of the result data. In summary, the NDWPSO can reveal very competitive results compared to other intelligent algorithms.

Conclusions and future works

An improved algorithm named NDWPSO is proposed to enhance the solving speed and improve the computational accuracy at the same time. The improved NDWPSO algorithm incorporates the search ideas of other intelligent algorithms (DE, WOA). Besides, we also proposed some new hybrid strategies to adjust the distribution of algorithm parameters (such as the inertia weight parameter, the acceleration coefficients, the initialization scheme, the position updating equation, and so on).

23 classical benchmark functions: indefinite unimodal (f1-f7), indefinite multimodal (f8-f13), and fixed-dimensional multimodal(f14-f23) are applied to evaluate the effective line and feasibility of the NDWPSO algorithm. Firstly, NDWPSO is compared with PSO, CDWPSO, and SDWPSO. The simulation results can prove the exploitative, exploratory, and local optima avoidance of NDWPSO. Secondly, the NDWPSO algorithm is compared with 5 other intelligent algorithms (WOA, HHO, GWO, AOA, EO). The NDWPSO algorithm also has better performance than other intelligent algorithms. Finally, 3 classical engineering problems are applied to prove that the NDWPSO algorithm shows superior results compared to other algorithms for the constrained engineering optimization problems.

Although the proposed NDWPSO is superior in many computation aspects, there are still some limitations and further improvements are needed. The NDWPSO performs a limit initialize on each particle by the strategy of “elite opposition-based learning”, it takes more computation time before speed update. Besides, the” local optimal jump-out” strategy also brings some random process. How to reduce the random process and how to improve the limit initialize efficiency are the issues that need to be further discussed. In addition, in future work, researchers will try to apply the NDWPSO algorithm to wider fields to solve more complex and diverse optimization problems.

Data availability

The datasets used and/or analyzed during the current study available from the corresponding author on reasonable request.

Sami, F. Optimize electric automation control using artificial intelligence (AI). Optik 271 , 170085 (2022).

Article   ADS   Google Scholar  

Li, X. et al. Prediction of electricity consumption during epidemic period based on improved particle swarm optimization algorithm. Energy Rep. 8 , 437–446 (2022).

Article   Google Scholar  

Sun, B. Adaptive modified ant colony optimization algorithm for global temperature perception of the underground tunnel fire. Case Stud. Therm. Eng. 40 , 102500 (2022).

Bartsch, G. et al. Use of artificial intelligence and machine learning algorithms with gene expression profiling to predict recurrent nonmuscle invasive urothelial carcinoma of the bladder. J. Urol. 195 (2), 493–498 (2016).

Article   PubMed   Google Scholar  

Bao, Z. Secure clustering strategy based on improved particle swarm optimization algorithm in internet of things. Comput. Intell. Neurosci. 2022 , 1–9 (2022).

Google Scholar  

Kennedy, J. & Eberhart, R. Particle swarm optimization. In: Proceedings of ICNN'95-International Conference on Neural Networks . IEEE, 1942–1948 (1995).

Lin, Q. et al. A novel artificial bee colony algorithm with local and global information interaction. Appl. Soft Comput. 62 , 702–735 (2018).

Abed-alguni, B. H. et al. Exploratory cuckoo search for solving single-objective optimization problems. Soft Comput. 25 (15), 10167–10180 (2021).

Brajević, I. A shuffle-based artificial bee colony algorithm for solving integer programming and minimax problems. Mathematics 9 (11), 1211 (2021).

Khan, A. T. et al. Non-linear activated beetle antennae search: A novel technique for non-convex tax-aware portfolio optimization problem. Expert Syst. Appl. 197 , 116631 (2022).

Brajević, I. et al. Hybrid sine cosine algorithm for solving engineering optimization problems. Mathematics 10 (23), 4555 (2022).

Abed-Alguni, B. H., Paul, D. & Hammad, R. Improved Salp swarm algorithm for solving single-objective continuous optimization problems. Appl. Intell. 52 (15), 17217–17236 (2022).

Nadimi-Shahraki, M. H. et al. Binary starling murmuration optimizer algorithm to select effective features from medical data. Appl. Sci. 13 (1), 564 (2022).

Nadimi-Shahraki, M. H. et al. A systematic review of the whale optimization algorithm: Theoretical foundation, improvements, and hybridizations. Archiv. Comput. Methods Eng. 30 (7), 4113–4159 (2023).

Fatahi, A., Nadimi-Shahraki, M. H. & Zamani, H. An improved binary quantum-based avian navigation optimizer algorithm to select effective feature subset from medical data: A COVID-19 case study. J. Bionic Eng. 21 (1), 426–446 (2024).

Abed-alguni, B. H. & AL-Jarah, S. H. IBJA: An improved binary DJaya algorithm for feature selection. J. Comput. Sci. 75 , 102201 (2024).

Yeh, W.-C. A novel boundary swarm optimization method for reliability redundancy allocation problems. Reliab. Eng. Syst. Saf. 192 , 106060 (2019).

Solomon, S., Thulasiraman, P. & Thulasiram, R. Collaborative multi-swarm PSO for task matching using graphics processing units. In: Proceedings of the 13th Annual Conference on Genetic and Evolutionary Computation 1563–1570 (2011).

Mukhopadhyay, S. & Banerjee, S. Global optimization of an optical chaotic system by chaotic multi swarm particle swarm optimization. Expert Syst. Appl. 39 (1), 917–924 (2012).

Duan, L. et al. Improved particle swarm optimization algorithm for enhanced coupling of coaxial optical communication laser. Opt. Fiber Technol. 64 , 102559 (2021).

Sun, F., Xu, Z. & Zhang, D. Optimization design of wind turbine blade based on an improved particle swarm optimization algorithm combined with non-gaussian distribution. Adv. Civ. Eng. 2021 , 1–9 (2021).

Liu, M. et al. An improved particle-swarm-optimization algorithm for a prediction model of steel slab temperature. Appl. Sci. 12 (22), 11550 (2022).

Article   MathSciNet   CAS   Google Scholar  

Gad, A. G. Particle swarm optimization algorithm and its applications: A systematic review. Archiv. Comput. Methods Eng. 29 (5), 2531–2561 (2022).

Article   MathSciNet   Google Scholar  

Feng, H. et al. Trajectory control of electro-hydraulic position servo system using improved PSO-PID controller. Autom. Constr. 127 , 103722 (2021).

Chen, Ke., Zhou, F. & Liu, A. Chaotic dynamic weight particle swarm optimization for numerical function optimization. Knowl. Based Syst. 139 , 23–40 (2018).

Bai, B. et al. Reliability prediction-based improved dynamic weight particle swarm optimization and back propagation neural network in engineering systems. Expert Syst. Appl. 177 , 114952 (2021).

Alsaidy, S. A., Abbood, A. D. & Sahib, M. A. Heuristic initialization of PSO task scheduling algorithm in cloud computing. J. King Saud Univ. –Comput. Inf. Sci. 34 (6), 2370–2382 (2022).

Liu, H., Cai, Z. & Wang, Y. Hybridizing particle swarm optimization with differential evolution for constrained numerical and engineering optimization. Appl. Soft Comput. 10 (2), 629–640 (2010).

Deng, W. et al. A novel intelligent diagnosis method using optimal LS-SVM with improved PSO algorithm. Soft Comput. 23 , 2445–2462 (2019).

Huang, M. & Zhen, L. Research on mechanical fault prediction method based on multifeature fusion of vibration sensing data. Sensors 20 (1), 6 (2019).

Article   ADS   PubMed   PubMed Central   Google Scholar  

Wolpert, D. H. & Macready, W. G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1 (1), 67–82 (1997).

Gandomi, A. H. et al. Firefly algorithm with chaos. Commun. Nonlinear Sci. Numer. Simul. 18 (1), 89–98 (2013).

Article   ADS   MathSciNet   Google Scholar  

Zhou, Y., Wang, R. & Luo, Q. Elite opposition-based flower pollination algorithm. Neurocomputing 188 , 294–310 (2016).

Li, G., Niu, P. & Xiao, X. Development and investigation of efficient artificial bee colony algorithm for numerical function optimization. Appl. Soft Comput. 12 (1), 320–332 (2012).

Xiong, G. et al. Parameter extraction of solar photovoltaic models by means of a hybrid differential evolution with whale optimization algorithm. Solar Energy 176 , 742–761 (2018).

Mirjalili, S. & Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 95 , 51–67 (2016).

Yao, X., Liu, Y. & Lin, G. Evolutionary programming made faster. IEEE Trans. Evol. Comput. 3 (2), 82–102 (1999).

Heidari, A. A. et al. Harris hawks optimization: Algorithm and applications. Fut. Gener. Comput. Syst. 97 , 849–872 (2019).

Mirjalili, S., Mirjalili, S. M. & Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 69 , 46–61 (2014).

Hashim, F. A. et al. Archimedes optimization algorithm: A new metaheuristic algorithm for solving optimization problems. Appl. Intell. 51 , 1531–1551 (2021).

Faramarzi, A. et al. Equilibrium optimizer: A novel optimization algorithm. Knowl. -Based Syst. 191 , 105190 (2020).

Pant, M. et al. Differential evolution: A review of more than two decades of research. Eng. Appl. Artif. Intell. 90 , 103479 (2020).

Coello, C. A. C. Use of a self-adaptive penalty approach for engineering optimization problems. Comput. Ind. 41 (2), 113–127 (2000).

Kannan, B. K. & Kramer, S. N. An augmented lagrange multiplier based method for mixed integer discrete continuous optimization and its applications to mechanical design. J. Mech. Des. 116 , 405–411 (1994).

Derrac, J. et al. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol. Comput. 1 (1), 3–18 (2011).

Download references

Acknowledgements

This work was supported by Key R&D plan of Shandong Province, China (2021CXGC010207, 2023CXGC01020); First batch of talent research projects of Qilu University of Technology in 2023 (2023RCKY116); Introduction of urgently needed talent projects in Key Supported Regions of Shandong Province; Key Projects of Natural Science Foundation of Shandong Province (ZR2020ME116); the Innovation Ability Improvement Project for Technology-based Small- and Medium-sized Enterprises of Shandong Province (2022TSGC2051, 2023TSGC0024, 2023TSGC0931); National Key R&D Program of China (2019YFB1705002), LiaoNing Revitalization Talents Program (XLYC2002041) and Young Innovative Talents Introduction & Cultivation Program for Colleges and Universities of Shandong Province (Granted by Department of Education of Shandong Province, Sub-Title: Innovative Research Team of High Performance Integrated Device).

Author information

Authors and affiliations.

School of Mechanical and Automotive Engineering, Qilu University of Technology (Shandong Academy of Sciences), Jinan, 250353, China

Jinwei Qiao, Guangyuan Wang, Zhi Yang, Jun Chen & Pengbo Liu

Shandong Institute of Mechanical Design and Research, Jinan, 250353, China

School of Information Science and Engineering, Northeastern University, Shenyang, 110819, China

Xiaochuan Luo

Fushun Supervision Inspection Institute for Special Equipment, Fushun, 113000, China

You can also search for this author in PubMed   Google Scholar

Contributions

Z.Y., J.Q., and G.W. wrote the main manuscript text and prepared all figures and tables. J.C., P.L., K.L., and X.L. were responsible for the data curation and software. All authors reviewed the manuscript.

Corresponding author

Correspondence to Zhi Yang .

Ethics declarations

Competing interests.

The authors declare no competing interests.

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary Information

Supplementary information., rights and permissions.

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Cite this article.

Qiao, J., Wang, G., Yang, Z. et al. A hybrid particle swarm optimization algorithm for solving engineering problem. Sci Rep 14 , 8357 (2024). https://doi.org/10.1038/s41598-024-59034-2

Download citation

Received : 11 January 2024

Accepted : 05 April 2024

Published : 10 April 2024

DOI : https://doi.org/10.1038/s41598-024-59034-2

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Particle swarm optimization
• Elite opposition-based learning
• Iterative mapping
• Convergence analysis

By submitting a comment you agree to abide by our Terms and Community Guidelines . If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

Quick links

• Explore articles by subject
• Guide to authors
• Editorial policies

Sign up for the Nature Briefing: AI and Robotics newsletter — what matters in AI and robotics research, free to your inbox weekly.

MCHIAO: a modified coronavirus herd immunity-Aquila optimization algorithm based on chaotic behavior for solving engineering problems

• Original Article
• Open access
• Published: 20 April 2024

Cite this article

You have full access to this open access article

• Heba Selim 1 ,
• Amira Y. Haikal 1 ,
• Labib M. Labib 1 &
• Mahmoud M. Saafan   ORCID: orcid.org/0000-0002-9279-1537 1  

This paper proposes a hybrid Modified Coronavirus Herd Immunity Aquila Optimization Algorithm (MCHIAO) that compiles the Enhanced Coronavirus Herd Immunity Optimizer (ECHIO) algorithm and Aquila Optimizer (AO). As one of the competitive human-based optimization algorithms, the Coronavirus Herd Immunity Optimizer (CHIO) exceeds some other biological-inspired algorithms. Compared to other optimization algorithms, CHIO showed good results. However, CHIO gets confined to local optima, and the accuracy of large-scale global optimization problems is decreased. On the other hand, although AO has significant local exploitation capabilities, its global exploration capabilities are insufficient. Subsequently, a novel metaheuristic optimizer, Modified Coronavirus Herd Immunity Aquila Optimizer (MCHIAO), is presented to overcome these restrictions and adapt it to solve feature selection challenges. In this paper, MCHIAO is proposed with three main enhancements to overcome these issues and reach higher optimal results which are cases categorizing, enhancing the new genes’ value equation using the chaotic system as inspired by the chaotic behavior of the coronavirus and generating a new formula to switch between expanded and narrowed exploitation. MCHIAO demonstrates it’s worth contra ten well-known state-of-the-art optimization algorithms (GOA, MFO, MPA, GWO, HHO, SSA, WOA, IAO, NOA, NGO) in addition to AO and CHIO. Friedman average rank and Wilcoxon statistical analysis ( p -value) are conducted on all state-of-the-art algorithms testing 23 benchmark functions. Wilcoxon test and Friedman are conducted as well on the 29 CEC2017 functions. Moreover, some statistical tests are conducted on the 10 CEC2019 benchmark functions. Six real-world problems are used to validate the proposed MCHIAO against the same twelve state-of-the-art algorithms. On classical functions, including 24 unimodal and 44 multimodal functions, respectively, the exploitative and explorative behavior of the hybrid algorithm MCHIAO is evaluated. The statistical significance of the proposed technique for all functions is demonstrated by the p -values calculated using the Wilcoxon rank-sum test, as these p -values are found to be less than 0.05.

Avoid common mistakes on your manuscript.

1 Introduction

We face a large number of optimization challenges in engineering, for which optimization methods are required [ 1 ]. Optimization algorithms help us in a variety of ways in our daily lives. Optimization algorithms can be used to reduce expenses and faults in any system or to increase profits in a financial firm. Optimization algorithms can be classified into two main categories: deterministic algorithms and stochastic algorithms.

Deterministic algorithms pursue a firm procedure where for the starting point the deterministic algorithm will follow up the same path whenever we run the program. On the other hand, stochastic algorithms are random in finding the optimum values. So, every time we run the program the solutions will be different [ 2 ]. Traditionally, deterministic algorithms are used to deal with optimization problems that are characterized as small dimensions and less complex problems. Despite their capability to reach an exact and specific solution to optimization problems, they experience some serious impasses, and they can easily fall into the local optimal solution [ 3 ]. We can say that stochastic algorithms can overcome deterministic algorithms’ impasses. Heuristic optimization algorithms are methods that improve the efficiency of a search process by sacrificing completeness, examples of these methods are Nearest Neighbor (Greedy Algorithm) and local search algorithms. Although they can reach a “near-optimal” solution in a short time and consume a small memory space, they cannot guarantee to reach the optimal solution or reach a solution that is "good enough" [ 4 ]. As a result, meta-heuristic algorithms emerged that combine heuristic techniques in an upper-level framework to explore a search space efficiently. Metaheuristic-based algorithms provide a framework for optimization that employs stochastic features that are controlled by tunable parameters with knowledge acquisition operators to improve the current solution until the best possible solution is found [ 5 ]. Interestingly enough, nature-inspired phenomena helped in generating the most meta-heuristic algorithms, which can be divided into categories as listed in Fig.  1 [ 6 ].

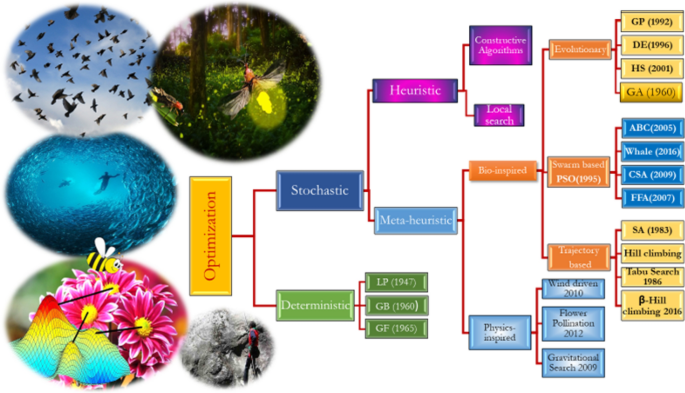
Optimization methods

Nevertheless, there is not a single optimization algorithm that can operate efficiently with all classes of optimization issues “according to the No Free Lunch (NFL) Theorem” [ 7 ]. The community-based behavior of animal flocks is often an inspiration for swarm-based algorithms. The ability to work together to survive is the main asset of such a class. Particle swarm optimization (PSO), which imitates the social behavior of flocking birds, is one of the first swarm-based algorithms [ 8 ]. The particles (solutions) search for the best position in their surroundings (search space) “global best”. Throughout the flight, the first-rate places (local best) on the road to the optimum locations are noted. The grasshopper optimization algorithm (GOA) is a novel swarm intelligence algorithm inspired by grasshoppers' natural foraging and swarming behavior [ 9 ]. Saremi et al. presented the GOA algorithm in [ 9 ], which is a fascinating new swarm intelligence system that simulates grasshopper foraging and swarming behaviors. Grasshoppers are insects that are well-known as pests that wreak havoc on agricultural production and agriculture [ 9 ]. Their life cycle is divided into two stages: nymph and adulthood. Small steps and gradual movements describe the nymph phase, but long-range and rapid movements represent the maturity phase. The intensification and diversification phases of GOA are defined by nymph and adult movements. Moth-Flame Optimization (MFO) algorithm is a new nature-inspired algorithm inspired by moths' transverse orientation mechanism [ 10 ]. MFO uses a set of moths to search the decision space, reporting fitness functions at each time step and tagging the best solution with a flame. The movement of moths is based on their flames spiraling around them in a spiral direction. The Marine Predators Algorithm (MPA) is another well-known nature-inspired optimization algorithm that follows the rules that regulate optimal foraging strategy and predator–prey encounter rates in marine ecosystems [ 11 ].

The main inspiration for MPA is a widely used foraging strategy in ocean predators, specifically Lévy and Brownian movements, as well as an optimal encounter rate policy in predator–prey biological interactions. While seeking food in a prey-scarce environment, marine predators (such as sharks, tunas, and marlines) use the Lévy strategy, but when foraging in a prey-abundant environment, the pattern is frequently shifted to Brownian motion [ 12 ]. In a biological interaction between predator and prey, the optimum encounter rate policy is also determined by the sort of movement that each predator/prey makes and the velocity ratio of prey to predator [ 13 ]. Grey Wolf Optimizer (GWO) is a new type of optimization approach for swarm intelligence inspired by grey wolves (Canis lupus) [ 14 ]. The GWO algorithm is simulated after the natural hierarchy of authority and hunting mechanism of grey wolves. For mimicking the leadership hierarchy, four types of grey wolves are used: alpha, beta, delta, and omega. Furthermore, the three basic processes of hunting are implemented: seeking prey, encircling prey, and attacking prey. Heidari et al. established Harris Hawks Optimization (HHO), a novel optimization algorithm inspired by the simulation of the behavior of Harris Hawks [ 15 ]. The algorithm's base is the simultaneous attack method of Harris Hawks from numerous directions. For the time being, comparing nature-inspired human-based algorithms such as HSA to other nature-inspired algorithms gives more pleasing results. The Salp swarm algorithm (SSA) is a newly developed bio-inspired optimization algorithm based on the swarming mechanism of salps, which was first presented in 2017 [ 16 ]. SSA is an evolutionary algorithm that mimics the natural swarming mechanism of salps. In 2016, the whale optimization algorithm (WOA) was proposed by Mirjalili and Lewis [ 17 ]. It's a swarm intelligence optimization system that mimics the hunting behavior of humpback whales. Metaheuristics solve intractable optimization problems. Since the initial metaheuristic was proposed, several new algorithms have been created [ 18 , 19 , 20 , 21 , 22 , 23 , 24 , 25 ]. The algorithm's main goal is to solve the objective problem by mimicking the predatory behavior of a whale. In this paper, a modification in the nature-inspired and human-based optimization technique which is known as “Coronavirus Herd Immunity Optimizer” is proposed. In the year 2019 in China, an evolution of a severe acute respiratory syndrome which is called coronavirus disease (COVID-19) caused a considerable global outbreak that gave rise to a major public health issue [ 26 ]. The coronavirus pandemic and specifically the herd immunity against COVID-19 gave the main concepts to the Coronavirus Herd Immunity Optimizer (CHIO) algorithm. Outperforming several other biologically inspired algorithms, the Coronavirus Herd Immunity Optimizer (CHIO) is a competitive human-based optimisation tool. Compared to other optimization approaches, CHIO performed efficiently. Nevertheless, CHIO can only handle local optima, which limits its accuracy in solving intricate global optimization problems. Consequently, the Coronavirus Herd Immunity Optimizer (CHIO) algorithm has a poor rate of convergence during the iterative process and is easily prone to falling into a local optimum in high-dimensional space, which is why we propose Enhanced Coronavirus Herd Immunity Optimizer (ECHIO). However, considering that AO has great local exploitation capabilities, its global exploration skills are restricted. The AO algorithm may exhibit early convergence and poor global exploration when used to optimize difficult, high-dimensional engineering problems. When optimizing complex multidimensional problems, the AO runs into challenges, such as poor exploration efficiency and poor convergence behavior. Then, in order to overcome these drawbacks, such as CHIO's poor exploitation skills and the AO algorithm's insufficient exploration capabilities, the Modified Coronavirus Herd Immunity Aquila Optimizer (MCHIAO), a novel metaheuristic optimizer, is presented. It is modified to handle feature selection issues. Three different contributions have been applied to the CHIO algorithm to increase exploration efficiency by keeping the ideal balance between it and the search's exploitation of an optimal solution. The main contributions of the current work can be summarized as:

Cases categorizing according to the status vector.

Enhancement of the gene's equations for new genes applying chaotic maps.

Generating a new formula for switching between narrowed and expanded exploitation.

Validate the proposed MCHIAO through testing against 12 state-of-the-art algorithms.

Wilcoxon statistical analysis and Friedman average rank are conducted to validate the proposed MCHIAO.

On 130 benchmark functions, the proposed hybrid algorithm's performance is evaluated. The benchmarks comprise 23 standard benchmark functions, 29 CEC-2017 test functions, 10 CEC-2019 test functions, 24 unimodal functions, and 44 multimodal functions.

Test the proposed MCHIAO algorithm on six real-world engineering problems.

The sections of this paper are organized in the following order:

Section  2 presents the CHIO algorithm, the inspiration beyond it, and its main concepts. The Aquila algorithm, its origins of inspiration, and its core perspectives are all presented in Sect.  3 . Section  4 outlines the proposed hybrid algorithm MCHIAO and the details of the contributions. Section  5 presents the results of a comparison between the MCHIAO algorithm, CHIO algorithm, Aquila algorithm, and other state-of-the-art algorithms applied to different benchmark functions with different dimensions and as well as 6 common real-world problems. Section  6 shows the conclusion and direction for future work.

2 Corona virus herd immunity optimization algorithm

2.1 inspiration.

The COVID-19 pandemic has been a global threat. Herd immunity is a highly effective method to tackle the COVID-19 pandemic [ 27 ]. The resistance to the spread of an infectious illness within a community or herd is known as “Herd Immunity.” On March 13th, the British Government’s chief scientific adviser, Sir Patrick Vallance pointed out that waiting for herd immunity would result in getting 60% of the population being infected with COVID-19. Herd immunity occurs when a considerable section of a community gets immune to a disease stopping its spread from one person to another. There are two ways to achieve herd immunity for COVID-19:

Without causing suffering or illness, vaccines create immunity and protect people against pandemics. Despite the effectiveness of the concept of vaccination, it has a serious drawback, some people may reject taking vaccines because of fear of the possible side effects and risks. Another drawback of the vaccine is that it may fade over time and requires revaccination. Natural infection is an effective path to obtaining herd immunity. It can be achieved when an appropriate portion of people in the community has recovered from a specific disease and have evolved antibodies that would work against future infection [ 28 ]. Herd immunity is suggested to be one of the mechanisms to control and slow down the COVID-19 widespread disease. Bear in mind that the CHIO algorithm put in an application “the survival of the fittest” principle from the Darwinian Theory. Herd immunity can be described as the indirect protection from contagion given to susceptible human beings when an appropriate proportion of immune persons exist in a population. The population-level effect is frequently considered in the vaccination programs which target to establish herd immunity for those who cannot be vaccinated and still be protected against contra disease. The susceptible-infectious-recovered (SIR) model has been widely utilized to survey the dynamic growth of COVID-19 in a large population [ 29 ]. The SIR model classifies the population into three categories:

Susceptible individuals: The virus has not yet infected these participants, but when a susceptible individual and an infectious individual come into infectious contact without following the recommended social distancing rules, they can be infected.

Infected individuals: Participants in this category have been verified to be infected, and they can spread the virus to others who are susceptible.

Recovered (immune) individuals: These are the individuals who are protected against the virus either because they have taken the vaccine or because they have been infected with the virus and recovered.

2.2 Mathematical model of CHIO [ 30 ]

In this section, the mathematical model of the CHIO algorithm is illustrated in steps

2.2.1 Initializing CHIO parameters

where \(f(x)\) is the objective function (immunity rate) and it is calculated for each case (individual).

where \({x}_{i}\) represents the gene (decision variable) indexed by \(i\) , while \(n\) represents the overall amount of decision variables in every case.

where \({lb}_{i}\) is the lower bound of the gene \({x}_{i}\) and \({ub}_{i}\) is the upper bound of it.

The CHIO algorithm has two control parameters:

Basic reproduction Rate ( \({BR}_{r}\) ): By spreading the virus among individuals, it controls the CHIO operators.

Maximum infected case age ( \({Max}_{Age}\) ): Determine the infected cases’ status when a case reaches \({Max}_{Age}\) , it is either recovered or died.

The CHIO algorithm has another four parameters:

\(Max\_Itr\) : Represents the maximum number of iterations.

\({C}_{0}\) : This value represents the number of primary infected cases, which is typically one.

\(HIS:\) Represents the population size.

\(n:\) Represents the problem dimensionality.

2.2.2 Generating herd immunity population:

Randomly CHIO generates a set of individuals (cases) as many as \(HIS\) . The set of the generated individuals is stored as a two-dimensional matrix of size \(n \times HIS\) in the herd immunity population ( \(HIP\) ) as follows:

where each row represents a case \({x}^{j}\) , which is calculated as follows:

For each case, the objective function is calculated using Eq. ( 1.1 ).

The fitness for each search agent is set as follows:

where \(S\) is the status vector of length \(HIS\) in the \(HIP\) for every case initiating from zero which means a case that is susceptible or rather one that represents an infected case.

2.2.3 Coronavirus herd immunity evolution

In this section, the main improvement loop of CHIO is presented. The gene ( \({x}_{i}^{j}\) ) of the case ( \({x}^{j}\) ) either remains the same or becomes classified as an infected, susceptible, or immune case according to the percentage of the basic reproduction rate ( \({BR}_{r}\) ) as follows:

where \(r\) is a random value between 0 and 1.

For infected cases:

where \({x}_{i}^{j}(t+1)\) is the new gene and the value \({x}_{i}^{c}(t)\) is chosen randomly based on the status vector ( \(S\) ) from any infected case \({x}^{c}\) as \(c= \left\{i|{S}_{i}=1\right\}\) and \(r\) is the random number between \(0\) and \(1\) .

For susceptible cases:

where \({x}_{i}^{j}(t+1)\) is the new gene and the value \({x}_{i}^{m}(t)\) is chosen randomly based on the status vector ( \(S\) ) from any susceptible case \({x}^{m}\) as \(m= \left\{i|{S}_{i}=0\right\}\) and \(r\) is the random number between \(0\) and \(1\) .

For immune cases:

where \({x}_{i}^{j}(t+1)\) is the new gene and the value \({x}_{i}^{v}(t)\) is chosen randomly based on the status vector ( \(S\) ) from any immuned case \({x}^{v}\) as \(f\left({x}^{v}\right)=arg {min}_{j\left\{k|{S}_{k}=2\right\}}f({x}^{j})\) .

2.2.4 Update the herd immunity population:

For each generated case \({x}^{j}\left(t+1\right)\) , the immunity rate \({f(x}_{i}^{j}\left(t+1\right))\) is calculated and if the generated case \({x}^{j}\left(t+1\right)\) is better than the present case \({x}^{j}\left(t\right)\) such as \(f\left({x}^{j}\left(t+1\right)\right)<f({x}^{j}(t))\) , the current case is replaced by the generated case.

If the status vector ( \({S}_{j}=1\) ), the age vector \(({A}_{j})\) is increased by one.

Based on the herd immunity threshold, for each case \({x}^{j}\left(t\right)\) the status vector ( \({S}^{j})\) is updated which employs the following equation:

where, \(\vartriangle f\left( x \right) = \frac{{\mathop \sum \nolimits_{i = 1}^{HIS} f\left( {x_{i} } \right)}}{HIS}\) .

Where \(is\_Corona({x}^{j}(t+1))\) represents a binary value that equals one in case of the new case \({x}^{j}(t+1)\) gained a value from the infected case and \(\Delta f(x)\) represents the mean value of the population immune rates.

2.2.5 Fatality cases

When the immunity rate \((f\left({x}^{j}\left(t+1\right)\right))\) of the current infected case does not improve for a specific time of iterations which is specified by the parameter \(Max\_Age\) such as \({A}_{j}\ge Max\_Age\) then this case is considered dead. Then, it is regenerated from scratch using the following equation:

where \(\forall i=\mathrm{1,2}, \dots , n\)

Over and above, \({A}_{j}\) and \({S}_{j}\) are set to zero.

2.2.6 Stop criterion

CHIO repeats the main loop until the maximum number of iterations is achieved. The entire number of immune cases in addition to the susceptible cases command the population and the infected individuals disappear. Figure  2 represents the flowchart of CHIO. The pseudo-code of the CHIO is described in algorithm 1.

CHIO flowchart [ 30 ]

CHIO pseudo-code [ 30 ].

3 Aquila optimization algorithm [ 31 ]

3.1 inspiration.

One of the most well-known raptors in the Northern Hemisphere is the Aquila. Aquila catches a variety of prey, primarily rabbits, hares, deeps, marmots, squirrels, and other ground animals, using its speed, agility, strong feet, and long, pointed talons. Aquila may be seen in nature, along with their peculiar behaviors.

Aquila may maintain 200 km2 or larger holdings. They build large nests on mountains and other high areas. They reproduce in the spring, and because they are monogamous, they are likely to remain together for the rest of their lives. Aquila is one of the most researched birds in the world because of its bold hunting behavior. Aquila hunt squirrels, rabbits, and many other creatures with their speed and razor-sharp talons. Even mature deer have been known to be attacked by them.

The Aquila is known to primarily employ four different hunting techniques, each of which has several notable variations. Depending on the circumstances, most Aquila can deftly and swiftly switch between different hunting techniques. The following statements describe Aquila's hunting techniques.

In the first method, the Aquila hunts birds in flight using the first technique, high soar with a vertical stoop, in which it soars far above the ground.

The Aquila undertakes a lengthy, low-angled glide after exploring its prey, increasing its speed as the wings continue to shut. The Aquila must have a height advantage over its prey for this strategy to be effective. To simulate a thunderclap just before the encounter, the wings and tail are opened, and the feet are propelled forward to seize the prey.

Aquila is known for using the second technique, contour flying with brief glide attack, the most frequently. In this technique, the Aquila climbs at a low height above the ground. The target is then pursued relentlessly, whether it is flying or running. This strategy is advantageous for pursuing seabirds, nesting grouse, or ground squirrels.

A low flight and a gradual descending assault are the third strategies. In this, the Aquila descends to the ground and then advances on the victim. The Aquila chooses its victim and attempts to enter by landing on the neck and back of the animal. For sluggish prey, such as rattlesnakes, hedgehogs, foxes, and tortoises, as well as any species lacking an escape reaction, this hunting technique is used.

The Aquila walks on the ground while attempting to draw its prey in the fourth technique, known as walking and grabbing prey. It is used to remove the young of big prey, such as sheep or deer, from the coverage area.

As a whole, Aquila is one of the most knowledgeable and proficient hunters—possibly second only to humans. The methods mentioned above formed the primary sources of inspiration for the suggested AO algorithm. These processes are modeled in the AO in the next subsections.

3.2 Mathematical model of AO

3.2.1 generating ao population.

The population of candidate solutions (X) as shown in Eq. ( 2.1 ), which is created stochastically between the upper limit (UB) and lower bound (LB) of the given problem, serves as the starting point for the optimization procedure in the population-based approach known as AO. In each iteration, the best answer so far is roughly decided to be the best candidate.

where N is the total number of candidate solutions (population), \({X}_{i}\) indicates the decision values (positions) of the \({i}^{th}\) solution, X is the set of current candidate solutions, which are generated randomly by applying Eq. ( 2.2 ), and Dim denotes the problem's dimension size.

When a rand is a random number, \({LB}_{j}\) refers to the \({j}^{th}\) lower bound, and \({UB}_{j}\) represents to the \({j}^{th}\) upper limit of the given issue.

3.2.2 Aquila algorithm evolution

In this section, the Aquila optimization algorithm's main steps are presented. The AO algorithm mimics Aquila's behavior during hunting by displaying the activities taken at each stage of the hunt. Thus, the four methods used in the proposed AO algorithm's optimization processes are high soar with a vertical stoop to select the search space; contour flight with a short glide attack to explore within a diverged search space; low flight with a slow descent attack to exploit within a converge search space; and walk and grab prey to swoop.

Based on this condition, if \(t\le (\frac{2}{3})\times T\) , the exploration steps will be thrilled; otherwise, the exploitation steps will be carried out, and the AO algorithm can switch from exploration steps to exploitation steps utilizing different behaviors.

Aquila behaviors are modeled as a mathematical optimization paradigm that chooses the optimum solution while taking into account several restrictions. The following is the mathematical representation of the AO.

3.2.2.1 Step 1: Expanded exploration ( \({{\varvec{X}}}_{1}\) )

In the initial method ( \({X}_{1}\) ), the Aquila determines the ideal hunting location by high-flying with a vertical stoop after identifying the prey region. Here, the AO extensively explores from a high altitude to pinpoint the location of the prey in the search space. The mathematical representation of this behavior is given in Eq. ( 2.3 ).

where \({{\varvec{X}}}_{1}({\varvec{t}}+1)\) is the result of the first search technique ( \({X}_{1}\) ) for the answer to the next iteration of the problem t. The best answer up until the \({t}^{th}\) iteration, \({{\varvec{X}}}_{{\varvec{b}}{\varvec{e}}{\varvec{s}}{\varvec{t}}}\left({\varvec{t}}\right)\) , represents the approximate location of the prey. The enlarged search (exploration) is managed through the number of iterations using the equation ( \(\frac{1 - t}{T}\) ). The location means the value of the connected current solutions at the \({t}^{th}\) iteration, or \({{\varvec{X}}}_{{\varvec{M}}}\left({\varvec{t}}\right),\) is determined using Eq. ( 2.4 ). A random number between 0 and 1 is called rand. The current iteration and the maximum number of iterations are represented, respectively, by t and T.

where N is the number of potential solutions (population size) and Dim is the problem's dimension size.

3.2.2.2 Step 2: Narrowed exploration ( \({{\varvec{X}}}_{2}\) )

In the second technique ( \({X}_{2}\) ), the Aquila circles over the intended prey, prepares the terrain, and then strikes after being spotted from a great height. Contour flying with a short glide attack is this technique.

Here, AO prepares for the attack by closely examining the chosen location of the intended victim. This behavior is represented quantitatively in Eq. ( 2.5 ).

where \({X}_{2}(t+1)\) is the result of the second search technique ( \({X}_{2}\) ) and represents the answer of the subsequent iteration of the problem t. Levy(D) is the levy flight distribution function that is determined using Eq. ( 2.6 ), where D is the dimension space.

At the \({i}^{th}\) iteration, \({X}_{R}(t)\) is a random solution selected from the interval [1 N].

where u and \(\upsilon\) are random numbers between 0 and 1, and s is a constant value set to 0.01. \(\sigma\) is determined by applying Eq. ( 2.7 ).

where \(\beta\) is a constant with the value 1.5.

The spiral form in the search is presented in Eq. ( 3.5 ) using the variables y and x, which are computed as follows.

For a set number of search cycles, \({{\varvec{r}}}_{1}\) takes a value between 1 and 20, and \({\varvec{U}}\) is an insignificant value fixed at 0.00565. \({D}_{1}\) Consists of integers from 1 to the search space's length (Dim), and \(\omega\) is a tiny value fixed at 0.005.

3.2.2.3 Step 3: Expanded exploitation ( \({{\varvec{X}}}_{3}\) )

In the third approach ( \({X}_{3}\) ), the Aquila descends vertically with an initial attack to ascertain the prey reaction after the prey region has been precisely designated and the Aquila is prepared for landing and attacking. Low flying with gradual descending assault is the name given to this tactic. Here, AO takes advantage of the target's chosen location to approach its victim and attack. The mathematical representation of this behavior is given in Eq. ( 2.13 ).

where \({X}_{3}(t+1)\) represents the result of the third search technique ( \({X}_{3}\) ) for the solution of the subsequent iteration of the constant t. The best-obtained solution, \({X}_{best}(t)\) , reflects the approximate position of the prey up until the \({i}^{th}\) iteration, and the mean value of the current solution at the \({t}^{th}\) iteration, \({X}_{M}(t),\) is determined using Eq. ( 2.4 ). A random number between 0 and 1 is called \(rand\) . The exploitation adjustment parameters \(\alpha\) and \(\delta\) , are set in this study at a low value (0.1). The given problem's \(LB\) and \(UB\) abbreviations stand for lower and upper bounds, respectively.

3.2.2.4 Step 4: Narrowed exploitation ( \({{\varvec{X}}}_{4}\) )

In the fourth technique ( \({X}_{4}\) ), the Aquila approaches the target and then assaults it over the land in accordance with its stochastic motions. This strategy is known as "walk and grab prey." Finally, AO engages the prey at the last position. The mathematical representation of this behavior is given in Eq. ( 2.14 ).

where \({X}_{4}(t+1)\) is the result of the fourth search technique ( \({X}_{4}\) ), which is created for the following iteration of t. The term "QF" refers to a quality function that is derived using Eq. ( 2.15 ) and is used to balance the search techniques. \({G}_{1}\) , which is produced using Eq. ( 2.16 ), stands for multiple AO movements that are employed to follow the prey during the hunt. The flight slope of the AO used to follow the prey during the journey from the starting position (1) to the last site (t), which is created using Eq. ( 2.17 ), is represented by \({G}_{2}\) by decreasing values from 2 to 0. The solution as of the \({t}^{th}\) iteration is X(t).

The quality function value at the \({t}^{th}\) iteration is denoted by \(QF(t)\) , and the random value, rand, is a number between 0 and 1. The current iteration and the maximum number of iterations are represented, respectively, by t and T. Using Eq. ( 2.6 ), we can derive the levy flight distribution function, \(Levy(D)\) .

Algorithm 2 explains the pseudo-code of the AO. The flowchart of the AO is presented in Fig. 3 .

Aquila flowchart [ 31 ]

Aquila Optimizer [ 31 ].

4 The proposed modified coronavirus herd immunity aquila optimization algorithm (MCHIAO)

This section outlines the hybrid algorithm that we developed by enhancing and fusing CHIO and AO, two distinct optimization algorithms. As AO is a population-based algorithm and CHIO is a human-based algorithm, they are both metaheuristic optimization algorithms. The suggested method comprises two phases: exploration and exploitation, with the exploration phase performed by ECHIO and the exploitation phase by the AO. The first of two modifications to CHIO is the categorization of cases, followed by applying chaotic maps to improve the equation values for the new genes. Based on this condition, if \(t\le (\frac{2}{3}) T\) , the exploration steps will be excited; otherwise, the exploitation steps will be carried out, and the MCHIAO algorithm can switch from exploration steps to exploitation steps utilizing this behavior. Finally, the two scenarios of exploitation using AO are used in the proposed algorithm in addition to an enhancement to the random value used to switch between narrowed and expanded exploitation. In the subsections that follow, the specifics of the proposed MCHIAO algorithm are covered.

4.1 Enhanced coronavirus herd immunity optimization algorithm (ECHIO)

4.1.1 cases categorizing.

For every search and optimization algorithm, exploration and exploitation exemplify influential characteristics. The inability to achieve the balance between both exploration and exploitation leads the optimization algorithms to fall into local optimum in optimization problems.

Supporting optimal “exploitation” of the existing results and promoting “exploration” for new ones is our main goal in this proposed contribution.

Instead of categorizing the cases (individuals) according to the basic reproduction rate ( \({BR}_{r}\) ) parameter which leads the CHIO algorithm to be trapped in the local optima, we use the status vector ( \(S\) ) in classifying the cases (individuals) that caused a local optima avoidance and a faster convergence curve as follows:

4.1.2 New genes’ value equation enhancement:

In the coronavirus herd immunity evolution for infected, susceptible, and immune cases instead of adding the current gene’s value to the dissimilarity among the existing gene’s value and a random gene adapted from infected, susceptible, and immune cases as shown in Eqs.  1.6 , 1.7 , and 1.8 , respectively, we use subtraction in Eqs.  3.2 , 3.3 , and 3.4 .

In addition, chaotic maps are used instead of random parameters due to their expected ability to increase the speed of convergence. Equations  3.2 , 3.3 , and 3.4 are modified to clarify the proposed claim. Chaotic systems or simply chaos can be described as behavior that falls between rigid regularity and randomness. One of the most essential characteristics of the chaotic system is that it exhibits extreme sensitivity to initial conditions. Many studies suggested that the spread of COVID-19 can be categorized as a chaotic system.

The chaotic behavior of the coronavirus inspired us to use the chaotic system by replacing the random parameter ( \(r\) ) with the parameter ( \(m\) ).

Local minima avoidance and rapid convergence rate are the main reasons for us to use chaos optimization. Chaos theory plays an important and effective role in overcoming these problems.

The main three important dynamic properties of chaos can be described as quasi-stochastic, ergodicity, and sensitive dependence on the initial conditions.

Quasi-stochastic can be described as the ability to replace random variables with the values of a chaotic map. Ergodicity expresses the ability of chaotic variables to search the non-recurrently of all states in a specified range.

Replacing the random parameter “ \(r\) ” with the chaotic value “ \(m\) ” allows an enormous effect on enhancing the exploration phase of the proposed ECHIO algorithm which assists in finding a new promising search region hopefully for the optimum solution.

The new enhanced equations for Eqs.  1.6 , 1.7 , and 1.8 respectively will be as follows:

where the m vector can be calculated as shown in Eq.  3.5 .

This chaotic behavior in the final stage aids in alleviating the two issues of entrapment in local optima and slow convergence rate while solving high-dimensional problems. In this article, 10 chaotic maps have been used to improve the performance of the CHIO algorithm as illustrated in Table  1 [ 31 ].

Figure  4 illustrates the flowchart of the proposed optimization algorithm ECHIO. Figure  5 presents the graphical description of the proposed ECHIO algorithm. The pseudo-code of the proposed algorithm ECHIO is illustrated in Algorithm 3.

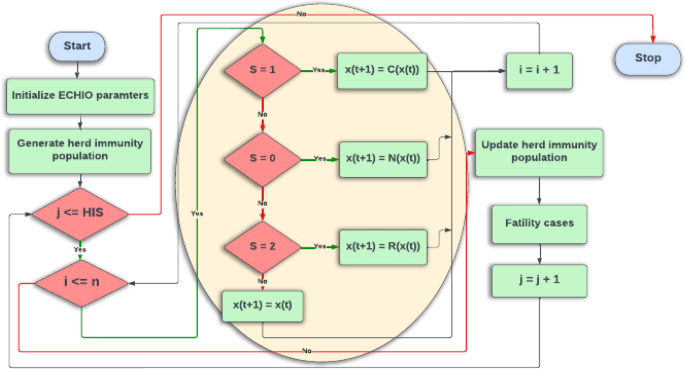
ECHIO flowchart

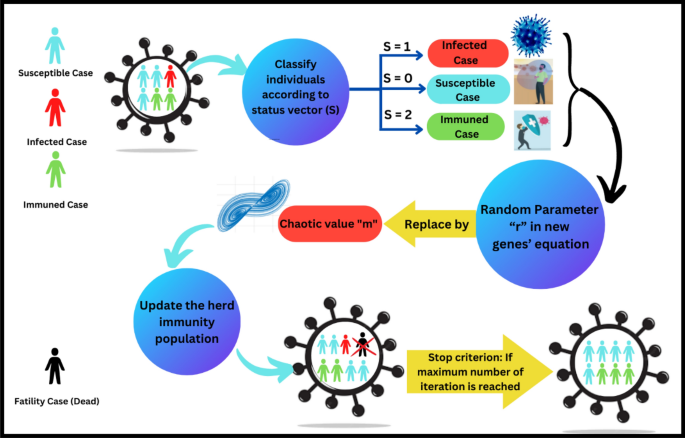
Description of the proposed ECHIO

The proposed ECHIO pseudo-code.

4.2 Selection between the narrowed and expanded exploitation in the AO algorithm

In the AO algorithm, a random value \(rand\) is used to switch between the Narrowed and Expanded exploitation cases, as \(rand\) is a random number between 0 and 1.

To improve the algorithm's performance, we modified \(rand\) value as shown in Eq.  3.6 .

As t represents the current iteration and T is the maximum number of iterations, respectively.

4.3 Hybrid ECHIO with AO algorithms (MCHIAO)

The Coronavirus Herd Immunity Optimizer (CHIO) outperforms certain other biologically-inspired algorithms as one of the competitive human-based optimisation techniques. CHIO performed well in comparison to other optimisation techniques. However, CHIO is limited to local optima, which reduces the precision of complex global optimisation issues. Therefore, in high-dimensional space, it is simple to fall into a local optimum, and the Coronavirus Herd Immunity Optimizer (CHIO) algorithm has a low rate of convergence during the iterative process. However, AO's global exploration skills are limited, despite the fact that it possesses strong local exploitation capabilities. When AO algorithm is applied to optimize challenging, high-dimensional engineering problems, it may experience early convergence and poor global exploration. The AO encounters issues while optimizing challenging multidimensional problems, including subpar convergence behavior and subpar exploration efficiency. The Modified Coronavirus Herd Immunity Aquila Optimizer (MCHIAO), a novel metaheuristic optimizer, is then introduced to get over these limitations such as the low exploitation skills in CHIO and the insufficient exploration abilities of the AO algorithm and modify it to address feature selection problems.

Figure  6 below illustrates the flowchart of the proposed optimization algorithm MCHIAO and the pseudo-code of the proposed algorithm MCHIAO is illustrated in Algorithm 4.

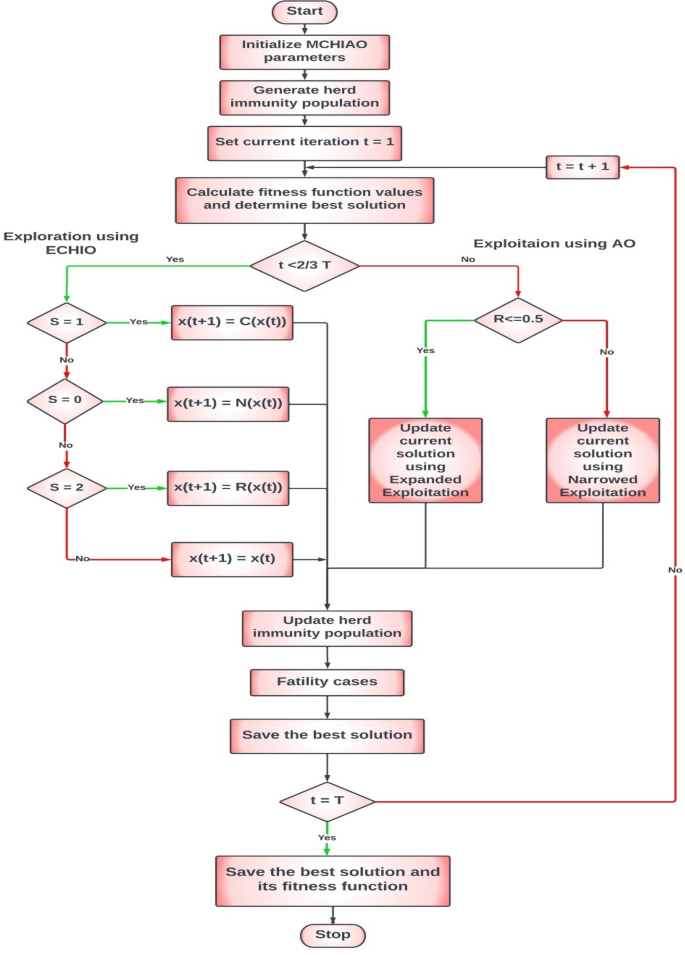
MCHIAO flowchart

The algorithm starts by initializing the MCHIAO parameters \({\varvec{H}}{\varvec{I}}{\varvec{S}}\) , \({{\varvec{S}}}_{{\varvec{r}}}\) , \({\varvec{\delta}}\) , \(\boldsymbol{\alpha },\) and \({{\varvec{M}}{\varvec{a}}{\varvec{x}}}_{{\varvec{a}}{\varvec{g}}{\varvec{e}}}\) . Herd immunity population is generated, and the fitness function of each search agent is calculated. Herd immunity evolution is initialized and the exploitation parameters \({G}_{1}, {G}_{2}, Levy(D)\) are updated. The selection between the exploration and the exploitation cases is based on the condition \(t \le \left(\frac{2}{3}\right)\times T\) . The exploration phase is handled by the proposed ECHIO algorithm, as the cases are categorized as infected, susceptible, and immune cases based on the status vector. The exploitation phase consists of two categories, expanded exploitation and narrowed exploitation. The selection between the two exploitation cases is based on the generated formula \(R.\) The herd immunity population is updated, and the new positions of the agents are calculated. After the fatality condition is met, the best solution is obtained.

The proposed MCHIAO pseudo-code.

5 Experimental results & analysis

The performance of the proposed MCHIAO is evaluated for variants benchmark functions including 23 CEC 2005, 29 CEC 2017, 10 CEC 2019, 24 unimodal, 44 multimodal test functions, and six different real-world problems. The proposed MCHIAO is compared as well against twelve state-of-the-art algorithms (GOA, MFO, MPA, GWO, HHO, SSA, WOA, IAO, NOA, NGO, AO, and CHIO), conducting Wilcoxon statistical analysis to statistically validate all outcomes. MATLAB/SIMULINK® 2018b is used to accomplish all simulations. The metrics used to define the performance of the algorithm against the twelve competitive state-of-the-art algorithms are mean, standard deviation, rank, percentage, and total rank. The experimental results include the mean value (Mean), standard deviation (Std), and rank order (Rank). In the case of the minimum problem, the algorithm's discovery of the optimal solution is more likely the smaller the best value; similarly, the algorithm's comprehensive optimization capabilities are enhanced by the lower the mean value; and the algorithm's stability is improved by the smaller standard deviation. The algorithms are ranked using a ranking based on the mean value, which allows for a more intuitive comparison based on the magnitude of the mean value. The algorithm with the highest ranking among those ranked equally is shown.

The Wilcoxon signed-rank test (also called the Wilcoxon signed-rank sum test) is a nonparametric test used to compare data. For within-group comparison of algorithms generally Wilcoxon signed-rank test can be applied to analyze each algorithm within-group. We have calculated the mean result for each algorithm as all of the algorithms are executed with a maximum of 500 iterations and 51 runs. The Friedman average rank test is used for evaluating the performance of the various optimization algorithms, with the best result of each measure in each function highlighted in bold in the result tables.

5.1 Case1: MCHIAO performance through 23 CEC 2005 benchmark

In this section, 23 benchmark functions are considered to evaluate the proposed MCHIAO’s performance. Each of these test functions is a minimization problem of varying size and difficulty. Table 2 shows the benchmark functions, where Dim represents the function's dimension, Range represents the function's search space boundaries, and \({f}_{min}\) is optimum.

5.1.1 MCHIAO Vs AO and CHIO

MCHIAO is run against the original CHIO and AO algorithms on the different functions of 23 benchmark. Numerical results in Table  3 demonstrate the mean, standard deviation, and rank of the used algorithms on every function, as it ranked first in all of the 23 benchmark functions (from Table  2 ) except for F_13 (x) where AO ranked the first. MCHIAO achieved total rank 1.

5.1.2 MCHIAO vs other algorithms

The proposed MCHIAO algorithm is compared against twelve different algorithms in a simulated experiment. These algorithms are GOA, MFO, MPA, GWO, HHO, WOA, SSA, IAO, NOA, NGO, AO, and CHIO. All of the algorithms are executed with a maximum of 500 iterations and 51 runs. In Fig.  7 and Table  4 , simulation results for all methods are presented. Table 4 presents the metrics calculated such as mean, standard deviation (Std), and Friedman average rank test for evaluating the performance of the various optimization techniques, with the best result of each measure in each function highlighted in bold.

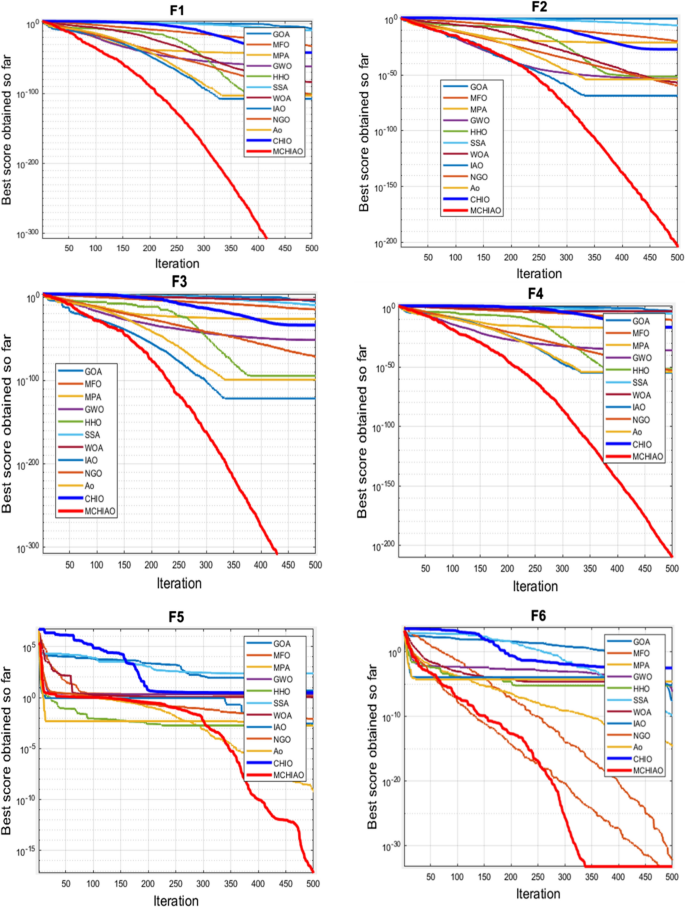
The 23 CEC2005 benchmark functions and convergence plots

These data show that the suggested algorithm MCHIAO performed well in both the multimodal functions from \({F}_{8}(x)\) to \({F}_{13}(x)\) and the unimodal functions from \({F}_{1}(x)\) to \({F}_{7}(x)\) , demonstrating the first rank except for \({F}_{6}(x)\) and \({F}_{13}(x)\) where NGO and MPA ranked the first, respectively. However, MCHIAO showed the greatest rate and placed first in all the fixed-dimension multimodal functions from \({F}_{14}(x)\) to \({F}_{23}(x)\) , except \({F}_{20}(x)\) where MPA ranked first. With a total rank of one, the findings showed that the suggested algorithm MCHIAO performed the best on the Standard benchmark functions. In Fig.  7 , the vertical axis shows the optimal solution to the function, while the horizontal axis shows the total number of iterations. It implies a comparison of the convergence curves of MCHIAO and other algorithms on common benchmark functions, demonstrating that MCHIAO has a favorable rate of convergence and the ability to find a more compact solution across all the benchmark functions, demonstrating one of its key strengths. In the majority of the twenty-three benchmark functions, it is seen that using the MCHIAO approach beats the other twelve evaluated algorithms. The Wilcoxon rank-sum test [ 32 ] is also applied in order to statically prove the efficiency of our proposed algorithm. Statistical study of the discrepancy results between two algorithms frequently makes use of the p-value of the Wilcoxon rank-sum test, which is useful in establishing if the two sets of data are significantly different. When p is less than 0.05, it indicates a substantial difference between the two methods in this test function, indicating the rejection of the null hypothesis. The comprehensive p -values in Table  5 were acquired by applying the Wilcoxon test with each of the twelve algorithms to the MCHIAO solution findings, 51 times separately on the 23 benchmark functions test. This was necessary because the test necessitates two independent data sets. These results prove the significance of the proposed algorithm for all functions because the p -values are less than 0.05.

From the previous table, the proposed algorithm MCHIAO outperforms or produces similar solutions in all functions except for \({F}_{6}(x), {F}_{13}(x)\) and \({F}_{20}(x)\) where the best algorithms are NGO and MPA respectively.

The convergence curves for all thirteen algorithms on the 23 standard benchmark functions are shown in Fig.  7 , where the vertical axis shows the optimal solution to the problem and the horizontal axis shows the total number of iterations. One of MCHIAO's assets is its remarkable convergence abilities, which are demonstrated by the algorithm's rate of convergence on CEC2005 benchmark functions and the ability to produce a more compact solution for all benchmark functions.

5.2 Case 2: MCHIAO performance on CEC2017 benchmark functions

The 29 CEC2017 benchmark functions are used to evaluate the proposed MCHIAO against all the same twelve state-of-the-art algorithms. The minimization problems in CEC2017 are divided into four categories: The first has three unimodal functions (F1–F3), the second has seven simple multimodal functions (F4–F10), the third has ten hybrid functions (F11–F20), and the fourth has ten composition functions (F21–F30). Table 6 shows how these functions operate. The objective function minimizes the difference between the optimal value of the \(i\) th function \({f}_{i}({x}^{*})\) and the best solution determined by the method \({f}_{i}(x)\) ; this function can be written as Eq. ( 4.1 ).

5.2.1 MCHIAO Vs AO and CHIO

Table 7 demonstrates the performance of the proposed MCHIAO against CHIO and AO as it ranked the first in all of the 29 functions except for \({F}_{28}(x),\) as it ranked second and CHIO ranked the first. MCHIAO scored a total rank 1.

5.2.2 MCHIAO vs other algorithms

Table 8 presents the experimental study findings of the suggested MCHIAO algorithm as well as the other comparator techniques in terms of mean results and standard derivation after 51 separate runs of each algorithm. The best outcomes are displayed in bold font in Tables  7 and 8 . Optimization results presented in Table  8 indicate that the proposed MCHIAO algorithm outperforms the other twelve algorithms in 17 out of the 29 CEC2017 benchmark functions and scored a total first rank against other optimization algorithms. Our proposed algorithm MCHIAO ranked first in the unimodal functions \({F}_{1}(x)\) and \({F}_{3}(x)\) . For the multimodal functions \({F}_{4}(x)\) to \({F}_{10}(x)\) , MCHIAO ranked first in \({F}_{4}(x), {F}_{5}(x),\,and\,{F}_{8}(x)\) . MPA ranked first in \({F}_{6}(x), {F}_{9}(x),\,and\,{F}_{10}(x)\) , and GOA ranked first in \({F}_{7}(x).\) In the hybrid functions \({F}_{11}(x)\) to \({F}_{20}(x)\) , MCHIAO ranked first in all functions except \({F}_{11}(x), {F}_{12}(x), {F}_{14}(x),\,and\,{F}_{17}(x)\) , where it ranked the second and MPA ranked first in \({F}_{11}(x), {F}_{14}(x),\,and\,{F}_{17}(x)\) , and NGO ranked first in \({F}_{12}(x).\) However, in the composition functions \({F}_{21}(x)\) to \({F}_{30}(x)\) , MCHIAO ranked first in all functions except \({F}_{25}(x), {F}_{26}(x), {F}_{28}(x),\,and\,{F}_{30}(x)\) where GOA, MPA, CHIO, and NGO ranked first, respectively. Therefore, with a total rank of 1, our suggested algorithm MCHIAO showed the greatest performance on the CEC2017 benchmark functions. Table 9 presents the p -values of MCHIAO which was acquired by applying the Wilcoxon test against all the other twelve algorithms for 29 CEC2017 benchmark functions. These results prove the significance of the proposed algorithm for all functions because the p -values are less than 0.05.

Figure  8 presents the convergence plots of the proposed MCHIAO algorithm against the same twelve algorithms for the 29 CEC2017 benchmark functions. The MCHIAO algorithm outperforms the other twelve evaluated algorithms in the majority of the 29 benchmark functions.

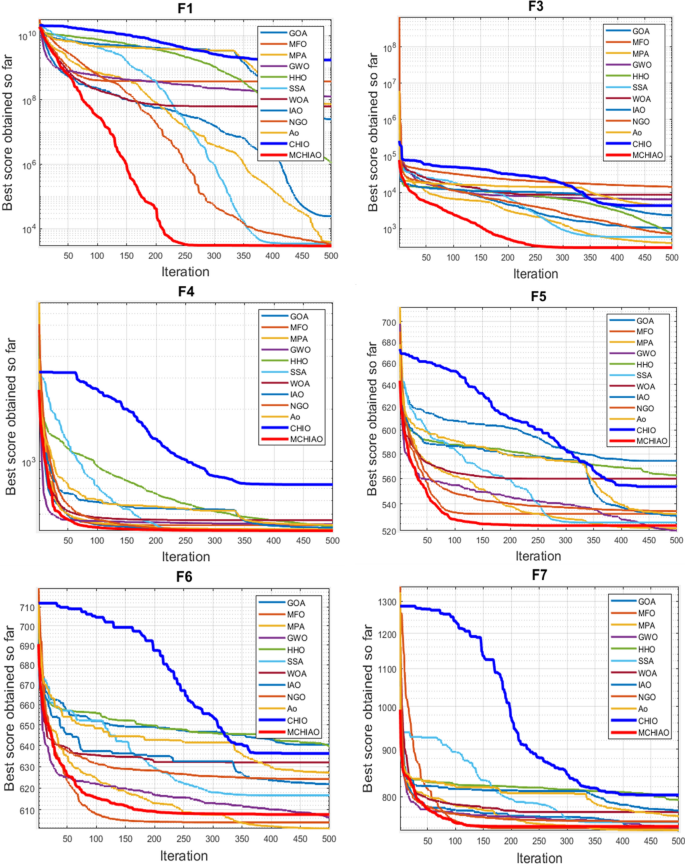
The 29 CEC2017 functions and convergence plots

5.3 Case 3: MCHIAO performance on CEC2019 benchmark functions

We chose one of the most relevant and challenging test suites from the numerical optimization competitions, CEC-2019 (which has ten functions) to further demonstrate the effectiveness of the proposed technique. Table 10 illustrates the ten CEC2019 benchmark functions.

5.3.1 MCHIAO Vs AO and CHIO

Table 11 shows that MCHIAO is ranked first against CHIO and AO in all the 10 CEC-2019 benchmark functions. For the total rank, MCHIAO scored 1.

5.3.2 MCHIAO vs other algorithms

Table 12 shows the performance of the proposed MCHIAO against the same twelve algorithms conducted on the ten CEC2019 functions after 500 iterations and 51 runs of each algorithm. The data analyzed for the mean value, standard deviation, and rank produced by the twelve unique state-of-the-art optimization methods are shown in Table  12 . With a high rate, our suggested algorithm MCHIAO placed first in CEC01, CEC02, CEC03, and CEC09, second in CEC08, fourth in CEC05, and fifth in CEC06, CEC07, and CEC10, and sixth in CEC04. With a total rank of 2, MCHIAO showed a promising overall performance on the CEC2019 benchmark functions. Table 13 presents the p -values of MCHIAO which was acquired by applying the Wilcoxon test against all the other twelve algorithms for ten CEC2019 benchmark functions. These results prove the significance of the proposed algorithm for all functions because the p -values are less than 0.05.

Figure  9 shows the convergence behavior of the proposed MCHIAO on CEC2019 functions.

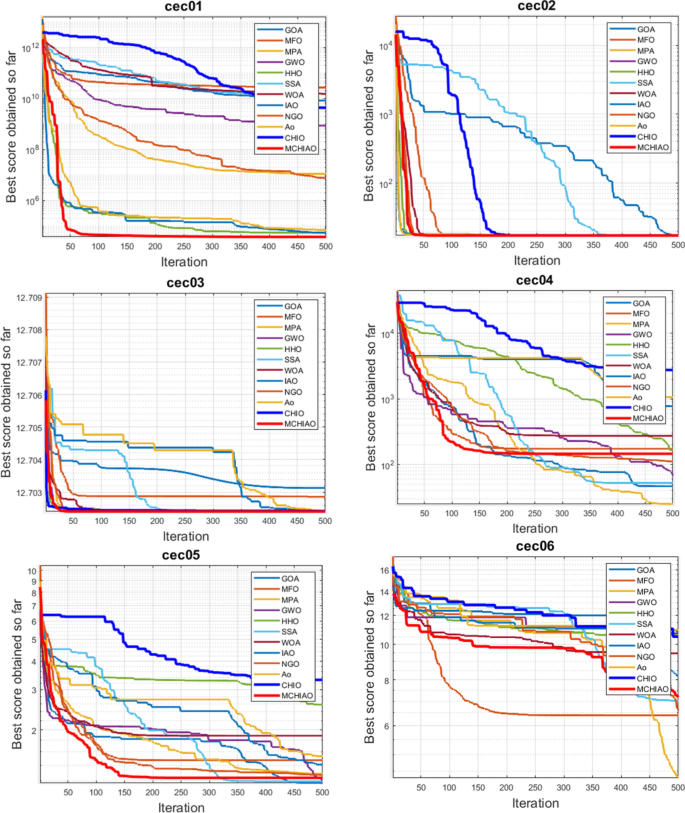
Convergence curves of CEC2019 functions and convergence plots

5.4 Case 4: performance of MCHIAO on Unimodal fixed-dimension problems

Table 14 represents the details of the unimodal fixed-dimension problems. Range specifies the lower and upper boundaries of the design variables, whereas \({{\varvec{f}}}_{{\varvec{m}}{\varvec{i}}{\varvec{n}}}\) signifies the overall minimum of the functions. Vars identifies the number of dimensions (design variables) of the functions.

5.4.1 MCHIAO Vs AO and CHIO

In Table  15 , MCHIAO is ranked the first in all 8 functions with a total rank 1, while CHIO ranked second and AO ranked third.

5.4.2 MCHIAO vs other algorithms

Tables 15 and 16 show the mean value, standard deviation, and rank attained by the proposed MCHIAO algorithm against CHIO and AO, and the other twelve unique state-of-the-art optimization algorithms, respectively. Table 16 shows that MCHIAO demonstrated the first rank in all unimodal fixed-dimension problems except for F6 in which it ranked second. With a total rank of 1, MCHIAO had the greatest overall performance on the unimodal fixed-dimension functions. The convergence curves of the various methods are shown in Fig.  10 , where the vertical axis shows the optimal solution to the function and the horizontal axis shows the total number of iterations. Table 17 presents the p -values of MCHIAO which was acquired by applying the Wilcoxon test against all the other twelve algorithms for the 8 Unimodal fixed-dimension functions. These results prove the significance of the proposed algorithm for all functions because the p -values are less than 0.05.

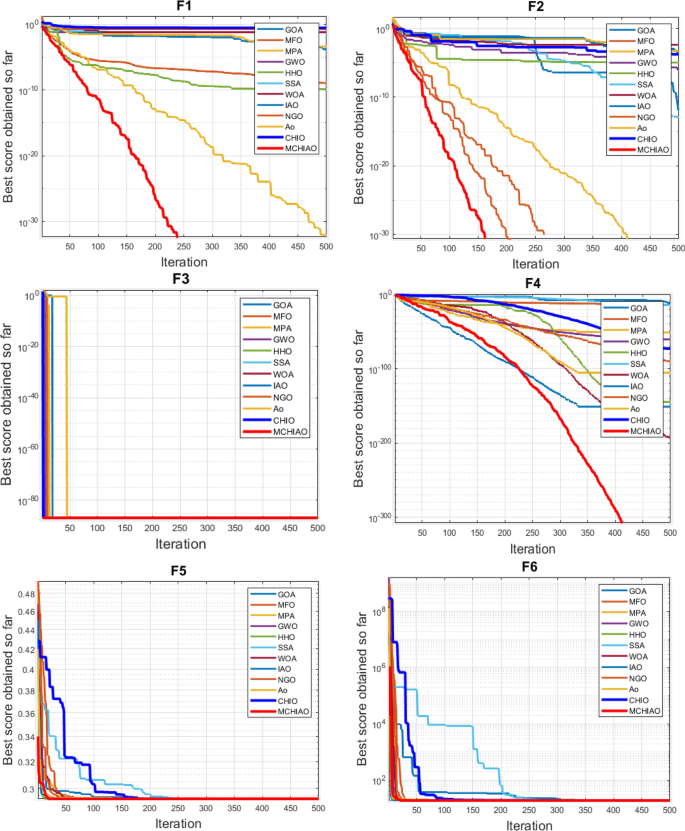
The 8 Unimodal fixed-dimension and convergence plots

5.5 Case 5: performance of MCHIAO on Unimodal variable-dimension problems

Table 18 represents the details of the unimodal variable-dimension functions.

5.5.1 MCHIAO Vs AO and CHIO

Table 19 demonstrates that MCHIAO obtained the first rank in all unimodal variable-dimension problems. For the total rank, MCHIAO ranked first, AO ranked second, and CHIO ranked third.

5.5.2 MCHIAO vs other algorithms

In comparison to the 12 existing meta-heuristics algorithms, Table  20 demonstrates that the novel hybrid MCHIAO algorithm offers the best attainable optimum values of the functions in terms of mean and standard values of the functions. Figure  11 addresses the convergence performance of the twelve competitive algorithms and MCHIAO variations in solving unimodal benchmark functions; the convergence solutions encountered show that the MCHIAO is better capable of finding the most optimum solution in the fewest iterations. Based on the results of variable and fixed dimension unimodal problems, we can say that MCHIAO has excellent exploitation capabilities and can produce superior results in difficult situations. Table 21 presents the p -values of MCHIAO which was acquired by applying the Wilcoxon test against all the other twelve algorithms for the 15 Unimodal variable-dimension functions. These results prove the significance of the proposed algorithm for all functions because the p -values are less than 0.05.

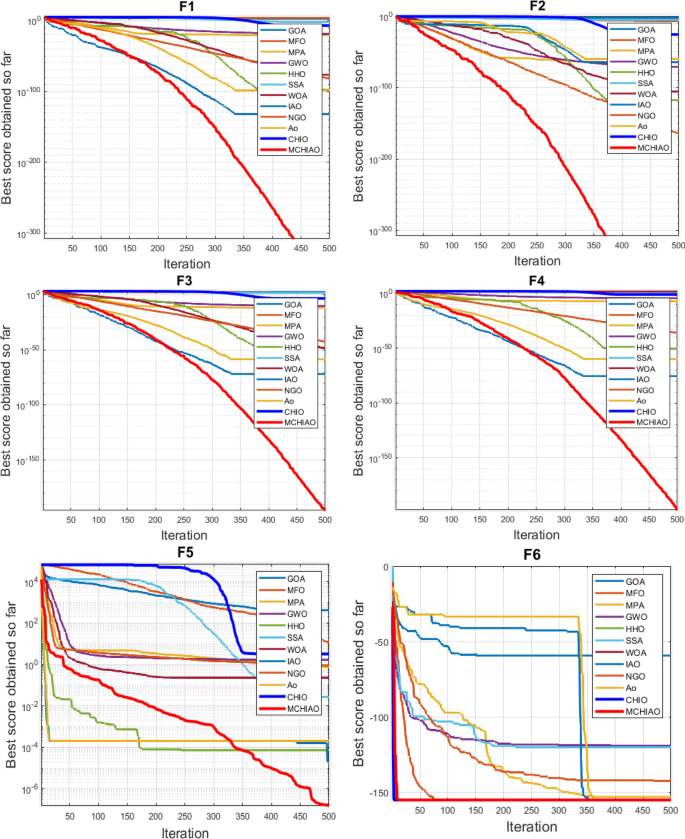
The Unimodal variable-dimension functions and convergence plots

5.6 Case 6: performance of MCHIAO on Multimodal fixed-dimension problems

The details of the multimodal fixed-dimension functions are presented in Table  22 .

5.6.1 MCHIAO Vs AO and CHIO

Table 23 presents the MCHIAO against CHIO and AO where it ranked first in all functions except \({F}_{14}(x)\) where AO ranked first. For the total rank, MCHIAO scored rank 1, AO rank 2, and CHIO rank 3.

5.6.2 MCHIAO vs other algorithms

Table 24 illustrates the outcomes of MCHIAO and the other algorithms for the fixed-dimension multimodal benchmarks. The results show that MCHIAO generally reaches the globally optimal values. If the results are compared, MCHIAO possesses first place for all functions other than f9, f14, and f15. An important feature that should be explored is the convergence of the MCHAIO for the optimal solutions throughout the iteration numbers, hence Fig.  12 demonstrates the best solutions so far across the iteration numbers. The acceleration convergence curves of the suggested MCHIAO have a discernible declining rate for the multimodal fixed-dimension functions. Table 25 presents the p-values of MCHIAO which was acquired by applying the Wilcoxon test against all the other twelve algorithms for the 27 multimodal fixed-dimension functions. These results prove the significance of the proposed algorithm for all functions because the p -values are less than 0.05.

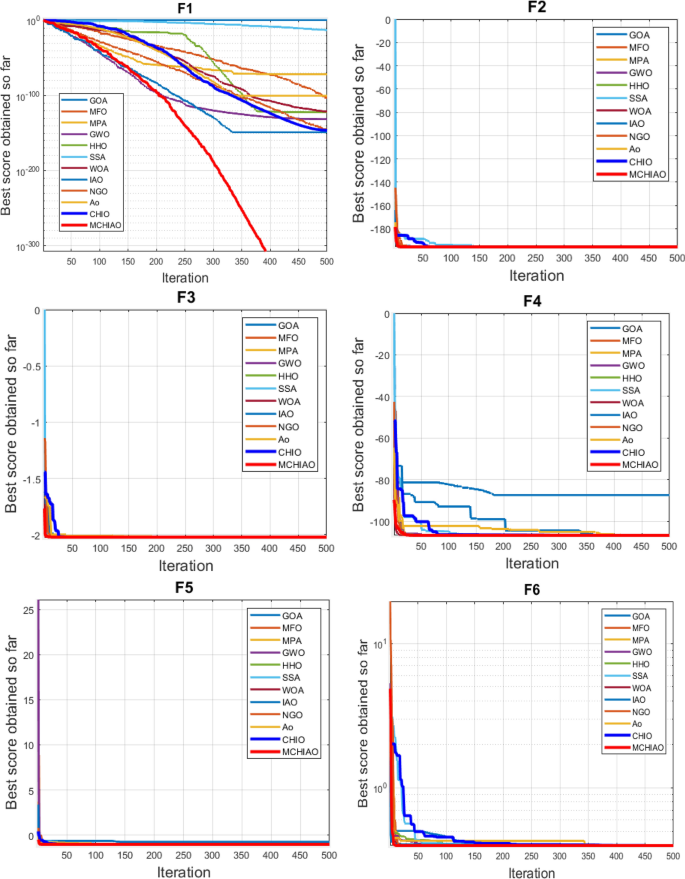
The Multimodal fixed-dimension functions and convergence plots

5.7 Case 7: performance of MCHIAO on Multimodal variable-dimension problems

The dimensionality of the variable-dimension multimodal benchmark functions, in addition to the local optima, increases the complexity and difficulty of optimization.

Table 26 presents the details of the multimodal variable-dimension problems. Vars specifies the number of dimensions (design variables) of the functions. Range identifies the lower and upper boundaries of the design variables, whereas \({{\varvec{f}}}_{{\varvec{m}}{\varvec{i}}{\varvec{n}}}\) signifies the overall minimum of the functions.

5.7.1 MCHIAO Vs AO and CHIO

MCHIAO is ranked first in all functions against CHIO and AO except for \({F}_{8}(x)\) and \({F}_{14}(x)\) where AO ranked the first, as shown in Table  27 . MCHIAO scored 1 for the total rank, while AO scored 2 and CHIO ranked rank 3.

5.7.2 MCHIAO vs other algorithms

In Table  28 , MCHIAO's ability to solve multimodal functions with variable dimensions is compared with the performance of other algorithms.

The results show that MCHAIO can fully explore the search space. Except for \({F}_{8}(x)\) , \({F}_{14}(x)\) , and \({F}_{17}(x)\) , MCHAIO consistently exceeds competitors; nonetheless, the results for these three functions are equally competitive. Table 29 presents the p-values of MCHIAO which was acquired by applying the Wilcoxon test against all the other twelve algorithms for the 17 multimodal variable-dimension functions. These results prove the significance of the proposed algorithm for all functions because the p-values are less than 0.05.

In Fig.  13 , MCHIAO's convergence curves for 17 multimodal variable-dimension functions are presented and compared with the twelve algorithms to demonstrate the convergence capabilities of MCHIAO.

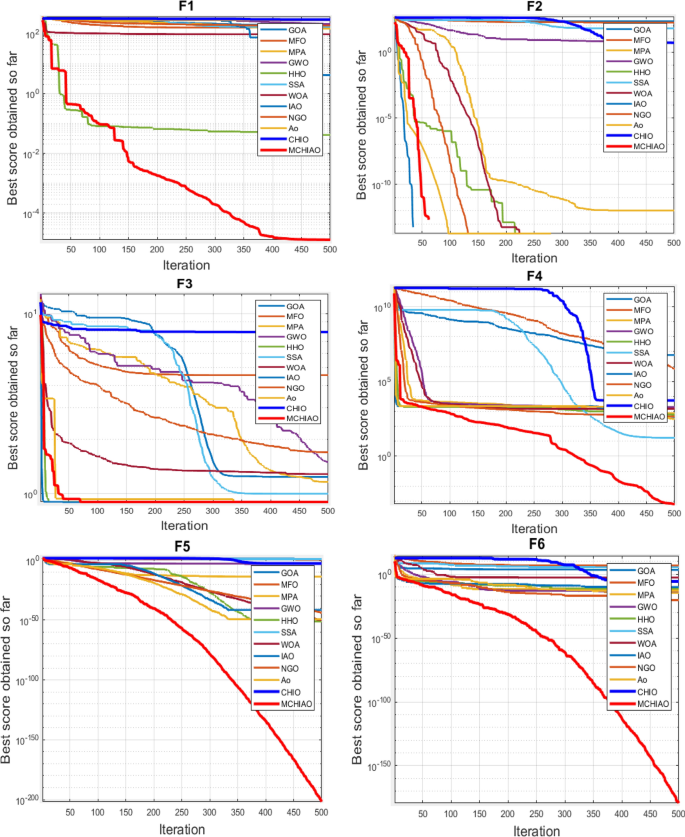
The Multimodal variable-dimension functions and convergence plots

5.8 Case 8: performance of MCHIAO on real-world problems

The majority of the search spaces for real-world issues are unknown and provide several challenges. Such challenges drastically reduce the performance of optimization algorithms in the sector, which previously excelled at benchmark functions or simple case studies [ 36 ].

Scientists and practitioners must recognize the obstacles and include the appropriate adjustments, alterations, and enhancements in the algorithms to address them in order to guarantee the quality of solutions to optimisation problems [ 37 ].

This section evaluates the performance of MCHIAO in real-world problems, this optimizer has been used to solve six engineering problems: welded beam design, pressure vessel design, tension/compression spring design, weight minimization of a speed reducer, three-bar truss design problem, and gear train design problem.

5.8.1 Tension/compression spring design

The goal is to obtain the least fabrication cost for spring. It is a weight minimization problem of a spring with three structural parameters: wire diameter (d or \({x}_{1}\) ), mean coil diameter (D or \({x}_{2}\) ), and the number of active coils (P or \({x}_{3}\) ). Figure  14 presents the spring and its parameters [ 38 ].

Tension/compression spring design problem

This problem has the following mathematical model:

The performance of the proposed MCHIAO is evaluated by solving the tension/compression spring design problem and compared against the same twelve state-of-the-art algorithms as shown in Table  30 . The performance of the MCHIAO algorithm is better than the twelve state-of-the-art algorithms.

For 500 iterations and 51 runs, MCHIAO outperforms the other twelve algorithms as proved in Table  31 . Table 31 presents the p -values of MCHIAO which was acquired by applying the Wilcoxon test against all the other twelve algorithms for the tension/compression spring design problem. These results prove the significance of the proposed algorithm for all functions because the p-values are less than 0.05.

Figure  15 presents the convergence curve of the MCHIAO optimization algorithm against the other twelve algorithms in the tension/compression spring design problem.

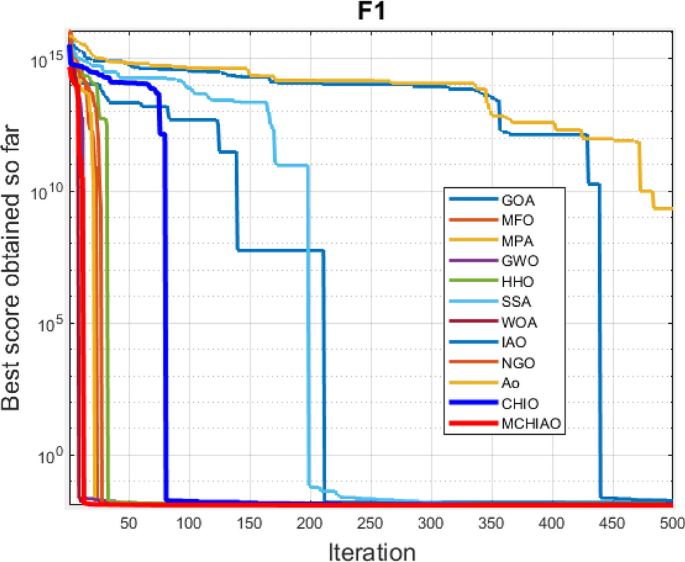
Convergence curves of the 13 algorithms on the tension/compression spring design

5.8.2 Pressure vessel design

The objective is to obtain a pressure vessel design with the minimum fabrication cost. Figure  16 demonstrates the pressure vessel and the design parameters [ 38 ].

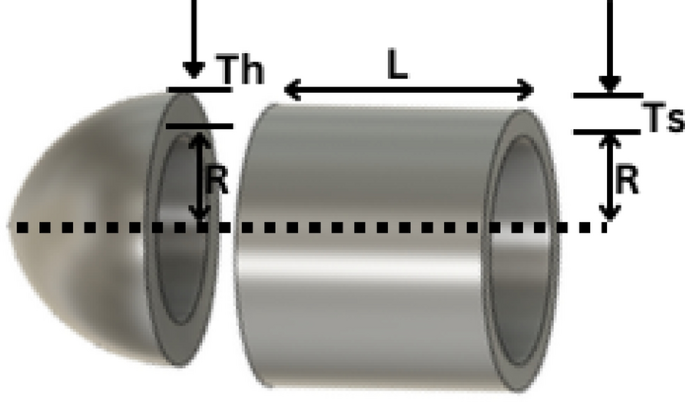
Schematic of pressure vessel design

The four decision variables in this problem are head Thickness ( \({T}_{h}\) ), shell thickness ( \({T}_{s}\) ), length of the cylindrical section neglecting head(L), and Inner radius (R). This problem's mathematical formulation is as follows:

\({x}_{1} \,and\, {x}_{2}\) are discrete while \({x}_{3}\, and\, {x}_{4}\) are continuous.

The fitness function is nonlinear with linear and nonlinear inequality constraints.

Table 32 provides the results of this problem for the proposed MCHIAO against the same twelve algorithms. Table 33 presents the p -values of MCHIAO which was acquired by applying the Wilcoxon test against all the other twelve algorithms for the pressure vessel design problem. These results prove the significance of the proposed algorithm for all functions because the p -values are less than 0.05.

Figure  17 represents the convergence curves of the MCHIAO against the other twelve optimization algorithms in the pressure vessel problem.

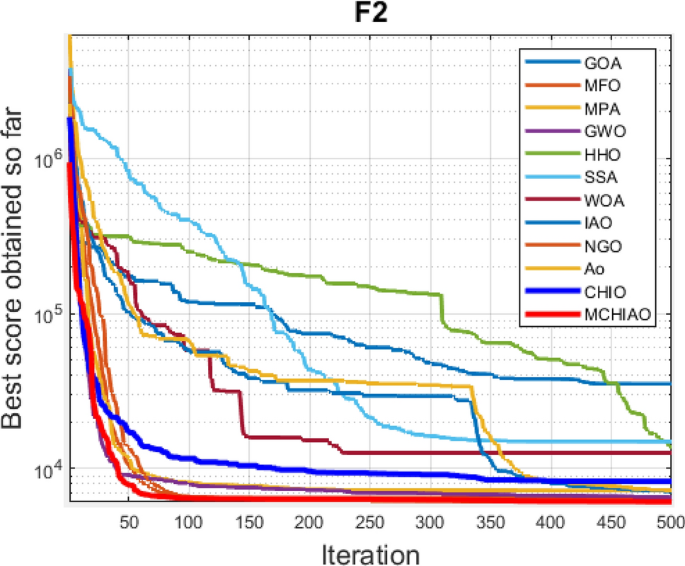
Convergence curves of the 13 algorithms on the pressure vessel design problem

5.8.3 Welded beam design

Another example used to assess MCHIAO performance in the engineering domain is a well-known welded beam design, as shown in Fig.  18 [ 22 ].

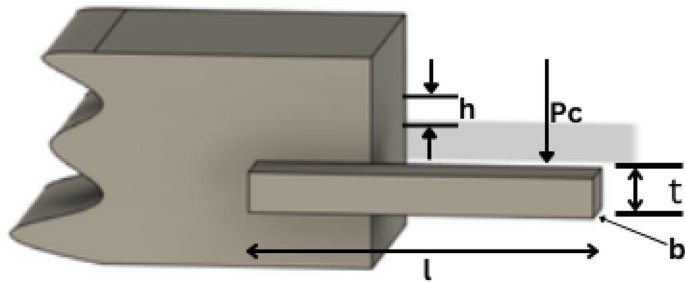
Schematic of welded beam design

In this problem, the aim is to establish the best design variables to minimize the overall manufacturing cost of a welded beam is subject to Shear stress (τ), Bending stress (θ), the bar’s buckling load (Pc), the beam end deflection (δ), and other constraints. The four variables in this problem are the bar length (l), the thickness of the weld (h), height (t), and thickness (b). The mathematical formulation of this problem is as follows:

where \({\uptau }\left( x \right) = \sqrt {{{\tau^{\prime}}} + \left( {2{{\tau \tau^{\prime}}}} \right)\frac{{x_{2} }}{2R} + \left( {{{\tau^{\prime\prime}}}} \right)^{2} } ,\)

Table 34 presents the optimization results of the welded beam design problem for the proposed MCHIAO against the same twelve algorithms. Table 35 presents the p-values of MCHIAO which was acquired by applying the Wilcoxon test against all the other twelve algorithms for the welded beam design problem. These results prove the significance of the proposed algorithm for all functions because the p -values are less than 0.05.

Figure  19 below illustrates the MCHIAO plot against the competitive optimization results in the welded beam design problem.

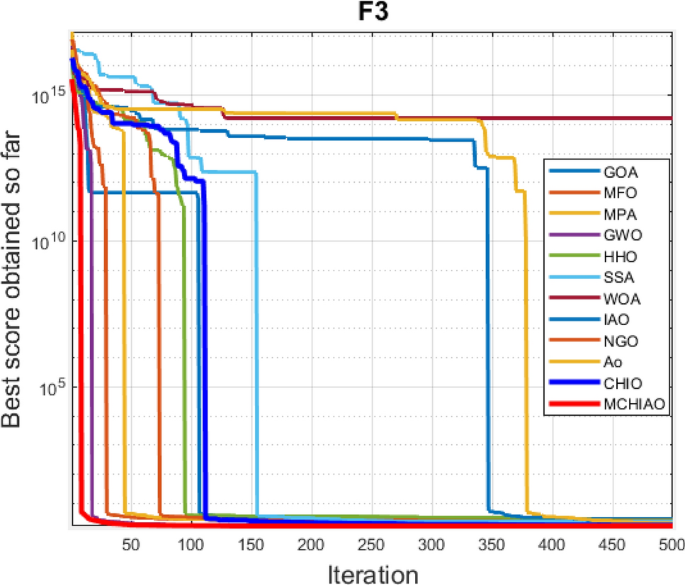
Convergence curves of the 13 algorithms on the welded beam design problem

5.8.4 Speed Reducer problem

It is a weight minimization problem that involves the design of a speed reducer for a small aircraft’s internal combustion engine. It is a challenging benchmark because it has seven design variables ( \({x}_{1}\, to\, {x}_{7}\) ). Figure  20 illustrates the problem's schematic [ 39 ].

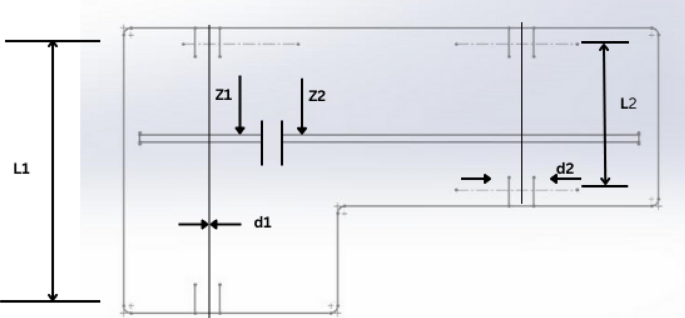
Speed reducer design

This problem's mathematical model is as follows:

Table 36 shows the results of this problem for the proposed MCHIAO against the same twelve algorithms. Table 37 presents the p -values of MCHIAO which was acquired by applying the Wilcoxon test against all the other twelve algorithms for the speed reducer design problem. These results prove the significance of the proposed algorithm for all functions because the p -values are less than 0.05.

Figure  21 illustrates the same 12 optimization algorithms’ convergence curves against the MCHIAO on the speed reducer problem.

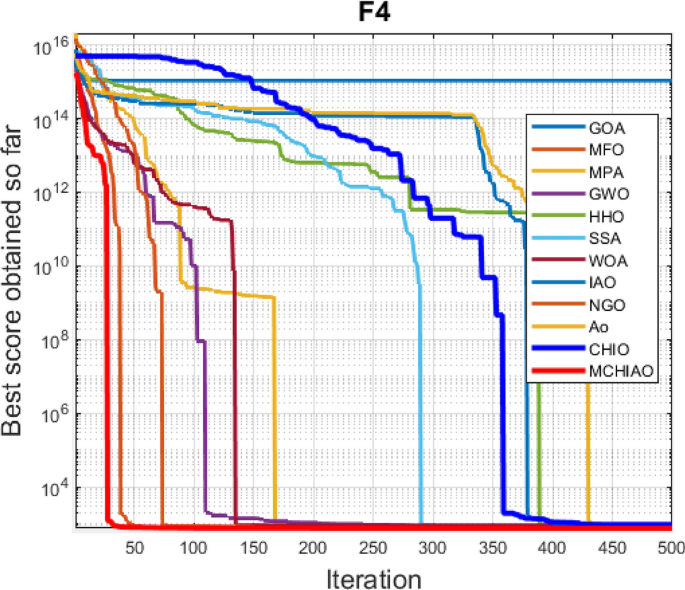
Convergence curves of the 13 algorithms on the speed reducer problem

5.8.5 Gear train design problem

The main goal of this problem is to minimize the gear ratio for preparing the compound gear train, as shown in Fig.  22 [ 39 ].

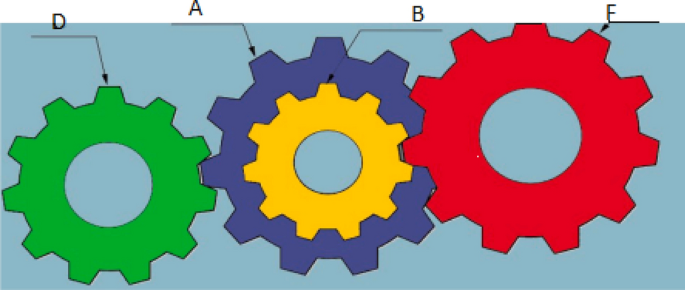
Gear train design

The objective is to achieve the optimal number of teeth for four train gears to minimize the gear ratio. The gear ratio is defined as:

The decision variables ( \({n}_{j}\) ) are discrete. Where \({n}_{j}\) stands for the number of gearwheel teeth \(j\) , with \(j=A, B, D, F.\)

Table 38 illustrates the results of this problem for the proposed MCHIAO against the same twelve algorithms. Table 39 presents the p -values of MCHIAO which was acquired by applying the Wilcoxon test against all the other twelve algorithms for the gear train design problem. These results prove the significance of the proposed algorithm for all functions because the p -values are less than 0.05.

Figure  23 demonstrates the diverse algorithms’ convergence curves against the proposed MCHIAO algorithm.

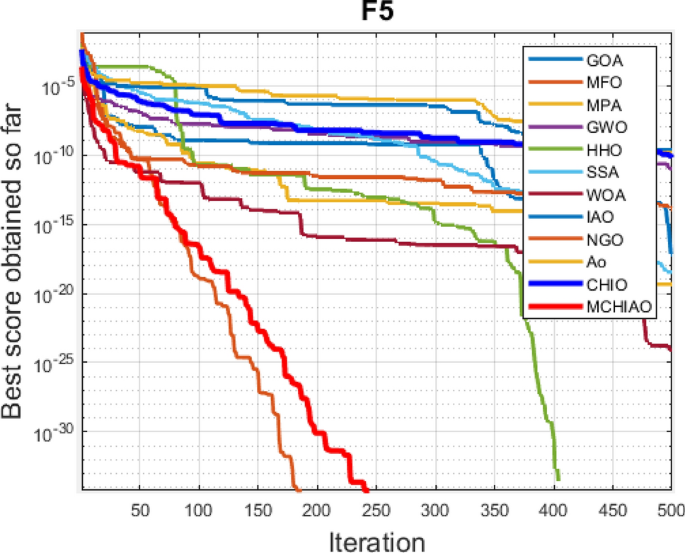
Convergence curves of the 13 algorithms on the gear train design problem

5.8.6 Three-bar truss design problem

The primary purpose of truss design is to reduce the weight of the bar structures. As a result, three bars should be placed as shown in Fig.  24 . As the goal is to reduce the weight of the bars in this position. This is an optimization problem with constraints. This problem has two design parameters \(({x}_{1},{x}_{2})\) and three restrictive functions: deflection constraints of each bar, buckling, and stress [ 22 ].

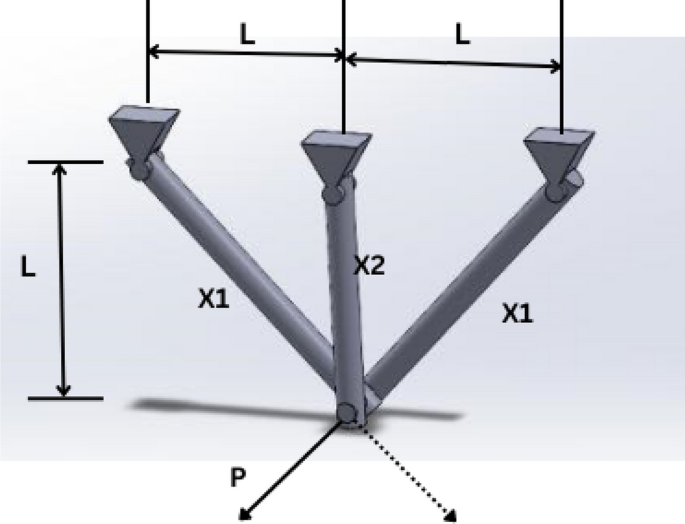
Three-bar truss design

The problem is mathematically expressed as follows:

The constants are as follows: \(L=100\, cm, P=2\frac{KN}{{cm}^{2}}.\) \(\mathrm{and}\,\sigma =2 KN/{cm}^{2}\) .

Table 40 presents the results of various algorithms on this problem for the proposed MCHIAO against the same twelve algorithms. Table 41 presents the p -values of MCHIAO which was acquired by applying the Wilcoxon test against all the other twelve algorithms for the three-bar truss design problem. These results prove the significance of the proposed algorithm for all functions because the p -values are less than 0.05.

Figure  25 below presents the various competitive optimization algorithms’ convergence curves.

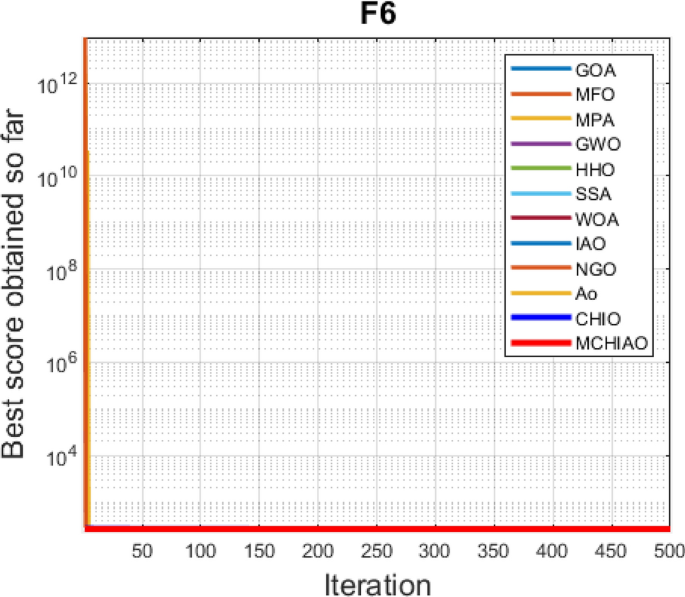
Three-bar truss design plots

6 Conclusions

In this study, Modified Coronavirus Herd Immunity Aquila Optimizer (MCHIAO) is an improved hybrid algorithm proposed as a contribution to a novel nature-inspired human-based metaheuristic optimization algorithm (CHIO) with Aquila optimization algorithm for global optimization problems. The proposed algorithm presents three main modifications that lead to better outcomes. The first modification is applying an improved case categorizing technique that implements a balance between the exploitation and exploration stages. The second enhancement is improving the equation of the new genes’ value which leads to more optimal values. Additionally, as many studies show that the COVID-19 pandemic possesses chaotic system characteristics, we applied the chaotic system in the case categorizing phase which leads to avoiding local minima and rapid convergence rate. The third enhancement is generating a new formula for the selection between the expanded exploitation and narrowed exploitation phases. The results reveal that the proposed MCHIAO can find optimal solutions and converge faster on most issues due to its strong exploration and exploitation capabilities. The proposed MCHIAO's effectiveness is evaluated using Wilcoxon statistical analyses and Friedman average rank through 23 well-known benchmark functions of various dimensions and complexity: seven unimodal, six multimodal with adjustable dimensions, and 10 multimodal with fixed dimensions. These functions have been widely used to evaluate newly proposed optimization methods in the literature. The MCHIAO is also compared to the performance of other well-known and most recent optimization techniques. The algorithms used in the comparison are GWO, GOA, MFO, MPA, HHO, SSA, WOA, IAO, NOA, NGO, AO, and the original CHIO. The comparative analysis reveals that MCHIAO is conspicuously competitive since it can acquire 21 out of the 23 benchmark functions. Further, to prove the efficiency of the proposed MCHIAO algorithm, both CEC 2017 and CEC 2019 benchmark functions are tested in which MCHIAO achieves the overall best results in 17 out of 29 CEC 2017 and 4 out of 10 CEC19 benchmark functions. The exploitative and explorative behavior of the hybrid algorithm MCHIAO is assessed on a variety of classical functions, including 24 unimodal and 44 multimodal functions, respectively. The proposed MCHIAO ranked top in all 15 functions for unimodal variable-dimension issues and first in 7 out of 8 functions for unimodal fixed-dimension problems. On the other hand, MCHIAO succeeds in 24 out of 27 functions for the multimodal fixed-dimension challenges and is placed top in 14 out of 17 functions for the multimodal variable-dimension problems. As well, the proposed MCHIAO defeats the competitive optimization algorithms in five out of six real-world application problems gear train design problem, speed reducer problem, welded beam design problem, pressure vessel design problem, and welded beam design problem and ranked second in the pressure vessel problem. MCHIAO has several limitations, much like any other suggested algorithm. First, the sensitivity to parameter issue in the original CHIO and AO has been resolved by MCHIAO. Results with the mentioned issues are encouraging. This might not work, though, for other issues. Second, convergence time grows with complexity, providing a new avenue for future study to address this problem. Finally, new algorithms with improved performance may be created as this field of study continues to advance.

Data availability

Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.

Shabani A, Asgarian B, Gharebaghi SA, Salido MA, Giret A (2019) A new optimization algorithm based on search and rescue operations. Math Probl Eng 2019:1–23

Article   Google Scholar  

Yang X (2021) Nature-inspired optimization algorithms: second edition, Mara Conner.

Wang FS, Chen LH (2013) Heuristic Optimization. In: Dubitzky W, Wolkenhauer O, Cho KH, Yokota H (eds) Encyclopedia of Systems Biology. Springer, New York, NY. https://doi.org/10.1007/978-1-4419-9863-7_411 .

Osman IH, Laporte G (1996) Metaheuristics: A bibliography. Ann Ope Res 63(5):511–623

Fausto F, Reyna-Orta A, Cuevas E, Andrade AG, Perez-Cisneros M (2019) From ants to whales: metaheuristics for all tastes. Artif Intell Rev 1–58

Saafan MM, El-Gendy EM (2021) IWOSSA: An improved whale optimization salp swarm algorithm for solving optimization problems. Exp Syst Appl 176: 114901. ISSN 0957–4174, https://doi.org/10.1016/j.eswa.2021.114901 .

Wolpert DH, Macready WG (1997) No free lunch theorems for optimization. IEEE Trans Evolut Comput 1(1):67–82.

Kennedy J, Eberhart R (1995) Particle swarm optimization. In: Proceedings of ICNN’95-International Conference on Neural Networks 4: 1942–1948. IEEE.

Saremi S, Mirjalili S, Lewis A (2017) Grasshopper optimisation algorithm: theory and application. Adv Eng Softw 105:30–47

Mirjalili S (2015) Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowl-Based Syst 89.

Faramarzi A, Heidarinejad M, Mirjalili S, Gandomi AH (2020) Marine predators algorithm: a nature-inspired metaheuristic. Exp Syst Appl 152: 113377, ISSN 0957–4174.

Humphries NE, Queiroz N, Dyer JRM, Pade NG, Musyl MK, Schaefer KM, Fuller DW, Brunnschweiler JM, Doyle TK, Houghton JDR, Hays GC, Jones CS, Noble LR, Wearmouth VJ, Southall EJ, Sims DW (2010) Environmental context explains Lévy and Brownian movement patterns of marine predators. Nature 465(7301):1066

Bartumeus F, Catalan J, Fulco UL, Lyra ML, Viswanathan GM (2002) Optimizing the encounter rate in biological interactions: Lévy versus Brownian strategies. Phys Rev Lett 88(9):097901

Mirjalili S, Mirjalili SM, Lewis A (2014) Grey wolf optimizer. J Adv Eng Softw 69:46–61

Heidari AA, Mirjalili S, Faris H, Aljarah I, Mafarja M, Chen H (2019) Harris hawks optimization: algorithm and applications. Future Gener Comput Syst 97:849–872

Mirjalili S, Gandomi AH, Mirjalili SZ, Saremi S, Faris H, Mirjalili SM (2017) Salp Swarm Algorithm: a bio-inspired optimizer for engineering design problems. Adv Eng Softw 114:163–191

Seyedali M, Andrew L (2016) The whale optimization algorithm. Adv Eng Softw 95:51–67

Balaha HM, El-Gendy EM, Saafan MM (2021) Covh2sd: A covid-19 detection approach based on harris hawks optimization and stacked deep learning. Expert Syst Appl 186:115805

Balaha HM, Saafan MM (2021) Automatic exam correction framework (aecf) for the mcqs, essays, and equations matching. IEEE Access 9:32368–33238

Balaha HM, El-Gendy EM, Saafan MM (2022) A complete framework for accurate recognition and prognosis of covid-19 patients based on deep transfer learning and feature classification approach. Artif Intell Rev 1–46.

Balaha HM, Shaban AO, El-Gendy EM, Saafan MM (2022) A multi-variate heart disease optimization and recognition framework. Neural Comput Appl 1–38.

Fahmy H, El-Gendy EM, Mohamed MA, Saafan MM (2023) ECH3OA: An Enhanced Chimp-Harris Hawks Optimization Algorithm for copyright protection in Color Images using watermarking techniques. Knowl-Based Syst 269: 110494, ISSN 0950–7051. https://doi.org/10.1016/j.knosys.2023.110494 .

Badr AA, Saafan MM, Abdelsalam MM et al (2023) Novel variants of grasshopper optimization algorithm to solve numerical problems and demand side management in smart grids. Artif Intell Rev. https://doi.org/10.1007/s10462-023-10431-5

Balaha MM, El-Kady S, Balaha HM et al (2023) A vision-based deep learning approach for independent-users Arabic sign language interpretation. Multimed Tools Appl 82:6807–6826. https://doi.org/10.1007/s11042-022-13423-9

Balaha HM, Antar ER, Saafan MM et al (2023) A comprehensive framework towards segmenting and classifying breast cancer patients using deep learning and Aquila optimizer. J Ambient Intell Human Comput. https://doi.org/10.1007/s12652-023-04600-1

Kwok KO, Lai F, Wei WI, Wong SYS, Tang JW (2020) Herd immunity–estimating the level required to halt the covid-19 epidemics in affected countries. J Infect 80(6):e32–e33

Tzanetos A, Dounias G (2021) Nature inspired optimization algorithms or simply variations of metaheuristics? Artif Intell Rev 54:1841–1862. https://doi.org/10.1007/s10462-020-09893-8

Xia Y, Zhong L, Tan J, Zhang Z, Lyu J, Chen Y, Zhao A, Huang L, Long Z, Liu NN, Wang H (2020) How to understand “Herd Immunity” in COVID-19 Pandemic. Front Cell Dev Biol 8:547314

Zhuang L, Cressie N (2014) Bayesian hierarchical statistical SIRS models. Stat Methods Appl 23:601–646. https://doi.org/10.1007/s10260-014-0280-9

Article   MathSciNet   Google Scholar  

Al-Betar MA, Alyasseri ZAA, Awadallah MA et al (2021) Coronavirus herd immunity optimizer (CHIO). Neural Comput & Applic 33:5011–5042. https://doi.org/10.1007/s00521-020-05296-6

Abualigah L, Yousri D, Abd Elaziz ME, Ewees AA, Al-qaness MAA, Gandomi AH (2021) Aquila optimizer: A novel meta-heuristic optimization algorithm. Comput Ind Eng 157: 107250, ISSN 0360–8352, https://doi.org/10.1016/j.cie.2021.107250 .

Salawudeen AT, Mu’azu MB, Sha’aban YA, Adedokun AE (2021) A novel smell agent optimization (SAO): An extensive CEC study and engineering application. Knowl-Based Syst. 232: 107486 (2021).

Ewees AA, Algamal ZY, Abualigah L, Al-qaness MAA, Yousri D, Ghoniem RM, AbdElaziz M (2022) Cox proportional-hazardsmodel based on improved aquilaoptimizer with whale optimizationalgorithm operators. Mathematics 10:1273. https://doi.org/10.3390/math10081273

Abdel-Basset M,Mohamed R, Jameel M, Abouhawwash M (2023) Nutcracker optimizer: A novel nature-inspired metaheuristic algorithm for global optimization and engineering design problems. Knowl-Based Syst, 262: 110248, ISSN 0950–7051, https://doi.org/10.1016/j.knosys.2022.110248 .

Dehghani M, Hubalovsky S, Trojovsky P (2021) Northern goshawk optimization: a new swarm-based algorithm for solving optimization problems. IEEE Access. 1–1. https://doi.org/10.1109/ACCESS.2021.3133286 .

Recioui A (2018) Application of teaching learning-based optimization to the optimal placement of phasor measurement units. Book chapter in: Handbook of Research on Emergent Applications of Optimization Algorithms, IGI Global.

Recioui A (2021) Home load-side management in smart grids using global optimization. Book chapter in: Research Anthology on Multi-Industry Uses of Genetic Programming and Algorithms, IGI Global.

El-Sherbiny A, Elhosseini MA, Haikal AY (2018) A new ABC variant for solving inverse kinematics problem in 5 DOF robot arm. Appl Soft Comput 73:24–38. https://doi.org/10.1016/j.asoc.2018.08.028

Guedria NB (2016) Improved accelerated PSO algorithm for mechanical engineering optimization problems. Appl Soft Comput 40: 455–467, ISSN 1568–4946, https://doi.org/10.1016/j.asoc.2015.10.048 .

Download references

Open access funding provided by The Science, Technology & Innovation Funding Authority (STDF) in cooperation with The Egyptian Knowledge Bank (EKB). Open access funding is provided by The Science, Technology, and Innovation Funding Authority (STDF) in cooperation with The Egyptian Knowledge Bank (EKB). No funding was received for this work.

Author information

Authors and affiliations.

Computers and Control Systems Engineering Department, Faculty of Engineering, Mansoura University, Mansoura, Egypt

Heba Selim, Amira Y. Haikal, Labib M. Labib & Mahmoud M. Saafan

You can also search for this author in PubMed   Google Scholar

Contributions

HS, AYH, LML, and MMS contributed to the design and implementation of the research and, the analysis of the results. All the authors have participated in writing the manuscript and have revised the final version. All authors read and approved the final manuscript.

Corresponding author

Correspondence to Mahmoud M. Saafan .

Ethics declarations

Conflict of interest.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper. There are no conflicts of interest. I would like to confirm that there were no known conflicts of interest associated with this publication and that there was no significant financial support for this work that could affect its outcome.

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

A glossary of acronyms and abbreviations is listed in Table  42 .

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Selim, H., Haikal, A.Y., Labib, L.M. et al. MCHIAO: a modified coronavirus herd immunity-Aquila optimization algorithm based on chaotic behavior for solving engineering problems. Neural Comput & Applic (2024). https://doi.org/10.1007/s00521-024-09533-0

Download citation

Received : 29 May 2023

Accepted : 22 January 2024

Published : 20 April 2024

DOI : https://doi.org/10.1007/s00521-024-09533-0

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Meta-heuristic algorithm
• Optimization
• Coronavirus
• Herd immunity
• Chaos theory
• Find a journal
• Publish with us
• Track your research

A quick post on Chen’s algorithm

Update (April 19): Yilei Chen announced the discovery of a bug in the algorithm, which he does not know how to fix. This was independently discovered by Hongxun Wu and Thomas Vidick. At present, the paper does not provide a polynomial-time algorithm for solving LWE.

If you’re a normal person — that is, a person who doesn’t obsessively follow the latest cryptography news — you probably missed last week’s cryptography bombshell. That news comes in the form of a new e-print authored by Yilei Chen, “ Quantum Algorithms for Lattice Problems “, which has roiled the cryptography research community. The result is now being evaluated by experts in lattices and quantum algorithm design ( and to be clear, I am not one! ) but if it holds up, it’s going to be quite a bad day/week/month/year for the applied cryptography community.

Rather than elaborate at length, here’s quick set of five bullet-points giving the background.

(1) Cryptographers like to build modern public-key encryption schemes on top of mathematical problems that are believed to be “hard”. In practice, we need problems with a specific structure: we can construct efficient solutions for those who hold a secret key, or “trapdoor”, and yet also admit no efficient solution for folks who don’t. While many problems have been considered (and often discarded), most schemes we use today are based on three problems: factoring (the RSA cryptosystem), discrete logarithm (Diffie-Hellman, DSA) and elliptic curve discrete logarithm problem (EC-Diffie-Hellman, ECDSA etc.)

(2) While we would like to believe our favorite problems are fundamentally “hard”, we know this isn’t really true. Researchers have devised algorithms that solve all of these problems quite efficiently (i.e., in polynomial time) — provided someone figures out how to build a quantum computer powerful enough to run the attack algorithms. Fortunately such a computer has not yet been built!

(3) Even though quantum computers are not yet powerful enough to break our public-key crypto, the mere threat of future quantum attacks has inspired industry, government and academia to join forces Fellowship-of-the-Ring-style in order to tackle the problem right now. This isn’t merely about future-proofing our systems: even if quantum computers take decades to build, future quantum computers could break encrypted messages we send today !

(4) One conspicuous outcome of this fellowship is NIST’s Post-Quantum Cryptography (PQC) competition : this was an open competition designed to standardize “post-quantum” cryptographic schemes . Critically, these schemes must be based on different mathematical problems — most notably, problems that don’t seem to admit efficient quantum solutions.

(5) Within this new set of schemes, the most popular class of schemes are based on problems related to mathematical objects called lattices . NIST-approved schemes based on lattice problems include Kyber and Dilithium (which I wrote about recently .) Lattice problems are also the basis of several efficient fully-homomorphic encryption (FHE) schemes.

This background sets up the new result.

Chen’s (not yet peer-reviewed) preprint claims a new quantum algorithm that efficiently solves the “shortest independent vector problem” (SIVP, as well as GapSVP) in lattices with specific parameters. If it holds up, the result could (with numerous important caveats) allow future quantum computers to break schemes that depend on the hardness of specific instances of these problems. The good news here is that even if the result is correct, the vulnerable parameters are very specific: Chen’s algorithm does not immediately apply to the recently-standardized NIST algorithms such as Kyber or Dilithium. Moreover, the exact concrete complexity of the algorithm is not instantly clear: it may turn out to be impractical to run, even if quantum computers become available.

But there is a saying in our field that attacks only get better. If Chen’s result can be improved upon, then quantum algorithms could render obsolete an entire generation of “post-quantum” lattice-based schemes, forcing cryptographers and industry back to the drawing board.

In other words, both a great technical result — and possibly a mild disaster.

As previously mentioned: I am neither an expert in lattice-based cryptography nor quantum computing. The folks who are those things are very busy trying to validate the writeup : and more than a few big results have fallen apart upon detailed inspection. For those searching for the latest developments, here’s a nice writeup by Nigel Smart that doesn’t tackle the correctness of the quantum algorithm (see updates at the bottom), but does talk about the possible implications for FHE and PQC schemes (TL;DR: bad for some FHE schemes, but really depends on the concrete details of the algorithm’s running time.) And here’s another brief note on a “bug” that was found in the paper , that seems to have been quickly addressed by the author.

Up until this week I had intended to write another long wonky post about complexity theory, lattices, and what it all meant for applied cryptography. But now I hope you’ll forgive me if I hold onto that one, for just a little bit longer.

• Cryptography
• cybersecurity
• quantum-computing

Leave a comment Cancel reply

• Already have a WordPress.com account? Log in now.
• Subscribe Subscribed
• Copy shortlink
• Report this content
• View post in Reader
• Manage subscriptions
• Collapse this bar

• School Guide
• Class 8 Syllabus
• Maths Notes Class 8
• Science Notes Class 8
• History Notes Class 8
• Geography Notes Class 8
• Civics Notes Class 8
• NCERT Soln. Class 8 Maths
• RD Sharma Soln. Class 8
• Math Formulas Class 8
• Working with Layers in Flash
• What is Download and Upload Speed?
• What is the Impact of E-Commerce on the Society?
• Factors Affecting Video Conferencing
• Add Text with Horizontal Type Tool in Photoshop
• What Factors one should Keep in Mind while doing E-Commerce?
• Audio and Video Conferencing
• What is EDI (Electronic Data Interchange)?
• How to Use the Timeline in Animate?
• Benefits of Video Conferencing
• How to Use Frames and Keyframes in Flash?
• Types of Animations in Flash
• How to Create a Shape Tween in Flash?
• What is Chatting? - Definition, Types, Platforms, Risks
• What is E-Commerce and E-Greetings?
• Preparing Files for Web Output in Photoshop
• Introduction to Macromedia Flash 8
• How to Use the Rectangle Tool in Photoshop?
• How to Create a Motion Tween in Flash?

How to Use Algorithms to Solve Problems?

An algorithm is a process or set of rules which must be followed to complete a particular task. This is basically the step-by-step procedure to complete any task. All the tasks are followed a particular algorithm, from making a cup of tea to make high scalable software. This is the way to divide a task into several parts. If we draw an algorithm to complete a task then the task will be easier to complete.

The algorithm is used for,

• To develop a framework for instructing computers.
• Introduced notation of basic functions to perform basic tasks.
• For defining and describing a big problem in small parts, so that it is very easy to execute.

Characteristics of Algorithm

• An algorithm should be defined clearly.
• An algorithm should produce at least one output.
• An algorithm should have zero or more inputs.
• An algorithm should be executed and finished in finite number of steps.
• An algorithm should be basic and easy to perform.
• Each step started with a specific indentation like, “Step-1”,
• There must be “Start” as the first step and “End” as the last step of the algorithm.

Let’s take an example to make a cup of tea,

Step 1: Start

Step 2: Take some water in a bowl.

Step 3: Put the water on a gas burner .

Step 4: Turn on the gas burner 

Step 5: Wait for some time until the water is boiled.  

Step 6: Add some tea leaves to the water according to the requirement.

Step 7: Then again wait for some time until the water is getting colorful as tea.

Step 8: Then add some sugar according to taste.

Step 9: Again wait for some time until the sugar is melted.

Step 10: Turn off the gas burner and serve the tea in cups with biscuits.

Step 11: End

Here is an algorithm for making a cup of tea. This is the same for computer science problems.

There are some basics steps to make an algorithm:

• Start – Start the algorithm
• Input – Take the input for values in which the algorithm will execute.
• Conditions – Perform some conditions on the inputs to get the desired output.
• Output – Printing the outputs.
• End – End the execution.

Let’s take some examples of algorithms for computer science problems.

Example 1. Swap two numbers with a third variable  

Step 1: Start Step 2: Take 2 numbers as input. Step 3: Declare another variable as “temp”. Step 4: Store the first variable to “temp”. Step 5: Store the second variable to the First variable. Step 6: Store the “temp” variable to the 2nd variable. Step 7: Print the First and second variables. Step 8: End

Example 2. Find the area of a rectangle

Step 1: Start Step 2: Take the Height and Width of the rectangle as input. Step 3: Declare a variable as “area” Step 4: Multiply Height and Width Step 5: Store the multiplication to “Area”, (its look like area = Height x Width) Step 6: Print “area”; Step 7: End

Example 3. Find the greatest between 3 numbers.

Step 1: Start Step 2: Take 3 numbers as input, say A, B, and C. Step 3: Check if(A>B and A>C) Step 4: Then A is greater Step 5: Print A Step 6 : Else Step 7: Check if(B>A and B>C) Step 8: Then B is greater Step 9: Print B Step 10: Else C is greater Step 11 : Print C Step 12: End

Advantages of Algorithm

• An algorithm uses a definite procedure.
• It is easy to understand because it is a step-by-step definition.
• The algorithm is easy to debug if there is any error happens.
• It is not dependent on any programming language
• It is easier for a programmer to convert it into an actual program because the algorithm divides a problem into smaller parts.

Disadvantages of Algorithms

• An algorithm is Time-consuming, there is specific time complexity for different algorithms.
• Large tasks are difficult to solve in Algorithms because the time complexity may be higher, so programmers have to find a good efficient way to solve that task.
• Looping and branching are difficult to define in algorithms.

Please Login to comment...

Similar reads.

• School Learning
• School Programming

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Avi Wigderson wins $1 million Turing Award for using randomness to change computer science

The 2023 Turing Award has been given to Avi Wigderson . The mathematician found that adding randomness into algorithms made them better at solving nondeterministic problems.

The 2023 Turing Award has been given to Avi Wigderson , a mathematician who discovered the strange connection between computation and randomness. 

Wigderson was announced the winner of the Association for Computing Machinery (ACM) A.M. Turing Award, often called the " Nobel Prize of Computing," on April 10, 2024.

The award, given with a prize of $1 million, comes just three years after Wigderson, a professor of mathematics at the Institute for Advanced Study in Princeton, New Jersey, won the 2021 Abel Award for his contributions to computer science. Wigderson's theoretical work has been key to the development of numerous advances in computing , from cloud networks to cryptography methods that underpin cryptocurrencies.

"Wigderson is a towering intellectual force in theoretical computer science, an exciting discipline that attracts some of the most promising young researchers to work on the most difficult challenges," Yannis Ioannidis , president of the ACM, said in a statement . "This year's Turing Award recognizes Wigderson's specific work on randomness, as well as the indirect but substantial impact he has had on the entire field of theoretical computer science."

Related: Scientists uncover hidden math that governs genetic mutations

Computer algorithms are deterministic by nature, which enables them to make predictions but also limits their grasp of the messy randomness found in the real world. In fact, many problems are considered computationally “hard”, and deterministic algorithms struggle to solve them efficiently.

— Newly discovered 'einstein' tile is a 13-sided shape that solves a decades-old math problem

— Centuries old 'impossible math problem cracked using physics of Schrödinger's cat

— Two mathematicians just solved a decades-old math riddle — and possibly the meaning of life

But Wigderson and his colleague Richard Karp , a computer scientist at the University of California, Berkeley, found a way to tame computational hardness. After inserting randomness into their algorithms, they found that they made some problems much easier to solve.

Sign up for the Live Science daily newsletter now

Get the world’s most fascinating discoveries delivered straight to your inbox.

Wigderson chased this observation, proving in later work that the reverse also applied: Randomness could always be stripped from probabilistic algorithms to transform them into deterministic ones. His findings illuminated the connection between computational hardness and randomness in ways that reshaped computer science.

"From the earliest days of computer science, researchers have recognized that incorporating randomness was a way to design faster algorithms for a wide range of applications," Jeff Dean , chief scientist at Google Research and Google DeepMind, said in the statement. "Efforts to better understand randomness continue to yield important benefits to our field, and Wigderson has opened new horizons in this area."

Ben Turner is a U.K. based staff writer at Live Science. He covers physics and astronomy, among other topics like tech and climate change. He graduated from University College London with a degree in particle physics before training as a journalist. When he's not writing, Ben enjoys reading literature, playing the guitar and embarrassing himself with chess.

Pi calculated to 105 trillion digits, smashing world record

Can you solve NASA's Pi Day 2024 riddle?

Scientists may have pinpointed the true origin of the Hope Diamond and other pristine gemstones

Most Popular

• 2 Nightmare fish may explain how our 'fight or flight' response evolved
• 3 Lyrid meteor shower 2024: How to watch stunning shooting stars and 'fireballs' during the event's peak this week
• 4 Scientists are one step closer to knowing the mass of ghostly neutrinos — possibly paving the way to new physics
• 5 What's the largest waterfall in the world?
• 2 Enormous dinosaur dubbed Shiva 'The Destroyer' is one of the biggest ever discovered
• 3 2,500-year-old skeletons with legs chopped off may be elites who received 'cruel' punishment in ancient China
• 4 Rare 'porcelain gallbladder' found in 100-year-old unmarked grave at Mississippi mental asylum cemetery

Intro Programming for Engrs

Engineering.

Engineering problem solving using computer programming. Topics include problem solving strategies, algorithm development, structured programming design, the interface of software with the physical world (e.g., the use of sensors or real world data), and the application of numerical techniques.

Engineering problem solving using computer programming. Topics include problem solving strategies, algorithm development, structured programming design, the interface of software with the physical world (e.g., the use of sensors) and the application of numerical techniques.

PREREQ.: MATH 100A or MATH 110A

Novel quantum algorithm proposed for high-quality solutions to combinatorial optimization problems

C ombinatorial optimization problems (COPs) have applications in many different fields such as logistics, supply chain management, machine learning, material design and drug discovery, among others, for finding the optimal solution to complex problems. These problems are usually very computationally intensive using classical computers and thus solving COPs using quantum computers has attracted significant attention from both academia and industry.

Quantum computers take advantage of the quantum property of superposition, using specialized qubits, that can exist in an infinite yet contained number of states of 0 or 1 or any combination of the two, to quickly solve large problems. However, when COPs involve constraints, conventional quantum algorithms like adiabatic quantum annealing struggle to obtain a near-optimal solution within the operation time of quantum computers.

Recent advances in quantum technology have led to devices such as quantum annealers and gate-type quantum devices that provide suitable platforms for solving COPs. Unfortunately, they are susceptible to noise, which limits their applicability to quantum algorithms with low computational costs.

To address this challenge, Assistant Professor Tatsuhiko Shirai and Professor Nozomu Togawa from the Department of Computer Science and Communications Engineering at Waseda University in Japan have recently developed a post-processing variationally scheduled quantum algorithm (pVSQA). Their study was published in the journal IEEE Transactions on Quantum Engineering .

"The two main methods for solving COPs with quantum devices are variational scheduling and post-processing. Our algorithm combines variational scheduling with a post-processing method that transforms infeasible solutions into feasible ones, allowing us to achieve near-optimal solutions for constrained COPs on both quantum annealers and gate-based quantum computers," explains Dr. Shirai.

The innovative pVSQA algorithm uses a quantum device to first generate a variational quantum state via quantum computation. This is then used to generate a probability distribution function which consists of all the feasible and infeasible solutions that are within the constraints of the COP.

Next, the post-processing method transforms the infeasible solutions into feasible ones, leaving the probability distribution with only feasible solutions. A classical computer is then used to calculate an energy expectation value of the cost function using this new probability distribution. Repeating this calculation results in a near-optimal solution.

The researchers analyzed the performance of this algorithm using both a simulator and real quantum devices such as a quantum annealer and a gate-type quantum device. The experiments revealed that pVSQA achieves a near-optimal performance within a predetermined time on the simulator and outperforms conventional quantum algorithms without post-processing on real quantum devices.

Dr. Shirai said, "Drastic social transformations are urgently needed to address various social issues. Examples include the realization of a carbon-neutral society to solve climate change issues and the realization of sustainable development goals to address issues such as increased energy demand and food shortage.

"Efficiently solving combinatorial optimization problems is at the heart of achieving these transformations. Our new method will play a significant role in realizing these long-term social transformations."

In conclusion, this study marks a significant step forward for using quantum computers for solving COPs, holding promise for addressing complex real-world problems across various domains.

More information: Tatsuhiko Shirai et al, Post-Processing Variationally Scheduled Quantum Algorithm for Constrained Combinatorial Optimization Problems, IEEE Transactions on Quantum Engineering (2024). DOI: 10.1109/TQE.2024.3376721

Provided by Waseda University