quasi assignment meaning

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

7.3 Quasi-Experimental Research

Learning objectives.

• Explain what quasi-experimental research is and distinguish it clearly from both experimental and correlational research.
• Describe three different types of quasi-experimental research designs (nonequivalent groups, pretest-posttest, and interrupted time series) and identify examples of each one.

The prefix quasi means “resembling.” Thus quasi-experimental research is research that resembles experimental research but is not true experimental research. Although the independent variable is manipulated, participants are not randomly assigned to conditions or orders of conditions (Cook & Campbell, 1979). Because the independent variable is manipulated before the dependent variable is measured, quasi-experimental research eliminates the directionality problem. But because participants are not randomly assigned—making it likely that there are other differences between conditions—quasi-experimental research does not eliminate the problem of confounding variables. In terms of internal validity, therefore, quasi-experiments are generally somewhere between correlational studies and true experiments.

Quasi-experiments are most likely to be conducted in field settings in which random assignment is difficult or impossible. They are often conducted to evaluate the effectiveness of a treatment—perhaps a type of psychotherapy or an educational intervention. There are many different kinds of quasi-experiments, but we will discuss just a few of the most common ones here.

Nonequivalent Groups Design

Recall that when participants in a between-subjects experiment are randomly assigned to conditions, the resulting groups are likely to be quite similar. In fact, researchers consider them to be equivalent. When participants are not randomly assigned to conditions, however, the resulting groups are likely to be dissimilar in some ways. For this reason, researchers consider them to be nonequivalent. A nonequivalent groups design , then, is a between-subjects design in which participants have not been randomly assigned to conditions.

Imagine, for example, a researcher who wants to evaluate a new method of teaching fractions to third graders. One way would be to conduct a study with a treatment group consisting of one class of third-grade students and a control group consisting of another class of third-grade students. This would be a nonequivalent groups design because the students are not randomly assigned to classes by the researcher, which means there could be important differences between them. For example, the parents of higher achieving or more motivated students might have been more likely to request that their children be assigned to Ms. Williams’s class. Or the principal might have assigned the “troublemakers” to Mr. Jones’s class because he is a stronger disciplinarian. Of course, the teachers’ styles, and even the classroom environments, might be very different and might cause different levels of achievement or motivation among the students. If at the end of the study there was a difference in the two classes’ knowledge of fractions, it might have been caused by the difference between the teaching methods—but it might have been caused by any of these confounding variables.

Of course, researchers using a nonequivalent groups design can take steps to ensure that their groups are as similar as possible. In the present example, the researcher could try to select two classes at the same school, where the students in the two classes have similar scores on a standardized math test and the teachers are the same sex, are close in age, and have similar teaching styles. Taking such steps would increase the internal validity of the study because it would eliminate some of the most important confounding variables. But without true random assignment of the students to conditions, there remains the possibility of other important confounding variables that the researcher was not able to control.

Pretest-Posttest Design

In a pretest-posttest design , the dependent variable is measured once before the treatment is implemented and once after it is implemented. Imagine, for example, a researcher who is interested in the effectiveness of an antidrug education program on elementary school students’ attitudes toward illegal drugs. The researcher could measure the attitudes of students at a particular elementary school during one week, implement the antidrug program during the next week, and finally, measure their attitudes again the following week. The pretest-posttest design is much like a within-subjects experiment in which each participant is tested first under the control condition and then under the treatment condition. It is unlike a within-subjects experiment, however, in that the order of conditions is not counterbalanced because it typically is not possible for a participant to be tested in the treatment condition first and then in an “untreated” control condition.

If the average posttest score is better than the average pretest score, then it makes sense to conclude that the treatment might be responsible for the improvement. Unfortunately, one often cannot conclude this with a high degree of certainty because there may be other explanations for why the posttest scores are better. One category of alternative explanations goes under the name of history . Other things might have happened between the pretest and the posttest. Perhaps an antidrug program aired on television and many of the students watched it, or perhaps a celebrity died of a drug overdose and many of the students heard about it. Another category of alternative explanations goes under the name of maturation . Participants might have changed between the pretest and the posttest in ways that they were going to anyway because they are growing and learning. If it were a yearlong program, participants might become less impulsive or better reasoners and this might be responsible for the change.

Another alternative explanation for a change in the dependent variable in a pretest-posttest design is regression to the mean . This refers to the statistical fact that an individual who scores extremely on a variable on one occasion will tend to score less extremely on the next occasion. For example, a bowler with a long-term average of 150 who suddenly bowls a 220 will almost certainly score lower in the next game. Her score will “regress” toward her mean score of 150. Regression to the mean can be a problem when participants are selected for further study because of their extreme scores. Imagine, for example, that only students who scored especially low on a test of fractions are given a special training program and then retested. Regression to the mean all but guarantees that their scores will be higher even if the training program has no effect. A closely related concept—and an extremely important one in psychological research—is spontaneous remission . This is the tendency for many medical and psychological problems to improve over time without any form of treatment. The common cold is a good example. If one were to measure symptom severity in 100 common cold sufferers today, give them a bowl of chicken soup every day, and then measure their symptom severity again in a week, they would probably be much improved. This does not mean that the chicken soup was responsible for the improvement, however, because they would have been much improved without any treatment at all. The same is true of many psychological problems. A group of severely depressed people today is likely to be less depressed on average in 6 months. In reviewing the results of several studies of treatments for depression, researchers Michael Posternak and Ivan Miller found that participants in waitlist control conditions improved an average of 10 to 15% before they received any treatment at all (Posternak & Miller, 2001). Thus one must generally be very cautious about inferring causality from pretest-posttest designs.

Does Psychotherapy Work?

Early studies on the effectiveness of psychotherapy tended to use pretest-posttest designs. In a classic 1952 article, researcher Hans Eysenck summarized the results of 24 such studies showing that about two thirds of patients improved between the pretest and the posttest (Eysenck, 1952). But Eysenck also compared these results with archival data from state hospital and insurance company records showing that similar patients recovered at about the same rate without receiving psychotherapy. This suggested to Eysenck that the improvement that patients showed in the pretest-posttest studies might be no more than spontaneous remission. Note that Eysenck did not conclude that psychotherapy was ineffective. He merely concluded that there was no evidence that it was, and he wrote of “the necessity of properly planned and executed experimental studies into this important field” (p. 323). You can read the entire article here:

http://psychclassics.yorku.ca/Eysenck/psychotherapy.htm

Fortunately, many other researchers took up Eysenck’s challenge, and by 1980 hundreds of experiments had been conducted in which participants were randomly assigned to treatment and control conditions, and the results were summarized in a classic book by Mary Lee Smith, Gene Glass, and Thomas Miller (Smith, Glass, & Miller, 1980). They found that overall psychotherapy was quite effective, with about 80% of treatment participants improving more than the average control participant. Subsequent research has focused more on the conditions under which different types of psychotherapy are more or less effective.

In a classic 1952 article, researcher Hans Eysenck pointed out the shortcomings of the simple pretest-posttest design for evaluating the effectiveness of psychotherapy.

Wikimedia Commons – CC BY-SA 3.0.

Interrupted Time Series Design

A variant of the pretest-posttest design is the interrupted time-series design . A time series is a set of measurements taken at intervals over a period of time. For example, a manufacturing company might measure its workers’ productivity each week for a year. In an interrupted time series-design, a time series like this is “interrupted” by a treatment. In one classic example, the treatment was the reduction of the work shifts in a factory from 10 hours to 8 hours (Cook & Campbell, 1979). Because productivity increased rather quickly after the shortening of the work shifts, and because it remained elevated for many months afterward, the researcher concluded that the shortening of the shifts caused the increase in productivity. Notice that the interrupted time-series design is like a pretest-posttest design in that it includes measurements of the dependent variable both before and after the treatment. It is unlike the pretest-posttest design, however, in that it includes multiple pretest and posttest measurements.

Figure 7.5 “A Hypothetical Interrupted Time-Series Design” shows data from a hypothetical interrupted time-series study. The dependent variable is the number of student absences per week in a research methods course. The treatment is that the instructor begins publicly taking attendance each day so that students know that the instructor is aware of who is present and who is absent. The top panel of Figure 7.5 “A Hypothetical Interrupted Time-Series Design” shows how the data might look if this treatment worked. There is a consistently high number of absences before the treatment, and there is an immediate and sustained drop in absences after the treatment. The bottom panel of Figure 7.5 “A Hypothetical Interrupted Time-Series Design” shows how the data might look if this treatment did not work. On average, the number of absences after the treatment is about the same as the number before. This figure also illustrates an advantage of the interrupted time-series design over a simpler pretest-posttest design. If there had been only one measurement of absences before the treatment at Week 7 and one afterward at Week 8, then it would have looked as though the treatment were responsible for the reduction. The multiple measurements both before and after the treatment suggest that the reduction between Weeks 7 and 8 is nothing more than normal week-to-week variation.

Figure 7.5 A Hypothetical Interrupted Time-Series Design

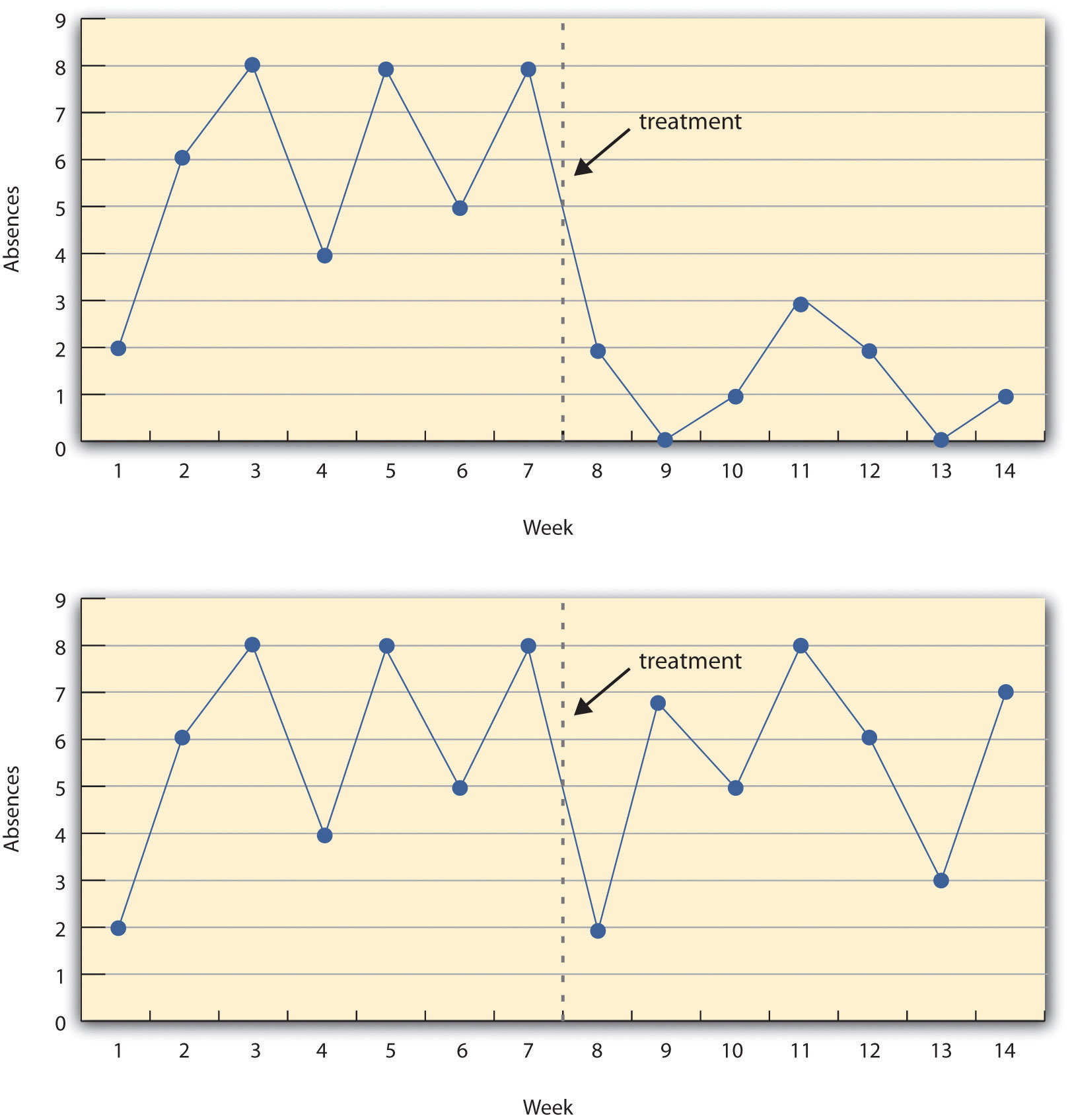
The top panel shows data that suggest that the treatment caused a reduction in absences. The bottom panel shows data that suggest that it did not.

Combination Designs

A type of quasi-experimental design that is generally better than either the nonequivalent groups design or the pretest-posttest design is one that combines elements of both. There is a treatment group that is given a pretest, receives a treatment, and then is given a posttest. But at the same time there is a control group that is given a pretest, does not receive the treatment, and then is given a posttest. The question, then, is not simply whether participants who receive the treatment improve but whether they improve more than participants who do not receive the treatment.

Imagine, for example, that students in one school are given a pretest on their attitudes toward drugs, then are exposed to an antidrug program, and finally are given a posttest. Students in a similar school are given the pretest, not exposed to an antidrug program, and finally are given a posttest. Again, if students in the treatment condition become more negative toward drugs, this could be an effect of the treatment, but it could also be a matter of history or maturation. If it really is an effect of the treatment, then students in the treatment condition should become more negative than students in the control condition. But if it is a matter of history (e.g., news of a celebrity drug overdose) or maturation (e.g., improved reasoning), then students in the two conditions would be likely to show similar amounts of change. This type of design does not completely eliminate the possibility of confounding variables, however. Something could occur at one of the schools but not the other (e.g., a student drug overdose), so students at the first school would be affected by it while students at the other school would not.

Finally, if participants in this kind of design are randomly assigned to conditions, it becomes a true experiment rather than a quasi experiment. In fact, it is the kind of experiment that Eysenck called for—and that has now been conducted many times—to demonstrate the effectiveness of psychotherapy.

Key Takeaways

• Quasi-experimental research involves the manipulation of an independent variable without the random assignment of participants to conditions or orders of conditions. Among the important types are nonequivalent groups designs, pretest-posttest, and interrupted time-series designs.
• Quasi-experimental research eliminates the directionality problem because it involves the manipulation of the independent variable. It does not eliminate the problem of confounding variables, however, because it does not involve random assignment to conditions. For these reasons, quasi-experimental research is generally higher in internal validity than correlational studies but lower than true experiments.
• Practice: Imagine that two college professors decide to test the effect of giving daily quizzes on student performance in a statistics course. They decide that Professor A will give quizzes but Professor B will not. They will then compare the performance of students in their two sections on a common final exam. List five other variables that might differ between the two sections that could affect the results.

Discussion: Imagine that a group of obese children is recruited for a study in which their weight is measured, then they participate for 3 months in a program that encourages them to be more active, and finally their weight is measured again. Explain how each of the following might affect the results:

• regression to the mean
• spontaneous remission

Cook, T. D., & Campbell, D. T. (1979). Quasi-experimentation: Design & analysis issues in field settings . Boston, MA: Houghton Mifflin.

Eysenck, H. J. (1952). The effects of psychotherapy: An evaluation. Journal of Consulting Psychology, 16 , 319–324.

Posternak, M. A., & Miller, I. (2001). Untreated short-term course of major depression: A meta-analysis of studies using outcomes from studies using wait-list control groups. Journal of Affective Disorders, 66 , 139–146.

Smith, M. L., Glass, G. V., & Miller, T. I. (1980). The benefits of psychotherapy . Baltimore, MD: Johns Hopkins University Press.

Research Methods in Psychology Copyright © 2016 by University of Minnesota is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Child Care and Early Education Research Connections

Experiments and quasi-experiments.

This page includes an explanation of the types, key components, validity, ethics, and advantages and disadvantages of experimental design.

An experiment is a study in which the researcher manipulates the level of some independent variable and then measures the outcome. Experiments are powerful techniques for evaluating cause-and-effect relationships. Many researchers consider experiments the "gold standard" against which all other research designs should be judged. Experiments are conducted both in the laboratory and in real life situations.

Types of Experimental Design

There are two basic types of research design:

• True experiments
• Quasi-experiments

The purpose of both is to examine the cause of certain phenomena.

True experiments, in which all the important factors that might affect the phenomena of interest are completely controlled, are the preferred design. Often, however, it is not possible or practical to control all the key factors, so it becomes necessary to implement a quasi-experimental research design.

Similarities between true and quasi-experiments:

• Study participants are subjected to some type of treatment or condition
• Some outcome of interest is measured
• The researchers test whether differences in this outcome are related to the treatment

Differences between true experiments and quasi-experiments:

• In a true experiment, participants are randomly assigned to either the treatment or the control group, whereas they are not assigned randomly in a quasi-experiment
• In a quasi-experiment, the control and treatment groups differ not only in terms of the experimental treatment they receive, but also in other, often unknown or unknowable, ways. Thus, the researcher must try to statistically control for as many of these differences as possible
• Because control is lacking in quasi-experiments, there may be several "rival hypotheses" competing with the experimental manipulation as explanations for observed results

Key Components of Experimental Research Design

The manipulation of predictor variables.

In an experiment, the researcher manipulates the factor that is hypothesized to affect the outcome of interest. The factor that is being manipulated is typically referred to as the treatment or intervention. The researcher may manipulate whether research subjects receive a treatment (e.g., antidepressant medicine: yes or no) and the level of treatment (e.g., 50 mg, 75 mg, 100 mg, and 125 mg).

Suppose, for example, a group of researchers was interested in the causes of maternal employment. They might hypothesize that the provision of government-subsidized child care would promote such employment. They could then design an experiment in which some subjects would be provided the option of government-funded child care subsidies and others would not. The researchers might also manipulate the value of the child care subsidies in order to determine if higher subsidy values might result in different levels of maternal employment.

Random Assignment

• Study participants are randomly assigned to different treatment groups
• All participants have the same chance of being in a given condition
• Participants are assigned to either the group that receives the treatment, known as the "experimental group" or "treatment group," or to the group which does not receive the treatment, referred to as the "control group"
• Random assignment neutralizes factors other than the independent and dependent variables, making it possible to directly infer cause and effect

Random Sampling

Traditionally, experimental researchers have used convenience sampling to select study participants. However, as research methods have become more rigorous, and the problems with generalizing from a convenience sample to the larger population have become more apparent, experimental researchers are increasingly turning to random sampling. In experimental policy research studies, participants are often randomly selected from program administrative databases and randomly assigned to the control or treatment groups.

Validity of Results

The two types of validity of experiments are internal and external. It is often difficult to achieve both in social science research experiments.

Internal Validity

• When an experiment is internally valid, we are certain that the independent variable (e.g., child care subsidies) caused the outcome of the study (e.g., maternal employment)
• When subjects are randomly assigned to treatment or control groups, we can assume that the independent variable caused the observed outcomes because the two groups should not have differed from one another at the start of the experiment
• For example, take the child care subsidy example above. Since research subjects were randomly assigned to the treatment (child care subsidies available) and control (no child care subsidies available) groups, the two groups should not have differed at the outset of the study. If, after the intervention, mothers in the treatment group were more likely to be working, we can assume that the availability of child care subsidies promoted maternal employment

One potential threat to internal validity in experiments occurs when participants either drop out of the study or refuse to participate in the study. If particular types of individuals drop out or refuse to participate more often than individuals with other characteristics, this is called differential attrition. For example, suppose an experiment was conducted to assess the effects of a new reading curriculum. If the new curriculum was so tough that many of the slowest readers dropped out of school, the school with the new curriculum would experience an increase in the average reading scores. The reason they experienced an increase in reading scores, however, is because the worst readers left the school, not because the new curriculum improved students' reading skills.

External Validity

• External validity is also of particular concern in social science experiments
• It can be very difficult to generalize experimental results to groups that were not included in the study
• Studies that randomly select participants from the most diverse and representative populations are more likely to have external validity
• The use of random sampling techniques makes it easier to generalize the results of studies to other groups

For example, a research study shows that a new curriculum improved reading comprehension of third-grade children in Iowa. To assess the study's external validity, you would ask whether this new curriculum would also be effective with third graders in New York or with children in other elementary grades.

Glossary terms related to validity:

• internal validity
• external validity
• differential attrition

It is particularly important in experimental research to follow ethical guidelines. Protecting the health and safety of research subjects is imperative. In order to assure subject safety, all researchers should have their project reviewed by the Institutional Review Boards (IRBS). The  National Institutes of Health  supplies strict guidelines for project approval. Many of these guidelines are based on the  Belmont Report  (pdf).

The basic ethical principles:

• Respect for persons  -- requires that research subjects are not coerced into participating in a study and requires the protection of research subjects who have diminished autonomy
• Beneficence  -- requires that experiments do not harm research subjects, and that researchers minimize the risks for subjects while maximizing the benefits for them
• Justice  -- requires that all forms of differential treatment among research subjects be justified

Advantages and Disadvantages of Experimental Design

The environment in which the research takes place can often be carefully controlled. Consequently, it is easier to estimate the true effect of the variable of interest on the outcome of interest.

Disadvantages

It is often difficult to assure the external validity of the experiment, due to the frequently nonrandom selection processes and the artificial nature of the experimental context.

Research Methodologies Guide

• Action Research
• Bibliometrics
• Case Studies
• Content Analysis
• Digital Scholarship This link opens in a new window
• Documentary
• Ethnography
• Focus Groups
• Grounded Theory
• Life Histories/Autobiographies
• Longitudinal
• Participant Observation
• Qualitative Research (General)

Quasi-Experimental Design

• Usability Studies

Quasi-Experimental Design is a unique research methodology because it is characterized by what is lacks. For example, Abraham & MacDonald (2011) state:

" Quasi-experimental research is similar to experimental research in that there is manipulation of an independent variable. It differs from experimental research because either there is no control group, no random selection, no random assignment, and/or no active manipulation. "

This type of research is often performed in cases where a control group cannot be created or random selection cannot be performed. This is often the case in certain medical and psychological studies. 

For more information on quasi-experimental design, review the resources below: 

Where to Start

Below are listed a few tools and online guides that can help you start your Quasi-experimental research. These include free online resources and resources available only through ISU Library.

• Quasi-Experimental Research Designs by Bruce A. Thyer This pocket guide describes the logic, design, and conduct of the range of quasi-experimental designs, encompassing pre-experiments, quasi-experiments making use of a control or comparison group, and time-series designs. An introductory chapter describes the valuable role these types of studies have played in social work, from the 1930s to the present. Subsequent chapters delve into each design type's major features, the kinds of questions it is capable of answering, and its strengths and limitations.
• Experimental and Quasi-Experimental Designs for Research by Donald T. Campbell; Julian C. Stanley. Call Number: Q175 C152e Written 1967 but still used heavily today, this book examines research designs for experimental and quasi-experimental research, with examples and judgments about each design's validity.

Online Resources

• Quasi-Experimental Design From the Web Center for Social Research Methods, this is a very good overview of quasi-experimental design.
• Experimental and Quasi-Experimental Research From Colorado State University.
• Quasi-experimental design--Wikipedia, the free encyclopedia Wikipedia can be a useful place to start your research- check the citations at the bottom of the article for more information.
• << Previous: Qualitative Research (General)
• Next: Sampling >>
• Last Updated: Dec 19, 2023 2:12 PM
• URL: https://instr.iastate.libguides.com/researchmethods

Nursing Shark

Your nursing school resource

Quasi-Experimental Design

Similar to a true experiment, a quasi-experimental design aims to establish a causal relationship between an independent and dependent variable . However, unlike true experiments, quasi-experiments do not utilize random assignment of participants to treatment and control groups. Instead, participants are assigned to groups based on pre-existing characteristics or circumstances, rather than through random selection.

Quasi-experimental designs are valuable research tools when conducting true experiments is not feasible or ethical due to practical or ethical constraints. They allow researchers to study cause-and-effect relationships in real-world situations where random assignment or manipulation of variables is challenging or impossible.

Differences between quasi-experiments and true experiments

Here’s a table highlighting the differences between true experimental designs and quasi-experimental designs in terms of assignment to treatment, control over treatment, and the use of control groups:

Example of a true experiment vs a quasi-experiment

Assume you are interested in studying the effects of a new tutoring program on student academic performance.

True Experiment:

A researcher wants to study the effect of a new teaching method on student performance in mathematics. The researcher randomly assigns students from the same school and grade level to either the treatment group (receives the new teaching method) or the control group (receives the traditional teaching method) . 

The researcher has control over the implementation of the teaching methods and ensures that all other factors, such as curriculum, instructional time, and classroom environment, are kept consistent between the two groups.

Quasi-Experiment:

A researcher wants to study the effect of a new school policy that provides additional tutoring services on student performance in reading. However, the researcher cannot randomly assign students to groups. Instead, the researcher selects two schools: one school that has implemented the new tutoring policy (treatment group) and another school that has not implemented the policy (control group). 

The researcher has no control over the implementation of the tutoring services or other factors that may differ between the two schools, such as teacher quality, socioeconomic status of the student population, or school resources.

In the true experiment, the random assignment of participants to groups and the researcher’s control over the treatment ensure that any observed differences in student performance can be attributed to the new teaching method, minimizing the influence of confounding variables.

In the quasi-experiment, the lack of random assignment and the researcher’s limited control over the treatment (tutoring policy) and other factors introduce potential confounding variables that may influence student performance. The researcher must account for these potential confounding variables in the analysis to strengthen the validity of the findings and draw more reliable conclusions about the effect of the tutoring policy.

Types of quasi-experimental designs

Quasi-experimental designs allow researchers to study phenomena and interventions in situations where true experiments are not feasible or ethical due to practical or ethical constraints.The three different types are:

Nonequivalent groups design

In this design, two or more groups are compared, but the participants are not randomly assigned to the groups. The groups may differ on important characteristics, and the researcher must account for these differences in the analysis.

Example : A researcher wants to study the effect of a new tutoring program on academic performance. Two existing classes are selected: one class receives the tutoring program (treatment group), and the other class does not (control group) . Since the classes already exist and students were not randomly assigned to them, this is a nonequivalent groups design.

Regression discontinuity

This design is used when participants are assigned to treatment or control groups based on a specific cutoff score or threshold on a continuous variable.

Example : A school district implements a new reading intervention program for students who score below a certain threshold on a standardized reading test. Students just below the cutoff score receive the intervention (treatment group) , while students just above the cutoff do not (control group) . The researcher can compare the reading scores of the two groups to evaluate the effectiveness of the intervention.

Natural experiments

These designs take advantage of naturally occurring events or circumstances that resemble experimental treatments. The researcher does not have control over the treatment or assignment to groups.

Example: A researcher wants to study the effect of a new state law that raises the minimum wage. Some cities in the state have already implemented the higher minimum wage (treatment group) , while others have not (control group) . The researcher can compare economic indicators, such as employment rates and consumer spending, between the two groups of cities to evaluate the impact of the minimum wage increase.

When to use quasi-experimental design

Quasi-experimental designs are often used when true experiments are not feasible or ethical due to practical or ethical constraints.

In some situations, it may be unethical or undesirable to randomly assign participants to treatment or control groups, especially when the treatment or intervention being studied involves potential risks or benefits. Quasi-experimental designs are suitable in these cases because they do not require random assignment.

For example , in medical research, it would be unethical to randomly assign participants to receive a potentially harmful treatment or to withhold a potentially beneficial treatment. In such cases, researchers may use a quasi-experimental design to study the effects of an existing treatment or intervention without randomly assigning participants.

In other cases, it may be difficult or impossible to randomly assign participants or manipulate the treatment due to practical constraints. Quasi-experimental designs are useful in these situations because they allow researchers to study phenomena in real-world settings or with pre-existing groups.

For instance, in educational research , it may not be feasible to randomly assign students to different teaching methods or interventions due to logistical or administrative constraints. In such cases, researchers may use a quasi-experimental design to study the effects of an educational program or policy by comparing existing groups of students or schools.

Advantages and disadvantages

Despite their limitations, quasi-experimental designs are valuable research methods when true experiments are not feasible or ethical. Here are some advantages and disadvantages:

• Allow researchers to study phenomena that cannot be manipulated experimentally due to ethical or practical constraints.
• Provide insights into real-world situations and naturalistic settings, enhancing external validity.
• Generally less expensive and time-consuming than true experiments, as they do not require extensive experimental controls or setups.

Disadvantages

• Lack of random assignment and control over treatment can introduce confounding variables and reduce internal validity, making it more difficult to establish cause-and-effect relationships.
• Potential for selection biases and other threats to validity due to the non-random assignment of participants to groups.
• Limited generalizability due to the specific context and sample used in the study, which may not be representative of the broader population.

Frequently asked questions

What is a quasi-experiment.

A quasi-experiment is a type of research design that attempts to establish a cause-and-effect relationship. The main difference between this and a true experiment is that the groups are not randomly assigned.

Frequently asked questions: Methodology

Quantitative observations involve measuring or counting something and expressing the result in numerical form, while qualitative observations involve describing something in non-numerical terms, such as its appearance, texture, or color.

To make quantitative observations , you need to use instruments that are capable of measuring the quantity you want to observe. For example, you might use a ruler to measure the length of an object or a thermometer to measure its temperature.

Scope of research is determined at the beginning of your research process , prior to the data collection stage. Sometimes called “scope of study,” your scope delineates what will and will not be covered in your project. It helps you focus your work and your time, ensuring that you’ll be able to achieve your goals and outcomes.

Defining a scope can be very useful in any research project, from a research proposal to a thesis or dissertation . A scope is needed for all types of research: quantitative , qualitative , and mixed methods .

To define your scope of research, consider the following:

• Budget constraints or any specifics of grant funding
• Your proposed timeline and duration
• Specifics about your population of study, your proposed sample size , and the research methodology you’ll pursue
• Any inclusion and exclusion criteria
• Any anticipated control , extraneous , or confounding variables that could bias your research if not accounted for properly.

Inclusion and exclusion criteria are predominantly used in non-probability sampling . In purposive sampling and snowball sampling , restrictions apply as to who can be included in the sample .

Inclusion and exclusion criteria are typically presented and discussed in the methodology section of your thesis or dissertation .

The purpose of theory-testing mode is to find evidence in order to disprove, refine, or support a theory. As such, generalisability is not the aim of theory-testing mode.

Due to this, the priority of researchers in theory-testing mode is to eliminate alternative causes for relationships between variables . In other words, they prioritise internal validity over external validity , including ecological validity .

Convergent validity shows how much a measure of one construct aligns with other measures of the same or related constructs .

On the other hand, concurrent validity is about how a measure matches up to some known criterion or gold standard, which can be another measure.

Although both types of validity are established by calculating the association or correlation between a test score and another variable , they represent distinct validation methods.

Validity tells you how accurately a method measures what it was designed to measure. There are 4 main types of validity :

• Construct validity : Does the test measure the construct it was designed to measure?
• Face validity : Does the test appear to be suitable for its objectives ?
• Content validity : Does the test cover all relevant parts of the construct it aims to measure.
• Criterion validity : Do the results accurately measure the concrete outcome they are designed to measure?

Criterion validity evaluates how well a test measures the outcome it was designed to measure. An outcome can be, for example, the onset of a disease.

Criterion validity consists of two subtypes depending on the time at which the two measures (the criterion and your test) are obtained:

• Concurrent validity is a validation strategy where the the scores of a test and the criterion are obtained at the same time
• Predictive validity is a validation strategy where the criterion variables are measured after the scores of the test

Attrition refers to participants leaving a study. It always happens to some extent – for example, in randomised control trials for medical research.

Differential attrition occurs when attrition or dropout rates differ systematically between the intervention and the control group . As a result, the characteristics of the participants who drop out differ from the characteristics of those who stay in the study. Because of this, study results may be biased .

Criterion validity and construct validity are both types of measurement validity . In other words, they both show you how accurately a method measures something.

While construct validity is the degree to which a test or other measurement method measures what it claims to measure, criterion validity is the degree to which a test can predictively (in the future) or concurrently (in the present) measure something.

Construct validity is often considered the overarching type of measurement validity . You need to have face validity , content validity , and criterion validity in order to achieve construct validity.

Convergent validity and discriminant validity are both subtypes of construct validity . Together, they help you evaluate whether a test measures the concept it was designed to measure.

• Convergent validity indicates whether a test that is designed to measure a particular construct correlates with other tests that assess the same or similar construct.
• Discriminant validity indicates whether two tests that should not be highly related to each other are indeed not related. This type of validity is also called divergent validity .

You need to assess both in order to demonstrate construct validity. Neither one alone is sufficient for establishing construct validity.

Face validity and content validity are similar in that they both evaluate how suitable the content of a test is. The difference is that face validity is subjective, and assesses content at surface level.

When a test has strong face validity, anyone would agree that the test’s questions appear to measure what they are intended to measure.

For example, looking at a 4th grade math test consisting of problems in which students have to add and multiply, most people would agree that it has strong face validity (i.e., it looks like a math test).

On the other hand, content validity evaluates how well a test represents all the aspects of a topic. Assessing content validity is more systematic and relies on expert evaluation. of each question, analysing whether each one covers the aspects that the test was designed to cover.

A 4th grade math test would have high content validity if it covered all the skills taught in that grade. Experts(in this case, math teachers), would have to evaluate the content validity by comparing the test to the learning objectives.

Content validity shows you how accurately a test or other measurement method taps  into the various aspects of the specific construct you are researching.

In other words, it helps you answer the question: “does the test measure all aspects of the construct I want to measure?” If it does, then the test has high content validity.

The higher the content validity, the more accurate the measurement of the construct.

If the test fails to include parts of the construct, or irrelevant parts are included, the validity of the instrument is threatened, which brings your results into question.

Construct validity refers to how well a test measures the concept (or construct) it was designed to measure. Assessing construct validity is especially important when you’re researching concepts that can’t be quantified and/or are intangible, like introversion. To ensure construct validity your test should be based on known indicators of introversion ( operationalisation ).

On the other hand, content validity assesses how well the test represents all aspects of the construct. If some aspects are missing or irrelevant parts are included, the test has low content validity.

• Discriminant validity indicates whether two tests that should not be highly related to each other are indeed not related

Construct validity has convergent and discriminant subtypes. They assist determine if a test measures the intended notion.

The reproducibility and replicability of a study can be ensured by writing a transparent, detailed method section and using clear, unambiguous language.

Reproducibility and replicability are related terms.

• A successful reproduction shows that the data analyses were conducted in a fair and honest manner.
• A successful replication shows that the reliability of the results is high.
• Reproducing research entails reanalysing the existing data in the same manner.
• Replicating (or repeating ) the research entails reconducting the entire analysis, including the collection of new data . 

Snowball sampling is a non-probability sampling method . Unlike probability sampling (which involves some form of random selection ), the initial individuals selected to be studied are the ones who recruit new participants.

Because not every member of the target population has an equal chance of being recruited into the sample, selection in snowball sampling is non-random.

Snowball sampling is a non-probability sampling method , where there is not an equal chance for every member of the population to be included in the sample .

This means that you cannot use inferential statistics and make generalisations – often the goal of quantitative research . As such, a snowball sample is not representative of the target population, and is usually a better fit for qualitative research .

Snowball sampling relies on the use of referrals. Here, the researcher recruits one or more initial participants, who then recruit the next ones. 

Participants share similar characteristics and/or know each other. Because of this, not every member of the population has an equal chance of being included in the sample, giving rise to sampling bias .

Snowball sampling is best used in the following cases:

• If there is no sampling frame available (e.g., people with a rare disease)
• If the population of interest is hard to access or locate (e.g., people experiencing homelessness)
• If the research focuses on a sensitive topic (e.g., extra-marital affairs)

Stratified sampling and quota sampling both involve dividing the population into subgroups and selecting units from each subgroup. The purpose in both cases is to select a representative sample and/or to allow comparisons between subgroups.

The main difference is that in stratified sampling, you draw a random sample from each subgroup ( probability sampling ). In quota sampling you select a predetermined number or proportion of units, in a non-random manner ( non-probability sampling ).

Random sampling or probability sampling is based on random selection. This means that each unit has an equal chance (i.e., equal probability) of being included in the sample.

On the other hand, convenience sampling involves stopping people at random, which means that not everyone has an equal chance of being selected depending on the place, time, or day you are collecting your data.

Convenience sampling and quota sampling are both non-probability sampling methods. They both use non-random criteria like availability, geographical proximity, or expert knowledge to recruit study participants.

However, in convenience sampling, you continue to sample units or cases until you reach the required sample size.

In quota sampling, you first need to divide your population of interest into subgroups (strata) and estimate their proportions (quota) in the population. Then you can start your data collection , using convenience sampling to recruit participants, until the proportions in each subgroup coincide with the estimated proportions in the population.

A sampling frame is a list of every member in the entire population . It is important that the sampling frame is as complete as possible, so that your sample accurately reflects your population.

Stratified and cluster sampling may look similar, but bear in mind that groups created in cluster sampling are heterogeneous , so the individual characteristics in the cluster vary. In contrast, groups created in stratified sampling are homogeneous , as units share characteristics.

Relatedly, in cluster sampling you randomly select entire groups and include all units of each group in your sample. However, in stratified sampling, you select some units of all groups and include them in your sample. In this way, both methods can ensure that your sample is representative of the target population .

When your population is large in size, geographically dispersed, or difficult to contact, it’s necessary to use a sampling method .

This allows you to gather information from a smaller part of the population, i.e. the sample, and make accurate statements by using statistical analysis. A few sampling methods include simple random sampling , convenience sampling , and snowball sampling .

The two main types of social desirability bias are:

• Self-deceptive enhancement (self-deception): The tendency to see oneself in a favorable light without realizing it.
• Impression managemen t (other-deception): The tendency to inflate one’s abilities or achievement in order to make a good impression on other people.

Response bias refers to conditions or factors that take place during the process of responding to surveys, affecting the responses. One type of response bias is social desirability bias .

Demand characteristics are aspects of experiments that may give away the research objective to participants. Social desirability bias occurs when participants automatically try to respond in ways that make them seem likeable in a study, even if it means misrepresenting how they truly feel.

Participants may use demand characteristics to infer social norms or experimenter expectancies and act in socially desirable ways, so you should try to control for demand characteristics wherever possible.

A systematic review is secondary research because it uses existing research. You don’t collect new data yourself.

Ethical considerations in research are a set of principles that guide your research designs and practices. These principles include voluntary participation, informed consent, anonymity, confidentiality, potential for harm, and results communication.

Scientists and researchers must always adhere to a certain code of conduct when collecting data from others .

These considerations protect the rights of research participants, enhance research validity , and maintain scientific integrity.

Research ethics matter for scientific integrity, human rights and dignity, and collaboration between science and society. These principles make sure that participation in studies is voluntary, informed, and safe.

Research misconduct means making up or falsifying data, manipulating data analyses, or misrepresenting results in research reports. It’s a form of academic fraud.

These actions are committed intentionally and can have serious consequences; research misconduct is not a simple mistake or a point of disagreement but a serious ethical failure.

Anonymity means you don’t know who the participants are, while confidentiality means you know who they are but remove identifying information from your research report. Both are important ethical considerations .

You can only guarantee anonymity by not collecting any personally identifying information – for example, names, phone numbers, email addresses, IP addresses, physical characteristics, photos, or videos.

You can keep data confidential by using aggregate information in your research report, so that you only refer to groups of participants rather than individuals.

Peer review is a process of evaluating submissions to an academic journal. Utilising rigorous criteria, a panel of reviewers in the same subject area decide whether to accept each submission for publication.

For this reason, academic journals are often considered among the most credible sources you can use in a research project – provided that the journal itself is trustworthy and well regarded.

In general, the peer review process follows the following steps:

• First, the author submits the manuscript to the editor.
• Reject the manuscript and send it back to author, or
• Send it onward to the selected peer reviewer(s)
• Next, the peer review process occurs. The reviewer provides feedback, addressing any major or minor issues with the manuscript, and gives their advice regarding what edits should be made.
• Lastly, the edited manuscript is sent back to the author. They input the edits, and resubmit it to the editor for publication.

Peer review can stop obviously problematic, falsified, or otherwise untrustworthy research from being published. It also represents an excellent opportunity to get feedback from renowned experts in your field.

It acts as a first defence, helping you ensure your argument is clear and that there are no gaps, vague terms, or unanswered questions for readers who weren’t involved in the research process.

Peer-reviewed articles are considered a highly credible source due to this stringent process they go through before publication.

Many academic fields use peer review , largely to determine whether a manuscript is suitable for publication. Peer review enhances the credibility of the published manuscript.

However, peer review is also common in non-academic settings. The United Nations, the European Union, and many individual nations use peer review to evaluate grant applications. It is also widely used in medical and health-related fields as a teaching or quality-of-care measure.

Peer assessment is often used in the classroom as a pedagogical tool. Both receiving feedback and providing it are thought to enhance the learning process, helping students think critically and collaboratively.

• In a single-blind study , only the participants are blinded.
• In a double-blind study , both participants and experimenters are blinded.
• In a triple-blind study , the assignment is hidden not only from participants and experimenters, but also from the researchers analysing the data.

Blinding is important to reduce bias (e.g., observer bias , demand characteristics ) and ensure a study’s internal validity .

If participants know whether they are in a control or treatment group , they may adjust their behaviour in ways that affect the outcome that researchers are trying to measure. If the people administering the treatment are aware of group assignment, they may treat participants differently and thus directly or indirectly influence the final results.

Blinding means hiding who is assigned to the treatment group and who is assigned to the control group in an experiment .

Explanatory research is a research method used to investigate how or why something occurs when only a small amount of information is available pertaining to that topic. It can help you increase your understanding of a given topic.

Explanatory research is used to investigate how or why a phenomenon occurs. Therefore, this type of research is often one of the first stages in the research process , serving as a jumping-off point for future research.

Exploratory research is a methodology approach that explores research questions that have not previously been studied in depth. It is often used when the issue you’re studying is new, or the data collection process is challenging in some way.

Exploratory research is often used when the issue you’re studying is new or when the data collection process is challenging for some reason.

You can use exploratory research if you have a general idea or a specific question that you want to study but there is no preexisting knowledge or paradigm with which to study it.

To implement random assignment , assign a unique number to every member of your study’s sample .

Then, you can use a random number generator or a lottery method to randomly assign each number to a control or experimental group. You can also do so manually, by flipping a coin or rolling a die to randomly assign participants to groups.

Random selection, or random sampling , is a way of selecting members of a population for your study’s sample.

In contrast, random assignment is a way of sorting the sample into control and experimental groups.

Random sampling enhances the external validity or generalisability of your results, while random assignment improves the internal validity of your study.

Random assignment is used in experiments with a between-groups or independent measures design. In this research design, there’s usually a control group and one or more experimental groups. Random assignment helps ensure that the groups are comparable.

In general, you should always use random assignment in this type of experimental design when it is ethically possible and makes sense for your study topic.

Clean data are valid, accurate, complete, consistent, unique, and uniform. Dirty data include inconsistencies and errors.

Dirty data can come from any part of the research process, including poor research design , inappropriate measurement materials, or flawed data entry.

Data cleaning takes place between data collection and data analyses. But you can use some methods even before collecting data.

For clean data, you should start by designing measures that collect valid data. Data validation at the time of data entry or collection helps you minimize the amount of data cleaning you’ll need to do.

After data collection, you can use data standardisation and data transformation to clean your data. You’ll also deal with any missing values, outliers, and duplicate values.

Data cleaning involves spotting and resolving potential data inconsistencies or errors to improve your data quality. An error is any value (e.g., recorded weight) that doesn’t reflect the true value (e.g., actual weight) of something that’s being measured.

In this process, you review, analyse, detect, modify, or remove ‘dirty’ data to make your dataset ‘clean’. Data cleaning is also called data cleansing or data scrubbing.

Data cleaning is necessary for valid and appropriate analyses. Dirty data contain inconsistencies or errors , but cleaning your data helps you minimise or resolve these.

Without data cleaning, you could end up with a Type I or II error in your conclusion. These types of erroneous conclusions can be practically significant with important consequences, because they lead to misplaced investments or missed opportunities.

Observer bias occurs when a researcher’s expectations, opinions, or prejudices influence what they perceive or record in a study. It usually affects studies when observers are aware of the research aims or hypotheses. This type of research bias is also called detection bias or ascertainment bias .

The observer-expectancy effect occurs when researchers influence the results of their own study through interactions with participants.

Researchers’ own beliefs and expectations about the study results may unintentionally influence participants through demand characteristics .

You can use several tactics to minimise observer bias .

• Use masking (blinding) to hide the purpose of your study from all observers.
• Triangulate your data with different data collection methods or sources.
• Use multiple observers and ensure inter-rater reliability.
• Train your observers to make sure data is consistently recorded between them.
• Standardise your observation procedures to make sure they are structured and clear.

Naturalistic observation is a valuable tool because of its flexibility, external validity , and suitability for topics that can’t be studied in a lab setting.

The downsides of naturalistic observation include its lack of scientific control , ethical considerations , and potential for bias from observers and subjects.

Naturalistic observation is a qualitative research method where you record the behaviours of your research subjects in real-world settings. You avoid interfering or influencing anything in a naturalistic observation.

You can think of naturalistic observation as ‘people watching’ with a purpose.

Closed-ended, or restricted-choice, questions offer respondents a fixed set of choices to select from. These questions are easier to answer quickly.

Open-ended or long-form questions allow respondents to answer in their own words. Because there are no restrictions on their choices, respondents can answer in ways that researchers may not have otherwise considered.

You can organise the questions logically, with a clear progression from simple to complex, or randomly between respondents. A logical flow helps respondents process the questionnaire easier and quicker, but it may lead to bias. Randomisation can minimise the bias from order effects.

Questionnaires can be self-administered or researcher-administered.

Self-administered questionnaires can be delivered online or in paper-and-pen formats, in person or by post. All questions are standardised so that all respondents receive the same questions with identical wording.

Researcher-administered questionnaires are interviews that take place by phone, in person, or online between researchers and respondents. You can gain deeper insights by clarifying questions for respondents or asking follow-up questions.

In a controlled experiment , all extraneous variables are held constant so that they can’t influence the results. Controlled experiments require:

• A control group that receives a standard treatment, a fake treatment, or no treatment
• Random assignment of participants to ensure the groups are equivalent

Depending on your study topic, there are various other methods of controlling variables .

An experimental group, also known as a treatment group, receives the treatment whose effect researchers wish to study, whereas a control group does not. They should be identical in all other ways.

A true experiment (aka a controlled experiment) always includes at least one control group that doesn’t receive the experimental treatment.

However, some experiments use a within-subjects design to test treatments without a control group. In these designs, you usually compare one group’s outcomes before and after a treatment (instead of comparing outcomes between different groups).

For strong internal validity , it’s usually best to include a control group if possible. Without a control group, it’s harder to be certain that the outcome was caused by the experimental treatment and not by other variables.

A questionnaire is a data collection tool or instrument, while a survey is an overarching research method that involves collecting and analysing data from people using questionnaires.

A Likert scale is a rating scale that quantitatively assesses opinions, attitudes, or behaviours. It is made up of four or more questions that measure a single attitude or trait when response scores are combined.

To use a Likert scale in a survey , you present participants with Likert-type questions or statements, and a continuum of items, usually with five or seven possible responses, to capture their degree of agreement.

Individual Likert-type questions are generally considered ordinal data , because the items have clear rank order, but don’t have an even distribution.

Overall Likert scale scores are sometimes treated as interval data. These scores are considered to have directionality and even spacing between them.

The type of data determines what statistical tests you should use to analyse your data.

A research hypothesis is your proposed answer to your research question. The research hypothesis usually includes an explanation (‘ x affects y because …’).

A statistical hypothesis, on the other hand, is a mathematical statement about a population parameter. Statistical hypotheses always come in pairs: the null and alternative hypotheses. In a well-designed study , the statistical hypotheses correspond logically to the research hypothesis.

A hypothesis states your predictions about what your research will find. It is a tentative answer to your research question that has not yet been tested. For some research projects, you might have to write several hypotheses that address different aspects of your research question.

A hypothesis is not just a guess. It should be based on existing theories and knowledge. It also has to be testable, which means you can support or refute it through scientific research methods (such as experiments, observations, and statistical analysis of data).

Cross-sectional studies are less expensive and time-consuming than many other types of study. They can provide useful insights into a population’s characteristics and identify correlations for further research.

Sometimes only cross-sectional data are available for analysis; other times your research question may only require a cross-sectional study to answer it.

Cross-sectional studies cannot establish a cause-and-effect relationship or analyse behaviour over a period of time. To investigate cause and effect, you need to do a longitudinal study or an experimental study .

Longitudinal studies and cross-sectional studies are two different types of research design . In a cross-sectional study you collect data from a population at a specific point in time; in a longitudinal study you repeatedly collect data from the same sample over an extended period of time.

Longitudinal studies are better to establish the correct sequence of events, identify changes over time, and provide insight into cause-and-effect relationships, but they also tend to be more expensive and time-consuming than other types of studies.

The 1970 British Cohort Study , which has collected data on the lives of 17,000 Brits since their births in 1970, is one well-known example of a longitudinal study .

Longitudinal studies can last anywhere from weeks to decades, although they tend to be at least a year long.

A correlation reflects the strength and/or direction of the association between two or more variables.

• A positive correlation means that both variables change in the same direction.
• A negative correlation means that the variables change in opposite directions.
• A zero correlation means there’s no relationship between the variables.

A correlational research design investigates relationships between two variables (or more) without the researcher controlling or manipulating any of them. It’s a non-experimental type of quantitative research .

A correlation coefficient is a single number that describes the strength and direction of the relationship between your variables.

Different types of correlation coefficients might be appropriate for your data based on their levels of measurement and distributions . The Pearson product-moment correlation coefficient (Pearson’s r ) is commonly used to assess a linear relationship between two quantitative variables.

Controlled experiments establish causality, whereas correlational studies only show associations between variables.

• In an experimental design , you manipulate an independent variable and measure its effect on a dependent variable. Other variables are controlled so they can’t impact the results.
• In a correlational design , you measure variables without manipulating any of them. You can test whether your variables change together, but you can’t be sure that one variable caused a change in another.

In general, correlational research is high in external validity while experimental research is high in internal validity .

The third variable and directionality problems are two main reasons why correlation isn’t causation .

The third variable problem means that a confounding variable affects both variables to make them seem causally related when they are not.

The directionality problem is when two variables correlate and might actually have a causal relationship, but it’s impossible to conclude which variable causes changes in the other.

As a rule of thumb, questions related to thoughts, beliefs, and feelings work well in focus groups . Take your time formulating strong questions, paying special attention to phrasing. Be careful to avoid leading questions , which can bias your responses.

Overall, your focus group questions should be:

• Open-ended and flexible
• Impossible to answer with ‘yes’ or ‘no’ (questions that start with ‘why’ or ‘how’ are often best)
• Unambiguous, getting straight to the point while still stimulating discussion
• Unbiased and neutral

Social desirability bias is the tendency for interview participants to give responses that will be viewed favourably by the interviewer or other participants. It occurs in all types of interviews and surveys , but is most common in semi-structured interviews , unstructured interviews , and focus groups .

Social desirability bias can be mitigated by ensuring participants feel at ease and comfortable sharing their views. Make sure to pay attention to your own body language and any physical or verbal cues, such as nodding or widening your eyes.

This type of bias in research can also occur in observations if the participants know they’re being observed. They might alter their behaviour accordingly.

A focus group is a research method that brings together a small group of people to answer questions in a moderated setting. The group is chosen due to predefined demographic traits, and the questions are designed to shed light on a topic of interest. It is one of four types of interviews .

The four most common types of interviews are:

• Structured interviews : The questions are predetermined in both topic and order.
• Semi-structured interviews : A few questions are predetermined, but other questions aren’t planned.
• Unstructured interviews : None of the questions are predetermined.
• Focus group interviews : The questions are presented to a group instead of one individual.

An unstructured interview is the most flexible type of interview, but it is not always the best fit for your research topic.

Unstructured interviews are best used when:

• You are an experienced interviewer and have a very strong background in your research topic, since it is challenging to ask spontaneous, colloquial questions
• Your research question is exploratory in nature. While you may have developed hypotheses, you are open to discovering new or shifting viewpoints through the interview process.
• You are seeking descriptive data, and are ready to ask questions that will deepen and contextualise your initial thoughts and hypotheses
• Your research depends on forming connections with your participants and making them feel comfortable revealing deeper emotions, lived experiences, or thoughts

A semi-structured interview is a blend of structured and unstructured types of interviews. Semi-structured interviews are best used when:

• You have prior interview experience. Spontaneous questions are deceptively challenging, and it’s easy to accidentally ask a leading question or make a participant uncomfortable.
• Your research question is exploratory in nature. Participant answers can guide future research questions and help you develop a more robust knowledge base for future research.

The interviewer effect is a type of bias that emerges when a characteristic of an interviewer (race, age, gender identity, etc.) influences the responses given by the interviewee.

There is a risk of an interviewer effect in all types of interviews , but it can be mitigated by writing really high-quality interview questions.

A structured interview is a data collection method that relies on asking questions in a set order to collect data on a topic. They are often quantitative in nature. Structured interviews are best used when:

• You already have a very clear understanding of your topic. Perhaps significant research has already been conducted, or you have done some prior research yourself, but you already possess a baseline for designing strong structured questions.
• You are constrained in terms of time or resources and need to analyse your data quickly and efficiently
• Your research question depends on strong parity between participants, with environmental conditions held constant

More flexible interview options include semi-structured interviews , unstructured interviews , and focus groups .

When conducting research, collecting original data has significant advantages:

• You can tailor data collection to your specific research aims (e.g., understanding the needs of your consumers or user testing your website).
• You can control and standardise the process for high reliability and validity (e.g., choosing appropriate measurements and sampling methods ).

However, there are also some drawbacks: data collection can be time-consuming, labour-intensive, and expensive. In some cases, it’s more efficient to use secondary data that has already been collected by someone else, but the data might be less reliable.

Data collection is the systematic process by which observations or measurements are gathered in research. It is used in many different contexts by academics, governments, businesses, and other organisations.

A mediator variable explains the process through which two variables are related, while a moderator variable affects the strength and direction of that relationship.

A confounder is a third variable that affects variables of interest and makes them seem related when they are not. In contrast, a mediator is the mechanism of a relationship between two variables: it explains the process by which they are related.

If something is a mediating variable :

• It’s caused by the independent variable
• It influences the dependent variable
• When it’s taken into account, the statistical correlation between the independent and dependent variables is higher than when it isn’t considered

Including mediators and moderators in your research helps you go beyond studying a simple relationship between two variables for a fuller picture of the real world. They are important to consider when studying complex correlational or causal relationships.

Mediators are part of the causal pathway of an effect, and they tell you how or why an effect takes place. Moderators usually help you judge the external validity of your study by identifying the limitations of when the relationship between variables holds.

You can think of independent and dependent variables in terms of cause and effect: an independent variable is the variable you think is the cause , while a dependent variable is the effect .

In an experiment, you manipulate the independent variable and measure the outcome in the dependent variable. For example, in an experiment about the effect of nutrients on crop growth:

• The  independent variable  is the amount of nutrients added to the crop field.
• The  dependent variable is the biomass of the crops at harvest time.

Defining your variables, and deciding how you will manipulate and measure them, is an important part of experimental design .

Discrete and continuous variables are two types of quantitative variables :

• Discrete variables represent counts (e.g., the number of objects in a collection).
• Continuous variables represent measurable amounts (e.g., water volume or weight).

Quantitative variables are any variables where the data represent amounts (e.g. height, weight, or age).

Categorical variables are any variables where the data represent groups. This includes rankings (e.g. finishing places in a race), classifications (e.g. brands of cereal), and binary outcomes (e.g. coin flips).

You need to know what type of variables you are working with to choose the right statistical test for your data and interpret your results .

Determining cause and effect is one of the most important parts of scientific research. It’s essential to know which is the cause – the independent variable – and which is the effect – the dependent variable.

You want to find out how blood sugar levels are affected by drinking diet cola and regular cola, so you conduct an experiment .

• The type of cola – diet or regular – is the independent variable .
• The level of blood sugar that you measure is the dependent variable – it changes depending on the type of cola.

No. The value of a dependent variable depends on an independent variable, so a variable cannot be both independent and dependent at the same time. It must be either the cause or the effect, not both.

Yes, but including more than one of either type requires multiple research questions .

For example, if you are interested in the effect of a diet on health, you can use multiple measures of health: blood sugar, blood pressure, weight, pulse, and many more. Each of these is its own dependent variable with its own research question.

You could also choose to look at the effect of exercise levels as well as diet, or even the additional effect of the two combined. Each of these is a separate independent variable .

To ensure the internal validity of an experiment , you should only change one independent variable at a time.

To ensure the internal validity of your research, you must consider the impact of confounding variables. If you fail to account for them, you might over- or underestimate the causal relationship between your independent and dependent variables , or even find a causal relationship where none exists.

A confounding variable is closely related to both the independent and dependent variables in a study. An independent variable represents the supposed cause , while the dependent variable is the supposed effect . A confounding variable is a third variable that influences both the independent and dependent variables.

Failing to account for confounding variables can cause you to wrongly estimate the relationship between your independent and dependent variables.

There are several methods you can use to decrease the impact of confounding variables on your research: restriction, matching, statistical control, and randomisation.

In restriction , you restrict your sample by only including certain subjects that have the same values of potential confounding variables.

In matching , you match each of the subjects in your treatment group with a counterpart in the comparison group. The matched subjects have the same values on any potential confounding variables, and only differ in the independent variable .

In statistical control , you include potential confounders as variables in your regression .

In randomisation , you randomly assign the treatment (or independent variable) in your study to a sufficiently large number of subjects, which allows you to control for all potential confounding variables.

In scientific research, concepts are the abstract ideas or phenomena that are being studied (e.g., educational achievement). Variables are properties or characteristics of the concept (e.g., performance at school), while indicators are ways of measuring or quantifying variables (e.g., yearly grade reports).

The process of turning abstract concepts into measurable variables and indicators is called operationalisation .

In statistics, ordinal and nominal variables are both considered categorical variables .

Even though ordinal data can sometimes be numerical, not all mathematical operations can be performed on them.

A control variable is any variable that’s held constant in a research study. It’s not a variable of interest in the study, but it’s controlled because it could influence the outcomes.

Control variables help you establish a correlational or causal relationship between variables by enhancing internal validity .

If you don’t control relevant extraneous variables , they may influence the outcomes of your study, and you may not be able to demonstrate that your results are really an effect of your independent variable .

‘Controlling for a variable’ means measuring extraneous variables and accounting for them statistically to remove their effects on other variables.

Researchers often model control variable data along with independent and dependent variable data in regression analyses and ANCOVAs . That way, you can isolate the control variable’s effects from the relationship between the variables of interest.

An extraneous variable is any variable that you’re not investigating that can potentially affect the dependent variable of your research study.

A confounding variable is a type of extraneous variable that not only affects the dependent variable, but is also related to the independent variable.

There are 4 main types of extraneous variables :

• Demand characteristics : Environmental cues that encourage participants to conform to researchers’ expectations
• Experimenter effects : Unintentional actions by researchers that influence study outcomes
• Situational variables : Eenvironmental variables that alter participants’ behaviours
• Participant variables : Any characteristic or aspect of a participant’s background that could affect study results

The difference between explanatory and response variables is simple:

• An explanatory variable is the expected cause, and it explains the results.
• A response variable is the expected effect, and it responds to other variables.

The term ‘ explanatory variable ‘ is sometimes preferred over ‘ independent variable ‘ because, in real-world contexts, independent variables are often influenced by other variables. This means they aren’t totally independent.

Multiple independent variables may also be correlated with each other, so ‘explanatory variables’ is a more appropriate term.

On graphs, the explanatory variable is conventionally placed on the x -axis, while the response variable is placed on the y -axis.

• If you have quantitative variables , use a scatterplot or a line graph.
• If your response variable is categorical, use a scatterplot or a line graph.
• If your explanatory variable is categorical, use a bar graph.

A correlation is usually tested for two variables at a time, but you can test correlations between three or more variables.

An independent variable is the variable you manipulate, control, or vary in an experimental study to explore its effects. It’s called ‘independent’ because it’s not influenced by any other variables in the study.

Independent variables are also called:

• Explanatory variables (they explain an event or outcome)
• Predictor variables (they can be used to predict the value of a dependent variable)
• Right-hand-side variables (they appear on the right-hand side of a regression equation)

A dependent variable is what changes as a result of the independent variable manipulation in experiments . It’s what you’re interested in measuring, and it ‘depends’ on your independent variable.

In statistics, dependent variables are also called:

• Response variables (they respond to a change in another variable)
• Outcome variables (they represent the outcome you want to measure)
• Left-hand-side variables (they appear on the left-hand side of a regression equation)

Deductive reasoning is commonly used in scientific research, and it’s especially associated with quantitative research .

In research, you might have come across something called the hypothetico-deductive method . It’s the scientific method of testing hypotheses to check whether your predictions are substantiated by real-world data.

Deductive reasoning is a logical approach where you progress from general ideas to specific conclusions. It’s often contrasted with inductive reasoning , where you start with specific observations and form general conclusions.

Deductive reasoning is also called deductive logic.

Inductive reasoning is a method of drawing conclusions by going from the specific to the general. It’s usually contrasted with deductive reasoning, where you proceed from general information to specific conclusions.

Inductive reasoning is also called inductive logic or bottom-up reasoning.

In inductive research , you start by making observations or gathering data. Then, you take a broad scan of your data and search for patterns. Finally, you make general conclusions that you might incorporate into theories.

Inductive reasoning is a bottom-up approach, while deductive reasoning is top-down.

Inductive reasoning takes you from the specific to the general, while in deductive reasoning, you make inferences by going from general premises to specific conclusions.

There are many different types of inductive reasoning that people use formally or informally.

Here are a few common types:

• Inductive generalisation : You use observations about a sample to come to a conclusion about the population it came from.
• Statistical generalisation: You use specific numbers about samples to make statements about populations.
• Causal reasoning: You make cause-and-effect links between different things.
• Sign reasoning: You make a conclusion about a correlational relationship between different things.
• Analogical reasoning: You make a conclusion about something based on its similarities to something else.

It’s often best to ask a variety of people to review your measurements. You can ask experts, such as other researchers, or laypeople, such as potential participants, to judge the face validity of tests.

While experts have a deep understanding of research methods , the people you’re studying can provide you with valuable insights you may have missed otherwise.

Face validity is important because it’s a simple first step to measuring the overall validity of a test or technique. It’s a relatively intuitive, quick, and easy way to start checking whether a new measure seems useful at first glance.

Good face validity means that anyone who reviews your measure says that it seems to be measuring what it’s supposed to. With poor face validity, someone reviewing your measure may be left confused about what you’re measuring and why you’re using this method.

Face validity is about whether a test appears to measure what it’s supposed to measure. This type of validity is concerned with whether a measure seems relevant and appropriate for what it’s assessing only on the surface.

Statistical analyses are often applied to test validity with data from your measures. You test convergent validity and discriminant validity with correlations to see if results from your test are positively or negatively related to those of other established tests.

You can also use regression analyses to assess whether your measure is actually predictive of outcomes that you expect it to predict theoretically. A regression analysis that supports your expectations strengthens your claim of construct validity .

When designing or evaluating a measure, construct validity helps you ensure you’re actually measuring the construct you’re interested in. If you don’t have construct validity, you may inadvertently measure unrelated or distinct constructs and lose precision in your research.

Construct validity is often considered the overarching type of measurement validity ,  because it covers all of the other types. You need to have face validity , content validity, and criterion validity to achieve construct validity.

Construct validity is about how well a test measures the concept it was designed to evaluate. It’s one of four types of measurement validity , which includes construct validity, face validity , and criterion validity.

There are two subtypes of construct validity.

• Convergent validity : The extent to which your measure corresponds to measures of related constructs
• Discriminant validity: The extent to which your measure is unrelated or negatively related to measures of distinct constructs

Attrition bias can skew your sample so that your final sample differs significantly from your original sample. Your sample is biased because some groups from your population are underrepresented.

With a biased final sample, you may not be able to generalise your findings to the original population that you sampled from, so your external validity is compromised.

There are seven threats to external validity : selection bias , history, experimenter effect, Hawthorne effect , testing effect, aptitude-treatment, and situation effect.

The two types of external validity are population validity (whether you can generalise to other groups of people) and ecological validity (whether you can generalise to other situations and settings).

The external validity of a study is the extent to which you can generalise your findings to different groups of people, situations, and measures.

Attrition bias is a threat to internal validity . In experiments, differential rates of attrition between treatment and control groups can skew results.

This bias can affect the relationship between your independent and dependent variables . It can make variables appear to be correlated when they are not, or vice versa.

Internal validity is the extent to which you can be confident that a cause-and-effect relationship established in a study cannot be explained by other factors.

There are eight threats to internal validity : history, maturation, instrumentation, testing, selection bias , regression to the mean, social interaction, and attrition .

A sampling error is the difference between a population parameter and a sample statistic .

A statistic refers to measures about the sample , while a parameter refers to measures about the population .

Populations are used when a research question requires data from every member of the population. This is usually only feasible when the population is small and easily accessible.

Systematic sampling is a probability sampling method where researchers select members of the population at a regular interval – for example, by selecting every 15th person on a list of the population. If the population is in a random order, this can imitate the benefits of simple random sampling .

There are three key steps in systematic sampling :

• Define and list your population , ensuring that it is not ordered in a cyclical or periodic order.
• Decide on your sample size and calculate your interval, k , by dividing your population by your target sample size.
• Choose every k th member of the population as your sample.

Yes, you can create a stratified sample using multiple characteristics, but you must ensure that every participant in your study belongs to one and only one subgroup. In this case, you multiply the numbers of subgroups for each characteristic to get the total number of groups.

For example, if you were stratifying by location with three subgroups (urban, rural, or suburban) and marital status with five subgroups (single, divorced, widowed, married, or partnered), you would have 3 × 5 = 15 subgroups.

You should use stratified sampling when your sample can be divided into mutually exclusive and exhaustive subgroups that you believe will take on different mean values for the variable that you’re studying.

Using stratified sampling will allow you to obtain more precise (with lower variance ) statistical estimates of whatever you are trying to measure.

For example, say you want to investigate how income differs based on educational attainment, but you know that this relationship can vary based on race. Using stratified sampling, you can ensure you obtain a large enough sample from each racial group, allowing you to draw more precise conclusions.

In stratified sampling , researchers divide subjects into subgroups called strata based on characteristics that they share (e.g., race, gender, educational attainment).

Once divided, each subgroup is randomly sampled using another probability sampling method .

Multistage sampling can simplify data collection when you have large, geographically spread samples, and you can obtain a probability sample without a complete sampling frame.

But multistage sampling may not lead to a representative sample, and larger samples are needed for multistage samples to achieve the statistical properties of simple random samples .

In multistage sampling , you can use probability or non-probability sampling methods.

For a probability sample, you have to probability sampling at every stage. You can mix it up by using simple random sampling , systematic sampling , or stratified sampling to select units at different stages, depending on what is applicable and relevant to your study.

Cluster sampling is a probability sampling method in which you divide a population into clusters, such as districts or schools, and then randomly select some of these clusters as your sample.

The clusters should ideally each be mini-representations of the population as a whole.

There are three types of cluster sampling : single-stage, double-stage and multi-stage clustering. In all three types, you first divide the population into clusters, then randomly select clusters for use in your sample.

• In single-stage sampling , you collect data from every unit within the selected clusters.
• In double-stage sampling , you select a random sample of units from within the clusters.
• In multi-stage sampling , you repeat the procedure of randomly sampling elements from within the clusters until you have reached a manageable sample.

Cluster sampling is more time- and cost-efficient than other probability sampling methods , particularly when it comes to large samples spread across a wide geographical area.

However, it provides less statistical certainty than other methods, such as simple random sampling , because it is difficult to ensure that your clusters properly represent the population as a whole.

If properly implemented, simple random sampling is usually the best sampling method for ensuring both internal and external validity . However, it can sometimes be impractical and expensive to implement, depending on the size of the population to be studied,

If you have a list of every member of the population and the ability to reach whichever members are selected, you can use simple random sampling.

The American Community Survey  is an example of simple random sampling . In order to collect detailed data on the population of the US, the Census Bureau officials randomly select 3.5 million households per year and use a variety of methods to convince them to fill out the survey.

Simple random sampling is a type of probability sampling in which the researcher randomly selects a subset of participants from a population . Each member of the population has an equal chance of being selected. Data are then collected from as large a percentage as possible of this random subset.

Sampling bias occurs when some members of a population are systematically more likely to be selected in a sample than others.

In multistage sampling , or multistage cluster sampling, you draw a sample from a population using smaller and smaller groups at each stage.

This method is often used to collect data from a large, geographically spread group of people in national surveys, for example. You take advantage of hierarchical groupings (e.g., from county to city to neighbourhood) to create a sample that’s less expensive and time-consuming to collect data from.

In non-probability sampling , the sample is selected based on non-random criteria, and not every member of the population has a chance of being included.

Common non-probability sampling methods include convenience sampling , voluntary response sampling, purposive sampling , snowball sampling , and quota sampling .

Probability sampling means that every member of the target population has a known chance of being included in the sample.

Probability sampling methods include simple random sampling , systematic sampling , stratified sampling , and cluster sampling .

Samples are used to make inferences about populations . Samples are easier to collect data from because they are practical, cost-effective, convenient, and manageable.

While a between-subjects design has fewer threats to internal validity , it also requires more participants for high statistical power than a within-subjects design .

Advantages:

• Prevents carryover effects of learning and fatigue.
• Shorter study duration.

Disadvantages:

• Needs larger samples for high power.
• Uses more resources to recruit participants, administer sessions, cover costs, etc.
• Individual differences may be an alternative explanation for results.

In a factorial design, multiple independent variables are tested.

If you test two variables, each level of one independent variable is combined with each level of the other independent variable to create different conditions.

Yes. Between-subjects and within-subjects designs can be combined in a single study when you have two or more independent variables (a factorial design). In a mixed factorial design, one variable is altered between subjects and another is altered within subjects.

Within-subjects designs have many potential threats to internal validity , but they are also very statistically powerful .

• Only requires small samples
• Statistically powerful
• Removes the effects of individual differences on the outcomes
• Internal validity threats reduce the likelihood of establishing a direct relationship between variables
• Time-related effects, such as growth, can influence the outcomes
• Carryover effects mean that the specific order of different treatments affect the outcomes

Quasi-experimental design is most useful in situations where it would be unethical or impractical to run a true experiment .

Quasi-experiments have lower internal validity than true experiments, but they often have higher external validity  as they can use real-world interventions instead of artificial laboratory settings.

In experimental research, random assignment is a way of placing participants from your sample into different groups using randomisation. With this method, every member of the sample has a known or equal chance of being placed in a control group or an experimental group.

In a between-subjects design , every participant experiences only one condition, and researchers assess group differences between participants in various conditions.

In a within-subjects design , each participant experiences all conditions, and researchers test the same participants repeatedly for differences between conditions.

The word ‘between’ means that you’re comparing different conditions between groups, while the word ‘within’ means you’re comparing different conditions within the same group.

A confounding variable , also called a confounder or confounding factor, is a third variable in a study examining a potential cause-and-effect relationship.

A confounding variable is related to both the supposed cause and the supposed effect of the study. It can be difficult to separate the true effect of the independent variable from the effect of the confounding variable.

In your research design , it’s important to identify potential confounding variables and plan how you will reduce their impact.

Triangulation can help:

• Reduce bias that comes from using a single method, theory, or investigator
• Enhance validity by approaching the same topic with different tools
• Establish credibility by giving you a complete picture of the research problem

But triangulation can also pose problems:

• It’s time-consuming and labour-intensive, often involving an interdisciplinary team.
• Your results may be inconsistent or even contradictory.

There are four main types of triangulation :

• Data triangulation : Using data from different times, spaces, and people
• Investigator triangulation : Involving multiple researchers in collecting or analysing data
• Theory triangulation : Using varying theoretical perspectives in your research
• Methodological triangulation : Using different methodologies to approach the same topic

Experimental designs are a set of procedures that you plan in order to examine the relationship between variables that interest you.

To design a successful experiment, first identify:

• A testable hypothesis
• One or more independent variables that you will manipulate
• One or more dependent variables that you will measure

When designing the experiment, first decide:

• How your variable(s) will be manipulated
• How you will control for any potential confounding or lurking variables
• How many subjects you will include
• How you will assign treatments to your subjects

Exploratory research explores the main aspects of a new or barely researched question.

Explanatory research explains the causes and effects of an already widely researched question.

The key difference between observational studies and experiments is that, done correctly, an observational study will never influence the responses or behaviours of participants. Experimental designs will have a treatment condition applied to at least a portion of participants.

An observational study could be a good fit for your research if your research question is based on things you observe. If you have ethical, logistical, or practical concerns that make an experimental design challenging, consider an observational study. Remember that in an observational study, it is critical that there be no interference or manipulation of the research subjects. Since it’s not an experiment, there are no control or treatment groups either.

These are four of the most common mixed methods designs :

• Convergent parallel: Quantitative and qualitative data are collected at the same time and analysed separately. After both analyses are complete, compare your results to draw overall conclusions. 
• Embedded: Quantitative and qualitative data are collected at the same time, but within a larger quantitative or qualitative design. One type of data is secondary to the other.
• Explanatory sequential: Quantitative data is collected and analysed first, followed by qualitative data. You can use this design if you think your qualitative data will explain and contextualise your quantitative findings.
• Exploratory sequential: Qualitative data is collected and analysed first, followed by quantitative data. You can use this design if you think the quantitative data will confirm or validate your qualitative findings.

Triangulation in research means using multiple datasets, methods, theories and/or investigators to address a research question. It’s a research strategy that can help you enhance the validity and credibility of your findings.

Triangulation is mainly used in qualitative research , but it’s also commonly applied in quantitative research . Mixed methods research always uses triangulation.

Operationalisation means turning abstract conceptual ideas into measurable observations.

For example, the concept of social anxiety isn’t directly observable, but it can be operationally defined in terms of self-rating scores, behavioural avoidance of crowded places, or physical anxiety symptoms in social situations.

Before collecting data , it’s important to consider how you will operationalise the variables that you want to measure.

Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics. It is used by scientists to test specific predictions, called hypotheses , by calculating how likely it is that a pattern or relationship between variables could have arisen by chance.

There are five common approaches to qualitative research :

• Grounded theory involves collecting data in order to develop new theories.
• Ethnography involves immersing yourself in a group or organisation to understand its culture.
• Narrative research involves interpreting stories to understand how people make sense of their experiences and perceptions.
• Phenomenological research involves investigating phenomena through people’s lived experiences.
• Action research links theory and practice in several cycles to drive innovative changes.

There are various approaches to qualitative data analysis , but they all share five steps in common:

• Prepare and organise your data.
• Review and explore your data.
• Develop a data coding system.
• Assign codes to the data.
• Identify recurring themes.

The specifics of each step depend on the focus of the analysis. Some common approaches include textual analysis , thematic analysis , and discourse analysis .

In mixed methods research , you use both qualitative and quantitative data collection and analysis methods to answer your research question .

Methodology refers to the overarching strategy and rationale of your research project . It involves studying the methods used in your field and the theories or principles behind them, in order to develop an approach that matches your objectives.

Methods are the specific tools and procedures you use to collect and analyse data (e.g. experiments, surveys , and statistical tests ).

In shorter scientific papers, where the aim is to report the findings of a specific study, you might simply describe what you did in a methods section .

In a longer or more complex research project, such as a thesis or dissertation , you will probably include a methodology section , where you explain your approach to answering the research questions and cite relevant sources to support your choice of methods.

The research methods you use depend on the type of data you need to answer your research question .

• If you want to measure something or test a hypothesis , use quantitative methods . If you want to explore ideas, thoughts, and meanings, use qualitative methods .
• If you want to analyse a large amount of readily available data, use secondary data. If you want data specific to your purposes with control over how they are generated, collect primary data.
• If you want to establish cause-and-effect relationships between variables , use experimental methods. If you want to understand the characteristics of a research subject, use descriptive methods.

Ask our team

Want to contact us directly? No problem. We are always here for you.

• Chat with us
• Email [email protected]
• Call +44 (0)20 3917 4242
• WhatsApp +31 20 261 6040

Our support team is here to help you daily via chat, WhatsApp, email, or phone between 9:00 a.m. to 11:00 p.m. CET.

Our APA experts default to APA 7 for editing and formatting. For the Citation Editing Service you are able to choose between APA 6 and 7.

Yes, if your document is longer than 20,000 words, you will get a sample of approximately 2,000 words. This sample edit gives you a first impression of the editor’s editing style and a chance to ask questions and give feedback.

How does the sample edit work?

You will receive the sample edit within 24 hours after placing your order. You then have 24 hours to let us know if you’re happy with the sample or if there’s something you would like the editor to do differently.

Read more about how the sample edit works

Yes, you can upload your document in sections.

We try our best to ensure that the same editor checks all the different sections of your document. When you upload a new file, our system recognizes you as a returning customer, and we immediately contact the editor who helped you before.

However, we cannot guarantee that the same editor will be available. Your chances are higher if

• You send us your text as soon as possible and
• You can be flexible about the deadline.

Please note that the shorter your deadline is, the lower the chance that your previous editor is not available.

If your previous editor isn’t available, then we will inform you immediately and look for another qualified editor. Fear not! Every Scribbr editor follows the  Scribbr Improvement Model  and will deliver high-quality work.

Yes, our editors also work during the weekends and holidays.

Because we have many editors available, we can check your document 24 hours per day and 7 days per week, all year round.

If you choose a 72 hour deadline and upload your document on a Thursday evening, you’ll have your thesis back by Sunday evening!

Yes! Our editors are all native speakers, and they have lots of experience editing texts written by ESL students. They will make sure your grammar is perfect and point out any sentences that are difficult to understand. They’ll also notice your most common mistakes, and give you personal feedback to improve your writing in English.

Every Scribbr order comes with our award-winning Proofreading & Editing service , which combines two important stages of the revision process.

For a more comprehensive edit, you can add a Structure Check or Clarity Check to your order. With these building blocks, you can customize the kind of feedback you receive.

You might be familiar with a different set of editing terms. To help you understand what you can expect at Scribbr, we created this table:

View an example

When you place an order, you can specify your field of study and we’ll match you with an editor who has familiarity with this area.

However, our editors are language specialists, not academic experts in your field. Your editor’s job is not to comment on the content of your dissertation, but to improve your language and help you express your ideas as clearly and fluently as possible.

This means that your editor will understand your text well enough to give feedback on its clarity, logic and structure, but not on the accuracy or originality of its content.

Good academic writing should be understandable to a non-expert reader, and we believe that academic editing is a discipline in itself. The research, ideas and arguments are all yours – we’re here to make sure they shine!

After your document has been edited, you will receive an email with a link to download the document.

The editor has made changes to your document using ‘Track Changes’ in Word. This means that you only have to accept or ignore the changes that are made in the text one by one.

It is also possible to accept all changes at once. However, we strongly advise you not to do so for the following reasons:

• You can learn a lot by looking at the mistakes you made.
• The editors don’t only change the text – they also place comments when sentences or sometimes even entire paragraphs are unclear. You should read through these comments and take into account your editor’s tips and suggestions.
• With a final read-through, you can make sure you’re 100% happy with your text before you submit!

You choose the turnaround time when ordering. We can return your dissertation within 24 hours , 3 days or 1 week . These timescales include weekends and holidays. As soon as you’ve paid, the deadline is set, and we guarantee to meet it! We’ll notify you by text and email when your editor has completed the job.

Very large orders might not be possible to complete in 24 hours. On average, our editors can complete around 13,000 words in a day while maintaining our high quality standards. If your order is longer than this and urgent, contact us to discuss possibilities.

Always leave yourself enough time to check through the document and accept the changes before your submission deadline.

Scribbr is specialised in editing study related documents. We check:

• Graduation projects
• Dissertations
• Admissions essays
• College essays
• Application essays
• Personal statements
• Process reports
• Reflections
• Internship reports
• Academic papers
• Research proposals
• Prospectuses

Calculate the costs

The fastest turnaround time is 24 hours.

You can upload your document at any time and choose between four deadlines:

At Scribbr, we promise to make every customer 100% happy with the service we offer. Our philosophy: Your complaint is always justified – no denial, no doubts.

Our customer support team is here to find the solution that helps you the most, whether that’s a free new edit or a refund for the service.

Yes, in the order process you can indicate your preference for American, British, or Australian English .

If you don’t choose one, your editor will follow the style of English you currently use. If your editor has any questions about this, we will contact you.

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Quasi-Experimental Research

The prefix  quasi  means “resembling.” Thus quasi-experimental research is research that resembles experimental research but is not true experimental research. Recall with a true between-groups experiment, random assignment to conditions is used to ensure the groups are equivalent and with a true within-subjects design counterbalancing is used to guard against order effects. Quasi-experiments are missing one of these safeguards. Although an independent variable is manipulated, either a control group is missing or participants are not randomly assigned to conditions (Cook & Campbell, 1979) [1] .

Because the independent variable is manipulated before the dependent variable is measured, quasi-experimental research eliminates the directionality problem associated with non-experimental research. But because either counterbalancing techniques are not used or participants are not randomly assigned to conditions—making it likely that there are other differences between conditions—quasi-experimental research does not eliminate the problem of confounding variables. In terms of internal validity, therefore, quasi-experiments are generally somewhere between non-experimental studies and true experiments.

Quasi-experiments are most likely to be conducted in field settings in which random assignment is difficult or impossible. They are often conducted to evaluate the effectiveness of a treatment—perhaps a type of psychotherapy or an educational intervention. There are many different kinds of quasi-experiments, but we will discuss just a few of the most common ones in this chapter. 

• Cook, T. D., & Campbell, D. T. (1979). Quasi-experimentation: Design & analysis issues in field settings . Boston, MA: Houghton Mifflin. ↵

Research Methods in Psychology Copyright © 2019 by Rajiv S. Jhangiani, I-Chant A. Chiang, Carrie Cuttler, & Dana C. Leighton is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Share This Book

• Privacy Policy

Home » Quasi-Experimental Research Design – Types, Methods

Quasi-Experimental Research Design – Types, Methods

Table of Contents

Quasi-Experimental Design

Quasi-experimental design is a research method that seeks to evaluate the causal relationships between variables, but without the full control over the independent variable(s) that is available in a true experimental design.

In a quasi-experimental design, the researcher uses an existing group of participants that is not randomly assigned to the experimental and control groups. Instead, the groups are selected based on pre-existing characteristics or conditions, such as age, gender, or the presence of a certain medical condition.

Types of Quasi-Experimental Design

There are several types of quasi-experimental designs that researchers use to study causal relationships between variables. Here are some of the most common types:

Non-Equivalent Control Group Design

This design involves selecting two groups of participants that are similar in every way except for the independent variable(s) that the researcher is testing. One group receives the treatment or intervention being studied, while the other group does not. The two groups are then compared to see if there are any significant differences in the outcomes.

Interrupted Time-Series Design

This design involves collecting data on the dependent variable(s) over a period of time, both before and after an intervention or event. The researcher can then determine whether there was a significant change in the dependent variable(s) following the intervention or event.

Pretest-Posttest Design

This design involves measuring the dependent variable(s) before and after an intervention or event, but without a control group. This design can be useful for determining whether the intervention or event had an effect, but it does not allow for control over other factors that may have influenced the outcomes.

Regression Discontinuity Design

This design involves selecting participants based on a specific cutoff point on a continuous variable, such as a test score. Participants on either side of the cutoff point are then compared to determine whether the intervention or event had an effect.

Natural Experiments

This design involves studying the effects of an intervention or event that occurs naturally, without the researcher’s intervention. For example, a researcher might study the effects of a new law or policy that affects certain groups of people. This design is useful when true experiments are not feasible or ethical.

Data Analysis Methods

Here are some data analysis methods that are commonly used in quasi-experimental designs:

Descriptive Statistics

This method involves summarizing the data collected during a study using measures such as mean, median, mode, range, and standard deviation. Descriptive statistics can help researchers identify trends or patterns in the data, and can also be useful for identifying outliers or anomalies.

Inferential Statistics

This method involves using statistical tests to determine whether the results of a study are statistically significant. Inferential statistics can help researchers make generalizations about a population based on the sample data collected during the study. Common statistical tests used in quasi-experimental designs include t-tests, ANOVA, and regression analysis.

Propensity Score Matching

This method is used to reduce bias in quasi-experimental designs by matching participants in the intervention group with participants in the control group who have similar characteristics. This can help to reduce the impact of confounding variables that may affect the study’s results.

Difference-in-differences Analysis

This method is used to compare the difference in outcomes between two groups over time. Researchers can use this method to determine whether a particular intervention has had an impact on the target population over time.

Interrupted Time Series Analysis

This method is used to examine the impact of an intervention or treatment over time by comparing data collected before and after the intervention or treatment. This method can help researchers determine whether an intervention had a significant impact on the target population.

Regression Discontinuity Analysis

This method is used to compare the outcomes of participants who fall on either side of a predetermined cutoff point. This method can help researchers determine whether an intervention had a significant impact on the target population.

Steps in Quasi-Experimental Design

Here are the general steps involved in conducting a quasi-experimental design:

• Identify the research question: Determine the research question and the variables that will be investigated.
• Choose the design: Choose the appropriate quasi-experimental design to address the research question. Examples include the pretest-posttest design, non-equivalent control group design, regression discontinuity design, and interrupted time series design.
• Select the participants: Select the participants who will be included in the study. Participants should be selected based on specific criteria relevant to the research question.
• Measure the variables: Measure the variables that are relevant to the research question. This may involve using surveys, questionnaires, tests, or other measures.
• Implement the intervention or treatment: Implement the intervention or treatment to the participants in the intervention group. This may involve training, education, counseling, or other interventions.
• Collect data: Collect data on the dependent variable(s) before and after the intervention. Data collection may also include collecting data on other variables that may impact the dependent variable(s).
• Analyze the data: Analyze the data collected to determine whether the intervention had a significant impact on the dependent variable(s).
• Draw conclusions: Draw conclusions about the relationship between the independent and dependent variables. If the results suggest a causal relationship, then appropriate recommendations may be made based on the findings.

Quasi-Experimental Design Examples

Here are some examples of real-time quasi-experimental designs:

• Evaluating the impact of a new teaching method: In this study, a group of students are taught using a new teaching method, while another group is taught using the traditional method. The test scores of both groups are compared before and after the intervention to determine whether the new teaching method had a significant impact on student performance.
• Assessing the effectiveness of a public health campaign: In this study, a public health campaign is launched to promote healthy eating habits among a targeted population. The behavior of the population is compared before and after the campaign to determine whether the intervention had a significant impact on the target behavior.
• Examining the impact of a new medication: In this study, a group of patients is given a new medication, while another group is given a placebo. The outcomes of both groups are compared to determine whether the new medication had a significant impact on the targeted health condition.
• Evaluating the effectiveness of a job training program : In this study, a group of unemployed individuals is enrolled in a job training program, while another group is not enrolled in any program. The employment rates of both groups are compared before and after the intervention to determine whether the training program had a significant impact on the employment rates of the participants.
• Assessing the impact of a new policy : In this study, a new policy is implemented in a particular area, while another area does not have the new policy. The outcomes of both areas are compared before and after the intervention to determine whether the new policy had a significant impact on the targeted behavior or outcome.

Applications of Quasi-Experimental Design

Here are some applications of quasi-experimental design:

• Educational research: Quasi-experimental designs are used to evaluate the effectiveness of educational interventions, such as new teaching methods, technology-based learning, or educational policies.
• Health research: Quasi-experimental designs are used to evaluate the effectiveness of health interventions, such as new medications, public health campaigns, or health policies.
• Social science research: Quasi-experimental designs are used to investigate the impact of social interventions, such as job training programs, welfare policies, or criminal justice programs.
• Business research: Quasi-experimental designs are used to evaluate the impact of business interventions, such as marketing campaigns, new products, or pricing strategies.
• Environmental research: Quasi-experimental designs are used to evaluate the impact of environmental interventions, such as conservation programs, pollution control policies, or renewable energy initiatives.

When to use Quasi-Experimental Design

Here are some situations where quasi-experimental designs may be appropriate:

• When the research question involves investigating the effectiveness of an intervention, policy, or program : In situations where it is not feasible or ethical to randomly assign participants to intervention and control groups, quasi-experimental designs can be used to evaluate the impact of the intervention on the targeted outcome.
• When the sample size is small: In situations where the sample size is small, it may be difficult to randomly assign participants to intervention and control groups. Quasi-experimental designs can be used to investigate the impact of an intervention without requiring a large sample size.
• When the research question involves investigating a naturally occurring event : In some situations, researchers may be interested in investigating the impact of a naturally occurring event, such as a natural disaster or a major policy change. Quasi-experimental designs can be used to evaluate the impact of the event on the targeted outcome.
• When the research question involves investigating a long-term intervention: In situations where the intervention or program is long-term, it may be difficult to randomly assign participants to intervention and control groups for the entire duration of the intervention. Quasi-experimental designs can be used to evaluate the impact of the intervention over time.
• When the research question involves investigating the impact of a variable that cannot be manipulated : In some situations, it may not be possible or ethical to manipulate a variable of interest. Quasi-experimental designs can be used to investigate the relationship between the variable and the targeted outcome.

Purpose of Quasi-Experimental Design

The purpose of quasi-experimental design is to investigate the causal relationship between two or more variables when it is not feasible or ethical to conduct a randomized controlled trial (RCT). Quasi-experimental designs attempt to emulate the randomized control trial by mimicking the control group and the intervention group as much as possible.

The key purpose of quasi-experimental design is to evaluate the impact of an intervention, policy, or program on a targeted outcome while controlling for potential confounding factors that may affect the outcome. Quasi-experimental designs aim to answer questions such as: Did the intervention cause the change in the outcome? Would the outcome have changed without the intervention? And was the intervention effective in achieving its intended goals?

Quasi-experimental designs are useful in situations where randomized controlled trials are not feasible or ethical. They provide researchers with an alternative method to evaluate the effectiveness of interventions, policies, and programs in real-life settings. Quasi-experimental designs can also help inform policy and practice by providing valuable insights into the causal relationships between variables.

Overall, the purpose of quasi-experimental design is to provide a rigorous method for evaluating the impact of interventions, policies, and programs while controlling for potential confounding factors that may affect the outcome.

Advantages of Quasi-Experimental Design

Quasi-experimental designs have several advantages over other research designs, such as:

• Greater external validity : Quasi-experimental designs are more likely to have greater external validity than laboratory experiments because they are conducted in naturalistic settings. This means that the results are more likely to generalize to real-world situations.
• Ethical considerations: Quasi-experimental designs often involve naturally occurring events, such as natural disasters or policy changes. This means that researchers do not need to manipulate variables, which can raise ethical concerns.
• More practical: Quasi-experimental designs are often more practical than experimental designs because they are less expensive and easier to conduct. They can also be used to evaluate programs or policies that have already been implemented, which can save time and resources.
• No random assignment: Quasi-experimental designs do not require random assignment, which can be difficult or impossible in some cases, such as when studying the effects of a natural disaster. This means that researchers can still make causal inferences, although they must use statistical techniques to control for potential confounding variables.
• Greater generalizability : Quasi-experimental designs are often more generalizable than experimental designs because they include a wider range of participants and conditions. This can make the results more applicable to different populations and settings.

Limitations of Quasi-Experimental Design

There are several limitations associated with quasi-experimental designs, which include:

• Lack of Randomization: Quasi-experimental designs do not involve randomization of participants into groups, which means that the groups being studied may differ in important ways that could affect the outcome of the study. This can lead to problems with internal validity and limit the ability to make causal inferences.
• Selection Bias: Quasi-experimental designs may suffer from selection bias because participants are not randomly assigned to groups. Participants may self-select into groups or be assigned based on pre-existing characteristics, which may introduce bias into the study.
• History and Maturation: Quasi-experimental designs are susceptible to history and maturation effects, where the passage of time or other events may influence the outcome of the study.
• Lack of Control: Quasi-experimental designs may lack control over extraneous variables that could influence the outcome of the study. This can limit the ability to draw causal inferences from the study.
• Limited Generalizability: Quasi-experimental designs may have limited generalizability because the results may only apply to the specific population and context being studied.

About the author

Muhammad Hassan

Researcher, Academic Writer, Web developer

You may also like

Questionnaire – Definition, Types, and Examples

Case Study – Methods, Examples and Guide

Observational Research – Methods and Guide

Quantitative Research – Methods, Types and...

Qualitative Research Methods

Explanatory Research – Types, Methods, Guide

The use and interpretation of quasi-experimental design

Last updated

6 February 2023

Reviewed by

Miroslav Damyanov

• What is a quasi-experimental design?

Commonly used in medical informatics (a field that uses digital information to ensure better patient care), researchers generally use this design to evaluate the effectiveness of a treatment – perhaps a type of antibiotic or psychotherapy, or an educational or policy intervention.

Even though quasi-experimental design has been used for some time, relatively little is known about it. Read on to learn the ins and outs of this research design.

Make research less tedious

Dovetail streamlines research to help you uncover and share actionable insights

• When to use a quasi-experimental design

A quasi-experimental design is used when it's not logistically feasible or ethical to conduct randomized, controlled trials. As its name suggests, a quasi-experimental design is almost a true experiment. However, researchers don't randomly select elements or participants in this type of research.

Researchers prefer to apply quasi-experimental design when there are ethical or practical concerns. Let's look at these two reasons more closely.

Ethical reasons

In some situations, the use of randomly assigned elements can be unethical. For instance, providing public healthcare to one group and withholding it to another in research is unethical. A quasi-experimental design would examine the relationship between these two groups to avoid physical danger.

Practical reasons

Randomized controlled trials may not be the best approach in research. For instance, it's impractical to trawl through large sample sizes of participants without using a particular attribute to guide your data collection .

Recruiting participants and properly designing a data-collection attribute to make the research a true experiment requires a lot of time and effort, and can be expensive if you don’t have a large funding stream.

A quasi-experimental design allows researchers to take advantage of previously collected data and use it in their study.

• Examples of quasi-experimental designs

Quasi-experimental research design is common in medical research, but any researcher can use it for research that raises practical and ethical concerns. Here are a few examples of quasi-experimental designs used by different researchers:

Example 1: Determining the effectiveness of math apps in supplementing math classes

A school wanted to supplement its math classes with a math app. To select the best app, the school decided to conduct demo tests on two apps before selecting the one they will purchase.

Scope of the research

Since every grade had two math teachers, each teacher used one of the two apps for three months. They then gave the students the same math exams and compared the results to determine which app was most effective.

Reasons why this is a quasi-experimental study

This simple study is a quasi-experiment since the school didn't randomly assign its students to the applications. They used a pre-existing class structure to conduct the study since it was impractical to randomly assign the students to each app.

Example 2: Determining the effectiveness of teaching modern leadership techniques in start-up businesses

A hypothetical quasi-experimental study was conducted in an economically developing country in a mid-sized city.

Five start-ups in the textile industry and five in the tech industry participated in the study. The leaders attended a six-week workshop on leadership style, team management, and employee motivation.

After a year, the researchers assessed the performance of each start-up company to determine growth. The results indicated that the tech start-ups were further along in their growth than the textile companies.

The basis of quasi-experimental research is a non-randomized subject-selection process. This study didn't use specific aspects to determine which start-up companies should participate. Therefore, the results may seem straightforward, but several aspects may determine the growth of a specific company, apart from the variables used by the researchers.

Example 3: A study to determine the effects of policy reforms and of luring foreign investment on small businesses in two mid-size cities

In a study to determine the economic impact of government reforms in an economically developing country, the government decided to test whether creating reforms directed at small businesses or luring foreign investments would spur the most economic development.

The government selected two cities with similar population demographics and sizes. In one of the cities, they implemented specific policies that would directly impact small businesses, and in the other, they implemented policies to attract foreign investment.

After five years, they collected end-of-year economic growth data from both cities. They looked at elements like local GDP growth, unemployment rates, and housing sales.

The study used a non-randomized selection process to determine which city would participate in the research. Researchers left out certain variables that would play a crucial role in determining the growth of each city. They used pre-existing groups of people based on research conducted in each city, rather than random groups.

• Advantages of a quasi-experimental design

Some advantages of quasi-experimental designs are:

Researchers can manipulate variables to help them meet their study objectives.

It offers high external validity, making it suitable for real-world applications, specifically in social science experiments.

Integrating this methodology into other research designs is easier, especially in true experimental research. This cuts down on the time needed to determine your outcomes.

• Disadvantages of a quasi-experimental design

Despite the pros that come with a quasi-experimental design, there are several disadvantages associated with it, including the following:

It has a lower internal validity since researchers do not have full control over the comparison and intervention groups or between time periods because of differences in characteristics in people, places, or time involved. It may be challenging to determine whether all variables have been used or whether those used in the research impacted the results.

There is the risk of inaccurate data since the research design borrows information from other studies.

There is the possibility of bias since researchers select baseline elements and eligibility.

• What are the different quasi-experimental study designs?

There are three distinct types of quasi-experimental designs:

Nonequivalent

Regression discontinuity, natural experiment.

This is a hybrid of experimental and quasi-experimental methods and is used to leverage the best qualities of the two. Like the true experiment design, nonequivalent group design uses pre-existing groups believed to be comparable. However, it doesn't use randomization, the lack of which is a crucial element for quasi-experimental design.

Researchers usually ensure that no confounding variables impact them throughout the grouping process. This makes the groupings more comparable.

Example of a nonequivalent group design

A small study was conducted to determine whether after-school programs result in better grades. Researchers randomly selected two groups of students: one to implement the new program, the other not to. They then compared the results of the two groups.

This type of quasi-experimental research design calculates the impact of a specific treatment or intervention. It uses a criterion known as "cutoff" that assigns treatment according to eligibility.

Researchers often assign participants above the cutoff to the treatment group. This puts a negligible distinction between the two groups (treatment group and control group).

Example of regression discontinuity

Students must achieve a minimum score to be enrolled in specific US high schools. Since the cutoff score used to determine eligibility for enrollment is arbitrary, researchers can assume that the disparity between students who only just fail to achieve the cutoff point and those who barely pass is a small margin and is due to the difference in the schools that these students attend.

Researchers can then examine the long-term effects of these two groups of kids to determine the effect of attending certain schools. This information can be applied to increase the chances of students being enrolled in these high schools.

This research design is common in laboratory and field experiments where researchers control target subjects by assigning them to different groups. Researchers randomly assign subjects to a treatment group using nature or an external event or situation.

However, even with random assignment, this research design cannot be called a true experiment since nature aspects are observational. Researchers can also exploit these aspects despite having no control over the independent variables.

Example of the natural experiment approach

An example of a natural experiment is the 2008 Oregon Health Study.

Oregon intended to allow more low-income people to participate in Medicaid.

Since they couldn't afford to cover every person who qualified for the program, the state used a random lottery to allocate program slots.

Researchers assessed the program's effectiveness by assigning the selected subjects to a randomly assigned treatment group, while those that didn't win the lottery were considered the control group.

• Differences between quasi-experiments and true experiments

There are several differences between a quasi-experiment and a true experiment:

Participants in true experiments are randomly assigned to the treatment or control group, while participants in a quasi-experiment are not assigned randomly.

In a quasi-experimental design, the control and treatment groups differ in unknown or unknowable ways, apart from the experimental treatments that are carried out. Therefore, the researcher should try as much as possible to control these differences.

Quasi-experimental designs have several "competing hypotheses," which compete with experimental manipulation to explain the observed results.

Quasi-experiments tend to have lower internal validity (the degree of confidence in the research outcomes) than true experiments, but they may offer higher external validity (whether findings can be extended to other contexts) as they involve real-world interventions instead of controlled interventions in artificial laboratory settings.

Despite the distinct difference between true and quasi-experimental research designs, these two research methodologies share the following aspects:

Both study methods subject participants to some form of treatment or conditions.

Researchers have the freedom to measure some of the outcomes of interest.

Researchers can test whether the differences in the outcomes are associated with the treatment.

• An example comparing a true experiment and quasi-experiment

Imagine you wanted to study the effects of junk food on obese people. Here's how you would do this as a true experiment and a quasi-experiment:

How to carry out a true experiment

In a true experiment, some participants would eat junk foods, while the rest would be in the control group, adhering to a regular diet. At the end of the study, you would record the health and discomfort of each group.

This kind of experiment would raise ethical concerns since the participants assigned to the treatment group are required to eat junk food against their will throughout the experiment. This calls for a quasi-experimental design.

How to carry out a quasi-experiment

In quasi-experimental research, you would start by finding out which participants want to try junk food and which prefer to stick to a regular diet. This allows you to assign these two groups based on subject choice.

In this case, you didn't assign participants to a particular group, so you can confidently use the results from the study.

When is a quasi-experimental design used?

Quasi-experimental designs are used when researchers don’t want to use randomization when evaluating their intervention.

What are the characteristics of quasi-experimental designs?

Some of the characteristics of a quasi-experimental design are:

Researchers don't randomly assign participants into groups, but study their existing characteristics and assign them accordingly.

Researchers study the participants in pre- and post-testing to determine the progress of the groups.

Quasi-experimental design is ethical since it doesn’t involve offering or withholding treatment at random.

Quasi-experimental design encompasses a broad range of non-randomized intervention studies. This design is employed when it is not ethical or logistically feasible to conduct randomized controlled trials. Researchers typically employ it when evaluating policy or educational interventions, or in medical or therapy scenarios.

How do you analyze data in a quasi-experimental design?

You can use two-group tests, time-series analysis, and regression analysis to analyze data in a quasi-experiment design. Each option has specific assumptions, strengths, limitations, and data requirements.

Should you be using a customer insights hub?

Do you want to discover previous research faster?

Do you share your research findings with others?

Do you analyze research data?

Start for free today, add your research, and get to key insights faster

Editor’s picks

Last updated: 11 January 2024

Last updated: 15 January 2024

Last updated: 17 January 2024

Last updated: 25 November 2023

Last updated: 12 May 2023

Last updated: 30 April 2024

Last updated: 13 May 2024

Latest articles

Related topics, .css-je19u9{-webkit-align-items:flex-end;-webkit-box-align:flex-end;-ms-flex-align:flex-end;align-items:flex-end;display:-webkit-box;display:-webkit-flex;display:-ms-flexbox;display:flex;-webkit-flex-direction:row;-ms-flex-direction:row;flex-direction:row;-webkit-box-flex-wrap:wrap;-webkit-flex-wrap:wrap;-ms-flex-wrap:wrap;flex-wrap:wrap;-webkit-box-pack:center;-ms-flex-pack:center;-webkit-justify-content:center;justify-content:center;row-gap:0;text-align:center;max-width:671px;}@media (max-width: 1079px){.css-je19u9{max-width:400px;}.css-je19u9>span{white-space:pre;}}@media (max-width: 799px){.css-je19u9{max-width:400px;}.css-je19u9>span{white-space:pre;}} decide what to .css-1kiodld{max-height:56px;display:-webkit-box;display:-webkit-flex;display:-ms-flexbox;display:flex;-webkit-align-items:center;-webkit-box-align:center;-ms-flex-align:center;align-items:center;}@media (max-width: 1079px){.css-1kiodld{display:none;}} build next, decide what to build next.

Users report unexpectedly high data usage, especially during streaming sessions.

Users find it hard to navigate from the home page to relevant playlists in the app.

It would be great to have a sleep timer feature, especially for bedtime listening.

I need better filters to find the songs or artists I’m looking for.

Log in or sign up

Get started for free

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

12.2: Pre-experimental and quasi-experimental design

• Last updated
• Save as PDF
• Page ID 25667

• Matthew DeCarlo
• Radford University via Open Social Work Education

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

• Identify and describe the various types of quasi-experimental designs
• Distinguish true experimental designs from quasi-experimental and pre-experimental designs
• Identify and describe the various types of quasi-experimental and pre-experimental designs

As we discussed in the previous section, time, funding, and ethics may limit a researcher’s ability to conduct a true experiment. For researchers in the medical sciences and social work, conducting a true experiment could require denying needed treatment to clients, which is a clear ethical violation. Even those whose research may not involve the administration of needed medications or treatments may be limited in their ability to conduct a classic experiment. When true experiments are not possible, researchers often use quasi-experimental designs.

Quasi-experimental designs are similar to true experiments, but they lack random assignment to experimental and control groups. The most basic of these quasi-experimental designs is the nonequivalent comparison groups design (Rubin & Babbie, 2017). [1] The nonequivalent comparison group design looks a lot like the classic experimental design, except it does not use random assignment. In many cases, these groups may already exist. For example, a researcher might conduct research at two different agency sites, one of which receives the intervention and the other does not. No one was assigned to treatment or comparison groups. Those groupings existed prior to the study. While this method is more convenient for real-world research, researchers cannot be sure that the groups are comparable. Perhaps the treatment group has a characteristic that is unique–for example, higher income or different diagnoses–that make the treatment more effective.

Quasi-experiments are particularly useful in social welfare policy research. Social welfare policy researchers like me often look for what are termed natural experiments , or situations in which comparable groups are created by differences that already occur in the real world. For example, Stratmann and Wille (2016) [2] were interested in the effects of a state healthcare policy called Certificate of Need on the quality of hospitals. They clearly cannot assign states to adopt one set of policies or another. Instead, researchers used hospital referral regions, or the areas from which hospitals draw their patients, that spanned across state lines. Because the hospitals were in the same referral region, researchers could be pretty sure that the client characteristics were pretty similar. In this way, they could classify patients in experimental and comparison groups without affecting policy or telling people where to live.

There are important examples of policy experiments that use random assignment, including the Oregon Medicaid experiment. In the Oregon Medicaid experiment, the wait list for Oregon was so long, state officials conducted a lottery to see who from the wait list would receive Medicaid (Baicker et al., 2013). [3] Researchers used the lottery as a natural experiment that included random assignment. People selected to be a part of Medicaid were the experimental group and those on the wait list were in the control group. There are some practical complications with using people on a wait list as a control group—most obviously, what happens when people on the wait list are accepted into the program while you’re still collecting data? Natural experiments aren’t a specific kind of experiment like quasi- or pre-experimental designs. Instead, they are more like a feature of the social world that allows researchers to use the logic of experimental design to investigate the connection between variables.

Matching is another approach in quasi-experimental design to assigning experimental and comparison groups. Researchers should think about what variables are important in their study, particularly demographic variables or attributes that might impact their dependent variable. Individual matching involves pairing participants with similar attributes. When this is done at the beginning of an experiment, the matched pair is split—with one participant going to the experimental group and the other to the control group. An ex post facto control group , in contrast, is when a researcher matches individuals after the intervention is administered to some participants. Finally, researchers may engage in aggregate matching , in which the comparison group is determined to be similar on important variables.

There are many different quasi-experimental designs in addition to the nonequivalent comparison group design described earlier. Describing all of them is beyond the scope of this textbook, but one more design is worth mentioning. The time series design uses multiple observations before and after an intervention. In some cases, experimental and comparison groups are used. In other cases where that is not feasible, a single experimental group is used. By using multiple observations before and after the intervention, the researcher can better understand the true value of the dependent variable in each participant before the intervention starts. Additionally, multiple observations afterwards allow the researcher to see whether the intervention had lasting effects on participants. Time series designs are similar to single-subjects designs, which we will discuss in Chapter 15.

When true experiments and quasi-experiments are not possible, researchers may turn to a pre-experimental design (Campbell & Stanley, 1963). [4] Pre-experimental designs are called such because they often happen before a true experiment is conducted. Researchers want to see if their interventions will have some effect on a small group of people before they seek funding and dedicate time to conduct a true experiment. Pre-experimental designs, thus, are usually conducted as a first step towards establishing the evidence for or against an intervention. However, this type of design comes with some unique disadvantages, which we’ll describe as we review the pre-experimental designs available.

If we wished to measure the impact of a natural disaster, such as Hurricane Katrina for example, we might conduct a pre-experiment by identifying an experimental group from a community that experienced the hurricane and a control group from a similar community that had not been hit by the hurricane. This study design, called a static group comparison , has the advantage of including a comparison group that did not experience the stimulus (in this case, the hurricane). Unfortunately, it is difficult to know those groups are truly comparable because the experimental and control groups were determined by factors other than random assignment. Additionally, the design would only allow for posttests, unless one were lucky enough to be gathering the data already before Katrina. As you might have guessed from our example, static group comparisons are useful in cases where a researcher cannot control or predict whether, when, or how the stimulus is administered, as in the case of natural disasters.

In cases where the administration of the stimulus is quite costly or otherwise not possible, a one- shot case study design might be used. In this instance, no pretest is administered, nor is a control group present. In our example of the study of the impact of Hurricane Katrina, a researcher using this design would test the impact of Katrina only among a community that was hit by the hurricane and would not seek a comparison group from a community that did not experience the hurricane. Researchers using this design must be extremely cautious about making claims regarding the effect of the stimulus, though the design could be useful for exploratory studies aimed at testing one’s measures or the feasibility of further study.

Finally, if a researcher is unlikely to be able to identify a sample large enough to split into control and experimental groups, or if she simply doesn’t have access to a control group, the researcher might use a one-group pre-/posttest design. In this instance, pre- and posttests are both taken, but there is no control group to which to compare the experimental group. We might be able to study of the impact of Hurricane Katrina using this design if we’d been collecting data on the impacted communities prior to the hurricane. We could then collect similar data after the hurricane. Applying this design involves a bit of serendipity and chance. Without having collected data from impacted communities prior to the hurricane, we would be unable to employ a one- group pre-/posttest design to study Hurricane Katrina’s impact.

As implied by the preceding examples where we considered studying the impact of Hurricane Katrina, experiments do not necessarily need to take place in the controlled setting of a lab. In fact, many applied researchers rely on experiments to assess the impact and effectiveness of various programs and policies. You might recall our discussion of arresting perpetrators of domestic violence in Chapter 6, which is an excellent example of an applied experiment. Researchers did not subject participants to conditions in a lab setting; instead, they applied their stimulus (in this case, arrest) to some subjects in the field and they also had a control group in the field that did not receive the stimulus (and therefore were not arrested).

Key Takeaways

• Quasi-experimental designs do not use random assignment.
• Comparison groups are often used in quasi-experiments.
• Matching is a way of improving the comparability of experimental and comparison groups.
• Quasi-experimental designs and pre-experimental designs are often used when experimental designs are impractical.
• Quasi-experimental and pre-experimental designs may be easier to carry out, but they lack the rigor of true experiments.
• Aggregate matching- when the comparison group is determined to be similar to the experimental group along important variables
• Ex post facto control group- a control group created when a researcher matches individuals after the intervention is administered
• Individual matching- pairing participants with similar attributes for the purpose of assignment to groups
• Natural experiments- situations in which comparable groups are created by differences that already occur in the real world
• Nonequivalent comparison group design- a quasi-experimental design similar to a classic experimental design but without random assignment
• One-group pre-/posttest design- a pre-experimental design that applies an intervention to one group but also includes a pretest
• One-shot case study- a pre-experimental design that applies an intervention to only one group without a pretest
• Pre-experimental designs- a variation of experimental design that lacks the rigor of experiments and is often used before a true experiment is conducted
• Quasi-experimental design- designs lack random assignment to experimental and control groups
• Static group design- uses an experimental group and a comparison group, without random assignment and pretesting
• Time series design- a quasi-experimental design that uses multiple observations before and after an intervention

Image attributions

cat and kitten matching avocado costumes on the couch looking at the camera by Your Best Digs CC-BY-2.0

• Rubin, C. & Babbie, S. (2017). Research methods for social work (9th edition) . Boston, MA: Cengage. ↵
• Stratmann, T. & Wille, D. (2016). Certificate-of-need laws and hospital quality . Mercatus Center at George Mason University, Arlington, VA. Retrieved from: https://www.mercatus.org/system/files/mercatus-stratmann-wille-con-hospital-quality-v1.pdf ↵
• Baicker, K., Taubman, S. L., Allen, H. L., Bernstein, M., Gruber, J. H., Newhouse, J. P., ... & Finkelstein, A. N. (2013). The Oregon experiment—effects of Medicaid on clinical outcomes. New England Journal of Medicine , 368 (18), 1713-1722. ↵
• Campbell, D., & Stanley, J. (1963). Experimental and quasi-experimental designs for research . Chicago, IL: Rand McNally. ↵

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Chapter 7: Nonexperimental Research

Quasi-Experimental Research

Learning Objectives

• Explain what quasi-experimental research is and distinguish it clearly from both experimental and correlational research.
• Describe three different types of quasi-experimental research designs (nonequivalent groups, pretest-posttest, and interrupted time series) and identify examples of each one.

The prefix  quasi  means “resembling.” Thus quasi-experimental research is research that resembles experimental research but is not true experimental research. Although the independent variable is manipulated, participants are not randomly assigned to conditions or orders of conditions (Cook & Campbell, 1979). [1] Because the independent variable is manipulated before the dependent variable is measured, quasi-experimental research eliminates the directionality problem. But because participants are not randomly assigned—making it likely that there are other differences between conditions—quasi-experimental research does not eliminate the problem of confounding variables. In terms of internal validity, therefore, quasi-experiments are generally somewhere between correlational studies and true experiments.

Quasi-experiments are most likely to be conducted in field settings in which random assignment is difficult or impossible. They are often conducted to evaluate the effectiveness of a treatment—perhaps a type of psychotherapy or an educational intervention. There are many different kinds of quasi-experiments, but we will discuss just a few of the most common ones here.

Nonequivalent Groups Design

Recall that when participants in a between-subjects experiment are randomly assigned to conditions, the resulting groups are likely to be quite similar. In fact, researchers consider them to be equivalent. When participants are not randomly assigned to conditions, however, the resulting groups are likely to be dissimilar in some ways. For this reason, researchers consider them to be nonequivalent. A  nonequivalent groups design , then, is a between-subjects design in which participants have not been randomly assigned to conditions.

Imagine, for example, a researcher who wants to evaluate a new method of teaching fractions to third graders. One way would be to conduct a study with a treatment group consisting of one class of third-grade students and a control group consisting of another class of third-grade students. This design would be a nonequivalent groups design because the students are not randomly assigned to classes by the researcher, which means there could be important differences between them. For example, the parents of higher achieving or more motivated students might have been more likely to request that their children be assigned to Ms. Williams’s class. Or the principal might have assigned the “troublemakers” to Mr. Jones’s class because he is a stronger disciplinarian. Of course, the teachers’ styles, and even the classroom environments, might be very different and might cause different levels of achievement or motivation among the students. If at the end of the study there was a difference in the two classes’ knowledge of fractions, it might have been caused by the difference between the teaching methods—but it might have been caused by any of these confounding variables.

Of course, researchers using a nonequivalent groups design can take steps to ensure that their groups are as similar as possible. In the present example, the researcher could try to select two classes at the same school, where the students in the two classes have similar scores on a standardized math test and the teachers are the same sex, are close in age, and have similar teaching styles. Taking such steps would increase the internal validity of the study because it would eliminate some of the most important confounding variables. But without true random assignment of the students to conditions, there remains the possibility of other important confounding variables that the researcher was not able to control.

Pretest-Posttest Design

In a  pretest-posttest design , the dependent variable is measured once before the treatment is implemented and once after it is implemented. Imagine, for example, a researcher who is interested in the effectiveness of an antidrug education program on elementary school students’ attitudes toward illegal drugs. The researcher could measure the attitudes of students at a particular elementary school during one week, implement the antidrug program during the next week, and finally, measure their attitudes again the following week. The pretest-posttest design is much like a within-subjects experiment in which each participant is tested first under the control condition and then under the treatment condition. It is unlike a within-subjects experiment, however, in that the order of conditions is not counterbalanced because it typically is not possible for a participant to be tested in the treatment condition first and then in an “untreated” control condition.

If the average posttest score is better than the average pretest score, then it makes sense to conclude that the treatment might be responsible for the improvement. Unfortunately, one often cannot conclude this with a high degree of certainty because there may be other explanations for why the posttest scores are better. One category of alternative explanations goes under the name of  history . Other things might have happened between the pretest and the posttest. Perhaps an antidrug program aired on television and many of the students watched it, or perhaps a celebrity died of a drug overdose and many of the students heard about it. Another category of alternative explanations goes under the name of  maturation . Participants might have changed between the pretest and the posttest in ways that they were going to anyway because they are growing and learning. If it were a yearlong program, participants might become less impulsive or better reasoners and this might be responsible for the change.

Another alternative explanation for a change in the dependent variable in a pretest-posttest design is  regression to the mean . This refers to the statistical fact that an individual who scores extremely on a variable on one occasion will tend to score less extremely on the next occasion. For example, a bowler with a long-term average of 150 who suddenly bowls a 220 will almost certainly score lower in the next game. Her score will “regress” toward her mean score of 150. Regression to the mean can be a problem when participants are selected for further study  because  of their extreme scores. Imagine, for example, that only students who scored especially low on a test of fractions are given a special training program and then retested. Regression to the mean all but guarantees that their scores will be higher even if the training program has no effect. A closely related concept—and an extremely important one in psychological research—is  spontaneous remission . This is the tendency for many medical and psychological problems to improve over time without any form of treatment. The common cold is a good example. If one were to measure symptom severity in 100 common cold sufferers today, give them a bowl of chicken soup every day, and then measure their symptom severity again in a week, they would probably be much improved. This does not mean that the chicken soup was responsible for the improvement, however, because they would have been much improved without any treatment at all. The same is true of many psychological problems. A group of severely depressed people today is likely to be less depressed on average in 6 months. In reviewing the results of several studies of treatments for depression, researchers Michael Posternak and Ivan Miller found that participants in waitlist control conditions improved an average of 10 to 15% before they received any treatment at all (Posternak & Miller, 2001) [2] . Thus one must generally be very cautious about inferring causality from pretest-posttest designs.

Does Psychotherapy Work?

Early studies on the effectiveness of psychotherapy tended to use pretest-posttest designs. In a classic 1952 article, researcher Hans Eysenck summarized the results of 24 such studies showing that about two thirds of patients improved between the pretest and the posttest (Eysenck, 1952) [3] . But Eysenck also compared these results with archival data from state hospital and insurance company records showing that similar patients recovered at about the same rate  without  receiving psychotherapy. This parallel suggested to Eysenck that the improvement that patients showed in the pretest-posttest studies might be no more than spontaneous remission. Note that Eysenck did not conclude that psychotherapy was ineffective. He merely concluded that there was no evidence that it was, and he wrote of “the necessity of properly planned and executed experimental studies into this important field” (p. 323). You can read the entire article here: Classics in the History of Psychology .

Fortunately, many other researchers took up Eysenck’s challenge, and by 1980 hundreds of experiments had been conducted in which participants were randomly assigned to treatment and control conditions, and the results were summarized in a classic book by Mary Lee Smith, Gene Glass, and Thomas Miller (Smith, Glass, & Miller, 1980) [4] . They found that overall psychotherapy was quite effective, with about 80% of treatment participants improving more than the average control participant. Subsequent research has focused more on the conditions under which different types of psychotherapy are more or less effective.

Interrupted Time Series Design

A variant of the pretest-posttest design is the  interrupted time-series design . A time series is a set of measurements taken at intervals over a period of time. For example, a manufacturing company might measure its workers’ productivity each week for a year. In an interrupted time series-design, a time series like this one is “interrupted” by a treatment. In one classic example, the treatment was the reduction of the work shifts in a factory from 10 hours to 8 hours (Cook & Campbell, 1979) [5] . Because productivity increased rather quickly after the shortening of the work shifts, and because it remained elevated for many months afterward, the researcher concluded that the shortening of the shifts caused the increase in productivity. Notice that the interrupted time-series design is like a pretest-posttest design in that it includes measurements of the dependent variable both before and after the treatment. It is unlike the pretest-posttest design, however, in that it includes multiple pretest and posttest measurements.

Figure 7.3 shows data from a hypothetical interrupted time-series study. The dependent variable is the number of student absences per week in a research methods course. The treatment is that the instructor begins publicly taking attendance each day so that students know that the instructor is aware of who is present and who is absent. The top panel of  Figure 7.3 shows how the data might look if this treatment worked. There is a consistently high number of absences before the treatment, and there is an immediate and sustained drop in absences after the treatment. The bottom panel of  Figure 7.3 shows how the data might look if this treatment did not work. On average, the number of absences after the treatment is about the same as the number before. This figure also illustrates an advantage of the interrupted time-series design over a simpler pretest-posttest design. If there had been only one measurement of absences before the treatment at Week 7 and one afterward at Week 8, then it would have looked as though the treatment were responsible for the reduction. The multiple measurements both before and after the treatment suggest that the reduction between Weeks 7 and 8 is nothing more than normal week-to-week variation.

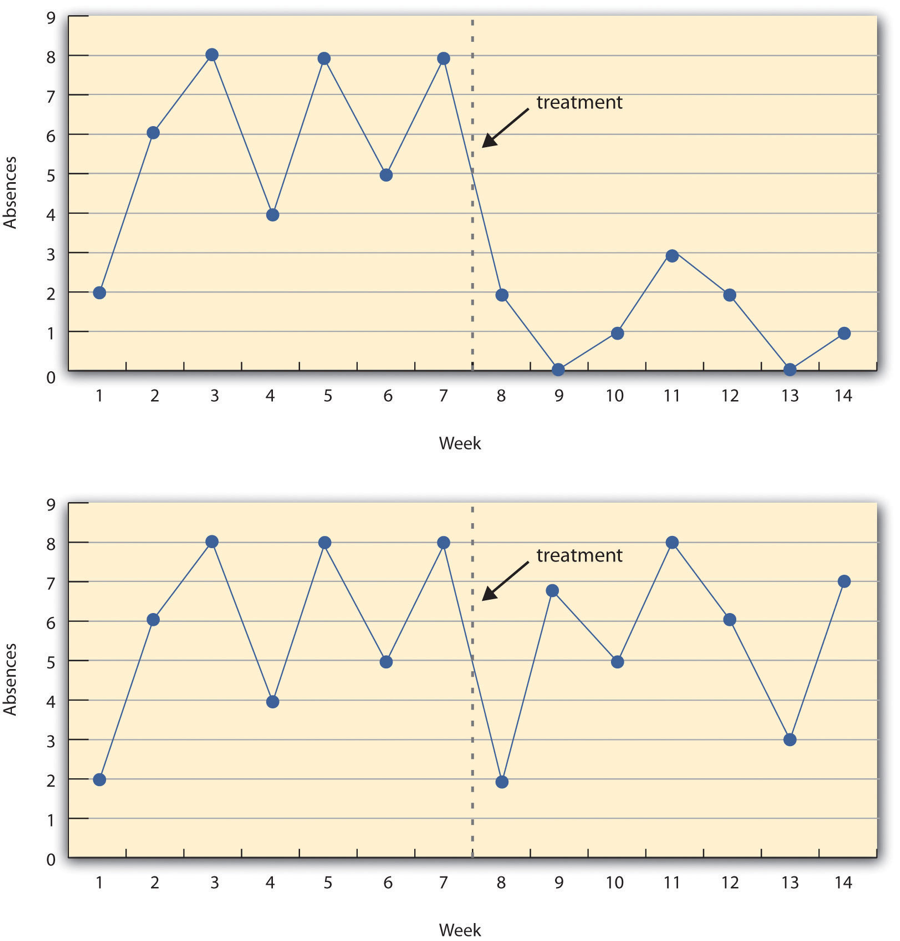
Combination Designs

A type of quasi-experimental design that is generally better than either the nonequivalent groups design or the pretest-posttest design is one that combines elements of both. There is a treatment group that is given a pretest, receives a treatment, and then is given a posttest. But at the same time there is a control group that is given a pretest, does  not  receive the treatment, and then is given a posttest. The question, then, is not simply whether participants who receive the treatment improve but whether they improve  more  than participants who do not receive the treatment.

Imagine, for example, that students in one school are given a pretest on their attitudes toward drugs, then are exposed to an antidrug program, and finally are given a posttest. Students in a similar school are given the pretest, not exposed to an antidrug program, and finally are given a posttest. Again, if students in the treatment condition become more negative toward drugs, this change in attitude could be an effect of the treatment, but it could also be a matter of history or maturation. If it really is an effect of the treatment, then students in the treatment condition should become more negative than students in the control condition. But if it is a matter of history (e.g., news of a celebrity drug overdose) or maturation (e.g., improved reasoning), then students in the two conditions would be likely to show similar amounts of change. This type of design does not completely eliminate the possibility of confounding variables, however. Something could occur at one of the schools but not the other (e.g., a student drug overdose), so students at the first school would be affected by it while students at the other school would not.

Finally, if participants in this kind of design are randomly assigned to conditions, it becomes a true experiment rather than a quasi experiment. In fact, it is the kind of experiment that Eysenck called for—and that has now been conducted many times—to demonstrate the effectiveness of psychotherapy.

Key Takeaways

• Quasi-experimental research involves the manipulation of an independent variable without the random assignment of participants to conditions or orders of conditions. Among the important types are nonequivalent groups designs, pretest-posttest, and interrupted time-series designs.
• Quasi-experimental research eliminates the directionality problem because it involves the manipulation of the independent variable. It does not eliminate the problem of confounding variables, however, because it does not involve random assignment to conditions. For these reasons, quasi-experimental research is generally higher in internal validity than correlational studies but lower than true experiments.
• Practice: Imagine that two professors decide to test the effect of giving daily quizzes on student performance in a statistics course. They decide that Professor A will give quizzes but Professor B will not. They will then compare the performance of students in their two sections on a common final exam. List five other variables that might differ between the two sections that could affect the results.
• regression to the mean
• spontaneous remission

Image Descriptions

Figure 7.3 image description: Two line graphs charting the number of absences per week over 14 weeks. The first 7 weeks are without treatment and the last 7 weeks are with treatment. In the first line graph, there are between 4 to 8 absences each week. After the treatment, the absences drop to 0 to 3 each week, which suggests the treatment worked. In the second line graph, there is no noticeable change in the number of absences per week after the treatment, which suggests the treatment did not work. [Return to Figure 7.3]

• Cook, T. D., & Campbell, D. T. (1979). Quasi-experimentation: Design & analysis issues in field settings . Boston, MA: Houghton Mifflin. ↵
• Posternak, M. A., & Miller, I. (2001). Untreated short-term course of major depression: A meta-analysis of studies using outcomes from studies using wait-list control groups. Journal of Affective Disorders, 66 , 139–146. ↵
• Eysenck, H. J. (1952). The effects of psychotherapy: An evaluation. Journal of Consulting Psychology, 16 , 319–324. ↵
• Smith, M. L., Glass, G. V., & Miller, T. I. (1980). The benefits of psychotherapy . Baltimore, MD: Johns Hopkins University Press. ↵

A between-subjects design in which participants have not been randomly assigned to conditions.

The dependent variable is measured once before the treatment is implemented and once after it is implemented.

A category of alternative explanations for differences between scores such as events that happened between the pretest and posttest, unrelated to the study.

An alternative explanation that refers to how the participants might have changed between the pretest and posttest in ways that they were going to anyway because they are growing and learning.

The statistical fact that an individual who scores extremely on a variable on one occasion will tend to score less extremely on the next occasion.

The tendency for many medical and psychological problems to improve over time without any form of treatment.

A set of measurements taken at intervals over a period of time that are interrupted by a treatment.

Research Methods in Psychology - 2nd Canadian Edition Copyright © 2015 by Paul C. Price, Rajiv Jhangiani, & I-Chant A. Chiang is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Share This Book

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

• Advanced Search
• Journal List
• HHS Author Manuscripts

Quasi-Experimental Designs for Causal Inference

When randomized experiments are infeasible, quasi-experimental designs can be exploited to evaluate causal treatment effects. The strongest quasi-experimental designs for causal inference are regression discontinuity designs, instrumental variable designs, matching and propensity score designs, and comparative interrupted time series designs. This article introduces for each design the basic rationale, discusses the assumptions required for identifying a causal effect, outlines methods for estimating the effect, and highlights potential validity threats and strategies for dealing with them. Causal estimands and identification results are formalized with the potential outcomes notations of the Rubin causal model.

Causal inference plays a central role in many social and behavioral sciences, including psychology and education. But drawing valid causal conclusions is challenging because they are warranted only if the study design meets a set of strong and frequently untestable assumptions. Thus, studies aiming at causal inference should employ designs and design elements that are able to rule out most plausible threats to validity. Randomized controlled trials (RCTs) are considered as the gold standard for causal inference because they rely on the fewest and weakest assumptions. But under certain conditions quasi-experimental designs that lack random assignment can also be as credible as RCTs ( Shadish, Cook, & Campbell, 2002 ).

This article discusses four of the strongest quasi-experimental designs for identifying causal effects: regression discontinuity design, instrumental variable design, matching and propensity score designs, and the comparative interrupted time series design. For each design we outline the strategy and assumptions for identifying a causal effect, address estimation methods, and discuss practical issues and suggestions for strengthening the basic designs. To highlight the design differences, throughout the article we use a hypothetical example with the following causal research question: What is the effect of attending a summer science camp on students’ science achievement?

POTENTIAL OUTCOMES AND RANDOMIZED CONTROLLED TRIAL

Before we discuss the four quasi-experimental designs, we introduce the potential outcomes notation of the Rubin causal model (RCM) and show how it is used in the context of an RCT. The RCM ( Holland, 1986 ) formalizes causal inference in terms of potential outcomes, which allow us to precisely define causal quantities of interest and to explicate the assumptions required for identifying them. RCM considers a potential outcome for each possible treatment condition. For a dichotomous treatment variable (i.e., a treatment and control condition), each subject i has a potential treatment outcome Y i (1), which we would observe if subject i receives the treatment ( Z i = 1), and a potential control outcome Y i (0), which we would observe if subject i receives the control condition ( Z i = 0). The difference in the two potential outcomes, Y i (1)− Y i (0), represents the individual causal effect.

Suppose we want to evaluate the effect of attending a summer science camp on students’ science achievement score. Then each student has two potential outcomes: a potential control score for not attending the science camp, and the potential treatment score for attending the camp. However, the individual causal effects of attending the camp cannot be inferred from data, because the two potential outcomes are never observed simultaneously. Instead, researchers typically focus on average causal effects. The average treatment effect (ATE) for the entire study population is defined as the difference in the expected potential outcomes, ATE = E [ Y i (1)] − E [ Y i (0)]. Similarly, we can also define the ATE for the treated subjects (ATT), ATT = E [ Y i (1) | Z i = 1] − E [ Y (0) | Z i =1]. Although the expectations of the potential outcomes are not directly observable because not all potential outcomes are observed, we nonetheless can identify ATE or ATT under some reasonable assumptions. In an RCT, random assignment establishes independence between the potential outcomes and the treatment status, which allows us to infer ATE. Suppose that students are randomly assigned to the science camp and that all students comply with the assigned condition. Then random assignment guarantees that the camp attendance indicator Z is independent of the potential achievement scores Y i (0) and Y i (1).

The independence assumption allows us to rewrite ATE in terms of observable expectations (i.e., with observed outcomes instead of potential outcomes). First, due to the independence (randomization), the unconditional expectations of the potential outcomes can be expressed as conditional expectations, E [ Y i (1)] = E [ Y i (1) | Z i = 1] and E [ Y i (0)] = E [ Y i (0) | Z i = 0] Second, because the potential treatment outcomes are actually observed for the treated, we can replace the potential treatment outcome with the observed outcome such that E [ Y i (1) | Z i = 1] = E [ Y i | Z i = 1] and, analogously, E [ Y i (0) | Z i = 0] = E [ Y i | Z i = 0] Thus, the ATE is expressible in terms of observable quantities rather than potential outcomes, ATE = E [ Y i (1)] − E [ Y i (0)] = E [ Y i | Z i = 1] – E [ Y i | Z i = 0], and we that say ATE is identified.

This derivation also rests on the stable-unit-treatment-value assumption (SUTVA; Imbens & Rubin, 2015 ). SUTVA is required to properly define the potential outcomes, that is, (a) the potential outcomes of a subject depend neither on the assignment mode nor on other subjects’ treatment assignment, and (b) there is only one unique treatment and one unique control condition. Without further mentioning, we assume SUTVA for all quasi-experimental designs discussed in this article.

REGRESSION DISCONTINUITY DESIGN

Due to ethical or budgetary reasons, random assignment is often infeasible in practice. Nonetheless, researchers may sometimes still retain full control over treatment assignment as in a regression discontinuity (RD) design where, based on a continuous assignment variable and a cutoff score, subjects are deterministically assigned to treatment conditions.

Suppose that the science camp is a remedial program and only students whose grade point average (GPA) score is less than or equal to 2.0 are eligible to participate. Figure 1 shows a scatterplot of hypothetical data where the x-axis represents the assignment variable ( GPA ) and the y -axis the outcome ( Science Score ). All subjects with a GPA score below the cutoff attended the camp (circles), whereas all subjects scoring above the cutoff do not attend (squares). Because all low-achieving students are in the treatment group and all high-achieving students in the control group, their respective GPA distributions do not overlap, not even at the cutoff. This lack of overlap complicates the identification of a causal effect because students in the treatment and control group are not comparable at all (i.e., they have a completely different distribution of the GPA scores).

A hypothetical example of regression discontinuity design. Note . GPA = grade point average.

One strategy of dealing with the lack of overlap is to rely on the linearity assumption of regression models and to extrapolate into areas of nonoverlap. However, if the linear models do not correctly specify the functional form, the resulting ATE estimate is biased. A safer strategy is to evaluate the treatment effect only at the cutoff score where treatment and control cases almost overlap, and thus functional form assumptions and extrapolation are almost no longer needed. Consider the treatment and control students that score right at the cutoff or just above it. Students with a GPA score of 2.0 participate in the science camp and students with a GPA score of 2.1 are in the control condition (the status quo condition or a different camp). The two groups of students are essentially equivalent because the difference in their GPA scores is negligibly small (2.1 − 2.0 = .1) and likely due to random chance (measurement error) rather than a real difference in ability. Thus, in the very close neighborhood around the cutoff score, the RD design is equivalent to an RCT; therefore, the ATE at the cutoff (ATEC) is identified.

CAUSAL ESTIMAND AND IDENTIFICATION

ATEC is defined as the difference in the expected potential treatment and control outcomes for the subjects scoring exactly at the cutoff: ATEC = E [ Y i (1) | A i = a c ] − E [ Y i (0) | A i = a c ], where A denotes assignment variable and a c the cutoff score. Because we observe only treatment subjects and not control subjects right at the cutoff, we need two assumptions in order to identify ATEC ( Hahn, Todd, & van Klaauw, 2001 ): (a) the conditional expectations of the potential treatment and control outcomes are continuous at the cutoff ( continuity ), and (b) all subjects comply with treatment assignment ( full compliance ).

The continuity assumption can be expressed in terms of limits as lim a ↓ a C E [ Y i ( 1 ) | A i = a ] = E [ Y i ( 1 ) | A i = a ] = lim a ↑ a C E [ Y i ( 1 ) | A i = a ] and lim a ↓ a C E [ Y i ( 0 ) | A i = a ] = E [ Y i ( 0 ) | A i = a ] = lim a ↑ a C E [ Y i ( 0 ) | A i = a ] . Thus, we can rewrite ATEC as the difference in limits, A T E C = lim a ↑ a C E [ Y i ( 1 ) | A i = a c ] − lim a ↓ a C E [ Y i ( 0 ) | A i = a c ] , which solves the issue that no control subjects are observed directly at the cutoff. Then, by the full compliance assumption, the potential treatment and control outcomes can be replaced with the observed outcomes such that A T E C = lim a ↑ a C E [ Y i | A i = a c ] − lim a ↓ a C E [ Y i | A i = a c ] is identified at the cutoff (i.e., ATEC is now expressed in terms of observable quantities). The difference in the limits represents the discontinuity in the mean outcomes exactly at the cutoff ( Figure 1 ).

Estimating ATEC

ATEC can be estimated with parametric or nonparametric regression methods. First, consider the parametric regression of the outcome Y on the treatment Z , the cutoff-centered assignment variable A − a c , and their interaction: Y = β 0 + β 1 Z + β 2 ( A − a c ) + β 3 ( Z × ( A − a c )) + e . If the model correctly specifies the functional form, then β ^ 1 is an unbiased estimator for ATEC. In practice, an appropriate model specification frequently involves also quadratic and cubic terms of the assignment variable plus their interactions with the treatment indicator.

To avoid overly strong functional form assumptions, semiparametric or nonparametric regression methods like generalized additive models or local linear kernel regression can be employed ( Imbens & Lemieux, 2008 ). These methods down-weight or even discard observations that are not in the close neighborhood around the cutoff. The R packages rdd ( Dimmery, 2013 ) and rdrobust ( Calonico, Cattaneo, & Titiunik, 2015 ), or the command rd in STATA ( Nichols, 2007 ) are useful for estimation and diagnostic purposes.

Practical Issues

A major validity threat for RD designs is the manipulation of the assignment score around the cutoff, which directly results in a violation of the continuity assumption ( Wong et al., 2012 ). For instance, if a teacher knows the assignment score in advance and he wants all his students to attend the science camp, the teacher could falsely report a GPA score of 2.0 or below for the students whose actual GPA score exceeds the cutoff value.

Another validity threat is noncompliance, meaning that subjects assigned to the control condition may cross over to the treatment and subjects assigned to the treatment do not show up. An RD design with noncompliance is called a fuzzy RD design (instead of a sharp RD design with full compliance). A fuzzy RD design still allows us to identify the intention-to-treat effect or the local average treatment effect at the cutoff (LATEC). The intention-to-treat effect refers to the effect of treatment assignment rather than the actual treatment receipt. LATEC estimates ATEC for the subjects who comply with treatment assignment. LATEC is identified if one uses the assignment status as an instrumental variable for treatment receipt (see the upcoming Instrumental Variable section).

Finally, generalizability and statistical power are often mentioned as major disadvantages of RD designs. Because RD designs identify the treatment effect only at the cutoff, ATEC estimates are not automatically generalizable to subjects scoring further away from the cutoff. Statistical power for detecting a significant effect is an issue because the lack of overlap on the assignment variable results in increased standard errors. With semi- or nonparametric regression methods, power further diminishes.

Strengthening RD Designs

To avoid systematic manipulations of the assignment variable, it is desirable to conceal the assignment rule from study participants and administrators. If the assignment rule is known to them, manipulations can hardly be ruled out, particularly when the stakes are high. Researchers can use the McCrary test ( McCrary, 2008 ) to check for potential manipulations. The test investigates whether there is a discontinuity in the distribution of the assignment variable right at the cutoff. Plotting baseline covariates against the assignment variable, and regressing the covariates on the assignment variable and the treatment indicator also help in detecting potential discontinuities at the cutoff.

The RD design’s validity can be increased by combining the basic RD design with other designs. An example is the tie-breaking RD design, which uses two cutoff scores. Subjects scoring between the two cutoff scores are randomly assigned to treatment conditions, whereas subjects scoring outside the cutoff interval receive the treatment or control condition according to the RD assignment rule ( Black, Galdo & Smith, 2007 ). This design combines an RD design with an RCT and is advantageous with respect to the correct specification of the functional form, generalizability, and statistical power. Similar benefits can be obtained by adding pretest measures of the outcome or nonequivalent comparison groups ( Wing & Cook, 2013 ).

Imbens and Lemieux (2008) and Lee and Lemieux (2010) provided comprehensive introductions to RD designs. Lee and Lemieux also summarized many applications from economics. Angrist and Lavy (1999) applied the design to investigate the effect of class size on student achievement.

INSTRUMENTAL VARIABLE DESIGN

In practice, researchers often have no or only partial control over treatment selection. In addition, they might also lack reliable knowledge of the selection process. Nonetheless, even with limited control and knowledge of the selection process it is still possible to identify a causal treatment effect if an instrumental variable (IV) is available. An IV is an exogenous variable that is related to the treatment but is completely unrelated to the outcome, except via treatment. An IV design requires researchers either to create an IV at the design stage (as in an encouragement design; see next) or to find an IV in the data set at hand or a related data base.

Consider the science camp example, but instead of random or deterministic treatment assignment, students decide on their own or together with their parents whether to attend the camp. Many factors may determine the decision, for instance, students’ science ability and motivation, parents’ socioeconomic status, or the availability of public transportation for the daily commute to the camp. Whereas the first three variables are presumably also related to the science outcome, public transportation might be unrelated to the science score (except via camp attendance). Thus, the availability of public transportation may qualify as an IV. Figure 2 illustrates such IV design: Public transportation (IV) directly affects camp attendance but has no direct or indirect effect on science achievement (outcome) other than through camp attendance (treatment). The question mark represents unknown or unobserved confounders, that is, variables that simultaneously affect both camp attendance and science achievement. The IV design allows us to identify a causal effect even if some or all confounders are unknown or unobserved.

A diagram of an example of instrumental variable design.

The strategy for identifying a causal effect is based on exploiting the variation in the treatment variable explained by IV. In Figure 2 , the total variation in the treatment consists of (a) the variation induced by the IV and (b) the variation induced by confounders (question mark) and other exogenous variables (not shown in the figure). The identification of the camp’s effect requires us to isolate the treatment variation that is related to public transportation (IV), and then to use the isolated variation to investigate the camp’s effect on the science score. Because we exploit the treatment variation exclusively induced by the IV but ignore the variation induced by unobserved or unknown confounders, the IV design identifies the ATE for the sub-population of compliers only. In our example, the compliers are the students who attend the camp because public transportation is available and do not attend because it is unavailable. For students whose parents always use their own car to drop them off and pick them up at the camp location, we cannot infer the causal effect, because their camp attendance is completely unrelated to the availability of public transportation.

Causal Estimand and Identification

The complier average treatment effect (CATE) is defined as the expected difference in potential outcomes for the sub-population of compliers: CATE = E [ Y i (1) | Complier ] − E [ Y i (0) | Complier ] = τ C .

Identification requires us to distinguish between four latent groups: compliers (C), who attend the camp if public transportation is available but do not attend if unavailable; always-takers (A), who always attend the camp regardless of whether or not public transportation is available; never-takers (N), who never attend the camp regardless of public transportation; and defiers (D), who do not attend if public transportation is available but attend if unavailable. Because group membership is unknown, it is impossible to directly infer CATE from the data of compliers. However, CATE is identified from the entire data set if (a) the IV is predictive of the treatment ( predictive first stage ), (b) the IV is unrelated to the outcome except via treatment ( exclusion restriction ), and (c) no defiers are present ( monotonicity ; Angrist, Imbens, & Rubin, 1996 ; see Steiner, Kim, Hall, & Su, 2015 , for a graphical explanation).

First, notice that the IV’s effects on the treatment (γ) and the outcome (δ) are directly identified from the observed data because the IV’s relation with the treatment and outcome is unconfounded. In our example ( Figure 2 ), γ denotes the effect of public transportation on camp attendance and δ the indirect effect of public transportation on the science score. Both effects can be written as weighted averages of the corresponding group-specific effects ( γ C , γ A , γ N , γ D and δ C , δ A , δ N , δ D for compliers, always-takers, never-takers, and defiers, respectively): γ = p ( C ) γ C + p ( A ) γA + p ( N ) γ N + p ( D ) γ D and δ = p ( C ) δ C + p ( A ) δ A + p ( N ) δ N + p ( D ) δ D where p (.) represents the portion of the respective latent group in the population and p ( C ) + p ( A ) + p ( N ) + p ( D ) = 1. Because the treatment choice of always-takers and never-takers is entirely unaffected by the instrument, the IV’s effect on the treatment is zero, γ A = γ N = .0, and together with the exclusion restriction , we also know δ A = δ N = 0, that is, the IV has no effect on the outcome. If no defiers are present, p ( D ) = 0 ( monotonicity ), then the IV’s effects on the treatment and outcome simplify to γ = p ( C ) γC and δ = p ( C ) δC , respectively. Because δ C = γ C τ C and γ ≠ 0 ( predictive first stage ), the ratio of the observable IV effects, γ and δ, identifies CATE: δ γ = p ( C ) γ C τ C p ( C ) γ C = τ C .

Estimating CATE

A two-stage least squares (2SLS) regression is typically used for estimating CATE. In the first stage, treatment Z is regressed on the IV, Z = β 0 + β 1 IV + e . The linear first-stage model applies with a dichotomous treatment variable (linear probability model). The second stage then regresses the outcome Y on the predicted values Z ^ from the first stage model, Y = π 0 + π 1 Z ^ + r , where π ^ 1 is the CATE estimator. The two stages are automatically performed by the 2SLS procedure, which also provides an appropriate standard error for the effect estimate. The STATA commands ivregress and ivreg2 ( Baum, Schaffer, & Stillman, 2007 ) or the sem package in R ( Fox, 2006 ) perform the 2SLS regression.

One challenge in implementing an IV design is to find a valid instrument that satisfies the assumptions just discussed. In particular, the exclusion restriction is untestable and frequently hard to defend in practice. In our example, if high-income families live in suburban areas with bad public transportation connections, then the availability of the public transportation is likely related to the science score via household income (or socioeconomic status). Although conditioning on the observed household income can transform public transportation into a conditional IV (see next), one can frequently come up with additional scenarios that explains why the IV is related to the outcome and thus violates the exclusion restriction.

Another issue arises from “weak” IVs that are only weakly related to treatment. Weak IVs cause efficiency problems ( Wooldridge, 2012 ). If the availability of public transportation barely affects camp attendance because most parents give their children a ride anyway, the IV’s effect on the treatment ( γ ) is close to zero. Because γ ^ is the denominator in the CATE estimator, τ ^ C = δ ^ / γ ^ , an imprecisely estimated γ ^ results in a considerable over- or underestimation of CATE. Moreover, standard errors will be large.

One also needs to keep in mind that the substantive meaning of CATE depends on the chosen IV. Consider two slightly different IVs with respect to public transportation: the availability of (a) a bus service and (b) subway service. For the first IV, the complier population consists of students who choose to (not) attend the camp depending on the availability of a bus service. For the second IV, the complier population refers to the availability of a subway service. Because the two complier populations are very likely different from each other (students who are willing to take the subway might not be willing to take the bus), the corresponding CATEs refer to different subpopulations.

Strengthening IV Designs

Given the challenges in identifying a valid instrument from observed data, researchers should consider creating an IV at the design stage of a study. Although it might be impossible to directly assign subjects to treatment conditions, one might still be able to encourage participants to take the treatment. Subjects are randomly encouraged to sign up for treatment, but whether they actually comply with the encouragement is entirely their own decision ( Imai et al., 2011 ). Random encouragement qualifies as an IV because it very likely meets the exclusion restriction. For example, instead of collecting data on public transportation, researchers may advertise and recommend the science camp in a letter to the parents of a randomly selected sample of students.

With observational data it is hard to identify a valid IV because covariates that strongly predict the treatment are usually also related to the outcome. However, these covariates can still qualify as an IV if they affect the outcome only indirectly via other observed variables. Such covariates can be used as conditional IVs, that is, they meet the IV requirements conditional on the observed variables ( Brito & Pearl, 2002 ). Assume the availability of public transportation (IV) is associated with the science score via household income. Then, controlling for the reliably measured household income in both stages of the 2SLS analysis blocks the IV’s relation to the science score and turns public transportation into a conditional IV. However, controlling for a large set of variables does not guarantee that the exclusion restriction is more likely met. It may even result in more bias as compared to an IV analysis with fewer covariates ( Ding & Miratrix, 2015 ; Steiner & Kim, in press ). The choice of a valid conditional IV requires researchers to carefully select the control variables based on subject-matter theory.

The seminal article by Angrist et al. (1996) provides a thorough discussion of the IV design, and Steiner, Kim, et al. (2015 ) proved the identification result using graphical models. Excellent introductions to IV designs can be found in Angrist and Pischke (2009 , 2015) . Angrist and Krueger (1992) is an example of a creative application of the design with birthday as the IV. For encouragement designs, see Holland (1988) and Imai et al. (2011) .

MATCHING AND PROPENSITY SCORE DESIGN

This section considers quasi-experimental designs in which researchers lack control over treatment selection but have good knowledge about the selection mechanism or at least the confounders that simultaneously determine the treatment selection and the outcome. Due to self or third-person selection of subjects into treatment, the resulting treatment and control groups typically differ in observed but also unobserved baseline covariates. If we have reliable measures of all confounding covariates, then matching or propensity score (PS) designs balance groups on observed baseline covariates and thus enable the identification of causal effects ( Imbens & Rubin, 2015 ). Regression analysis and the analysis of covariance can also remove the confounding bias, but because they rely on functional form assumptions and extrapolation we discuss only nonparametric matching and PS designs.

Suppose that students decide on their own whether to attend the science camp. Although many factors can affect students’ decision, teachers with several years of experience of running the camp may know that selection is mostly driven by students’ science ability, liking of science, and their parents’ socioeconomic status. If all the selection-relevant factors that also affect the outcome are known, the question mark in Figure 2 can be replaced by the known confounding covariates.

Given the set of confounding covariates, causal inference with matching or PS designs is straightforward, at least theoretically. The basic one-to-one matching design matches each treatment subject to a control subject that is equivalent or at least very similar in observed covariates. To illustrate the idea of matching, consider a camp attendee with baseline measures of 80 on the science pre-test, 6 on liking science, and 50 on the socioeconomic status. Then a multivariate matching strategy tries to find a nonattendee with exactly the same or at least very similar baseline measures. If we succeed in finding close matches for all camp attendee, the matched samples of attendees and nonattendees will have almost identical covariate distributions.

Although multivariate matching works well when the number of confounders is small and the pool of control subjects is large relative to the number of treatment subjects, it is usually difficult to find close matches with a large set of covariates or a small pool of control subjects. Matching on the PS helps to overcome this issue because the PS is a univariate score computed from the observed covariates ( Rosenbaum & Rubin, 1983 ). The PS is formally defined as the conditional probability of receiving the treatment given the set of observed covariates X : PS = Pr( Z = 1 | X ).

Matching and PS designs usually investigate ATE = E [ Y i (1)] − E [ Y i (0)] or ATT = E [ Y i (1) | Z i = 1] – E [ Y i (0) | Z i = 1]. Both causal effects are identified if (a) the potential outcomes are statistically independent of the treatment indicator given the set of observed confounders X , { Y (1), Y (0)}⊥ Z | X ( unconfoundedness ; ⊥ denotes independence), and (b) the treatment probability is strictly between zero and one, 0 < Pr( Z = 1 | X ) < 1 ( positivity ).

By the positivity assumption we get E [ Y i (1)] = E X [ E [ Y i (1) | X ]] and E [ Y i (0)] = E X [ E [ Y i (0) | X ]]. If the unconfoundedness assumption holds, we can write the inner expectations as E [ Y i (1) | X ] = E [ Y i (1) | Z i =1; X ] and E [ Y i (0) | X ] = E [ Y i (0) | Z i = 0; X ]. Finally, because the treatment (control) outcomes of the treatment (control) subjects are actually observed, ATE is identified because it can be expressed in terms of observable quantities: ATE = E X [ E [ Y i | Z i = 1; X ]] – E X [ E [ Y i | Z i = 0; X ]]. The same can be shown for ATT. The unconfoundedness and positivity assumption are frequently referred to jointly as the strong ignorability assumption. Rosenbaum and Rubin (1983) proved that if the assignment is strongly ignorable given X , then it is also strongly ignorable given the PS alone.

Estimating ATE and ATT

Matching designs use a distance measure for matching each treatment subject to the closest control subject. The Mahalanobis distance is usually used for multivariate matching and the Euclidean distance on the logit of the PS for PS matching. Matching strategies differ with respect to the matching ratio (one-to-one or one-to-many), replacement of matched subjects (with or without replacement), use of a caliper (treatment subjects that do not have a control subject within a certain threshold remain unmatched), and the matching algorithm (greedy, genetic, or optimal matching; Sekhon, 2011 ; Steiner & Cook, 2013 ). Because we try to find at least one control subject for each treatment subject, matching estimators typically estimate ATT. Once treatment and control subjects are matched, ATT is computed as the difference in the mean outcome of the treatment and control group. An alternative matching strategy that allows for estimating ATE is full matching, which stratifies all subjects into the maximum number of strata, where each stratum contains at least one treatment and one control subject ( Hansen, 2004 ).

The PS can also be used for PS stratification and inverse-propensity weighting. PS stratification stratifies the treatment and control subjects into at least five strata and estimates the treatment effect within each stratum. ATE or ATT is then obtained as the weighted average of the stratum-specific treatment effects. Inverse-propensity weighting follows the same logic as inverse-probability weighting in survey research ( Horvitz & Thompson, 1952 ) and requires the computation of weights that refer to either the overall population (ATE) or the population of treated subjects only (ATT). Given the inverse-propensity weights, ATE or ATT is usually estimated via weighted least squares regression.

Because the true PSs are unknown, they need to be estimated from the observed data. The most common method for estimating the PS is logistic regression, which regresses the binary treatment indicator Z on predictors of the observed covariates. The PS model is specified according to balance criteria (instead of goodness of fit criteria), that is, the estimated PSs should remove all baseline differences in observed covariates ( Imbens & Rubin, 2015 ). The predicted probabilities from the PS model represent the estimated PSs.

All three PS designs—matching, stratification, and weighting—can benefit from additional covariance adjustments in an outcome regression. That is, for the matched, stratified or weighted data, the outcome is regressed on the treatment indicator and the additional covariates. Combining the PS design with a covariance adjustment gives researchers two chances to remove the confounding bias, by correctly specifying either the PS model or the outcome model. These combined methods are said to be doubly robust because they are robust against either the misspecification of the PS model or the misspecification of the outcome model ( Robins & Rotnitzky, 1995 ). The R packages optmatch ( Hansen & Klopfer, 2006 ) and MatchIt ( Ho et al., 2011 ) and the STATA command teffects , in particular teffects psmatch ( StataCorp, 2015 ), can be useful for matching or PS analyses.

The most challenging issue with matching and PS designs is the selection of covariates for establishing unconfoundedness. Ideally, subject-matter theory about the selection process and the outcome-generating model is used for selecting a set of covariates that removes all the confounding ( Pearl, 2009 ). If strong subject-matter theories are not available, selecting the right covariates is difficult. In the hope to remove a major part of the confounding bias—if not all of it—a frequently applied strategy is to match on as many covariates as possible. However, recent literature shows that thoughtless inclusion of covariates may increase rather than reduce the confounding bias ( Pearl, 2010 ; Steiner & Kim, in press). The risk of increasing bias can be reduced if the observed covariates cover a broad range of heterogeneous construct domains, including at least one reliable pretest measure of the outcome ( Steiner, Cook, et al., 2015 ). Besides having the right covariates, they also need to be reliably measured. The unreliable measurement of confounding covariates has a similar effect as the omission of a confounder: It results in a violation of the unconfoundedness assumption and thus in a biased effect estimate ( Steiner, Cook, & Shadish, 2011 ; Steiner & Kim, in press ).

Even if the set of reliably measured covariates establishes unconfoundedness, we still need to correctly specify the functional form of the PS model. Although parametric models like logistic regression, including higher order terms, might frequently approximate the correct functional form, they still rely on the linearity assumption. The linearity assumption can be relaxed if one estimates the PS with statistical learning algorithms like classification trees, neural networks, or the LASSO ( Keller, Kim, & Steiner, 2015 ; McCaffrey, Ridgeway, & Morral, 2004 ).

Strengthening Matching and PS Designs

The credibility of matching and PS designs heavily relies on the unconfoundedness assumption. Although empirically untestable, there are indirect ways for assessing unconfoundedness. First, unaffected (nonequivalent) outcomes that are known to be unaffected by the treatment can be used ( Shadish et al., 2002 ). For instance, we may expect that attendance in the science camp does not significantly affect the reading score. Thus, if we observe a significant group difference in the reading score after the PS adjustment, bias due to unobserved confounders (e.g., general intelligence) is still likely. Second, adding a second but conceptually different control group allows for a similar test as with the unaffected outcome ( Rosenbaum, 2002 ).

Because researchers rarely know whether the unconfoundedness assumption is actually met with the data at hand, it is important to assess the effect estimate’s sensitivity to potentially unobserved confounders. Sensitivity analyses investigate how strongly an estimate’s magnitude and significance changes if a confounder of a certain strength would have been omitted from the analyses. Causal conclusions are much more credible if the effect’s direction, magnitude, and significance is rather insensitive to omitted confounders ( Rosenbaum, 2002 ). However, despite the value of sensitivity analyses, they are not informative about whether hidden bias is actually present.

Schafer and Kang (2008) and Steiner and Cook (2013) provided a comprehensive introduction. Rigorous formalization and technical details of PS designs can be found in Imbens and Rubin (2015) . Rosenbaum (2002) discussed many important design issues in these designs.

COMPARATIVE INTERRUPTED TIME SERIES DESIGN

The designs discussed so far require researchers to have either full control over treatment assignment or reliable knowledge of the exogenous (IV) or endogenous part of the selection mechanism (i.e., the confounders). If none of these requirements are met, a comparative interrupted time series (CITS) design might be a viable alternative if (a) multiple measurements of the outcome ( time series ) are available for both the treatment and a comparison group and (b) the treatment group’s time series has been interrupted by an intervention.

Suppose that all students of one class in a school (say, an advanced science class) attend the camp, whereas all students of another class in the same school do not attend. Also assume that monthly measures of science achievement before and after the science camp are available. Figure 3 illustrates such a scenario where the x -axis represents time in Months and the y -axis the Science Score (aggregated at the class level). The filled symbols indicate the treatment group (science camp), open symbols the comparison group (no science camp). The science camp intervention divides both time series into a preintervention time series (circles) and a postintervention time series (squares). The changes in the levels and slopes of the pre- and postintervention regression lines represent the camp’s impact but possibly also the effect of other events that co-occur with the intervention. The dashed lines extrapolate the preintervention growth curves into the postintervention period, and thus represent the counterfactual situation where the intervention but also other co-occurring events are absent.

A hypothetical example of comparative interrupted time series design.

The strength of a CITS design is its ability to discriminate between the intervention’s effect and the effects of co-occurring events. Such events might be other potentially competing interventions (history effects) or changes in the measurement of the outcome (instrumentation), for instance. If the co-occurring events affect the treatment and comparison group to the same extent, then subtracting the changes in the comparison group’s growth curve from the changes in the treatment group’s growth curve provides a valid estimate of the intervention’s impact. Because we investigate the difference in the changes (= differences) of the two growth curves, the CITS design is a special case of the difference-in-differences design ( Somers et al., 2013 ).

Assume that a daily TV series about Albert Einstein was broadcast in the evenings of the science camp week and that students of both classes were exposed to the same extent to the TV series. It follows that the comparison group’s change in the growth curve represents the TV series’ impact. The comparison group’s time series in Figure 3 indicates that the TV series might have had an immediate impact on the growth curve’s level but almost no effect on the slope. On the other hand, the treatment group’s change in the growth curve is due to both the science camp and the TV series. Thus, in differencing out the TV series’ effect (estimated from the comparison group) we can identify the camp effect.

Let t c denote the time point of the intervention, then the intervention’s effect on the treated (ATT) at a postintervention time point t ≥ t c is defined as τ t = E [ Y i t T ( 1 ) ] − E [ Y i t T ( 0 ) ] , where Y i t T ( 0 ) and Y i t T ( 1 ) are the potential control and treatment outcomes of subject i in the treatment group ( T ) at time point t . The time series of the expected potential outcomes can be formalized as sum of nonparametric but additive time-dependent functions. The treatment group’s expected potential control outcome can be represented as E [ Y i t T ( 0 ) ] = f 0 T ( t ) + f E T ( t ) , where the control function f 0 T ( t ) generates the expected potential control outcomes in absence of any interventions ( I ) or co-occurring events ( E ), and the event function f E T ( t ) adds the effects of co-occurring events. Similarly, the expected potential treatment outcome can be written as E [ Y i t T ( 1 ) ] = f 0 T ( t ) + f E T ( t ) + f I T ( t ) , which adds the intervention’s effect τ t = f I T ( t ) to the control and event function. In the absence of a comparison group, we can try to identify the impact of the intervention by comparing the observable postintervention outcomes to the extrapolated outcomes from the preintervention time series (dashed line in Figure 3 ). Extrapolation is necessary because we do not observe any potential control outcomes in the postintervention period (only potential treatment outcomes are observed). Let f ^ 0 T ( t ) denote the parametric extrapolation of the preintervention control function f 0 T ( t ) , then the observable pre–post-intervention difference ( PP T ) in the expected control outcome is P P t T = f 0 T ( t ) + f E T ( t ) + f I T ( t ) − f ^ 0 T ( t ) = f I T ( t ) + ( f 0 T ( t ) − f ^ 0 T ( t ) ) + f E T ( t ) . Thus, in the absence of a comparison group, ATT is identified (i.e., P P t T = f I T ( t ) = τ t ) only if the control function is correctly specified ( f 0 T ( t ) = f ^ 0 T ( t ) ) and if no co-occurring events are present ( f E T ( t ) = 0 ).

The comparison group in a CITS design allows us to relax both of these identifying assumptions. In order to see this, we first define the expected control outcomes of the comparison group ( C ) as a sum of two time-dependent functions as before: E [ Y i t C ( 0 ) ] = f 0 C ( t ) + f E C ( t ) . Then, in extrapolating the comparison group’s preintervention function into the postintervention period, f ^ 0 C ( t ) , we can compute the pre–post-intervention difference for the comparison group: P P t C = f 0 C ( t ) + f E C ( t ) − f ^ 0 C ( t ) = f E C ( t ) + ( f 0 C ( t ) − f ^ 0 C ( t ) ) If the control function is correctly specified f 0 C ( t ) = f ^ 0 C ( t ) , the effect of co-occurring events is identified P P t C = f E C ( t ) . However, we do not necessarily need a correctly specified control function, because in a CITS design we focus on the difference in the treatment and comparison group’s pre–post-intervention differences, that is, P P t T − P P t C = f I T ( t ) + { ( f 0 T ( t ) − f ^ 0 T ( t ) ) − ( f 0 C ( t ) − f ^ 0 C ( t ) ) } + { f E T ( t ) − f E C ( t ) } . Thus, ATT is identified, P P t T − P P t C = f I T ( t ) = τ t , if (a) both control functions are either correctly specified or misspecified to the same additive extent such that ( f 0 T ( t ) − f ^ 0 T ( t ) ) = ( f 0 C ( t ) − f ^ 0 C ( t ) ) ( no differential misspecification ) and (b) the effect of co-occurring events is identical in the treatment and comparison group, f E T ( t ) = f E C ( t ) ( no differential event effects ).

Estimating ATT

CITS designs are typically analyzed with linear regression models that regress the outcome Y on the centered time variable ( T – t c ), the intervention indicator Z ( Z = 0 if t < t c , otherwise Z = 1), the group indicator G ( G = 1 for the treatment group and G = 0 for the control group), and the corresponding two-way and three-way interactions:

Depending on the number of subjects in each group, fixed or random effects for the subjects are included as well (time fixed or random effect can also be considered). β ^ 5 estimates the intervention’s immediate effect at the onset of the intervention (change in intercept) and β ^ 7 the intervention’s effect on the growth rate (change in slope). The inclusion of dummy variables for each postintervention time point (plus their interaction with the intervention and group indicators) would allow for a direct estimation of the time-specific effects. If the time series are long enough (at least 100 time points), then a more careful modeling of the autocorrelation structure via time series models should be considered.

Compared to other designs, CITS designs heavily rely on extrapolation and thus on functional form assumptions. Therefore, it is crucial that the functional forms of the pre- and postintervention time series (including their extrapolations) are correctly specified or at least not differentially misspecified. With short time series or measurement points that inadequately capture periodical variations, the correct specification of the functional form is very challenging. Another specification aspect concerns serial dependencies among the data points. Failing to model serial dependencies can bias effect estimates and their standard errors such that significance tests might be misleading. Accounting for serial dependencies requires autoregressive models (e.g., ARIMA models), but the time series should have at least 100 time points ( West, Biesanz, & Pitts, 2000 ). Standard fixed effects or random effects models deal at least partially with the dependence structure. Robust standard errors (e.g., Huber-White corrected ones) or the bootstrap can also be used to account for dependency structures.

Events that co-occur with the intervention of interest, like history or instrumentation effects, are a major threat to the time series designs that lack a comparison group ( Shadish et al., 2002 ). CITS designs are rather robust to co-occurring events as long as the treatment and comparison groups are affected to the same additive extent. However, there is no guarantee that both groups are exposed to the same events and affected to the same extent. For example, if students who do not attend the camp are less likely to watch the TV series, its effect cannot be completely differenced out (unless the exposure to the TV series is measured). If one uses aggregated data like class or school averages of achievement scores, then differential compositional shifts over time can also invalidate the CITS design. Compositional shifts occur due to dropouts or incoming subjects over time.

Strengthening CITS Designs

If the treatment and comparison group’s preintervention time series are very different (different levels and slopes), then the assumption that history or instrumentation threats affect both groups to the same additive extent may not hold. Matching treatment and comparison subjects prior to the analysis can increase the plausibility of this assumption. Instead of using all nonparticipating students of the comparison class, we may select only those students who have a similar level and growth in the preintervention science scores as the students participating in the camp. We can also match on additional covariates like socioeconomic status or motivation levels. Multivariate or PS matching can be used for this purpose. If the two groups are similar, it is more likely that they are affected by co-occurring events to the same extent.

As with the matching and PS designs, using an unaffected outcome in CITS designs helps to probe the untestable assumptions ( Coryn & Hobson, 2011 ; Shadish et al., 2002 ). For instance, we might expect that attending the science camp does not affect students’ reading scores but that some validity threats (e.g., attrition) operate on both the reading and science outcome. If we find a significant camp effect on the reading score, the validity of the CITS design for evaluating the camp’s impact on the science score is in doubt.

Another strategy to avoid validity threats is to control the time point of the intervention if possible. Researchers can wait with the implementation of the treatment until they have enough preintervention measures for reliably estimating the functional form. They can also choose to intervene when threats to validity are less likely (avoiding the week of the TV series). Control over the intervention also allows researchers to introduce and remove the treatment in subsequent time intervals, maybe even with switching replications between two (or more) groups. If the treatment is effective, we expect that the pattern of the intervention scheme is directly reflected in the time series of the outcome (for more details, see Shadish et al., 2002 ; for the literature on single case designs, see Kazdin, 2011 ).

A comprehensive introduction to CITS design can be found in Shadish et al. (2002) , which also addresses many classical applications. For more technical details of its identification, refer to Lechner (2011) . Wong, Cook, and Steiner (2009) evaluated the effect of No Child Left Behind using a CITS design.

CONCLUDING REMARKS

This article discussed four of the strongest quasi-experimental designs for causal inference when randomized experiments are not feasible. For each design we highlighted the identification strategies and the required assumptions. In practice, it is crucial that the design assumptions are met, otherwise biased effect estimates result. Because most important assumptions like the exclusion restriction or the unconfoundedness assumption are not directly testable, researchers should always try to assess their plausibility via indirect tests and investigate the effect estimates’ sensitivity to violations of these assumptions.

Our discussion of RD, IV, PS, and CITS designs made it also very clear that, in comparison to RCTs, quasi-experimental designs rely on more or stronger assumptions. With prefect control over treatment assignment and treatment implementation (as in an RCT), causal inference is warranted by a minimal set of assumptions. But with limited control over and knowledge about treatment assignment and implementation, stronger assumptions are required and causal effects might be identifiable only for local subpopulations. Nonetheless, observational data sometimes meet the assumptions of a quasi-experimental design, at least approximately, such that causal conclusions are credible. If so, the estimates of quasi-experimental designs—which exploit naturally occurring selection processes and real-world implementations of the treatment—are frequently better generalizable than the results from a controlled laboratory experiment. Thus, if external validity is a major concern, the results of randomized experiments should always be complemented by findings from valid quasi-experiments.

• Angrist JD, Imbens GW, & Rubin DB (1996). Identification of causal effects using instrumental variables . Journal of the American Statistical Association , 91 , 444–455. [ Google Scholar ]
• Angrist JD, & Krueger AB (1992). The effect of age at school entry on educational attainment: An application of instrumental variables with moments from two samples . Journal of the American Statistical Association , 87 , 328–336. [ Google Scholar ]
• Angrist JD, & Lavy V (1999). Using Maimonides’ rule to estimate the effect of class size on scholastic achievment . Quarterly Journal of Economics , 114 , 533–575. [ Google Scholar ]
• Angrist JD, & Pischke JS (2009). Mostly harmless econometrics: An empiricist’s companion . Princeton, NJ: Princeton University Press. [ Google Scholar ]
• Angrist JD, & Pischke JS (2015). Mastering’metrics: The path from cause to effect . Princeton, NJ: Princeton University Press. [ Google Scholar ]
• Baum CF, Schaffer ME, & Stillman S (2007). Enhanced routines for instrumental variables/generalized method of moments estimation and testing . The Stata Journal , 7 , 465–506. [ Google Scholar ]
• Black D, Galdo J, & Smith JA (2007). Evaluating the bias of the regression discontinuity design using experimental data (Working paper) . Chicago, IL: University of Chicago. [ Google Scholar ]
• Brito C, & Pearl J (2002). Generalized instrumental variables In Darwiche A & Friedman N (Eds.), Uncertainty in artificial intelligence (pp. 85–93). San Francisco, CA: Morgan Kaufmann. [ Google Scholar ]
• Calonico S, Cattaneo MD, & Titiunik R (2015). rdrobust: Robust data-driven statistical inference in regression-discontinuity designs (R package ver. 0.80) . Retrieved from http://CRAN.R-project.org/package=rdrobust
• Coryn CLS, & Hobson KA (2011). Using nonequivalent dependent variables to reduce internal validity threats in quasi-experiments: Rationale, history, and examples from practice . New Directions for Evaluation , 131 , 31–39. [ Google Scholar ]
• Dimmery D (2013). rdd: Regression discontinuity estimation (R package ver. 0.56) . Retrieved from http://CRAN.R-project.org/package=rdd
• Ding P, & Miratrix LW (2015). To adjust or not to adjust? Sensitivity analysis of M-bias and butterfly-bias . Journal of Causal Inference , 3 ( 1 ), 41–57. [ Google Scholar ]
• Fox J (2006). Structural equation modeling with the sem package in R . Structural Equation Modeling , 13 , 465–486. [ Google Scholar ]
• Hahn J, Todd P, & Van der Klaauw W (2001). Identification and estimation of treatment effects with a regression–discontinuity design . Econometrica , 69 ( 1 ), 201–209. [ Google Scholar ]
• Hansen BB (2004). Full matching in an observational study of coaching for the SAT . Journal of the American Statistical Association , 99 , 609–618. [ Google Scholar ]
• Hansen BB, & Klopfer SO (2006). Optimal full matching and related designs via network flows . Journal of Computational and Graphical Statistics , 15 , 609–627. [ Google Scholar ]
• Ho D, Imai K, King G, & Stuart EA (2011). MatchIt: Nonparametric preprocessing for parametric causal inference . Journal of Statistical Software , 42 ( 8 ), 1–28. Retrieved from http://www.jstatsoft.org/v42/i08/ [ Google Scholar ]
• Holland PW (1986). Statistics and causal inference . Journal of the American Statistical Association , 81 , 945–960. [ Google Scholar ]
• Holland PW (1988). Causal inference, path analysis and recursive structural equations models . ETS Research Report Series . doi: 10.1002/j.2330-8516.1988.tb00270.x [ CrossRef ] [ Google Scholar ]
• Horvitz DG, & Thompson DJ (1952). A generalization of sampling without replacement from a finite universe . Journal of the American Statistical Association , 47 , 663–685. [ Google Scholar ]
• Imai K, Keele L, Tingley D, & Yamamoto T (2011). Unpacking the black box of causality: Learning about causal mechanisms from experimental and observational studies . American Political Science Review , 105 , 765–789. [ Google Scholar ]
• Imbens GW, & Lemieux T (2008). Regression discontinuity designs: A guide to practice . Journal of Econometrics , 142 , 615–635. [ Google Scholar ]
• Imbens GW, & Rubin DB (2015). Causal inference in statistics, social, and biomedical sciences . New York, NY: Cambridge University Press. [ Google Scholar ]
• Kazdin AE (2011). Single-case research designs: Methods for clinical and applied settings . New York, NY: Oxford University Press. [ Google Scholar ]
• Keller B, Kim JS, & Steiner PM (2015). Neural networks for propensity score estimation: Simulation results and recommendations In van der Ark LA, Bolt DM, Chow S-M, Douglas JA, & Wang W-C (Eds.), Quantitative psychology research (pp. 279–291). New York, NY: Springer. [ Google Scholar ]
• Lechner M (2011). The estimation of causal effects by difference-in-difference methods . Foundations and Trends in Econometrics , 4 , 165–224. [ Google Scholar ]
• Lee DS, & Lemieux T (2010). Regression discontinuity designs in economics . Journal of Economic Literature , 48 , 281–355. [ Google Scholar ]
• McCaffrey DF, Ridgeway G, & Morral AR (2004). Propensity score estimation with boosted regression for evaluating causal effects in observational studies . Psychological Methods , 9 , 403–425. [ PubMed ] [ Google Scholar ]
• McCrary J (2008). Manipulation of the running variable in the regression discontinuity design: A density test . Journal of Econometrics , 142 , 698–714. [ Google Scholar ]
• Nichols A (2007). rd: Stata modules for regression discontinuity estimation . Retrieved from http://ideas.repec.org/c/boc/bocode/s456888.html
• Pearl J (2009). C ausality: Models, reasoning, and inference (2nd ed.). New York, NY: Cambridge University Press. [ Google Scholar ]
• Pearl J (2010). On a class of bias-amplifying variables that endanger effect estimates In Proceedings of the Twenty-Sixth Conference on Uncertainty in Artificial Intelligence (pp. 425–432). Corvallis, OR: Association for Uncertainty in Artificial Intelligence. [ Google Scholar ]
• Robins JM, & Rotnitzky A (1995). Semiparametric efficiency in multivariate regression models with missing data . Journal of the American Statistical Association , 90 ( 429 ), 122–129. [ Google Scholar ]
• Rosenbaum PR (2002). Observational studies . New York, NY: Springer. [ Google Scholar ]
• Rosenbaum PR, & Rubin DB (1983). The central role of the propensity score in observational studies for causal effects . Biometrika , 70 ( 1 ), 41–55. [ Google Scholar ]
• Schafer JL, & Kang J (2008). Average causal effects from nonrandomized studies: A practical guide and simulated example . Psychological Methods , 13 , 279–313. [ PubMed ] [ Google Scholar ]
• Sekhon JS (2011). Multivariate and propensity score matching software with automated balance optimization: The matching package for R . Journal of Statistical Software , 42 ( 7 ), 1–52. [ Google Scholar ]
• Shadish WR, Cook TD, & Campbell DT (2002). Experimental and quasi-experimental designs for generalized causal inference . Boston, MA: Houghton-Mifflin. [ Google Scholar ]
• Somers M, Zhu P, Jacob R, & Bloom H (2013). The validity and precision of the comparative interrupted time series design and the difference-in-difference design in educational evaluation (MDRC working paper in research methodology) . New York, NY: MDRC. [ Google Scholar ]
• StataCorp. (2015). Stata treatment-effects reference manual: Potential outcomes/counterfactual outcomes . College Station, TX: Stata Press; Retrieved from http://www.stata.com/manuals14/te.pdf [ Google Scholar ]
• Steiner PM, & Cook D (2013). Matching and propensity scores In Little T (Ed.), The Oxford handbook of quantitative methods in psychology (Vol. 1 , pp. 237–259). New York, NY: Oxford University Press. [ Google Scholar ]
• Steiner PM, Cook TD, Li W, & Clark MH (2015). Bias reduction in quasi-experiments with little selection theory but many covariates . Journal of Research on Educational Effectiveness , 8 , 552–576. [ Google Scholar ]
• Steiner PM, Cook TD, & Shadish WR (2011). On the importance of reliable covariate measurement in selection bias adjustments using propensity scores . Journal of Educational and Behavioral Statistics , 36 , 213–236. [ Google Scholar ]
• Steiner PM, & Kim Y (in press). The mechanics of omitted variable bias: Bias amplification and cancellation of offsetting biases . Journal of Causal Inference . [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Steiner PM, Kim Y, Hall CE, & Su D (2015). Graphical models for quasi-experimental designs . Sociological Methods & Research. Advance online publication . doi: 10.1177/0049124115582272 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• West SG, Biesanz JC, & Pitts SC (2000). Causal inference and generalization in field settings: Experimental and quasi-experimental designs In Reis HT & Judd CM (Eds.), Handbook of research methods in social and personality psychology (pp. 40–84). New York, NY: Cambridge University Press. [ Google Scholar ]
• Wing C, & Cook TD (2013). Strengthening the regression discontinuity design using additional design elements: A within-study comparison . Journal of Policy Analysis and Management , 32 , 853–877. [ Google Scholar ]
• Wong M, Cook TD, & Steiner PM (2009). No Child Left Behind: An interim evaluation of its effects on learning using two interrupted time series each with its own non-equivalent comparison series (Working Paper No. WP-09–11) . Evanston, IL: Institute for Policy Research, Northwestern University. [ Google Scholar ]
• Wong VC, Wing C, Steiner PM, Wong M, & Cook TD (2012). Research designs for program evaluation . Handbook of Psychology , 2 , 316–341. [ Google Scholar ]
• Wooldridge J (2012). Introductory econometrics: A modern approach (5th ed.). Mason, OH: South-Western Cengage Learning. [ Google Scholar ]

• Skip to main content
• Skip to primary sidebar
• Skip to footer
• QuestionPro

• Solutions Industries Gaming Automotive Sports and events Education Government Travel & Hospitality Financial Services Healthcare Cannabis Technology Use Case NPS+ Communities Audience Contactless surveys Mobile LivePolls Member Experience GDPR Positive People Science 360 Feedback Surveys
• Resources Blog eBooks Survey Templates Case Studies Training Help center

Home Market Research Research Tools and Apps

Quasi-experimental Research: What It Is, Types & Examples

Much like an actual experiment, quasi-experimental research tries to demonstrate a cause-and-effect link between a dependent and an independent variable. A quasi-experiment, on the other hand, does not depend on random assignment, unlike an actual experiment. The subjects are sorted into groups based on non-random variables.

What is Quasi-Experimental Research?

“Resemblance” is the definition of “quasi.” Individuals are not randomly allocated to conditions or orders of conditions, even though the regression analysis is changed. As a result, quasi-experimental research is research that appears to be experimental but is not.

The directionality problem is avoided in quasi-experimental research since the regression analysis is altered before the multiple regression is assessed. However, because individuals are not randomized at random, there are likely to be additional disparities across conditions in quasi-experimental research.

As a result, in terms of internal consistency, quasi-experiments fall somewhere between correlational research and actual experiments.

The key component of a true experiment is randomly allocated groups. This means that each person has an equivalent chance of being assigned to the experimental group or the control group, depending on whether they are manipulated or not.

Simply put, a quasi-experiment is not a real experiment. A quasi-experiment does not feature randomly allocated groups since the main component of a real experiment is randomly assigned groups. Why is it so crucial to have randomly allocated groups, given that they constitute the only distinction between quasi-experimental and actual  experimental research ?

Let’s use an example to illustrate our point. Let’s assume we want to discover how new psychological therapy affects depressed patients. In a genuine trial, you’d split half of the psych ward into treatment groups, With half getting the new psychotherapy therapy and the other half receiving standard  depression treatment .

And the physicians compare the outcomes of this treatment to the results of standard treatments to see if this treatment is more effective. Doctors, on the other hand, are unlikely to agree with this genuine experiment since they believe it is unethical to treat one group while leaving another untreated.

A quasi-experimental study will be useful in this case. Instead of allocating these patients at random, you uncover pre-existing psychotherapist groups in the hospitals. Clearly, there’ll be counselors who are eager to undertake these trials as well as others who prefer to stick to the old ways.

These pre-existing groups can be used to compare the symptom development of individuals who received the novel therapy with those who received the normal course of treatment, even though the groups weren’t chosen at random.

If any substantial variations between them can be well explained, you may be very assured that any differences are attributable to the treatment but not to other extraneous variables.

As we mentioned before, quasi-experimental research entails manipulating an independent variable by randomly assigning people to conditions or sequences of conditions. Non-equivalent group designs, pretest-posttest designs, and regression discontinuity designs are only a few of the essential types.

What are quasi-experimental research designs?

Quasi-experimental research designs are a type of research design that is similar to experimental designs but doesn’t give full control over the independent variable(s) like true experimental designs do.

In a quasi-experimental design, the researcher changes or watches an independent variable, but the participants are not put into groups at random. Instead, people are put into groups based on things they already have in common, like their age, gender, or how many times they have seen a certain stimulus.

Because the assignments are not random, it is harder to draw conclusions about cause and effect than in a real experiment. However, quasi-experimental designs are still useful when randomization is not possible or ethical.

The true experimental design may be impossible to accomplish or just too expensive, especially for researchers with few resources. Quasi-experimental designs enable you to investigate an issue by utilizing data that has already been paid for or gathered by others (often the government). 

Because they allow better control for confounding variables than other forms of studies, they have higher external validity than most genuine experiments and higher  internal validity  (less than true experiments) than other non-experimental research.

Is quasi-experimental research quantitative or qualitative?

Quasi-experimental research is a quantitative research method. It involves numerical data collection and statistical analysis. Quasi-experimental research compares groups with different circumstances or treatments to find cause-and-effect links. 

It draws statistical conclusions from quantitative data. Qualitative data can enhance quasi-experimental research by revealing participants’ experiences and opinions, but quantitative data is the method’s foundation.

Quasi-experimental research types

There are many different sorts of quasi-experimental designs. Three of the most popular varieties are described below: Design of non-equivalent groups, Discontinuity in regression, and Natural experiments.

Design of Non-equivalent Groups

Example: design of non-equivalent groups, discontinuity in regression, example: discontinuity in regression, natural experiments, example: natural experiments.

However, because they couldn’t afford to pay everyone who qualified for the program, they had to use a random lottery to distribute slots.

Experts were able to investigate the program’s impact by utilizing enrolled people as a treatment group and those who were qualified but did not play the jackpot as an experimental group.

How QuestionPro helps in quasi-experimental research?

QuestionPro can be a useful tool in quasi-experimental research because it includes features that can assist you in designing and analyzing your research study. Here are some ways in which QuestionPro can help in quasi-experimental research:

Design surveys

Randomize participants, collect data over time, analyze data, collaborate with your team.

With QuestionPro, you have access to the most mature market research platform and tool that helps you collect and analyze the insights that matter the most. By leveraging InsightsHub, the unified hub for data management, you can ​​leverage the consolidated platform to organize, explore, search, and discover your  research data  in one organized data repository . 

Optimize Your quasi-experimental research with QuestionPro. Get started now!

FREE TRIAL         LEARN MORE

MORE LIKE THIS

I Am Disconnected – Tuesday CX Thoughts

May 21, 2024

20 Best Customer Success Tools of 2024

May 20, 2024

AI-Based Services Buying Guide for Market Research (based on ESOMAR’s 20 Questions) 

Data Information vs Insight: Essential differences

May 14, 2024

Other categories

• Academic Research
• Artificial Intelligence
• Assessments
• Brand Awareness
• Case Studies
• Communities
• Consumer Insights
• Customer effort score
• Customer Engagement
• Customer Experience
• Customer Loyalty
• Customer Research
• Customer Satisfaction
• Employee Benefits
• Employee Engagement
• Employee Retention
• Friday Five
• General Data Protection Regulation
• Insights Hub
• Life@QuestionPro
• Market Research
• Mobile diaries
• Mobile Surveys
• New Features
• Online Communities
• Question Types
• Questionnaire
• QuestionPro Products
• Release Notes
• Research Tools and Apps
• Revenue at Risk
• Survey Templates
• Training Tips
• Uncategorized
• Video Learning Series
• What’s Coming Up
• Workforce Intelligence

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

8.2 Quasi-experimental and pre-experimental designs

Learning objectives.

• Identify and describe the various types of quasi-experimental designs
• Distinguish true experimental designs from quasi-experimental and pre-experimental designs
• Identify and describe the various types of quasi-experimental and pre-experimental designs

As we discussed in the previous section, time, funding, and ethics may limit a researcher’s ability to conduct a true experiment. For researchers in the medical sciences and social work, conducting a true experiment could require denying needed treatment to clients, which is a clear ethical violation. Even those whose research may not involve the administration of needed medications or treatments may be limited in their ability to conduct a classic experiment. When true experiments are not possible, researchers often use quasi-experimental designs.

Quasi-experimental designs

Quasi-experimental designs are similar to true experiments, but they lack random assignment to experimental and control groups. Quasi-experimental designs have a comparison group that is similar to a control group except assignment to the comparison group is not determined by random assignment. The most basic of these quasi-experimental designs is the nonequivalent comparison groups design (Rubin & Babbie, 2017).  The nonequivalent comparison group design looks a lot like the classic experimental design, except it does not use random assignment. In many cases, these groups may already exist. For example, a researcher might conduct research at two different agency sites, one of which receives the intervention and the other does not. No one was assigned to treatment or comparison groups. Those groupings existed prior to the study. While this method is more convenient for real-world research, it is less likely that that the groups are comparable than if they had been determined by random assignment. Perhaps the treatment group has a characteristic that is unique–for example, higher income or different diagnoses–that make the treatment more effective.

Quasi-experiments are particularly useful in social welfare policy research. Social welfare policy researchers often look for what are termed natural experiments , or situations in which comparable groups are created by differences that already occur in the real world. Natural experiments are a feature of the social world that allows researchers to use the logic of experimental design to investigate the connection between variables. For example, Stratmann and Wille (2016) were interested in the effects of a state healthcare policy called Certificate of Need on the quality of hospitals. They clearly could not randomly assign states to adopt one set of policies or another. Instead, researchers used hospital referral regions, or the areas from which hospitals draw their patients, that spanned across state lines. Because the hospitals were in the same referral region, researchers could be pretty sure that the client characteristics were pretty similar. In this way, they could classify patients in experimental and comparison groups without dictating state policy or telling people where to live.

Matching is another approach in quasi-experimental design for assigning people to experimental and comparison groups. It begins with researchers thinking about what variables are important in their study, particularly demographic variables or attributes that might impact their dependent variable. Individual matching involves pairing participants with similar attributes. Then, the matched pair is split—with one participant going to the experimental group and the other to the comparison group. An ex post facto control group , in contrast, is when a researcher matches individuals after the intervention is administered to some participants. Finally, researchers may engage in aggregate matching , in which the comparison group is determined to be similar on important variables.

Time series design

There are many different quasi-experimental designs in addition to the nonequivalent comparison group design described earlier. Describing all of them is beyond the scope of this textbook, but one more design is worth mentioning. The time series design uses multiple observations before and after an intervention. In some cases, experimental and comparison groups are used. In other cases where that is not feasible, a single experimental group is used. By using multiple observations before and after the intervention, the researcher can better understand the true value of the dependent variable in each participant before the intervention starts. Additionally, multiple observations afterwards allow the researcher to see whether the intervention had lasting effects on participants. Time series designs are similar to single-subjects designs, which we will discuss in Chapter 15.

Pre-experimental design

When true experiments and quasi-experiments are not possible, researchers may turn to a pre-experimental design (Campbell & Stanley, 1963).  Pre-experimental designs are called such because they often happen as a pre-cursor to conducting a true experiment.  Researchers want to see if their interventions will have some effect on a small group of people before they seek funding and dedicate time to conduct a true experiment. Pre-experimental designs, thus, are usually conducted as a first step towards establishing the evidence for or against an intervention. However, this type of design comes with some unique disadvantages, which we’ll describe below.

A commonly used type of pre-experiment is the one-group pretest post-test design . In this design, pre- and posttests are both administered, but there is no comparison group to which to compare the experimental group. Researchers may be able to make the claim that participants receiving the treatment experienced a change in the dependent variable, but they cannot begin to claim that the change was the result of the treatment without a comparison group.   Imagine if the students in your research class completed a questionnaire about their level of stress at the beginning of the semester.  Then your professor taught you mindfulness techniques throughout the semester.  At the end of the semester, she administers the stress survey again.  What if levels of stress went up?  Could she conclude that the mindfulness techniques caused stress?  Not without a comparison group!  If there was a comparison group, she would be able to recognize that all students experienced higher stress at the end of the semester than the beginning of the semester, not just the students in her research class.

In cases where the administration of a pretest is cost prohibitive or otherwise not possible, a one- shot case study design might be used. In this instance, no pretest is administered, nor is a comparison group present. If we wished to measure the impact of a natural disaster, such as Hurricane Katrina for example, we might conduct a pre-experiment by identifying  a community that was hit by the hurricane and then measuring the levels of stress in the community.  Researchers using this design must be extremely cautious about making claims regarding the effect of the treatment or stimulus. They have no idea what the levels of stress in the community were before the hurricane hit nor can they compare the stress levels to a community that was not affected by the hurricane.  Nonetheless, this design can be useful for exploratory studies aimed at testing a measures or the feasibility of further study.

In our example of the study of the impact of Hurricane Katrina, a researcher might choose to examine the effects of the hurricane by identifying a group from a community that experienced the hurricane and a comparison group from a similar community that had not been hit by the hurricane. This study design, called a static group comparison , has the advantage of including a comparison group that did not experience the stimulus (in this case, the hurricane). Unfortunately, the design only uses for post-tests, so it is not possible to know if the groups were comparable before the stimulus or intervention.  As you might have guessed from our example, static group comparisons are useful in cases where a researcher cannot control or predict whether, when, or how the stimulus is administered, as in the case of natural disasters.

As implied by the preceding examples where we considered studying the impact of Hurricane Katrina, experiments, quasi-experiments, and pre-experiments do not necessarily need to take place in the controlled setting of a lab. In fact, many applied researchers rely on experiments to assess the impact and effectiveness of various programs and policies. You might recall our discussion of arresting perpetrators of domestic violence in Chapter 2, which is an excellent example of an applied experiment. Researchers did not subject participants to conditions in a lab setting; instead, they applied their stimulus (in this case, arrest) to some subjects in the field and they also had a control group in the field that did not receive the stimulus (and therefore were not arrested).

Key Takeaways

• Quasi-experimental designs do not use random assignment.
• Comparison groups are used in quasi-experiments.
• Matching is a way of improving the comparability of experimental and comparison groups.
• Quasi-experimental designs and pre-experimental designs are often used when experimental designs are impractical.
• Quasi-experimental and pre-experimental designs may be easier to carry out, but they lack the rigor of true experiments.
• Aggregate matching – when the comparison group is determined to be similar to the experimental group along important variables
• Comparison group – a group in quasi-experimental design that does not receive the experimental treatment; it is similar to a control group except assignment to the comparison group is not determined by random assignment
• Ex post facto control group – a control group created when a researcher matches individuals after the intervention is administered
• Individual matching – pairing participants with similar attributes for the purpose of assignment to groups
• Natural experiments – situations in which comparable groups are created by differences that already occur in the real world
• Nonequivalent comparison group design – a quasi-experimental design similar to a classic experimental design but without random assignment
• One-group pretest post-test design – a pre-experimental design that applies an intervention to one group but also includes a pretest
• One-shot case study – a pre-experimental design that applies an intervention to only one group without a pretest
• Pre-experimental designs – a variation of experimental design that lacks the rigor of experiments and is often used before a true experiment is conducted
• Quasi-experimental design – designs lack random assignment to experimental and control groups
• Static group design – uses an experimental group and a comparison group, without random assignment and pretesting
• Time series design – a quasi-experimental design that uses multiple observations before and after an intervention

Image attributions

cat and kitten   matching avocado costumes on the couch looking at the camera by Your Best Digs CC-BY-2.0

Foundations of Social Work Research Copyright © 2020 by Rebecca L. Mauldin is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Share This Book

Étale cohomology of algebraizable rigid analytic varieties via nearby cycles over general bases

• Open access
• Published: 22 May 2024

Cite this article

You have full access to this open access article

• Hiroki Kato   ORCID: orcid.org/0000-0003-0513-0878 1  

We prove a finiteness theorem and a comparison theorem in the theory of étale cohomology of rigid analytic varieties. By a result of Huber, for a quasi-compact separated morphism of rigid analytic varieties with target being of dimension \(\le 1\) , the compactly supported higher direct image preserves quasi-constructibility. Though the analogous statement for morphisms with higher dimensional target fails in general, we prove that, in the algebraizable case, it holds after replacing the target with a modification. We deduce it from a known finiteness result in the theory of nearby cycles over general bases and a new comparison result, which gives an identification of the compactly supported higher direct image sheaves, up to modification of the target, in terms of nearby cycles over general bases.

Avoid common mistakes on your manuscript.

1 Introduction

We prove a new finiteness theorem and a new comparison theorem on étale cohomology of rigid analytic varieties, more specifically, on the compactly supported higher direct image sheaves for algebraizable morphisms of algebraizable rigid analytic varieties.

1.1 Finiteness and modification

Let k be a non-archimedean field and \(k^\circ \) denote the subring of power pounded elements of k , i.e, the ring of integers. Let \(\mathsf f:\mathsf X\rightarrow \mathsf Y\) be a quasi-compact separated morphism of adic spaces locally of finite type over \(\mathop {\textrm{Spa}}\nolimits (k,k^\circ )\) and \(\mathsf F\) be a quasi-constructible sheaf of \({\mathbb {Z}}/n{\mathbb {Z}}\) -modules on \(\mathsf X_\mathrm{\acute{e}t}\) , with n an integer invertible in \(k^\circ \) . A finiteness theorem of Huber ([ 11 , Theorem 2.1]) states that, if the characteristic of k is zero and if \(\dim \mathsf Y\le 1\) , then the compactly supported higher direct image sheaves \(R^i\mathsf f_!\mathsf F\) are again quasi-constructible. Here, roughly speaking, a quasi-constructible sheaf is a sheaf which étale locally admits a stratification by intersections of constructible locally closed subsets and Zariski locally closed subsets such that the restriction to each stratum is locally constant. (See [ 10 , 12 ] for variants of this finiteness result.)

We note that the analogous statement for \(\mathsf f\) with \(\dim \mathsf Y\ge 2\) fails as pointed out in [ 11 , Example 2.2]. Nonetheless, the author expects that there exists a modification \(\pi :\mathsf Y'\rightarrow \mathsf Y\) such that the pullback \(\pi ^*R^i\mathsf f_!\mathsf F\) is quasi-constructible, and we prove this expectation in the case where \(\mathsf f:\mathsf X\rightarrow \mathsf Y\) and \(\mathsf F\) are algebraizable.

To be precise, let us introduce some notations. For a scheme X locally of finite type over \(k^\circ \) , let \(X^\textrm{rig}\) denote the Raynaud generic fiber of the \(\varpi \) -adic completion of X for some pseudo-uniformizor \(\varpi \in k^\circ \) , viewed as an adic space. For a morphism \(f:X\rightarrow Y\) of schemes locally of finite type over \(k^\circ \) , let \(f^\textrm{rig}\) denote the associated morphism \(X^\textrm{rig}\rightarrow Y^\textrm{rig}\) . Finally, for a sheaf \(\mathcal F\) on the generic fiber \(X_{\eta ,\mathrm{\acute{e}t}}\) of a scheme X locally of finite type over \(k^\circ \) , let \(\mathcal F^\textrm{rig}\) denote the sheaf on \(X^\textrm{rig}_\mathrm{\acute{e}t}\) obtained by pulling back \(\mathcal F\) .

Now we can state our finiteness result:

Theorem 1.1

(Theorem 5.5 ) Let k be a non-archimedean field and n be an integer invertible in \(k^\circ \) . Let \(f:X\rightarrow Y\) be a morphism of schemes of finite type over \(k^\circ \) which is separated and of finite presentation. Let \(\mathcal F\) be a constructible sheaf of \({\mathbb {Z}}/n{\mathbb {Z}}\) -modules on the generic fiber \(X_{\eta ,\mathrm{\acute{e}t}}\) . Then there exists a modification \(\pi :Y'\rightarrow Y\) such that the sheaves \(\pi ^{\textrm{rig}*}R^if^\textrm{rig}_!\mathcal F^\textrm{rig}\) are quasi-constructible.

Our proof is totally different from Huber’s and reproves his finiteness result in the algebraizable case. Contrary to Huber’s case, we do not need any assumption on the characteristic of k . In fact, we will not make any reference to the base field in the proof and will work with much more general setting (see § 5 for details).

Further, our approach gives a remarkable simplification of the proof. We do not need any of complicated reduction arguments that Huber made in [ 11 ]. We do not rely on deep results used in his proof, namely, the preservation of constructibility by smooth compactly supported pushforward [ 9 , Theorem 6.2.2], and the p -adic Riemann’s existence theorem due to Lütkebohmert [ 17 , Theorem 2.2], which requires the assumption on the characteristic of k . We prove Theorem 1.1 as a direct consequence of the following two results: One is a known finiteness result in the theory of nearby cycles over general bases due to Orgogozo [ 20 ], and the other is a new comparison result, which gives an identification of the compactly supported higher direct image sheaves, up to modification of the target, in terms of nearby cycles over general bases. This comparison result is the heart of this paper and will be briefly explained in the next subsection.

The idea of our approach comes from a recent work of K. Ito [ 16 ], in which the theory of nearby cycles over general bases is used to study étale cohomology of rigid analytic varieties. Though his aim is different from proving a finiteness result, his work includes a new proof of a special case of Huber’s finiteness result; namely the special case of Theorem 1.1 where \(\dim Y^\textrm{rig}=1\) and \(\mathcal F\) is constant ([ 16 , Theorem 6.10]). Let us mention that his proof does not rely on the p -adic Riemann existence theorem, but still relies on the preservation of constructibility by smooth compactly supported pushforward.

It is natural to ask if one can also apply our argument to higher direct image sheaves without support. The author expects that a similar statement with “quasi-constructible” replaced by “oc-quasi-constructible” (see [ 10 ] for the definition and the case where \(\dim \mathsf Y=1\) ) holds. However, it seems much more difficult and he does not know how to address it even in the algebraizable case (see Remark 5.6 ).

One of typical applications of a finiteness result of higher direct image is the existence of a tubular neighborhood that does not change the cohomology. For instance, in [ 11 ], the following is proved as a consequence of his finiteness result: Under the assumption that k is of characteristic zero, every hypersurface in an affinoid adic space of finite type over \(\mathop {\textrm{Spa}}\nolimits (k,k^\circ )\) admits a tubular (closed) neighborhood that does not change the compactly supported cohomology (see [ 10 , 11 , 16 ] for variants). In a celebrated paper of Scholze [ 22 ], such a existence result is used in the proof of the weight monodromy conjecture for varieties of complete intersection.

1.2 Comparison result

One of the most fundamental results in the theory of étale cohomology of rigid analytic varieties is the comparison theorem between the étale cohomology of an algebraizable rigid analytic variety and the nearby cycle cohomology, due to Fujiwara and Huber ( [ 5 , Corollary 6.6.2], [ 9 , Theorem 5.7.6]). More generally, the results in Huber’s book [ 9 ] show the following description of the stalks of the compactly supported higher direct image sheaves. Let k be a non-archimedean field. Let \(f:X\rightarrow Y\) be a separated morphism of schemes of finite type over \(k^\circ \) and \(\mathcal F\) a sheaf of \({\mathbb {Z}}/n{\mathbb {Z}}\) -modules on the generic fiber \(X_{\eta ,\mathrm{\acute{e}t}}\) , for an integer n . We consider the higher direct image \(Rf^\textrm{rig}_!\mathcal F^\textrm{rig}\) by the morphism \(f^\textrm{rig}:X^\textrm{rig}\rightarrow Y^\textrm{rig}\) between the Raynaud generic fibers. For every geometric point \(\xi \) (possibly of higher rank) of \(Y^\textrm{rig}\) , the stalk \((Rf^\textrm{rig}_!\mathcal F^\textrm{rig})_\xi \) is canonically isomorphic to the cohomology of the nearby cycle taken over the valuation ring \(\kappa (\xi )^+\) corresponding to \(\xi \) .

Thus, we know that there is a comparison isomorphism at each geometric point between the stalk of \(Rf^\textrm{rig}_!\mathcal F^\textrm{rig}\) and a suitable nearby cycle cohomology. The main discovery of this article is a uniform construction of those separately constructed isomorphisms. More precisely, we construct a relative variant of nearby cycle cohomology as a complex on \(Y^\textrm{rig}_\mathrm{\acute{e}t}\) and a canonical morphism to \(Rf^\textrm{rig}_!\mathcal F\) . Then we prove that the canonical morphism becomes an isomorphism after a modification of Y , under the assumption that n is invertible in \(k^\circ \) and that \(\mathcal F\) is constructible.

For the construction, we use the theory of nearby cycles over general bases as in [ 14 ]. We first construct a relative variant of nearby cycle cohomology as a complex \(\Xi _f\mathcal F\) on the topos \(Y\overleftarrow{\times }_YY\) called the vanishing topos of Y (see § 2.3 for details). Roughly speaking, the vanishing topos \(Y\overleftarrow{\times }_YY\) is a topos whose points correspond to specializations \(y\leftarrow z\) of two geometric points of Y , and the complex \(\Xi _f\mathcal F\) is a complex whose stalk at \(y\leftarrow z\) is canonically isomorphic to the cohomology of the nearby cycle taken with respect to the specialization \(y\leftarrow z\) over the strict henselization \(Y_{(y)}\) . Here, as mentioned in Illusie’s survey article [ 13 , 6.4], the vanishing topos \(Y\overleftarrow{\times }_YY\) receives a canonical morphism of topoi \(\widetilde{\lambda }_Y:(Y^\textrm{rig}_\mathrm{\acute{e}t})^\sim \rightarrow Y\overleftarrow{\times }_YY\) from the étale topos of \(Y^\textrm{rig}\) which sends a geometric point \(\xi \) of \(Y^\textrm{rig}\) to the specialization defined by the closed point and the generic point of the spectrum of the valuation ring \(\kappa (\xi )^+\) . Then the desired complex on \(Y^\textrm{rig}_\mathrm{\acute{e}t}\) is defined to be the pullback \(\widetilde{\lambda }^*_Y\Xi _f\mathcal F\) .

Theorem 1.2

Let \(f:X\rightarrow Y\) be a compactifiable morphism of schemes of finite type over \(k^\circ \) and \(\mathcal F\) be a sheaf of \({\mathbb {Z}}/n{\mathbb {Z}}\) -modules on the generic fiber \(X_{\eta ,\mathrm{\acute{e}t}}\) , for an integer n . Then there exists a canonical morphism

satisfying the following: Assume that n is invertible in \(k^\circ \) , that f is of finite presentation, and that \(\mathcal F\) is constructible. Then, after replacing Y by a modification and f by the base change, the morphism \(\theta _f\) becomes an isomorphism.

We note that the nearby cycle appearing in the description of \((Rf^\textrm{rig}_!\mathcal F^\textrm{rig})_\xi \) is taken over the valuation ring \(\kappa (\xi )^+\) , while that appearing in \((\widetilde{\lambda }_Y^*\Xi _f\mathcal F)_\xi \) is taken over the strict henselization \(Y_{(y_\xi )}\) , where \(y_\xi \) is the image of the closed geometric point of \(\mathop {\textrm{Spec}}\nolimits \kappa (\xi )^+\) by the natural map \(\mathop {\textrm{Spec}}\nolimits \kappa (\xi )^+\rightarrow Y\) . In general, the formation of nearby cycle does not commute with base change, and in particular, the above two nearby cycles are different (and \(\theta _f\) can be non-isomorphic as seen in Example 4.13 ). But, as proved by Orgogozo in [ 20 ], it commutes with base change after a modification, i.e, after replacing Y by a modification and f by the base change, the formation of the nearby cycle commutes with base change. In particular, the above two nearby cycles agree after this replacement.

Once we have proved Theorem 1.2 , we can easily deduce Theorem 1.1 from the constructibility of the complex \(\Xi _f\mathcal F\) on the vanishing topos \(Y\overleftarrow{\times }_YY\) , which is a consequence of finiteness results on nearby cycles over general bases due to Orgogozo [ 20 ].

The canonical morphism \(\theta _f\) in Theorem 1.2 is constructed as a certain base change morphism with respect to a certain square diagram involving the vanishing topoi of X and Y (see Construction 4.7 ). To check that \(\theta _f\) becomes isomorphic after modification, we show that, using results of Orgogozo in [ 20 ], after replacing Y by a modification and f by the base change, the formation of \(\Xi _f\mathcal F\) commutes with base change. After this replacement, the morphism \((\theta _f)_\xi \) induced on the stalks at each geometric point \(\xi \) of \(Y^\textrm{rig}\) is identified with the comparison morphism constructed by Huber.

1.3 Organization of the article

We recall basic definitions and some results on the theory of nearby cycles over general bases in § 2 . After a preliminary section § 3 concerning on adic spaces, we give in § 4 the key constructions and prove Theorem 1.2 . We deduce Theorem 1.1 from Theorem 1.2 in § 5 . Finally we deduce the existence of a good tubular neighborhood for families in § 6 .

Convention For a scheme, or a pseudo-adic space X , we denote the associated étale site by \(X_\mathrm{\acute{e}t}\) . We use the same letter X for the associated étale topos by abuse of notation.

A morphism \(f:X\rightarrow Y\) of schemes is called compactifiable if there exist a proper morphism \({{\bar{f}}}:{{\bar{X}}}\rightarrow Y\) and an open immersion \(j:X\rightarrow {{\bar{X}}}\) such that \(f={{\bar{f}}}j\) . Note that, by Nagata’s compactification theorem ([ 4 , Chapter II, Theorem F.1.1]), if f is separated and of finite type and if Y is quasi-compact and quasi-separated, then f is compactifiable.

2 Vanishing topos and Nearby cycles over general bases

2.1 review of definition.

Let \(f:X\rightarrow S\) and \(g:Y\rightarrow S\) be morphisms of topoi. For the definition of the oriented product \(X\overleftarrow{\times }_SY\) , we refer to [ 14 ]. It comes with morphisms \(p_1:X\overleftarrow{\times }_SY\rightarrow X\) and \(p_2:X\overleftarrow{\times }_SY\rightarrow Y\) and a 2-morphism \(\tau :gp_2\rightarrow fp_1\) , and is universal for these data. Recall that giving a 2-morphism \(a\rightarrow b\) between two morphisms \(a,b:X\rightarrow Y\) of topoi is equivalent to giving a morphism \(a_*\rightarrow b_*\) of functors ( [ 7 , 3.2]).

If \(f:X\rightarrow S\) and \(g:Y\rightarrow S\) are morphisms of schemes, then a point of the topos \(X\overleftarrow{\times }_SY\) , i.e., a morphism from the punctual topos, is described by a triple ( x ,  y ,  c ) consisting of a geometric point x of X , a geometric point y of Y , and a specialization \(c:g(y)\rightarrow f(x)\) of geometric points, i.e, a morphism \(g(y)\rightarrow S_{(f(x))}\) of schemes. We use the notation \(x\leftarrow y\) for the triple ( x ,  y ,  c ).

For a morphism \(f:X\rightarrow S\) of schemes, the topos \(X\overleftarrow{\times }_SS\) is called the vanishing topos and we have the natural morphism \(\Psi _f:X\rightarrow X\overleftarrow{\times }_SS\) induced from \(\textrm{id}_X:X\rightarrow X\) , \(f:X\rightarrow S\) , and the 2-morphism \(\textrm{id}:f\rightarrow f\) by the universal property of \(X\overleftarrow{\times }_SS\) . For a ring \(\Lambda \) , the nearby cycle functor \(R\Psi _f:D^+(X,\Lambda )\rightarrow D^+(X\overleftarrow{\times }_YY,\Lambda )\) is defined to be the derived functor \(R(\Psi _f)_*\) .

Let X be a scheme and \(\Lambda \) be a ring. We consider the 2-commutative diagram

Recall that the morphism \(p_2^*\rightarrow R\Psi _\textrm{id}\) of functors \(D^+(X,\Lambda )\rightarrow D^+(X\overleftarrow{\times }_XX,\Lambda )\) induced by \(p_2\Psi _\textrm{id}\cong \textrm{id}\) is an isomorphism [ 14 , Proposition 4.7].

For a morphism \(f:X\rightarrow S\) of schemes, we have the 2-commutative diagram

Thus, we have canonical isomorphisms

Notation 2.2

(Sliced nearby cycles) Let \(f:X\rightarrow S\) be a morphism of schemes and \(s\leftarrow t\) be a point of \(S\overleftarrow{\times }_SS\) . We consider the diagram

of schemes, where the first map is induced by the specialization map \(S_{(t)}\rightarrow S_{(s)}\) corresponding to \(s\leftarrow t\) . The functor \(i_s^*Rj_{(t)*}:D^+(X\times _SS_{(t)},\Lambda )\rightarrow D^+(X_s,\Lambda )\) (or \(D^+(X,\Lambda )\rightarrow D^+(X_s,\Lambda )\) ) is denoted by \(R\psi _f^{s\leftarrow t}\) . We call it the sliced nearby cycle functor over \(s\leftarrow t\) for f . As in [ 15 , 1.3], denoting the composite \(X_s\cong X_s\overleftarrow{\times }_St\rightarrow X\overleftarrow{\times }_SS\) by \(\iota _{s\leftarrow t}\) , we have a canonical isomorphism

of functors \(D^+(X,\Lambda )\rightarrow D^+(X_s,\Lambda )\) .

2.2 Base change morphisms

We recall the base change morphism for \(R\Psi \) . For a morphism \(f:X\rightarrow Y\) of schemes, we consider base change by a morphism \(Y^\prime \rightarrow Y\) . Consider the Cartesian diagram

of schemes, which induces the diagram of topoi

We consider the base change morphism

Definition 2.3

Let \(f:X\rightarrow Y\) be a morphism of schemes, \(\Lambda \) a ring, and \(\mathcal F\) an object of \(D^+(X,\Lambda )\) . We say that the formation of \(R\Psi _f\mathcal F\) commutes with base change if, for every morphism \(Y'\rightarrow Y\) of schemes, the base change morphism

defined above is an isomorphism.

The following analogue of the proper base change theorem is indispensable in our construction.

be a commutative diagram of schemes with the upper square being Cartesian. We assume that f is proper. We consider the diagram of topoi

Let \(\Lambda \) be a torsion ring. Then the base change morphism

is an isomorphism of functors \(D^+(X\overleftarrow{\times }_SS,\Lambda )\rightarrow D^+(Y'\overleftarrow{\times }_{S'}S',\Lambda )\) .

Though this is essentially proved in [ 20 , Lemme 10.1], we include a proof for completeness.

Recall that, if \(X\rightarrow S\) and \(Y\rightarrow S\) are coherent morphisms of coherent topoi, then the oriented product \(X\overleftarrow{\times }_SY\) is also coherent [ 14 , Lemma 2.5]. Thus, by [ 6 , Proposition 9.0], it has enough points, that is, a morphism \(\mathcal F\rightarrow \mathcal G\) of objects of \(X\overleftarrow{\times }_SY\) is an isomorphism if and only if the morphism \(\mathcal F_{x\leftarrow y}\rightarrow \mathcal G_{x\leftarrow y}\) is bijective for any point \(x\leftarrow y\) of \(X\overleftarrow{\times }_SY\) [ 6 , Définition IV.6.4.1]. This implies that for any diagram \(X\rightarrow S\leftarrow Y\) of schemes, the oriented product \(X\overleftarrow{\times }_SY\) has enough points.

Proof (Proof of Lemma 2.4)

[Proof of Lemma 2.4 ] For each object \(\mathcal F\) of \(D^+(X\overleftarrow{\times }_SS,\Lambda )\) and for each point \(y'\leftarrow t'\) of \(Y'\overleftarrow{\times }_{S'}S'\) , we check that the morphism induced on the stalks is an isomorphism. For this, we may assume that \(Y'=Y'_{(y')}\) and \(Y=Y_{(y)}\) , where y is the image of \(y'\) . Further, by [ 14 , 1.12 and 1.13], we may assume that \(S'=S'_{(s')}\) and \(S=S_{(s)}\) are strictly local, where \(s'\) and s are the images of \(y'\) in \(S'\) and S respectively. We denote the image of \(t'\) in S by t . Then the morphism \((R(f\overleftarrow{\times }\textrm{id})_*\mathcal F)_{y\leftarrow t}\rightarrow (R(f'\overleftarrow{\times }\textrm{id})_*{\varphi '}^*\mathcal F)_{y'\leftarrow t'}\) induced on the stalks is identified with the morphism

induced by the adjunction morphism \(\textrm{id}\rightarrow R\varphi '_*{\varphi '}^*\) . We consider the diagram

The morphism in question is identified with

Then, by the (usual) proper base change theorem, it suffices to show that the base change morphism \(g^*Rp_{1*}\mathcal F\rightarrow Rp'_{1*}{\varphi '}^*\mathcal F\) is an isomorphism. We check that, for each geometric point \(x'\) of \(X'\) , the morphism \((Rp_{1*}\mathcal F)_x\rightarrow (Rp'_{1*}{\varphi '}^*\mathcal F)_{x'}\) induced on the stalks is an isomorphism, where x is the image of \(x'\) . But it is identified with the natural morphism \(R\Gamma (X_{(x)}\overleftarrow{\times }_SS_{(t)},\mathcal F)\rightarrow R\Gamma (X'_{(x')}\overleftarrow{\times }_{S'}S'_{(t')},{\varphi '}^*\mathcal F)\) , which is an isomorphism since \(\varphi ':X'_{(x')}\overleftarrow{\times }_{S'}S'_{(t')}\rightarrow X_{(x)}\overleftarrow{\times }_SS_{(t)}\) is a local morphism of local topoi [ 14 , Corollaire 2.3.2]. Thus, the assertion follows. \(\square \)

2.3 Higher direct image with compact support for vanishing topoi

Let S be a scheme and \(f:X\rightarrow Y\) be a morphism of S -schemes. We consider the natural morphism

We assume that \(f:X\rightarrow Y\) is compactifiable and choose a proper morphism \({{\bar{f}}}:{{\bar{X}}}\rightarrow Y\) with an open immersion \(j:X\rightarrow {{\bar{X}}}\) such that \({{\bar{f}}}j=f\) . Note that the topos \(X\overleftarrow{\times }_SS\) is an open subtopos of \({{\bar{X}}}\overleftarrow{\times }_SS\) (in the sense of [ 7 , 9.2.1]), and hence, the functor \((j\overleftarrow{\times }\textrm{id})^*\) admits a left adjoint \((j\overleftarrow{\times }\textrm{id})_!\) by [ 7 , Proposition 9.2.4]. For a torsion ring \(\Lambda \) , we define a functor

to be the composite \(R({{\bar{f}}}\overleftarrow{\times }\textrm{id})_*\circ (j\overleftarrow{\times }\textrm{id})_!\) (cf. [ 18 , Construction 1.8]). Lemma 2.4 (together with [ 3 , 3.3]) implies that the composite \(R({{\bar{f}}}\overleftarrow{\times }\textrm{id})_*\circ (j\overleftarrow{\times }\textrm{id})_!\) is independent of the choice of a compactification up to a canonical isomorphism. Lemma 2.4 also implies the following:

Let notation be as in Lemma 2.4 . We assume that f is compactifiable. Then we have a canonical isomorphism

of functors \(D^+(X\overleftarrow{\times }_SS,\Lambda )\rightarrow D^+(Y'\overleftarrow{\times }_{S'}S',\Lambda )\) .

We consider a pair \((X,L_X)\) of a scheme X and a constructible closed subset \(L_X\) of X . We call such a pair a scheme with support. A morphism \(f:(X,L_X)\rightarrow (Y,L_Y)\) of schemes with support is a morphism \(f:X\rightarrow Y\) of schemes such that \(L_X\subset f^{-1}(L_Y)\) . We often regard \(L_X\) as a subscheme of X with the reduced scheme structure.

Let \(f:(X,L_X)\rightarrow (Y,L_Y)\) be a morphism of schemes with support such that \(f:X\rightarrow Y\) is compactifiable. Let \(\Lambda \) be a torsion ring and \(\mathcal F\) be an object of \(D^+(X,\Lambda )\) . We are interested in the complex \(R(f\overleftarrow{\times }\textrm{id})_!R\Psi _f\mathcal F\) on \(L_Y\overleftarrow{\times }_YY\) , where \(f\overleftarrow{\times }\textrm{id}\) denotes the natural morphism \(L_X\overleftarrow{\times }_YY\rightarrow L_Y\overleftarrow{\times }_YY\) , and where the restriction of \(R\Psi _f\mathcal F\) to \(L_X\overleftarrow{\times }_YY\) is also denoted by \(R\Psi _f\mathcal F\) . This complex plays a role of a family of nearby cycle cohomology, which was denoted by \(\Xi _f\mathcal F\) in the introduction: more precisely, with Notation 2.2 , for a point \(y\leftarrow z\) of the topos \(L_Y\overleftarrow{\times }_YY\) , the stalk of \(R(f\overleftarrow{\times }\textrm{id})_!R\Psi _f\mathcal F\) at \(y\leftarrow z\) is identified with the compactly supported cohomology of the sliced nearby cycle complex over \(y\leftarrow z\) for f , i.e., we have a canonical isomorphism

Construction 2.6

Let \(\mathcal F\) be an object of \(D^+(X,\Lambda )\) . We study a base change morphism for the complex \(R(f\overleftarrow{\times }\textrm{id})_!R\Psi _f\mathcal F\) . Let

be a Cartesian diagram of schemes with support (being Cartesian means that the underlying diagram of schemes is Cartesian and \({f'}^{-1}(L_{Y'})\cap {g'}^{-1}(L_X)=L_{X'}\) ). Recall that we have the base change morphism

where \(\overleftarrow{g'}\) is the natural morphism \(L_{X'}\overleftarrow{\times }_{Y'}Y'\rightarrow L_{X}\overleftarrow{\times }_YY\) (see the beginning of § 2.2 ). Combining this with the base change isomorphism in Lemma 2.5 , we obtain

where \(\overleftarrow{g}\) denotes the natural morphism \(L_{Y'}\overleftarrow{\times }_{Y'}Y'\rightarrow L_Y\overleftarrow{\times }_YY\) .

The morphism \(\alpha \) is not an isomorphism in general (see § 2.5 ).

By Lemma 2.5 , if the formation of \(R\Psi _f\mathcal F\) commutes with base change, then so does that of \(R(f\overleftarrow{\times }\textrm{id})_!R\Psi _f\mathcal F\) .

The morphism \(\alpha \) is an isomorphism if f is proper and if \(\Lambda \) is killed by an integer invertible on Y (even when the formation of \(R\Psi _f\mathcal F\) does not commute). In fact, for each point \(y'\leftarrow z'\) of \(Y'\overleftarrow{\times }_{Y'}Y'\) , by the proper base change theorem, the morphism induced by \(\alpha \) on the stalks is identified with the canonical morphism \(R\Gamma (X_z,\mathcal F)\rightarrow R\Gamma (X'_{z'},\mathcal F)\) , which is an isomorphism by the invariance of the étale cohomology under change of base separably closed field ([ 2 , Corollaire 1.6]).

It will be convenient to prepare the following notation.

Definition 2.8

For a morphism \(f:(X,L_X)\rightarrow (Y,L_Y)\) of schemes with support with \(f:X\rightarrow Y\) being compactifiable, we consider the natural morphism \(\overleftarrow{f}:L_X\overleftarrow{\times }_XX\rightarrow L_Y\overleftarrow{\times }_YY\) of topoi. We define a functor

by \(R\overleftarrow{f}_!=R(f\overleftarrow{\times }\textrm{id})_!R(\textrm{id}\overleftarrow{\times }f)_*\) .

Let \(f:(X,L_X)\rightarrow (Y,L_Y)\) be a morphism of schemes with support such that \(f:X\rightarrow Y\) is compactifiable. We take morphisms \((X,L_X)\overset{j}{\rightarrow }({{\bar{X}}},L_{{{\bar{X}}}})\overset{{{\bar{f}}}}{\rightarrow } (Y,L_Y)\) of schemes with support such that \({{\bar{f}}}:{{\bar{X}}}\rightarrow Y\) is a proper morphism, \(j:X\rightarrow {{\bar{X}}}\) and \(L_X\rightarrow L_{{{\bar{X}}}}\) are open immersions, and \({{\bar{f}}}j=f\) . Then we have a canonical isomorphism

where \(\overleftarrow{{{\bar{f}}}}\) denotes the natural morphism \(L_{{{\bar{X}}}}\overleftarrow{\times }_{{{\bar{X}}}}{{\bar{X}}}\rightarrow L_Y\overleftarrow{\times }_YY\) and \(\overleftarrow{j}\) denotes the natural open immersion \(L_X\overleftarrow{\times }_XX=L_X\overleftarrow{\times }_{{{\bar{X}}}}{{\bar{X}}}\rightarrow L_{{{\bar{X}}}}\overleftarrow{\times }_{{{\bar{X}}}}{{\bar{X}}}\) .

Consider the diagram of topoi

which induces a natural isomorphism

Its inverse induces a morphism

By adjunction, we obtain

Now let i denote the closed immersion \(Z=L_{{{\bar{X}}}}{\setminus } L_X\rightarrow L_{{{\bar{X}}}}\) . Then the base change morphism

is an isomorphism by the proof of [ 18 , Corollary 1.2]. Thus, the morphism ( 2.1 ) is an isomorphism, and hence, we obtain a canonical isomorphism \(R\overleftarrow{f}_!\cong R\overleftarrow{{{\bar{f}}}}_*\overleftarrow{j}_!\) .

\(\square \)

Let \(f:(X,L_X)\rightarrow (Y,L_Y)\) be a morphism of schemes with support such that \(f:X\rightarrow Y\) is compactifiable. We consider the following morphisms of topoi:

We note that, by Remark 2.1 , we have a canonical isomorphism \(R\overleftarrow{f}_!p_2^*\cong R(f\overleftarrow{\times }\textrm{id})_!R\Psi _f\) .

The following will be used (only) in the proof of Lemma 4.9 .

Construction 2.10

Again we consider a Cartesian diagram

of schemes with support. We consider the diagram

This induces a base change morphism

of functors \(D^+(L_X\overleftarrow{\times }_XX,\Lambda )\rightarrow D^+(L_{Y'}\overleftarrow{\times }_{Y'}Y',\Lambda )\) . For an object \(\mathcal F\) of \(D^+(X,\Lambda )\) , we have the following commutative diagram

in \(D^+(L_{Y'}\overleftarrow{\times }_{Y'}Y',\Lambda )\) .

2.4 Constructibility

For a scheme or a morphism of schemes, being coherent means being quasi-compact and quasi-separated.

Definition 2.11

([ 20 , §§8–9]) Let \(X\rightarrow S\) and \(Y\rightarrow S\) be coherent morphisms of coherent schemes. Let \(\Lambda \) be a noetherian ring. We say that a sheaf \(\mathcal F\) of \(\Lambda \) -modules on \(X\overleftarrow{\times }_SY\) is constructible if there exist partitions \(X=\coprod _{i\in I}X_i\) and \(Y=\coprod _{j\in J}Y_i\) by finitely many locally closed constructible subsets \(X_i\subset X\) and \(Y_j\subset Y\) such that the restriction of \(\mathcal F\) to the subtopos \(X_i\overleftarrow{\times }_SY_j\) is locally constant of finite type for every \((i,j)\in I\times J\) .

The full subcategory of the category of sheaves of \(\Lambda \) -modules on \(X\overleftarrow{\times }_SY\) consisting of constructible sheaves is a thick subcategory, i.e., closed under extensions. Thus, complexes \(\mathcal K\) such that the cohomology sheaves \(\mathcal H^i(\mathcal K)\) are constructible for all i form a triagulated subcategory of \(D^b(X\overleftarrow{\times }_SY,\Lambda )\) , which is denoted by \(D^b_c(X\overleftarrow{\times }_SY,\Lambda )\) .

Remark 2.12

Let \(f:X\rightarrow Y\) be a morphism of finite presentation of coherent schemes with Y having only finitely many irreducible components. Let \(\mathcal F\) be an object of \(D^b_c(X,{\mathbb {Z}}/n{\mathbb {Z}})\) , for an integer n invertible on Y . Then, by [ 20 , Théorème 8.1, Lemme 10.5], if the formation of \(R\Psi _f\mathcal F\) commutes with base change, then \(R\Psi _f\mathcal F\) is an object of \(D_c^b(X\overleftarrow{\times }_YY,{\mathbb {Z}}/n{\mathbb {Z}})\) .

Let \(f:(X,L_X)\rightarrow (Y,L_Y)\) be a morphism of schemes with support (§ 2.3 ) such that Y is a coherent scheme having only finitely many irreducible components and \(f:X\rightarrow Y\) is a separated morphism of finite presentation. Let n be an integer invertible on Y and \(\mathcal F\) an object of \(D^b_c(X,{\mathbb {Z}}/n{\mathbb {Z}})\) . We assume that the formation of \(R\Psi _f\mathcal F\) commutes with base change. Then the complex \(R(f\overleftarrow{\times }\textrm{id})_!R\Psi _f\mathcal F\) is an object of \(D^b_c(L_Y\overleftarrow{\times }_YY,{\mathbb {Z}}/n{\mathbb {Z}})\) , where \(f\overleftarrow{\times }\textrm{id}\) denotes the natural morphism \(L_X\overleftarrow{\times }_YY\rightarrow L_Y\overleftarrow{\times }_YY\) and \(R\Psi _f\mathcal F\) also denotes its restriction to \(L_X\overleftarrow{\times }_YY\) .

By Remark 2.12 , the complex \(R\Psi _f\mathcal F\) is an object of \(D^b_c(X\overleftarrow{\times }_YY,{\mathbb {Z}}/n{\mathbb {Z}})\) . Then the assertion follows from [ 20 , Proposition 10.2] together with a standard limit argument. \(\square \)

Remark 2.14

We only need to assume that the formation of \(R(f\overleftarrow{\times }\textrm{id})_!R\Psi _f\mathcal F\) (instead of \(R\Psi _f\mathcal F\) ) commutes with base change (which holds when f is proper as mentioned in Remark 2.7 .3). In fact, by [ 20 , Lemme 10.5], we may replace f with the base change along a modification \(Y'\rightarrow Y\) . Then, by [ 20 , Théorème 2.1], we may assume that the formation of \(R\Psi _f\mathcal F\) commutes with base change.

2.5 An example

Recall that the formation of \(R\Psi _f\mathcal F\) does not commute with base change in general (see [ 20 , §11] for an example). In this subsection, we give an example where the formation of \(R(f\overleftarrow{\times }\textrm{id})_!R\Psi _f\mathcal F\) does not commute with base change, and provide an explicit modification that makes the formation commute with base change.

Let A be a strictly henselian regular local ring and \(s,t\in A\) be a part of a system of regular parameters. Let \(\pi :\widetilde{Y}\rightarrow Y=\mathop {\textrm{Spec}}\nolimits A\) be the blowup along the ideal ( s ,  t ) and \(Z\subset \widetilde{Y}\) be the proper transform of the closed subscheme \(\mathop {\textrm{Spec}}\nolimits A/(t)\) of Y (so \(Z\cong \mathop {\textrm{Spec}}\nolimits A/(t)\) ). Let \(f:X=\widetilde{Y}{\setminus } Z\rightarrow Y\) denote the restriction of \(\pi \) . Let \(\Lambda \) be a noetherian torsion ring. Then the formation of \(R(f\overleftarrow{\times }\textrm{id})_!R\Psi _f\Lambda \) does not commute with base change.

To see this, we consider a strictly henselian discrete valuation ring \(A'\) together with a local homomorphism \(A/(t)\rightarrow A'\) such that the image of s is non-zero, and the induced morphism \(g:Y'\rightarrow Y\) (e.g., \(A'=\mathop {\textrm{Spec}}\nolimits A/(t,t_1,\ldots ,t_n)\) for a system of regular parameters \((s,t,t_1,\ldots ,t_n)\) of A ). Then, letting \(f'\) denote the base change \(X'=X\times _YY'\rightarrow Y'\) of f , we claim that the canonical morphism

from Construction 2.6 is not an isomorphism. In fact, as we show in the following claim, it is not an isomorphism at the point \(y\leftarrow \xi \) of the topos \(Y'\overleftarrow{\times }_{Y'}Y'\) , where y (resp. \(\xi \) ) denotes a closed (resp. generic) geometric point of \(Y'\) .

With Notation 2.2 , the complex of sliced nearby cycle cohomology over \(y\leftarrow \xi \) for f is nonzero, while that for \(f'\) is zero, i.e., we have

Since \(X'\times _{Y'}Y'_{(\xi )}=X\times _Y\xi =\emptyset \) , the second equality holds. We consider the distinguished triangle

By the proper base change theorem, the middle term is isomorphic to \(R\Gamma (\widetilde{Y}_\xi ,\Lambda )=R\Gamma (\xi ,\Lambda )= \Lambda \) . We claim that the 0-th cohomology group of the third term is not finitely generated, which we show by following the argument given in [ 20 , §11].

First of all, since \(Z_y\) consists of a single geometric point z , the third term is identified with \(R\Gamma (\widetilde{Y}_{(z)}\times _{Y}Y_{(\xi )},\Lambda )\) . Denoting the field of fractions of Y (resp. \(\widetilde{Y}_{(z)}\) , resp. \(Y_{(\xi )}\) ) by K (resp. \(K_{(z)}\) , resp. \(K_{(\xi )}\) ), the 0-th cohomology group of the latter complex is identified with \(\Gamma (\mathop {\textrm{Spec}}\nolimits (K_{(z)}\otimes _KK_{(\xi )}),\Lambda )\) . To show that this group is not finitely generated, we take an element \(f\in K\) which does not have zeros or poles at z (e.g., \(f=\frac{s+t}{s}\) ). Then, the \(\widetilde{Y}\) -scheme \(\widetilde{Y}[f^{\pm 1},f^{1/m}]\) is an étale neighborhood of z for any integer m that is prime to the characteristic of the residue field of A , and hence, the both \(K_{(z)}\) and \(K_{(\xi )}\) contain \(L=\bigcup _mK(f^{1/m})\) , which is an infinite algebraic extension of K . Since the natural map \(\Gamma (\mathop {\textrm{Spec}}\nolimits (L\otimes _KL),\Lambda )\rightarrow \Gamma (\mathop {\textrm{Spec}}\nolimits (K_{(z)}\otimes _KK_{(\xi )}),\Lambda )\) is injective, and since the source is not finitely generated, the assertion follows. \(\square \)

Let n be an integer that is invertible on Y (and take \(\Lambda \) to be \({\mathbb {Z}}/n{\mathbb {Z}}\) ). Similarly to [ 20 , §11], base changing along the blowup \(\widetilde{Y}\rightarrow Y\) makes the formation of \(R\Psi _f{\mathbb {Z}}/n{\mathbb {Z}}\) commute with base change.

We consider the second projection \(\textrm{pr}_2:\widetilde{Y}\times _Y\widetilde{Y}\rightarrow \widetilde{Y}\) and let \(\widetilde{f}:X\times _Y\widetilde{Y}\rightarrow \widetilde{Y}\) be the base change of f . Then the following hold.

The formation of \(R\Psi _{\textrm{pr}_2}{\mathbb {Z}}/n{\mathbb {Z}}\) commutes with base change. In particular, so does that of \(R\Psi _{\widetilde{f}}{\mathbb {Z}}/n{\mathbb {Z}}\) .

The formation of \(R(\widetilde{f}\overleftarrow{\times }\textrm{id})_!R\Psi _{\widetilde{f}}{\mathbb {Z}}/n{\mathbb {Z}}\) commutes with base change.

In the case where Y is the strict henselization of k [ s ,  t ] at the maximal ideal ( s ,  t ) for a separably closed field k , assertion 1 is explained in [ 20 , §11]. In general, it is proven by a “global-to-local” argument as in the proof of [ 20 , Proposition 6.1] (explained in the proof of Lemma 2.17 ).

As the formation of \(R(\widetilde{f}\overleftarrow{\times }\textrm{id})_!\) commutes with base change by Lemma 2.5 , assertion 2 follows from assertion 1. Since assertion 1 is a local problem, it suffices to show the claim about \(\textrm{pr}_2\) .

At each geometric point y of \(\widetilde{Y}\) , the base change \(X\times _Y\widetilde{Y}_{(y)}\) to \(\widetilde{Y}_{(y)}=\mathop {\textrm{Spec}}\nolimits B\) can be locally identified (over \(\widetilde{Y}_{(y)}\) ) with \(\mathop {\textrm{Spec}}\nolimits B[T]/(uT)\) for a nonzero element u of B . Since the problem is local, the assertion follows from Lemma 2.17 below. \(\square \)

Let \(S=\mathop {\textrm{Spec}}\nolimits B\) be an affine scheme, \(u\in B\) be a (non-zero) element, X be the S -scheme \(\mathop {\textrm{Proj}}\nolimits B[T_0,T_1]/(uT_1)\) , and \(f:X\rightarrow S\) denote the structural morphism. Then, for an integer n invertible in B , the formation of \(R\Psi _f{\mathbb {Z}}/n{\mathbb {Z}}\) commutes with base change.

We have to show that for any morphism \(S'\rightarrow S\) of schemes and any point \(x'\leftarrow t'\) of \(X'\overleftarrow{\times }_{S'}S'\) , where \(X'=X\times _SS'\) , the canonical morphism

is an isomorphism, where x , s , and \(s'\) (resp. t ) denote the geometric points induced by \(x'\) (resp. \(t'\) ).

When x maps into the open subset defined by \(u\ne 0\) , this holds as f is isomorphic on that locus. We note that, away from the locus where \(T_1=0\) , X maps smoothly onto \(Z=\mathop {\textrm{Spec}}\nolimits B/(u)\) and that the Milnor tube \(X_{(x)}\times _SS_{(t)}\) is identified with \(X_{(x)}\times _{Z}Z_{(t)}\) . Thus, by the local acyclicity of smooth morphisms ([ 1 , Théorème 2.1]), morphism ( 2.2 ) is an isomorphism when x maps into the open subset define by \(T_1\ne 0\) .

We now assume that x maps into the closed subset of X defined by \(u=T=0\) and show that the canonical morphism

is an isomorphism, where g denotes the natural morphism \(X'_{s'}\rightarrow X_s\) . Let C denotes the cone of this morphism. Then, by what we have observed above, it is supported on the closed subset defined by \(u=T=0\) of \(X'_{s'}\) , which consists of a single point, so that we have \(R\Gamma (X'_{s'},C)\cong C_{x'}\) . But, by the proper base change theorem, \(R\Gamma (X'_{s'},C)\) is identified with the cone of \(R\Gamma (X_t,{\mathbb {Z}}/n{\mathbb {Z}})\rightarrow R\Gamma (X'_{t'},{\mathbb {Z}}/n{\mathbb {Z}})\) . This last morphism is an isomorphism by the invariance of the étale cohomology group under change of separably closed base field ( [ 2 , Corollaire 1.6]). Thus, the assertion follows. \(\square \)

3 Preliminaries on analytic adic spaces

We refer to [ 8 , 9 ] for details on adic spaces.

3.1 Analytic adic spaces

We first recall from [ 9 , 1.9] the analytic adic space associated to a formal scheme. We consider a formal scheme \(\mathfrak X\) satisfying the following condition from [ 9 , 1.9]:

Any point of \(\mathfrak X\) admits an affine neighborhood \(\mathop {\textrm{Spf}}\nolimits A\subset \mathfrak X\) such that the topology of A is \(\varpi \) -adic for some element \(\varpi \in A\) and the ring \(A[1/\varpi ]\) equipped with the topology induced from A is a strongly noetherian Tate ring (see [ 8 , §2] or [ 9 , 1.1] for the definition of being strongly noetherian).

Then we can consider the analytic adic space \(d(\mathfrak X)\) associated to \(\mathfrak X\) defined in [ 9 , Proposition 1.9.1]: if \(\mathfrak X=\mathop {\textrm{Spf}}\nolimits A\) is affine with the topology of A being \(\varpi \) -adic for some \(\varpi \in A\) and if \(A[1/\varpi ]\) is strongly noetherian, then \(d(\mathfrak X)=\mathop {\textrm{Spa}}\nolimits (A[1/\varpi ],A^+)\) , where \(A^+\) is the integral closure of A in \(A[1/\varpi ]\) . The adic space \(d(\mathfrak X)\) comes with a natural morphism \(\lambda _{\mathfrak X}:d(\mathfrak X)\rightarrow \mathfrak X\) of topologically ringed spaces. It induces a natural morphism \(d(\mathfrak X)_\mathrm{\acute{e}t}\rightarrow \mathfrak X_\mathrm{\acute{e}t}\) of sites as in [ 9 , Lemma 3.5.1], which we denote again by \(\lambda _{\mathfrak X}\) and call the specialization morphism. In this article we focus on formal schemes coming from schemes.

Definition 3.1

Let X be a scheme and \(X_0\) the closed subset defined by vanishing of a locally finitely generated ideal sheaf. Consider the formal completion \(\widehat{X}\) of X along a locally finitely generated ideal sheaf defining \(X_0\) (note that \(\widehat{X}\) is independent of the choice of a locally finitely generated ideal sheaf). The pair \((X,X_0)\) is called an admissible pair if \(\widehat{X}\) satisfies the condition (*). A morphism \((X,X_0)\rightarrow (Y,Y_0)\) of admissible pairs is a morphism \(f:X\rightarrow Y\) of schemes such that \(X_0=f^{-1}(Y_0)\) .

For an admissible pair \((X,X_0)\) , let \(\widehat{X}\) denote the formal completion of X along a locally finitely generated ideal sheaf defining \(X_0\) and let \((X,X_0)^a\) be the associated analytic adic space \(d(\widehat{X})\) . The assignment \((X,X_0)\mapsto (X,X_0)^a\) defines a functor from the category of admissible pairs to that of analytic adic spaces. If there is no risk of confusion, we simply write \(X^a\) for \((X,X_0)^a\) .

Let U denote the complementary open \(X\setminus X_0\) . The adic space \(X^a\) comes with the following two natural morphisms of sites;

\(\lambda _X:X^a_\mathrm{\acute{e}t}\rightarrow X_{0,\mathrm{\acute{e}t}}\) defined to be the composite of the specialization morphism \(\lambda _{\widehat{X}}:X^a_\mathrm{\acute{e}t}\rightarrow \widehat{X}_\mathrm{\acute{e}t}\) and the natural equivalence \(\widehat{X}_\mathrm{\acute{e}t}\cong X_{0,\mathrm{\acute{e}t}}\) ,

\(\varphi _X:X^a_\mathrm{\acute{e}t}\rightarrow U_\mathrm{\acute{e}t}\) defined in [ 9 , 3.5.12], which we call the analytification morphism.

Example 3.2

Let k be a non-archimedean field and X a scheme locally of finite type over \(k^\circ \) . Then we can form an admissible pair \((X,X_0)\) by letting \(X_0\) be the closed fiber of X . Then the analytic adic space \((X,X_0)^a\) is nothing but the Raynaud generic fiber ([ 21 , 8 , Remark 4.6.ii], [ 9 , Example 1.9.2.ii]) viewed as an adic space, which is denoted by \(X^\textrm{rig}\) . Similarly, for a morphism \(f:X\rightarrow Y\) , we denote the associated morphism \(X^\textrm{rig}\rightarrow Y^\textrm{rig}\) by \(f^\textrm{rig}\) . For a sheaf \(\mathcal F\) on \(X_\mathrm{\acute{e}t}\) , we denote the pullback \(\varphi _X^*\mathcal F\) by \(\mathcal F^\textrm{rig}\) .

3.2 Analytic pseudo-adic spaces

In the proof of Theorem 1.2 , we will need to consider geometric points of adic spaces, for which we need to work with the framework of pseudo-adic spaces. We refer to [ 9 , 1.10] for details on pseudo-adic spaces. Let us just recall that a pseudo-adic space is a pair \(X=({\underline{X}},|X|)\) of an adic space \({\underline{X}}\) and a subset | X | of \({\underline{X}}\) satisfying certain conditions. A morphism \(f:({\underline{X}},|X|)\rightarrow ({\underline{Y}},|Y|)\) of pseudo-adic spaces is a morphism \(f:{\underline{X}}\rightarrow {\underline{Y}}\) of adic spaces such that \(f(|X|)\subset |Y|\) . We often regard an adic space X as a pseudo-adic space via the fully faithful functor \(X\mapsto (X,X)\) from the category of adic spaces to that of pseudo-adic spaces.

As in [ 9 , 3.5.3], to a pair \((\mathfrak X,L)\) of a formal scheme \(\mathfrak X\) satisfying (*) and a locally closed subset L of \(\mathfrak X\) , we can associate an analytic pseudo-adic space \((d(\mathfrak X),\lambda _{\mathfrak X}^{-1}(L))\) , which is denoted by \(d(\mathfrak X,L)\) . It comes with a natural morphism \(\lambda _{(\mathfrak X,L)}:d(\mathfrak X,L)_\mathrm{\acute{e}t}\rightarrow L_\mathrm{\acute{e}t}\) of sites [ 9 , 3.5.3, 3.5.5], where L is regarded as a subscheme of \(\mathfrak X\) with reduced scheme structure. We call \(\lambda _{(\mathfrak X,L)}\) the specialization morphism.

We define an algebro-geometric datum which gives an analytic pseudo-adic space.

Definition 3.3

An admissible triple is a triple \((X,X_0,L)\) with \((X,X_0)\) being an admissible pair (Definition 3.1 ) and L being a constructible closed subset of \(X_0\) . A morphism \((X,X_0,L)\rightarrow (Y,Y_0,M)\) of admissible triples is a morphism \(f:(X,X_0)\rightarrow (Y,Y_0)\) of admissible pairs such that \(f(L)\subset M\) .

For an admissible triple \((X,X_0,L)\) , we can consider the pseudo-adic space \(d(\widehat{X},L)\) associated to the pair \((\widehat{X},L)\) , which we denote by \((X,X_0,L)^a\) , or simply by \(X^a\) . The assignment \((X,X_0,L)\mapsto (X,X_0,L)^a\) defines a functor from the category of admissible triples to that of analytic pseudo-adic spaces. We often regard L as a closed subscheme with reduced scheme structure. By taking L to be \(X_0\) , we recover the adic space associated to the admissible pair \((X,X_0)\) , that is, we have \((X,X_0,X_0)^a=(X,X_0)^a\) .

Let \((X,X_0,L)\) be an admissible triple and U denote the open subscheme \(X\setminus X_0\) . Similarly to the case of admissible pairs, the associated analytic pseudo-adic space \(X^a\) comes with the two natural morphisms of sites;

the specialization morphism \(\lambda _X=\lambda _{(\widehat{X},L)}:X^a_\mathrm{\acute{e}t}\rightarrow L_\mathrm{\acute{e}t}\) ,

\(\varphi _X:X^a_\mathrm{\acute{e}t}\rightarrow U_\mathrm{\acute{e}t}\) defined to be the composite \(X^a_\mathrm{\acute{e}t}=(X,X_0,L)^a_\mathrm{\acute{e}t}\rightarrow (X,X_0)^a_\mathrm{\acute{e}t}\rightarrow U_\mathrm{\acute{e}t}\) .

Important examples of admissible triples are those coming from schemes of finite type over a microbial valuation ring. Recall that a valuation ring B is called microbial if B has a prime ideal of height one ([ 9 , Definition 1.1.4]). For instance, any finitely dimensional valuation ring is microbial.

Definition 3.4

[cf. [ 9 , Example 1.9.2.i]] Let B be a microbial valuation ring. The admissible triple \((S,S_0,L_S)\) associated to B is defined as follows. Put \(S=\mathop {\textrm{Spec}}\nolimits B\) , let \(S_0\) be the closed set defined by vanishing of the unique height one prime ideal \({\mathfrak {p}}\) of B , and \(L_S\) the singleton consisting of the closed point of S . Note that, as a finitely generated ideal defining \(S_0\) , we can take the ideal generated by a nonzero element of \({\mathfrak {p}}\) .

Let a be a nonzero element of \({\mathfrak {p}}\) . Note that the a -adic topology on B coincides with the valuation topology, and hence the formal completion of S along the ideal generated by a is isomorphic to the formal spectrum \(\mathop {\textrm{Spf}}\nolimits B\) with B being equipped with the valuation topology.

Let K denote the field of fractions of B and \(S^a\) the pseudo-adic space associated to \((S,S_0,L_S)\) . Then the analytification morphism \(\varphi _S:S^a\rightarrow \mathop {\textrm{Spec}}\nolimits K\) gives an equivalence of topoi [ 9 , Proposition 2.3.10]. In particular, if K is separably closed, then the topos \(S^a\) is equivalent to the punctual topos.

Example 3.6

Let \((Y,Y_0,L_Y)\) be an admissible triple and \(Y^a\) denote the associated pseudo-adic space. Let \(\xi =(\mathop {\textrm{Spa}}\nolimits (\kappa (\xi ),\kappa (\xi )^+),\{*\})\rightarrow Y^a\) be a geometric point, i.e, \(\kappa (\xi )^+\) is a microbial valuation ring with separably closed field of fractions \(\kappa (\xi )\) and \(*\) is the closed point of \(\mathop {\textrm{Spa}}\nolimits (\kappa (\xi ),\kappa (\xi )^+)\) ( [ 9 , Definition 2.5.1]). Let \((S,S_0,L)\) denote the pseudo-adic space associated to the microbial valuation ring \(\kappa (\xi )^+\) . Then \(\xi \) is identified with the pseudo-adic space \(S^a\) associated to the admissible triple \((S,S_0,L)\) . Note that we have a natural morphism \((S,S_0,L_S)\rightarrow (Y,Y_0,L_S)\) of admissible triples. The associated morphism \(S^a\rightarrow Y^a\) is canonically identified with the geometric point \(\xi \rightarrow Y^a\) .

3.3 Adic spaces and vanishing topoi

For an admissible triple \((X,X_0,L)\) , we construct a canonical morphism \(\widetilde{\lambda }_X:X^a\rightarrow L\overleftarrow{\times }_XX\) of topoi (cf. [ 13 , 6.4]). We denote the complement of \(X_0\) by U . Then we have a natural diagram of topoi

with a natural 2-map \(\tau :j\varphi _X\rightarrow i\lambda _X\) defined as follows (cf. the proof of [ 9 , Theorem 3.5.13]): For an object V of \(X_\mathrm{\acute{e}t}\) , we have a natural morphism

from [ 9 , 1.9.5], which induces, for a sheaf \(\mathcal F\) on \((X^a)_\mathrm{\acute{e}t}\) , a morphism

Thus, by the universal property of the vanishing topos \(L\overleftarrow{\times }_XU\) , the above diagram induces a canonical morphism of topoi

We denote the composite \(X^a\rightarrow L\overleftarrow{\times }_XU\rightarrow L\overleftarrow{\times }_XX\) also by \(\widetilde{\lambda }_X\) when there is no risk of confusion.

4 Compactly supported direct image for rigid analytic varieties

Our main interest in this section is the compactly supported direct image \(Rf^a_!\) for a morphism \(f:(X,X_0,L_X)\rightarrow (Y,Y_0,L_Y)\) of admissible triples (Definition 3.3 ) with \(f:X\rightarrow Y\) compactifiable, where \(f^a\) denotes the induced morphism \(X^a\rightarrow Y^a\) of analytic pseudo-adic spaces.

We note that a compactification of \(f:X\rightarrow Y\) induces a compactification of \(f^a:X^a\rightarrow Y^a\) . More precisely, we make the following construction.

Construction 4.1

Let \({{\bar{f}}}:{{\bar{X}}}\rightarrow Y\) be a proper morphism with an open immersion \(j:X\rightarrow {{\bar{X}}}\) such that \(f={{\bar{f}}}j\) . Let \({{\bar{X}}}_0\) be the pullback \({{\bar{f}}}^{-1}(Y_0)\) and \(L_{{{\bar{X}}}}\) be the closure of \(L_X\) in \({{\bar{X}}}_0\) , so that we have morphisms \((X,X_0,L_X)\overset{j}{\rightarrow }({{\bar{X}}},{{\bar{X}}}_0,L_{{{\bar{X}}}})\overset{{{\bar{f}}}}{\rightarrow }(Y,Y_0,L_Y)\) of admissible triples whose composite is f . Let \({{\bar{X}}}^a\) denote the pseudo-adic space associated to \(({{\bar{X}}},{{\bar{X}}}_0,L_{{{\bar{X}}}})\) . Then \(j^a:X^a\rightarrow {{\bar{X}}}^a\) is an open immersion and \({{\bar{f}}}^a:{{\bar{X}}}^a\rightarrow Y^a\) is a proper morphism (this can be checked using [ 9 , Corollary 1.3.9, Lemma 1.3.10], see also [ 19 , Lemma 3.5]). Thus, by the definition of the compactly supported direct image [ 9 , Definition 5.4.4], we have an identification \(Rf^a_!=R{{\bar{f}}}^a_*\circ j^a_!\) of functors \(D^+(X^a,\Lambda )\rightarrow D^+(Y^a,\Lambda )\) , for a torsion ring \(\Lambda \) .

4.1 Cohomology of fibers via nearby cycle

Let \((X,X_0,L)\) be an admissible triple (Definition 3.3 ) and U the complement of \(X_0\) . For a torsion ring \(\Lambda \) and an object \(\mathcal F\) of \(D^+(U,\Lambda )\) , we put \(\mathcal F^a=\varphi _X^*\mathcal F\) . The diagram ( 3.1 ) induces a canonical morphism

which is an isomorphism by the proof of [ 9 , Corollary 3.5.15] (cf. [ 5 , Theorem 6.5.4]).

Here, we give an interpretation of the canonical morphism ( 4.1 ) via vanishing topos. We consider the diagram of topoi

with canonical 2-morphisms \(jp_2\rightarrow ip_1\) and \(p_1\widetilde{\lambda }_{X}\cong \lambda _X\) . This diagram induces the morphisms

whose composite is identified with the morphism ( 4.1 ).

The two morphisms in ( 4.3 ) are isomorphisms.

The first one is an isomorphism by [ 14 , Théorème 2.4], and so is the second, since the composite is an isomorphism as mentioned above. \(\square \)

Construction 4.3

Let \((S,S_0,L_S)\) be the admissible triple associated to a microbial valuation ring with separably closed field of fractions (Definition 3.4 ). Let \(f:(X,X_0,L_X)\rightarrow (S,S_0,L_S)\) be a morphism of admissible triples with \(f:X\rightarrow S\) being locally of finite type. Then we have the associated morphism \(f^a:X^a\rightarrow S^a\) of pseudo-adic spaces, which is locally of finite type.

We denote the generic point (resp. closed point) of S by \(\eta \) (resp. s ). For a torsion ring \(\Lambda \) and a sheaf \(\mathcal F\) of \(\Lambda \) -modules on \(X_{\eta ,\mathrm{\acute{e}t}}\) , we consider the nearby cycle complex \(R\psi _S\mathcal F=i^*Rj_*\mathcal F\) over S , where j is the natural open immersion \(X_\eta \rightarrow X\) and i is the natural closed immersion \(X_s\rightarrow X\) . We denote by \(\mathcal F^a\) the pullback of \(\mathcal F\) by the analytification morphism \(\varphi _X:X^a_\mathrm{\acute{e}t}\rightarrow X_{\eta ,\mathrm{\acute{e}t}}\) . Then the canonical isomorphism \(R\psi _S\mathcal F\cong R\lambda _{X*}\mathcal F^a\) induces a canonical isomorphism

Construction 4.4

In the situation of Construction 4.3 , we assume that the morphism \(f:X\rightarrow S\) is compactifiable. We recall the construction of a canonical isomorphism from [ 9 , Theorem 5.7.8]

We take a proper morphism \({{\bar{f}}}:{{\bar{X}}}\rightarrow S\) with an open immersion \(j:X\rightarrow {{\bar{X}}}\) such that \(f={{\bar{f}}}j\) . Let \({{\bar{X}}}_0\) be the pullback \({{\bar{f}}}^{-1}(S_0)\) and \(L_{{{\bar{X}}}}\) be the closure of \(L_X\) in \({{\bar{X}}}_0\) , so that we have morphisms \((X,X_0,L_X)\overset{j}{\rightarrow }({{\bar{X}}},{{\bar{X}}}_0,L_{{{\bar{X}}}})\overset{{{\bar{f}}}}{\rightarrow }(S,S_0,L_S)\) of admissible triples whose composite is f . The induced morphism \({{\bar{f}}}^a:{{\bar{X}}}^a\rightarrow S^a\) is proper, and \(j^a:X^a\rightarrow {{\bar{X}}}^a\) is an open immersion, as recalled in the beginning of this section. We consider the diagram of topoi

The isomorphism \(R\psi _S\mathcal F\cong R\lambda _{X*}\mathcal F^a\) and the canonical isomorphism \(j_!R\lambda _{X*}\cong R\lambda _{{{\bar{X}}}*}j^a_!\) from [ 9 , Corollary 3.5.11] induce

4.2 Compactly supported direct image via nearby cycles over general bases

We globalize Huber’s construction of the isomorphism between the étale cohomology of an algebraizable rigid analytic variety and the nearby cycle cohomology.

We frequently use the fact that the étale topos of any pseudo-adic space has enough points ([ 9 , Proposition 2.5.5], see also [ 9 , Proposition 2.5.17]).

Construction 4.5

Let \(f:(X,X_0,L_X)\rightarrow (Y,Y_0,L_Y)\) be a morphism of admissible triples (Definition 3.3 ) and let \(f^a:X^a\rightarrow Y^a\) denote the induced morphism of analytic pseudo-adic spaces. We consider the natural diagram of topoi

Here \(\widetilde{\lambda }_X\) and \(\widetilde{\lambda }_Y\) denote the morphisms defined in § 3.3 . We denote the natural morphism \(L_X\overleftarrow{\times }_XX\rightarrow L_Y\overleftarrow{\times }_YY\) by \(\overleftarrow{f}\) . The diagram above induces the base change morphism \(\widetilde{\lambda }_Y^*R\overleftarrow{f}_*\rightarrow Rf^{a}_*\widetilde{\lambda }_X^*\) .

Let \(\Lambda \) be a ring and \(\mathcal F\) be an object of \(D^+(X,\Lambda )\) . Note that we have canonical isomorphisms \(R\Psi _f\mathcal F\cong R(\textrm{id}\overleftarrow{\times }f)_*R\Psi _\textrm{id}\mathcal F\cong R(\textrm{id}\overleftarrow{\times }f)_*p_2^*\mathcal F\) from Remark 2.1 . Thus, the base change morphism \(\widetilde{\lambda }_Y^*R\overleftarrow{f}_*\rightarrow Rf^{a}_*\widetilde{\lambda }_X^*\) induces

We also give a variant for higher direct image with compact support. For the construction, we use the following lemma.

Let \(j:(X,X_0,L_X)\rightarrow ({{\bar{X}}},{{\bar{X}}}_0,L_{{{\bar{X}}}})\) be a morphism of admissible triples such that \(j:X\rightarrow {{\bar{X}}}\) is an open immersion and that the image of \(L_X\) is open in \(L_{{{\bar{X}}}}\) . Let \(j^a:X^a\rightarrow {{\bar{X}}}^a\) denote the induced open immersion of analytic pseudo-adic spaces. We consider the diagram of topoi

Let \(\Lambda \) be a ring. Then the natural morphism

of functors \(D^+(L_X\overleftarrow{\times }_XX,\Lambda )\rightarrow D^+({{\bar{X}}}^a,\Lambda )\) is an isomorphism.

Let \(\mathcal F\) be an object of \(D^+(L_X\overleftarrow{\times }_XX,\Lambda )\) . We show that, for each geometric point \(\xi \) of \({{\bar{X}}}^a\) , the morphism \((j^a_!\widetilde{\lambda }_X^*\mathcal F)_\xi \rightarrow (\widetilde{\lambda }_{{{\bar{X}}}}^*\overleftarrow{j}_!\mathcal F)_\xi \) induced on the stalks is an isomorphism. For this, it suffices to show that \(\xi \) lies over \(X^a\) if \(x\leftarrow \xi \) lies over \(L_X\overleftarrow{\times }_XX\) , where \(x\leftarrow \xi \) denotes, by abuse of notation, the image of \(\xi \) by \(\widetilde{\lambda }_{{{\bar{X}}}}\) . Since \(x\leftarrow \xi \) lies over \(L_X\overleftarrow{\times }_XX\) if and only if x lies over \(L_X\) , the assertion follows from the fact that \(\lambda _{{{\bar{X}}}}^{-1}(L_X)=X^a\) as a subset of \({{\bar{X}}}^a\) . \(\square \)

Construction 4.7

Let \(f:(X,X_0,L_X)\rightarrow (Y,Y_0,L_Y)\) be a morphism of admissible triples (Definition 3.3 ) and let \(f^a:X^a\rightarrow Y^a\) denote the induced morphism. We now assume that \(f:X\rightarrow Y\) is compactifiable and let \((X,X_0,L_X)\overset{j}{\rightarrow }({{\bar{X}}},{{\bar{X}}}_0,L_{{{\bar{X}}}})\overset{{{\bar{f}}}}{\rightarrow }(Y,Y_0,L_Y)\) be a decomposition as in Construction 4.1 .

Let \({{\bar{X}}}^a\) denote the pseudo-adic space associated to \(({{\bar{X}}},{{\bar{X}}}_0,L_{{{\bar{X}}}})\) . Then \(j^a:X^a\rightarrow {{\bar{X}}}^a\) is an open immersion and \({{\bar{f}}}^a:{{\bar{X}}}^a\rightarrow Y^a\) is a proper morphism, as recalled in the beginning of this section.

Let \(\Lambda \) be a torsion ring. Then we have the following sequence of canonical morphisms of functors \(D^+(L_X\overleftarrow{\times }_XX,\Lambda )\rightarrow D^+(Y^a,\Lambda )\) ;

where the first isomorphism comes from Lemma 2.9 , the second is the base change morphism induced by the diagram ( 4.5 ) for \({{\bar{f}}}:{{\bar{X}}}\rightarrow Y\) , and the third one comes from Lemma 4.6 .

Let \(\mathcal F\) be an object of \(D^+(X,\Lambda )\) . By considering \(p_2^*\mathcal F\) , we obtain a canonical morphism

To state the compatibility of the canonical morphism \(\theta _f\) with base change, we make the following construction.

Construction 4.8

be a commutative diagram of admissible triples. We assume that \(f:X\rightarrow Y\) is compactifiable and that the diagram is Cartesian, i.e, the diagram

is a Cartesian diagram of schemes and \({f'}^{-1}(L_{Y'})\cap {g'}^{-1}(L_{X})=L_{X'}\) .

Then, for a torsion ring \(\Lambda \) and an object \(\mathcal F\) of \(D^+(X,\Lambda )\) , we have the base change morphism

defined in Construction 2.6 . On the other hand, we have a Cartesian diagram

of pseudo-adic spaces, which induces the base change morphism

Thus, we have the diagram

in \(D^+({Y'}^a,\Lambda )\) .

The diagram ( 4.6 ) is commutative.

If the formation of \(R\Psi _f\mathcal F\) commutes with base change, then the morphism \(\alpha \) is an isomorphism.

The morphism \(\beta \) is an isomorphism if one of the following conditions is satisfied:

\(\Lambda \) is killed by an integer invertible in Y ,

\((Y',Y'_0,L_{Y'})\) is the admissible triple associated to a geometric point \(\xi \) of \(Y^a\) (Example 3.6 ) and \(g:(Y',Y'_0,L_{Y'})\rightarrow (Y,Y_0,L_Y)\) is the natural morphism.

1. By Construction 2.10 , the morphism \(\alpha \) is identified with the base change morphism

induced by the diagram

Thus, both of \(\theta _{f'}\circ \widetilde{\lambda }_{Y'}^*\alpha \) and \(\beta \circ ({g^a})^*\theta _{f}\) are identified with the base change morphism induced by the diagram

2. This is clear from the definition of \(\alpha \) .

3. This follows from [ 9 , Theorem 5.3.9, Corollary 5.3.10]. \(\square \)

Let \((S,S_0,L_S)\) be the admissible triple associated to a microbial valuation ring with separably closed field of fractions (Definition 3.4 ). Let \(f:(X,X_0,L_X)\rightarrow (S,S_0,L_S)\) be a morphism of admissible triples with \(f:X\rightarrow S\) being compactifiable. Let \(\Lambda \) be a torsion ring and \(\mathcal F\) an object of \(D^+(X,\Lambda )\) . Then the morphism

in \(D^+(S^a,\Lambda )\) is identified with the morphism ( 4.4 ) in Construction 4.4 via the equivalence \(R\Gamma (S^a,-):D^+(S^a,\Lambda )\cong D^+(\Lambda )\) (Remark 3.5 .2), and hence is an isomorphism.

Since \(S^a\) and \(L_S\overleftarrow{\times }_S\eta \) , where \(\eta \) is the generic point of S , are equivalent to the punctual topos, the morphism ( 4.7 ) is identified with the morphism

induced by the adjunction morphism \(\theta :p_2^*\mathcal F\rightarrow R\widetilde{\lambda }_{X*}\widetilde{\lambda }_X^*p_2^*\mathcal F=R\widetilde{\lambda }_{X*}\mathcal F^a\) . We consider the diagram of topoi

The morphism ( 4.8 ) is identified with the morphism

induced from the above diagram. Then the assertion follows from Lemma 4.2 . \(\square \)

Theorem 4.11

Let \(f:(X,X_0,L_X)\rightarrow (Y,Y_0,L_Y)\) be a morphism of admissible triples (Definition 3.3 ) with \(f:X\rightarrow Y\) being compactifiable. Let \(\Lambda \) be a torsion ring and \(\mathcal F\) an object of \(D^+(X,\Lambda )\) . We assume that the formation of \(R\Psi _f\mathcal F\) commutes with base change. Then the morphism

from Construction 4.7 is an isomorphism.

We prove that \(\theta _f\) induces an isomorphism of the stalks at each geometric point \(\xi \) of \(Y^a\) . Example 3.6 shows that we have the natural morphism \((S,S_0,L_S)\rightarrow (Y,Y_0,L_Y)\) of admissible triples such that the associated morphism \(S^a\rightarrow Y^a\) of pseudo-adic spaces is canonically identified with the geometric point \(\xi \rightarrow Y^a\) . By forming a Cartesian diagram

of admissible triples and applying Lemma 4.9 to it, the problem is reduced to the case where \((Y,Y_0,L_Y)=(S,S_0,L_S)\) . Then the assertion follows from Lemma 4.10 . \(\square \)

Proof (Proof of Theorem 1.2)

[Proof of Theorem 1.2 ] Follows from Theorem 4.11 and [ 20 , Théorème 2.1].

Remark 4.12

In Theorem 4.11 , it is strictly necessary to assume that the formation of \(R\Psi _f\mathcal F\) commutes with base change as seen in Example 4.13 below. See also Remark 5.6 .1.

It seems impossible to give a similar comparison isomorphism for \(Rf^a_*\) (see Remark 5.6 .2).

We now explicitly see that \(\theta _f\) can be non-isomorphic.

Example 4.13

We let k be a strictly henselian discrete valuation field and use the notation established in Example 3.2 . We fix a uniformizor \(\varpi \in k^\circ \) . Let A be a regular ring that is flat and of finite type over \(k^\circ \) and \(Y=\mathop {\textrm{Spec}}\nolimits A\) . We take a regular sequence \(s,t\in A\) satisfying the following three conditions (we assume that there exists such a regular sequence: see below for explicit choices).

\(Z=\mathop {\textrm{Spec}}\nolimits A/(t)\) is regular and flat over \(k^\circ \) ,

A /( s ,  t ) is regular,

\(A/(\varpi ,s,t)\ne 0\) .

Let \(\pi :\widetilde{Y}\rightarrow Y\) be the blowup along the ideal ( s ,  t ). We consider the complement X of the proper transform of Z and let \(f:X\rightarrow Y\) denote the restriction of \(\pi \) . Then the canonical morphism

from Construction 4.7 is not an isomorphism.

To see this, we take a maximal ideal \(\mathfrak m\) of A that contains \((\varpi ,s,t)\) , which exists by c), and then take a prime ideal \(\mathfrak p\subset \mathfrak m\) that is maximal among those satisfying \(t\in \mathfrak p\) and \(s\varpi \notin \mathfrak p\) , which exists as \(s\varpi \ne 0\) in A /( t ) by a). Then, we consider the normalization \(A'\) of the integral local domain \(A/\mathfrak p\) , which is a finite extension of \(k^\circ \) . Setting \(Y'=\mathop {\textrm{Spec}}\nolimits A'\) , we obtain a morphism \((Y')^\textrm{rig}\rightarrow Y^\textrm{rig}\) . Let \(\nu \) be a geometric point of \((Y')^\textrm{rig}\) . Then the stalk of the right hand side at \(\nu \) is zero since \(X^\textrm{rig}\times _{Y^\textrm{rig}}(Y')^\textrm{rig}=\emptyset \) .

On the other hand, the stalk of the left hand side is described as follows. Let \(\nu _s\) (resp. \(\nu _\eta \) ) be the closed (resp. generic) geometric point of \(Y'\) . Then, by construction (see § 2.3 and § 3.3 ), we have a canonical isomorphism

The latter complex is non-zero by Claim 2.15 . Thus, the morphism \(\theta _f\) is not an isomorphism.

Let n be an integer invertible in \(k^\circ \) and take \(\Lambda \) to be \({\mathbb {Z}}/n{\mathbb {Z}}\) . Then the morphism \(\theta _f\) becomes an isomorphism after base changing along \(\pi :\widetilde{Y}\rightarrow Y\) . More precisely, let \(\widetilde{f}:X\times _Y\widetilde{Y}\rightarrow \widetilde{Y}\) be the base change of f . Then, by Claim 2.16 , the formation of \(R\Psi _{\widetilde{f}}{\mathbb {Z}}/n{\mathbb {Z}}\) commutes with base change. Thus, the morphism \(\theta _{\widetilde{f}}\) is an isomorphism by Theorem 4.11 .

The above example includes the following two suggestive cases.

When \(A=k^\circ [T]\) , \(s=\varpi \) , \(t=T\) , the blowup \(\pi :\widetilde{Y}\rightarrow Y\) is an admissible blowup and the morphism \(f^\textrm{rig}:X^\textrm{rig}\rightarrow Y^\textrm{rig}\) is identified with the natural open immersion from the annuli defined by \(|\varpi |\le |T|\le 1\) to the unit disk. In this case, we can take \(\nu \) to be a geometric point over the origin of the unit disk \(Y^\textrm{rig}\) .

When \(A=\mathop {\textrm{Spec}}\nolimits k^\circ [S,T]\) , \(s=S\) , \(t=T\) , the morphism \(f^\textrm{rig}:X^\textrm{rig}\rightarrow Y^\textrm{rig}\) is identified with the morphism f in [ 11 , Example 2.2], or equivalently with the morphism \(\mathop {\textrm{Spa}}\nolimits (k\langle S,T\rangle ,k^\circ \langle S,T\rangle )\rightarrow \mathop {\textrm{Spa}}\nolimits (k\langle S,T\rangle ,k^\circ \langle S,T\rangle )\) given by \((S,T)\mapsto (ST,T)\) . In this case, we can take \(\nu \) to be a geometric point over the point \((\varpi ,0)\in (k^\circ )^2=Y^\textrm{rig}(k)\) .

5 Quasi-constructibility

In § 5.1 , we state and deduce from Theorem 4.11 our finiteness result (Theorem 5.5 ). In § 5.2 , we focus on the case where the target is the 2-dimensional disk to give a concrete consequence (Corollary 5.11 ) of Theorem 5.5 .

5.1 Modification and finiteness

Definition 5.1.

Let \(\mathsf X\) be an analytic pseudo-adic space which is quasi-compact and quasi-separated. Let \(\Lambda \) be a noetherian ring.

Let \(\mathsf F\) be a sheaf of \(\Lambda \) -modules on \(\mathsf X\) . We say that \(\mathsf F\) is strictly quasi-constructible if there exist a finite partition \(\mathsf X=\coprod _{i\in I}\mathsf L_i\) by locally closed constructible subsets \(\mathsf L_i\) and a finite partition \(\mathsf X=\coprod _{j\in J} \mathsf Z_j\) by Zariski locally closed subsets \(\mathsf Z_j\) such that the restriction of \(\mathsf F\) to \(\mathsf L_i\cap \mathsf Z_j\) is locally constant of finite type for every \((i,j)\in I\times J\) .

Let \(\mathsf F\) be an object of \(D^b(\mathsf X,\Lambda )\) . We say that \(\mathsf F\) is strictly quasi-constructible if the all cohomology sheaves \(\mathcal H^i(\mathsf F)\) are strictly quasi-constructible.

If \(\mathsf F\) is strictly quasi-constructible, then \(\mathsf F\) is quasi-constructible in the sense of [ 11 , Definition 1.1].

Let \((X,X_0,L_X)\) be an admissible triple (Definition 3.3 ) with X being quasi-compact and quasi-separated and let \(X^a\) denote the associated analytic pseudo-adic space (§ 3.2 ). We consider the natural morphism \(\widetilde{\lambda }_X:X^a\rightarrow L_X\overleftarrow{\times }_XU\) defined in § 3.3 , where U is the complement of \(X_0\) . Let \(\Lambda \) be a noetherian ring and \(\mathcal K\) an object of \(D_c^b(L_X\overleftarrow{\times }_XU,\Lambda )\) . Then \(\widetilde{\lambda }_X^*\mathcal K\) is strictly quasi-constructible.

We may assume that \(L_X=X_0\) . We take finite partitions \(X_0=\coprod _{i\in I}L_i\) and \(U=\coprod _{j\in J}Z_j\) by locally closed subsets \(L_i\subset X_0\) and \(Z_j\subset U\) such that \(\mathcal K\) is locally constant on \(L_i\overleftarrow{\times }_XZ_j\) . Let \(\mathsf L_i\) be the pullback of \(L_i\) by the map \(\lambda _X:X^a\rightarrow X_0\) and \(\mathsf Z_i\) the pullback of \(Z_i\) by the map \(\varphi _X:X^a\rightarrow U\) . Then each \(\mathsf L_i\) is a constructible locally closed subset, and each \(\mathsf Z_j\) is a Zariski locally closed subset. Further, the restriction of \(\widetilde{\lambda }_X^*\mathcal K\) to \(\mathsf L_i\cap \mathsf Z_j\) is locally constant. Thus, \(\widetilde{\lambda }_X^*\mathcal K\) is quasi-constructible.

Definition 5.4

A morphism \(X'\rightarrow X\) of schemes is called a modification if it is proper and surjective, if there exists a dense open subscheme U of X such that the restriction \(X'\times _XU\rightarrow U\) is an isomorphism, and if every generic point (i.e, maximal point) of \(X'\) is sent to a generic point of X .

Theorem 5.5

Let \(f:(X,X_0,L_X)\rightarrow (Y,Y_0,L_Y)\) be a morphism of admissible triples (Definition 3.3 ). We assume that Y is a coherent scheme having only finitely many irreducible components and that \(f:X\rightarrow Y\) is separated and of finite presentation. Let n be an integer invertible on Y and \(\mathcal F\) be an object of \(D^b_c(X,{\mathbb {Z}}/n{\mathbb {Z}})\) . Then there exists a modification \(\pi :Y'\rightarrow Y\) such that the complex \({\pi ^a}^*Rf^a_!\mathcal F^a\) is strictly quasi-constructible. Here \(\pi ^a\) is the morphism \((Y')^a\rightarrow Y^a\) of pseudo-adic spaces induced by the morphism \(\pi :(Y',\pi ^{-1}(Y_0),\pi ^{-1}(L_Y))\rightarrow (Y,Y_0,L_Y)\) of admissible triples.

Recall that the formation of \(Rf^a_!\) commutes with base change ( [ 9 , Theorem 5.3.9]). Hence, we can freely replace Y by a modification. By [ 20 , Théorème 2.1], there exists a modification \(Y'\rightarrow Y\) such that the formation of \(R\Psi _{f'}\mathcal F'\) commutes with base change, where \(f'\) is the base change \(X'=X\times _YY'\rightarrow Y'\) and \(\mathcal F'\) is the pullback of \(\mathcal F\) by the projection \(X'\rightarrow X\) . Thus, we may assume that the formation of \(R\Psi _f\mathcal F\) commutes with base change. Then, by Theorem 4.11 , we have \(\widetilde{\lambda }_Y^*R(f\overleftarrow{\times }\textrm{id})_!R\Psi _f\mathcal F\cong Rf^a_!\mathcal F^a\) . On the other hand, by Lemma 2.13 , \(R(f\overleftarrow{\times }\textrm{id})_!R\Psi _f\mathcal F\) is constructible. Thus, by Lemma 5.3 , \(Rf^a_!\mathcal F^a\) is strictly quasi-constructible. \(\square \)

In particular, Theorem 1.1 follows.

As mentioned in the introduction, the modification is strictly necessary in Theorem 1.1 . In fact, if \(f:X\rightarrow Y\) is as in Example 4.13 .2, the complex \(Rf^\textrm{rig}_!{\mathbb {Z}}/n{\mathbb {Z}}\) is not quasi-constructible as shown in [ 11 , Example 2.2].

The above theorem does not hold for the direct image without support. In general, the complex \(Rf^a_*\mathcal F^a\) is not quasi-constructible even after any modification as seen in [ 10 , Example 1.1].

5.2 Quasi-constructible sheaves on the 2-dimensional disk

In this subsection, we fix a non-archimedean field k and use the notations in Example 3.2 .

Proposition 5.7

Let \(\pi :S'\rightarrow S=\mathop {\textrm{Spec}}\nolimits k^\circ [s,t]\) be a modification and \(\mathsf F\) a sheaf of \(\Lambda \) -modules on \(S^\textrm{rig}\cong \mathop {\textrm{Spa}}\nolimits (k\langle s,t\rangle ,k^\circ \langle s,t\rangle )\) , for a noetherian ring \(\Lambda \) . We assume that \({\pi ^\textrm{rig}}^{*}\mathsf F\) is strictly quasi-constructible. Then there exist an integer \(\nu \ge 0\) and \(\delta \in |k^\times |\) such that \(\mathsf F\) is locally constant on the open subset \(\{x\in S^\textrm{rig}\mid 0<|s(x)|\le |t^\nu (x)| \text { and }|t(x)|\le \delta \}\) .

The aim of this subsection is to prove this propositioin and use it to obtain a concrete consequence (Corollary 5.11 ) of Theorem 5.5 . To this end, we prepare some lemmas (Lemmas 5.8 and 5.10 ).

Let \(\pi :S'\rightarrow S=\mathop {\textrm{Spec}}\nolimits k^\circ [s,t]\) be a modification. For an integer \(\nu \ge 0\) , we consider the S -scheme \(S_\nu =\mathop {\textrm{Spec}}\nolimits k^\circ [\frac{s}{t^\nu },t]\) , that is, the scheme \(\mathop {\textrm{Spec}}\nolimits k^\circ [s',t]\) with S -scheme structure given by the \(k^\circ [t]\) -algebra homomorphism \(k^\circ [s,t]\rightarrow k^\circ [s',t]\) sending s to \(s't^\nu \) . Then there exist an integer \(\nu \ge 0\) , an open neighborhood \(\mathsf U\subset (S_\nu )^\textrm{rig}\) of the origin, and a commutative diagram

Applying Lemma 5.9 below to the regular local ring \(k[s,t]_{(s,t)}\) , we can find a commutative diagram

for some \(\nu \ge 1\) and \(f\in k[\frac{s}{t^\nu },t]\) which does not belong to the maximal ideal \((\frac{s}{t^\nu },t)\) . We take \(\mathsf U\) to be the fiber product \(U\times _SS^\textrm{rig}\) ([ 8 , Proposition 3.8]). Since we have a natural isomorphism \((S')^\textrm{rig}\cong S'\times _SS^\textrm{rig}\) ([ 9 , Proposition 1.9.6]), we obtain a desired commutative diagram by applying \(\times _SS^\textrm{rig}\) to the above commutative diagram. \(\square \)

The following elementary lemma is used in the above proof.

Let A be a regular local ring of dimension 2 with regular parameters s ,  t . Let \(\pi :X\rightarrow \mathop {\textrm{Spec}}\nolimits A\) be a modification. Then there exist an integer \(\nu \ge 0\) and a commutative diagram

where \(\pi _\nu \) is the natural morphism.

By the valuative criterion of proper morphisms, it suffices to show that the ring \({\widetilde{A}}=\varinjlim _\nu A[\frac{s}{t^\nu }]_{(\frac{s}{t^\nu },t)}\) is a valuation ring.

To see this, we claim that any nonzero element \(f\in A\) can be written as \(f=s^nt^m(g+\frac{s}{t^m}h)\) for some integers \(n,m\ge 0\) and some elements \(g\in A^\times \) and \(h\in A\) . This can be checked as follows: take the maximum \(n\in {\mathbb {Z}}\) with \(f\in s^nA\) so that \(f=s^nf_1\) for some \(f_1\in A\setminus sA\) ; take the maximum \(m\in {\mathbb {Z}}\) with \(f\mod s\in t^m(A/sA)\) so that \(f_1\mod s=t^m{{\bar{g}}}\) for some \({{\bar{g}}}\in (A/sA){\setminus } t(A/sA)\) ; then \(f_1=t^mg+sh\) for some \(g\in A{\setminus }(s,t)=A^\times \) and \(h\in A\) . Thus, any \(f\in A\) can be written in the claimed way.

We consider the map \(v:A\setminus \{0\}\rightarrow {\mathbb {Z}}^2\) sending f to ( n ,  m ) taken as above. This defines a valuation with respect to the lexicographic order on \({\mathbb {Z}}^2\) and canonically extends to a valuation on the field of fractions of A . Let V be the corresponding valuation ring. Then we have \(\widetilde{A}\subset V\) , as we have \(v(\frac{s}{t^\nu })=(1,-\nu )\ge 0\) and \(v(u)=0\) for any \(u\in A[\frac{s}{t^\nu }]{\setminus }(\frac{s}{t^\nu },t)\) . On the other hand, since the factor \(g+\frac{s}{t^m}h\) is a unit in \(A[\frac{s}{t^m}]_{(\frac{s}{t^m},t)}\) , any nonzero element of V can be written as \(s^nt^mu\) for some \((n,m)\ge 0\) and some unit u of \({\widetilde{A}}\) . Thus, we have \(\widetilde{A}=V\) . \(\square \)

Let \(\mathsf U\subset \mathop {\textrm{Spa}}\nolimits (k\langle s,t\rangle ,k^\circ \langle s,t\rangle )\) be an open neighborhood of the origin and \(\mathsf Z\subsetneq \mathsf U\) be a proper Zariski closed subset. Then there exist an integer \(\nu \ge 0\) and \(\delta \in |k^\times |\) such that \(\mathsf U\setminus \mathsf Z\) contains the open subset

We may assume that \(\mathsf U=\mathop {\textrm{Spa}}\nolimits (k\langle s,t\rangle ,k^\circ \langle s,t\rangle )\) . We take a nonzero function \(f\in k\langle s,t\rangle \) such that the zero of f contains \(\mathsf Z\) , i.e, a nonzero element in an ideal defining \(\mathsf Z\) . We may assume that \(\mathsf Z\) is the Zariski closed subset defined by f . Since we do not care about points x with \(|s(x)|=0\) , we may assume that f is not divided by s . Then, by replacing f by cf for some \(c\in k^\times \) if needed, we can write

with \(a\in k^\times \) , \(g\in k^\circ \langle t\rangle \) , and \(h\in k^\circ \langle s,t\rangle \) . Take \(\delta \in |k^\times |\) such that \(\delta <|a|\) . Let \(x\in \mathop {\textrm{Spa}}\nolimits (k\langle s,t\rangle ,k^\circ \langle s,t\rangle )\) be a point which satisfies \(0<|s(x)|\le |t^{\nu +1}(x)|\) and \(|t(x)|\le \delta \) . Then we have

and hence, \(|f(x)|\ne 0\) . This proves the assertion. \(\square \)

Proof (Proof of Proposition 5.7)

[Proof of Proposition 5.7 ] By Lemma 5.8 , the problem is reduced to the case where \(\mathcal F\) is strictly quasi-constructible. Then there exists a constructible subset \(\mathsf L\) which contains the origin of \({\mathbb {B}}^2_k=\mathop {\textrm{Spa}}\nolimits (k\langle s,t\rangle ,k^\circ \langle s,t\rangle )\) and a Zariski closed subset \(\mathsf Z\subset {\mathbb {B}}^2_k\) such that \(\mathcal F\) is locally constant on \(\mathsf L\setminus (\mathsf L\cap \mathsf Z)\) . Note that, since the origin is a maximal point, \(\mathsf L\) contains an open neighborhood of the origin. Then the assertion follows from Lemma 5.10 . \(\square \)

Corollary 5.11

Let \(f:X\rightarrow S=\mathop {\textrm{Spec}}\nolimits k^\circ [s,t]\) be a morphism separated of finite presentation and \(\mathcal F\) be a constructible sheaf of \({\mathbb {Z}}/n{\mathbb {Z}}\) -modules on X , for an integer n invertible in \(k^\circ \) . Then there exist an integer \(\nu \ge 0\) and \(\delta \in |k^\times |\) such that the cohomology sheaves of \(Rf^\textrm{rig}_!\mathcal F^\textrm{rig}\) are locally constant on the open subset \(S^\textrm{rig}=\mathop {\textrm{Spa}}\nolimits (k\langle s,t\rangle ,k^\circ \langle s,t\rangle )\) defined by \(0<|s|\le |t^\nu |\) and \(|t|\le \delta \) .

By Theorem 5.5 , there exists a modification \(\pi :S'\rightarrow S\) such that \(\pi ^{\textrm{rig}*}Rf^\textrm{rig}_!\mathcal F^\textrm{rig}\) is strictly quasi-constructible. As \(Rf^\textrm{rig}_!\) has finite cohomological dimension ([ 9 , Corollary 0.5.8]), the assertion follows from Proposition 5.7 . \(\square \)

6 Tubular neighborhoods

In this section, we fix a non-archimedean field k and assume that k is of characteristic zero. We also fix an integer n invertible in \(k^\circ \) . We introduce some notations. The rigid affine line \(\mathop {\textrm{Spec}}\nolimits k[t]\times _{\mathop {\textrm{Spec}}\nolimits k}\mathop {\textrm{Spa}}\nolimits (k,k^\circ )\) ([ 8 , Proposition 3.8]) is denoted by \({\mathbb {A}}\) . For \(r\in |k^\times |\) , the disk (resp. punctured disk) of radius r , i.e, the open subset \(\{x\in {\mathbb {A}}\mid |t(x)|\le r\}\) (resp. \(\{x\in {\mathbb {A}}\mid 0<|t(x)|\le r\}\) ) is denoted by \({\mathbb {B}}(r)\) (resp. \({\mathbb {B}}^*(r)\) ). We put \({\mathbb {B}}={\mathbb {B}}(1)\) and \({\mathbb {B}}^*={\mathbb {B}}^*(1)\) .

Let \(p:P\rightarrow \mathop {\textrm{Spec}}\nolimits k^\circ [t]\) be a morphism of schemes separated of finite type and X a closed subscheme of P defined by a global function \(g\in \mathcal O_P(P)\) . We denote the natural morphism \(X\rightarrow \mathop {\textrm{Spec}}\nolimits k^\circ [t]\) by f . For an integer \(\nu \ge 0\) and an element \(\varepsilon \in |k^\times |\) , we consider the closed subset \(X^\textrm{rig}_{\nu ,\varepsilon }=\{x\in P^\textrm{rig}\times _{{\mathbb {B}}}{\mathbb {B}}^*\mid |g(x)|<\varepsilon \cdot |t^\nu (x)|\}\) and denote the natural morphism \(X^\textrm{rig}_{\nu ,\varepsilon }\rightarrow {\mathbb {B}}^*\) of pseudo-adic spaces by \(f^\textrm{rig}_{\nu ,\varepsilon }\) .

Proposition 6.1

Let \(\mathcal F\) be a constructible sheaf of \({\mathbb {Z}}/n{\mathbb {Z}}\) -modules on P . There exist an integer \(\nu \ge 0\) and an element \(\varepsilon _0\in |k^\times |\) satisfying the following property. For every \(\varepsilon \in |k^\times |\) with \(\varepsilon \le \varepsilon _0\) , there exists an element \(\delta \in |k^\times |\) such that the natural morphism

is an isomorphism on \({\mathbb {B}}^*(\delta )\) .

We prove this proposition at the end of this section. To this end, we recall a structure theorem of finite étale coverings of annuli due to Lütkebohmert. For this, we introduce a terminology:

Definition 6.2

Assume that k is algebraically closed. Let \(r,R\in |k^\times |\) be elements with \(r\le R\) and \(X\rightarrow {\mathbb {B}}(r,R)=\{x\in {\mathbb {A}}\mid r\le |t(x)|\le R\}\) be a finite étale covering. We say \(X\rightarrow {\mathbb {B}}(r,R)\) is of Kummer type if it is isomorphic to the cover

Then Lütkebohmert’s structure theorem states the following.

Theorem 6.3

( [ 17 , Theorem 2.2]) Let \(d\ge 1\) be an integer and k be an algebraically closed complete non-archimedean field extension of \({\mathbb {Q}}_p\) . Then there exists an element \(\beta \in |k^\times |\) with \(\beta \le 1 \) such that every finite étale covering \(X\rightarrow {\mathbb {B}}(r,R)\) of degree d , for every \(r\le R\in |k^\times |\) with \(\beta ^{-1}r\le \beta R\) , is of Kummer type over \({\mathbb {B}}(\beta ^{-1}r,\beta R)\) .

For \(r\in |k^\times |\) , the closed disk (resp. punctured closed disk) of radius r , i.e, the subset \(\{x\in {\mathbb {A}}\mid |t(x)|< r\}\) (resp. \(\{x\in {\mathbb {A}}\mid 0<|t(x)|< r\}\) ) is denoted by \({\mathbb {D}}(r)\) (resp. \({\mathbb {D}}^*(r)\) ). We put \({\mathbb {D}}={\mathbb {D}}(1)\) and \({\mathbb {D}}^*={\mathbb {D}}^*(1)\) . We regard \({\mathbb {D}}(r)\) and \({\mathbb {D}}^*(r)\) as pseudo-adic spaces.

[c.f. (II) in the proof of [ 11 , Theorem 2.5]] Assume that k is algebraically closed and let \(d\ge 1\) be an integer. There exists an element \(\varepsilon _0(d)\in |k^\times |\) satisfying the following condition. Let \(\mathcal M\) be a locally constant constructible sheaf of \({\mathbb {Z}}/n{\mathbb {Z}}\) -modules on \({\mathbb {B}}^*\) that is trivialized by a finite étale cover \(X\rightarrow {\mathbb {B}}^*\) of degree d . Then for every \(\varepsilon \le \varepsilon _0(d)\) , we have \(R\Gamma _c({\mathbb {D}}^*(\varepsilon ),\mathcal M)=0\) .

We follow the proof of [ 16 , Lemma 6.12].

Take \(\varepsilon _0\) to be an element \(\beta \) as in Theorem 6.3 . Since \(H^i_c({\mathbb {D}}^*(\beta ),\mathcal M)\cong \varinjlim _{r\in |k^\times |}H^i_c({\mathbb {D}}(\beta ){\setminus }{\mathbb {D}}(r),\mathcal M)\) , it suffices to prove that \(R\Gamma _c({\mathbb {D}}(\beta )\setminus {\mathbb {D}}(r),\mathcal M)=0\) . By Theorem 6.3 , we may assume that \(\mathcal M\) is a constant sheaf. Then the explicit description \(R\Gamma _c({\mathbb {D}}(r),{\mathbb {Z}}/n{\mathbb {Z}})\cong {\mathbb {Z}}/n{\mathbb {Z}}\) as in [ 9 , Example 0.2.5] shows the assertion. \(\square \)

Let \({\mathbb {B}}^2_k=\mathop {\textrm{Spa}}\nolimits (k\langle s,t\rangle ,k^\circ \langle s,t\rangle )\) and \(\nu \ge 0\) an integer. For an element \(\varepsilon \in |k^\times |\) , we consider the subsets \(\mathsf U_\varepsilon =\{x\in {\mathbb {B}}^2_k\mid 0<|s(x)|\le \varepsilon \cdot |t^\nu (x)|\}\) and \(\mathsf U_\varepsilon '=\{x\in {\mathbb {B}}^2_k\mid 0<|s(x)|<\varepsilon \cdot |t^\nu (x)|\}\) , which we regard as pseudo-adic spaces. We denote the second projection \(\mathsf U'_\varepsilon \rightarrow {\mathbb {B}}=\mathop {\textrm{Spa}}\nolimits (k\langle t\rangle ,k^\circ \langle t\rangle )\) by \(\textrm{pr}'_{\varepsilon ,2}\) . Let \(\mathcal M\) be a locally constant constructible sheaf of \({\mathbb {Z}}/n{\mathbb {Z}}\) -modules on \(\mathsf U_1\) . Then there exists an element \(\varepsilon _0\in |k^\times |\) satisfying the following condition. For every element \(\varepsilon \in |k^\times |\) with \(\varepsilon \le \varepsilon _0\) , there exists an element \(\delta \in |k^\times |\) such that the restriction of \(R\textrm{pr}'_{\varepsilon ,2!}(\mathcal M|_{\mathsf U'_\varepsilon })\) to \({\mathbb {B}}^*(\delta )\) vanishes.

We may assume that k is algebraically closed. Considering the isomorphism \(\varphi _\nu :\mathsf U_1\cong {\mathbb {B}}^*\times {\mathbb {B}}^*;(s,t)\mapsto (s/t^\nu ,t)\) of adic spaces, we may assume that \(\nu =0\) . We denote the natural immersion \(\mathsf U'_\varepsilon \rightarrow {\mathbb {B}}^2_k\) by u . Then the sheaf \(u_!\mathcal M\) is strictly quasi-constructible (in particular, quasi-constructible). Thus, by [ 11 , Theorem 2.1] and [ 11 , 1.2.iv)], there exists an element \(\delta \in |k^\times |\) such that the restriction of \(R\textrm{pr}'_{\varepsilon ,2!}\mathcal M\) to \({\mathbb {B}}^*(\delta )\) is locally constant of finite type. Note that, for a classical point x of \({\mathbb {B}}^*(\delta )\) , we have \((R\textrm{pr}'_{\varepsilon ,2!}\mathcal M)_x\cong R\Gamma _c({\mathbb {D}}^*(\varepsilon ),\mathcal M|_{{\mathbb {D}}^*(\varepsilon )\times x})\) by [ 9 , Theorem 5.3.9]. We take a finite étale cover of that trivializes \(\mathcal M\) and let d denote its degree. Take \(\varepsilon _0=\varepsilon _0(d)\) to be an element as in Lemma 6.4 . Then, if \(\varepsilon \le \varepsilon _0\) , then the stalk \((R\textrm{pr}'_{\varepsilon ,2!}\mathcal M)_x\cong R\Gamma _c({\mathbb {D}}^*(\varepsilon ),\mathcal M|_{{\mathbb {D}}^*(\varepsilon )\times x})\) , and hence \(R\textrm{pr}'_{\varepsilon ,2!}\mathcal M\) vanishes. \(\square \)

Proof (Proof of Proposition 6.1)

[Proof of Proposition 6.1 ] We consider the morphism \(g:P\rightarrow S=\mathop {\textrm{Spec}}\nolimits k^\circ [s,t]\) over \(\mathop {\textrm{Spec}}\nolimits k^\circ [t]\) defined by \(s\mapsto g\in \mathcal O_{P}(P)\) . By Corollary 5.11 , we can apply Lemma 6.5 to the restriction of \(R^ig^\textrm{rig}_!\mathcal F^\textrm{rig}\) to the subset \(\{x\in S^\textrm{rig}\mid 0<|s(x)|\le |t^\nu (x)|\}\) , which proves the assertion. \(\square \)

It would be straightforward to extend Proposition 6.1 to the case where the closed subscheme X is not necessarily defined by one global equation, i.e, the case of general closed subschemes X .

It might be also possible to remove the assumption on the characteristic of the base field k by an argument similar to the proof of [ 16 , Lemma 7.1].

Artin, M.: Morphismes acycliques, Séminaire de Géométrie Algébrique du Bois-Marie 1963–1964 (SGA 4 III), exposé XV, Lecture Notes in Mathematics, vol. 305. Springer-Verlag (1973)

Artin, M.: Théoréme de changement de base par un morphisme lisse, et applications, Séminaire de Géométrie Algébrique du Bois-Marie 1963–1964 (SGA 4 III), exposé XVI, Lecture Notes in Mathematics, vol. 305. Springer-Verlag (1973)

Deligne, P.: Cohomologie á support propre, Séminaire de Géométrie Algébrique du Bois-Marie 1963–1964 (SGA 4 III), exposé XVII, Lecture Notes in Mathematics, vol. 305. Springer-Verlag (1973)

Fujiwara, K., Kato, F.: Foundations of Rigid Geometry. I, EMS Monographs in Mathematics. European Mathematical Society (EMS), Zürich (2018). MR3752648

Fujiwara, K.: Theory of tubular neighborhood in étale topology. Duke Math. J. 80 (1), 15–57 (1995)

Grothendieck, A., Verdier, J.-L. Conditions de finitude. topos et sites fibrés. Applications aux questions de passage à la limite., Séminaire de Géométrie Algébrique du Bois-Marie 1963–1964 (SGA 4 II), exposé VI, Lecture Notes in Mathematics, vol. 270. Springer-Verlag (1972)

Grothendieck, A., Verdier, J.-L.: Topos, Séminaire de Géométrie Algébrique du Bois-Marie 1963–1964 (SGA 4 I), exposé IV, Lecture Notes in Mathematics, vol. 269. Springer-Verlag (1972)

Huber, R.: A generalization of formal schemes and rigid analytic varieties. Math. Z. 217 (4), 513–551 (1994)

Article   MathSciNet   Google Scholar  

Huber, R.: Étale cohomology of rigid analytic varieties and Adic spaces. In: Aspects of Mathematics. Vieweg, Braunschweig (1996)

Google Scholar  

Huber, R.: A finiteness result for direct image sheaves on the étale site of rigid analytic varieties. J. Algebr. Geom. 7 (2), 359–403 (1998)

Huber, R.: A finiteness result for the compactly supported cohomology of rigid analytic varieties. J. Algebr. Geom. 7 (2), 313–357 (1998)

Huber, R.: A finiteness result for the compactly supported cohomology of rigid analytic varieties. II. Ann. Inst. Fourier (Grenoble) 57 (3), 973–1017 (2007)

Illusie, L.: Vanishing cycles over general bases after P. Deligne, O. Gabber, G. Laumon and F. Orgogozo, https://www.imo.universite-paris-saclay.fr/~illusie/vanishing1b.pdf (2006)

Illusie, L.: Exposé XI. Produits orientés, no. 363–364, 2014, Travaux de Gabber sur l’uniformisation locale et la cohomologie étale des schémas quasi-excellents, pp. 213–234. MR3329780

Illusie, L.: Around the Thom-Sebastiani theorem, with an appendix by Weizhe Zheng. Manuscr. Math. 152 (1–2), 61–125 (2017)

Ito, K.: Uniform local constancy of étale cohomology of rigid analytic varieties. J. Inst. Math. Jussieu 23 , no.2, 839–896 (2024)

Lütkebohmert, W.: Riemann’s existence problem for AP-ADIC field. Invent. Math. 111 (1), 309–330 (1993)

Lu, Q., Zheng, W.: Compatible systems and ramification. Compos. Math. 155 (12), 2334–2353 (2019)

Mieda, Yoichi: On the action of the Weil group on the \(\ell \) -adic cohomology of rigid spaces over local fields. Int. Math. Res. Not. 2006 (9), 16429–16429 (2006)

MathSciNet   Google Scholar  

Orgogozo, F.: Modifications et cycles proches sur une base générale. Int. Math. Res. Not. 25315, 38. MR2249998 (2006)

Raynaud, M.: Géométrie analytique rigide d’aprés Tate, Kiehl,.... Table Ronde d’Analyse Non Archimédienne (Paris, 1972), pp. 319–327. Supplément au Bull. Soc. Math. France, vol. Tome 102, Soc. Math. France, Paris, (1974). MR470254

Scholze, P.: Perfectoid spaces. Publ. Math. Inst. Hautes Études Sci. 116 , 245–313 (2012)

Download references

Acknowledgements

The author would like to thank Teruhisa Koshikawa for pointing out mistakes in an earlier attempt of the author to directly generalize the proof in [ 11 ] and for suggesting to use nearby cycles over general bases. He is grateful to Kazuhiro Ito for explaining his work [ 16 ] to the author, especially how to apply nearby cycles over general bases to the theory of étale cohomology of rigid analytic varieties. He would also like to thank Daichi Takeuchi for various helpful discussions, especially for pointing out a mistake in Remark 3.5 of the earlier draft and suggesting to fix Definition 3.1 and Definition 3.4 . He would like to express his gratitude to Takeshi Saito for various helpful discussion and for constant encouragement. Finally, the author thanks the referee for reading the manuscript carefully and giving numerous amount of advice. This project has received funding from Iwanami Fujukai Foundation and the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 851146), and funding through the Max Planck Institute for Mathematics in Bonn, Germany (report number MPIM-Bonn-2023).

Open Access funding enabled and organized by Projekt DEAL.

Author information

Authors and affiliations.

Max Planck Institut für Mathematik, Bonn, Germany

Hiroki Kato

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Hiroki Kato .

Ethics declarations

Data availability statement.

This manuscript has no associated data.

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Kato, H. Étale cohomology of algebraizable rigid analytic varieties via nearby cycles over general bases. manuscripta math. (2024). https://doi.org/10.1007/s00229-024-01564-0

Download citation

Received : 07 September 2021

Accepted : 18 April 2024

Published : 22 May 2024

DOI : https://doi.org/10.1007/s00229-024-01564-0

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

Mathematics Subject Classification

• Find a journal
• Publish with us
• Track your research