quadratic assignment problem programming

• Analysis of Algorithms
• Backtracking
• Dynamic Programming
• Divide and Conquer
• Geometric Algorithms
• Mathematical Algorithms
• Pattern Searching
• Bitwise Algorithms
• Branch & Bound
• Randomized Algorithms

Quadratic Assignment Problem (QAP)

• Channel Assignment Problem
• Assignment Operators In C++
• Solidity - Assignment Operators
• Job Assignment Problem using Branch And Bound
• Range Minimum Query with Range Assignment
• Transportation Problem | Set 1 (Introduction)
• Transportation Problem | Set 2 (NorthWest Corner Method)
• Transportation Problem | Set 3 (Least Cost Cell Method)
• Transportation Problem | Set 4 (Vogel's Approximation Method)
• Assignment Operators in C
• QA - Placement Quizzes | Profit and Loss | Question 7
• QA - Placement Quizzes | Profit and Loss | Question 4
• QA - Placement Quizzes | Profit and Loss | Question 12
• QA - Placement Quizzes | Profit and Loss | Question 10
• QA - Placement Quizzes | Profit and Loss | Question 8
• QA - Placement Quizzes | Age | Question 4
• QA - Placement Quizzes | Profit and Loss | Question 9
• QA - Placement Quizzes | Profit and Loss | Question 11
• IBM Placement Paper | Quantitative Analysis Set - 5

The Quadratic Assignment Problem (QAP) is an optimization problem that deals with assigning a set of facilities to a set of locations, considering the pairwise distances and flows between them.

The problem is to find the assignment that minimizes the total cost or distance, taking into account both the distances and the flows.

The distance matrix and flow matrix, as well as restrictions to ensure each facility is assigned to exactly one location and each location is assigned to exactly one facility, can be used to formulate the QAP as a quadratic objective function.

The QAP is a well-known example of an NP-hard problem , which means that for larger cases, computing the best solution might be difficult. As a result, many algorithms and heuristics have been created to quickly identify approximations of answers.

There are various types of algorithms for different problem structures, such as:

• Precise algorithms
• Approximation algorithms
• Metaheuristics like genetic algorithms and simulated annealing
• Specialized algorithms

Example: Given four facilities (F1, F2, F3, F4) and four locations (L1, L2, L3, L4). We have a cost matrix that represents the pairwise distances or costs between facilities. Additionally, we have a flow matrix that represents the interaction or flow between locations. Find the assignment that minimizes the total cost based on the interactions between facilities and locations. Each facility must be assigned to exactly one location, and each location can only accommodate one facility.

Facilities cost matrix:

Flow matrix:

To solve the QAP, various optimization techniques can be used, such as mathematical programming, heuristics, or metaheuristics. These techniques aim to explore the search space and find the optimal or near-optimal solution.

The solution to the QAP will provide an assignment of facilities to locations that minimizes the overall cost.

The solution generates all possible permutations of the assignment and calculates the total cost for each assignment. The optimal assignment is the one that results in the minimum total cost.

To calculate the total cost, we look at each pair of facilities in (i, j) and their respective locations (location1, location2). We then multiply the cost of assigning facility1 to facility2 (facilities[facility1][facility2]) with the flow from location1 to location2 (locations[location1][location2]). This process is done for all pairs of facilities in the assignment, and the costs are summed up.

Overall, the output tells us that assigning facilities to locations as F1->L1, F3->L2, F2->L3, and F4->L4 results in the minimum total cost of 44. This means that Facility 1 is assigned to Location 1, Facility 3 is assigned to Location 2, Facility 2 is assigned to Location 3, and Facility 4 is assigned to Location 4, yielding the lowest cost based on the given cost and flow matrices.This example demonstrates the process of finding the optimal assignment by considering the costs and flows associated with each facility and location. The objective is to find the assignment that minimizes the total cost, taking into account the interactions between facilities and locations.

Applications of the QAP include facility location, logistics, scheduling, and network architecture, all of which require effective resource allocation and arrangement.

Please Login to comment...

Similar reads, improve your coding skills with practice.

What kind of Experience do you want to share?

Quadratic programming

This web page is a duplicate of https://optimization.mccormick.northwestern.edu/index.php/Quadratic_programming

Author: Jack Heider (ChE 345 Spring 2015) Steward: Dajun Yue, Fengqi You

• 1 Introduction
• 2.1 Global solutions
• 2.2 KKT conditions
• 2.3 Solution strategies
• 3 Numerical example
• 4 Applications
• 5 Conclusion
• 6 References

Introduction

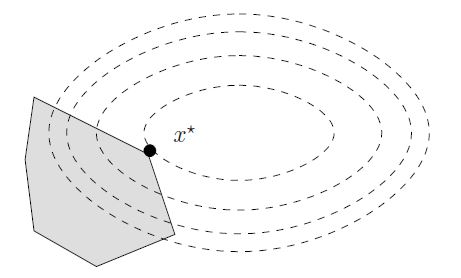
Quadratic programming (QP) is the problem of optimizing a quadratic objective function and is one of the simplests form of non-linear programming. 1 The objective function can contain bilinear or up to second order polynomial terms, 2 and the constraints are linear and can be both equalities and inequalities. QP is widely used in image and signal processing, to optimize financial portfolios, to perform the least-squares method of regression, to control scheduling in chemical plants, and in sequential quadratic programming , a technique for solving more complex non-linear programming problems. 3,4 The problem was first explored in the early 1950s, most notably by Princeton University's Wolfe and Frank , who developed its theoretical background, 1 and by Harry Markowitz , who applied it to portfolio optimization, a subfield of finance.

Problem formulation

A general quadratic programming formulation contains a quadratic objective function and linear equality and inequality constraints: 2,5,6

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{min} f(x)=q^{T}x+\frac{1}{2}x^{T}Qx} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle s.t. Ax=a} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Bx\le b} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x\ge0}

The objective function is arranged such that the vector Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q} contains all of the (singly-differentiated) linear terms and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q} contains all of the (twice-differentiated) quadratic terms. Put more simply, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Q} is the Hessian matrix of the objective function and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q} is its gradient. By convention, any constants contained in the objective function are left out of the general formulation. 6 The one-half in front of the quadratic term is included to remove the coefficient (2) that results from taking the derivative of a second-order polynomial.

As for the constraints, the matrix equation Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Ax=a} contains all of the linear equality constraints, and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Bx \le b} are the linear inequality constraints.

When there are only inequality constraints ( Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Bx\le b} ), the Lagrangean is: 6 Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L(x,\lambda,\mu)=q^{T}x+\frac{1}{2}x^{T}Qx+{\lambda}^T(Ax-a)+{\mu}^T(Bx-b)=0}

Global solutions

If the objective function is convex, then any local minimum found is also the sole global minimum. To analyze the function’s convexity, one can compute its Hessian matrix and verify that all eigenvalues are positive, or, equivalently, one can verify that the matrix Q is positive definite. 6 This is a sufficient condition, meaning that it is not required to be true in order for a local minimum to be the unique global minimum, but will guarantee this property holds if true.

KKT conditions

Solutions can be tested for optimality using Karush-Kuhn-Tucker conditions just as is done for other nonlinear problems: 5

Condition 1: sum of gradients is zero: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangledown L({x}^*,{\lambda}^*,{\mu}^*)=q^{T}+\frac{1}{2}x^{T}Q+{\lambda}^{*T}A+{\mu}^{*T}B}

Condition 2: all constraints satisfied: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Ax^*-a=0} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Bx^*-b\le0}

Condition 3: complementary conditions: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\mu}^TBx-b=0} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {x}^{T},{\lambda}^{T},{\mu}^T\ge0}

Solution strategies

Because quadratic programming problems are a simple form of nonlinear problem, they can be solved in the same manner as other non-linear programming problems. An unconstrained quadratic programming problem is most straightforward to solve: simply set the derivative (gradient) of the objective function equal to zero and solve. 7 More practical (constrained) formulations are more difficult to solve. The typical solution technique when the objective function is strictly convex and there are only equality constraints is the conjugate gradient method . If there are inequality constraints ( Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Bx\le b} ), then the interior point and active set methods are the preferred solution methods. When there is a range on the allowable values of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} (in the form Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^L\le x\le x^U} , which is the case for image and signal processing applications, trust-region methods are most frequently used. 4 For all convex cases, an NLP solver in the optimization utility GAMS, such as KNITRO, MINOS, or CONOPT, can find solutions for quadratic programming problems.

Numerical example

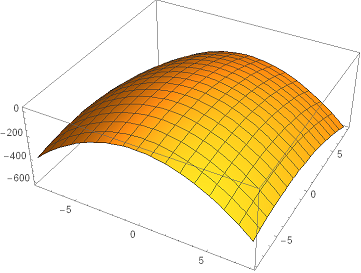
This example demonstrates how to determine the KKT point of a specific QP problem:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{min}} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x)=3{x_1}^2+{x_2}^2+2{x_1}{x_2}+x_1+6{x_2}+2} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{s.t.}} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2{x_1}+3{x_2} \ge 4} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {x_1},{x_2} \ge 0}

Rewrite the constraints. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g_1=-2{x_1}-3{x_2}+4\le 0} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g_2=-{x_1} \le 0} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g_3=-{x_2} \le 0}

Construct the gradients. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangledown f= \begin{bmatrix} 6{x_1}+2{x_2}+1 \\ 2{x_1}+2{x_2}+6 \end{bmatrix}, \triangledown {g_1}= \begin{bmatrix} -2 \\ -3 \end{bmatrix}, \triangledown {g_2}= \begin{bmatrix} -1 \\ 0 \end{bmatrix}, \triangledown {g_3}= \begin{bmatrix} 0 \\ -1 \end{bmatrix} }

Assuming all constraints are satisfied, set the gradient equal to zero to attempt to find an optima. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 6{x_1}+2{x_2}+1=0} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2{x_1}+2{x_2}+6=0}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {x_1}=\frac{5}{4}} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {x_2}=-\frac{17}{4}}

Make constraints Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g_1} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g_3} , which are violated, active. Set both equal to zero. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {g_1} = -2{x_1}-3{x_2}+4=0} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {g_3} = -{x_2}=0}

Solve the resulting system of equations. Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangledown f+ {\mu_1} \triangledown {g_1}+ {\mu_3} \triangledown {g_3} =0} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {g_1}=0} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {g_3}=0}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{bmatrix} 6{x_1}+2{x_2}+1 \\ 2{x_1}+2{x_2}+6 \end{bmatrix} +{\mu_1} \begin{bmatrix} -2 \\ -3 \end{bmatrix} +{\mu_3} \begin{bmatrix} 0 \\ -1 \end{bmatrix} } Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -2{x_1}-3{x_2}+4=0} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -{x_2}=0}

Formulating the system as one matrix and row reducing is one of the simplest ways to solve. Doing so yields: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {x_1}=2, {x_2}=0, {\mu_1}=6.5, {\mu_3}=-9.5}

Drop constraint Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g_3} because Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\mu_3}} is negative and resolve the system. Doing so yields: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {x_1}=0.5, {x_2}=1, {\mu_1}=3}

Which yields an objective function value of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f=11.25}

Verify linear dependence of the gradient: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \triangledown f+ {\mu_1} \triangledown {g_1}} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{bmatrix} 6 \\ 9 \end{bmatrix} +3 \begin{bmatrix} -2 \\ -3 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} \therefore }

Verify the uniqueness of the solution: Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\triangledown}^2 f(x)= \begin{bmatrix} 6 & 2 \\ 2 & 1 \end{bmatrix} \rightarrow \begin{bmatrix} 6-\lambda & 2 \\ 2 & 1-\lambda \end{bmatrix} =0 \rightarrow \lambda = 0.298, 6.702}

Because both eigenvalues are positive, the Hessian matrix is positive determinant, and this local minimum is the global minimum of the objective function given these constraints.

Applications

A few of the many quadratic programming applications are discussed in more detail and accompanied with general models below, and a list of other areas in which QP is important is presented as well.

• Quadratic knapsack problem (QKP)

In the standard knapsack problem, there are a number of items with different weights and values, and the items are selected based on which combination yields the highest overall value without exceeding the overall weight limit of the knapsack.

In the quadratic knapsack problem, the objective function is quadratic or, more specifically, bilinear, and the constraints are the same as in the typical knapsack problem. 8 QKP's are used in designing email servers and to optimize the locations of "nodes" in applications such as positioning transportation hubs like airports and train stations. 8 Additionally, the problem can model situations in which a limited number of people are assigned to complete specific objectives that require them to interact. 9 One formulation is presented below: 8 Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{max or min}} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^{T}Qx} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Ax \le a} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x \in {B}^{n} }

The quadratic knapsack problem, although it looks very simple, is NP-hard and is thus difficult to solve. To make obtaining solutions easier, these problems are often linearized. 8

• Model predictive control

Quadratic programming also has important applications in chemical engineering. Model predictive control (MPC) is a group of algorithms that help manage production in chemical plants by dictating production in each batch. While often formulated as linear programs because the resulting models are more stable, robust and easier to solve, MPC models are sometimes made with quadratic programming. 11 As an example of its utility, quadratic programming was used by Di Ruscio in an MPC algorithm for a thermomechanical pulping process, which a method for making paper. 11

• Least squares

Least squares regression is one of the most common types of regression, and works by minimizing the sum of the squares of the difference between data points and a proposed fit. Quadratic optimization is one method that can be used to perform a least squares regression and is more flexible than most linear methods. One formulation for a quadratic programming regression model is as follows: 3

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{min}} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e'Ie} Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e = Y-X \beta}

In this model, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e} are the unknown regression parameters, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I} is an identity matrix, and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Y} contain data about the independent and dependent variables respectively. 3

• Other applications

Quadratic programming is used in a wide range of applications not touched upon in the sample presented above. Other major areas in which QP's are relied upon include signal and image processing 12 and a subfield of optimization called partial differential constrained optimization. 3 QP's are also extensively used in finance, as variance, which is used to measure risk, is a function containing squares. 13,14,15 More specifically, Markowitz won the 1990 Nobel Prize in Economics for his widely-used model that employs quadratic programming to optimizes the amount of risk taken on based on variances. 14

Additionally, Sequential quadratic programming , an algorithm for solving more complicated NLP's that uses QP subproblems, is one of the most important applications.

Quadratic programming, the problem of optimizing a quadratic function, have been widely used since its development in the 1950s because it is a simple type of non-linear programming that can accurately model many real world systems, notably ones dependent on two variables. Problems formulated this way are straightforward to optimize when the objective function is convex. QP has applications in finance, various types of computer systems, statistics, chemical production, and in algorithms to solve more complex NLP's.

1. Frank, Marguerite, and Philip Wolfe. "An Algorithm for Quadratic Programming." Naval Research Logistics Quarterly 3 (1956): 95-110. Web. 4 June 2015. 2. Floudas, Christodoulos A., and V. Visweswaran. "Quadratic Optimization." Nonconvex Optimization and Its Applications, 2 (1995): 217-69. Web. 23 May 2015. 3. McCarl, Bruce A., Moskowitz, Herbert, and Harley Furtan. "Quadratic Programming Applications." The International Journal of Management Science, 5 (1977): 43-55. 4. Geletu, Abele. "Quadratic programming problems." Ilmenau University of Technology. Web. 23 May 2015. 5. Bradley, Hax, and Magnanti. Applied Mathematical Programming. Boston: Addison-Wesley, 1997. 421-40. Web. 23 May 2015. 6. Jensen, Paul A., and Jonathan F. Bard. "Quadratic Programming." Operations Research Models and Methods. The University of Texas at Austin. Web. 23 May 2015. 7. Binner, David. "Quadratic programming example - no constraints." Miscellaneous mathematical utilities. AKiTi. Web. 23 May 2015. 8. Pisinger, David. "The Quadratic Knapsack Problem – A Survey." Discrete Applied Mathematics, 155 (2007): 623 – 648. Web. 23 May 2015. 9. "Quadratic Multiple Knapsack Problem." Optimization of Complex System. Optiscom Project. 2012. Web. 6 June 2015. 10. Gallo, G., P. L. Hammer, and B. Simeone. "Quadratic Knapsack Problems." Mathematical Programming 12 (1980): 132-149. Web. 24 May 2015. 11. Di Ruscio, David. "Model Predictive Control and Optimization." Telemark University College. Mar. 2001. Web. 24 May 2015. 12. Ma, W. K. "Signal Processing Optimization Techniques." The Chinese University of Hong Kong. Web. 24 May 2015. 13. Tütüncü, Reha H. "Optimization in Finance." Tokyo Institute of Technology. Spring 2003. Web. 23 May 2015. 14. Van Slyke, R. "Portfolio Optimization." NYU Polytechnic School of Engineering. 16 Nov. 2007. Web. 24 May 2015. 15. "Portfolio Optimization." SAS/OR(R) 9.2 User's Guide: Mathematical Programming. SAS Institute. Web. 23 May 2015.

• Pages with math errors
• Pages with math render errors

Navigation menu

Quadratic Assignment Problem

The objective of the Quadratic Assignment Problem (QAP) is to assign \(n\) facilities to \(n\) locations in such a way as to minimize the assignment cost. The assignment cost is the sum, over all pairs, of the flow between a pair of facilities multiplied by the distance between their assigned locations.

Problem Statement

The quadratic assignment problem (QAP) was introduced by Koopmans and Beckman in 1957 in the context of locating “indivisible economic activities”. The objective of the problem is to assign a set of facilities to a set of locations in such a way as to minimize the total assignment cost. The assignment cost for a pair of facilities is a function of the flow between the facilities and the distance between the locations of the facilities.

Consider a facility location problem with four facilities (and four locations). One possible assignment is shown in the figure below: facility 2 is assigned to location 1, facility 1 is assigned to location 2, facility 4 is assigned to location 3, and facility 4 is assigned to location 3. This assignment can be written as the permutation \(p = \{2, 1, 4, 3\}\), which means that facility 2 is assigned to location 1, facility 1 is assigned to location 2, facility 4 is assigned to location 3, and facility 4 is assigned to location 3. In the figure, the line between a pair of facilities indicates that there is required flow between the facilities, and the thickness of the line increases with the value of the flow.

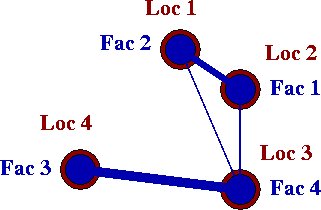
To calculate the assignment cost of the permutation, the required flows between facilities and the distances between locations are needed.

Then, the assignment cost of the permutation can be computed as \(f(1,2) \cdot d(2,1) + f(1,4) \cdot d(2,3) + f(2,4) \cdot d(1,3) + f(3,4) \cdot d(3,4)\) = \(3 \cdot 22 + 2 \cdot 40 + 1 \cdot 53 + 4 \cdot 55\) = 419. Note that this permutation is not the optimal solution.

Mathematical Formulation

Here we present the Koopmans-Beckmann formulation of the QAP. Given a set of facilities and locations along with the flows between facilities and the distances between locations, the objective of the Quadratic Assignment Problem is to assign each facility to a location in such a way as to minimize the total cost.

Sets \(N = \{1, 2, \cdots, n\}\) \(S_n = \phi: N \rightarrow N\) is the set of all permutations

Parameters \(F = (f_{ij})\) is an \(n \times n\) matrix where \(f_{ij}\) is the required flow between facilities \(i\) and \(j\) \(D = (d_{ij})\) is an \(n \times n\) matrix where \(d_{ij}\) is the distance between locations \(i\) and \(j\)

Optimization Problem \(\text{min}_{\phi \in S_n} \sum_{i=1}^n \sum_{j=1}^n f_{ij} \cdot d_{\phi(i) \phi(j)}\)

The assignment of facilities to locations is represented by a permutation \(\phi\), where \(\phi(i)\) is the location to which facility \(i\) is assigned. Each individual product \(f_{ij} \cdot d_{\phi(i) \phi(j)}\) is the cost of assigning facility \(i\) to location \(\phi(i)\) and facility \(j\) to location \(\phi(j)\).

Solve some QAPs!

Follow the links below to test your skill at finding good solutions to QAPs of various sizes. Notice that as the problem size increases, it becomes much more difficult to find an optimal solution. As \(n\) increases beyond a small number, it becomes impossible to enumerate and evaluate all possible assignment vectors. Instead, advanced solution algorithms are required to solve larger instances.

QAP of size 4

Qap of size 5, qap of size 6, qap of size 7, qap of size 8, qap of size 9.

• Anstreicher, K.M. 2003. Recent advances in the solution of quadratic assignment problems. Mathematical Programming Series B 97 , 27 - 42.
• Çela, E. 1998. The Quadratic Assignment Problem: Theory and Algorithms . Kluwer Academic Publishers, Dordrecht.
• Koopmans, T. C. and M. J. Beckmann. 1957. Assignment problems and the location of economic activities. Econometrica 25 , 53 - 76.
• QAPLIB Home Page

quadratic_assignment(method=’faq’) #

Solve the quadratic assignment problem (approximately).

This function solves the Quadratic Assignment Problem (QAP) and the Graph Matching Problem (GMP) using the Fast Approximate QAP Algorithm (FAQ) [1] .

Quadratic assignment solves problems of the following form:

where \(\mathcal{P}\) is the set of all permutation matrices, and \(A\) and \(B\) are square matrices.

Graph matching tries to maximize the same objective function. This algorithm can be thought of as finding the alignment of the nodes of two graphs that minimizes the number of induced edge disagreements, or, in the case of weighted graphs, the sum of squared edge weight differences.

Note that the quadratic assignment problem is NP-hard. The results given here are approximations and are not guaranteed to be optimal.

The square matrix \(A\) in the objective function above.

The square matrix \(B\) in the objective function above.

The algorithm used to solve the problem. This is the method-specific documentation for ‘faq’. ‘2opt’ is also available.

OptimizeResult containing the following fields.

Column indices corresponding to the best permutation found of the nodes of B .

The objective value of the solution.

The number of Frank-Wolfe iterations performed.

For documentation for the rest of the parameters, see scipy.optimize.quadratic_assignment

Maximizes the objective function if True .

Fixes part of the matching. Also known as a “seed” [2] .

Each row of partial_match specifies a pair of matched nodes: node partial_match[i, 0] of A is matched to node partial_match[i, 1] of B . The array has shape (m, 2) , where m is not greater than the number of nodes, \(n\) .

numpy.random.RandomState }, optional

If seed is None (or np.random ), the numpy.random.RandomState singleton is used. If seed is an int, a new RandomState instance is used, seeded with seed . If seed is already a Generator or RandomState instance then that instance is used.

Initial position. Must be a doubly-stochastic matrix [3] .

If the initial position is an array, it must be a doubly stochastic matrix of size \(m' \times m'\) where \(m' = n - m\) .

If "barycenter" (default), the initial position is the barycenter of the Birkhoff polytope (the space of doubly stochastic matrices). This is a \(m' \times m'\) matrix with all entries equal to \(1 / m'\) .

If "randomized" the initial search position is \(P_0 = (J + K) / 2\) , where \(J\) is the barycenter and \(K\) is a random doubly stochastic matrix.

Set to True to resolve degenerate gradients randomly. For non-degenerate gradients this option has no effect.

Integer specifying the max number of Frank-Wolfe iterations performed.

Tolerance for termination. Frank-Wolfe iteration terminates when \(\frac{||P_{i}-P_{i+1}||_F}{\sqrt{m')}} \leq tol\) , where \(i\) is the iteration number.

The algorithm may be sensitive to the initial permutation matrix (or search “position”) due to the possibility of several local minima within the feasible region. A barycenter initialization is more likely to result in a better solution than a single random initialization. However, calling quadratic_assignment several times with different random initializations may result in a better optimum at the cost of longer total execution time.

J.T. Vogelstein, J.M. Conroy, V. Lyzinski, L.J. Podrazik, S.G. Kratzer, E.T. Harley, D.E. Fishkind, R.J. Vogelstein, and C.E. Priebe, “Fast approximate quadratic programming for graph matching,” PLOS one, vol. 10, no. 4, p. e0121002, 2015, DOI:10.1371/journal.pone.0121002

D. Fishkind, S. Adali, H. Patsolic, L. Meng, D. Singh, V. Lyzinski, C. Priebe, “Seeded graph matching”, Pattern Recognit. 87 (2019): 203-215, DOI:10.1016/j.patcog.2018.09.014

“Doubly stochastic Matrix,” Wikipedia. https://en.wikipedia.org/wiki/Doubly_stochastic_matrix

As mentioned above, a barycenter initialization often results in a better solution than a single random initialization.

However, consider running from several randomized initializations and keeping the best result.

The ‘2-opt’ method can be used to further refine the results.

Navigation Menu

Search code, repositories, users, issues, pull requests..., provide feedback.

We read every piece of feedback, and take your input very seriously.

Saved searches

Use saved searches to filter your results more quickly.

To see all available qualifiers, see our documentation .

quadratic-assignment-problem

Here are 30 public repositories matching this topic..., thinklab-sjtu / thinkmatch.

A research protocol for deep graph matching.

• Updated Apr 8, 2024

theochem / procrustes

Python library for finding the optimal transformation(s) that makes two matrices as close as possible to each other.

• Updated Jan 3, 2023

Lolik-Bolik / Quadratic_Assign_Problem

Solution quadratic assign problem via LS(local search), ILS(iterated local search), GLS(guided local search)

• Updated May 11, 2020

CodeSopranos / LocalSearch

The research work on local search algorithms

• Updated May 9, 2020
• Jupyter Notebook

emanuele / DSPFP

This is a Python implementation of the Doubly Stochastic Projected Fixed Point (DSPFP) algorithm for solving the Quadratic Assignment Problem / Graph Matching..

• Updated Feb 21, 2020

jjosenaldo / QAP-algorithms

Algorithms for solving the Quadratic Assignment Problem

• Updated Oct 5, 2019

Giant316 / quadraticAssignment

Implementation of different algorithms: heuristic search, Simulated Annealing, Ant Colony Algorithm and Tabu Search to a Quadratic Assignment Problem.

• Updated Dec 6, 2020

ebrahimpichka / QAP-RL

Unofficial implemnetation of "Solving Quadratic Assignemt Problem using Deep Reinforcement Learning" ( https://arxiv.org/abs/2310.01604 )

• Updated Dec 29, 2023

ssk1328 / mcmf

Mapping and routing of a data flow network mapped on an mesh NoC

• Updated Jul 6, 2017

flixpar / QuadraticAssignmentProblem.jl

Algorithms for solving the quadratic assignment problem (QAP) implemented in Julia.

• Updated May 20, 2021

FanwangM / procrustes

This package supports general, orthogonal, rotation, permutation, projection, and symmetric Procrustes problems, including both the normal one-sided approach and (for orthogonal and permutation Procrustes) two-sided approaches, where both the rows and columns are transformed.

mhahsler / qap

Heuristics for the Quadratic Assignment Problem (QAP) - R package

• Updated Apr 20, 2024

Venopacman / comb_opt_lessons

laboratory works for combinatoric optimization course

• Updated Nov 25, 2018

ScottWalkerAU / QAPES

Quadratic Assignment Problem, an Enhanced Solver

• Updated Dec 12, 2021

sidneyrachel / quadratic-assignment-problem

Solving quadratic assignment problem using iterated local search, improved hybrid genetic algorithm, tabu search, and constraint solving.

• Updated Jan 28, 2022

TzeLun / QAPSolver

A simple Quadratic Assignment Problem solver using heuristics and metaheuristics

• Updated Dec 10, 2023

thomasWeise / moptipyapps

Applications of Metaheuristic Optimization in Python

• Updated May 18, 2024

JuanDa14Sa / QAP-instance-Genetic-algorithm

Solving a QAP instance using genetic algorithms

• Updated Jan 26, 2022

HeddaCohenIndelman / Learning-Constrained-Structured-Spaces-with-Application-to-Multi-Graph-Matching

This is the official code for the AISTATS 2023 paper "Learning Constrained Structured Spaces with Application to Multi-Graph Matching"

• Updated Jun 4, 2023

gzlupko / social_network_analysis

This repository utilizes social network analysis (SNA) to analyze multiple social networks. Clustering algorithms were used to explore sub-groups and QAP was implemented for non-parametric multiple regression analysis.

• Updated Mar 10, 2021

Improve this page

Add a description, image, and links to the quadratic-assignment-problem topic page so that developers can more easily learn about it.

Curate this topic

Add this topic to your repo

To associate your repository with the quadratic-assignment-problem topic, visit your repo's landing page and select "manage topics."

• Help & FAQ

Semidefinite programming approach for the quadratic assignment problem with a sparse graph

• Mathematics
• Center for Statistics & Machine Learning

Research output : Contribution to journal › Article › peer-review

The matching problem between two adjacency matrices can be formulated as the NP-hard quadratic assignment problem (QAP). Previous work on semidefinite programming (SDP) relaxations to the QAP have produced solutions that are often tight in practice, but such SDPs typically scale badly, involving matrix variables of dimension n 2 where n is the number of nodes. To achieve a speed up, we propose a further relaxation of the SDP involving a number of positive semidefinite matrices of dimension O(n) no greater than the number of edges in one of the graphs. The relaxation can be further strengthened by considering cliques in the graph, instead of edges. The dual problem of this novel relaxation has a natural three-block structure that can be solved via a convergent Alternating Direction Method of Multipliers in a distributed manner, where the most expensive step per iteration is computing the eigendecomposition of matrices of dimension O(n). The new SDP relaxation produces strong bounds on quadratic assignment problems where one of the graphs is sparse with reduced computational complexity and running times, and can be used in the context of nuclear magnetic resonance spectroscopy to tackle the assignment problem.

All Science Journal Classification (ASJC) codes

• Control and Optimization
• Computational Mathematics
• Applied Mathematics
• Alternating direction method of multipliers
• Convex relaxation
• Graph matching
• Quadratic assignment problem
• Semidefinite programming

Access to Document

• 10.1007/s10589-017-9968-8

Other files and links

• Link to publication in Scopus
• Link to the citations in Scopus

Fingerprint

• Quadratic Assignment Problem Mathematics 100%
• Sparse Graphs Mathematics 86%
• Semidefinite Programming Mathematics 83%
• Relaxation Engineering & Materials Science 67%
• Semidefinite Programming Relaxation Mathematics 66%
• Nuclear Magnetic Resonance Mathematics 36%
• Graph in graph theory Mathematics 33%
• Method of multipliers Mathematics 32%

T1 - Semidefinite programming approach for the quadratic assignment problem with a sparse graph

AU - Bravo Ferreira, José F.S.

AU - Khoo, Yuehaw

AU - Singer, Amit

N1 - Publisher Copyright: © 2017, Springer Science+Business Media, LLC, part of Springer Nature.

PY - 2018/4/1

Y1 - 2018/4/1

N2 - The matching problem between two adjacency matrices can be formulated as the NP-hard quadratic assignment problem (QAP). Previous work on semidefinite programming (SDP) relaxations to the QAP have produced solutions that are often tight in practice, but such SDPs typically scale badly, involving matrix variables of dimension n2 where n is the number of nodes. To achieve a speed up, we propose a further relaxation of the SDP involving a number of positive semidefinite matrices of dimension O(n) no greater than the number of edges in one of the graphs. The relaxation can be further strengthened by considering cliques in the graph, instead of edges. The dual problem of this novel relaxation has a natural three-block structure that can be solved via a convergent Alternating Direction Method of Multipliers in a distributed manner, where the most expensive step per iteration is computing the eigendecomposition of matrices of dimension O(n). The new SDP relaxation produces strong bounds on quadratic assignment problems where one of the graphs is sparse with reduced computational complexity and running times, and can be used in the context of nuclear magnetic resonance spectroscopy to tackle the assignment problem.

AB - The matching problem between two adjacency matrices can be formulated as the NP-hard quadratic assignment problem (QAP). Previous work on semidefinite programming (SDP) relaxations to the QAP have produced solutions that are often tight in practice, but such SDPs typically scale badly, involving matrix variables of dimension n2 where n is the number of nodes. To achieve a speed up, we propose a further relaxation of the SDP involving a number of positive semidefinite matrices of dimension O(n) no greater than the number of edges in one of the graphs. The relaxation can be further strengthened by considering cliques in the graph, instead of edges. The dual problem of this novel relaxation has a natural three-block structure that can be solved via a convergent Alternating Direction Method of Multipliers in a distributed manner, where the most expensive step per iteration is computing the eigendecomposition of matrices of dimension O(n). The new SDP relaxation produces strong bounds on quadratic assignment problems where one of the graphs is sparse with reduced computational complexity and running times, and can be used in the context of nuclear magnetic resonance spectroscopy to tackle the assignment problem.

KW - Alternating direction method of multipliers

KW - Convex relaxation

KW - Graph matching

KW - Quadratic assignment problem

KW - Semidefinite programming

UR - http://www.scopus.com/inward/record.url?scp=85034241306&partnerID=8YFLogxK

UR - http://www.scopus.com/inward/citedby.url?scp=85034241306&partnerID=8YFLogxK

U2 - 10.1007/s10589-017-9968-8

DO - 10.1007/s10589-017-9968-8

M3 - Article

AN - SCOPUS:85034241306

SN - 0926-6003

JO - Computational Optimization and Applications

JF - Computational Optimization and Applications

Help | Advanced Search

Quantum Physics

Title: utilising a quantum hybrid solver for bi-objective quadratic assignment problems.

Abstract: The intersection between quantum computing and optimisation has been an area of interest in recent years. There have been numerous studies exploring the application of quantum and quantum-hybrid solvers to various optimisation problems. This work explores scalarisation methods within the context of solving the bi-objective quadratic assignment problem using a quantum-hybrid solver. We show results that are consistent with previous research on a different Ising machine.

Submission history

Access paper:.

• HTML (experimental)
• Other Formats

References & Citations

• INSPIRE HEP
• Google Scholar
• Semantic Scholar

BibTeX formatted citation

Bibliographic and Citation Tools

Code, data and media associated with this article, recommenders and search tools.

• Institution

arXivLabs: experimental projects with community collaborators

arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website.

Both individuals and organizations that work with arXivLabs have embraced and accepted our values of openness, community, excellence, and user data privacy. arXiv is committed to these values and only works with partners that adhere to them.

Have an idea for a project that will add value for arXiv's community? Learn more about arXivLabs .

A zeroing feedback gradient-based neural dynamics model for solving dynamic quadratic programming problems with linear equation constraints in finite time

• Original Article
• Published: 27 May 2024

Cite this article

• Shangfeng Du 1 ,
• Dongyang Fu   ORCID: orcid.org/0000-0003-0426-4356 1 ,
• Long Jin 2 ,
• Yang Si 1 &
• Yongze Li 1  

Gradient-based neural dynamics (GND) models are a classical algorithm for solving optimization problems, but it has non-negligible flaws in solving dynamic problems. In this study, a novel GND model, namely the zeroing feedback gradient-based neural dynamics (ZF-GND) models, is proposed based on the original GND model for tracking down the exact solution of dynamic quadratic programming problem (DQP). Further, a nonlinear projection function is designed to accelerate the convergence of the model. An upper bound on the convergence time of the ZF-GND model is rigorously defined through theoretical analysis. The superior effect of the ZF-GND model in terms of convergence is verified through comparison experiments. Finally, an application of robot motion planning is introduced to verify the practicality of the ZF-GND model.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Price includes VAT (Russian Federation)

Instant access to the full article PDF.

Rent this article via DeepDyve

Institutional subscriptions

Data availability

The data that support the findings this study are available from the corresponding author upon reasonable request.

Mattingley J, Boyd S (2010) Real-Time convex optimization in signal processing. IEEE Signal Process Mag 27(3):50–61

Article   Google Scholar  

Jiang C, Xiao X, Liu D, Huang H, Xiao H, Lu H (2021) Nonconvex and bound constraint zeroing neural network for solving time-varying complex-valued quadratic programming problem. IEEE Trans Ind Informat 17(10):6864–6874

Liao-McPherson D, Huang M, Kolmanovsky I (2019) A regularized and smoothed fischer-burmeister method for quadratic programming with applications to model predictive control. IEEE Trans Autom Control 64(7):2937–2944

Article   MathSciNet   Google Scholar  

Wang G, Hao Z, Huang H, Zhang B (2023) A proportional-integral iterative algorithm for time-variant equality-constrained quadratic programming problem with applications. Artif Intell Rev 56:4535–4556

Fu D, Huang H, Xiao X, Xia L, Jin L (2022) A generalized complex-valued constrained energy minimization scheme for the arctic sea ice extraction aided with neural algorithm. IEEE Trans Geosci Remote Sens 60(4303017):1–17

Google Scholar  

Minet J, Taboury J, Goudail F, Pèalat M, Roux N, Lonnoy J, Ferrec Y (2011) Influence of band selection and target estimation error on the performance of the matched filter in hyperspectral imaging. Appl Opt 50(22):4276–4285

Manolakis D, Lockwood R, Cooley T, Jacobson J (2009) Hyperspectral detection algorithms: use covariances or subspaces? Proc. SPIE 7457, Imaging Spectrometry XIV, Aug

Si Y, Wang D, Chou Y, Fu D (2023) Non-convex activated zeroing neural network model for solving time-varying nonlinear minimization problems with finite-time convergence, Knowl.-Based Syst., vol. 274, Aug

Yaǧmur N, Alagöz BB (2019) Comparision of solutions of numerical gradient descent method and continous time gradient descent dynamics and lyapunov stability. In: Proceedings on 2019 27th signal processing and communications applications conference (SIU), pp. 1–4

Li W, Swetits J (1993) A Newton method for convex regression, data smoothing, and quadratic programming with bounded constraints. SIAM J Optim 3(3):466–488

Liu M, Chen L, Du X, Jin L, Shang M (2023) Activated gradients for deep neural networks. IEEE Trans Neural Netw Learn Syst 34(4):2156–2168

Plevris V, Papadrakakis M (2010) A hybrid particle swarm?gradient algorithm for global structural optimization. Comput-Aided Civ Infrastruct Eng 26(1):48–68

Andrei N (2014) An accelerated subspace minimization three-term conjugate gradient algorithm for unconstrained optimization. Numer. Algor. 65:859–874

Wang F, Jian J, Wang C (2014) A model-hybrid approach for unconstrained optimization problems. Numer Algor 66:741–759

Mathews JH, Fink KD (2004) Numerical Methods using MATLAB., Englewood Cliffs, NJ, USA: Prentice-Hall

Zhang Y, Jiang D, Wang J (2002) A recurrent neural network for solving sylvester equation with time-varying coefficients. IEEE Trans Neural Netw 13(5):1053–1063

Sun B, Cao Y, Guo Z, Yan Z, Wen S (2020) Synchronization of discrete-time recurrent neural networks with time-varying delays via quantized sliding mode control. Appl Math Comput 375:125093

MathSciNet   Google Scholar  

Zhang X, Chen L, Li S, Stanimirović P, Zhang J, Jin L (2021) Design and analysis of recurrent neural network models with non-linear activation functions for solving time-varying quadratic programming problems. CAAI Trans Intell Technol 6(4):394–404

Jia C, Kong D, Du L (2022) Recursive terminal Sliding-Mode control method for nonlinear system based on double hidden layer fuzzy emotional recurrent neural network. IEEE Access 10:118012–118023

Zhang Z, Zheng L, Yu J, Li Y, Yu Z (2017) Three recurrent neural networks and three numerical methods for solving a repetitive motion planning scheme of redundant robot manipulators. IEEE / ASME Trans Mechatr 22(3):1423–1434

Zhang Y, Wang J (2001) Recurrent neural networks for nonlinear output regulation. Automatica 37:1161–1173

Chen D, Zhang Y (2018) Robust zeroing neural-dynamics and its time-varying disturbances suppression model applied to mobile robot manipulators. IEEE Trans Neural Netw Learn Syst 29(9):4385–4397

Wang G, Li Q, Liu S, Xiao H, Zhang B (2022) New zeroing neural network with finite-time convergence for dynamic complex-value linear equation and its applications. Chaos Soliton Fractal 164:112674

Chen D, Li S, Wu Q (2021) A novel supertwisting zeroing neural network with application to mobile robot manipulators. IEEE Trans Neural Netw Learn Syst 32(4):1776–1787

Shi Y, Sheng W, Li S, Li B, Sun X (2023) Neurodynamics for equality-constrained time-variant nonlinear optimization using discretization. IEEE Trans Ind Inf. https://doi.org/10.1109/TII.2023.3290187

Shi Y, Wang J, Li S, Li B, Sun X (2023) Tracking control of cable-driven planar robot based on discrete-time recurrent neural network with immediate discretization method. IEEE Trans Ind Inf 19(6):7414–7423

Shi Y, Zhao W, Li S, Li B, Sun X (2023) Novel discrete-time recurrent neural network for robot manipulator: a direct discretization technical route. IEEE Trans Neural Netw Learn Syst 34(6):2781–2790

Shi Y, Jin L, Li S, Li J, Qiang J, Gerontitis DK (2022) Novel discrete-time recurrent neural networks handling discrete-form time-variant multi-augmented Sylvester matrix problems and manipulator application. IEEE Trans. Neural Netw. Learn. Syst. 33(2):587–599

Liao B, Zhang Y, Jin L (2016) Taylor \(O(h^{3})\) discretization of ZNN models for dynamic equality-constrained quadratic programming with application to manipulators. IEEE Trans Neural Netw Learn Syst 27(2):225–237

Liao S, Liu J, Qi Y, Huang H, Zheng R, Xiao X (2022) An adaptive gradient neural network to solve dynamic linear matrix equations. IEEE Trans, Syst, Man, Cybern, Syst 52(9):5913–5924

Liao S, Liu J, Xiao X, Fu D, Wang G, Jin L (2020) Modified gradient neural networks for solving the time-varying sylvester equation with adaptive coefficients and elimination of matrix inversion. Neurocomputing 379:1–11

Wang G, Hao Z, Li H, Zhang B (2023) An activated variable parameter gradient-based neural network for time-variant constrained quadratic programming and its applications. CAAI Trans Intell Technol, pp. 1–10, Feb

Li W, Han L, Xiao X et al (2022) A gradient-based neural network accelerated for vision-based control of an RCM-constrained surgical endoscope robot. Neural Comput Appl 34:1329–1343

Liufu Y, Jin L, Xu J, Xiao X, Fu D (2022) Reformative noise-immune neural network for equality-constrained optimization applied to image target detection. IEEE Trans Emerg Top Comput 10(2):973–984

Liu B, Fu D, Qi Y, Huang H, Jin L (2021) Noise-tolerant gradient-oriented neurodynamic model for solving the sylvester equation. Appl Soft Comput J, vol. 109

Jin L, Li S, Wang H, Zhang Z (2018) Nonconvex projection activated zeroing neurodynamic models for time-varying matrix pseudoinversion with accelerated finite-time convergence. Appl Soft Comput J 62:840–850

Jin L, Li S, Liao B, Zhang Z (2017) Zeroing neural networks: a survey. Neurocomputing 267:597–604

Zhang Y, Chen K, Tan H-Z (2009) Performance analysis of gradient neural network exploited for online Time-Varying matrix inversion. IEEE Trans Autom Control 54(8):1940–1945

Jin L, Wei L, Li S (2023) Gradient-based differential neural-solution to time-dependent nonlinear optimization. IEEE Trans Autom Control 68(1):620–627

Jarlebring E, Poloni F (2019) Iterative methods for the delay Lyapunov equation with T-Sylvester preconditioning. Appl Numer Math 135(1):173–185

Hunger R (2005) Floating point operations in matrix-vector calculus[M]. Munich, Germany: Munich University of Technology, Inst. for Circuit Theory and Signal Processing

Zuo Q, Li K, Xiao L, Wang Y, Li K (2021) On generalized zeroing neural network under discrete and distributed time delays and its application to dynamic Lyapunov equation. IEEE Trans Syst, Man, Cybern, Syst 52:5114–5126

Xiao L, Song W, Jia L, Li X (2022) ZNN for time-variant nonlinear inequality systems: A finite-time solution. Neurocomputing 500:319–328

Zhang Y, Li Z, Guo D, Chen K, Chen P (2013) Superior robustness of using power-sigmoid activation functions in Z-type models for time-varying problems solving. ICMLC., pp. 759–764

Zuo Q, Li K, Xiao L, Wang Y, Li K (2022) On generalized zeroing neural network under discrete and distributed time delays and its application to dynamic Lyapunov Equation. IEEE Trans Syst, Man, Cybernet: Syst 52(8):5114–5126. https://doi.org/10.1109/TSMC.2021.3115555

Download references

Acknowledgements

This research was funded in part by the National Key Research and Development Program of China under Grant No. 2022YFC3103101, Key Special Project for Introduced Talents Team of Southern Marine Science and Engineering Guangdong Laboratory under Contract GML2021GD0809, National Natural Science Foundation of China under Contract 42206187, Key projects of the Guangdong Education Department under Grant No. 2023ZDZX4009.

Author information

Authors and affiliations.

School of Electronic and Information Engineering, Guangdong Ocean University, Zhanjiang, 524088, China

Shangfeng Du, Dongyang Fu, Yang Si & Yongze Li

School of Information Science and Engineering, Lanzhou University, Lanzhou, 730000, China

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Dongyang Fu .

Ethics declarations

Ethical approval.

We confirm that the manuscript has been read and approved by all named authors and that there are no other persons who satisfied the criteria for authorship but are not listed. We further confirm that the other of authors listed in the manuscript has been approved by all of us. We confirm that we have given due consideration to the protection of intellectual property associated with this work and that there are no impediments to publication, including the timing of publication, with respect to intellectual property. In so doing we confirm that we have followed the regulations of our institutions concerning intellectual property. We understand that the Corresponding Author is the sole contact for the Editorial process (including Editorial Manager and direct communications with the office). He is responsible for communicating with the other authors about progress, submissions of revision, and final approval of proof. We confirm that we have provided a current email address, which is accessible by the corresponding author, which has been configured to accept email from the Neural Computing and Applications Editorial Office.

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Du, S., Fu, D., Jin, L. et al. A zeroing feedback gradient-based neural dynamics model for solving dynamic quadratic programming problems with linear equation constraints in finite time. Neural Comput & Applic (2024). https://doi.org/10.1007/s00521-024-09762-3

Download citation

Received : 27 July 2023

Accepted : 25 March 2024

Published : 27 May 2024

DOI : https://doi.org/10.1007/s00521-024-09762-3

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Zeroing feedback gradient-based neural dynamic (ZF-GND) model
• Nonlinear projection function
• Robotic motion planning
• Find a journal
• Publish with us
• Track your research