statement of the problem in mathematics research

Have a language expert improve your writing

Run a free plagiarism check in 10 minutes, generate accurate citations for free.

• Knowledge Base
• Starting the research process
• How to Write a Problem Statement | Guide & Examples

How to Write a Problem Statement | Guide & Examples

Published on November 6, 2022 by Shona McCombes and Tegan George. Revised on November 20, 2023.

A problem statement is a concise and concrete summary of the research problem you seek to address. It should:

• Contextualize the problem. What do we already know?
• Describe the exact issue your research will address. What do we still need to know?
• Show the relevance of the problem. Why do we need to know more about this?
• Set the objectives of the research. What will you do to find out more?

Table of contents

When should you write a problem statement, step 1: contextualize the problem, step 2: show why it matters, step 3: set your aims and objectives.

Problem statement example

Other interesting articles

Frequently asked questions about problem statements.

There are various situations in which you might have to write a problem statement.

In the business world, writing a problem statement is often the first step in kicking off an improvement project. In this case, the problem statement is usually a stand-alone document.

In academic research, writing a problem statement can help you contextualize and understand the significance of your research problem. It is often several paragraphs long, and serves as the basis for your research proposal . Alternatively, it can be condensed into just a few sentences in your introduction .

A problem statement looks different depending on whether you’re dealing with a practical, real-world problem or a theoretical issue. Regardless, all problem statements follow a similar process.

Prevent plagiarism. Run a free check.

The problem statement should frame your research problem, giving some background on what is already known.

Practical research problems

For practical research, focus on the concrete details of the situation:

• Where and when does the problem arise?
• Who does the problem affect?
• What attempts have been made to solve the problem?

Theoretical research problems

For theoretical research, think about the scientific, social, geographical and/or historical background:

• What is already known about the problem?
• Is the problem limited to a certain time period or geographical area?
• How has the problem been defined and debated in the scholarly literature?

The problem statement should also address the relevance of the research. Why is it important that the problem is addressed?

Don’t worry, this doesn’t mean you have to do something groundbreaking or world-changing. It’s more important that the problem is researchable, feasible, and clearly addresses a relevant issue in your field.

Practical research is directly relevant to a specific problem that affects an organization, institution, social group, or society more broadly. To make it clear why your research problem matters, you can ask yourself:

• What will happen if the problem is not solved?
• Who will feel the consequences?
• Does the problem have wider relevance? Are similar issues found in other contexts?

Sometimes theoretical issues have clear practical consequences, but sometimes their relevance is less immediately obvious. To identify why the problem matters, ask:

• How will resolving the problem advance understanding of the topic?
• What benefits will it have for future research?
• Does the problem have direct or indirect consequences for society?

Finally, the problem statement should frame how you intend to address the problem. Your goal here should not be to find a conclusive solution, but rather to propose more effective approaches to tackling or understanding it.

The research aim is the overall purpose of your research. It is generally written in the infinitive form:

• The aim of this study is to determine …
• This project aims to explore …
• This research aims to investigate …

The research objectives are the concrete steps you will take to achieve the aim:

• Qualitative methods will be used to identify …
• This work will use surveys to collect …
• Using statistical analysis, the research will measure …

The aims and objectives should lead directly to your research questions.

Learn how to formulate research questions

Receive feedback on language, structure, and formatting

Professional editors proofread and edit your paper by focusing on:

• Academic style
• Vague sentences
• Style consistency

See an example

You can use these steps to write your own problem statement, like the example below.

Step 1: Contextualize the problem A family-owned shoe manufacturer has been in business in New England for several generations, employing thousands of local workers in a variety of roles, from assembly to supply-chain to customer service and retail. Employee tenure in the past always had an upward trend, with the average employee staying at the company for 10+ years. However, in the past decade, the trend has reversed, with some employees lasting only a few months, and others leaving abruptly after many years.

Step 2: Show why it matters As the perceived loyalty of their employees has long been a source of pride for the company, they employed an outside consultant firm to see why there was so much turnover. The firm focused on the new hires, concluding that a rival shoe company located in the next town offered higher hourly wages and better “perks”, such as pizza parties. They claimed this was what was leading employees to switch. However, to gain a fuller understanding of why the turnover persists even after the consultant study, in-depth qualitative research focused on long-term employees is also needed. Focusing on why established workers leave can help develop a more telling reason why turnover is so high, rather than just due to salaries. It can also potentially identify points of change or conflict in the company’s culture that may cause workers to leave.

Step 3: Set your aims and objectives This project aims to better understand why established workers choose to leave the company. Qualitative methods such as surveys and interviews will be conducted comparing the views of those who have worked 10+ years at the company and chose to stay, compared with those who chose to leave.

If you want to know more about the research process , methodology , research bias , or statistics , make sure to check out some of our other articles with explanations and examples.

Methodology

• Sampling methods
• Simple random sampling
• Stratified sampling
• Cluster sampling
• Likert scales
• Reproducibility

 Statistics

• Null hypothesis
• Statistical power
• Probability distribution
• Effect size
• Poisson distribution

Research bias

• Optimism bias
• Cognitive bias
• Implicit bias
• Hawthorne effect
• Anchoring bias
• Explicit bias

Once you’ve decided on your research objectives , you need to explain them in your paper, at the end of your problem statement .

Keep your research objectives clear and concise, and use appropriate verbs to accurately convey the work that you will carry out for each one.

I will compare …

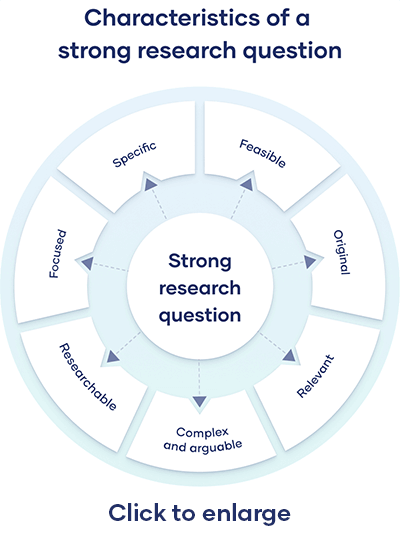
All research questions should be:

• Focused on a single problem or issue
• Researchable using primary and/or secondary sources
• Feasible to answer within the timeframe and practical constraints
• Specific enough to answer thoroughly
• Complex enough to develop the answer over the space of a paper or thesis
• Relevant to your field of study and/or society more broadly

Research objectives describe what you intend your research project to accomplish.

They summarize the approach and purpose of the project and help to focus your research.

Your objectives should appear in the introduction of your research paper , at the end of your problem statement .

Your research objectives indicate how you’ll try to address your research problem and should be specific:

Cite this Scribbr article

If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.

McCombes, S. & George, T. (2023, November 20). How to Write a Problem Statement | Guide & Examples. Scribbr. Retrieved October 8, 2024, from https://www.scribbr.com/research-process/problem-statement/

Is this article helpful?

Shona McCombes

Other students also liked, how to choose a dissertation topic | 8 steps to follow, how to define a research problem | ideas & examples, writing strong research questions | criteria & examples, what is your plagiarism score.

• Resources Home 🏠
• Try SciSpace Copilot
• Search research papers
• Add Copilot Extension
• Try AI Detector
• Try Paraphraser
• Try Citation Generator
• April Papers
• June Papers
• July Papers

How to Write a Statement of the Problem in Research

Table of Contents

The problem statement is a foundation of academic research writing , providing a precise representation of an existing gap or issue in a particular field of study.

Crafting a sharp and focused problem statement lays the groundwork for your research project.

• It highlights the research's significance .
• Emphasizes its potential to influence the broader academic community.
• Represents the initial step for you to make a meaningful contribution to your discipline.

Therefore, in this article, we will discuss what is a statement of the problem in research and how to craft a compelling research problem statement.

What is a research problem statement?

A research problem statement is a concise, clear, and specific articulation of a gap in current knowledge that your research aims to bridge. It not only sets forth the scope and direction of your research but also establishes its relevance and significance.

Your problem statement in your research paper aims to:

• Define the gap : Clearly identify and articulate a specific gap or issue in the existing knowledge.
• Provide direction : Serve as a roadmap, guiding the course of your research and ensuring you remain focused.
• Establish relevance : Highlight the importance and significance of the problem in the context of your field or the broader world.
• Guide inquiry :  Formulate the research questions or hypotheses you'll explore.
• Communicate intent : Succinctly convey the core purpose of your research to stakeholders, peers, and any audience.
• Set boundaries : Clearly define the scope of your research to ensure it's focused and achievable.

When should you write a problem statement in research?

Initiate your research by crafting a clear problem statement. This should be done before any data collection or analysis, serving as a foundational anchor that clearly identifies the specific issue you aim to address.

By establishing this early on, you shape the direction of your research, ensuring it targets a genuine knowledge gap.

Furthermore, an effective and a concise statement of the problem in research attracts collaborators, funders, and supporters, resonating with its clarity and purpose. Remember, as your research unfolds, the statement might evolve, reflecting new insights and staying pertinent.

But how do you distinguish between a well-crafted problem statement and one that falls short?

Effective vs. ineffective research problem statements

Imagine a scenario where medical researchers aim to tackle a new strain of virus. Their effective problem statement wouldn't merely state the existence of the virus. Instead, it would delve into the specifics — the regions most affected, the demographics most vulnerable, and the current limitations in medical interventions.

Whereas an ineffective research problem statement is vague, overly broad, or ambiguous, failing to provide a clear direction for the research. It may not be rooted in existing literature, might lack clarity on its significance, or could be framed in a way that makes the research objectives unachievable or irrelevant.

To understand it better, let's consider the topic of “Remote work and employee productivity.”

Effective problem statement

“Over the past decade, there has been a 70% increase in organizations adopting remote work policies. While some studies suggest remote work enhances employee productivity, others indicate potential declines due to distractions at home.

However, there’s a lack of comprehensive research examining the specific factors in a remote environment that influence productivity. This study aims to identify and analyze these factors, providing organizations with actionable insights to optimize remote work policies.”

Why is this statement of a problem in research effective?

• Specificity : The statement provides a clear percentage to highlight the rise in remote work.
• Context : It acknowledges existing research and the conflicting findings.
• Clear gap identification : It points out the lack of comprehensive research on specific factors affecting productivity in remote work.
• Purpose : The statement concludes with a clear aim for the research.

Ineffective problem statement

"People are working from home a lot now, especially since there are so many internet tools. Some say it's good; others say it's not that great. This research will just look into the whole work-from-home thing and see what's up."

Why is this statement of a problem in research ineffective?

• Informal language : Phrases like "what's up" and "the whole work-from-home thing" are not suitable for academic writing.
• Vagueness : The statement doesn't provide any specific data or context about the rise of remote work.
• Lack of clear focus : It's unclear what aspect of remote work the research will address.
• Ambiguous purpose : The statement doesn't specify the research's objectives or expected outcomes.

After gaining an understanding of what an effective research problem statement looks like, let's dive deeper into how to write one.

How to write a problem statement in research?

Drafting your research problem statement at the onset of your research journey ensures that your research remains anchored. That means by defining and articulating the main issue or challenge you intend to address at the very beginning of your research process; you provide a clear focus and direction for the entire study.

Here's a detailed guide to how you can write an effective statement of the problem in research.

Identify the research area : Before addressing a specific problem, you need to know the broader domain or field of your study. This helps in contextualizing your research and ensuring it aligns with existing academic disciplines.

Example: If you're curious about the effects of digital technology on human behavior, your broader research area might be Digital Sociology or Media Studies.

Conduct preliminary literature review : Familiarize yourself with existing research related to your topic. This will help you understand what's already known and, more importantly, identify gaps or unresolved questions in the existing knowledge. This step also ensures you're advancing upon existing work rather than replicating it.

Example: Upon reviewing literature on digital technology and behavior, you find many studies on social media's impact on youth but fewer on its effects on the elderly.

Read how to conduct an effective literature review .

Define the specific problem : After thoroughly reviewing the literature, pinpoint a particular issue that your research will address. Ensure that this chosen issue is not only of substantial importance in its field but also realistically approachable given your resources and expertise. To define it precisely, you might consider:

• Highlighting discrepancies or contradictions in existing literature.
• Emphasizing the real-world implications of this gap.
• Assessing the feasibility of exploring this issue within your means and timeframe.

Example: You decide to investigate how digital technology, especially social media, affects the mental well-being of the elderly, given the limited research in this area.

Articulate clearly and concisely : Your problem statement should be straightforward and devoid of jargon. It needs to convey the essence of your research issue in a manner that's understandable to both experts and non-experts.

Example: " The impact of social media on the mental well-being of elderly individuals remains underexplored, despite the growing adoption of digital technology in this age group. "

Highlight the significance : Explain why your chosen research problem matters. This could be due to its real-world implications, its potential to fill a knowledge gap or its relevance to current events or trends.

Example: As the elderly population grows and becomes more digitally connected, understanding the psychological effects of social media on this demographic could inform digital literacy programs and mental health interventions.

Ensure feasibility : Your research problem should be something you can realistically study, given your resources, timeframe, and expertise. It's essential to ensure that you can gather data, conduct experiments, or access necessary materials or participants.

Example: You plan to survey elderly individuals in local community centers about their social media usage and perceived mental well-being, ensuring you have the means to reach this demographic.

Seek feedback : Discuss your preliminary problem statement with peers, mentors, or experts in the field. They can provide insights, point out potential pitfalls, or suggest refinements.

Example: After discussing with a gerontologist, you decide to also consider the role of digital training in moderating the effects of social media on the elderly.

Refine and Revise : Based on feedback and further reflection, revise and improve your problem statement. This iterative process ensures clarity, relevance, and precision.

Example: Your refined statement reads: Despite the increasing digital connectivity of the elderly, the effects of social media on their mental well-being, especially in the context of digital training, remain underexplored.

By following these detailed steps, you can craft a research problem statement that is both compelling and academically rigorous.

Having explored the details of crafting a research problem statement, it's crucial to distinguish it from another fundamental element in academic research: the thesis statement.

Difference between a thesis statement and a problem statement

While both terms are central to research, a thesis statement presents your primary claim or argument, whereas a problem statement describes the specific issue your research aims to address.

Think of the thesis statement as the conclusion you're driving towards, while the problem statement identifies a specific gap in current knowledge.

For instance, a problem statement might highlight the rising mental health issues among teenagers, while the thesis statement could propose that increased screen time is a significant contributor.

Refer to the comparison table between what is a thesis and a problem statement in the research below:

Common mistakes to avoid in writing statement of the problem in research

Mistakes in the research problem statement can lead to a domino effect, causing misalignment in research objectives, wasted resources, and even inconclusive or irrelevant results.

Recognizing and avoiding these pitfalls not only strengthens the foundation of your research but also ensures that your efforts concede impactful insights.

Here's a detailed exploration of frequent subjective, qualitative, quantitative and measurable mistakes and how you can sidestep them.

Being too broad or too narrow

A problem statement that's too broad can lack focus, making it challenging to derive specific research questions or objectives. Conversely, a statement that's too narrow might limit the scope of your research or make it too trivial.

Example of mistake: "Studying the effects of diet on health" is too broad, while "Studying the effects of eating green apples at 3 pm on heart health" is overly narrow.

You can refine the scope based on preliminary research. The correct way to write this problem statement will be "Studying the effects of a high-fiber diet on heart health in adults over 50." This statement is neither too broad nor too narrow, and it provides a clear direction for the research.

Using unnecessary jargon or technical language

While academic writing often involves academic terms, overloading your problem statement with jargon can alienate readers and obscure the actual problem.

Example of Mistake: "Examining the diurnal variations in macronutrient ingestion vis-à-vis metabolic homeostasis."

To ensure it’s not complicated, you can simplify and clarify. "Examining how daily changes in nutrient intake affect metabolic balance" conveys the same idea more accessible.

Not emphasizing the "Why" of the problem

It's not enough to state a problem; you must also convey its significance. Why does this problem matter? What are the implications of not addressing it?

Example of Mistake: "Many students are not engaging with online learning platforms."

You can proceed with the approach of highlighting the significance here. "Many students are not engaging with online learning platforms, leading to decreased academic performance and widening educational disparities."

Circular reasoning and lack of relevance

Your problem statement should be grounded in existing research or observed phenomena. Avoid statements that assume what they set out to prove or lack a clear basis in current knowledge.

Example of Mistake: "We need to study X because not enough research has been done on X."

Instead, try grounding your statement based on already-known facts. "While several studies have explored Y, the specific impact of X remains unclear, necessitating further research."

Being overly ambitious

While it's commendable to aim high, your problem statement should reflect a challenge that's achievable within your means, timeframe, and resources.

Example of Mistake: "This research will solve world hunger."

Here, you need to be realistic and focused. "This research aims to develop sustainable agricultural techniques to increase crop yields in arid regions."

By being mindful of these common mistakes, you can craft a problem statement that is clear, relevant and sets a solid foundation for your research.

Over-reliance on outdated data

Using data that is no longer relevant can mislead the direction of your research. It's essential to ensure that the statistics or findings you reference are current and pertinent to the present scenario.

Example of Mistake: "According to a 1995 study, only 5% of the population uses the internet for daily tasks."

You always cross-check the dates and relevance of the data you're using. For a contemporary study on internet usage, you'd want to reference more recent statistics.

Not specifying the sample size or demographic

A problem statement should be clear about the population or sample size being studied, especially when making generalizations or claims.

Example of Mistake: "People prefer online shopping to in-store shopping."

Here, you would benefit from specifying the demographic or sample size when presenting data to avoid overgeneralization. " In a survey of 1,000 urban residents aged 18-35, 70% expressed a preference for online shopping over in-store shopping. "

Ignoring conflicting data

Cherry-picking data that supports your hypothesis while ignoring conflicting data can lead to a biased problem statement.

Example of Mistake: "Research shows that all students benefit from online learning."

You’ve to ensure a balanced view by considering all relevant data, even if it contradicts your hypothesis. " While many studies highlight the advantages of online learning for students, some research points to challenges such as decreased motivation and lack of face-to-face interaction. "

Making unsubstantiated predictions

Projecting future trends without solid data can weaken the credibility of your problem statement.

Example of Mistake: "The demand for electric cars will increase by 500% in the next year."

Base your predictions on current trends and reliable data sources, avoiding hyperbolic or unsupported claims. " With the current growth rate and recent advancements in battery technology, there's potential for a significant rise in the demand for electric cars. "

Wrapping Up

A well-crafted problem statement ensures that your research is focused, relevant, and contributes meaningfully to the broader academic community.

However, the consequences of an incorrect or poorly constructed problem statement can be severe. It can lead to misdirected research efforts, wasted resources, compromised credibility, and even ethical concerns. Such pitfalls underscore the importance of dedicating time and effort to craft a precise and impactful problem statement.

So, as you start your research journey , remember that a well-defined problem statement is not just a starting point; it guides your entire research journey, ensuring clarity, relevance, and meaningful contributions to your field.

Frequently Asked Questions

A problem statement is a clear, concise and specific articulation of a gap in current knowledge that your research aims to bridge.

The Problem Statement should highlight existing gaps in current knowledge and also the significance of the research. It should also include the research question and purpose of the research.

Clear articulation of the problem and establishing relevance; Working thesis (methods to solve the problem); Purpose and scope of study — are the 3 parts of the problem statement.

While the statement of the problem articulates and delineates a particular research problem, Objectives designates the aims, purpose and strategies to address the particular problem.

Here’s an example — “The study aims to identify and analyze the specific factors that impact employee productivity, providing organizations with actionable insights to optimize remote work policies.”

You might also like

Consensus GPT vs. SciSpace GPT: Choose the Best GPT for Research

Literature Review and Theoretical Framework: Understanding the Differences

Types of Essays in Academic Writing - Quick Guide (2024)

ORIGINAL RESEARCH article

Mathematical problem-solving through cooperative learning—the importance of peer acceptance and friendships.

• 1 Department of Education, Uppsala University, Uppsala, Sweden
• 2 Department of Education, Culture and Communication, Malardalen University, Vasteras, Sweden
• 3 School of Natural Sciences, Technology and Environmental Studies, Sodertorn University, Huddinge, Sweden
• 4 Faculty of Education, Gothenburg University, Gothenburg, Sweden

Mathematical problem-solving constitutes an important area of mathematics instruction, and there is a need for research on instructional approaches supporting student learning in this area. This study aims to contribute to previous research by studying the effects of an instructional approach of cooperative learning on students’ mathematical problem-solving in heterogeneous classrooms in grade five, in which students with special needs are educated alongside with their peers. The intervention combined a cooperative learning approach with instruction in problem-solving strategies including mathematical models of multiplication/division, proportionality, and geometry. The teachers in the experimental group received training in cooperative learning and mathematical problem-solving, and implemented the intervention for 15 weeks. The teachers in the control group received training in mathematical problem-solving and provided instruction as they would usually. Students (269 in the intervention and 312 in the control group) participated in tests of mathematical problem-solving in the areas of multiplication/division, proportionality, and geometry before and after the intervention. The results revealed significant effects of the intervention on student performance in overall problem-solving and problem-solving in geometry. The students who received higher scores on social acceptance and friendships for the pre-test also received higher scores on the selected tests of mathematical problem-solving. Thus, the cooperative learning approach may lead to gains in mathematical problem-solving in heterogeneous classrooms, but social acceptance and friendships may also greatly impact students’ results.

Introduction

The research on instruction in mathematical problem-solving has progressed considerably during recent decades. Yet, there is still a need to advance our knowledge on how teachers can support their students in carrying out this complex activity ( Lester and Cai, 2016 ). Results from the Program for International Student Assessment (PISA) show that only 53% of students from the participating countries could solve problems requiring more than direct inference and using representations from different information sources ( OECD, 2019 ). In addition, OECD (2019) reported a large variation in achievement with regard to students’ diverse backgrounds. Thus, there is a need for instructional approaches to promote students’ problem-solving in mathematics, especially in heterogeneous classrooms in which students with diverse backgrounds and needs are educated together. Small group instructional approaches have been suggested as important to promote learning of low-achieving students and students with special needs ( Kunsch et al., 2007 ). One such approach is cooperative learning (CL), which involves structured collaboration in heterogeneous groups, guided by five principles to enhance group cohesion ( Johnson et al., 1993 ; Johnson et al., 2009 ; Gillies, 2016 ). While CL has been well-researched in whole classroom approaches ( Capar and Tarim, 2015 ), few studies of the approach exist with regard to students with special educational needs (SEN; McMaster and Fuchs, 2002 ). This study contributes to previous research by studying the effects of the CL approach on students’ mathematical problem-solving in heterogeneous classrooms, in which students with special needs are educated alongside with their peers.

Group collaboration through the CL approach is structured in accordance with five principles of collaboration: positive interdependence, individual accountability, explicit instruction in social skills, promotive interaction, and group processing ( Johnson et al., 1993 ). First, the group tasks need to be structured so that all group members feel dependent on each other in the completion of the task, thus promoting positive interdependence. Second, for individual accountability, the teacher needs to assure that each group member feels responsible for his or her share of work, by providing opportunities for individual reports or evaluations. Third, the students need explicit instruction in social skills that are necessary for collaboration. Fourth, the tasks and seat arrangements should be designed to promote interaction among group members. Fifth, time needs to be allocated to group processing, through which group members can evaluate their collaborative work to plan future actions. Using these principles for cooperation leads to gains in mathematics, according to Capar and Tarim (2015) , who conducted a meta-analysis on studies of cooperative learning and mathematics, and found an increase of .59 on students’ mathematics achievement scores in general. However, the number of reviewed studies was limited, and researchers suggested a need for more research. In the current study, we focused on the effect of CL approach in a specific area of mathematics: problem-solving.

Mathematical problem-solving is a central area of mathematics instruction, constituting an important part of preparing students to function in modern society ( Gravemeijer et al., 2017 ). In fact, problem-solving instruction creates opportunities for students to apply their knowledge of mathematical concepts, integrate and connect isolated pieces of mathematical knowledge, and attain a deeper conceptual understanding of mathematics as a subject ( Lester and Cai, 2016 ). Some researchers suggest that mathematics itself is a science of problem-solving and of developing theories and methods for problem-solving ( Hamilton, 2007 ; Davydov, 2008 ).

Problem-solving processes have been studied from different perspectives ( Lesh and Zawojewski, 2007 ). Problem-solving heuristics Pólya, (1948) has largely influenced our perceptions of problem-solving, including four principles: understanding the problem, devising a plan, carrying out the plan, and looking back and reflecting upon the suggested solution. Schoenfield, (2016) suggested the use of specific problem-solving strategies for different types of problems, which take into consideration metacognitive processes and students’ beliefs about problem-solving. Further, models and modelling perspectives on mathematics ( Lesh and Doerr, 2003 ; Lesh and Zawojewski, 2007 ) emphasize the importance of engaging students in model-eliciting activities in which problem situations are interpreted mathematically, as students make connections between problem information and knowledge of mathematical operations, patterns, and rules ( Mousoulides et al., 2010 ; Stohlmann and Albarracín, 2016 ).

Not all students, however, find it easy to solve complex mathematical problems. Students may experience difficulties in identifying solution-relevant elements in a problem or visualizing appropriate solution to a problem situation. Furthermore, students may need help recognizing the underlying model in problems. For example, in two studies by Degrande et al. (2016) , students in grades four to six were presented with mathematical problems in the context of proportional reasoning. The authors found that the students, when presented with a word problem, could not identify an underlying model, but rather focused on superficial characteristics of the problem. Although the students in the study showed more success when presented with a problem formulated in symbols, the authors pointed out a need for activities that help students distinguish between different proportional problem types. Furthermore, students exhibiting specific learning difficulties may need additional support in both general problem-solving strategies ( Lein et al., 2020 ; Montague et al., 2014 ) and specific strategies pertaining to underlying models in problems. The CL intervention in the present study focused on supporting students in problem-solving, through instruction in problem-solving principles ( Pólya, 1948 ), specifically applied to three models of mathematical problem-solving—multiplication/division, geometry, and proportionality.

Students’ problem-solving may be enhanced through participation in small group discussions. In a small group setting, all the students have the opportunity to explain their solutions, clarify their thinking, and enhance understanding of a problem at hand ( Yackel et al., 1991 ; Webb and Mastergeorge, 2003 ). In fact, small group instruction promotes students’ learning in mathematics by providing students with opportunities to use language for reasoning and conceptual understanding ( Mercer and Sams, 2006 ), to exchange different representations of the problem at hand ( Fujita et al., 2019 ), and to become aware of and understand groupmates’ perspectives in thinking ( Kazak et al., 2015 ). These opportunities for learning are created through dialogic spaces characterized by openness to each other’s perspectives and solutions to mathematical problems ( Wegerif, 2011 ).

However, group collaboration is not only associated with positive experiences. In fact, studies show that some students may not be given equal opportunities to voice their opinions, due to academic status differences ( Langer-Osuna, 2016 ). Indeed, problem-solvers struggling with complex tasks may experience negative emotions, leading to uncertainty of not knowing the definite answer, which places demands on peer support ( Jordan and McDaniel, 2014 ; Hannula, 2015 ). Thus, especially in heterogeneous groups, students may need additional support to promote group interaction. Therefore, in this study, we used a cooperative learning approach, which, in contrast to collaborative learning approaches, puts greater focus on supporting group cohesion through instruction in social skills and time for reflection on group work ( Davidson and Major, 2014 ).

Although cooperative learning approach is intended to promote cohesion and peer acceptance in heterogeneous groups ( Rzoska and Ward, 1991 ), previous studies indicate that challenges in group dynamics may lead to unequal participation ( Mulryan, 1992 ; Cohen, 1994 ). Peer-learning behaviours may impact students’ problem-solving ( Hwang and Hu, 2013 ) and working in groups with peers who are seen as friends may enhance students’ motivation to learn mathematics ( Deacon and Edwards, 2012 ). With the importance of peer support in mind, this study set out to investigate whether the results of the intervention using the CL approach are associated with students’ peer acceptance and friendships.

The Present Study

In previous research, the CL approach has shown to be a promising approach in teaching and learning mathematics ( Capar and Tarim, 2015 ), but fewer studies have been conducted in whole-class approaches in general and students with SEN in particular ( McMaster and Fuchs, 2002 ). This study aims to contribute to previous research by investigating the effect of CL intervention on students’ mathematical problem-solving in grade 5. With regard to the complexity of mathematical problem-solving ( Lesh and Zawojewski, 2007 ; Degrande et al., 2016 ; Stohlmann and Albarracín, 2016 ), the CL approach in this study was combined with problem-solving principles pertaining to three underlying models of problem-solving—multiplication/division, geometry, and proportionality. Furthermore, considering the importance of peer support in problem-solving in small groups ( Mulryan, 1992 ; Cohen, 1994 ; Hwang and Hu, 2013 ), the study investigated how peer acceptance and friendships were associated with the effect of the CL approach on students’ problem-solving abilities. The study aimed to find answers to the following research questions:

a) What is the effect of CL approach on students’ problem-solving in mathematics?

b) Are social acceptance and friendship associated with the effect of CL on students’ problem-solving in mathematics?

Participants

The participants were 958 students in grade 5 and their teachers. According to power analyses prior to the start of the study, 1,020 students and 51 classes were required, with an expected effect size of 0.30 and power of 80%, provided that there are 20 students per class and intraclass correlation is 0.10. An invitation to participate in the project was sent to teachers in five municipalities via e-mail. Furthermore, the information was posted on the website of Uppsala university and distributed via Facebook interest groups. As shown in Figure 1 , teachers of 1,165 students agreed to participate in the study, but informed consent was obtained only for 958 students (463 in the intervention and 495 in the control group). Further attrition occurred at pre- and post-measurement, resulting in 581 students’ tests as a basis for analyses (269 in the intervention and 312 in the control group). Fewer students (n = 493) were finally included in the analyses of the association of students’ social acceptance and friendships and the effect of CL on students’ mathematical problem-solving (219 in the intervention and 274 in the control group). The reasons for attrition included teacher drop out due to sick leave or personal circumstances (two teachers in the control group and five teachers in the intervention group). Furthermore, some students were sick on the day of data collection and some teachers did not send the test results to the researchers.

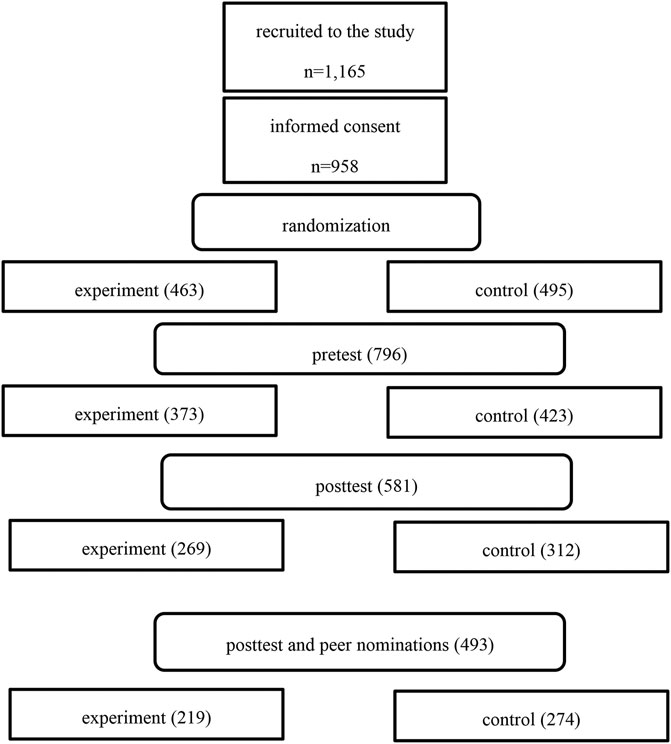
FIGURE 1 . Flow chart for participants included in data collection and data analysis.

As seen in Table 1 , classes in both intervention and control groups included 27 students on average. For 75% of the classes, there were 33–36% of students with SEN. In Sweden, no formal medical diagnosis is required for the identification of students with SEN. It is teachers and school welfare teams who decide students’ need for extra adaptations or special support ( Swedish National Educational Agency, 2014 ). The information on individual students’ type of SEN could not be obtained due to regulations on the protection of information about individuals ( SFS 2009 ). Therefore, the information on the number of students with SEN on class level was obtained through teacher reports.

TABLE 1 . Background characteristics of classes and teachers in intervention and control groups.

Intervention

The intervention using the CL approach lasted for 15 weeks and the teachers worked with the CL approach three to four lessons per week. First, the teachers participated in two-days training on the CL approach, using an especially elaborated CL manual ( Klang et al., 2018 ). The training focused on the five principles of the CL approach (positive interdependence, individual accountability, explicit instruction in social skills, promotive interaction, and group processing). Following the training, the teachers introduced the CL approach in their classes and focused on group-building activities for 7 weeks. Then, 2 days of training were provided to teachers, in which the CL approach was embedded in activities in mathematical problem-solving and reading comprehension. Educational materials containing mathematical problems in the areas of multiplication and division, geometry, and proportionality were distributed to the teachers ( Karlsson and Kilborn, 2018a ). In addition to the specific problems, adapted for the CL approach, the educational materials contained guidance for the teachers, in which problem-solving principles ( Pólya, 1948 ) were presented as steps in problem-solving. Following the training, the teachers applied the CL approach in mathematical problem-solving lessons for 8 weeks.

Solving a problem is a matter of goal-oriented reasoning, starting from the understanding of the problem to devising its solution by using known mathematical models. This presupposes that the current problem is chosen from a known context ( Stillman et al., 2008 ; Zawojewski, 2010 ). This differs from the problem-solving of the textbooks, which is based on an aim to train already known formulas and procedures ( Hamilton, 2007 ). Moreover, it is important that students learn modelling according to their current abilities and conditions ( Russel, 1991 ).

In order to create similar conditions in the experiment group and the control group, the teachers were supposed to use the same educational material ( Karlsson and Kilborn, 2018a ; Karlsson and Kilborn, 2018b ), written in light of the specified view of problem-solving. The educational material is divided into three areas—multiplication/division, geometry, and proportionality—and begins with a short teachers’ guide, where a view of problem solving is presented, which is based on the work of Polya (1948) and Lester and Cai (2016) . The tasks are constructed in such a way that conceptual knowledge was in focus, not formulas and procedural knowledge.

Implementation of the Intervention

To ensure the implementation of the intervention, the researchers visited each teachers’ classroom twice during the two phases of the intervention period, as described above. During each visit, the researchers observed the lesson, using a checklist comprising the five principles of the CL approach. After the lesson, the researchers gave written and oral feedback to each teacher. As seen in Table 1 , in 18 of the 23 classes, the teachers implemented the intervention in accordance with the principles of CL. In addition, the teachers were asked to report on the use of the CL approach in their teaching and the use of problem-solving activities embedding CL during the intervention period. As shown in Table 1 , teachers in only 11 of 23 classes reported using the CL approach and problem-solving activities embedded in the CL approach at least once a week.

Control Group

The teachers in the control group received 2 days of instruction in enhancing students’ problem-solving and reading comprehension. The teachers were also supported with educational materials including mathematical problems Karlsson and Kilborn (2018b) and problem-solving principles ( Pólya, 1948 ). However, none of the activities during training or in educational materials included the CL approach. As seen in Table 1 , only 10 of 25 teachers reported devoting at least one lesson per week to mathematical problem-solving.

Tests of Mathematical Problem-Solving

Tests of mathematical problem-solving were administered before and after the intervention, which lasted for 15 weeks. The tests were focused on the models of multiplication/division, geometry, and proportionality. The three models were chosen based on the syllabus of the subject of mathematics in grades 4 to 6 in the Swedish National Curriculum ( Swedish National Educational Agency, 2018 ). In addition, the intention was to create a variation of types of problems to solve. For each of these three models, there were two tests, a pre-test and a post-test. Each test contained three tasks with increasing difficulty ( Supplementary Appendix SA ).

The tests of multiplication and division (Ma1) were chosen from different contexts and began with a one-step problem, while the following two tasks were multi-step problems. Concerning multiplication, many students in grade 5 still understand multiplication as repeated addition, causing significant problems, as this conception is not applicable to multiplication beyond natural numbers ( Verschaffel et al., 2007 ). This might be a hindrance in developing multiplicative reasoning ( Barmby et al., 2009 ). The multi-step problems in this study were constructed to support the students in multiplicative reasoning.

Concerning the geometry tests (Ma2), it was important to consider a paradigm shift concerning geometry in education that occurred in the mid-20th century, when strict Euclidean geometry gave way to other aspects of geometry like symmetry, transformation, and patterns. van Hiele (1986) prepared a new taxonomy for geometry in five steps, from a visual to a logical level. Therefore, in the tests there was a focus on properties of quadrangles and triangles, and how to determine areas by reorganising figures into new patterns. This means that structure was more important than formulas.

The construction of tests of proportionality (M3) was more complicated. Firstly, tasks on proportionality can be found in many different contexts, such as prescriptions, scales, speeds, discounts, interest, etc. Secondly, the mathematical model is complex and requires good knowledge of rational numbers and ratios ( Lesh et al., 1988 ). It also requires a developed view of multiplication, useful in operations with real numbers, not only as repeated addition, an operation limited to natural numbers ( Lybeck, 1981 ; Degrande et al., 2016 ). A linear structure of multiplication as repeated addition leads to limitations in terms of generalization and development of the concept of multiplication. This became evident in a study carried out in a Swedish context ( Karlsson and Kilborn, 2018c ). Proportionality can be expressed as a/b = c/d or as a/b = k. The latter can also be expressed as a = b∙k, where k is a constant that determines the relationship between a and b. Common examples of k are speed (km/h), scale, and interest (%). An important pre-knowledge in order to deal with proportions is to master fractions as equivalence classes like 1/3 = 2/6 = 3/9 = 4/12 = 5/15 = 6/18 = 7/21 = 8/24 … ( Karlsson and Kilborn, 2020 ). It was important to take all these aspects into account when constructing and assessing the solutions of the tasks.

The tests were graded by an experienced teacher of mathematics (4 th author) and two students in their final year of teacher training. Prior to grading, acceptable levels of inter-rater reliability were achieved by independent rating of students’ solutions and discussions in which differences between the graders were resolved. Each student response was to be assigned one point when it contained a correct answer and two points when the student provided argumentation for the correct answer and elaborated on explanation of his or her solution. The assessment was thus based on quality aspects with a focus on conceptual knowledge. As each subtest contained three questions, it generated three student solutions. So, scores for each subtest ranged from 0 to 6 points and for the total scores from 0 to 18 points. To ascertain that pre- and post-tests were equivalent in degree of difficulty, the tests were administered to an additional sample of 169 students in grade 5. Test for each model was conducted separately, as students participated in pre- and post-test for each model during the same lesson. The order of tests was switched for half of the students in order to avoid the effect of the order in which the pre- and post-tests were presented. Correlation between students’ performance on pre- and post-test was .39 ( p < 0.000) for tests of multiplication/division; .48 ( p < 0.000) for tests of geometry; and .56 ( p < 0.000) for tests of proportionality. Thus, the degree of difficulty may have differed between pre- and post-test.

Measures of Peer Acceptance and Friendships

To investigate students’ peer acceptance and friendships, peer nominations rated pre- and post-intervention were used. Students were asked to nominate peers who they preferred to work in groups with and who they preferred to be friends with. Negative peer nominations were avoided due to ethical considerations raised by teachers and parents ( Child and Nind, 2013 ). Unlimited nominations were used, as these are considered to have high ecological validity ( Cillessen and Marks, 2017 ). Peer nominations were used as a measure of social acceptance, and reciprocated nominations were used as a measure of friendship. The number of nominations for each student were aggregated and divided by the number of nominators to create a proportion of nominations for each student ( Velásquez et al., 2013 ).

Statistical Analyses

Multilevel regression analyses were conducted in R, lme4 package Bates et al. (2015) to account for nestedness in the data. Students’ classroom belonging was considered as a level 2 variable. First, we used a model in which students’ results on tests of problem-solving were studied as a function of time (pre- and post) and group belonging (intervention and control group). Second, the same model was applied to subgroups of students who performed above and below median at pre-test, to explore whether the CL intervention had a differential effect on student performance. In this second model, the results for subgroups of students could not be obtained for geometry tests for subgroup below median and for tests of proportionality for subgroup above median. A possible reason for this must have been the skewed distribution of the students in these subgroups. Therefore, another model was applied that investigated students’ performances in math at both pre- and post-test as a function of group belonging. Third, the students’ scores on social acceptance and friendships were added as an interaction term to the first model. In our previous study, students’ social acceptance changed as a result of the same CL intervention ( Klang et al., 2020 ).

The assumptions for the multilevel regression were assured during the analyses ( Snijders and Bosker, 2012 ). The assumption of normality of residuals were met, as controlled by visual inspection of quantile-quantile plots. For subgroups, however, the plotted residuals deviated somewhat from the straight line. The number of outliers, which had a studentized residual value greater than ±3, varied from 0 to 5, but none of the outliers had a Cook’s distance value larger than 1. The assumption of multicollinearity was met, as the variance inflation factors (VIF) did not exceed a value of 10. Before the analyses, the cases with missing data were deleted listwise.

What Is the Effect of the CL Approach on Students’ Problem-Solving in Mathematics?

As seen in the regression coefficients in Table 2 , the CL intervention had a significant effect on students’ mathematical problem-solving total scores and students’ scores in problem solving in geometry (Ma2). Judging by mean values, students in the intervention group appeared to have low scores on problem-solving in geometry but reached the levels of problem-solving of the control group by the end of the intervention. The intervention did not have a significant effect on students’ performance in problem-solving related to models of multiplication/division and proportionality.

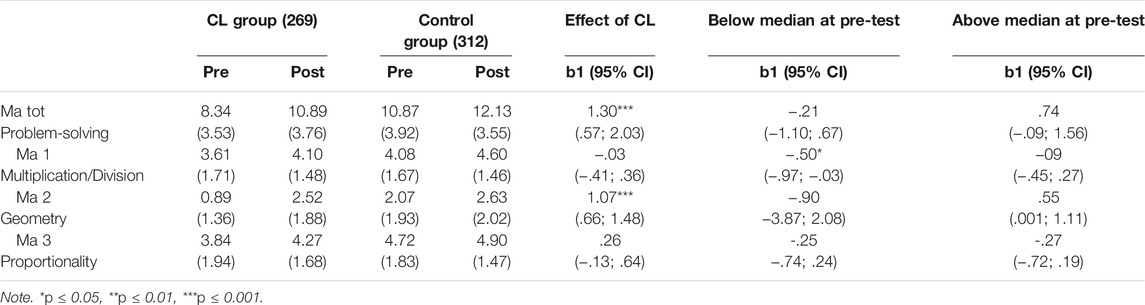
TABLE 2 . Mean scores (standard deviation in parentheses) and unstandardized multilevel regression estimates for tests of mathematical problem-solving.

The question is, however, whether CL intervention affected students with different pre-test scores differently. Table 2 includes the regression coefficients for subgroups of students who performed below and above median at pre-test. As seen in the table, the CL approach did not have a significant effect on students’ problem-solving, when the sample was divided into these subgroups. A small negative effect was found for intervention group in comparison to control group, but confidence intervals (CI) for the effect indicate that it was not significant.

Is Social Acceptance and Friendships Associated With the Effect of CL on Students’ Problem-Solving in Mathematics?

As seen in Table 3 , students’ peer acceptance and friendship at pre-test were significantly associated with the effect of the CL approach on students’ mathematical problem-solving scores. Changes in students’ peer acceptance and friendships were not significantly associated with the effect of the CL approach on students’ mathematical problem-solving. Consequently, it can be concluded that being nominated by one’s peers and having friends at the start of the intervention may be an important factor when participation in group work, structured in accordance with the CL approach, leads to gains in mathematical problem-solving.

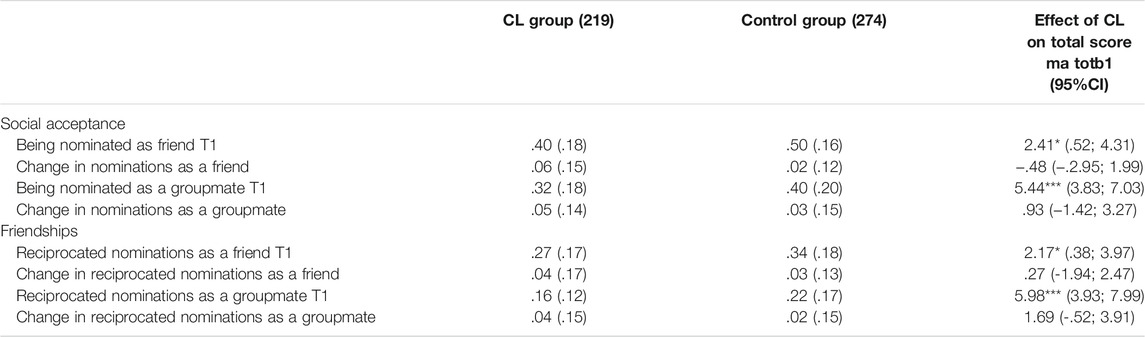
TABLE 3 . Mean scores (standard deviation in parentheses) and unstandardized multilevel regression estimates for tests of mathematical problem-solving, including scores of social acceptance and friendship in the model.

In light of the limited number of studies on the effects of CL on students’ problem-solving in whole classrooms ( Capar and Tarim, 2015 ), and for students with SEN in particular ( McMaster and Fuchs, 2002 ), this study sought to investigate whether the CL approach embedded in problem-solving activities has an effect on students’ problem-solving in heterogeneous classrooms. The need for the study was justified by the challenge of providing equitable mathematics instruction to heterogeneous student populations ( OECD, 2019 ). Small group instructional approaches as CL are considered as promising approaches in this regard ( Kunsch et al., 2007 ). The results showed a significant effect of the CL approach on students’ problem-solving in geometry and total problem-solving scores. In addition, with regard to the importance of peer support in problem-solving ( Deacon and Edwards, 2012 ; Hwang and Hu, 2013 ), the study explored whether the effect of CL on students’ problem-solving was associated with students’ social acceptance and friendships. The results showed that students’ peer acceptance and friendships at pre-test were significantly associated with the effect of the CL approach, while change in students’ peer acceptance and friendships from pre- to post-test was not.

The results of the study confirm previous research on the effect of the CL approach on students’ mathematical achievement ( Capar and Tarim, 2015 ). The specific contribution of the study is that it was conducted in classrooms, 75% of which were composed of 33–36% of students with SEN. Thus, while a previous review revealed inconclusive findings on the effects of CL on student achievement ( McMaster and Fuchs, 2002 ), the current study adds to the evidence of the effect of the CL approach in heterogeneous classrooms, in which students with special needs are educated alongside with their peers. In a small group setting, the students have opportunities to discuss their ideas of solutions to the problem at hand, providing explanations and clarifications, thus enhancing their understanding of problem-solving ( Yackel et al., 1991 ; Webb and Mastergeorge, 2003 ).

In this study, in accordance with previous research on mathematical problem-solving ( Lesh and Zawojewski, 2007 ; Degrande et al., 2016 ; Stohlmann and Albarracín, 2016 ), the CL approach was combined with training in problem-solving principles Pólya (1948) and educational materials, providing support in instruction in underlying mathematical models. The intention of the study was to provide evidence for the effectiveness of the CL approach above instruction in problem-solving, as problem-solving materials were accessible to teachers of both the intervention and control groups. However, due to implementation challenges, not all teachers in the intervention and control groups reported using educational materials and training as expected. Thus, it is not possible to draw conclusions of the effectiveness of the CL approach alone. However, in everyday classroom instruction it may be difficult to separate the content of instruction from the activities that are used to mediate this content ( Doerr and Tripp, 1999 ; Gravemeijer, 1999 ).

Furthermore, for successful instruction in mathematical problem-solving, scaffolding for content needs to be combined with scaffolding for dialogue ( Kazak et al., 2015 ). From a dialogical perspective ( Wegerif, 2011 ), students may need scaffolding in new ways of thinking, involving questioning their understandings and providing arguments for their solutions, in order to create dialogic spaces in which different solutions are voiced and negotiated. In this study, small group instruction through CL approach aimed to support discussions in small groups, but the study relies solely on quantitative measures of students’ mathematical performance. Video-recordings of students’ discussions may have yielded important insights into the dialogic relationships that arose in group discussions.

Despite the positive findings of the CL approach on students’ problem-solving, it is important to note that the intervention did not have an effect on students’ problem-solving pertaining to models of multiplication/division and proportionality. Although CL is assumed to be a promising instructional approach, the number of studies on its effect on students’ mathematical achievement is still limited ( Capar and Tarim, 2015 ). Thus, further research is needed on how CL intervention can be designed to promote students’ problem-solving in other areas of mathematics.

The results of this study show that the effect of the CL intervention on students’ problem-solving was associated with students’ initial scores of social acceptance and friendships. Thus, it is possible to assume that students who were popular among their classmates and had friends at the start of the intervention also made greater gains in mathematical problem-solving as a result of the CL intervention. This finding is in line with Deacon and Edwards’ study of the importance of friendships for students’ motivation to learn mathematics in small groups ( Deacon and Edwards, 2012 ). However, the effect of the CL intervention was not associated with change in students’ social acceptance and friendship scores. These results indicate that students who were nominated by a greater number of students and who received a greater number of friends did not benefit to a great extent from the CL intervention. With regard to previously reported inequalities in cooperation in heterogeneous groups ( Cohen, 1994 ; Mulryan, 1992 ; Langer Osuna, 2016 ) and the importance of peer behaviours for problem-solving ( Hwang and Hu, 2013 ), teachers should consider creating inclusive norms and supportive peer relationships when using the CL approach. The demands of solving complex problems may create negative emotions and uncertainty ( Hannula, 2015 ; Jordan and McDaniel, 2014 ), and peer support may be essential in such situations.

Limitations

The conclusions from the study must be interpreted with caution, due to a number of limitations. First, due to the regulation of protection of individuals ( SFS 2009 ), the researchers could not get information on type of SEN for individual students, which limited the possibilities of the study for investigating the effects of the CL approach for these students. Second, not all teachers in the intervention group implemented the CL approach embedded in problem-solving activities and not all teachers in the control group reported using educational materials on problem-solving. The insufficient levels of implementation pose a significant challenge to the internal validity of the study. Third, the additional investigation to explore the equivalence in difficulty between pre- and post-test, including 169 students, revealed weak to moderate correlation in students’ performance scores, which may indicate challenges to the internal validity of the study.

Implications

The results of the study have some implications for practice. Based on the results of the significant effect of the CL intervention on students’ problem-solving, the CL approach appears to be a promising instructional approach in promoting students’ problem-solving. However, as the results of the CL approach were not significant for all subtests of problem-solving, and due to insufficient levels of implementation, it is not possible to conclude on the importance of the CL intervention for students’ problem-solving. Furthermore, it appears to be important to create opportunities for peer contacts and friendships when the CL approach is used in mathematical problem-solving activities.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Ethics Statement

The studies involving human participants were reviewed and approved by the Uppsala Ethical Regional Committee, Dnr. 2017/372. Written informed consent to participate in this study was provided by the participants’ legal guardian/next of kin.

Author Contributions

NiK was responsible for the project, and participated in data collection and data analyses. NaK and WK were responsible for intervention with special focus on the educational materials and tests in mathematical problem-solving. PE participated in the planning of the study and the data analyses, including coordinating analyses of students’ tests. MK participated in the designing and planning the study as well as data collection and data analyses.

The project was funded by the Swedish Research Council under Grant 2016-04,679.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We would like to express our gratitude to teachers who participated in the project.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2021.710296/full#supplementary-material

Barmby, P., Harries, T., Higgins, S., and Suggate, J. (2009). The array representation and primary children's understanding and reasoning in multiplication. Educ. Stud. Math. 70 (3), 217–241. doi:10.1007/s10649-008-914510.1007/s10649-008-9145-1

CrossRef Full Text | Google Scholar

Bates, D., Mächler, M., Bolker, B., and Walker, S. (2015). Fitting Linear Mixed-Effects Models Usinglme4. J. Stat. Soft. 67 (1), 1–48. doi:10.18637/jss.v067.i01

Capar, G., and Tarim, K. (2015). Efficacy of the cooperative learning method on mathematics achievement and attitude: A meta-analysis research. Educ. Sci-theor Pract. 15 (2), 553–559. doi:10.12738/estp.2015.2.2098

Child, S., and Nind, M. (2013). Sociometric methods and difference: A force for good - or yet more harm. Disabil. Soc. 28 (7), 1012–1023. doi:10.1080/09687599.2012.741517

Cillessen, A. H. N., and Marks, P. E. L. (2017). Methodological choices in peer nomination research. New Dir. Child Adolesc. Dev. 2017, 21–44. doi:10.1002/cad.20206

PubMed Abstract | CrossRef Full Text | Google Scholar

Clarke, B., Cheeseman, J., and Clarke, D. (2006). The mathematical knowledge and understanding young children bring to school. Math. Ed. Res. J. 18 (1), 78–102. doi:10.1007/bf03217430

Cohen, E. G. (1994). Restructuring the classroom: Conditions for productive small groups. Rev. Educ. Res. 64 (1), 1–35. doi:10.3102/00346543064001001

Davidson, N., and Major, C. H. (2014). Boundary crossings: Cooperative learning, collaborative learning, and problem-based learning. J. Excell. Coll. Teach. 25 (3-4), 7.

Google Scholar

Davydov, V. V. (2008). Problems of developmental instructions. A Theoretical and experimental psychological study . New York: Nova Science Publishers, Inc .

Deacon, D., and Edwards, J. (2012). Influences of friendship groupings on motivation for mathematics learning in secondary classrooms. Proc. Br. Soc. Res. into Learn. Math. 32 (2), 22–27.

Degrande, T., Verschaffel, L., and van Dooren, W. (2016). “Proportional word problem solving through a modeling lens: a half-empty or half-full glass?,” in Posing and Solving Mathematical Problems, Research in Mathematics Education . Editor P. Felmer.

Doerr, H. M., and Tripp, J. S. (1999). Understanding how students develop mathematical models. Math. Thinking Learn. 1 (3), 231–254. doi:10.1207/s15327833mtl0103_3

Fujita, T., Doney, J., and Wegerif, R. (2019). Students' collaborative decision-making processes in defining and classifying quadrilaterals: a semiotic/dialogic approach. Educ. Stud. Math. 101 (3), 341–356. doi:10.1007/s10649-019-09892-9

Gillies, R. (2016). Cooperative learning: Review of research and practice. Ajte 41 (3), 39–54. doi:10.14221/ajte.2016v41n3.3

Gravemeijer, K. (1999). How Emergent Models May Foster the Constitution of Formal Mathematics. Math. Thinking Learn. 1 (2), 155–177. doi:10.1207/s15327833mtl0102_4

Gravemeijer, K., Stephan, M., Julie, C., Lin, F.-L., and Ohtani, M. (2017). What mathematics education may prepare students for the society of the future? Int. J. Sci. Math. Educ. 15 (S1), 105–123. doi:10.1007/s10763-017-9814-6

Hamilton, E. (2007). “What changes are needed in the kind of problem-solving situations where mathematical thinking is needed beyond school?,” in Foundations for the Future in Mathematics Education . Editors R. Lesh, E. Hamilton, and Kaput (Mahwah, NJ: Lawrence Erlbaum ), 1–6.

Hannula, M. S. (2015). “Emotions in problem solving,” in Selected Regular Lectures from the 12 th International Congress on Mathematical Education . Editor S. J. Cho. doi:10.1007/978-3-319-17187-6_16

Hwang, W.-Y., and Hu, S.-S. (2013). Analysis of peer learning behaviors using multiple representations in virtual reality and their impacts on geometry problem solving. Comput. Edu. 62, 308–319. doi:10.1016/j.compedu.2012.10.005

Johnson, D. W., Johnson, R. T., and Johnson Holubec, E. (2009). Circle of Learning: Cooperation in the Classroom . Gurgaon: Interaction Book Company .

Johnson, D. W., Johnson, R. T., and Johnson Holubec, E. (1993). Cooperation in the Classroom . Gurgaon: Interaction Book Company .

Jordan, M. E., and McDaniel, R. R. (2014). Managing uncertainty during collaborative problem solving in elementary school teams: The role of peer influence in robotics engineering activity. J. Learn. Sci. 23 (4), 490–536. doi:10.1080/10508406.2014.896254

Karlsson, N., and Kilborn, W. (2018a). Inclusion through learning in group: tasks for problem-solving. [Inkludering genom lärande i grupp: uppgifter för problemlösning] . Uppsala: Uppsala University .

Karlsson, N., and Kilborn, W. (2018c). It's enough if they understand it. A study of teachers 'and students' perceptions of multiplication and the multiplication table [Det räcker om de förstår den. En studie av lärares och elevers uppfattningar om multiplikation och multiplikationstabellen]. Södertörn Stud. Higher Educ. , 175.

Karlsson, N., and Kilborn, W. (2018b). Tasks for problem-solving in mathematics. [Uppgifter för problemlösning i matematik] . Uppsala: Uppsala University .

Karlsson, N., and Kilborn, W. (2020). “Teacher’s and student’s perception of rational numbers,” in Interim Proceedings of the 44 th Conference of the International Group for the Psychology of Mathematics Education , Interim Vol., Research Reports . Editors M. Inprasitha, N. Changsri, and N. Boonsena (Khon Kaen, Thailand: PME ), 291–297.

Kazak, S., Wegerif, R., and Fujita, T. (2015). Combining scaffolding for content and scaffolding for dialogue to support conceptual breakthroughs in understanding probability. ZDM Math. Edu. 47 (7), 1269–1283. doi:10.1007/s11858-015-0720-5

Klang, N., Olsson, I., Wilder, J., Lindqvist, G., Fohlin, N., and Nilholm, C. (2020). A cooperative learning intervention to promote social inclusion in heterogeneous classrooms. Front. Psychol. 11, 586489. doi:10.3389/fpsyg.2020.586489

Klang, N., Fohlin, N., and Stoddard, M. (2018). Inclusion through learning in group: cooperative learning [Inkludering genom lärande i grupp: kooperativt lärande] . Uppsala: Uppsala University .

Kunsch, C. A., Jitendra, A. K., and Sood, S. (2007). The effects of peer-mediated instruction in mathematics for students with learning problems: A research synthesis. Learn. Disabil Res Pract 22 (1), 1–12. doi:10.1111/j.1540-5826.2007.00226.x

Langer-Osuna, J. M. (2016). The social construction of authority among peers and its implications for collaborative mathematics problem solving. Math. Thinking Learn. 18 (2), 107–124. doi:10.1080/10986065.2016.1148529

Lein, A. E., Jitendra, A. K., and Harwell, M. R. (2020). Effectiveness of mathematical word problem solving interventions for students with learning disabilities and/or mathematics difficulties: A meta-analysis. J. Educ. Psychol. 112 (7), 1388–1408. doi:10.1037/edu0000453

Lesh, R., and Doerr, H. (2003). Beyond Constructivism: Models and Modeling Perspectives on Mathematics Problem Solving, Learning and Teaching . Mahwah, NJ: Erlbaum .

Lesh, R., Post, T., and Behr, M. (1988). “Proportional reasoning,” in Number Concepts and Operations in the Middle Grades . Editors J. Hiebert, and M. Behr (Hillsdale, N.J.: Lawrence Erlbaum Associates ), 93–118.

Lesh, R., and Zawojewski, (2007). “Problem solving and modeling,” in Second Handbook of Research on Mathematics Teaching and Learning: A Project of the National Council of Teachers of Mathematics . Editor L. F. K. Lester (Charlotte, NC: Information Age Pub ), vol. 2.

Lester, F. K., and Cai, J. (2016). “Can mathematical problem solving be taught? Preliminary answers from 30 years of research,” in Posing and Solving Mathematical Problems. Research in Mathematics Education .

Lybeck, L. (1981). “Archimedes in the classroom. [Arkimedes i klassen],” in Göteborg Studies in Educational Sciences (Göteborg: Acta Universitatis Gotoburgensis ), 37.

McMaster, K. N., and Fuchs, D. (2002). Effects of Cooperative Learning on the Academic Achievement of Students with Learning Disabilities: An Update of Tateyama-Sniezek's Review. Learn. Disabil Res Pract 17 (2), 107–117. doi:10.1111/1540-5826.00037

Mercer, N., and Sams, C. (2006). Teaching children how to use language to solve maths problems. Lang. Edu. 20 (6), 507–528. doi:10.2167/le678.0

Montague, M., Krawec, J., Enders, C., and Dietz, S. (2014). The effects of cognitive strategy instruction on math problem solving of middle-school students of varying ability. J. Educ. Psychol. 106 (2), 469–481. doi:10.1037/a0035176

Mousoulides, N., Pittalis, M., Christou, C., and Stiraman, B. (2010). “Tracing students’ modeling processes in school,” in Modeling Students’ Mathematical Modeling Competencies . Editor R. Lesh (Berlin, Germany: Springer Science+Business Media ). doi:10.1007/978-1-4419-0561-1_10

Mulryan, C. M. (1992). Student passivity during cooperative small groups in mathematics. J. Educ. Res. 85 (5), 261–273. doi:10.1080/00220671.1992.9941126

OECD (2019). PISA 2018 Results (Volume I): What Students Know and Can Do . Paris: OECD Publishing . doi:10.1787/5f07c754-en

CrossRef Full Text

Pólya, G. (1948). How to Solve it: A New Aspect of Mathematical Method . Princeton, N.J.: Princeton University Press .

Russel, S. J. (1991). “Counting noses and scary things: Children construct their ideas about data,” in Proceedings of the Third International Conference on the Teaching of Statistics . Editor I. D. Vere-Jones (Dunedin, NZ: University of Otago ), 141–164., s.

Rzoska, K. M., and Ward, C. (1991). The effects of cooperative and competitive learning methods on the mathematics achievement, attitudes toward school, self-concepts and friendship choices of Maori, Pakeha and Samoan Children. New Zealand J. Psychol. 20 (1), 17–24.

Schoenfeld, A. H. (2016). Learning to think mathematically: Problem solving, metacognition, and sense making in mathematics (reprint). J. Edu. 196 (2), 1–38. doi:10.1177/002205741619600202

SFS 2009:400. Offentlighets- och sekretesslag. [Law on Publicity and confidentiality] . Retrieved from https://www.riksdagen.se/sv/dokument-lagar/dokument/svensk-forfattningssamling/offentlighets--och-sekretesslag-2009400_sfs-2009-400 on the 14th of October .

Snijders, T. A. B., and Bosker, R. J. (2012). Multilevel Analysis. An Introduction to Basic and Advanced Multilevel Modeling . 2nd Ed. London: SAGE .

Stillman, G., Brown, J., and Galbraith, P. (2008). Research into the teaching and learning of applications and modelling in Australasia. In H. Forgasz, A. Barkatas, A. Bishop, B. Clarke, S. Keast, W. Seah, and P. Sullivan (red.), Research in Mathematics Education in Australasiae , 2004-2007 , p.141–164. Rotterdam: Sense Publishers .doi:10.1163/9789087905019_009

Stohlmann, M. S., and Albarracín, L. (2016). What is known about elementary grades mathematical modelling. Edu. Res. Int. 2016, 1–9. doi:10.1155/2016/5240683

Swedish National Educational Agency (2014). Support measures in education – on leadership and incentives, extra adaptations and special support [Stödinsatser I utbildningen – om ledning och stimulans, extra anpassningar och särskilt stöd] . Stockholm: Swedish National Agency of Education .

Swedish National Educational Agency (2018). Syllabus for the subject of mathematics in compulsory school . Retrieved from https://www.skolverket.se/undervisning/grundskolan/laroplan-och-kursplaner-for-grundskolan/laroplan-lgr11-for-grundskolan-samt-for-forskoleklassen-och-fritidshemmet?url=-996270488%2Fcompulsorycw%2Fjsp%2Fsubject.htm%3FsubjectCode%3DGRGRMAT01%26tos%3Dgr&sv.url=12.5dfee44715d35a5cdfa219f ( on the 32nd of July, 2021).

van Hiele, P. (1986). Structure and Insight. A Theory of Mathematics Education . London: Academic Press .

Velásquez, A. M., Bukowski, W. M., and Saldarriaga, L. M. (2013). Adjusting for Group Size Effects in Peer Nomination Data. Soc. Dev. 22 (4), a–n. doi:10.1111/sode.12029

Verschaffel, L., Greer, B., and De Corte, E. (2007). “Whole number concepts and operations,” in Second Handbook of Research on Mathematics Teaching and Learning: A Project of the National Council of Teachers of Mathematics . Editor F. K. Lester (Charlotte, NC: Information Age Pub ), 557–628.

Webb, N. M., and Mastergeorge, A. (2003). Promoting effective helping behavior in peer-directed groups. Int. J. Educ. Res. 39 (1), 73–97. doi:10.1016/S0883-0355(03)00074-0

Wegerif, R. (2011). “Theories of Learning and Studies of Instructional Practice,” in Theories of learning and studies of instructional Practice. Explorations in the learning sciences, instructional systems and Performance technologies . Editor T. Koschmann (Berlin, Germany: Springer ). doi:10.1007/978-1-4419-7582-9

Yackel, E., Cobb, P., and Wood, T. (1991). Small-group interactions as a source of learning opportunities in second-grade mathematics. J. Res. Math. Edu. 22 (5), 390–408. doi:10.2307/749187

Zawojewski, J. (2010). Problem Solving versus Modeling. In R. Lesch, P. Galbraith, C. R. Haines, and A. Hurford (red.), Modelling student’s mathematical modelling competencies: ICTMA , p. 237–243. New York, NY: Springer .doi:10.1007/978-1-4419-0561-1_20

Keywords: cooperative learning, mathematical problem-solving, intervention, heterogeneous classrooms, hierarchical linear regression analysis

Citation: Klang N, Karlsson N, Kilborn W, Eriksson P and Karlberg M (2021) Mathematical Problem-Solving Through Cooperative Learning—The Importance of Peer Acceptance and Friendships. Front. Educ. 6:710296. doi: 10.3389/feduc.2021.710296

Received: 15 May 2021; Accepted: 09 August 2021; Published: 24 August 2021.

Reviewed by:

Copyright © 2021 Klang, Karlsson, Kilborn, Eriksson and Karlberg. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.

*Correspondence: Nina Klang, [email protected]

Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.

Academia.edu no longer supports Internet Explorer.

To browse Academia.edu and the wider internet faster and more securely, please take a few seconds to  upgrade your browser .

Enter the email address you signed up with and we'll email you a reset link.

• We're Hiring!
• Help Center

Download Free PDF

STUDENTS’ DIFFICULTIES IN COMPREHENDING MATHEMATICAL WORD PROBLEMS IN ENGLISH LANGUAGE LEARNING CONTEXTS

Related papers

This paper attempts to provide some insights on students' various approaches towards solving words problems in Mathematics. 15 students were randomly selected from SSIII students of Demonstration Secondary School, Azare Bauchi State. Three (3) visits were scheduled to the school for interview, questions administration on words problem and discussions, the findings revealed that the students lack necessary knowledge and skills to solve word problems. It is recommended that teachers should employ various heuristics when teaching words problem to enable the students develop necessary skills needed to solve words problems.

Mathematics Education Trends and Research, 2014

Diversity Dimensions in Mathematics and Language Learning, 2021

Issues in Educational Research, 2020

Understanding the challenges pertaining to the teaching and learning of mathematics word problems is important in order to formulate effective strategies that will address the challenges. The qualitative case study reported in this article describes the teachers’ and the learners’ experiences regarding mathematics word problems. Data were collected through focus group discussions and reflection sessions, through the use of the free attitude interview technique used to initiate the conversations. Thematic analysis was used to analyse data. Analysis of data revealed challenges related to lack of English proficiency, limited knowledge of mathematical vocabulary, the effects of “out of context” meanings and lack of understanding mathematical language and structure to be the sources of difficulty for teaching and learning mathematics word problems. Findings of the study suggest the need for challenges to be understood in context in order for meaningful possible solutions to be formulated...

Dirāsāt. Al-'ulūm al-insāniyyaẗ wa-al-iǧtimā'iyyaẗ/Dirāsāt. Al-ʻulūm al-insāniyyaẗ wa-al-iǧtimāʻiyyaẗ, 2024

Advances in Social Science, Education and Humanities Research, 2022

International Journal of Scientific and Research Publications (IJSRP)

The study was conducted on selected students of the University of Southern Mindanao from July to August 2013 and included 34 respondents. The main objective of the study was to identify the challenges encountered by students in solving Algebra word problems. Descriptive method was used. A prepared assessment tool was administered to the respondents who were conveniently chosen. Data were analyzed using mean frequency and percentage. Result of the study shows that the students encountered challenges were difficulty in translating the word problems in mathematical phrase. With this dilemma, students usually opted to give up than find ways to answer the problem. Students look for numerical values in the problem and apply any of the fundamental operations where they think would work. This can be call Guess and Check method but students usually misused it because they disregard the conditions given in the problem. Students cannot combine learned rules and principles into mixed or combination of using those rules and principles. Students lack the skills needed to solve word problems such as understanding the language of algebra; concepts of LCM, decimals, percentage; and simplifying algebraic expressions. Based on the results of this study the researcher conclude that failure to solve algebraic word problems is due to lack of prerequisite skills, haven’t understand the concepts of rules and principles in algebra , that’s why they cannot apply their learned rules and principles into complex conditions that needs combinations of those rules and principles. Students memorize the process of their teacher in solving the problems that’s why when they encounter parallel problems they cram and blame the teacher because for not teaching about it. They don’t understand the concept deeply so they say their teacher hasn’t taught it where in fact it’s a parallel problem. To sum up the findings, challenges encountered by the students were difficulty in translating the word problems to mathematical phrase because they have not learned the language of algebra and in simplifying algebraic equation.

Humanities & social sciences communications, 2022

Jurnal Gantang

This study aims to understand better student errors in solving mathematics word problems. A Word problem is a problem that has a story or arrangement based on sentences. The qualitative research approach was used. The data were collected by giving tests and interviewing two male high achievers senior high school students in mathematics. The student error analysis adopted the Newman error analysis system. The source triangulation was used to ensure the data validity. Based on the collecting data and data analysis, the decoding/reading error happened caused by students&#39; common understanding or unfamiliarity of the mathematical terms used in the problem. The subjects showed inconsistency in interpreting problem sentences and misused mathematical symbols. Furthermore, the subject encountered difficulties with the arithmetic process, especially fractions and their operation. This research identified students&#39; difficulties in solving problem mathematics word problems. Moreover, th...

Loading Preview

Sorry, preview is currently unavailable. You can download the paper by clicking the button above.

Faculty of Natural and Applied Sciences Journal of Mathematics and Science Education, 2022

Asian Journal of Social Sciences and Management Studies

EURASIA Journal of Mathematics, Science and Technology Education, 2016

Journal of Physics: Conference Series, 2020

Frontiers in psychology, 2016

Educatum Journal of Science Mathematic and Technology/EDUCATUM : Journal of Science Mathematics and Technology, 2021

Psychology and Education: A Multidisciplinary Journal, 2023

Education and New Developments 2019, 2019

Azim Premji University, 2016

LACLIL - Latin American Journal of Content and Language integrated Learning, 2019

International Electronic Journal of Mathematics Education, 2013

Bolema: Boletim de Educação Matemática, 2012

Educational Psychology, 2008

International Journal of Learning and Teaching

Al-Jabar, 2023

Health Psychology Report, 2014

•   We're Hiring!
•   Help Center
• Find new research papers in:
• Health Sciences
• Earth Sciences
• Cognitive Science
• Mathematics
• Computer Science
• Academia ©2024

Exploring the Effect of Mathematics Skills on Student Performance in Physics Problem-Solving: A Structural Equation Modeling Analysis

• Open access
• Published: 07 October 2024

Cite this article

You have full access to this open access article

• Tong Tong 1 ,
• Feipeng Pi 1 ,
• Siyan Zheng 1 ,
• Yi Zhong 1 ,
• Xiaochun Lin 1 &
• Yajun Wei   ORCID: orcid.org/0000-0003-4871-9682 1  

Students’ success in physics problem-solving extends beyond conceptual knowledge of physics, relying significantly on their mathematics skills. Understanding the specific contributions of different mathematics skills to physics problem-solving can offer valuable insights for enhancing physics education. Yet such studies are rare, particularly at the high school level. This study addresses the underexplored area of this topic in secondary education by investigating the associations between physics problem-solving performance using a robust methodological framework. We applied exploratory factor analysis (EFA) to identify latent sub-mathmetics skills relevant to physics problem-solving and employed structural equation modeling (SEM) to examine the causal impact of these skills on students’ performance in physics. The study analyzed data from a municipal-wide assessment involving 1,878 grade 12 students in Southern China. The results demonstrate that mathematics skills impacting high school students’ physics problem-solving performance can be categorized into two sub skills, algebraic skills and geometric skills. It also indicates that algebraic skills have a stronger direct effect on physics problem-solving performance compared to geometric skills in high school setting. These findings suggest that integrating focused algebraic training within physics education can significantly improve student outcomes in STEM fields. We recommend that educators design curricula and instructional strategies that emphasize the development of algebraic skills necessary for solving complex physics problems. Additionally, these findings have important implications for policymakers, who should consider integrating targeted mathematics training within physics curricula to foster interdisciplinary learning and better prepare students for challenges in STEM education.

Avoid common mistakes on your manuscript.

Introduction

In the landscape of STEM education, mathematics is often recognized as the foundational pillar that supports scientific learning (Dierdorp et al., 2014 ; Nakakoji & Wilson, 2018 ; Turşucu et al., 2020 ). For example, physics problem-solving is not merely a function of conceptual understanding; it critically depends on students’ ability to apply mathematical principles to analyze and interpret physical phenomena. As such, mathematics serves as a crucial tool in navigating the quantitative aspects of problem-solving in physics (Dierdorp et al., 2014 ). Despite the well-established interdependence of these disciplines, there remains a gap in our understanding of how specific mathematics skills—particularly geometric and algebraic skills—contribute to physics problem-solving performance, particularly at the secondary school level.

Many studies have explored the impact of mathematics learning in science education, particularly in physics education. These studies often highlight a strong correlation between students’ mathematics skills and their performance in physics (Arbabifar, 2021 ; Dehipawala et al., 2014 ; Matthews et al., 2009 ). Yet, further study on this topic is necessary for two major reasons. Firstly, much of this previous research has focused on university education settings but research findings at the university level might not automatically apply to a high school setting. (Jackson & Johnson, 2013 ; Meltzer, 2002 ; Rylands & Coady, 2009 ). The first research question in this study is to check if such a strong correlation, well documented at the college level, is evident among high school students, who are known to differ from adults in terms of factors influencing academic outcomes (Breitwieser & Brod, 2020 ; Dunlosky et al., 2013 ; Schneider & Preckel, 2017 ). Secondly, while previous research has documented correlations between general mathematics ability and science problem-solving, the specific roles of distinct mathematics skills—such as geometric and algebraic skills—remain underexplored, particularly in the context of secondary education. In other words, the second research question seeks to determine which skill, algebraic or geometric, has a higher impact, or if their impact levels are the same.

Using data from a municipal-wide assessment in Southern China with 1,878 grade 12 students, we employ exploratory factor analysis (EFA) and structural equation modeling (SEM) to evaluate the contributions of these skills. Our findings indicate that algebraic skills have a more significant impact on physics problem-solving than geometric skills, highlighting the importance of incorporating targeted mathematics instruction within physics curricula. This approach can better equip students with the tools necessary to tackle complex scientific problems, ultimately enhancing STEM education outcomes.

Literature Review

The relationship between mathematics and physics problem-solving in secondary education.

Physics, being an elemental science, inherently involves problem-solving, which plays a crucial role in evaluating students’ knowledge and skills in physics education (Reddy & Panacharoensawad, 2017 ; Ince, 2018 ). Successful problem-solving in physics is not solely dependent on students’ understanding of physics concepts but also significantly relies on their ability to apply mathematics principles (Redish & Kuo, 2015 ). Mathematics provides the language and tools necessary for the precise expression and application of physics laws and relationships, effectively bridging the gap between physics cognition and practical application (Bing & Redish, 2009 ; Franestian, 2020 ). In this way, mathematics plays a vital role in enabling students to navigate the quantitative aspects of physics problem-solving, making it indispensable for achieving success in this field.

Prior studies have established that students’ mathematics skills are closely associated with their performance in physics problem-solving. For example, Ogunleye ( 2011 ) identified poor mathematics proficiency as a major obstacle to students’ ability to solve physics problems, while Panorkou and Germia ( 2021 ) demonstrated that strong mathematics skills support a deeper understanding of physical phenomena, such as gravity, and enhance problem-solving abilities in this domain. These studies underscore the importance of integrating mathematics instruction with physics education to improve students’ problem-solving skills and overall academic performance.

However, most research exploring the relationship between mathematics and physics has been conducted at the post-secondary level, focusing primarily on college students (Jackson & Johnson, 2013 ; Meltzer, 2002 ; Rylands & Coady, 2009 ). These studies have often highlighted correlations between general mathematics ability and success in physics courses (Arbabifar, 2021 ; Dehipawala et al., 2014 ; Matthews et al., 2009 ). While valuable, the findings from these studies may not be directly applicable to high school students, who differ from college students in significant ways (Talsma et al., 2018a ; Schneider & Preckel, 2017 ).

Teenagers are distinct from adult learners in several respects, including their cognitive processes, learning habits, emotional development, and self-efficacy (Richardson et al., 2012 ; Talsma et al., 2018a ). Also, teenager’s approach to learning and problem-solving is often less mature and more variable compared to that of college students, who have generally developed more advanced reasoning skills and learning habits (Schneider & Preckel, 2017 ). Consequently, the strategies and educational interventions that are effective for college students may not necessarily be effective for teenagers. This underscores the importance of studying the relationship between mathematics skills and physics problem-solving specifically within the high school context. By focusing on high school students, this study aims to provide insights that are directly relevant to secondary education, helping to bridge the gap between theory and practice in STEM education at this crucial stage of development.

Latent Mathematics Skills Needed for Physics Problem-Solving

When studying problem-solving tasks in physics, researchers and practitioners have identified several latent mathematics skills necessary for successfully solving these tasks (Awodun et al., 2013 ; Panorkou & Germia, 2021 ; Redish, 2023 ; Rebello et al., 2007 ). Awodun et al. ( 2013 ) explored the mathematics skills required to tackle physics questions among upper secondary school students, identifying six key skills: computation skills, geometry skills, graph and table interpretation skills, probability and statistics skills, algebraic skills, and measurement skills. Similarly, Daniel et al. ( 2020 ) concluded that deficiencies in analytical skills, algebraic processing skills, geometric skills, computational skills, as well as table and graph interpretation skills, were the primary reasons behind students’ poor performance in physics. Despite the recognition of these various sub-mathematics skills, little effort has been made to determine the relative importance of these skills. This gap in the literature calls for a deeper investigation into which sub-mathematics skill plays a more critical role in improving students’ physics problem-solving abilities.

Algebraic Skills and Physics Problem-Solving

Algebra is a fundamental component of mathematics and serves as a powerful tool in physics (Monk, 1994 ). Algebraic skills in mathematics education include the ability to manipulate variables, solve equations, create formulas, work with functions, and apply these concepts to solve problems (Drijvers, 2011 ). Physics problem-solving benefits from the correct understanding and proper use of algebraic skills (Erdoğan et al., 2014 ). Research has shown that students with strong algebraic skills are more likely to succeed in physics problem-solving compared to those who struggle with algebra (Kanderakis, 2016 ; Rebello et al., 2007 ). Awodun et al. ( 2013 ) also found a positive impact of algebraic skills on problem-solving performance in secondary school physics.

Geometric Skills and Physics Problem-Solving

Geometric skills involve the ability to recognize and work with geometric shapes, visualize spatial relationships, sketch images, and apply geometric concepts to solve problems (Astuti et al., 2018 ). According to Hoffer ( 1981 ), geometric skills in mathematics encompass five types: visual skills, language skills, drawing skills, logical skills, and applied skills. These skills are essential in various physics problem-solving scenarios, such as analyzing forces, understanding light reflection and refraction, and evaluating projectile motion. The application of geometric skills is common in many areas of physics, and mastering these skills is vital for solving problems in this subject. Studies have consistently shown that geometric skills positively impact students’ performance in physics problem-solving at the secondary school level (Basson, 2002 ; Daniel et al., 2020 ).

Other Skills and Physics Problem-Solving

In addition to algebraic and geometric skills, graph and table interpretation skills, as well as probability and statistics skills, have been found to be closely related to students’ performance in physics (Awodun et al., 2013 ; Daniel et al., 2020 ). For instance, when analyzing a velocity-time graph, a student who cannot interpret the graph will struggle to determine whether an object is accelerating, decelerating, or moving at a constant speed. Research has consistently shown that graph and table interpretation plays a significant role in physics performance (McKenzie & Padilla, 1986 ; Redish, 2023 ). Moreover, probability and statistics skills are closely tied to logical thinking in mathematics and encompass five key competencies: understanding probability concepts, applying these concepts, calculating probability values, interpreting these values accurately, and visualizing and communicating probabilities and their implications (Puspitasari et al., 2019 ; Tiro et al., 2021 ). These skills are particularly relevant in the thermodynamics of physics; for example, students use them to grasp concepts like entropy and the second law from a microscopic perspective (Malgieri et al., 2016 ).

Research Questions

In summary, previous research has identified various sub-mathematics skills required for high performance in physics problem-solving, but little effort has been made to explore which specific sub-mathemtaics skill plays a more significant role in enhancing physics learning. Furthermore, most studies examining the relationship between mathematics and physics problem-solving have focused on college students, leaving a gap in understanding how these skills function among high school students, who differ significantly from adult learners.

This study aims to investigate the causal relationship between mathematics and physics problem-solving in upper secondary school physics education. Based on the data of a large scale assessment, we use exploratory factor analysis (EFA) to identify the latent mathematics skills involved in solving physics problems. Additionally, we employ structural equation modeling (SEM) to evaluate the relative strength of specific sub-mathematics skills’ impact on physics problem-solving for high school students. The specific research questions are as follows:

Q1: Does the association between students’ mathematics skills and physics problem-solving performance also hold in a high school setting?

Q2: What sub-mathematics skill plays a more important role in enhancing high school students’ physics problem-solving performance?

Methodology

The methodology of this study involved analyzing data from a municipal-wide assessment of 1,878 grade 12 students in Southern China, who were in the final year of a non-calculus-based physics course. The assessment included physics and mathematics tests, with the physics test comprising multiple-choice, blank-filling, and open-ended items, and the mathematics test featuring similar formats. Data analysis proceeded through three stages: assessing internal consistency and data collinearity, conducting exploratory factor analysis (EFA) to identify latent mathematics skills, and applying structural equation modeling (SEM) to explore the causal relationships between these skills and students’ performance in physics problem-solving.

The data were obtained from a well-developed municipal-wide assessment for evaluating upper secondary school students’ knowledge and problem-solving skills in physics. At the time of the test, the students were in the last year (grade 12) of a three-year-long physics course at upper secondary schools in a city in Southern China. The course, which is non-calculus-based, covers classical mechanics, electromagnetism, optics, and thermal physics, thereby preparing students for further studies in STEM subjects at university. These topics of physics are all covered in the first two years of the course, and the third year is solely dedicated to revision and training in physics problem-solving.

1,900 students were in grade 12 of the school, but 22 (1.16%) didn’t participate in either the physics or mathematics test of the assessment. Excluding these non-participants resulted in a valid sample size of 1,878. The data obtained from the school administration was anonymized, containing only a temporary test taker’s identification number (not real ID number) and performance scores on each item. The data did not contain students’ detailed demographic information, but the participants were nearly all aged 17 or 18 years, in accordance with the country’s strict age requirement for enrollment in K-12 education.

Instruments

The municipal-wide high school students’ knowledge and problem-solving skills physics assessment was structured with 10 multiple-choice items (7 single-correct-choice items, 3 multiple-correct-choice items), 2 blank-filling items, and 3 open-ended items. The assessment was a mock exam of the college entrance examination, with its content constructed by a panel of physics education experts and reviewed and validated by another team of experts independently. Table  1 lists the measurement indicators of students’ physics knowledge for each item in this test.

We scored the items dichotomously or polytomously based on the item formats. For the single-correct-choice items, which are multiple-choice problems with only one correct solution out of four options, students received a score of 1 if they answered the item correctly and a score of 0 otherwise. For the multiple-correct-choice items, which are multiple-choice problems with one to four possible correct solutions out of the list of four, students received a score of 2 if they picked all the correct options, a score of 1 if they picked some of the correct options, and a score of 0 if they picked any incorrect options. For the blank-filling items and open-ended items, we assigned a score of 1 to students whose item scores were higher than the average item score and a score of 0 to the rest, due to the discrete distribution. The Cronbach’s alpha of the 15 items ranged from 0.80 to 0.85 (Table  1 ). The overall Cronbach’s alpha was 0.83, indicating the high reliability of the physics assessment.

The municipal-wide upper secondary school students’ mathematics skills assessment was structured with 11 multiple-choice items (8 single-correct-choice items, 3 multiple-correct-choice items), 3 blank-filling items, and 5 open-ended items. They were scored in the same way as the physics test. We scaled the scores of the students’ mathematics skills assessment to make the average assessment scores equal to 0 due to the discrete distribution. The overall Cronbach’s alpha of the assessment was 0.74, indicating the acceptable reliability of the physics assessment.

Both the physics and mathematics assessments were part of a municipal-wide mock exam for the national college entrance examination, which is taken very seriously. All problem items were composed by a panel of six science and mathematics education experts, including university professors and experienced secondary school teachers, and were independently reviewed by another panel of such experts. The students took the 120-minute mathematics assessment on April 22, 2024, and the 75-minute physics assessment one day later.

Data Analysis

Almost all grade 12 students in the megalopolis municipal, with a population of 15 million, attend this municipal-wide mock exam in April 2024. Our data is extracted from one district of the municipality. This district has 1.5 million residents, with 1,900 grade 12 students who take science in high school. Among those 1,900 students, 1,878 successfully took both the mathematics and physics assessments. All of the 1,878 data points are included in this study.

To answer the research questions, we implemented three stages to analyze the data. Firstly, we computed the covariances across items to evaluate the items’ internal consistency and data collinearity issues. Then, exploratory factor analysis (EFA) with eigenvalues and model fit was conducted to explore the latent factors of the mathematics skills in solving physics assessment items. The third stage was to conduct structural equation modeling (SEM) to estimate the causal relationships between students’ mathematics skills and their performance in physics problem-solving, given the latent mathematics skills Figure  1 .

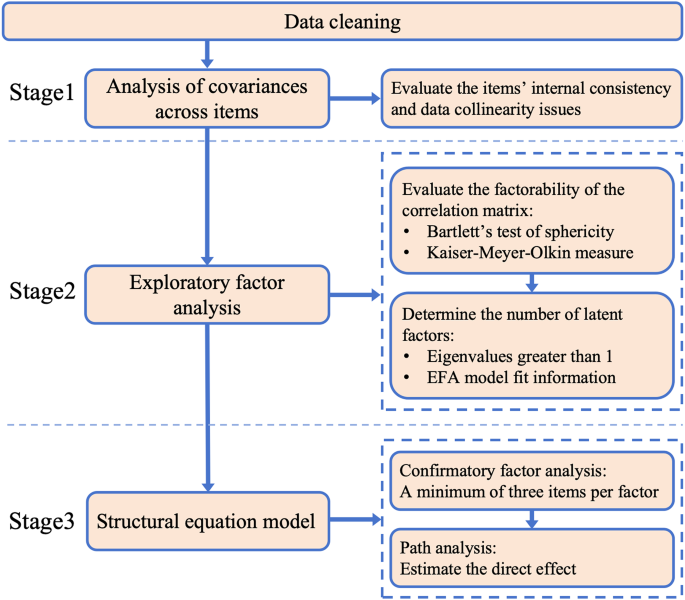
Procedure of data analysis

Exploring and Extracting Latent Factors

Before implementing the EFA, we initially assessed the assumption of sphericity through Bartlett’s test (Bartlett, 1954 ) to ensure that the correlation matrix was not random and evaluated sampling adequacy by the Kaiser-Meyer-Olkin (KMO test; Kaiser, 1974 ) measure. According to widely accepted evaluation criteria (Khine et al., 2018 ; Tabachnick & Fidell, 2007 ), EFA can proceed without violating assumptions or inflating estimated bias when the p-value of Bartlett’s test is less than 0.05, and the KMO test is greater than 0.5.

Following the assumption evaluation, we structured EFA using the weighted least squares estimation and the promax oblique rotation (Hendrickson & White, 1964 ), as we assumed the latent factors were correlated, and implemented three criteria to determine the number of latent factors. One criterion was based on the mathematical rules, as recommended by Cliff ( 1988 ), indicating that the eigenvalues should be larger than 1. This criterion was conducted using the ‘psych’ package (Revelle, 2023 ) in R version 4.3.1.

The second criterion was based on the EFA model fit information, which included the chi-square test, Tucker-Lewis Index (TLI; Tucker & Lewis, 1973 ), Bentler Comparative Fit Index (CFI; Bentler, 1990 ), Root Mean Square Error of Approximation (RMSEA; Steiger, 1990 ), and standardized root mean square residual (SRMR). We extracted the number of latent factors when the chi-square p-value was smaller than 0.05, the CFI and TLI exceeded 0.95 (Hu & Bentler, 1999 ), and the RMSEA and SRMR were lower than 0.05 (Browne & Cudeck, 1993 ). These model fit indexes indicate a close fit of a model to data (Kline, 2016 ). This analysis was conducted using the ‘lavaan’ package (Rosseel, 2012 ) in R version 4.3.1.

After extracting the number of factors, we named the latent factors based on the EFA factor loading outcomes. Additionally, items with factor loadings no less than 0.40 were selected as having a moderate or even strong association between the item and the latent factor (Stevens, 1992 ).

Estimating Causal Relationships via SEM

The SEM was structured in two parts. The first part involved the confirmatory factor analysis (CFA), which included a minimum of three items per factor to ensure the identification of model performance (Kline, 2016 ). The second part involved the structural part, including the path analysis for the direct effects in light of our hypothesis in the current study.

The CFA was conducted using the ‘lavaan’ package (Rosseel, 2012 ) with the method of maximum likelihood estimation. The model fit was evaluated by the chi-square test, Comparative Fit Index (CFI), Tucker-Lewis Index (TLI), Standardized Root Mean Square Residual (SRMR), and Root Mean Square Error of Approximation (RMSEA). The CFI and TLI exceeded 0.95 (Hu & Bentler, 1999 ), while the SRMR was below 0.05 (Hu & Bentler, 1999 ). Additionally, RMSEA was lower than 0.05 (Browne & Cudeck, 1993 ), indicating a perfect fit (Kline, 2016 ).

For the path analysis, we estimated the direct effect of students’ mathematics skills on each extracted latent factor. The number of paths in the structural part was the same as the number of extracted factors.

Covariances across Items

Table  2 shows the correlation between physics items and the mathematics assessment, none of which is smaller than 0.01. Therefore, we did not rule out any physics items in the following exploratory factor analysis.

Exploratory Factor Analysis

The result of Bartlett’s test of sphericity was significant, with a p -value smaller than 0.001 ( \(\:{\chi\:}^{2}\) (105) = 5419.5514, p  < .001) and the KMO test was 0.93. Both Bartlett’s test and the Kaiser-Meyer-Olkin measure indicated that the data were appropriate to proceed with the EFA.

Figure  2 is the scree plot visualizing the eigenvalues outcomes. The eigenvalues-greater-than-1 criterion suggested extracting two latent factors. The EFA model fit information with two factors, as shown in Table  3 , indicated that its TLI and CFI were larger than 0.950, and the RMSEA and SRMR were smaller than 0.050, all of which were acceptable values, indicating the extraction of two latent factors Figure  3 .

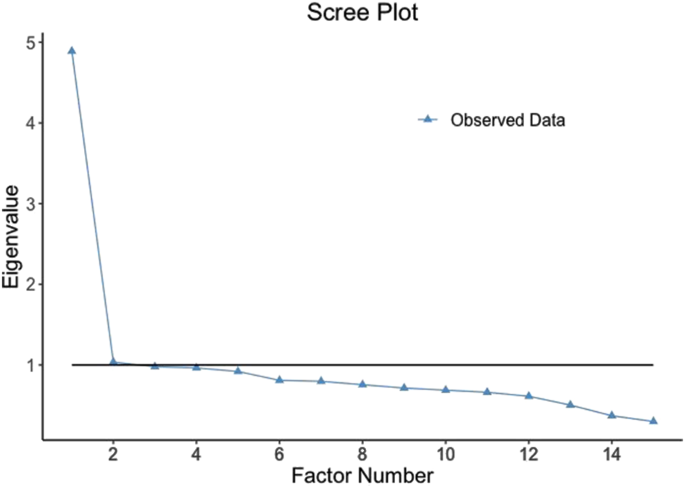
Scree plot of eigenvalues

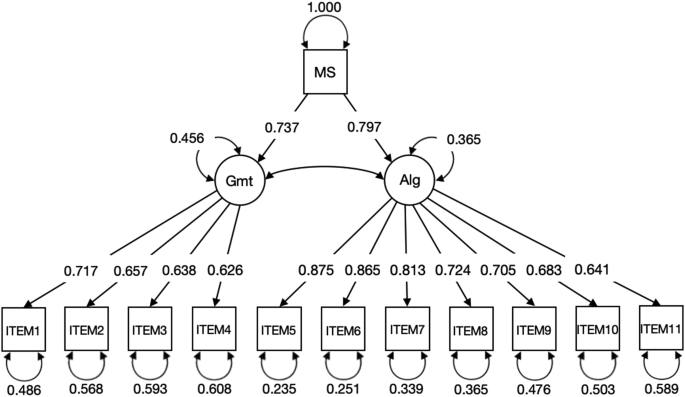
Structural model with standardized estimates Note MS: Mathematics Skill; Gmt: Geometric Skills; Alg: Algebraic Skills

Given the most salient manifest variables that latent factors have in common (Watkins, 2018 ), the two factors were named as follows: Factor 1: Geometric Skills with three items and Factor 2: Algebraic Skills with seven items.

Structural Equation Modeling Results

The final fitted structural model had a perfect fit ( \(\:{\chi\:}^{2}\) (52) = 71.969, p  < .05, CFI = 0.992, TLI = 0.991 SRMR = 0.039, and RMSEA = 0.014), as shown in Fig.  2 .

Table  5 lists the standardized factor loadings in the CFA part. The factor loadings of the 11 items ranged between 0.62 and 0.88, all of which were above 0.50. Each item had a statistically significant p -value smaller than 0.001.

In the structural part, there were two paths: students’ mathematics skills to algebraic skills in physics problem-solving and students’ mathematics skills to geometric skills in physics problem-solving. The standardized coefficient of the path from mathematics skills to the item responses involving algebraic skills was 0.797, indicating that students’ achievement increases by 0.797 scores in this category of physics problem-solving items as their mathematics skills increase by one unit. Likewise, the standardized coefficient of the path from mathematics skills to the item responses involving geometric skills was 0.737, indicating that students’ achievement increases by 0.737 scores in this category of physics problem-solving items as their mathematics skills increase by one unit.

Interpretation of the Results

This study aimed to investigate the causal effects of students’ mathematics skills on their physics problem-solving performance at the upper secondary school level. To achieve this, we employed Exploratory Factor Analysis (EFA) to identify the latent mathematics skills underlying physics problem-solving tasks. Subsequently, Structural Equation Modeling (SEM) was utilized to assess how these identified skills impacted students’ performance across different types of problem-solving tasks.

This study reaffirms the strong relationship between mathematics skills and physics problem-solving performance observed in prior research. Our observation of the strong association between mathematics scores and physics scores in 1,878 students is consistent with many previous studies. For example, Arbabifar ( 2021 ), Dehipawala et al. ( 2014 ), and Matthews et al. ( 2009 ) highlighted correlations between general mathematics ability and success in physics courses among college students. Similarly, Ogunleye ( 2011 ) identified poor mathematics proficiency as a major obstacle in students’ ability to solve physics problems, while Panorkou and Germia ( 2021 ) demonstrated that strong mathematics skills support a deeper understanding of physical phenomena, such as gravity, and enhance problem-solving abilities in this domain. Our research confirms that mathematics skills significantly influence students’ ability to solve physics problems.

Compared to college and university, physics education is sparsely researched at high school level (Kanim & Cid, 2020 ). Yet previous studies suggest that teaching methods and educational research findings that are effective for college students might not automatically apply to teenagers, highlighting the need for more empirical studies to understand their learning (Breitwieser & Brod, 2020 ; Dunlosky et al., 2013 ; Schneider & Preckel, 2017 ). Our results from this group effectively bridge this critical gap in this topic of exploring the association between mathematics skills and physics problem solving, delivering insights essential for developing age-appropriate teaching strategies. Along with few studies targeted at teenage learners (Roorda, 2015 ; Turşucu, 2020), we extend this association from college students to high school teenage learners.

Awodun et al. ( 2013 ) explored the underlying mathematics skills required to tackle physics questions among upper secondary school students, identifying six key skills: computation skills, geometry skills, graph and table interpretation skills, probability and statistics skills, algebraic skills, and measurement skills. Similarly, Daniel et al. ( 2020 ) concluded that deficiencies in analytical skills, algebraic processing skills, geometric skills, computational skills, as well as table and graph interpretation skills, were the primary reasons behind students’ poor performance in physics. Unlike these studies, our result indicates that mathematics skills influencing high school physics problem solving fall into only two categories, algebraic and geometric skills. We suggest this is because some other skills considered in those previous studies might potentially be included in either algebraic skills or geometric skills. For instance, computational skills may mainly be included in algebraic skills and graph interpretation skills may mainly fall into geometric skills. Also, some skills, such as analytical skill, are not subject-specific skill, as it doesn’t need mathematics conceptual knowledge and it is also an essential skill for other subjects (Powers & Enright, 1987 ; Bravo et al., 2016 ; Wei, 2024 ).

Furthermore, despite previous research has identified various sub-mathematics skills required for high performance in physics (Panorkou & Germia, 2021 ; Redish, 2023 ; Rebello et al., 2007 ), little effort has been made to explore which specific sub-mathematics skill plays a more significant role in enhancing physics learning. Our findings clearly suggest the more critical role of algebraic skills in enhancing physics problem-solving abilities among high school students. This aspect of the research provides actionable insights that can guide curriculum developers and educators in refining their teaching strategies and educational content.

Contribution to the Literature

The contributions of this research to the current body of literature in this field are twofold. Firstly, by extending the exploration to high school students, this study enriches the sparse body of high school-level research (Kanim & Cid, 2020 ), providing robust, data-driven evidence. Secondly, the study introduces an empirical comparison of sub-mathematics skills, marking the first time such a data-driven analysis of algebraic versus geometric skills has been conducted, to the best of our knowledge.

In response to our research questions, the evidence clearly shows that an association between students’ mathematics skills and physics problem-solving performance does indeed hold in a high school setting. Furthermore, the evidence decisively indicates that algebraic skills are more critical than geometric skills for solving physics problems, underscoring the need for a curricular focus on enhancing algebraic training. These insights should compel policymakers to advocate for educational reforms that prioritize these skills. Educators and practitioners can leverage our findings to develop targeted instructional strategies, thereby better equipping students to tackle complex physics problems effectively.

Teaching Strategies

These results are particularly relevant when considering the implications for educational practices. Given the pronounced impact of algebraic skills on physics problem-solving, it is imperative that physics curricula include targeted algebra training. By systematically integrating algebraic problem-solving techniques into physics instruction, educators can better prepare students to navigate complex analytical tasks, thereby enhancing their overall performance. We suggest that educators adopt targeted strategies to enhance students’ problem-solving proficiency. Initially, educators should identify the specific mathematics skills required for each physics problem-solving task. They can then focus on strengthening these skills, helping students translate physics problems into mathematical terms and apply these concepts to various physical scenarios. Such preparation allows students to better understand and tackle problem-solving tasks by effectively using their knowledge of both mathematics and science.

Furthermore, our findings indicate that mathematics skills significantly influence students’ success in physics problem-solving, particularly when tasks demand strong algebraic skills. For instance, when addressing Newton’s second law of motion, students who possess a strong foundation in algebraic manipulation—such as solving equations involving multiple variables—are significantly more likely to succeed. This illustrates the practical necessity of embedding algebraic training within the physics curriculum.

To foster a practical integration of physics and mathematics, we propose that educators and policymakers implement a coordinated teaching approach, similar to the “Mathematical Methods in Physics” format (Arbabifar, 2021 ). Such an approach would involve collaboration between mathematics and physics teachers to cover problem-solving tasks. For instance, in a scenario involving vehicle pursuits, mathematics teachers would focus on algebra, geometry, and data interpretation, while physics teachers would concentrate on the relevant physical principles, such as Newton’s laws. This collaborative teaching ensures that students receive a unified and coherent learning experience, enhancing their understanding and ability to apply mathematics skills in physics contexts.

Additionally, we recommend enhancing communication and collaboration between mathematics and physics teachers to develop integrated teaching strategies. By forming instructional groups, educators can share insights and strategies for translating physics problems into mathematical language and vice versa. This approach not only helps teachers address their instructional challenges but also enriches the student learning experience by linking theoretical concepts with practical applications.

Policy Making

A review of education policies across various countries reveals a universal emphasis on the role of mathematics in science education (Department for Education, 2015 ; NGSS Lead States, 2013 ; MOE of PRC, 2020 ). For example, the Principles and Standards for School Mathematics highlight the necessity of mathematics education in preparing students for careers as engineers, scientists, and other related professions (NCTM, 2000 ). Similarly, the Next Generation Science Standards advocate for integrating rigorous scientific content with the mathematics skills commonly used by scientists and engineers (NGSS Lead States, 2013 ). This interdisciplinary approach is crucial for students’ overall development and equips them for future academic and professional challenges.

In light of these insights and the findings of this research, we present specific recommendations for policymakers. Firstly, to better equip students for interdisciplinary challenges, we recommend the establishment of integrated mathematics and physics curricula. This approach ensures that students can apply mathematics skills in physics contexts with greater efficacy, reflecting the interconnected nature of these disciplines in both academic and professional environments.

Secondly, teacher training programs for physics educators should focus on enhancing mathematics skills, especially algebraic skills. This aligns with Turşucu et al. ( 2020 ), who suggest that the ability to explain fundamental mathematics should be a required competency for physics teachers. Accordingly, our study recommends a concentrated effort on developing algebraic skills in pre-service physics teachers to better prepare them for teaching complex physics problems.

Implementing these strategies promises significant improvements in secondary school students’ abilities to solve physics problems, ultimately leading to enhanced outcomes in physics education and laying a robust foundation for their future endeavors.

Limitations and Future Research

While this study provides valuable insight into secondary school students’ mathematics skills and physics problem-solving performance, with practical implications for both practitioners and policymakers, it is important to acknowledge several limitations.

Firstly, the physics problem-solving tasks in our empirical data encompassed multiple fields of physics knowledge, such as mechanics, thermodynamics, kinematics, and electromagnetism, rather than focusing on a single field. Each field may have varying degrees of association with mathematics skills, given the different latent mathematics skills involved in problem-solving tasks. In this study, we treated all physics knowledge as a whole to investigate the relationship between students’ problem-solving achievement and their mathematics skills, due to the limited number of items in our empirical data. Therefore, we suggest further refining the categorization of physics knowledge to gain a more comprehensive understanding of the specific impact of mathematics skills in different fields of physics, providing more targeted guidance for teaching practice.

Secondly, the sample of the present study was limited to one city in southern China with a similar ethnic background. This limits our ability to generalize the findings to a broader population with different ethnic backgrounds or in other settings, such as rural schools. However, the problem-solving items in the empirical research are commonly included in the national physics assessment for upper secondary school students. Given that our sample was large enough to meet the requirements of a normal distribution, the identified sub-mathematics skills for physics problem-solving tasks are still informative. The conclusions of the current study, to some extent, provide valuable insights into teaching problem-solving in physics education in upper secondary schools. In future research, we recommend that researchers collect samples across multiple regions to draw more comprehensive and generalizable conclusions. Collecting samples from different countries for comparison, and combining the education policies of different countries for discussion, may help to draw more in-depth conclusions and promote the development of science education.

Thirdly, the reliance on quantitative data may overlook the nuanced interplay between students’ cognitive, motivational, and contextual factors that can affect their performance in physics problem-solving. Qualitative data could enrich our understanding of how students apply their mathematics skills in physics contexts and the challenges they face in real-time problem-solving scenarios.

Lastly, the study’s focus on the causal relationships between mathematics skills and physics problem-solving may not fully capture the dynamic and iterative processes that students undergo when learning and applying these skills. Future studies could benefit from longitudinal designs that track changes in students’ problem-solving capabilities and mathematics skills development over time, offering deeper insights into the learning trajectories and educational interventions that are most effective.

Although the current study delved into the relationship between upper secondary school students’ mathematics skills and their performance in solving physics problems, the conclusions have the potential to be applied more broadly to science education. Other subjects within science, such as chemistry and biology, are also closely linked with mathematics. For example, in chemistry, mathematics is used to describe the relationship between conductivity and concentration (Shang, 2021 ). Secondary school chemistry courses covering stoichiometry problems, Avogadro’s number, balancing equations, and other areas require a robust understanding of mathematics (Weisman, 1981 ). In biology, mathematical methods are employed to understand the diversity and complexity of living systems (Kauffman, 1993 ). As biology and biotechnology continue to evolve, there is an increasing demand for quantitative skills (Gross, 2004 ; Karsai & Kampis, 2010 ).

This study’s methodological lens, focusing on the causal relationships facilitated by quantitative analysis through EFA and SEM, could serve as a model for similar research in other disciplines. By applying this proven approach, researchers and practitioners in fields like chemistry and biology could further investigate the pivotal role that mathematics plays in understanding and solving complex scientific problems. Therefore, we recommend that researchers and practitioners in other fields of science who share our research goal explore in-depth the causal relationship between mathematics ability and student achievement in problem-solving, considering various mathematics skills.

Conclusions and Implications

While prior studies exploring the relationship between mathematics skills and physics problem-solving at the high school level exist, they are rarer compared to those conducted at the college level. This study enriches this modest corpus by providing robust, data-driven evidence that highlights the distinct roles of algebraic and geometric skills in secondary physics education. Our analysis of the mathematics and physics assessment of 1878 grade 12 students using EFA and SEM demonstrates that mathematics skills needed for physics problem-solving in high school settings can be categorized into two sub-skills, with algebraic skills having a much more pronounced impact on physics problem-solving capabilities than geometric skills. These findings not only corroborate but also deepen our understanding of science education at this crucial academic stage.

Implications for Educational Practice

The significant influence of algebraic skills on physics problem-solving uncovered in this study suggests a need for strategic educational approaches. Physics educators are encouraged to integrate focused algebra training within their curricula, which could include the development of specific modules or interactive workshops that emphasize the application of algebraic concepts to physical problems. Such targeted training can equip students with the necessary tools to tackle complex scientific problems, thereby enhancing their overall academic success in STEM fields.

Policy Recommendations

This research underscores the importance of supportive educational policies that advocate for the integration of mathematics and physics education at the high school level. Policymakers should consider initiatives that fund and develop resources facilitating such integrated curricula. These policies could significantly contribute to creating a cohesive learning environment that effectively prepares students for advanced studies and careers in STEM disciplines.

Conclusions

This study significantly contributes to the limited but growing body of literature on high school students’ mathematics skills and their effect on physics problem-solving. By offering concrete, data-backed insights into the specific mathematics skills that most influence physics problem-solving success, our research provides a valuable foundation for further studies and informs both current educational practices and policy-making in STEM education. As STEM fields continue to evolve, the need for robust educational frameworks that prepare students through an interdisciplinary approach becomes increasingly crucial. The insights gained from this study not only contribute to academic discourse but also have practical implications for shaping future educational practices and policies.

Data availability

The raw data supporting the conclusions of this article will be made available by the authors on reasonable request.

Arbabifar, F. (2021). Transfer of learning in a mathematical methods in physics course for undergraduate students of physics. European Journal of Physics , 42 (4), 1–15. https://doi.org/10.1088/1361-6404/abf0db

Article   Google Scholar  

Astuti, R., Suryadi, D., & Turmudi (2018). Analysis on geometry skills of junior high school students on the concept congruence based on Van Hiele’s geometric thinking level. Journal of Physic: Conference Series , 1132 (1), 1–5. https://doi.org/10.1088/1742-6596/1132/1/012036

Awodun, O. A., & Adeniyi, O. (2013). Mathematics skills as predictors of physics students’ performance in senior secondary schools. International Journal of Science and Research , 2 (7), 391–394.

Google Scholar  

Bartlett, M. S. (1954). A note on the multiplying factors for various chi square approximations. Journal of the Royal Statistical Society Series B (Methodological) , 16 (2), 296–298. https://www.jstor.org/stable/2984057

Basson, I. (2002). Physics and mathematics as interrelated fields of thought development using acceleration as an example. International Journal of Mathematical Education in Science & Technology , 33 (5), 679–690. https://doi.org/10.1080/00207390210146023

Bentler, P. M. (1990). Comparative fit indexes in structural models. Psychological Bulletin , 107 (2), 238–246.

Bing, T. J., & Redish, E. F. (2009). Analyzing problem solving using math in physics: Epistemological framing via warrants. Physical Review Physics Education Research , 5 (2), 1–15. https://doi.org/10.1103/PhysRevSTPER.5.020108

Bravo, A., Porzecanski, A., Sterling, E., Bynum, N., Cawthorn, M., & Fernandez, D. S. (2016). Teaching for higher levels of thinking: Developing quantitative and analytical skills in environmental science courses. Ecosphere , 7 (4). https://doi.org/10.1002/ecs2.1290

Breitwieser, J., & Brod, G. (2020). Cognitive prerequisites for generative learning: Why some learning strategies are more effective than others. Child Development , 92 (1), 258–272. https://doi.org/10.1111/cdev.13393

Browne, M. W., & Cudeck, R. (1993). Alternative way of assessing model fit. In K. A. Bollen & J. S. Long (Eds.), Testing structural equation models (pp. 136–162).

Cliff, N. (1988). The eigenvalues-greater-than-one rule and the reliability of components. Psychological Bulletin , 103 (2), 276–79. https://doi.org/10.1037/0033-2909.103.2.276

Daniel, T. O., Umaru, R. J., Suraju, K. O., & Ajah, A. O. (2020). Investigation of the role of mathematics on students’ performance in physics. Research in Science and Technological Education , 5 (2), 101–108.

Dehipawala, S., Shekoyan, V., & Yao, H. (2014, April). Using mathematics review to enhance problem solving skills in general physics classes. In Proceedings of the 2014 Zone 1 Conference of the American Society for Engineering Education (pp. 1–4). IEEE. https://doi.org/10.1109/ASEEZone1.2014.6820631

Departament for Education. (2015). National curriculum in England: Science programmes of study . Departament for Education.

Dierdorp, A., Bakker, A., van Maanen, J. A., & Eijkelhof, H. M. (2014). Meaningful statistics in professional practices as a bridge between mathematics and science: An evaluation of a design research project. International Journal of STEM Education , 1 , 1–15. https://doi.org/10.1186/s40594-014-0009-1

Drijvers, P. (2011). Secondary algebra education: Revisiting topics and themes and exploring the unknown . Sense.

Dunlosky, J., Rawson, K. A., Marsh, E. J., Nathan, M. J., & Willingham, D. T. (2013). Improving students’ learning with effective learning techniques: Promising directions from cognitive and educational psychology. Psychological Science in the Public Interest , 14 (1), 4–58. https://doi.org/10.1177/1529100612453266

Erdoğan, A., Kurudirek, A., & Akça, H. (2014). The effect of mathematical misconception on students’ success in kinematics teaching. Education Journal , 3 (2), 90–94. https://doi.org/10.11648/j.edu.20140302.18

Franestian, I. D., Suyanta, & Wiyono, A. (2020). Analysis problem solving skills of student in Junior High School. Journal of Physic: Conference Series, 1440 (1), 1–5. https://doi.org/10.1088/1742-6596/1440/1/012089

Gross, L. (2004). Scientific illiteracy and the partisan takeover of biology. PLoS Biology , 4 (5), 680–683. https://doi.org/10.1371/journal.pbio.0040167

Hendrickson, A. E., & White, P. O. (1964). Promax: A quick method for rotation to oblique simple structure. British Journal of Statistical Psychology , 17 (1), 65–70. https://doi.org/10.1111/j.2044-8317.1964.tb00244.x

Hoffer, A. (1981). Geometry is more than proof. NCTM Journal , 74 (1), 11–18. https://doi.org/10.5951/MT.74.1.0011

Hu, L. T., & Bentler, P. M. (1999). Cutoff criteria for fit indexes in covariance structure analysis: Conventional criteria versus new alternatives. Structural Equation Modelling: A Multidisciplinary Journal , 6 (1), 1–55. https://doi.org/10.1080/10705519909540118

Ince, E. (2018). An overview of problem solving studies in physics education. Journal of Education and Learning , 7 (4), 191–200. https://doi.org/10.5539/jel.v7n4p191

Jackson, D. C., & Johnson, E. D. (2013). A hybrid model of mathematics support for science students emphasizing basic skills and discipline relevance. International Journal of Mathematical Education in Science and Technology , 44 (6), 846–864. https://doi.org/10.1080/0020739X.2013.808769

Kaiser, H. F. (1974). An index of factorial simplicity. Psychometrika , 39 , 31–36. https://doi.org/10.1007/BF02291575

Kanderakis, N. (2016). The mathematics of high school physics: Models, symbols, algorithmic operations and meaning. Science & Education , 25 (7–8), 837–868. https://doi.org/10.1007/s11191-016-9851-5

Kanim, S., & Cid, X. C. (2020). Demographics of physics education research. Physical Review Physics Education Research , 16 (2), 1–23. https://doi.org/10.1103/PhysRevPhysEducRes.16.020106

Karsai, I., & Kampis, G. (2010). The crossroads between biology and mathematics: The scientific method as the basics of scientific literacy. BioScience , 60 (8), 632–638. https://doi.org/10.1525/bio.2010.60.8.9

Kauffman, S. (1993). The origins of order: Self-organization and selection in evolution . Oxford University Press.

Khine, M. S., Fraser, B. J., Afari, E., Oo, Z., & Kyaw, T. T. (2018). Students’ perceptions of the learning environment in tertiary science classrooms in Myanmar. Learning Environ Res , 21 , 135–152. https://doi.org/10.1007/s10984-017-9250-0

Kline, R. B. (2016). Principles and practice of structural equation modeling (4th ed.). Guilford Press.

Malgieri, M., Onorato, P., Valentini, A., & Ambrosis, A. D. (2016). Improving the connection between the microscopic and macroscopic approaches to thermodynamics in high school. Physics Education , 51 (6), 1–13. https://doi.org/10.1088/0031-9120/51/6/065010

Matthews, K. E., Adams, P., & Goos, M. (2009). Putting it into perspective: Mathematics in the undergraduate science curriculum. International Journal of Mathematical Education in Science and Technology , 40 (7), 891–902. https://doi.org/10.1080/00207390903199244

McKenzie, D. L., & Padilla, M. J. (1986). The construction and validation of the test of graphing in science. Journal of Research in Science Teaching , 23 (7), 1–9. https://doi.org/10.1002/tea.3660230702

Meltzer, D. E. (2002). The relationship between mathematics preparation and conceptual learning gains in physics: A possible hidden variable in diagnostic pretest scores. American Journal of Physics , 70 (12), 1259–1268. https://doi.org/10.1119/1.1514215

Ministry of Education of the People’s Republic of China. (2020). Physics curriculum standards for senior high schools . People’s Education. (in Chinese).

Monk, M. (1994). Mathematics in physics education: A case of more haste less speed. Physics Education , 29 (4), 209–211. https://doi.org/10.1088/0031-9120/29/4/005

Nakakoji, Y., & Wilson, R. (2018). First-year mathematics and its application to science: Evidence of transfer of learning to physics and engineering. Education Sciences , 8 (1), 1–16. https://doi.org/10.3390/educsci8010008

National Council of Teachers of Mathematics. (2000). Principles and standards for school mathematics . Reston.

NGSS Lead States. (2013). Next generation science standards: For states, by states . National Academies.

Ogunleye, A. O. (2011). Teachers and students perceptions of students problem-solving difficulties in physics: Implications for remediation. Journal of College Teaching & Learning , 6 (7), 85–90. https://doi.org/10.19030/TLC.V6I7.1129

Panorkou, N., & Germia, E. F. (2021). Integrating math and science content through covariational reasoning: The case of gravity. Mathematical Thinking and Learning , 23 (4), 318–343. https://doi.org/10.1080/10986065.2020.1814977

Powers, D. E., & Enright, M. K. (1987). Analytical reasoning skills involved in graduate study: Perceptions of faculty in six fields. The Journal of Higher Education , 58 (6), 658–682. https://doi.org/10.2307/1981103

Puspitasari, N., Afriansyah, E. A., Nuraeni, R., Madio, S. S., & Margana, A. (2019). What are the difficulties in statistics and probability? Journal of Physics: Conference Series , 1402 (7), 1–5. https://doi.org/10.1088/1742-6596/1402/7/077092

Rebello, N. S., Cui, L., Bennett, A. G., Zollman, D. A., & Ozimek, D. J. (2007). Transfer of learning in problem solving in the context of mathematics and physics. In D. H. Jonassen (Eds.), Learning to Solve Complex Scientific Problems , (pp. 223–246). Routledge. https://doi.org/10.4324/9781315091938-10

Reddy, M. V. B., & Panacharoensawad, B. (2017). Students problem-solving difficulties and implications in physics: An empirical study on influencing factors. Journal of Education and Practice , 8 (14).

Redish, E. F. (2023). Using Math in Physics: 6. Reading the physics in a graph. The Physics Teacher , 61 (8), 651–656. https://doi.org/10.1119/5.0150860

Redish, E. F., & Kuo, E. (2015). Language of physics, Language of math: Disciplinary culture and dynamic epistemology. Science & Education , 24 (5–6), 561–590. https://doi.org/10.1007/s11191-015-9749-7

Revelle, W. (2023). psych: Procedures for Psychological, Psychometric, and Personality Research (Version 2.3.6.) [Computer Software]. https://CRAN.R-project.org/package=psych

Richardson, M., Abraham, C., & Bond, R. (2012). Psychological correlates of university students’ academic performance: A systematic review and meta-analysis. Psychological Bulletin , 138 (2), 353–387. https://doi.org/10.1037/a0026838

Roorda, G., Vos, P., & Goedhart, M. J. (2015). An actor-oriented transfer perspective on high school students’ development of the use of procedures to solve problems on rate of change. International Journal of Science and Mathematics Education , 13 (4), 863–889. https://doi.org/10.1007/s10763-013-9501-1

Rosseel, Y. (2012). Lavaan: An R package for structural equation modeling. Journal of Statistical Software , 48 (2), 1–36. https://doi.org/10.18637/jss.v048.i02

Rylands, L. J., & Coady, C. (2009). Performance of students with weak mathematics in first-year mathematics and science. International Journal of Mathematical Education in Science and Technology , 40 (6), 741–753. https://doi.org/10.1080/00207390902914130

Schneider, M., & Preckel, F. (2017). Variables associated with achievement in higher education: A systematic review of meta-analyses. Psychological Bulletin , 143 (6), 565. https://doi.org/10.1037/bul000009

Shang, H. (2021). Connecting chemistry to mathematics by establishing the relationship between conductivity and concentration in an interdisciplinary, computer-based project for high school chemistry students. Journal of Chemical Education , 98 (3), 796–804. https://doi.org/10.1021/acs.jchemed.0c01179

Steiger, J. H. (1990). Structural model evaluation and modification: An interval estimation approach. Multivariate Behavioral Research , 25 (2), 173–180. https://doi.org/10.1207/s15327906mbr2502_4

Stevens, J. (1992). Applied multivariate statistics for the social sciences (2nd ed.). Lawrence Erlbaum Associates.

Tabachnick, B. G., & Fidell, L. S. (2007). Using multivariate statistics (5th ed.). Pearson Education.

Talsma, K., Schüz, B., Schwarzer, R., & Norris, K. (2018). Miscalibration of self-efficacy and academic performance: Self-efficacy ≠ self-fulfilling prophecy. Learning and Individual Differences , 69 , 182–195. https://doi.org/10.1016/j.lindif.2018.11.002

Talsma, K., Schüz, B., Schwarzer, R., & Norris, K. (2018a). I believe, therefore i achieve (and vice versa): A meta-analytic cross-lagged panel analysis of self-efficacy and academic performance. Learning and Individual Differences , 61 , 136–150. https://doi.org/10.1016/j.lindif.2017.11.015

Tiro, M. A., Ruliana, & Aswi, A. (2021). Literacy description of probability for the senior secondary school students in makassar city. Journal of Physics: Conference Series, 1863 (1), 1–9. https://doi.org/10.1088/1742-6596/1863/1/012013

Tucker, L. R., & Lewis, C. (1973). A reliability coefficient for maximum likelihood factor analysis. Psychometrika , 38 (1), 1–10. https://doi.org/10.1007/BF02291170

Turşucu, S., Spandaw, J., & de Vries, M. J. (2020). The effectiveness of activation of prior mathematical knowledge during problem-solving in physics. Eurasia Journal of Mathematics Science and Technology Education , 16 (4), 1–24. https://doi.org/10.29333/ejmste/116446

Watkins, M. W. (2018). Exploratory factor analysis: A guide to best practice. Journal of Black Psychology , 44 (3), 219–246. https://doi.org/10.1177/0095798418771807

Wei, Y., Chen, X., Zhong, Y., Liu, G., Wang, M., Pi, F., & Li, C. (2024). Recorded video versus narrated animation in teaching physics problem-solving: The influence of problem difficulty level. Journal of Baltic Science Education , 23 (3), 570–587. https://doi.org/10.33225/jbse/24.23.570

Weisman, R. L. (1981). A mathematics readiness test for prospective chemistry students. Journal of Chemical Education , 58 (7), 564. https://doi.org/10.1021/ed058p564

Download references

No funding was received to assist with the preparation of this manuscript.

Author information

Authors and affiliations.

School of Physics and Materials Science, Guangzhou University, Building of Administration West 401, No. 230, West Waihuan Street, Higher Education Mega Center, Panyu District, Guangzhou City, Guangdong Province, China

Tong Tong, Feipeng Pi, Siyan Zheng, Yi Zhong, Xiaochun Lin & Yajun Wei

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Yajun Wei .

Ethics declarations

Competing interests.

The authors declare that they have no competing interests.

Additional information

Publisher’s note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Tong, T., Pi, F., Zheng, S. et al. Exploring the Effect of Mathematics Skills on Student Performance in Physics Problem-Solving: A Structural Equation Modeling Analysis. Res Sci Educ (2024). https://doi.org/10.1007/s11165-024-10201-5

Download citation

Accepted : 18 September 2024

Published : 07 October 2024

DOI : https://doi.org/10.1007/s11165-024-10201-5

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Physics problem-solving
• Mathematics skills
• Secondary education
• Structural equation modeling
• Find a journal
• Publish with us
• Track your research