
Child Login
- Kindergarten
- Number charts
- Skip Counting
- Place Value
- Number Lines
- Subtraction
- Multiplication
- Word Problems
- Comparing Numbers
- Ordering Numbers
- Odd and Even
- Prime and Composite
- Roman Numerals
- Ordinal Numbers
- In and Out Boxes
- Number System Conversions
- More Number Sense Worksheets
- Size Comparison
- Measuring Length
- Metric Unit Conversion
- Customary Unit Conversion
- Temperature
- More Measurement Worksheets
- Writing Checks
- Profit and Loss
- Simple Interest
- Compound Interest
- Tally Marks
- Mean, Median, Mode, Range
- Mean Absolute Deviation
- Stem-and-leaf Plot
- Box-and-whisker Plot
- Permutation and Combination
- Probability
- Venn Diagram
- More Statistics Worksheets
- Shapes - 2D
- Shapes - 3D
- Lines, Rays and Line Segments
- Points, Lines and Planes
- Transformation
- Quadrilateral
- Ordered Pairs
- Midpoint Formula
- Distance Formula
- Parallel, Perpendicular and Intersecting Lines
- Scale Factor
- Surface Area
- Pythagorean Theorem
- More Geometry Worksheets
- Converting between Fractions and Decimals
- Significant Figures
- Convert between Fractions, Decimals, and Percents
- Proportions
- Direct and Inverse Variation
- Order of Operations
- Squaring Numbers
- Square Roots
- Scientific Notations
- Speed, Distance, and Time
- Absolute Value
- More Pre-Algebra Worksheets
- Translating Algebraic Phrases
- Evaluating Algebraic Expressions
- Simplifying Algebraic Expressions
- Algebraic Identities
- Quadratic Equations
- Systems of Equations
- Polynomials
- Inequalities
- Sequence and Series
- Complex Numbers
- More Algebra Worksheets
- Trigonometry
- Math Workbooks
- English Language Arts
- Summer Review Packets
- Social Studies
- Holidays and Events
- Worksheets >
- Geometry >

Slope Worksheets
The slope (or gradient) of a line is a number that denotes the 'steepness' of the line, also commonly called 'rise over run'. Knowledge of relevant formulae is a must for students of grade 6 through high school to solve some of these pdf worksheets. This page consists of printable exercises like introduction to slopes such as identifying the type and counting the rise and run; finding the slope using ratio method, slope-intercept formula and two-point formula; drawing lines through coordinates and much more! Employ our free worksheets to sample our work. Answer keys are included.
Printing Help - Please do not print slope worksheets directly from the browser. Kindly download them and print.
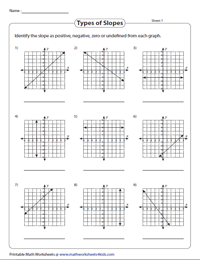
Identify the Types of Slopes
Introduction to slopes: Based on the position of the line on the graph, identify the type of slope - positive, negative, zero or undefined. This exercise is recommended for 6th grade and 7th grade children.
- Download the set

Draw Lines on a Graph: Types of Slopes
The first part of worksheets require students to plot the points on the graph, draw the line and identify the type of slope. In the next section, draw a line through the single-point plotted on the graph to represent the type of slope mentioned.

Count the Rise and Run
Based on the two points plotted on a graph, calculate the rise and run to find the slope of the line in the first level of worksheets. Find the rise and run between any two x- and y- coordinates on the line provided in the second level of worksheets. This practice resource is ideal for 7th grade and 8th grade students.

Graph the Line
Draw a line through a point plotted on the graph based on the slope provided in this set of pdf worksheets which is suitable for 9th grade children.

Fun Activity: Slope of the Roof
This set of fun activitiy worksheets contains houses with roofs of various sizes. Find the slope of the roof of each house. Answers must be in the form of positive slopes.

Find the Slope: Ratio Method
Use the x- and y- coordinates provided to find the slope (rise and run) of a line using the ratio method. A worked out example along with the formula is displayed at the top of each worksheet for easy reference.

Find the Slope: Line segments in a Triangle
Triangles are represented on each graph in this assembly of printable 8th grade worksheets. Learners will need to identify the rise and run for each of the three line segments that are joined to form a triangle.

Two-Point Formula
Employ the two-point formula that is featured atop every worksheet along with a worked out example. Substitute each pair of x- and y- coordinates in the given formula to find the slope of a line.

Plot the Points and Find the Slope
Plot the points on the graph based on the x- and y-coordinates provided. Then, find the slope of each line, so derived. Some problems contain x- and y-intercepts as well.

Find the Missing Coordinates
In this series of high school pdf worksheets, the slope and the co-ordinates are provided. Use the slope formula to find the missing coordinate.

Slope-Intercept Form
This set of printable worksheets features linear equations. Students are required to find the slopes by writing linear equations in slope-intercept form.
Related Worksheets
» Point-Slope Form
» Slope-Intercept Form
» Two-Point Form
» Equation of a Line
Become a Member
Membership Information
Privacy Policy
What's New?
Printing Help
Testimonial
Copyright © 2024 - Math Worksheets 4 Kids
This is a members-only feature!


- Parallelogram
- Quadrilateral
- Parallelepiped
- Tetrahedron
- Dodecahedron
- Fraction Calculator
- Mixed Fraction Calculator
- Greatest Common Factor Calulator
- Decimal to Fraction Calculator
- Whole Numbers
- Rational Numbers
- Place Value
- Irrational Numbers
- Natural Numbers
- Binary Operation
- Numerator and Denominator
- Order of Operations (PEMDAS)
- Scientific Notation
By Subjects
- Trigonometry
Slope Intercept Form Worksheets
The worksheets given here need students to have sound knowledge of the slope-intercept form of an equation as they got to work with the y-intercepts and slopes while solving the questions.

- Privacy Policy
Join Our Newsletter
© 2024 Mathmonks.com . All rights reserved. Reproduction in whole or in part without permission is prohibited.
Slope Formula Worksheets
Related Topics: More Math Worksheets More Printable Math Worksheets 7th Grade Math
There are six sets of coordinate geometry worksheets:
- Midpoint Formula
- Distance Formula
Slope Formula
- Standard Form & Slope-Intercept Form
- Parallel Lines
- Perpendicular Lines
Examples, solutions, videos, and worksheets to help grade 7 students learn how to use the slope formula to find the slope of a line passing through two points on the coordinate plane.
How to use the Slope Formula to find the slope of a line passing through two points?
The slope formula is used to calculate the slope of a line that passes through two points in a two-dimensional Cartesian coordinate system (x, y). The slope (m) represents the rate at which the line rises or falls as you move from left to right. The formula for calculating the slope between two points (x 1 , y 1 ) and (x 2 , y 2 ) is as follows:
m = (y 2 - y 1 ) / (x 2 - x 1 )
In this formula:
- (x 1 , y 1 ) are the coordinates of the first point on the line.
- (x 2 , y 2 ) are the coordinates of the second point on the line.
- m is the slope of the line that passes through these two points.
To calculate the slope between two points, you subtract the y-coordinates (vertical change) and divide it by the difference of the x-coordinates (horizontal change) between the two points.
Example: Use the slope formula to find the slope of the line passing through these two points A(3, 4) and B(6, 8). m = (8 - 4) / (6 - 3) m = 4 / 3
So, the slope of the line passing through points A and B is 4/3.
Click on the following worksheet to get a printable pdf document. Scroll down the page for more Slope Formula Worksheets .
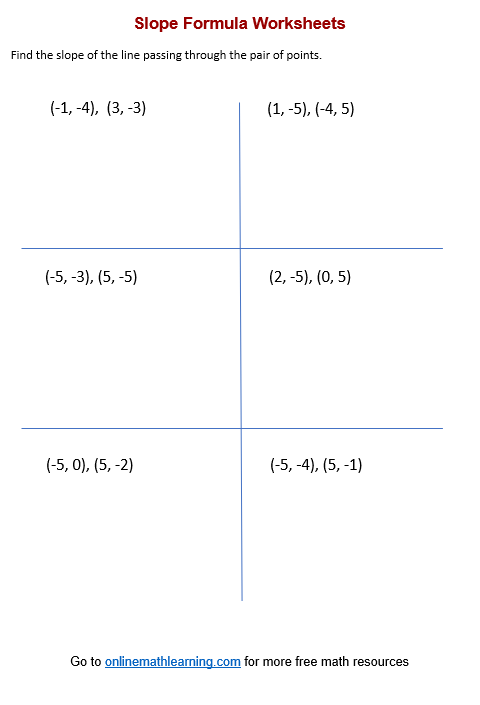

More Slope Formula Worksheets
Printable (Answers on the second page.) Slope Formula Worksheet #1
Online Quadrants of Coordinates Slope of a Line Slope and Intercept of a Line Midpoint Formula 1 Midpoint Formula 2 Distance Formula 1 Distance Formula 2
Related Lessons & Worksheets
More Printable Worksheets

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

Point Slope Worksheet and Answer Key
Students will practice working with the point slope form of a line by writing its equation from slope and 1 point, from 2 points, from the graph and more.

Example Questions
Find the equation of a line with the given slope and y-intercept .
Express your answer in point slope form.

Find the equation of the line that passes through the following two points. Express your answer in point slope form.

Write the equation of the line graphed below. Express your answer in point slope form.

Convert each point slope equation to slope intercept form .

Other Details
This is a 4 part worksheet:
- Part I Model Problems
- Part II Practice
- Part III Challenge Problems
- Part IV Answer Key
- Interactive Slope : explore the formula of slope by clicking and dragging two points.
- Pictures of Slope of a Line (formula, graphs etc..)
- Slope Intercept to Point Slope Form
- Standard Form to Point Slope Form
- Point Slope to Standard Form
- Point Slope to Slope Intercept Form
Ultimate Math Solver (Free) Free Algebra Solver ... type anything in there!
Popular pages @ mathwarehouse.com.

by Hall, Prentice
Chapter 5 - linear functions - 5-3 slope-intercept form - practice and problem-solving exercises - page 310: 7, work step by step, update this answer.
You can help us out by revising, improving and updating this answer.
After you claim an answer you’ll have 24 hours to send in a draft. An editor will review the submission and either publish your submission or provide feedback.

Slope calculate mcqs

IMAGES
VIDEO
COMMENTS
Lesson 6 Problem-Solving Practice Slope and Similar Triangles 1. The slope of a roof line is also called the pitch. Find the pitch of the roof shown. y O x B A 2. A carpenter is building a set of steps for a bunk bed. The plan for the steps is shown below. Using points A and B, find the slope of the line up the steps. Then
Free printable worksheet (pdf) and Answer Key on slope includes visual aides, model problems, exploratory activities, practice problems, and an online component
Draw a line through a point plotted on the graph based on the slope provided in this set of pdf worksheets which is suitable for 9th grade children. This set of fun activitiy worksheets contains houses with roofs of various sizes. Find the slope of the roof of each house. Answers must be in the form of positive slopes.
Practice Equations of Lines Write an equation in slope-intercept form of the line having the given slope and ... - 10 y = - −7 x 9 - −1 2 y = 4.5x + 0.25 Write equations in point-slope form of the line having the given slope that contains the given point. Then graph the line.
Example 1 Write the equation of the line with slope 2 that has y-intercept 5. y = mx + b Write the slope -intercept formula. y = 2x + 5 Substitute m = 2 and b = 5 The answer is y = 2x + 5. To find the equation of a line given the slope and one point on the line, plug in the slope and the coordinates of the point to solve for b, the y-intercept.
Slope-Intercept Form: We can describe slope in terms of "rise over run" or change in y over change in x. The y-intercept refers to where the line crosses the y-axis. In the case of a linear function with equation y=mx+b, b represents the y-intercept and will have coordinate points at (0,b). For example, the linear equation y=3x-2 has a ...
Determining Slope and y-Intercept Practice and Problem Solving: A/B Find the slope and y-intercept of the line in each graph. 1. 2. ... Practice and Problem Solving: C 1. a. $120 to rent the truck; $0.50 per mile b. $47.50; (45 miles × $0.50 per mile + $120) ÷ 3 = $47.50 2. The rate of change is $2.50 per ride.
Lesson 8 Homework Practice Slope For Exercises 1 and 2, graph the data. Then find the slope. Explain what the slope represents. 1. ENVELOPES The table shows the number of envelopes stuffed for various times. Time (min) 5 101520 Envelopes Stuffed 30 60 90 120 2. MEASUREMENT There are 3 feet for every yard. 3. Use the graph that shows the number ...
Rate of Change and Slope Practice and Problem Solving: D Tell whether the rates of change are constant or variable. The first one is done for you. 1. calories per serving _____ 2. distance jumped _____ Servings 1 2 5 7 Jumps 2 4 7 10 Calories 150 300 750 1,050 Distance (ft) 12 24 35 55 Find the slope of each line.
slope of 1 and a slope of 2 and a slope of −1 and a 3 y-intercept of -4. y-intercept of -3. y-intercept of 1. Graph each equation using the slope and the y-intercept. 13. y = 3x - 3 14. y = -x + 1 15. y = −1 2 x - 2 16. y = 4x - 2 17. y = - −3 2 x + 1 18. y = −2 x 3 - 3 Lesson 4 Skills Practice Slope-Intercept Form y Ox y x y O x y O xO ...
Slope Intercept Form Worksheets. The worksheets given here need students to have sound knowledge of the slope-intercept form of an equation as they got to work with the y-intercepts and slopes while solving the questions. Download PDF. Download PDF.
Free worksheet(pdf) and answer key on slope intercept form. 29 scaffolded questions that start relatively easy and end with some real challenges. Plus model problems explained step by step
To calculate the slope between two points, you subtract the y-coordinates (vertical change) and divide it by the difference of the x-coordinates (horizontal change) between the two points. Example: Use the slope formula to find the slope of the line passing through these two points A (3, 4) and B (6, 8). m = (8 - 4) / (6 - 3)
Practice and Problem Solving: A/B Find the slope of each line. 1. slope ! _____ 2. slope ! _____ Solve. 3. Jasmine bought 7 yards of fabric. The total cost was $45.43. What was ... Explain your answer. ...
Rate of Change and Slope Practice and Problem Solving: A/B Class 2. slope = Find the slope of each line. 1. slope = Solve. 3. Jasmine bought 7 yards of fabric. The total cost was $45.43. ... Explain your answer. Water in a Tank 01 23 Time (min) 7. A line passes through (l, 1), (—2, 4), and (6, n). Find the value of n.
Practice and Problem Solving: A/B Find the slope and y-intercept of the line in each graph. 1. 2. ... slope m = _____ slope m = _____ y-intercept b = _____ y-intercept b = _____ Find and interpret the rate of change and the initial value. 5. A pizzeria charges $8 for a large cheese pizza, plus $2 for each topping. The total cost for a large ...
Slope-intercept equation from graph. Find the equation of the line. Use exact numbers. Learn for free about math, art, computer programming, economics, physics, chemistry, biology, medicine, finance, history, and more. Khan Academy is a nonprofit with the mission of providing a free, world-class education for anyone, anywhere.
Example Questions. Find the equation of a line with the given slope and y-intercept. Express your answer in point slope form. Find the equation of the line that passes through the following two points. Express your answer in point slope form. Write the equation of the line graphed below. Express your answer in point slope form.
points and find the slope. Since that was impossible, the intercepts must have represented the same point. This can only happen if both intercepts are 0. The line passes through (0, 0). Practice and Problem Solving: Modified 1. rise = 1, run = 3, slope = 1 3 2. rise = 2, run = 1, slope = 2 3. rise = −3, run = 2, slope = 3 2 − 4. zero 5 ...
What is the slope of the line? Do 4 problems. Learn for free about math, art, computer programming, economics, physics, chemistry, biology, medicine, finance, history, and more. Khan Academy is a nonprofit with the mission of providing a free, world-class education for anyone, anywhere.
Algebra 1 answers to Chapter 5 - Linear Functions - 5-3 Slope-Intercept Form - Practice and Problem-Solving Exercises - Page 310 7 including work step by step written by community members like you. Textbook Authors: Hall, Prentice, ISBN-10: 0133500403, ISBN-13: 978--13350-040-0, Publisher: Prentice Hall
Slope Practice Problems (MCQs) Types of Slope Slope Worksheets Examples Practice Problem FAQs ... Slope Calculator will find slope of line using two points or equation of line. It also finds slope-intercept form, x-intercept, y-intercept, and other values along with slope.
4. Find the slope of CD. 5. Study with Quizlet and memorize flashcards containing terms like 2. Find the slope of AB, 3. Find the slope of BC, 4. Find the slope of CD and more.