practice and problem solving 1 3 compare and order real numbers

Have an account?

Suggestions for you See more

Ordering Rational Numbers

Place value and rounding, least common multiple, greatest common factor and least common ..., 6th -  8th  .

Lesson 1.3: Ordering Real Numbers

Mathematics.

15 questions

Introducing new   Paper mode

No student devices needed.   Know more

• 1. Multiple Choice Edit 3 minutes 1 pt Order 3π, √ 10 , and 3.25 from least to greatest. √ 10, 3π, 3.25 √ 10, 3.25, 3π 3π, 3.25, √ 10  3.25, √ 10, 3π
• 2. Multiple Choice Edit 5 minutes 1 pt List the following numbers from least to greatest: -64 , 3.5 , √27 , 6.666... -64 , 3.5 , √27 , 6.666... 3.5 , √27 , 6.666..., -64 3.5, -64, √27, 6.666... 6.666, √27, -64, 3.5

List the following numbers from least to greatest :

-64 , 3.5 , √27 , 6.666...

3.5 , √27 , 6.666..., -64

3.5, -64, √27, 6.666...

6.666, √27, -64, 3.5

Order 10.5, √105 , and 3π + 1 from greatest to least .

√ 105 , 3π + 1, 10.5

3π + 1,√ 105 , 10.5

√ 105 , 10.5, 3π + 1

10.5, √ 105 , 3π + 1

• 5. Multiple Choice Edit 1 minute 1 pt Put in the symbol to make the statement true... -17.5   _________ -√121 > < =

Between which if these does √27 lay on a number line?

• 8. Multiple Choice Edit 3 minutes 1 pt The √40 is between which two integers? 7 & 8 6 & 7 5 & 6 4 & 5

Which number is the smallest?

Which number is the greatest?

Order the following from least to greatest:

√16, -3, √23, 16/5, -4.5

-3, -4.5, 16/5, √16, √23

-4.5, -3, √16, 16/5, √23

-3, -4.5, √16, 16/5, √23

-4.5, -3, 16/5, √16, √23

Is the left side <, >, or = to the right side:

√2 + 4 ---------- 2 + √4

√12 + 6 ---------- √6 + 12

√17 - 3 ---------- -2 + √5

When ordering from least to greatest, which number comes third?

√7, 2, √8/2

Explore all questions with a free account

Continue with email

Continue with phone

Free Guide to Start Creating Teacher Resources

Comparing and Ordering Real Numbers

Before diving into comparing and ordering real numbers, we start with reviewing the square roots of perfect squares and estimating square roots. As you likely know, number sense is crucial for being successful in a math classroom. This unit sets the foundation for the REST of the year. As a result, I have learned to take it slow and to do formative assessments with every single skill (exit tickets are my BFF). After reading this post, you will have some lesson ideas along with teaching tips that will set your students up for success! Plus, there’s a freebie inside that you can use all year long!

Square Roots of Perfect Squares and Non-Perfect Squares

I love introducing this skill with color tiles. Start by giving students a bucket of color tiles. I like to provide them with 3 minutes to play with them before we start the activity. You can put them in partners if you are limited on color tiles!

After they finish playing, tell them to try to create a square with as few tiles as they can. This should be 1 tile. Then, ask them how many square tiles they need to make another square. This should be 4 tiles. Review how to find the area of a square.

Most will say A = l x w. Suggest they use s2 since we are working with squares. Then work your way up to at least 36 if you can. At this point, students will likely need to start sharing tiles.

Something new I added this year was an idea from my math coach and it is a KEEPER! We worked through this as we worked with the tiles.

Using a black pen, students could draw the radical to show the side length is the square root. This was actually kinda fun! In the future, I may have them make posters…somehow! After this, we took guided notes on perfect squares of square roots so students would have a resource to refer back to.

We ended by playing square roots bingo, this was our first time for the year and they’ve been asking to play more bingo!

Estimating Square Roots

So what about non-perfect squares? We started with slides 11-20 of this free Desmos activity: Square Dance Desmos activity . It’s basically like using color tiles digitally! I had students work through it at their own pace for about 15 minutes and then we took guided notes (of course)!

One thing I was sure to reinforce this year was using a number line. So we started with a clothesline activity to see if students could put the non-perfect squares in order. I gave each kid a card and then put them in groups of 7. Their task was to organize themselves in order!

An idea from my math coach that I will try next year: Project a hundreds chart and have students color in the perfect squares. And then ask, “What about all of the other numbers? Do they have square roots?” I was able to try this for struggling learners after the lesson and it was super helpful! They were able to quickly see where the non-perfect squares were.

I then had students complete a scavenger hunt with a partner around the room where they had to place non-perfect and perfect squares on a number line. The number line was great because they received immediate feedback, if it spelled a word they did it correctly!

Independently, they completed an estimating square roots drag and drop activity to reinforce the idea!

Even though my students can use Desmos calculators (thank goodness), I noticed that they really struggled to understand that 41.2% was a percent and not a decimal in standard notation. One downside of Desmos is they attempt to type the “41.2%” into the calculator and that does not work unless they type “41.2% of 1” , and they quite simply don’t remember to do that! In addition, I had students looking at a number like “3” and saying, “there’s no decimal point…so it isn’t a decimal.” At this point, I realized I needed to do two things:

• Change my language. instead of only saying decimal, I started saying “simplified into the standard format”. I also started doing a number of the day so they could visually see the different formats for writing rational numbers.
• Introduce them to invisible math! I had students turn to the invisible math page of their binder and pointed out that any number without a visible decimal point has an invisible one and a zero. Well, the next day, this same student came back and said, “Didn’t you say 0.3 is the same as 3 because of the invisible decimal point?” YIKES. Language change again…”Any number without a visible decimal point has an invisible one and a zero BEHIND IT!”

Another super tip? Use the same grid paper from square roots of perfect squares to help students them with comparing and ordering real numbers. Have them line up the decimal points.

Hey, I'm Asia!

Welcome to my Blog! I started The Sassy Math Teacher in 2020 to help teachers like you increase classroom engagement and teach with confidence! I also love to share about my life as a teacher including my favorite outfits, home items, gadgets and trips!

FREE DOWNLOAD

NEW PRODUCTS

Integer Activities and Games for 7th Graders

Adding and Subtracting Integers Task Cards – Enrichment – Critical Thinking – Color by Number – Integer Riddles

Comparing and Ordering Integers on a Number Line Integer Operations Task Cards

Mixed Operations with Integers Math Game Bingo Activity

3 responses.

Thank you so much for sharing this post! I am a resource teacher in a middle school, and I have used your guided notes and activities to teach and reinforce concepts, especially for my struggling 8th graders. This blog post is a really neat insight into how you use your resources in your classroom. I especially love all the different types of activities — hands-on, guided notes, and digital — as they allow students to experience the concepts in such different ways. Please keep blogging about what you are doing in your classroom, and please allow me to “steal” (purchase your resources, use ideas from your blog) ideas for my own classroom!

Hi Natasha! I am so very happy that you’ve found my blogs helpful! You are more than welcome to “steal” all of the ideas!!!

• Pingback: Teaching Real Numbers - The Sassy Math Teacher

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.

YOU MIGHT ALSO LIKE...

8th Grade Math Review with More than Just A Worksheet

Challenge Your Students to March Mathness in Math Class

Unpacking the New 2023 VDOE Math Standards

Math Lesson Ideas

Classroom Ideas

Make Your Own Resources

Teacher Life

Canvas for Teachers

TPT Store Audits

Copyright 2022 | Asia Hines | All Rights Reserved

• Math Lessons
• YouTube Videos
• TikTok Videos

Comparing and ordering real numbers

In order to compare numbers, you must be able to convert the numbers to a similar format. Sometimes, you will be given a list of numbers or organize that are in different formats such as decimals, whole numbers, fractions and radicals, or square roots. Converting each number into a decimal is the best way to compare them to each other. If you aren't familiar with converting numbers to decimals, see our previous videos on how to convert a fraction to a decimal and perfect square and cube roots.

Once your numbers are in decimal form, you will sort them by first looking at the whole numbers, the digits before the decimal place in each number, and sort them from smallest to the largest. If 2 numbers have the same whole number, then you will next compare the digits after the decimal to determine which is smaller and write them in order from smallest to largest.

Any numbers with a negative, or minus sign (⁻) , before it will be listed first. It may help to picture a number line with zero in the middle. The farther away you move from the zero into the negative range, the larger the number gets. So ⁻5 is smaller than ⁻2 and 2 is smaller than 5 .

Negative Integers                Positive Integers

Comparing and Ordering Real Numbers Printable Worksheet Practice Problems Solution Video Next Lesson in This Series: Rounding numbers

Personal Tutoring Option

If you need more personalized help with any of these topics, I offer a limited number of personal tutoring sessions each week and will be happy to work with you. The tutoring page includes details of how to register for a tutoring session.

Information on the Accuplacer Arithmetic Test for College Math Placement:

The first test in the math series, the Next Generation Arithmetic Test, includes questions from a variety of topics needed as a foundation for higher level college math courses. Some of the topics included on the Next Generation Arithmetic Test are order of operations, rounding, estimation, comparing values, ordering numbers in different formats, identifying equivalent values when presented in different formats, and basic number sense as well as computation skills with addition, subtraction, multiplication, and division with whole numbers, decimals and fractions. These skills are measured through the online Next Generation Accuplacer Arithmetic Test by presenting questions that are formatted as multiple choice. Questions will include both straight computational questions and questions where the mathematics skills will be presented in context through the use of word problems. The primary skills measured on this test include whole number operations, fraction operations, decimal operations, percent, number comparisons and equivalents. More information about the Accuplacer tests and College Board resources can be found at https://accuplacer.collegeboard.org/students .

Information on the Math Section of the GED:

© 2024 Grown Up Math [email protected]

Comparing and Ordering Numbers: Definition with Examples

What are comparing and ordering numbers, what is ordering numbers, comparing and ordering real numbers using a number line, solved examples on comparing and ordering, practice problems on comparing and ordering, frequently asked questions on comparing and ordering.

Have you ever compared your height and your friend’s height to decide who is taller? Or has the teacher ever asked your class to stand in increasing order of height? 

This type of situation can be answered by comparing and ordering numbers. “Comparing” in math is the process in which we observe similar properties of different persons or objects or things. Ordering a list of numbers means stating the numbers from the least to the greatest or from the greatest to the least. Before we learn how to compare and order numbers, let us first introduce the meaning of comparing numbers.

Comparing Numbers Meaning

Comparing in math refers to viewing something in relation to another. So, what is comparing numbers? Comparing numbers in math is defined as a process or method in which one can determine whether a number is smaller, greater, or equal to another number according to its values. 

The definition of comparison in math is all about identifying a quantity greater, smaller, or equal in relation with the given number.

Related Worksheets

Symbols for Comparing Numbers

The symbols used for comparing numbers are $\gt,\; \lt,$ or $=$.

• $“\gt”$ means “greater than”
• $“\lt”$ means “less than”
• $“=”$ means “equal to”

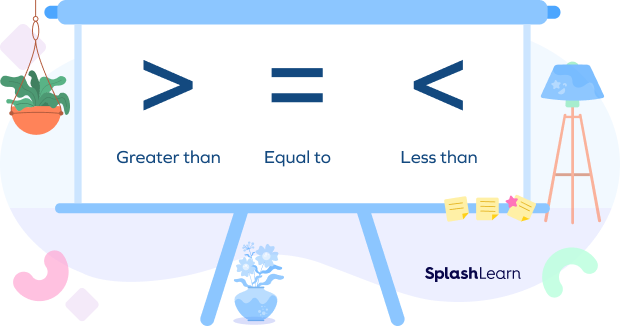
We also use the following symbols for comparing two quantities.

means “less than or equal to”

means “greater than or equal to”

Example: Let’s understand this visually using vertical bars composed of blocks. Each small block is of the same size. We can compare the numbers by comparing the heights of the bars.

On comparing two numbers, we can find out by how much a number is greater or smaller. 

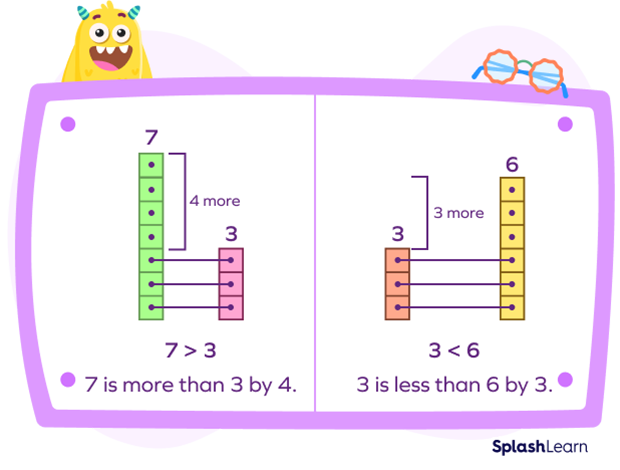
• In the first example, $7 \gt 3$ since the green bar is taller than the pink bar. We can also say that 7 is more or greater than 3 by $7 \;−\; 3 = 4$.
• In the second part, $3 \lt 6$ since the red bar is shorter than the yellow bar.  We can also say that 3 is less or smaller than 6 by $6 \;−\; 3 = 3$.

Steps for Comparing Numbers

Step 1: Compare the number of digits. The number with the more digits, is greater. Note that 0 placed at the beginning of a number is insignificant.

Example: $358 \lt 9104$

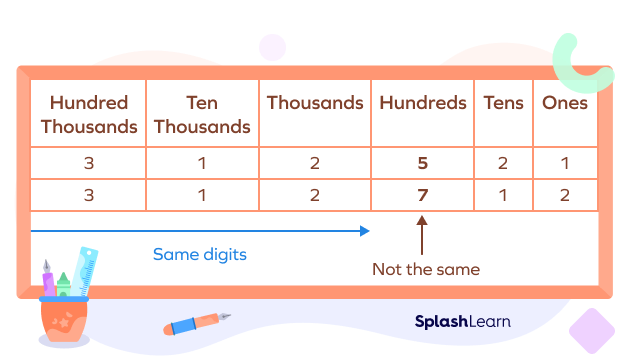
Step 2: If the number of digits are the same, we start by comparing the highest place values.

Example: In the following example, $312521 \lt 312712$ since $5 \lt 7$ at the hundreds place.

Ordering a list of numbers means arranging the numbers from least to greatest or greatest to least. In other words, we can say that ordering numbers means arranging numbers either in increasing order or decreasing order.

• Ascending order

Arrangement of numbers in increasing order, from the smallest to the greatest, is called ascending order.

For example $2 \lt 4 \lt 6 \lt 8 \lt 10$

• Descending order

Arrangement of numbers in decreasing order, from the greatest to smallest, is called descending order.

For example, $10 \gt 8 \gt 6 \gt 4 \gt 2$ 

On a number line, the numbers increase as we go from left to right. Thus, the number on the right is always greater than the number on the left. Thus, any two real numbers can be compared based on their position on the number line.

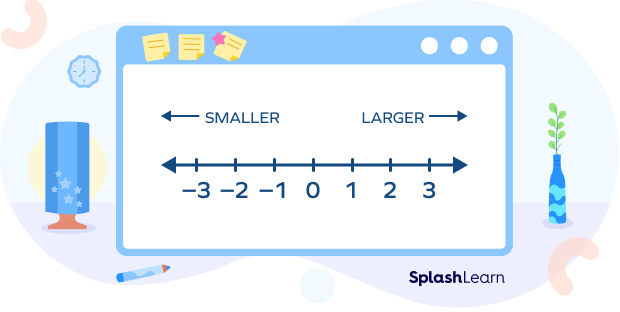
Example: Compare – 9 and 8 on the number line. 

-9 lies on the left side of 8.

Thus, -9 < 8.

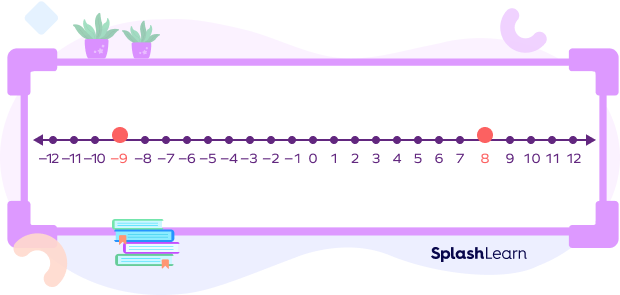
We can order the integers in increasing order as shown below

$…\; \lt -9 \lt -8 \lt -7 \lt -6 \lt …\lt -2 \lt -1 \lt 0 \lt 1 \lt 2 \lt 3 \lt 4 \lt …$

Similarly, $0.5 \lt 1.4$ since 0.5 lies on the left side of 1.4.

Comparing Rational Numbers

Comparing two or more rational numbers is similar to comparing fractions. We just need to keep in mind that:

• All negative rational numbers are smaller than 0.
• All positive rational numbers are greater than 0.
• All positive rational numbers are greater than all negative rational numbers.

As we know that rational numbers include whole numbers, integers, fractional, and decimal numbers in it, hence comparing two or more rational numbers can be categorized as

Comparing Whole Numbers

Comparing integers, comparing fractions, comparing decimals.

Let’s discuss steps for comparing numbers for each category one by one.

There are some steps through which we can compare two or more whole numbers:

Step 1: We should compare the number of digits. If there are more digits, it means the number is greater. For example $15 \gt 9,\; 125 \gt 32$, etc.

Step 2: If the number of digits is the same in both numbers, then we should compare the highest place values or the digit to the extreme left of the numbers. For example, $65 \gt 57,\; 243 \gt 127$, etc.

Step 3: If the digits at the highest place value are the same, we should compare the digits in the next digits to the right or the second highest place value. For example $76 \gt 72,\; 358 \gt 348$, etc.

Step 4: We keep comparing digits with the same place value until we find digits that are different. The number with the greater face value is the greater number. $109 \gt 102,\; 557 \gt 552$ etc.

• Comparing two positive integers is the same as comparing whole numbers except comparing with a negative integer.
• A positive integer is always greater or more than a negative integer. 

For example $5 \gt \;−\;5,\; 80 \gt \;−\; 80$, etc.

For comparing two negative numbers, we say that the greater number with a negative sign is the smallest of two negative integers.

For example $−\;80 \lt \;−\;75,\; −\;15 \lt \;−\;5$, etc.

• Negative integers are less than 0 and positive integers are greater than 0.

For example $−\;5 \lt 0, \;−\;12 \lt 0,\; 8 \gt 0$, etc.

When two or more fractions share the same denominator, the fractions are called “like fractions.” When two or more fractions have different denominators, they are called “unlike fractions.”

Comparing Like Fractions

To compare two or more like fractions, we just have to compare the numerators.

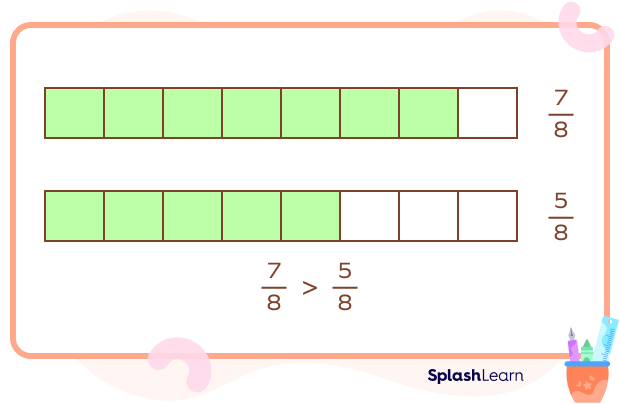
In the above figure, since $7 \gt 5$, hence $78\gt58$.

Comparing Unlike Fractions

To compare two or more unlike fractions, we can use different methods.

• Cross Multiplication Method

We multiply the numerator of the first fraction by the denominator of the second fraction and write the answer.

For example, we have to compare $\frac{5}{8}$ and $\frac{6}{11}$.

So, we multiply 5 and 11 together and 8 and 6 together, and we get

$5 \times 11 = 55$ and $6 \times 8 = 48$

After that, we can compare them like two whole numbers.

$55 \gt 48$

Finally, we replace the numbers with fractions. 

$\frac{5}{8} \gt \frac{6}{11}$

• Making the Denominators the Same 

In this method, we first find the LCM of both denominators. 

Let us take the above example, i.e., compare $\frac{5}{8}$ and $\frac{6}{11}$.

LCM $(8,\; 11) = 88$

To make the denominator the same, multiply the numerator and denominator by a relevant number. 

$\frac{5 \times 11}{8 \times 11} = \frac{55}{88}$ and $\frac{6\times8}{11\times8} = \frac{48}{88}$

After the denominators become the same, we compare the numerator. 

$55 > 48$

Finally, we replace the numbers with fractions.

$\frac{55}{88} \gt \frac{48}{88} \Rightarrow \frac{5}{8}\gt\frac{6}{11}$

We can compare two or more decimals by using the following steps:

Step 1: Firstly, compare the whole number part (i.e., compare the digits before the decimal). If they are different, you can compare the numbers as you would for any whole number. If they are the same, then follow the next step.

Step 2: Compare the tenth place. If they are different, then compare the numbers as you would for whole numbers. If they match, then move on to the next digit.

Step 3: Compare the hundredths place. If they are different, then compare those digits as you would for whole numbers. If they match, then move on to the next digit.

Example: Compare 23.56 and 23.289.

The numbers before the decimal are the same. So, we move to the next step, i.e., comparing the tenth place. Since $5 \gt 3,\; 23.56 \gt 23.289$.

In this article, we have discussed the meaning and symbols of comparing numbers, the method of comparing numbers, ordering, ascending and descending order as well as some important facts, and problems based on comparing and ordering numbers.

• Compare the numbers 425 and 412.

Given numbers 425 and 412.

Since the number of digits is the same in both numbers and the first digit is also the same, i.e., 4. But the digit at tens places 2 > 1.

Therefore, $425 \gt 412$

Hence, 425 is greater than 412.

• Which number is smaller out of $−612$ and $−625$ ?

Therefore, $−625 \lt −612$

Hence, $−625$ is smaller than $−612$.

• Compare $\frac{3}{5}$ and $\frac{5}{9}$ .

We have to compare $\frac{3}{5}$ and $\frac{5}{9}$.

Using the cross multiplication method,

$\frac{3}{5} = \frac{3 \times 9}{5 \times 9} = \frac{27}{45}$

$\frac{5}{9} = \frac{5 \times 5}{9 \times 5} = \frac{25}{45}$

Here, $27 \gt 25$

So, $\frac{27}{45} \gt \frac{25}{45}$

Finally, we replace the numbers with fractions $\frac{3}{5} \gt \frac{5}{9}$ .

• Compare the numbers 5, 0, 10, and $−15$ . Also, arrange them in ascending order.

Given a list of numbers $5, 0, 10,$ and $−15$.

Since a positive integer is always greater than a negative integer, $−15$ is smaller than all of the given numbers.

Also, negative integers are less than 0 and positive integers are greater than 0.

Hence, $−15 \lt 0 \lt 5 \lt 10$ (ascending order).

• Which is greater: 3.025 or 3.003?

Since the ones and tenth place of both the numbers are the same. So, we will see the hundredth place. Since $2 \gt 0$.

Hence, $3.025 \gt 3.003$.

Attend this quiz & Test your knowledge.

Which of the following is not a sign of comparing two numbers?

Which of the following is greater than $−5$, choose the correct sign for blank space: $\frac{13}{19}$ ——— $\frac{17}{19}$., ordering of a list of numbers in increasing order is called _________ order..

Why is comparing numbers important in our daily lives?

We compare numbers in our daily lives. For example, for comparing weights, for comparing the prices of everyday items, comparing the height of two or more people, etc.

How is comparing numbers different from ordering numbers?

Comparing numbers is a method of identifying greater, smaller, or equal numbers. Ordering numbers means arranging them in an ascending or descending order.

What is a quick way of comparing numbers?

The easiest way to compare numbers is by marking the numbers on a number line.

What are the different ways to compare numbers?

We can use different approaches to compare numbers, such as comparing numbers on a number line, by counting the number of digits, using place values of the numbers, etc.

RELATED POSTS

• Diagonals of Parallelogram: Formula, Examples
• Word form – Definition with Examples
• Convert Percent to Fraction –  Definition, Steps, Examples
• Percent Difference Formula: Examples, Facts, Practice Problems
• CPCTC: Definition, Postulates, Theorem, Proof, Examples

Math & ELA | PreK To Grade 5

Kids see fun., you see real learning outcomes..

Make study-time fun with 14,000+ games & activities, 450+ lesson plans, and more—free forever.

Parents, Try for Free Teachers, Use for Free

1.1 Real Numbers: Algebra Essentials

Learning objectives.

In this section, you will:

• Classify a real number as a natural, whole, integer, rational, or irrational number.
• Perform calculations using order of operations.
• Use the following properties of real numbers: commutative, associative, distributive, inverse, and identity.
• Evaluate algebraic expressions.
• Simplify algebraic expressions.

It is often said that mathematics is the language of science. If this is true, then an essential part of the language of mathematics is numbers. The earliest use of numbers occurred 100 centuries ago in the Middle East to count, or enumerate items. Farmers, cattle herders, and traders used tokens, stones, or markers to signify a single quantity—a sheaf of grain, a head of livestock, or a fixed length of cloth, for example. Doing so made commerce possible, leading to improved communications and the spread of civilization.

Three to four thousand years ago, Egyptians introduced fractions. They first used them to show reciprocals. Later, they used them to represent the amount when a quantity was divided into equal parts.

But what if there were no cattle to trade or an entire crop of grain was lost in a flood? How could someone indicate the existence of nothing? From earliest times, people had thought of a “base state” while counting and used various symbols to represent this null condition. However, it was not until about the fifth century CE in India that zero was added to the number system and used as a numeral in calculations.

Clearly, there was also a need for numbers to represent loss or debt. In India, in the seventh century CE, negative numbers were used as solutions to mathematical equations and commercial debts. The opposites of the counting numbers expanded the number system even further.

Because of the evolution of the number system, we can now perform complex calculations using these and other categories of real numbers. In this section, we will explore sets of numbers, calculations with different kinds of numbers, and the use of numbers in expressions.

Classifying a Real Number

The numbers we use for counting, or enumerating items, are the natural numbers : 1, 2, 3, 4, 5, and so on. We describe them in set notation as { 1 , 2 , 3 , ... } { 1 , 2 , 3 , ... } where the ellipsis (…) indicates that the numbers continue to infinity. The natural numbers are, of course, also called the counting numbers . Any time we enumerate the members of a team, count the coins in a collection, or tally the trees in a grove, we are using the set of natural numbers. The set of whole numbers is the set of natural numbers plus zero: { 0 , 1 , 2 , 3 , ... } . { 0 , 1 , 2 , 3 , ... } .

The set of integers adds the opposites of the natural numbers to the set of whole numbers: { ... , −3 , −2 , −1 , 0 , 1 , 2 , 3 , ... } . { ... , −3 , −2 , −1 , 0 , 1 , 2 , 3 , ... } . It is useful to note that the set of integers is made up of three distinct subsets: negative integers, zero, and positive integers. In this sense, the positive integers are just the natural numbers. Another way to think about it is that the natural numbers are a subset of the integers.

The set of rational numbers is written as { m n | m and  n are integers and  n ≠ 0 } . { m n | m and  n are integers and  n ≠ 0 } . Notice from the definition that rational numbers are fractions (or quotients) containing integers in both the numerator and the denominator, and the denominator is never 0. We can also see that every natural number, whole number, and integer is a rational number with a denominator of 1.

Because they are fractions, any rational number can also be expressed as a terminating or repeating decimal. Any rational number can be represented as either:

• ⓐ a terminating decimal: 15 8 = 1.875 , 15 8 = 1.875 , or
• ⓑ a repeating decimal: 4 11 = 0.36363636 … = 0. 36 ¯ 4 11 = 0.36363636 … = 0. 36 ¯

We use a line drawn over the repeating block of numbers instead of writing the group multiple times.

Writing Integers as Rational Numbers

Write each of the following as a rational number.

Write a fraction with the integer in the numerator and 1 in the denominator.

• ⓐ 7 = 7 1 7 = 7 1
• ⓑ 0 = 0 1 0 = 0 1
• ⓒ −8 = − 8 1 −8 = − 8 1

Identifying Rational Numbers

Write each of the following rational numbers as either a terminating or repeating decimal.

• ⓐ − 5 7 − 5 7
• ⓑ 15 5 15 5
• ⓒ 13 25 13 25

Write each fraction as a decimal by dividing the numerator by the denominator.

• ⓐ − 5 7 = −0. 714285 ——— , − 5 7 = −0. 714285 ——— , a repeating decimal
• ⓑ 15 5 = 3 15 5 = 3 (or 3.0), a terminating decimal
• ⓒ 13 25 = 0.52 , 13 25 = 0.52 , a terminating decimal
• ⓐ 68 17 68 17
• ⓑ 8 13 8 13
• ⓒ − 17 20 − 17 20

Irrational Numbers

At some point in the ancient past, someone discovered that not all numbers are rational numbers. A builder, for instance, may have found that the diagonal of a square with unit sides was not 2 or even 3 2 , 3 2 , but was something else. Or a garment maker might have observed that the ratio of the circumference to the diameter of a roll of cloth was a little bit more than 3, but still not a rational number. Such numbers are said to be irrational because they cannot be written as fractions. These numbers make up the set of irrational numbers . Irrational numbers cannot be expressed as a fraction of two integers. It is impossible to describe this set of numbers by a single rule except to say that a number is irrational if it is not rational. So we write this as shown.

Differentiating Rational and Irrational Numbers

Determine whether each of the following numbers is rational or irrational. If it is rational, determine whether it is a terminating or repeating decimal.

• ⓑ 33 9 33 9
• ⓓ 17 34 17 34
• ⓔ 0.3033033303333 … 0.3033033303333 …
• ⓐ 25 : 25 : This can be simplified as 25 = 5. 25 = 5. Therefore, 25 25 is rational.

So, 33 9 33 9 is rational and a repeating decimal.

• ⓒ 11 : 11 11 : 11 is irrational because 11 is not a perfect square and 11 11 cannot be expressed as a fraction.

So, 17 34 17 34 is rational and a terminating decimal.

• ⓔ 0.3033033303333 … 0.3033033303333 … is not a terminating decimal. Also note that there is no repeating pattern because the group of 3s increases each time. Therefore it is neither a terminating nor a repeating decimal and, hence, not a rational number. It is an irrational number.
• ⓐ 7 77 7 77
• ⓒ 4.27027002700027 … 4.27027002700027 …
• ⓓ 91 13 91 13

Real Numbers

Given any number n , we know that n is either rational or irrational. It cannot be both. The sets of rational and irrational numbers together make up the set of real numbers . As we saw with integers, the real numbers can be divided into three subsets: negative real numbers, zero, and positive real numbers. Each subset includes fractions, decimals, and irrational numbers according to their algebraic sign (+ or –). Zero is considered neither positive nor negative.

The real numbers can be visualized on a horizontal number line with an arbitrary point chosen as 0, with negative numbers to the left of 0 and positive numbers to the right of 0. A fixed unit distance is then used to mark off each integer (or other basic value) on either side of 0. Any real number corresponds to a unique position on the number line.The converse is also true: Each location on the number line corresponds to exactly one real number. This is known as a one-to-one correspondence. We refer to this as the real number line as shown in Figure 1 .

Classifying Real Numbers

Classify each number as either positive or negative and as either rational or irrational. Does the number lie to the left or the right of 0 on the number line?

• ⓐ − 10 3 − 10 3
• ⓒ − 289 − 289
• ⓓ −6 π −6 π
• ⓔ 0.615384615384 … 0.615384615384 …
• ⓐ − 10 3 − 10 3 is negative and rational. It lies to the left of 0 on the number line.
• ⓑ 5 5 is positive and irrational. It lies to the right of 0.
• ⓒ − 289 = − 17 2 = −17 − 289 = − 17 2 = −17 is negative and rational. It lies to the left of 0.
• ⓓ −6 π −6 π is negative and irrational. It lies to the left of 0.
• ⓔ 0.615384615384 … 0.615384615384 … is a repeating decimal so it is rational and positive. It lies to the right of 0.
• ⓑ −11.411411411 … −11.411411411 …
• ⓒ 47 19 47 19
• ⓓ − 5 2 − 5 2
• ⓔ 6.210735 6.210735

Sets of Numbers as Subsets

Beginning with the natural numbers, we have expanded each set to form a larger set, meaning that there is a subset relationship between the sets of numbers we have encountered so far. These relationships become more obvious when seen as a diagram, such as Figure 2 .

Sets of Numbers

The set of natural numbers includes the numbers used for counting: { 1 , 2 , 3 , ... } . { 1 , 2 , 3 , ... } .

The set of whole numbers is the set of natural numbers plus zero: { 0 , 1 , 2 , 3 , ... } . { 0 , 1 , 2 , 3 , ... } .

The set of integers adds the negative natural numbers to the set of whole numbers: { ... , −3 , −2 , −1 , 0 , 1 , 2 , 3 , ... } . { ... , −3 , −2 , −1 , 0 , 1 , 2 , 3 , ... } .

The set of rational numbers includes fractions written as { m n | m and  n are integers and  n ≠ 0 } . { m n | m and  n are integers and  n ≠ 0 } .

The set of irrational numbers is the set of numbers that are not rational, are nonrepeating, and are nonterminating: { h | h is not a rational number } . { h | h is not a rational number } .

Differentiating the Sets of Numbers

Classify each number as being a natural number ( N ), whole number ( W ), integer ( I ), rational number ( Q ), and/or irrational number ( Q′ ).

• ⓔ 3.2121121112 … 3.2121121112 …
• ⓐ − 35 7 − 35 7
• ⓔ 4.763763763 … 4.763763763 …

Performing Calculations Using the Order of Operations

When we multiply a number by itself, we square it or raise it to a power of 2. For example, 4 2 = 4 ⋅ 4 = 16. 4 2 = 4 ⋅ 4 = 16. We can raise any number to any power. In general, the exponential notation a n a n means that the number or variable a a is used as a factor n n times.

In this notation, a n a n is read as the n th power of a , a , or a a to the n n where a a is called the base and n n is called the exponent . A term in exponential notation may be part of a mathematical expression, which is a combination of numbers and operations. For example, 24 + 6 ⋅ 2 3 − 4 2 24 + 6 ⋅ 2 3 − 4 2 is a mathematical expression.

To evaluate a mathematical expression, we perform the various operations. However, we do not perform them in any random order. We use the order of operations . This is a sequence of rules for evaluating such expressions.

Recall that in mathematics we use parentheses ( ), brackets [ ], and braces { } to group numbers and expressions so that anything appearing within the symbols is treated as a unit. Additionally, fraction bars, radicals, and absolute value bars are treated as grouping symbols. When evaluating a mathematical expression, begin by simplifying expressions within grouping symbols.

The next step is to address any exponents or radicals. Afterward, perform multiplication and division from left to right and finally addition and subtraction from left to right.

Let’s take a look at the expression provided.

There are no grouping symbols, so we move on to exponents or radicals. The number 4 is raised to a power of 2, so simplify 4 2 4 2 as 16.

Next, perform multiplication or division, left to right.

Lastly, perform addition or subtraction, left to right.

Therefore, 24 + 6 ⋅ 2 3 − 4 2 = 12. 24 + 6 ⋅ 2 3 − 4 2 = 12.

For some complicated expressions, several passes through the order of operations will be needed. For instance, there may be a radical expression inside parentheses that must be simplified before the parentheses are evaluated. Following the order of operations ensures that anyone simplifying the same mathematical expression will get the same result.

Order of Operations

Operations in mathematical expressions must be evaluated in a systematic order, which can be simplified using the acronym PEMDAS :

P (arentheses) E (xponents) M (ultiplication) and D (ivision) A (ddition) and S (ubtraction)

Given a mathematical expression, simplify it using the order of operations.

• Step 1. Simplify any expressions within grouping symbols.
• Step 2. Simplify any expressions containing exponents or radicals.
• Step 3. Perform any multiplication and division in order, from left to right.
• Step 4. Perform any addition and subtraction in order, from left to right.

Using the Order of Operations

Use the order of operations to evaluate each of the following expressions.

• ⓐ ( 3 ⋅ 2 ) 2 − 4 ( 6 + 2 ) ( 3 ⋅ 2 ) 2 − 4 ( 6 + 2 )
• ⓑ 5 2 − 4 7 − 11 − 2 5 2 − 4 7 − 11 − 2
• ⓒ 6 − | 5 − 8 | + 3 ( 4 − 1 ) 6 − | 5 − 8 | + 3 ( 4 − 1 )
• ⓓ 14 − 3 ⋅ 2 2 ⋅ 5 − 3 2 14 − 3 ⋅ 2 2 ⋅ 5 − 3 2
• ⓔ 7 ( 5 ⋅ 3 ) − 2 [ ( 6 − 3 ) − 4 2 ] + 1 7 ( 5 ⋅ 3 ) − 2 [ ( 6 − 3 ) − 4 2 ] + 1
• ⓐ ( 3 ⋅ 2 ) 2 − 4 ( 6 + 2 ) = ( 6 ) 2 − 4 ( 8 ) Simplify parentheses. = 36 − 4 ( 8 ) Simplify exponent. = 36 − 32 Simplify multiplication. = 4 Simplify subtraction. ( 3 ⋅ 2 ) 2 − 4 ( 6 + 2 ) = ( 6 ) 2 − 4 ( 8 ) Simplify parentheses. = 36 − 4 ( 8 ) Simplify exponent. = 36 − 32 Simplify multiplication. = 4 Simplify subtraction.

Note that in the first step, the radical is treated as a grouping symbol, like parentheses. Also, in the third step, the fraction bar is considered a grouping symbol so the numerator is considered to be grouped.

• ⓒ 6 − | 5 − 8 | + 3 | 4 − 1 | = 6 − | −3 | + 3 ( 3 ) Simplify inside grouping symbols. = 6 - ( 3 ) + 3 ( 3 ) Simplify absolute value. = 6 - 3 + 9 Simplify multiplication. = 12 Simplify addition. 6 − | 5 − 8 | + 3 | 4 − 1 | = 6 − | −3 | + 3 ( 3 ) Simplify inside grouping symbols. = 6 - ( 3 ) + 3 ( 3 ) Simplify absolute value. = 6 - 3 + 9 Simplify multiplication. = 12 Simplify addition.

In this example, the fraction bar separates the numerator and denominator, which we simplify separately until the last step.

• ⓔ 7 ( 5 ⋅ 3 ) − 2 [ ( 6 − 3 ) − 4 2 ] + 1 = 7 ( 15 ) − 2 [ ( 3 ) − 4 2 ] + 1 Simplify inside parentheses. = 7 ( 15 ) − 2 ( 3 − 16 ) + 1 Simplify exponent. = 7 ( 15 ) − 2 ( −13 ) + 1 Subtract. = 105 + 26 + 1 Multiply. = 132 Add. 7 ( 5 ⋅ 3 ) − 2 [ ( 6 − 3 ) − 4 2 ] + 1 = 7 ( 15 ) − 2 [ ( 3 ) − 4 2 ] + 1 Simplify inside parentheses. = 7 ( 15 ) − 2 ( 3 − 16 ) + 1 Simplify exponent. = 7 ( 15 ) − 2 ( −13 ) + 1 Subtract. = 105 + 26 + 1 Multiply. = 132 Add.
• ⓐ 5 2 − 4 2 + 7 ( 5 − 4 ) 2 5 2 − 4 2 + 7 ( 5 − 4 ) 2
• ⓑ 1 + 7 ⋅ 5 − 8 ⋅ 4 9 − 6 1 + 7 ⋅ 5 − 8 ⋅ 4 9 − 6
• ⓒ | 1.8 − 4.3 | + 0.4 15 + 10 | 1.8 − 4.3 | + 0.4 15 + 10
• ⓓ 1 2 [ 5 ⋅ 3 2 − 7 2 ] + 1 3 ⋅ 9 2 1 2 [ 5 ⋅ 3 2 − 7 2 ] + 1 3 ⋅ 9 2
• ⓔ [ ( 3 − 8 ) 2 − 4 ] − ( 3 − 8 ) [ ( 3 − 8 ) 2 − 4 ] − ( 3 − 8 )

Using Properties of Real Numbers

For some activities we perform, the order of certain operations does not matter, but the order of other operations does. For example, it does not make a difference if we put on the right shoe before the left or vice-versa. However, it does matter whether we put on shoes or socks first. The same thing is true for operations in mathematics.

Commutative Properties

The commutative property of addition states that numbers may be added in any order without affecting the sum.

We can better see this relationship when using real numbers.

Similarly, the commutative property of multiplication states that numbers may be multiplied in any order without affecting the product.

Again, consider an example with real numbers.

It is important to note that neither subtraction nor division is commutative. For example, 17 − 5 17 − 5 is not the same as 5 − 17. 5 − 17. Similarly, 20 ÷ 5 ≠ 5 ÷ 20. 20 ÷ 5 ≠ 5 ÷ 20.

Associative Properties

The associative property of multiplication tells us that it does not matter how we group numbers when multiplying. We can move the grouping symbols to make the calculation easier, and the product remains the same.

Consider this example.

The associative property of addition tells us that numbers may be grouped differently without affecting the sum.

This property can be especially helpful when dealing with negative integers. Consider this example.

Are subtraction and division associative? Review these examples.

As we can see, neither subtraction nor division is associative.

Distributive Property

The distributive property states that the product of a factor times a sum is the sum of the factor times each term in the sum.

This property combines both addition and multiplication (and is the only property to do so). Let us consider an example.

Note that 4 is outside the grouping symbols, so we distribute the 4 by multiplying it by 12, multiplying it by –7, and adding the products.

To be more precise when describing this property, we say that multiplication distributes over addition. The reverse is not true, as we can see in this example.

A special case of the distributive property occurs when a sum of terms is subtracted.

For example, consider the difference 12 − ( 5 + 3 ) . 12 − ( 5 + 3 ) . We can rewrite the difference of the two terms 12 and ( 5 + 3 ) ( 5 + 3 ) by turning the subtraction expression into addition of the opposite. So instead of subtracting ( 5 + 3 ) , ( 5 + 3 ) , we add the opposite.

Now, distribute −1 −1 and simplify the result.

This seems like a lot of trouble for a simple sum, but it illustrates a powerful result that will be useful once we introduce algebraic terms. To subtract a sum of terms, change the sign of each term and add the results. With this in mind, we can rewrite the last example.

Identity Properties

The identity property of addition states that there is a unique number, called the additive identity (0) that, when added to a number, results in the original number.

The identity property of multiplication states that there is a unique number, called the multiplicative identity (1) that, when multiplied by a number, results in the original number.

For example, we have ( −6 ) + 0 = −6 ( −6 ) + 0 = −6 and 23 ⋅ 1 = 23. 23 ⋅ 1 = 23. There are no exceptions for these properties; they work for every real number, including 0 and 1.

Inverse Properties

The inverse property of addition states that, for every real number a , there is a unique number, called the additive inverse (or opposite), denoted by (− a ), that, when added to the original number, results in the additive identity, 0.

For example, if a = −8 , a = −8 , the additive inverse is 8, since ( −8 ) + 8 = 0. ( −8 ) + 8 = 0.

The inverse property of multiplication holds for all real numbers except 0 because the reciprocal of 0 is not defined. The property states that, for every real number a , there is a unique number, called the multiplicative inverse (or reciprocal), denoted 1 a , 1 a , that, when multiplied by the original number, results in the multiplicative identity, 1.

For example, if a = − 2 3 , a = − 2 3 , the reciprocal, denoted 1 a , 1 a , is − 3 2 − 3 2 because

Properties of Real Numbers

The following properties hold for real numbers a , b , and c .

Use the properties of real numbers to rewrite and simplify each expression. State which properties apply.

• ⓐ 3 ⋅ 6 + 3 ⋅ 4 3 ⋅ 6 + 3 ⋅ 4
• ⓑ ( 5 + 8 ) + ( −8 ) ( 5 + 8 ) + ( −8 )
• ⓒ 6 − ( 15 + 9 ) 6 − ( 15 + 9 )
• ⓓ 4 7 ⋅ ( 2 3 ⋅ 7 4 ) 4 7 ⋅ ( 2 3 ⋅ 7 4 )
• ⓔ 100 ⋅ [ 0.75 + ( −2.38 ) ] 100 ⋅ [ 0.75 + ( −2.38 ) ]
• ⓐ 3 ⋅ 6 + 3 ⋅ 4 = 3 ⋅ ( 6 + 4 ) Distributive property. = 3 ⋅ 10 Simplify. = 30 Simplify. 3 ⋅ 6 + 3 ⋅ 4 = 3 ⋅ ( 6 + 4 ) Distributive property. = 3 ⋅ 10 Simplify. = 30 Simplify.
• ⓑ ( 5 + 8 ) + ( −8 ) = 5 + [ 8 + ( −8 ) ] Associative property of addition. = 5 + 0 Inverse property of addition. = 5 Identity property of addition. ( 5 + 8 ) + ( −8 ) = 5 + [ 8 + ( −8 ) ] Associative property of addition. = 5 + 0 Inverse property of addition. = 5 Identity property of addition.
• ⓒ 6 − ( 15 + 9 ) = 6 + [ ( −15 ) + ( −9 ) ] Distributive property. = 6 + ( −24 ) Simplify. = −18 Simplify. 6 − ( 15 + 9 ) = 6 + [ ( −15 ) + ( −9 ) ] Distributive property. = 6 + ( −24 ) Simplify. = −18 Simplify.
• ⓓ 4 7 ⋅ ( 2 3 ⋅ 7 4 ) = 4 7 ⋅ ( 7 4 ⋅ 2 3 ) Commutative property of multiplication. = ( 4 7 ⋅ 7 4 ) ⋅ 2 3 Associative property of multiplication. = 1 ⋅ 2 3 Inverse property of multiplication. = 2 3 Identity property of multiplication. 4 7 ⋅ ( 2 3 ⋅ 7 4 ) = 4 7 ⋅ ( 7 4 ⋅ 2 3 ) Commutative property of multiplication. = ( 4 7 ⋅ 7 4 ) ⋅ 2 3 Associative property of multiplication. = 1 ⋅ 2 3 Inverse property of multiplication. = 2 3 Identity property of multiplication.
• ⓔ 100 ⋅ [ 0.75 + ( − 2.38 ) ] = 100 ⋅ 0.75 + 100 ⋅ ( −2.38 ) Distributive property. = 75 + ( −238 ) Simplify. = −163 Simplify. 100 ⋅ [ 0.75 + ( − 2.38 ) ] = 100 ⋅ 0.75 + 100 ⋅ ( −2.38 ) Distributive property. = 75 + ( −238 ) Simplify. = −163 Simplify.
• ⓐ ( − 23 5 ) ⋅ [ 11 ⋅ ( − 5 23 ) ] ( − 23 5 ) ⋅ [ 11 ⋅ ( − 5 23 ) ]
• ⓑ 5 ⋅ ( 6.2 + 0.4 ) 5 ⋅ ( 6.2 + 0.4 )
• ⓒ 18 − ( 7 −15 ) 18 − ( 7 −15 )
• ⓓ 17 18 + [ 4 9 + ( − 17 18 ) ] 17 18 + [ 4 9 + ( − 17 18 ) ]
• ⓔ 6 ⋅ ( −3 ) + 6 ⋅ 3 6 ⋅ ( −3 ) + 6 ⋅ 3

Evaluating Algebraic Expressions

So far, the mathematical expressions we have seen have involved real numbers only. In mathematics, we may see expressions such as x + 5 , 4 3 π r 3 , x + 5 , 4 3 π r 3 , or 2 m 3 n 2 . 2 m 3 n 2 . In the expression x + 5 , x + 5 , 5 is called a constant because it does not vary and x is called a variable because it does. (In naming the variable, ignore any exponents or radicals containing the variable.) An algebraic expression is a collection of constants and variables joined together by the algebraic operations of addition, subtraction, multiplication, and division.

We have already seen some real number examples of exponential notation, a shorthand method of writing products of the same factor. When variables are used, the constants and variables are treated the same way.

In each case, the exponent tells us how many factors of the base to use, whether the base consists of constants or variables.

Any variable in an algebraic expression may take on or be assigned different values. When that happens, the value of the algebraic expression changes. To evaluate an algebraic expression means to determine the value of the expression for a given value of each variable in the expression. Replace each variable in the expression with the given value, then simplify the resulting expression using the order of operations. If the algebraic expression contains more than one variable, replace each variable with its assigned value and simplify the expression as before.

Describing Algebraic Expressions

List the constants and variables for each algebraic expression.

• ⓑ 4 3 π r 3 4 3 π r 3
• ⓒ 2 m 3 n 2 2 m 3 n 2
• ⓐ 2 π r ( r + h ) 2 π r ( r + h )
• ⓑ 2( L + W )
• ⓒ 4 y 3 + y 4 y 3 + y

Evaluating an Algebraic Expression at Different Values

Evaluate the expression 2 x − 7 2 x − 7 for each value for x.

• ⓐ x = 0 x = 0
• ⓑ x = 1 x = 1
• ⓒ x = 1 2 x = 1 2
• ⓓ x = −4 x = −4
• ⓐ Substitute 0 for x . x . 2 x − 7 = 2 ( 0 ) − 7 = 0 − 7 = −7 2 x − 7 = 2 ( 0 ) − 7 = 0 − 7 = −7
• ⓑ Substitute 1 for x . x . 2 x − 7 = 2 ( 1 ) − 7 = 2 − 7 = −5 2 x − 7 = 2 ( 1 ) − 7 = 2 − 7 = −5
• ⓒ Substitute 1 2 1 2 for x . x . 2 x − 7 = 2 ( 1 2 ) − 7 = 1 − 7 = −6 2 x − 7 = 2 ( 1 2 ) − 7 = 1 − 7 = −6
• ⓓ Substitute −4 −4 for x . x . 2 x − 7 = 2 ( − 4 ) − 7 = − 8 − 7 = −15 2 x − 7 = 2 ( − 4 ) − 7 = − 8 − 7 = −15

Evaluate the expression 11 − 3 y 11 − 3 y for each value for y.

• ⓐ y = 2 y = 2
• ⓑ y = 0 y = 0
• ⓒ y = 2 3 y = 2 3
• ⓓ y = −5 y = −5

Evaluate each expression for the given values.

• ⓐ x + 5 x + 5 for x = −5 x = −5
• ⓑ t 2 t −1 t 2 t −1 for t = 10 t = 10
• ⓒ 4 3 π r 3 4 3 π r 3 for r = 5 r = 5
• ⓓ a + a b + b a + a b + b for a = 11 , b = −8 a = 11 , b = −8
• ⓔ 2 m 3 n 2 2 m 3 n 2 for m = 2 , n = 3 m = 2 , n = 3
• ⓐ Substitute −5 −5 for x . x . x + 5 = ( −5 ) + 5 = 0 x + 5 = ( −5 ) + 5 = 0
• ⓑ Substitute 10 for t . t . t 2 t − 1 = ( 10 ) 2 ( 10 ) − 1 = 10 20 − 1 = 10 19 t 2 t − 1 = ( 10 ) 2 ( 10 ) − 1 = 10 20 − 1 = 10 19
• ⓒ Substitute 5 for r . r . 4 3 π r 3 = 4 3 π ( 5 ) 3 = 4 3 π ( 125 ) = 500 3 π 4 3 π r 3 = 4 3 π ( 5 ) 3 = 4 3 π ( 125 ) = 500 3 π
• ⓓ Substitute 11 for a a and –8 for b . b . a + a b + b = ( 11 ) + ( 11 ) ( −8 ) + ( −8 ) = 11 − 88 − 8 = −85 a + a b + b = ( 11 ) + ( 11 ) ( −8 ) + ( −8 ) = 11 − 88 − 8 = −85
• ⓔ Substitute 2 for m m and 3 for n . n . 2 m 3 n 2 = 2 ( 2 ) 3 ( 3 ) 2 = 2 ( 8 ) ( 9 ) = 144 = 12 2 m 3 n 2 = 2 ( 2 ) 3 ( 3 ) 2 = 2 ( 8 ) ( 9 ) = 144 = 12
• ⓐ y + 3 y − 3 y + 3 y − 3 for y = 5 y = 5
• ⓑ 7 − 2 t 7 − 2 t for t = −2 t = −2
• ⓒ 1 3 π r 2 1 3 π r 2 for r = 11 r = 11
• ⓓ ( p 2 q ) 3 ( p 2 q ) 3 for p = −2 , q = 3 p = −2 , q = 3
• ⓔ 4 ( m − n ) − 5 ( n − m ) 4 ( m − n ) − 5 ( n − m ) for m = 2 3 , n = 1 3 m = 2 3 , n = 1 3

An equation is a mathematical statement indicating that two expressions are equal. The expressions can be numerical or algebraic. The equation is not inherently true or false, but only a proposition. The values that make the equation true, the solutions, are found using the properties of real numbers and other results. For example, the equation 2 x + 1 = 7 2 x + 1 = 7 has the solution of 3 because when we substitute 3 for x x in the equation, we obtain the true statement 2 ( 3 ) + 1 = 7. 2 ( 3 ) + 1 = 7.

A formula is an equation expressing a relationship between constant and variable quantities. Very often, the equation is a means of finding the value of one quantity (often a single variable) in terms of another or other quantities. One of the most common examples is the formula for finding the area A A of a circle in terms of the radius r r of the circle: A = π r 2 . A = π r 2 . For any value of r , r , the area A A can be found by evaluating the expression π r 2 . π r 2 .

Using a Formula

A right circular cylinder with radius r r and height h h has the surface area S S (in square units) given by the formula S = 2 π r ( r + h ) . S = 2 π r ( r + h ) . See Figure 3 . Find the surface area of a cylinder with radius 6 in. and height 9 in. Leave the answer in terms of π . π .

Evaluate the expression 2 π r ( r + h ) 2 π r ( r + h ) for r = 6 r = 6 and h = 9. h = 9.

The surface area is 180 π 180 π square inches.

A photograph with length L and width W is placed in a mat of width 8 centimeters (cm). The area of the mat (in square centimeters, or cm 2 ) is found to be A = ( L + 16 ) ( W + 16 ) − L ⋅ W . A = ( L + 16 ) ( W + 16 ) − L ⋅ W . See Figure 4 . Find the area of a mat for a photograph with length 32 cm and width 24 cm.

Simplifying Algebraic Expressions

Sometimes we can simplify an algebraic expression to make it easier to evaluate or to use in some other way. To do so, we use the properties of real numbers. We can use the same properties in formulas because they contain algebraic expressions.

Simplify each algebraic expression.

• ⓐ 3 x − 2 y + x − 3 y − 7 3 x − 2 y + x − 3 y − 7
• ⓑ 2 r − 5 ( 3 − r ) + 4 2 r − 5 ( 3 − r ) + 4
• ⓒ ( 4 t − 5 4 s ) − ( 2 3 t + 2 s ) ( 4 t − 5 4 s ) − ( 2 3 t + 2 s )
• ⓓ 2 m n − 5 m + 3 m n + n 2 m n − 5 m + 3 m n + n
• ⓐ 3 x − 2 y + x − 3 y − 7 = 3 x + x − 2 y − 3 y − 7 Commutative property of addition. = 4 x − 5 y − 7 Simplify. 3 x − 2 y + x − 3 y − 7 = 3 x + x − 2 y − 3 y − 7 Commutative property of addition. = 4 x − 5 y − 7 Simplify.
• ⓑ 2 r − 5 ( 3 − r ) + 4 = 2 r − 15 + 5 r + 4 Distributive property. = 2 r + 5 r − 15 + 4 Commutative property of addition. = 7 r − 11 Simplify. 2 r − 5 ( 3 − r ) + 4 = 2 r − 15 + 5 r + 4 Distributive property. = 2 r + 5 r − 15 + 4 Commutative property of addition. = 7 r − 11 Simplify.
• ⓒ ( 4 t − 5 4 s ) − ( 2 3 t + 2 s ) = 4 t − 5 4 s − 2 3 t − 2 s Distributive property. = 4 t − 2 3 t − 5 4 s − 2 s Commutative property of addition. = 10 3 t − 13 4 s Simplify. ( 4 t − 5 4 s ) − ( 2 3 t + 2 s ) = 4 t − 5 4 s − 2 3 t − 2 s Distributive property. = 4 t − 2 3 t − 5 4 s − 2 s Commutative property of addition. = 10 3 t − 13 4 s Simplify.
• ⓓ 2 m n − 5 m + 3 m n + n = 2 m n + 3 m n − 5 m + n Commutative property of addition. = 5 m n − 5 m + n Simplify. 2 m n − 5 m + 3 m n + n = 2 m n + 3 m n − 5 m + n Commutative property of addition. = 5 m n − 5 m + n Simplify.
• ⓐ 2 3 y − 2 ( 4 3 y + z ) 2 3 y − 2 ( 4 3 y + z )
• ⓑ 5 t − 2 − 3 t + 1 5 t − 2 − 3 t + 1
• ⓒ 4 p ( q − 1 ) + q ( 1 − p ) 4 p ( q − 1 ) + q ( 1 − p )
• ⓓ 9 r − ( s + 2 r ) + ( 6 − s ) 9 r − ( s + 2 r ) + ( 6 − s )

Simplifying a Formula

A rectangle with length L L and width W W has a perimeter P P given by P = L + W + L + W . P = L + W + L + W . Simplify this expression.

If the amount P P is deposited into an account paying simple interest r r for time t , t , the total value of the deposit A A is given by A = P + P r t . A = P + P r t . Simplify the expression. (This formula will be explored in more detail later in the course.)

Access these online resources for additional instruction and practice with real numbers.

• Simplify an Expression.
• Evaluate an Expression 1.
• Evaluate an Expression 2.

1.1 Section Exercises

Is 2 2 an example of a rational terminating, rational repeating, or irrational number? Tell why it fits that category.

What is the order of operations? What acronym is used to describe the order of operations, and what does it stand for?

What do the Associative Properties allow us to do when following the order of operations? Explain your answer.

For the following exercises, simplify the given expression.

10 + 2 × ( 5 − 3 ) 10 + 2 × ( 5 − 3 )

6 ÷ 2 − ( 81 ÷ 3 2 ) 6 ÷ 2 − ( 81 ÷ 3 2 )

18 + ( 6 − 8 ) 3 18 + ( 6 − 8 ) 3

−2 × [ 16 ÷ ( 8 − 4 ) 2 ] 2 −2 × [ 16 ÷ ( 8 − 4 ) 2 ] 2

4 − 6 + 2 × 7 4 − 6 + 2 × 7

3 ( 5 − 8 ) 3 ( 5 − 8 )

4 + 6 − 10 ÷ 2 4 + 6 − 10 ÷ 2

12 ÷ ( 36 ÷ 9 ) + 6 12 ÷ ( 36 ÷ 9 ) + 6

( 4 + 5 ) 2 ÷ 3 ( 4 + 5 ) 2 ÷ 3

3 − 12 × 2 + 19 3 − 12 × 2 + 19

2 + 8 × 7 ÷ 4 2 + 8 × 7 ÷ 4

5 + ( 6 + 4 ) − 11 5 + ( 6 + 4 ) − 11

9 − 18 ÷ 3 2 9 − 18 ÷ 3 2

14 × 3 ÷ 7 − 6 14 × 3 ÷ 7 − 6

9 − ( 3 + 11 ) × 2 9 − ( 3 + 11 ) × 2

6 + 2 × 2 − 1 6 + 2 × 2 − 1

64 ÷ ( 8 + 4 × 2 ) 64 ÷ ( 8 + 4 × 2 )

9 + 4 ( 2 2 ) 9 + 4 ( 2 2 )

( 12 ÷ 3 × 3 ) 2 ( 12 ÷ 3 × 3 ) 2

25 ÷ 5 2 − 7 25 ÷ 5 2 − 7

( 15 − 7 ) × ( 3 − 7 ) ( 15 − 7 ) × ( 3 − 7 )

2 × 4 − 9 ( −1 ) 2 × 4 − 9 ( −1 )

4 2 − 25 × 1 5 4 2 − 25 × 1 5

12 ( 3 − 1 ) ÷ 6 12 ( 3 − 1 ) ÷ 6

For the following exercises, evaluate the expression using the given value of the variable.

8 ( x + 3 ) – 64 8 ( x + 3 ) – 64 for x = 2 x = 2

4 y + 8 – 2 y 4 y + 8 – 2 y for y = 3 y = 3

( 11 a + 3 ) − 18 a + 4 ( 11 a + 3 ) − 18 a + 4 for a = –2 a = –2

4 z − 2 z ( 1 + 4 ) – 36 4 z − 2 z ( 1 + 4 ) – 36 for z = 5 z = 5

4 y ( 7 − 2 ) 2 + 200 4 y ( 7 − 2 ) 2 + 200 for y = –2 y = –2

− ( 2 x ) 2 + 1 + 3 − ( 2 x ) 2 + 1 + 3 for x = 2 x = 2

For the 8 ( 2 + 4 ) − 15 b + b 8 ( 2 + 4 ) − 15 b + b for b = –3 b = –3

2 ( 11 c − 4 ) – 36 2 ( 11 c − 4 ) – 36 for c = 0 c = 0

4 ( 3 − 1 ) x – 4 4 ( 3 − 1 ) x – 4 for x = 10 x = 10

1 4 ( 8 w − 4 2 ) 1 4 ( 8 w − 4 2 ) for w = 1 w = 1

For the following exercises, simplify the expression.

4 x + x ( 13 − 7 ) 4 x + x ( 13 − 7 )

2 y − ( 4 ) 2 y − 11 2 y − ( 4 ) 2 y − 11

a 2 3 ( 64 ) − 12 a ÷ 6 a 2 3 ( 64 ) − 12 a ÷ 6

8 b − 4 b ( 3 ) + 1 8 b − 4 b ( 3 ) + 1

5 l ÷ 3 l × ( 9 − 6 ) 5 l ÷ 3 l × ( 9 − 6 )

7 z − 3 + z × 6 2 7 z − 3 + z × 6 2

4 × 3 + 18 x ÷ 9 − 12 4 × 3 + 18 x ÷ 9 − 12

9 ( y + 8 ) − 27 9 ( y + 8 ) − 27

( 9 6 t − 4 ) 2 ( 9 6 t − 4 ) 2

6 + 12 b − 3 × 6 b 6 + 12 b − 3 × 6 b

18 y − 2 ( 1 + 7 y ) 18 y − 2 ( 1 + 7 y )

( 4 9 ) 2 × 27 x ( 4 9 ) 2 × 27 x

8 ( 3 − m ) + 1 ( − 8 ) 8 ( 3 − m ) + 1 ( − 8 )

9 x + 4 x ( 2 + 3 ) − 4 ( 2 x + 3 x ) 9 x + 4 x ( 2 + 3 ) − 4 ( 2 x + 3 x )

5 2 − 4 ( 3 x ) 5 2 − 4 ( 3 x )

Real-World Applications

For the following exercises, consider this scenario: Fred earns $40 at the community garden. He spends $10 on a streaming subscription, puts half of what is left in a savings account, and gets another $5 for walking his neighbor’s dog.

Write the expression that represents the number of dollars Fred keeps (and does not put in his savings account). Remember the order of operations.

How much money does Fred keep?

For the following exercises, solve the given problem.

According to the U.S. Mint, the diameter of a quarter is 0.955 inches. The circumference of the quarter would be the diameter multiplied by π . π . Is the circumference of a quarter a whole number, a rational number, or an irrational number?

Jessica and her roommate, Adriana, have decided to share a change jar for joint expenses. Jessica put her loose change in the jar first, and then Adriana put her change in the jar. We know that it does not matter in which order the change was added to the jar. What property of addition describes this fact?

For the following exercises, consider this scenario: There is a mound of g g pounds of gravel in a quarry. Throughout the day, 400 pounds of gravel is added to the mound. Two orders of 600 pounds are sold and the gravel is removed from the mound. At the end of the day, the mound has 1,200 pounds of gravel.

Write the equation that describes the situation.

Solve for g .

For the following exercise, solve the given problem.

Ramon runs the marketing department at their company. Their department gets a budget every year, and every year, they must spend the entire budget without going over. If they spend less than the budget, then the department gets a smaller budget the following year. At the beginning of this year, Ramon got $2.5 million for the annual marketing budget. They must spend the budget such that 2,500,000 − x = 0. 2,500,000 − x = 0. What property of addition tells us what the value of x must be?

For the following exercises, use a graphing calculator to solve for x . Round the answers to the nearest hundredth.

0.5 ( 12.3 ) 2 − 48 x = 3 5 0.5 ( 12.3 ) 2 − 48 x = 3 5

( 0.25 − 0.75 ) 2 x − 7.2 = 9.9 ( 0.25 − 0.75 ) 2 x − 7.2 = 9.9

If a whole number is not a natural number, what must the number be?

Determine whether the statement is true or false: The multiplicative inverse of a rational number is also rational.

Determine whether the statement is true or false: The product of a rational and irrational number is always irrational.

Determine whether the simplified expression is rational or irrational: −18 − 4 ( 5 ) ( −1 ) . −18 − 4 ( 5 ) ( −1 ) .

Determine whether the simplified expression is rational or irrational: −16 + 4 ( 5 ) + 5 . −16 + 4 ( 5 ) + 5 .

The division of two natural numbers will always result in what type of number?

What property of real numbers would simplify the following expression: 4 + 7 ( x − 1 ) ? 4 + 7 ( x − 1 ) ?

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/college-algebra-2e/pages/1-introduction-to-prerequisites

• Authors: Jay Abramson
• Publisher/website: OpenStax
• Book title: College Algebra 2e
• Publication date: Dec 21, 2021
• Location: Houston, Texas
• Book URL: https://openstax.org/books/college-algebra-2e/pages/1-introduction-to-prerequisites
• Section URL: https://openstax.org/books/college-algebra-2e/pages/1-1-real-numbers-algebra-essentials

© Jan 9, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

comparing and ordering real numbers

All Formats

Resource types, all resource types.

• Rating Count
• Price (Ascending)
• Price (Descending)
• Most Recent

Comparing and ordering real numbers

Compare and Order Real Numbers Activity (Rational & Irrational) Partner Games

Comparing and Ordering Real Numbers Task Cards - PDF and Google Form

• Google Apps™
• Easel Activity

Comparing and Ordering Real Numbers Task Cards | TEKS 8.2D

Comparing and Ordering Real Numbers Notes & Practice | Guided Notes

Ordering and Comparing Real Numbers Guided Notes PDF 8.NS.A.2 Go Math

Comparing and Ordering Real Numbers Task Cards

Compare and Order Real Numbers

Comparing and Ordering Real Numbers - Editable Foldable Notes

Comparing & Ordering Real Numbers - Drag & Drop - Digital

• Google Drive™ folder

Comparing and Ordering Real Numbers Activity Scavenger Hunt Digital Printable

Compare and Order Real Numbers Google Forms Homework

Comparing and Ordering Real Numbers Boom Cards--Digital Task Cards

• Internet Activities

Real Numbers - Order and Compare Rational & Irrational Numbers 30 problems

Comparing and Ordering Real Numbers Digital Activity FREE

Order and Compare Real Numbers FOLDABLE

Compare and Order Real Numbers Binder Notes for 8th Grade Math Pre-Algebra

8th Grade Math - Comparing and Ordering Real Numbers : Lesson and Activities

Compare and Order Real Numbers - Guided Notes and Practice

8th Grade - enVision Math Lesson Plan 1-3: Compare and Order Real Numbers

• Word Document File

Comparing and Ordering Real Numbers Game

Comparing and Ordering Real Numbers Task Cards | Real Numbers Practice Activity

8.2D Compare & Order Real Numbers Task Cards | Warm-Up, Stations, Centers

Compare & Order Real Numbers Cut & Paste Activity

• We're hiring
• Help & FAQ
• Privacy policy
• Student privacy
• Terms of service
• Tell us what you think

The website is not compatible for the version of the browser you are using. Not all the functionality may be available. Please upgrade your browser to the latest version.

• Social Media
• Access Points
• Print/Export Standards
• Computer Science Standards
• Coding Scheme
• B.E.S.T. Standards
• Standards Viewer App
• Course Descriptions
• Graduation Requirements
• Course Reports
• Gifted Coursework
• Career and Technical Education (CTE) Programs
• Browse/Search
• Original Student Tutorials
• MEAs - STEM Lessons
• Perspectives STEM Videos
• STEM Reading Resources
• Math Formative Assessments
• CTE Related Resources
• Our Review Process
• Professional Development Programs
• iCPALMS Tools
• Resource Development Programs
• Partnership Programs
• User Testimonials
• iCPALMS Account

• Account Information Profile and Notification Settings
• Administration Manage Site Features
• Recycle Bin Delete Items From Your Account
• Not a member yet? SIGN UP
• Account Information
• Administration
• Recycle Bin
• Home of CPALMS
• Standards Info. & Resources
• Course Descriptions & Directory
• Resources Vetted by Peers & Experts
• PD Programs Self-paced Training
• About CPALMS Initiatives & Partnerships
• iCPALMS Florida's Platform

MA.3.NSO.1.3

6 Lesson Plans

1 Problem-Solving Task

Clarifications

Clarification 2: Number lines, scaled by 50s, 100s or 1,000s, must be provided and can be a representation of any range of numbers.

Clarification 3: Within this benchmark, the expectation is to use symbols (<, > or =).

Benchmark Instructional Guide

Connecting benchmarks/horizontal alignment.

• MA.3.NSO.1.1 
• MA.3.NSO.1.2 
• MA.3.AR.2.2

Terms from the K-12 Glossary

• Number Line 
• Whole Number

Vertical Alignment

Previous Benchmarks MA.2.NSO.1.3 Next Benchmarks MA.4.NSO.1.3

Purpose and Instructional Strategies

• Instruction should use the terms greater than, less, than, and equal. Students should use place value strategies and number lines (horizontal and vertical) to justify how they compare numbers and explain their reasoning. Instruction should not rely on tricks for determining the direction of the inequality symbols. Students should read entire statements (e.g., read 7,309 > 7,039, “7,309 is greater than 7,039” and vice versa) ( MTR.2.1 , MTR.3.1 ). 
• It is imperative for teachers to define the meaning of the ≠ symbol through instruction. It is recommend that students use = and ≠ symbols first. Once students have determined that numbers are not equal, then they can determine “how” they are not equal, with the understanding now the number is either < or >. If students cannot determine if amounts are ≠ or = then they will struggle with < or >. This will build understanding of statements of inequality and help students determine differences between inequalities and equations ( MTR.6.1 ).

Common Misconceptions or Errors

• Often students think of these relational symbols as operational symbols instead. In order to address this misconception, allow students to have practice using the number line and/or place value blocks to see the relationship between one number and the other.

Strategies to Support Tiered Instruction

• For example, the teacher uses a number line and relational symbols to compare 487 and 623, labeling the endpoints of the number line 0 and 1,000. The teacher asks students to place 487 and 623 on the number line, discussing the placement of the numbers and distance from zero. Next, the teacher uses the number line to demonstrate that 487 is closer to zero than 623 so 487 < 623 and that 623 is farther from zero so 623 > 487. Then, the teacher explains that 487 and 623 are not the same point on the number line so 487 ≠ 623 and asks students to identify numbers that are greater than... and less than.... Finally, the teacher repeats with two four-digit numbers (number line endpoints of 0 and 10,000) and discusses the placement of the other numbers on the number line and if their values are greater than or less than other numbers. 

• For example, the teacher uses base-ten blocks, a place value chart and relational symbols to compare 274 and 312. The teacher begins by having students represent 274 and 312 using base-ten blocks and a place value chart and asking students to compare these numbers, beginning with the greatest place value. Next, the teacher explains that the number 274 has 2 hundreds and the number 312 has 3 hundreds so 274 < 312 and 312 > 274 and that 274 and 312 have different digits in the hundreds place so 274 ≠ 312.

Instructional Tasks

Instructional Task 1 

• Plot the numbers 3,790, 3,890, 3,799, 3,809 on the number line below. 

Choose two values from the list and compare them using >, <, or =.  Choose a number between 3,799 and 3,809 and plot it on the number line.  Use evidence from your number line to justify which number is greatest.

Instructional Items

Instructional Item 1 

• a. 6,909 < 6,099, because the value of the 9 in the tens place of 6,099 is greater than the value of the 0 in the tens place of 6,909.
• b. 6,909 > 6,099, because the value of the 9 in the tens place of 6,099 is greater than the value of the 0 in the tens place of 6,909. 
• c. 6,909 < 6,099, because the value of the 9 in the hundreds place of 6,909 is greater than the value of the 0 in the hundreds place of  6,099. 
• d. 6,909 > 6,099, because the value of the 9 in the hundreds place of 6,909 is greater than the value of the 0 in the hundreds place of  6,099. 

Related Courses

Related access points, related resources, lesson plans.

In this lesson, students will analyze voting data and perform mathematical procedures to determine the answer to specific questions. Students will compare the population of the community vs. the number of votes counted. Students will discuss the contribution each citizen is making when voting and the effects on the results when citizens do not vote.

Type: Lesson Plan

Students will apply their understanding of place value to plot, order, and compare event descriptions related to key figures in history. The key figures used in this lesson are James Madison, Alexander Hamilton, Booker T. Washington, Susan B. Anthony, William Pope Duval, William Dunn Mosely and Josiah T. Walls. Students will make connections between using a number line to plot, order and compare numbers, to real-world careers that use timelines for historical purposes in this integrated lesson plan.

In this lesson, students will gain fluency with rounding numbers to the nearest 10s and 100s place. The lesson has number lines to help students understand rounding.

The focus of this lesson is to find the halfway point and use it to round numbers.  The lesson rounds numbers 0 to 100 to the nearest ten and 0 to 1000 to the nearest ten and hundred. 

In this lesson, students will engage in tellling jokes and doing outside activities to discover rounding concepts. Students will use a vertical number line to round numbers from 0 to 1,000.

This lesson uses a relay game  to provide students with practice for their rounding skills.

Problem-Solving Task

It is common for students to compare multi-digit numbers just by comparing the first digit, then the second digit, and so on. This task includes three-digit numbers with large hundreds digits and four-digit numbers with small thousands digits so that students must infer the presence of a 0 in the thousands place in order to compare. It also includes numbers with strategically placed zeros and an unusual request to order them from greatest to least in addition to the more traditional least to greatest.

Type: Problem-Solving Task

Student Resources

Parent resources.

Like us on Facebook

Stay in touch with CPALMS

Follow Us on Twitter

Loading....

• Get started
• Pre-Algebra

A quicker path to better grades

We have gathered all your curriculum-based courses, assignments, hints, tests, and solutions in one easy-to-use place

• Integrated I
• Integrated II
• Integrated III

Can't find your textbook?

More math. less studying.

A personal private tutor for each student. Free from preassure and study anxiety.

Exercise 1 Page   22

Can you approximate irrational numbers ? How?

Check the answer

See solution.

We are asked how we to compare and order rational and irrational numbers. Let's take a look at an example. We will try to compare two irrational numbers sqrt(23) and 4.205639 ... and a rational number 4.3. Let's begin by finding an approximation of sqrt(23). We will do this using perfect squares . The two closest perfect squares to the number 23 are 16 and 25. 16 < 23 < 25 Now we can rewrite the above inequality with square roots . We will also calculate the square roots of the perfect squares. sqrt(16) < sqrt(23) < sqrt(25) ⇕ 4 < sqrt(23) < 5 We found that sqrt(23) is somewhere between 4 and 5. However, the two other numbers we want to compare it with are also between 4 and 5, which means that we need a better approximation. Let's use decimals. Let's see if sqrt(23) is greater than 4.5. 4.5 * 4.5 = 20.25 4.5 < sqrt(23) < 5 Now we know that sqrt(23) is somewhere between 4.5 and 5, which is a better approximation. Let's approximate 4.205639 ... as a rational number by rounding it to the nearest tenth . 4.205639 ... ≈ 4.2 Finally, we can plot each number on a number line to compare them. We know that sqrt(23) is somewhere between 4.5 and 5, so we will plot it between these numbers.

As we can see, to compare rational and irrational numbers, we must first find rational approximations of the irrational numbers. We can do this using perfect squares or by rounding.

• Texas Go Math
• Big Ideas Math
• enVision Math
• EngageNY Math
• McGraw Hill My Math
• 180 Days of Math
• Math in Focus Answer Key
• Math Expressions Answer Key
• Privacy Policy

Texas Go Math Grade 8 Lesson 1.3 Answer Key Ordering Real Numbers

Refer to our  Texas Go Math Grade 8 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 8 Lesson 1.3 Answer Key Ordering Real Numbers.

Essential Question How do you order a set of real numbers?

Question 1. If 7 + \(\sqrt{5}\) is equal to \(\sqrt{5}\) plus a number, what do you know about the number? Why? Answer: We are told that 7 + \(\sqrt{5}\) is equal to\(\sqrt{5}\) plus a number. Lets denote with x the unknown number. We have: 7 + \(\sqrt{5}\) = \(\sqrt{5}\) + x If we subtract \(\sqrt{5}\) in both sides we get: 7 + \(\sqrt{5}\) – \(\sqrt{5}\) = \(\sqrt{5}\) + x – \(\sqrt{5}\) x = 7

The unknown number is 7 (whole number, integer, rational, real number).

Go Math Grade 8 Algebra Lesson 1.3 Question 2. What are the closest two integers that \(\sqrt{300}\) is between? Answer: \(\sqrt{300}\) Given 289 < 300 < 324 Find the perfect squares of the number that 300 is between

17 < \(\sqrt{300}\) < 18 Take square roots The close two integers are $17$ and $18$

Compare. Write <, >, or .

\(\sqrt{6}\) is between 2 and 3 Approximate \(\sqrt{6}\)

\(\sqrt{12}\) + 6 is between 9 and 10 Use approximations to simply the expressions 12 + \(\sqrt{6}\) is between 14 and 15 \(\sqrt{12}\) + 6 < 12 + \(\sqrt{6}\) Compare

Order the numbers from least to greatest. Then graph them on the number line.

Math Talk Mathematical Processes If real numbers a, b, and c are in order from least to greatest, what is the order of their opposites from least to greatest? Explain.

Texas Go Math Grade 8 Lesson 1.3 Guided Practice Answer Key 

Compare. Write <, >, or =. (Example 1)

\(\sqrt{11}\) + 15 > \(\sqrt{8}\) + 15

4 < 6 < 9 Approximate \(\sqrt{6}\) \(\sqrt{4}\) < \(\sqrt{6}\) < \(\sqrt{9}\) 2 < \(\sqrt{6}\) < 3

4 < 5 < 9 Approximate \(\sqrt{5}\) \(\sqrt{4}\) < \(\sqrt{5}\) < \(\sqrt{9}\) 2 < \(\sqrt{5}\) < 3 \(\sqrt{6}\) + 5 is between 7 and 8 Use approximately to simplify the expressions 6 + \(\sqrt{5}\) is between 8 and 9 \(\sqrt{6}\) + 5 < 6 + \(\sqrt{5}\) Compare

\(\sqrt{17}\) – 3 is between 1 and 2 Use approximations to simplify the expressions -2 + \(\sqrt{5}\) is between 0 and 1 \(\sqrt{17}\) – 3 > -2 + \(\sqrt{5}\) Compare

10 – \(\sqrt{8}\) is between 8 and 7 Use approximations to simplify the expressions 12 – \(\sqrt{2}\) is between 11 and 10

10 – \(\sqrt{8}\) < 12 – \(\sqrt{2}\) Compare

\(\sqrt{7}\) + 2 is between 4 and 5 Use approximations to simplify the expressions \(\sqrt{10}\) – 1 is between 2 and 3

\(\sqrt{7}\) + 2 > \(\sqrt{10}\) – 1 Compare

\(\sqrt{17}\) + 3 is between 7 and 8 Use approximations to simplify the expressions 3 + \(\sqrt{11}\) is between 6 and 7

\(\sqrt{7}\) + 3 > 3 + \(\sqrt{11}\) Compare

From least to greatest, the numbers are 1.5, \(\sqrt{3}\), 2π. Click for the graph.

Essential Question Check-in

Question 11. Explain how to order a set of real numbers. Answer: To order real numbers first express them in the decimal form. If all numbers can’t be calculated to a finite decimal, approximate them to a chosen accuracy (number of digits behind the decimal point, where more digits equal higher accuracy). Then you can easily place them on a number line.

Express numbers in decimal form and approximate.

Texas Go Math Grade 8 Lesson 1.3 Independent Practice Answer Key 

Order the numbers from least to greatest.

Question 12. \(\sqrt{7}\), 2, \(\frac{\sqrt{8}}{2}\) Answer: \(\sqrt{7}\), 2, \(\frac{\sqrt{8}}{2}\) Given \(\sqrt{7}\) Estimate the value of \(\sqrt{7}\) \(\sqrt{7}\) is between 2 and 3 Since, $7$ is closer to $9$, $2.65^{2} = 7.02$, hence the estimated value is $2.65$

Go Math Grade 8 Answer Key Algebra Lesson 1.3 Question 13. \(\sqrt{10}\), π, 3.5 Answer: \(\sqrt{10}\) is between 3.1 and 3.2. In some cases, this approximation is precise enough, but this is not the case. Since we have a given number π ≈ 3.14 that ¡s also between 3.1 and 3.2 we must be more precise. So, an even better approximation is 3.15 because 3.15 2 ≈ 9.92. π ≈ 3.14

We can now order the numbers from [east to greatest easily: Because 3.14 < 3.15 < 3.5 it follows that π < \(\sqrt{10}\) < 3.5 Numbers from least to greatest π < \(\sqrt{10}\) < 3.5

Ordering Real Numbers 8th Grade Question 16. Your sister is considering two different shapes for her garden. One is a square with side lengths of 3.5 meters, and the other is a circle with a diameter of 4 meters. a. Find the area of the square. _______ Answer: To find the area of a square use the formula: A = x 2 where x is the side of the square and the area is represented by A. So, A = 35 2 = 12.25

To find the area of a square use the formula: B = r 2 π where r is the radius of the circle and the area is represented by B. So, B = 2 2 π = 12.57 (Diameter d is twice the radius r, so r = 2.)

The garden shaped like a circle would give her more space to plant because it has a bigger area. A = 3.5 2 = 12.25

b. Find the area of the circle. ____ Answer: B = 2 2 π = 12.57

c. Compare your answers from parts a and b. Which garden would give your sister the most space to plant? Answer: The circle-shaped garden has more space to plant.

b. Winnie’s father estimated the distance across his ranch to be \(\sqrt{56}\) km. How does this distance compare to Winnie’s estimate? Answer: \(\sqrt{56}\) ≈ 7.4833 Using claculator They are nearly identical

Give an example of each type of number.

Question 18. a real number between \(\sqrt{13}\) and \(\sqrt{14}\) _____ Answer: Since, \(\sqrt{13}\) ≈ 3.61 < 3.7 < \(\sqrt{14}\) ≈ 3.74 3.7 is a good example of a real. number that is in between \(\sqrt{13}\) and \(\sqrt{14}\)

Question 19. an irrational number between 5 and 7 _________ Answer: Square the given numbers to find their perfect squares and then a square root of any number in between those two is an example of an irrational number between 5 and 7: 5 2 = 25 7 2 = 49 So, one example is \(\sqrt{31}\) \(\sqrt{31}\)

Neither are right The numbers aren’t in any order.

Question 21. Math History There is a famous irrational number called Euler’s number, often symbolized with an e. Like π, it never seems to end. The first few digits of e are 2.7182818284.

a. Between which two square roots of integers could you find this number? Answer: 2.718281828 The square of e lies between 7 and 8 2.72 2 = 7.3984 Hence, it lies between $\sqrt{7} = 2.65$ and $\sqrt{8} = 2.82$

b. Between which two square roots of integers can you find π? Answer: The square of π lies between 9 and 10 3.142 3.14 2 = 9.8596 Hence, it lies between $\sqrt{9} = 3$ and $\sqrt{1ø} = 3.16$

Texas Go Math Grade 8 Lesson 1.3 H.O.T. Focus On Higher Order Thinking Answer Key 

Question 22. Analyze Relationships There are several approximations used for π, including 3.14 and \(\frac{22}{7}\).π is approximately 3.14159265358979…

b. Which of the two approximations is a better estimate for π? Explain. Answer: As we can see from the number line, \(\frac{22}{7}\) is closer to π, so we can conclude that \(\frac{22}{7}\) is a better estimation for π.

c. Find a whole number x in \(\frac{x}{113}\) so that the ratio is a better estimate for π than the two given approximations. ______ Answer: \(\frac{355}{113}\) is a better estimation for π, because \(\frac{355}{113}\) = 3.14159292035 ≈ 3.14159265358979 = π

Go Math 8th Grade Lesson 1.3 Compare and Order Real Numbers Question 23. Communicate Mathematical Ideas If a set of six numbers that include both rational and irrational numbers is graphed on a number line, what is the fewest number of distinct points that need to be graphed? Explain. Answer: The fewest number of distinct points that need to be graphed is 2. Because there are both rational and irrational numbers in the set and every rational number is not irrational and every irrational is not rational they can’t all be the same. Therefore it could be that there are some numbers that repeat but there are at least two different numbers.

Two. Click for proof.

Question 24. Critique Reasoning Jill says that \(12 . \overline{6}\) is less than 12.63. Explain her error. Answer: The line over the digit 6 means that it is repeating forever. So, \(12 . \overline{6}\) = 12.666666…. If we round that number to two decimal Places we have \(12 . \overline{6}\) ≈ 12.67. Obviously, 12.67 > 12.63

12.67 > 12.63. Click for proof.

Share this:

Leave a comment cancel reply.

You must be logged in to post a comment.